Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation
Abstract
1. Introduction
2. Computational Methods
2.1. Molecular Dynamics Simulation
2.1.1. Cross-Linking of the Polymer during the Curing Process
- It was assumed that the primary and secondary amines have the same reactivity with the reaction cutoff distance of 5 Ǻ.
- The system was checked for the bond formation at every 50 ps after each equilibration.
- The constants in the equation of the newly-formed bonds were decreased in the first equilibration level and progressively elevated to the real values [47].
- The outputs were examined to update the topology parameters according to the new bonds.
- An annealing process was implemented to release the residual stresses. In this process, the temperature was increased to 450 K and then cooled to 300 K gradually over 2 × 106 time-steps.
- Steps 2 through 5 were iterated to obtain about 80% cross-linking.
- Finally, the last NPT equilibration in an interval time of 3 ns was applied to the RVE.
2.1.2. Tensile Separation Process
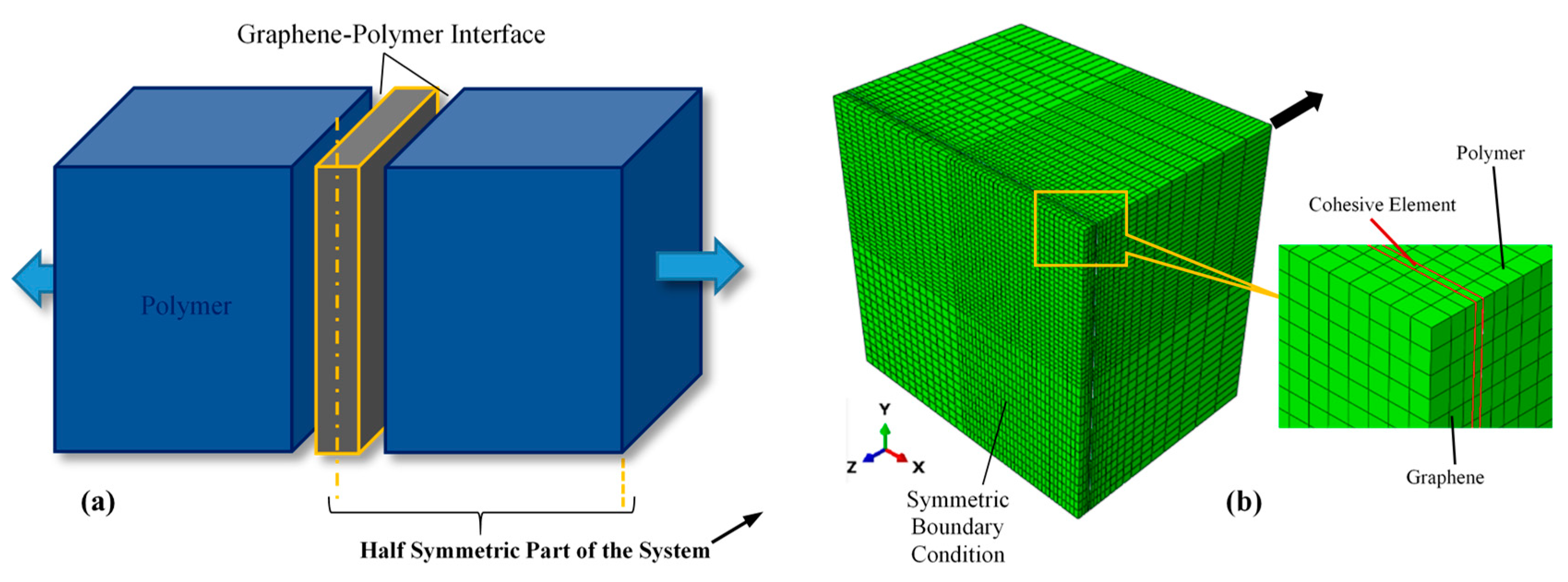
2.2. Continuum Mechanics Simulation
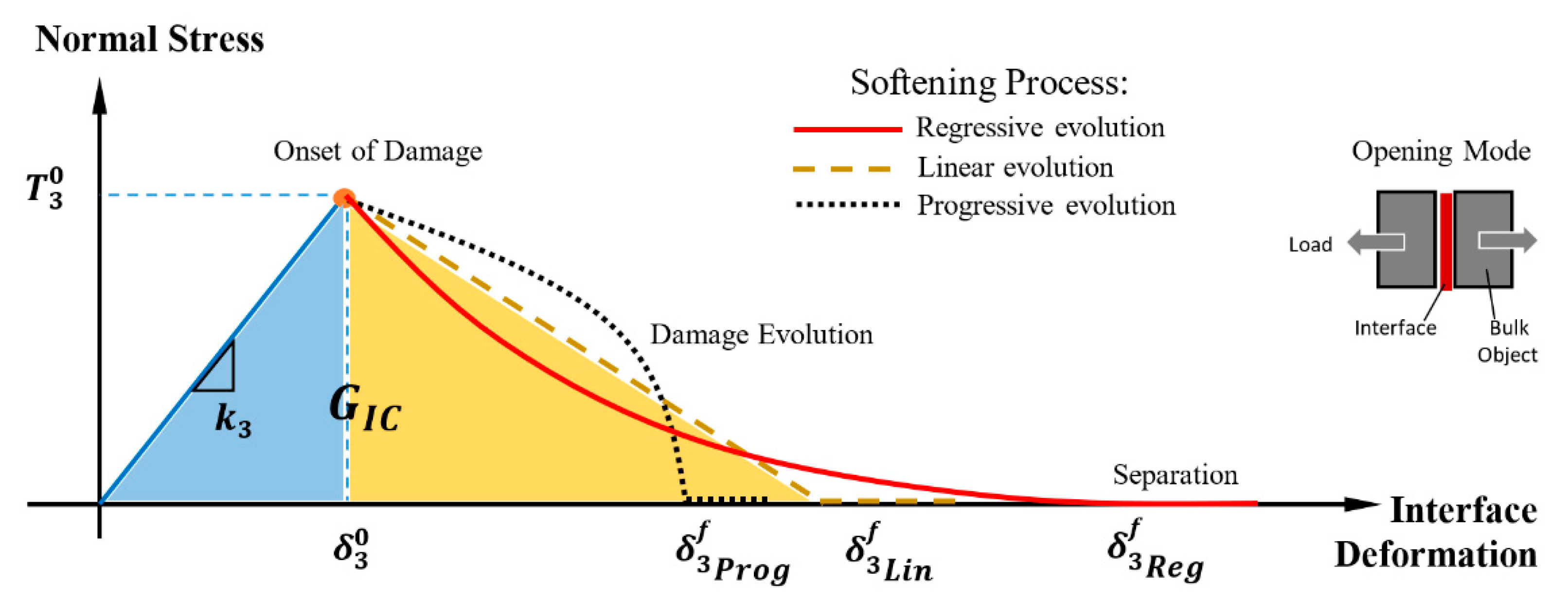
2.2.1. Cohesive Zone Model
2.2.2. Damage Initiation and Propagation Criterion
2.2.3. Finite Element Simulation
3. Results and Discussion
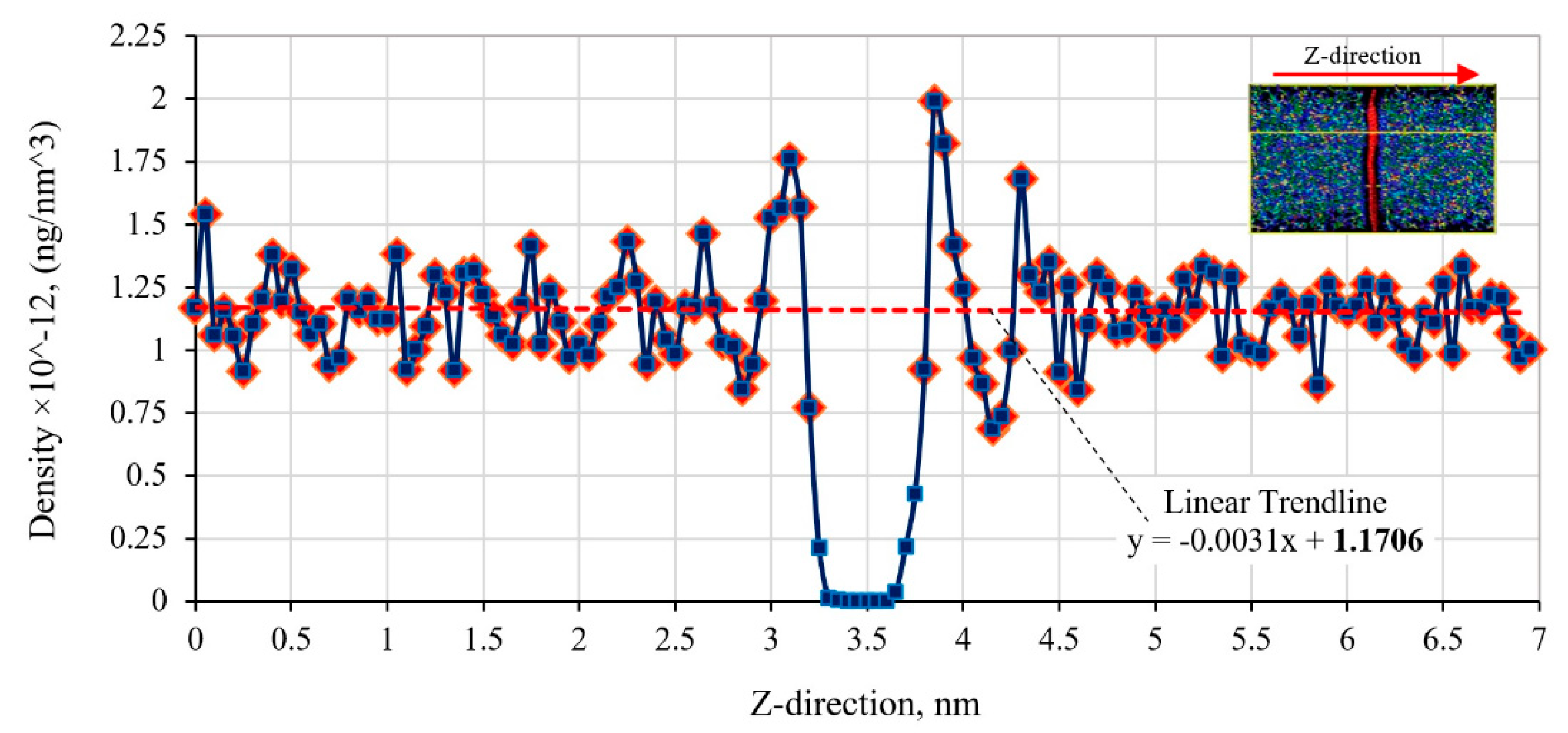
3.1. Thickness of the Graphene and Graphene/Polymer Interface
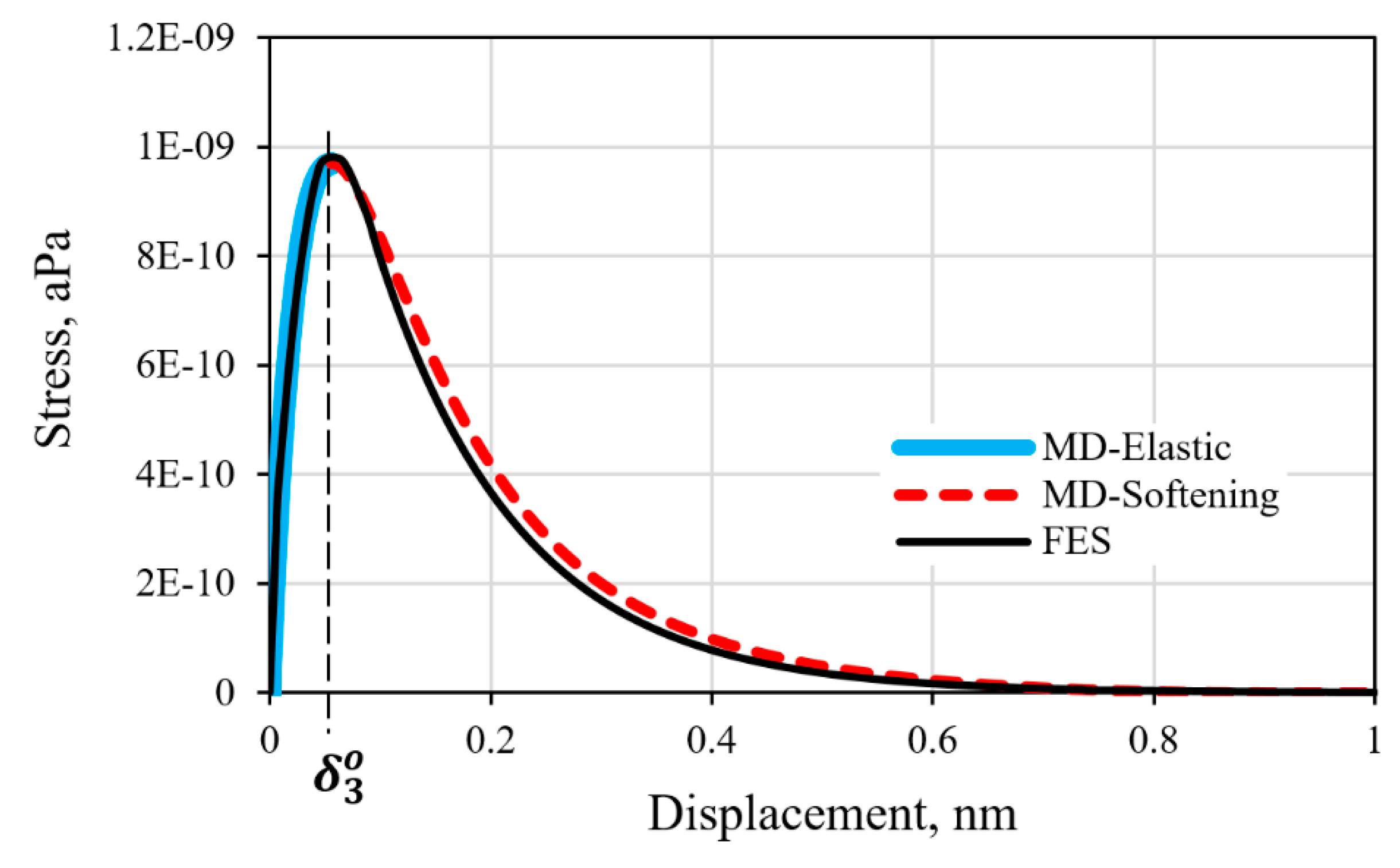
3.2. Nanomechanical Behaviors of Graphene/Polymer Interface
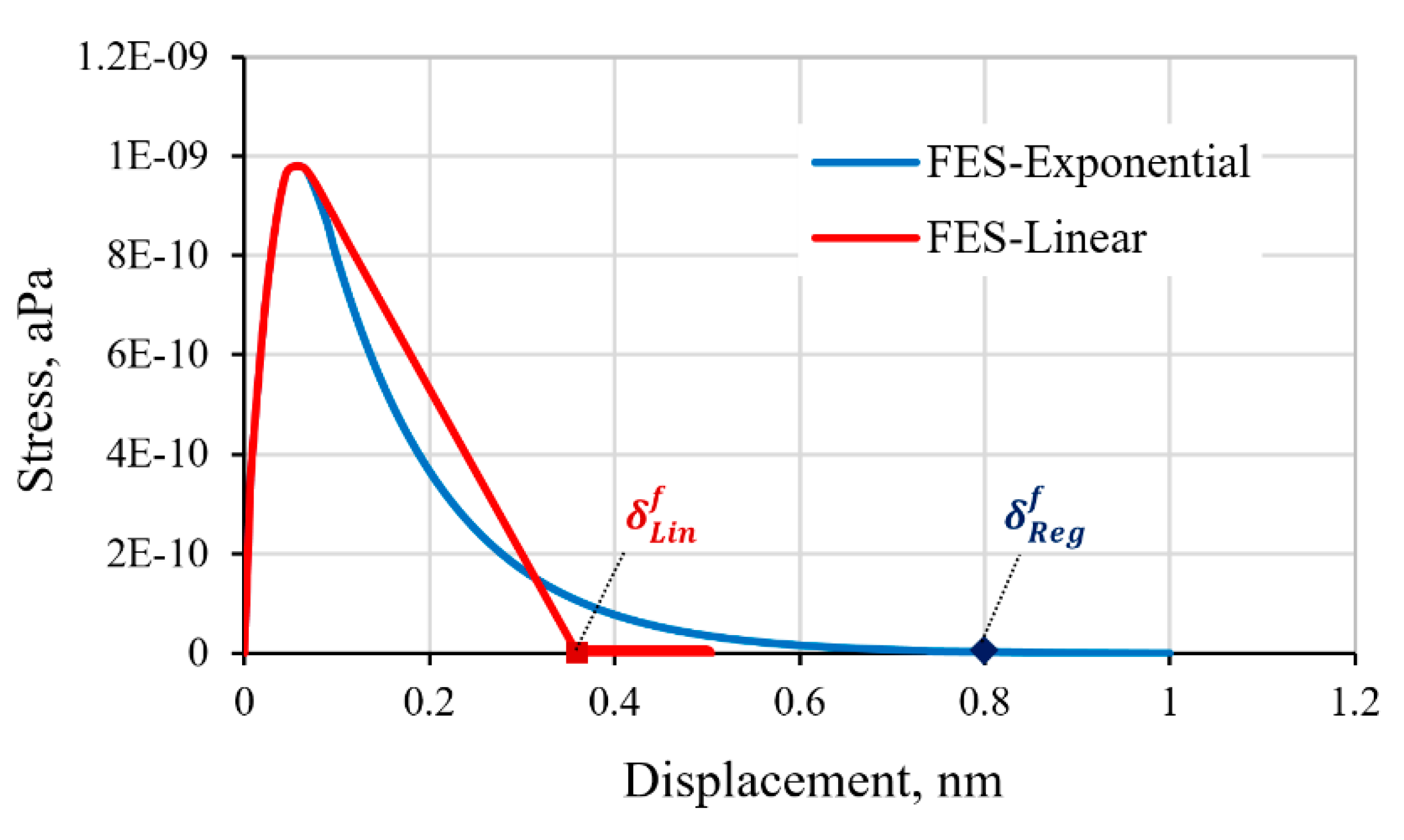
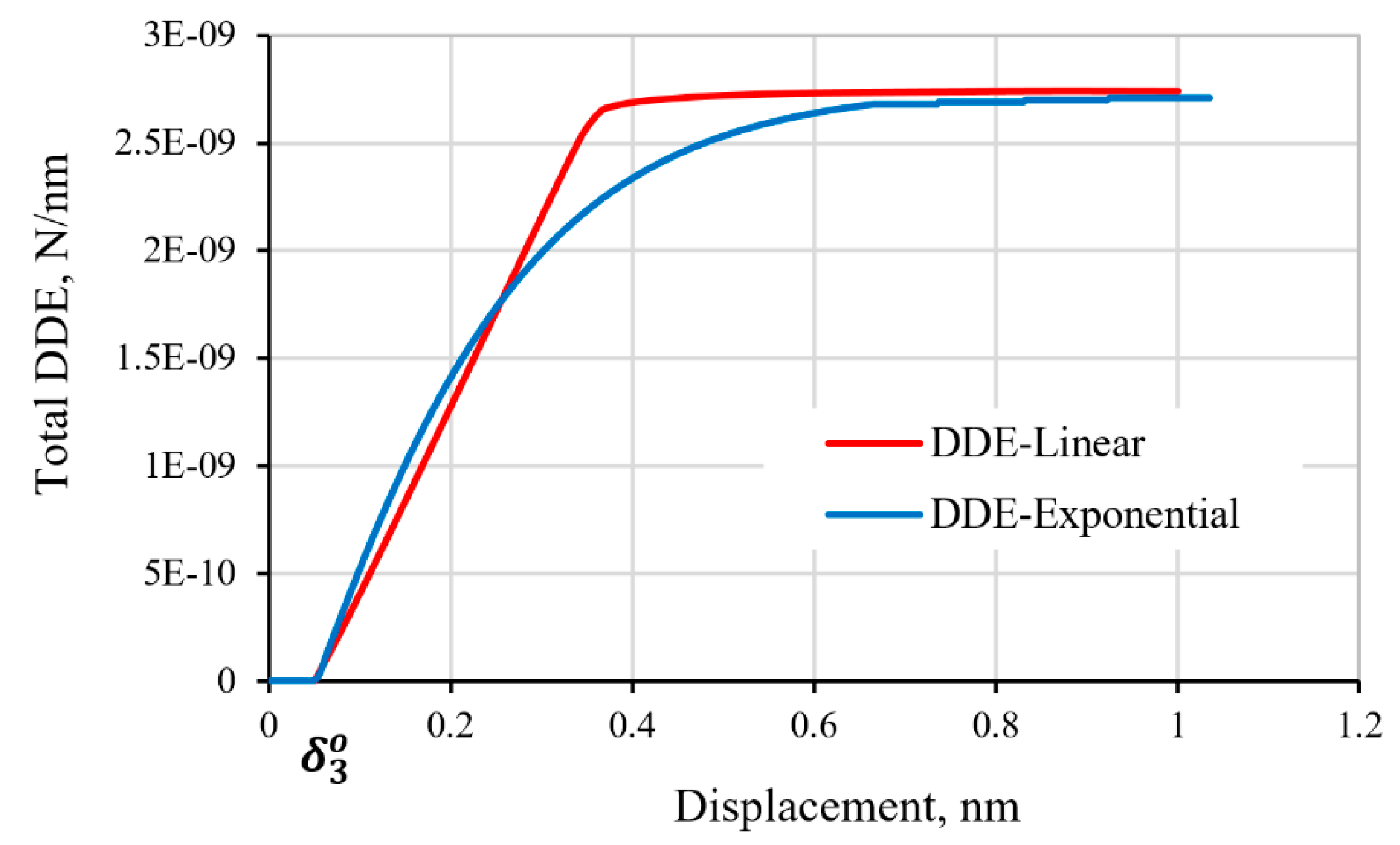
3.3. Response of the Graphene/Epoxy Interface Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Du, Y.; Li, D.; Liu, L.; Gai, G. Recent achievements of self-healing graphene/polymer composites. Polymers 2018, 10, 114. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Huang, F.; Guo, Y.; Chen, J.; Chen, X.; Hui, D.; He, P.; Zhou, X.; Zhou, Z. In situ intercalation polymerization approach to polyamide-6/graphite nanoflakes for enhanced thermal conductivity. Compos. Part B Eng. 2017, 117, 165–173. [Google Scholar] [CrossRef]
- Meng, F.; Zhong, J.; Chen, Y.; Liu, X. The influence of cross-linking reaction on the mechanical and thermal properties of polyarylene ether nitrile. J. Appl. Polym. Sci. 2011, 120, 1822–1828. [Google Scholar] [CrossRef]
- Kim, H.; Abdala, A.A.; Macosko, C.W. Graphene/polymer nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Stankovich, S.; Dikin, D.A.; Dommett, G.H.B.; Kohlhaas, K.M.; Zimney, E.J.; Stach, E.A.; Piner, R.D.; Nguyen, S.T.; Ruoff, R.S. Graphene-based composite materials. Nature 2006, 442, 282. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.-L.; Wu, H.-H.; Jeng, Y.-C.; Liang, W.-Z. Electrospun graphene nanosheet-filled poly(trimethylene terephthalate) composite fibers: Effects of the graphene nanosheet content on morphologies, electrical conductivity, crystallization behavior, and mechanical properties. Polymers 2019, 11, 164. [Google Scholar] [CrossRef]
- Kim, S.; Do, I.; Drzal, L.T. Multifunctional xgnp/lldpe nanocomposites prepared by solution compounding using various screw rotating systems. Macromol. Mater. Eng. 2009, 294, 196–205. [Google Scholar] [CrossRef]
- Rahimian-Koloor, S.M.; Moshrefzadeh-Sani, H.; Hashemianzadeh, S.M.; Shokrieh, M.M. The effective stiffness of an embedded graphene in a polymeric matrix. Curr. Appl. Phys. 2018, 18, 559–566. [Google Scholar] [CrossRef]
- Díez-Pascual, M.A.; Luceño Sánchez, A.J.; Peña Capilla, R.; García Díaz, P. Recent developments in graphene/polymer nanocomposites for application in polymer solar cells. Polymers 2018, 10, 217. [Google Scholar] [CrossRef]
- Dewapriya, M.A.N.; Rajapakse, R.K.N.D. Development of a homogenous nonlinear spring model characterizing the interfacial adhesion properties of graphene with surface defects. Compos. Part B Eng. 2016, 98, 339–349. [Google Scholar] [CrossRef]
- Ahmad, A.I.; Koziol, K.K.; Deveci, S.; Kim, H.-K.; Kumar, V.R. Advancing the use of high-performance graphene-based multimodal polymer nanocomposite at scale. Nanomaterials 2018, 8, 947. [Google Scholar] [CrossRef] [PubMed]
- Meng, F.; Ishida, H.; Liu, X. Introduction of benzoxazine onto the graphene oxide surface by click chemistry and the properties of graphene oxide reinforced polybenzoxazine nanohybrids. RSC Adv. 2014, 4, 9471–9475. [Google Scholar] [CrossRef]
- Agnihotri, P.K.; Kar, K.K.; Basu, S. Cohesive zone model of carbon nanotube-coated carbon fiber/polyester composites. Model. Simul. Mater. Sci. Eng. 2012, 20, 035014. [Google Scholar] [CrossRef]
- Azoti, W.L.; Elmarakbi, A. Multiscale modelling of graphene platelets-based nanocomposite materials. Compos. Struct. 2017, 168, 313–321. [Google Scholar] [CrossRef]
- Dandekar, C.R.; Shin, Y.C. Molecular dynamics based cohesive zone law for describing al–sic interface mechanics. Compos. Part A Appl. Sci. Manuf. 2011, 42, 355–363. [Google Scholar] [CrossRef]
- Awasthi, A.P.; Lagoudas, D.C.; Hammerand, D.C. Modeling of graphene–polymer interfacial mechanical behavior using molecular dynamics. Model. Simul. Mater. Sci. Eng. 2008, 17, 015002. [Google Scholar] [CrossRef]
- Kolanthai, E.; Bose, S.; Bhagyashree, K.S.; Bhat, S.V.; Asokan, K.; Kanjilal, D.; Chatterjee, K. Graphene scavenges free radicals to synergistically enhance structural properties in a gamma-irradiated polyethylene composite through enhanced interfacial interactions. Phys. Chem. Chem. Phys. 2015, 17, 22900–22910. [Google Scholar] [CrossRef]
- Ji, X.-Y.; Cao, Y.-P.; Feng, X.-Q. Micromechanics prediction of the effective elastic moduli of graphene sheet-reinforced polymer nanocomposites. Model. Simul. Mater. Sci. Eng. 2010, 18, 045005. [Google Scholar] [CrossRef]
- Shiu, S.-C.; Tsai, J.-L. Characterizing thermal and mechanical properties of graphene/epoxy nanocomposites. Compos. Part B Eng. 2014, 56, 691–697. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Tu, J.-F. Characterizing mechanical properties of graphite using molecular dynamics simulation. Mater. Des. 2010, 31, 194–199. [Google Scholar] [CrossRef]
- Firouz-Abadi, R.D.; Moshrefzadeh-Sany, H.; Mohammadkhani, H.; Sarmadi, M. A modified molecular structural mechanics model for the buckling analysis of single layer graphene sheet. Solid State Commun. 2016, 225, 12–16. [Google Scholar] [CrossRef]
- Pontefisso, A.; Mishnaevsky, L. Nanomorphology of graphene and cnt reinforced polymer and its effect on damage: Micromechanical numerical study. Compos. Part B Eng. 2016, 96, 338–349. [Google Scholar] [CrossRef]
- Liu, F.; Hu, N.; Han, M.; Atobe, S.; Ning, H.; Liu, Y.; Wu, L. Investigation of interfacial mechanical properties of graphene-polymer nanocomposites. Mol. Simul. 2016, 42, 1165–1170. [Google Scholar] [CrossRef]
- Lin, F.; Xiang, Y.; Shen, H.-S. Temperature dependent mechanical properties of graphene reinforced polymer nanocomposites – a molecular dynamics simulation. Compos. Part B Eng. 2017, 111, 261–269. [Google Scholar] [CrossRef]
- Hosseini Kordkheili, S.A.; Moshrefzadeh-Sani, H. Mechanical properties of double-layered graphene sheets. Comput. Mater. Sci. 2013, 69, 335–343. [Google Scholar] [CrossRef]
- Rissanou, N.A.; Power, J.A.; Harmandaris, V. Structural and dynamical properties of polyethylene/graphene nanocomposites through molecular dynamics simulations. Polymers 2015, 7, 390–417. [Google Scholar] [CrossRef]
- Tsai, J.-L.; Tzeng, S.-H.; Chiu, Y.-T. Characterizing elastic properties of carbon nanotubes/polyimide nanocomposites using multi-scale simulation. Compos. Part B Eng. 2010, 41, 106–115. [Google Scholar] [CrossRef]
- Montazeri, A.; Rafii-Tabar, H. Multiscale modeling of graphene- and nanotube-based reinforced polymer nanocomposites. Phys. Lett. A 2011, 375, 4034–4040. [Google Scholar] [CrossRef]
- Taherzadeh, M.; Baghani, M.; Baniassadi, M.; Abrinia, K.; Safdari, M. Modeling and homogenization of shape memory polymer nanocomposites. Compos. Part B Eng. 2016, 91, 36–43. [Google Scholar] [CrossRef]
- Dai, G.; Mishnaevsky, L. Graphene reinforced nanocomposites: 3d simulation of damage and fracture. Comput. Mater. Sci. 2014, 95, 684–692. [Google Scholar] [CrossRef]
- Rahimian-Koloor, S.M.; Moshrefzadeh-Sani, H.; Shokrieh, M.M.; Hashemianzadeh, S.M. On the behavior of isolated and embedded carbon nano-tubes in a polymeric matrix. Mater. Res. Express 2018, 5, 025019. [Google Scholar] [CrossRef]
- Elices, M.; Guinea, G.V.; Gómez, J.; Planas, J. The cohesive zone model: Advantages, limitations and challenges. Eng. Fract. Mech. 2002, 69, 137–163. [Google Scholar] [CrossRef]
- Koloor, S.S.R.; Tamin, M.N. Mode-ii interlaminar fracture and crack-jump phenomenon in cfrp composite laminate materials. Compos. Struct. 2018, 204, 594–606. [Google Scholar] [CrossRef]
- Guin, L.; Raphanel, J.L.; Kysar, J.W. Atomistically derived cohesive zone model of intergranular fracture in polycrystalline graphene. J. Appl. Phys. 2016, 119, 245107. [Google Scholar] [CrossRef]
- Dávila, C.G.; Camanho, P.P. Analysis of the Effects of Residual Strains and Defects on Skin/Stiffener Debonding Using Decohesion Elements; NASA Langley Research Center: Hampton, VA, USA; Norfolk, VA, USA, 2003. [Google Scholar]
- Campilho, R.D.S.G.; Banea, M.D.; Neto, J.A.B.P.; da Silva, L.F.M. Modelling adhesive joints with cohesive zone models: Effect of the cohesive law shape of the adhesive layer. Int. J. Adhes. Adhes. 2013, 44, 48–56. [Google Scholar] [CrossRef]
- ASTM. Astm d5528–13, Standard Test Method for Mode i Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2013. [Google Scholar]
- ASTM. Astm d7905/d7905m-14, Standard Test Method for Determination of the Mode ii Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Spearot, D.E.; Jacob, K.I.; McDowell, D.L. Non-local separation constitutive laws for interfaces and their relation to nanoscale simulations. Mech. Mater. 2004, 36, 825–847. [Google Scholar] [CrossRef]
- Yamakov, V.; Saether, E.; Glaessgen, E.H. Multiscale modeling of intergranular fracture in aluminum: Constitutive relation for interface debonding. J. Mater. Sci. 2008, 43, 7488–7494. [Google Scholar] [CrossRef][Green Version]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. Packmol: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Hadden, C.M.; Jensen, B.D.; Bandyopadhyay, A.; Odegard, G.M.; Koo, A.; Liang, R. Molecular modeling of epon-862/graphite composites: Interfacial characteristics for multiple crosslink densities. Compos. Sci. Technol. 2013, 76, 92–99. [Google Scholar] [CrossRef]
- Aghadavoudi, F.; Golestanian, H.; Tadi Beni, Y. Investigating the effects of resin crosslinking ratio on mechanical properties of epoxy-based nanocomposites using molecular dynamics. Polym. Compos. 2017, 38, E433–E442. [Google Scholar] [CrossRef]
- Alian, A.R.; Meguid, S.A. Molecular dynamics simulations of the effect of waviness and agglomeration of cnts on interface strength of thermoset nanocomposites. Phys. Chem. Chem. Phys. 2017, 19, 4426–4434. [Google Scholar] [CrossRef] [PubMed]
- Alian, A.R.; Kundalwal, S.I.; Meguid, S.A. Multiscale modeling of carbon nanotube epoxy composites. Polymer 2015, 70, 149–160. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A molecular dynamics study of epoxy-based networks: Cross-linking procedure and prediction of molecular and material properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Yarovsky, I.; Evans, E. Computer simulation of structure and properties of crosslinked polymers: Application to epoxy resins. Polymer 2002, 43, 963–969. [Google Scholar] [CrossRef]
- Brown, E.N.; White, S.R.; Sottos, N.R. Microcapsule induced toughening in a self-healing polymer composite. J. Mater. Sci. 2004, 39, 1703–1710. [Google Scholar] [CrossRef]
- Garcia, F.G.; Soares, B.G.; Pita, V.J.R.R.; Sánchez, R.; Rieumont, J. Mechanical properties of epoxy networks based on dgeba and aliphatic amines. J. Appl. Polym. Sci. 2007, 106, 2047–2055. [Google Scholar] [CrossRef]
- Vijayaraghavan, V.; Wong, C.H. Temperature, defect and size effect on the elastic properties of imperfectly straight carbon nanotubes by using molecular dynamics simulation. Comput. Mater. Sci. 2013, 71, 184–191. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A reactive potential for hydrocarbons with intermolecular interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Sun, H.; Mumby, S.J.; Maple, J.R.; Hagler, A.T. An ab initio cff93 all-atom force field for polycarbonates. J. Am. Chem. Soc. 1994, 116, 2978–2987. [Google Scholar] [CrossRef]
- Lordi, V.; Yao, N. Molecular mechanics of binding in carbon-nanotube–polymer composites. J. Mater. Res. 2000, 15, 2770–2779. [Google Scholar] [CrossRef]
- Desgranges, C.; Delhommelle, J. Evaluation of the grand-canonical partition function using expanded wang-landau simulations. Iii. Impact of combining rules on mixtures properties. J. Chem. Phys. 2014, 140, 104109. [Google Scholar] [CrossRef] [PubMed]
- Shenogina, N.B.; Tsige, M.; Patnaik, S.S.; Mukhopadhyay, S.M. Molecular modeling of elastic properties of thermosetting polymers using a dynamic deformation approach. Polymer 2013, 54, 3370–3376. [Google Scholar] [CrossRef]
- Yang, S.; Yu, S.; Cho, M. Influence of thrower–stone–wales defects on the interfacial properties of carbon nanotube/polypropylene composites by a molecular dynamics approach. Carbon 2013, 55, 133–143. [Google Scholar] [CrossRef]
- Lu, Q.; Bhattacharya, B. The role of atomistic simulations in probing the small-scale aspects of fracture—A case study on a single-walled carbon nanotube. Eng. Fract. Mech. 2005, 72, 2037–2071. [Google Scholar] [CrossRef]
- Martyna, G.J.; Tobias, D.J.; Klein, M.L. Constant pressure molecular dynamics algorithms. J. Chem. Phys. 1994, 101, 4177–4189. [Google Scholar] [CrossRef]
- Dassault Systemes. Abaqus Documentation; Dassault Systemes: Vélizy-Villacoublay, France, 2009. [Google Scholar]
- Koloor, S.S.R.; Ayatollahi, M.; Tamin, M. Elastic-damage deformation response of fiber-reinforced polymer composite laminates with lamina interfaces. J. Reinf. Plast. Compos. 2017, 36, 832–849. [Google Scholar] [CrossRef]
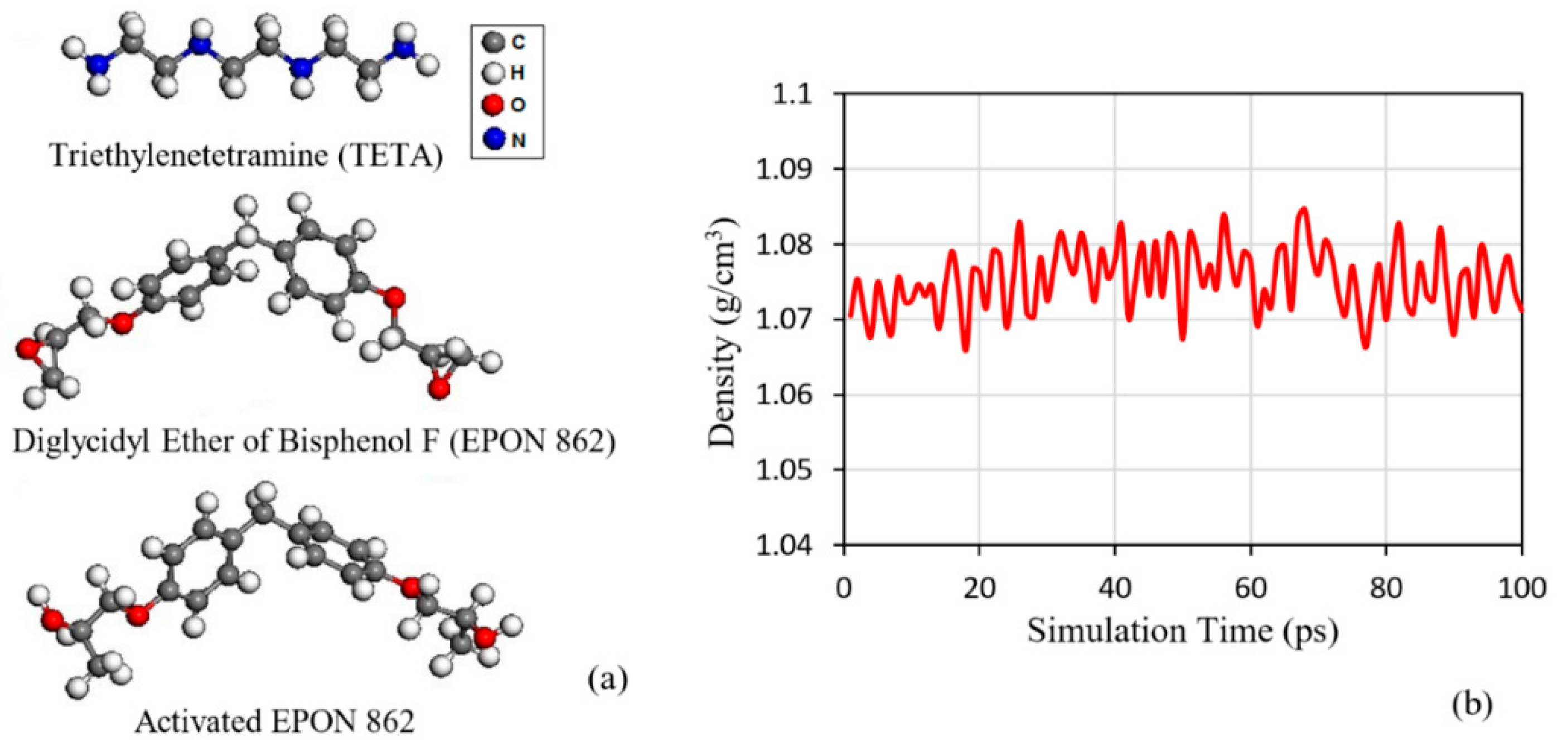


| Configuration of RVE | Graphene Sheet Length (nm) | Box Volume (nm3) | Number of Epoxy Molecules | Number of Hardener Molecules | Density after Curing Process and Final NPT Equilibration (g/cm3) |
|---|---|---|---|---|---|
| Long | 4.540 × 4.520 | 143.653 | 258 | 86 | 1.1865 |
| Parameter | MD Simulation | Experiments |
|---|---|---|
| Density, g/cm3 | 1.14 | 1.16 |
| Poisson’s ratio | 0.39 | 0.3–0.4 |
| Young’s modulus, GPa | 2.77 | 2.4–3.4 |
| Shear modulus, GPa | 1.03 | 1.0–1.5 |
| Parameter | Symbol (Unit) | Value |
|---|---|---|
| Tensile stiffness | k3, (aPa·nm−1) | 5 × 10−8 |
| Tensile strength | , (aPa) | 9.75 × 10−10 |
| Displacement at damage initiation | , (nm) | 0.0653 |
| Displacement at separation | , (nm) | 0.8 |
| Exponent for the regressive softening law, (Equation (8)) | α | 7.74 |
| Critical Mode I strain energy release rate | GIC, (N·nm−1) | 2.1 × 10−10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koloor, S.S.R.; Rahimian-Koloor, S.M.; Karimzadeh, A.; Hamdi, M.; Petrů, M.; Tamin, M.N. Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers 2019, 11, 1435. https://doi.org/10.3390/polym11091435
Koloor SSR, Rahimian-Koloor SM, Karimzadeh A, Hamdi M, Petrů M, Tamin MN. Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers. 2019; 11(9):1435. https://doi.org/10.3390/polym11091435
Chicago/Turabian StyleKoloor, S. S. R., S. M. Rahimian-Koloor, A. Karimzadeh, M. Hamdi, Michal Petrů, and M. N. Tamin. 2019. "Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation" Polymers 11, no. 9: 1435. https://doi.org/10.3390/polym11091435
APA StyleKoloor, S. S. R., Rahimian-Koloor, S. M., Karimzadeh, A., Hamdi, M., Petrů, M., & Tamin, M. N. (2019). Nano-Level Damage Characterization of Graphene/Polymer Cohesive Interface under Tensile Separation. Polymers, 11(9), 1435. https://doi.org/10.3390/polym11091435







