In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial
Abstract
:1. Introduction
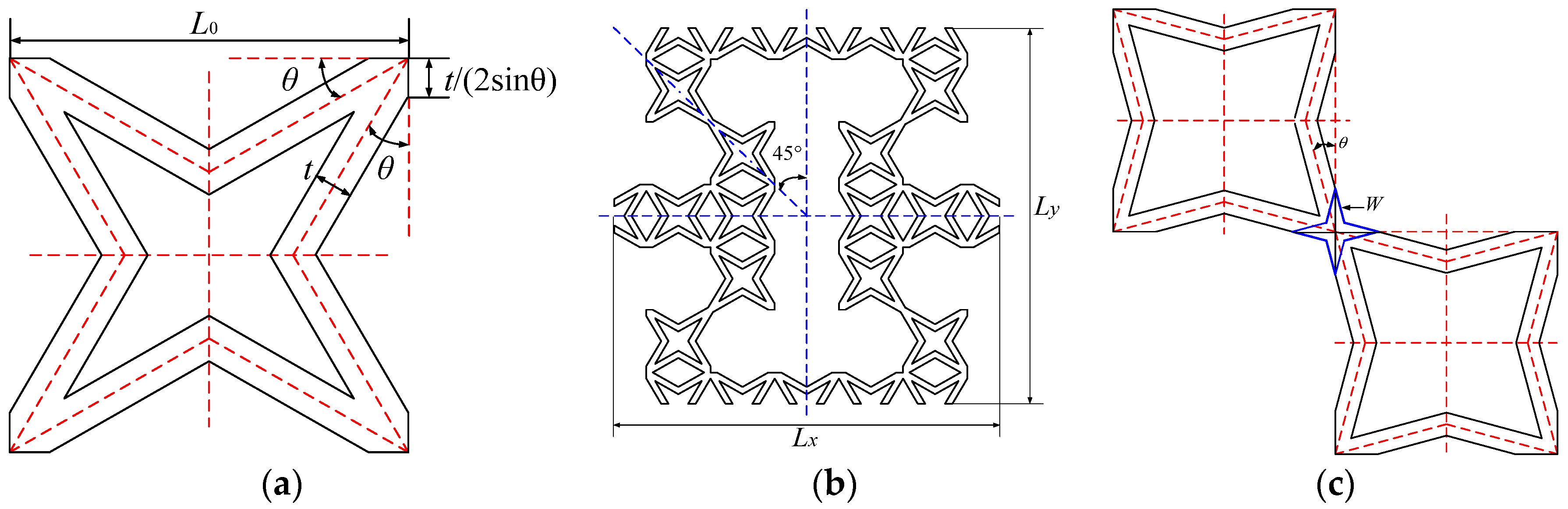
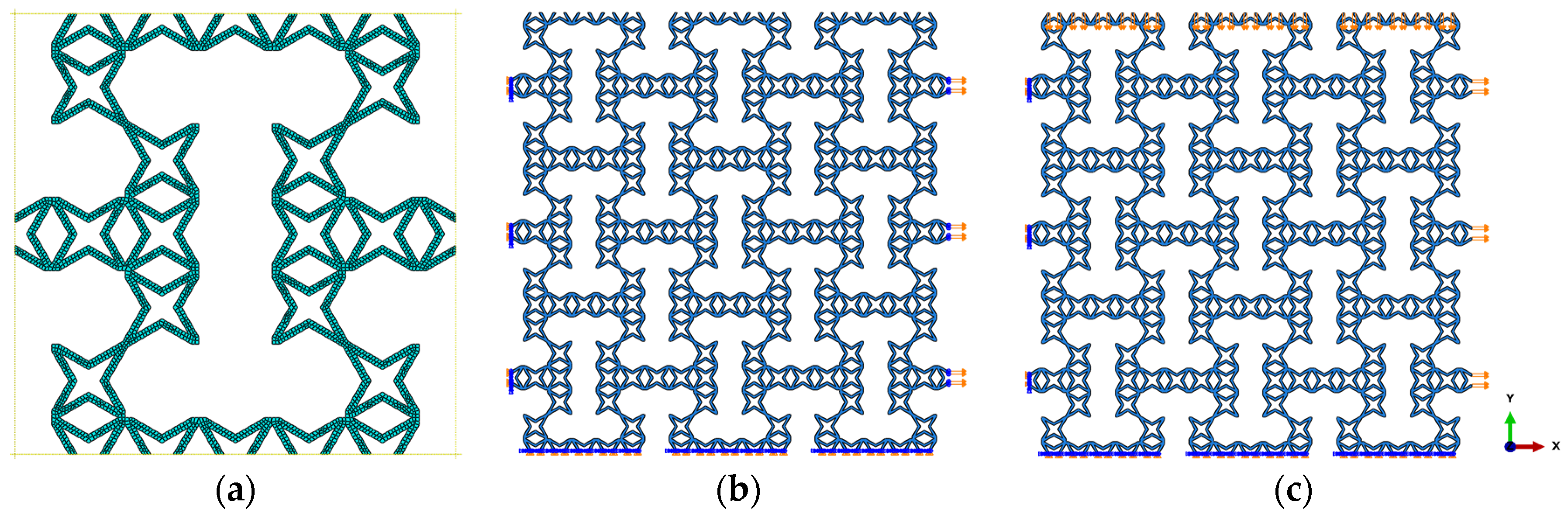
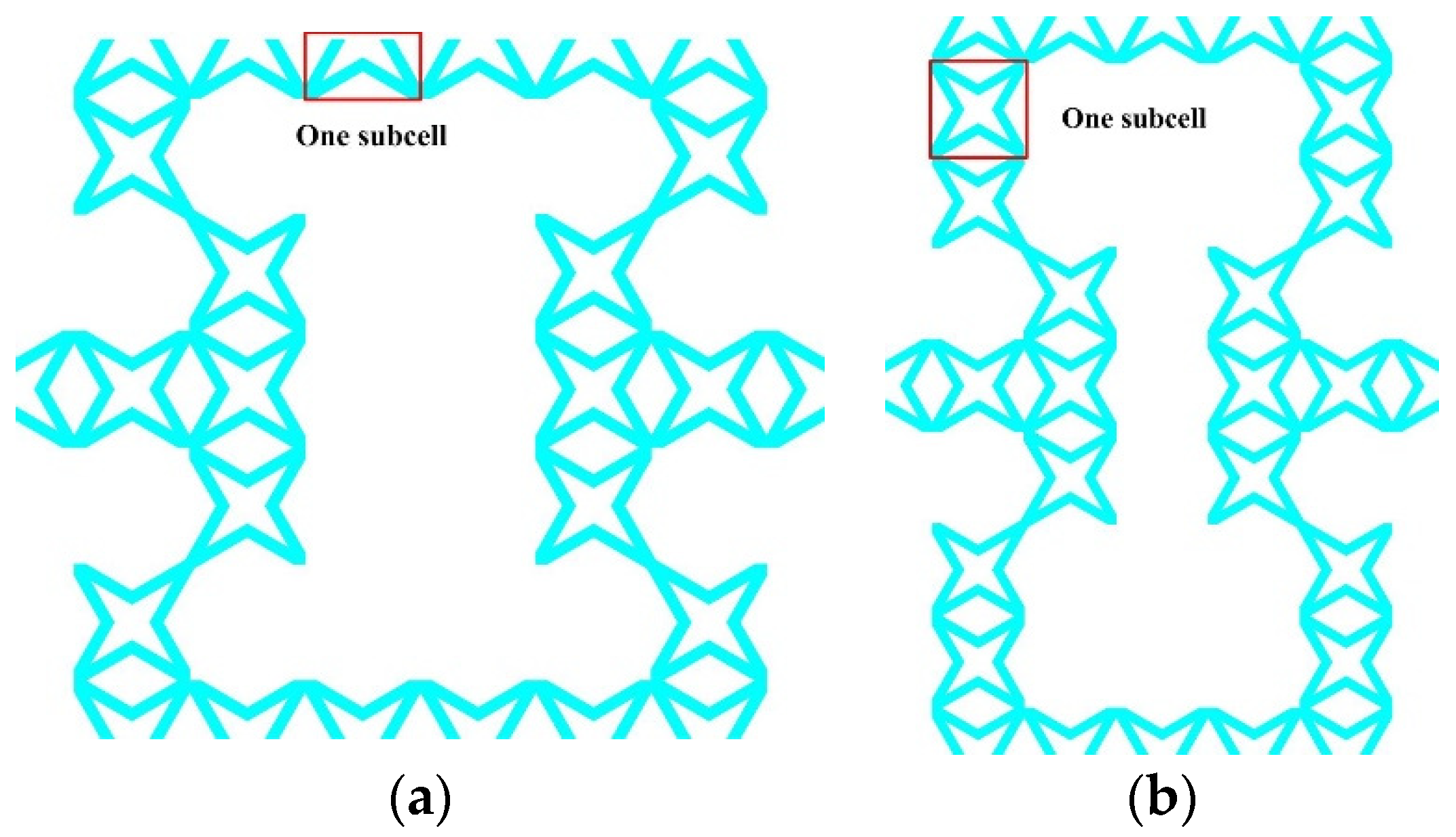
2. Materials and Methods
3. Results and Discussion
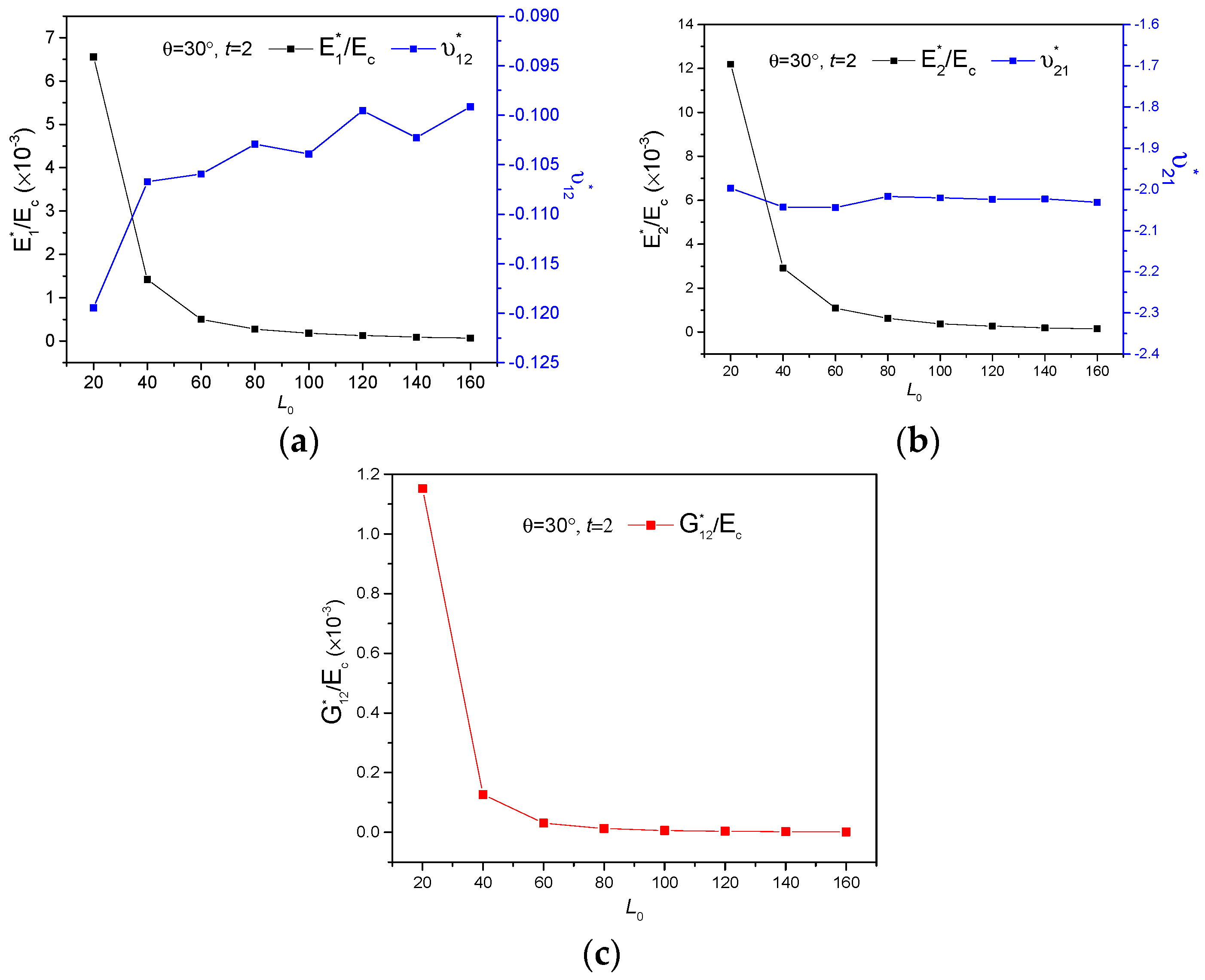
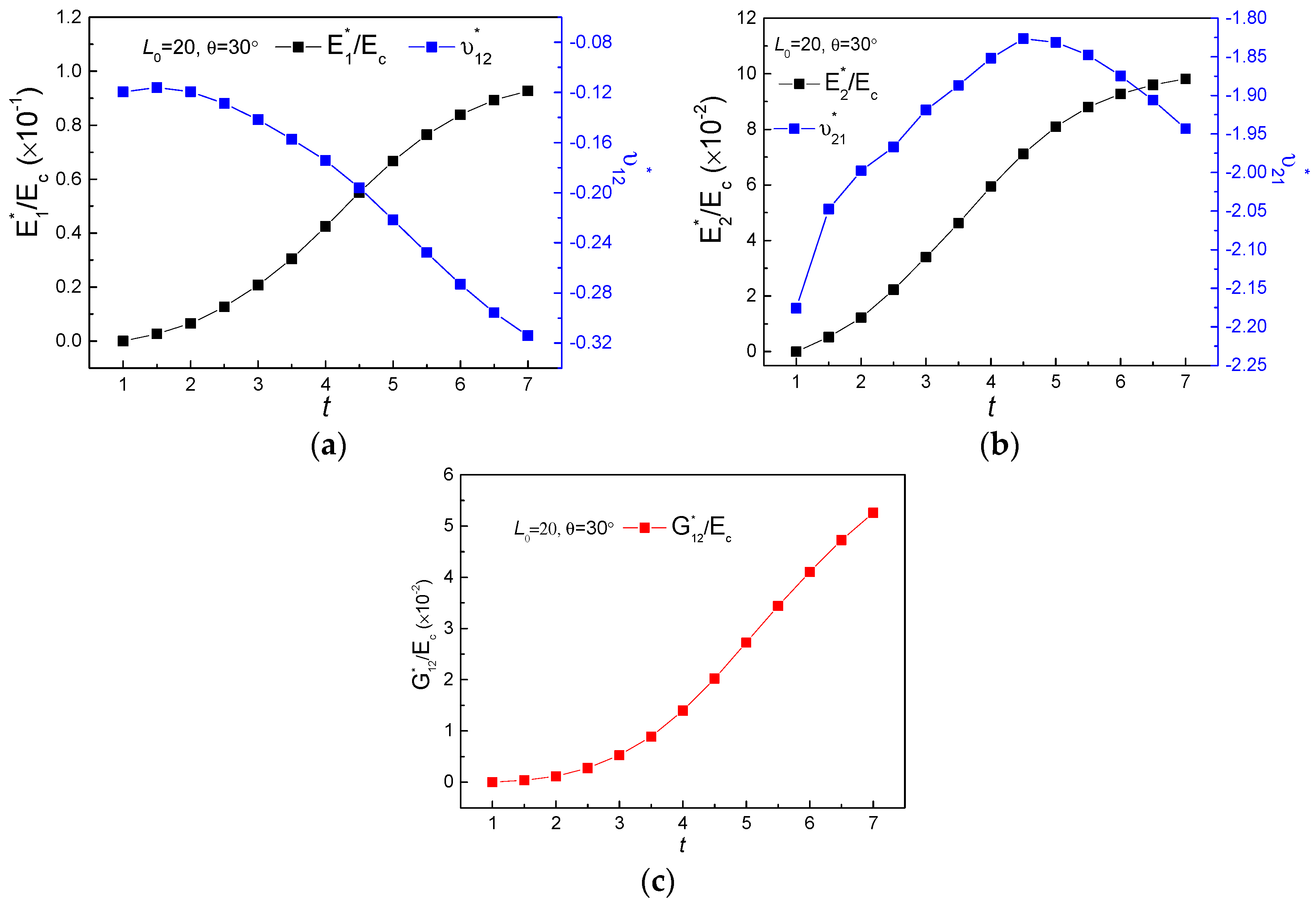
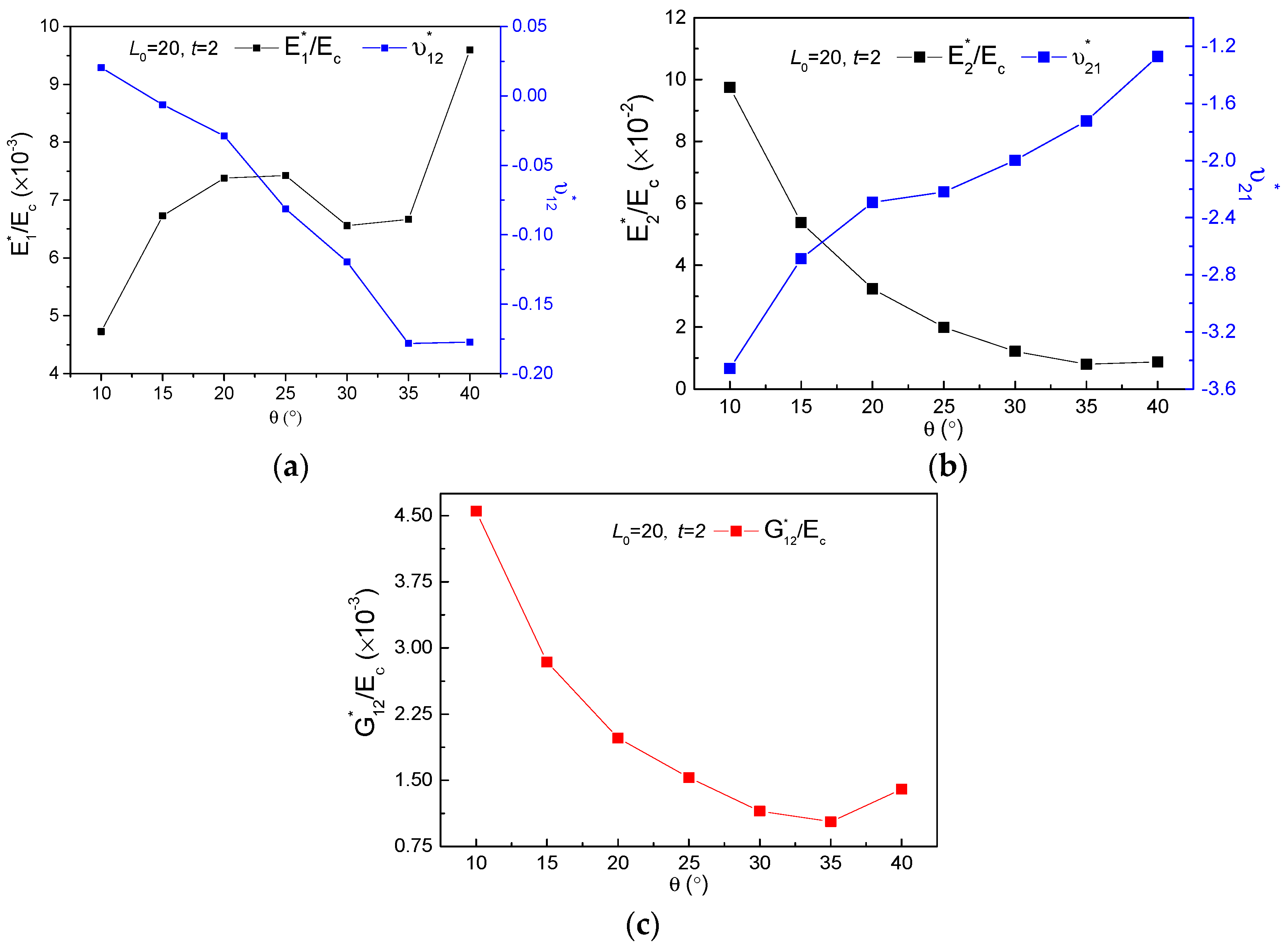
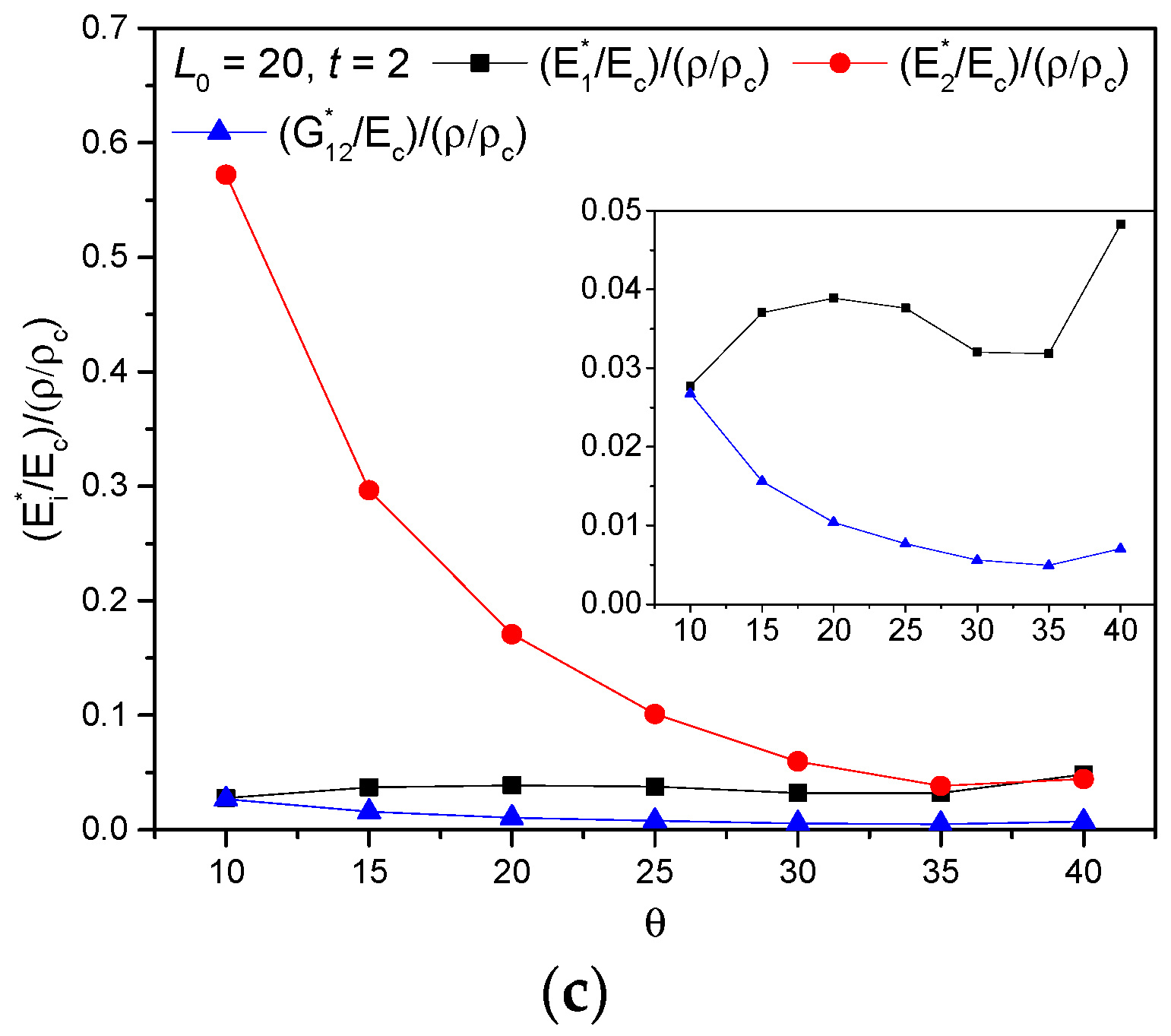
3.1. The Geometry Effects of Star Subordinate Cell
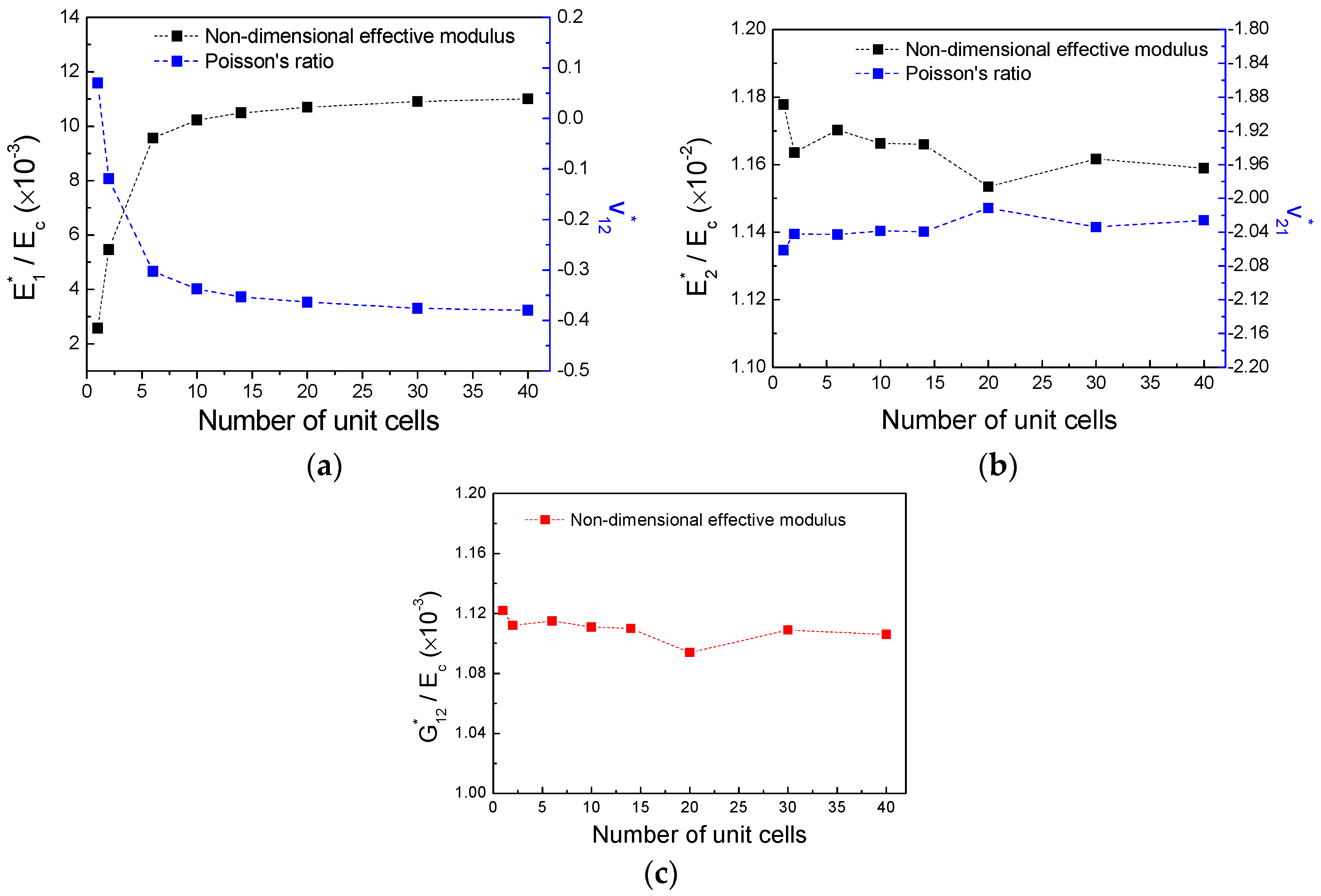
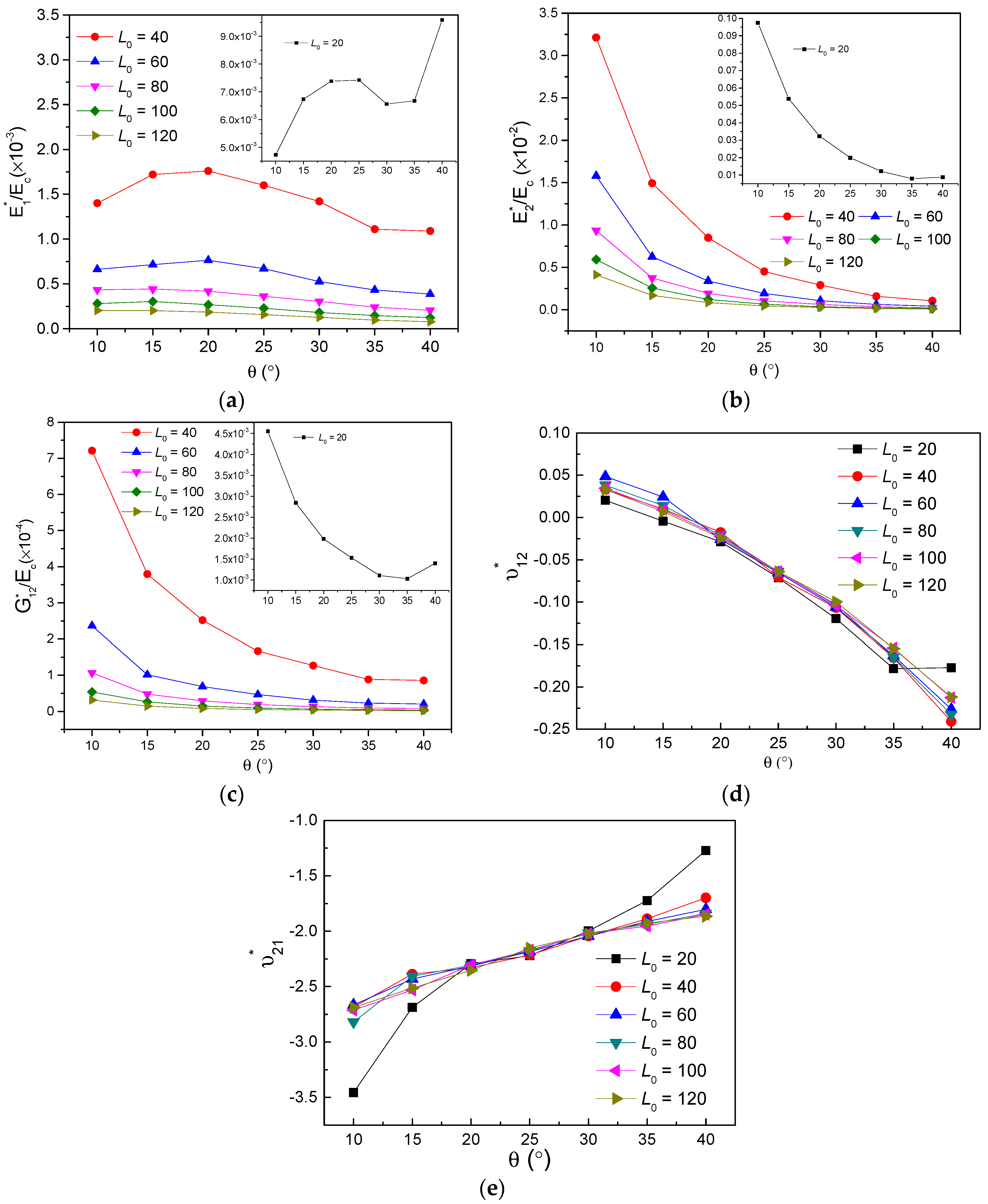
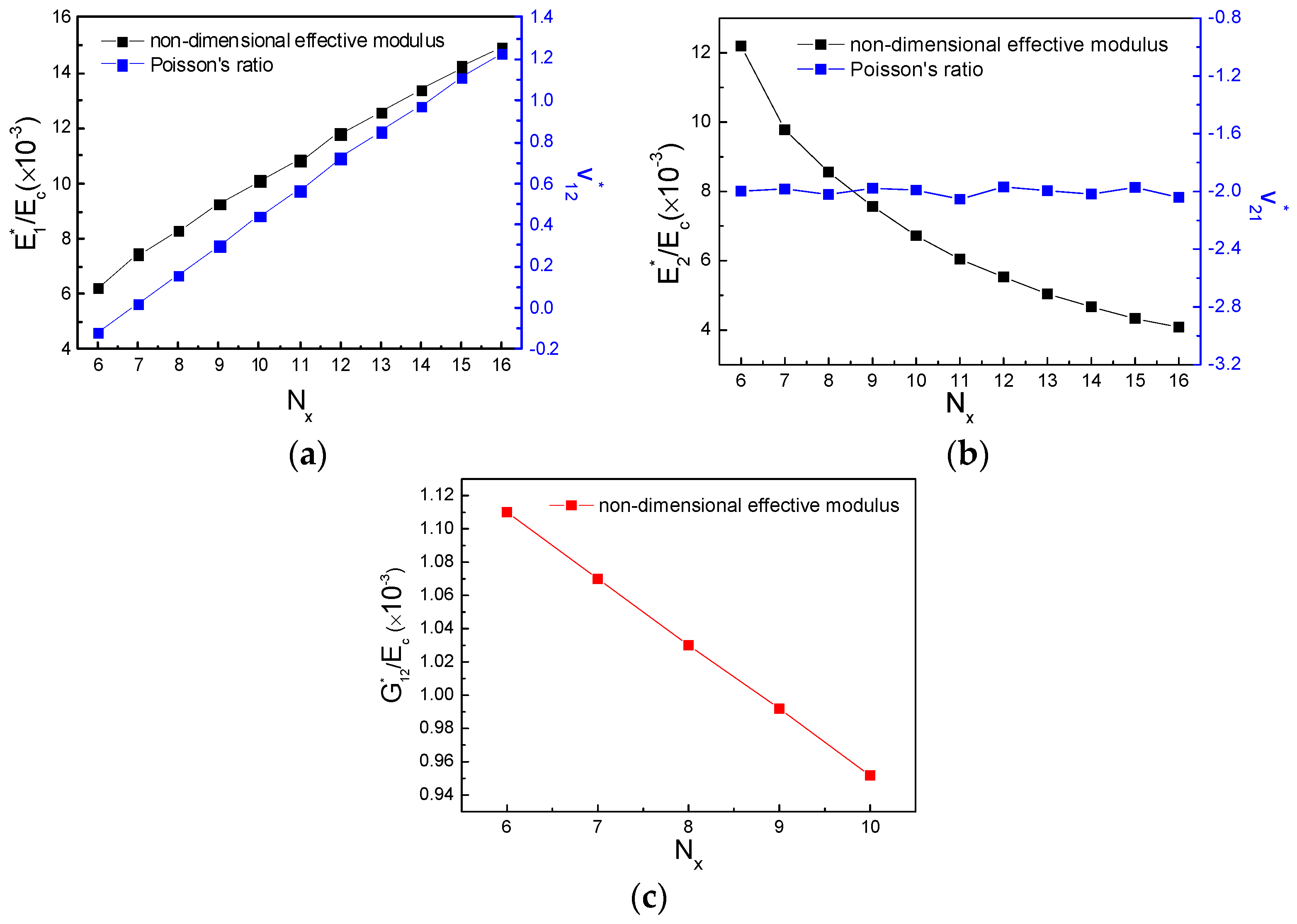
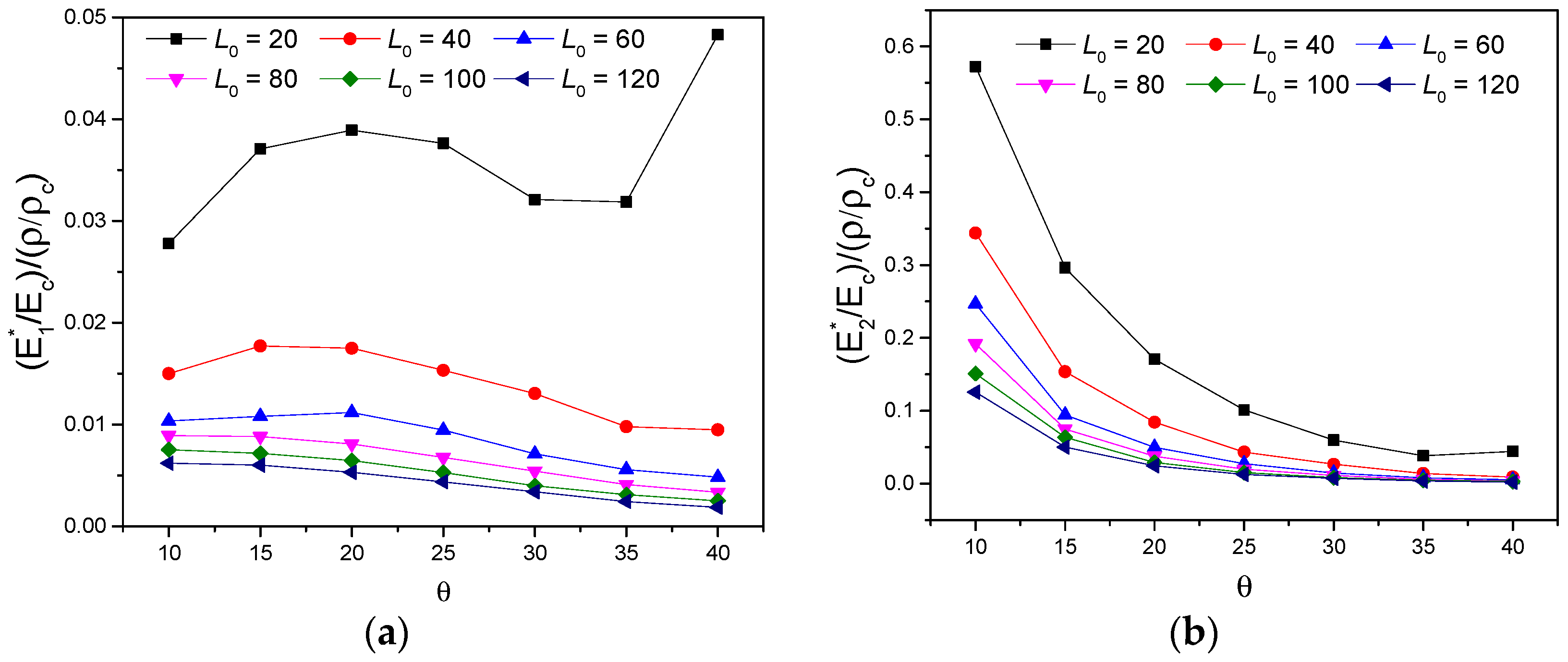
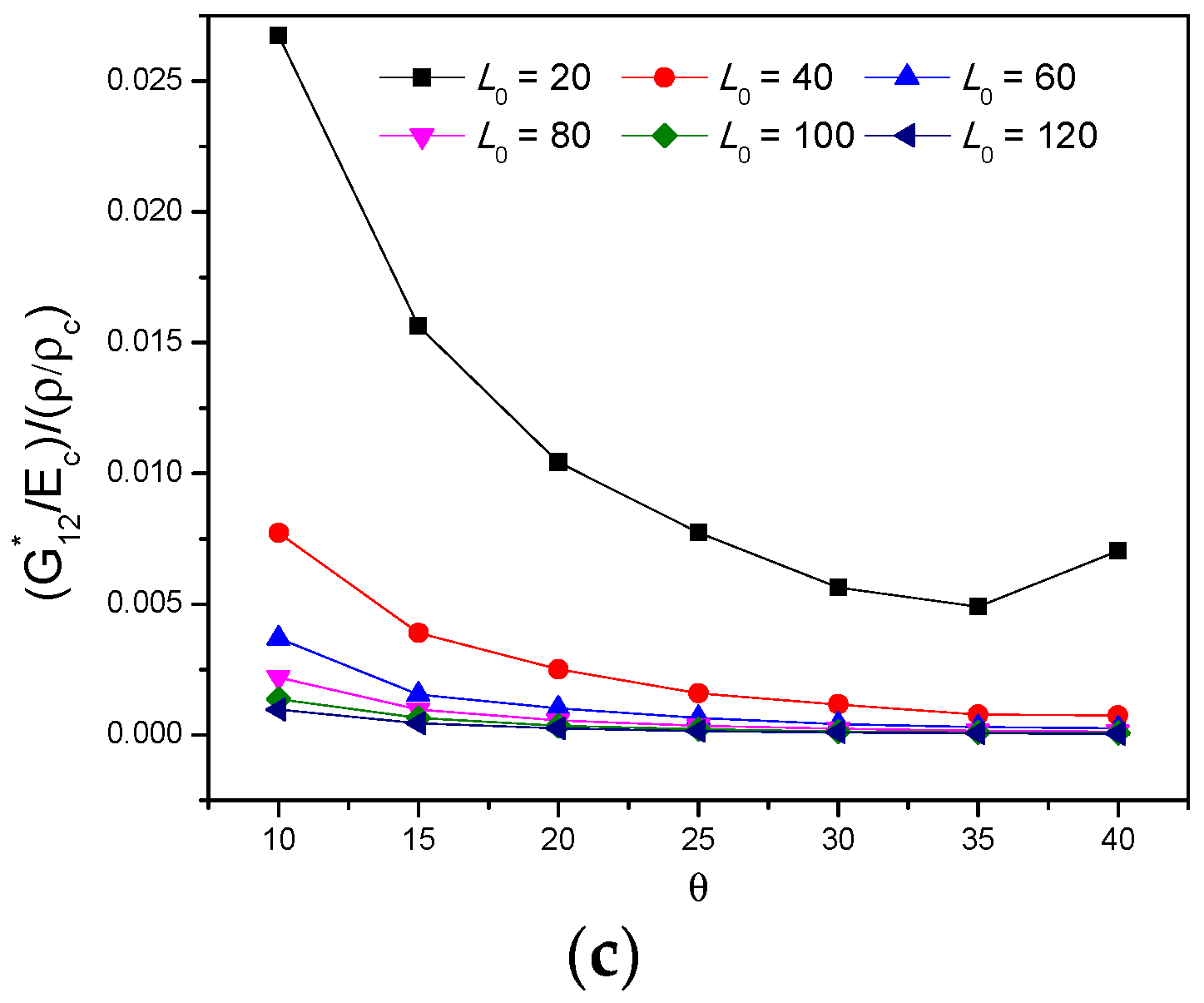
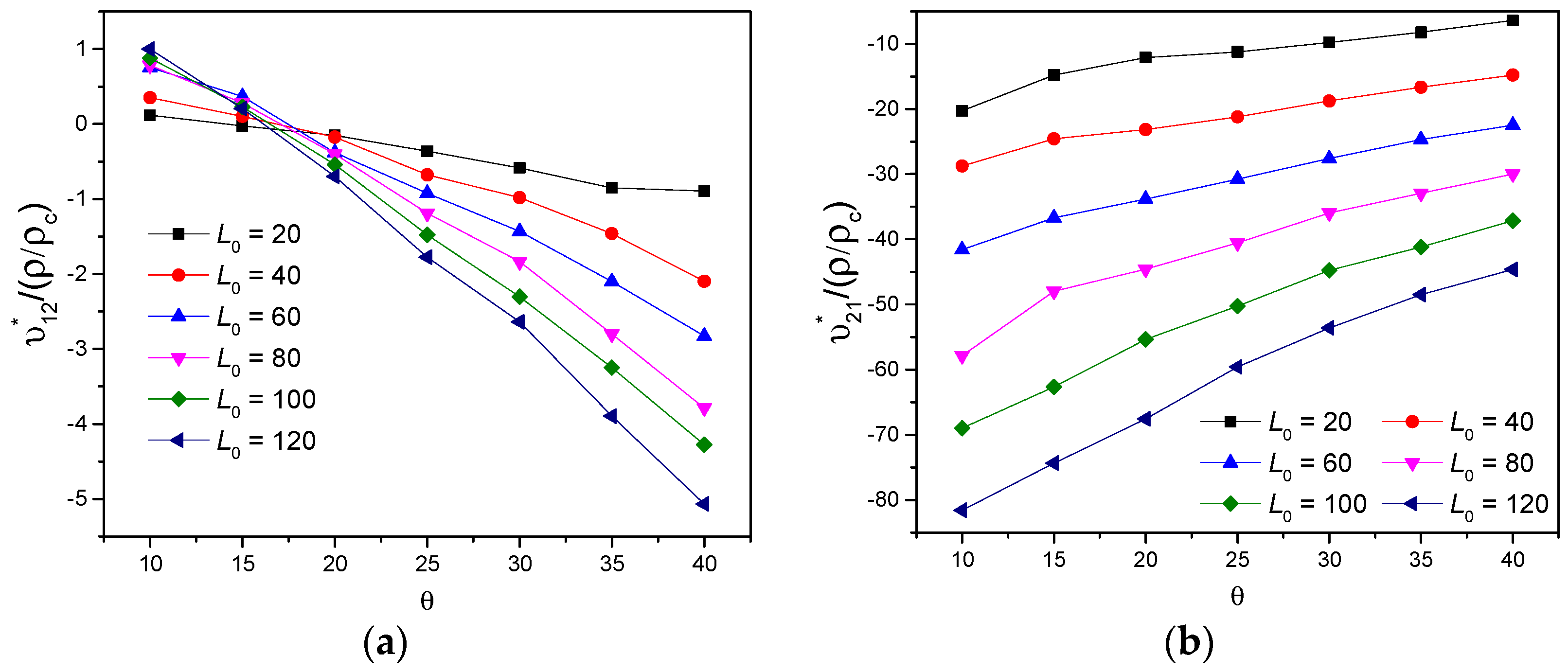
3.2. The Effects of Subordinate Cell Amount
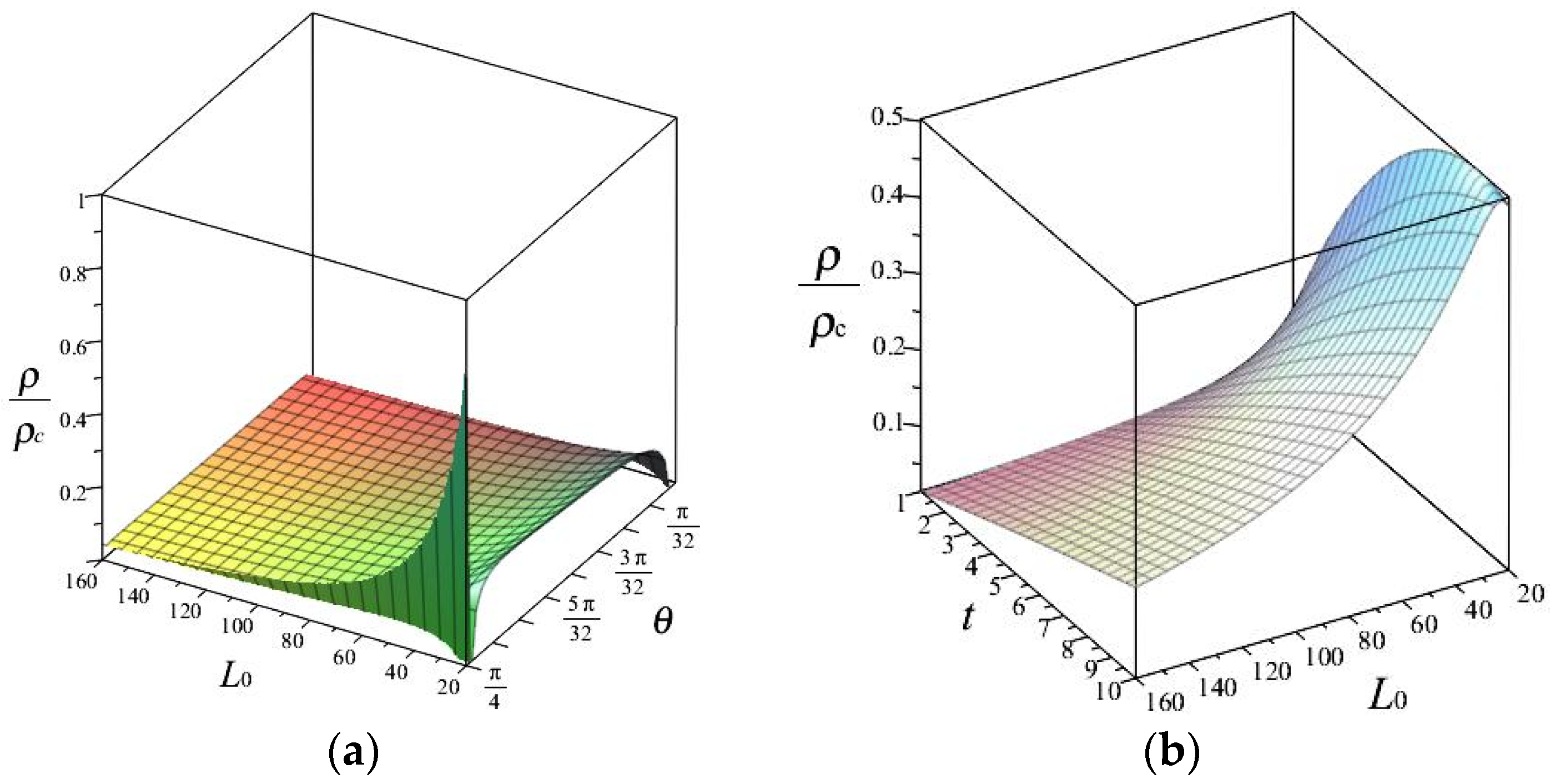
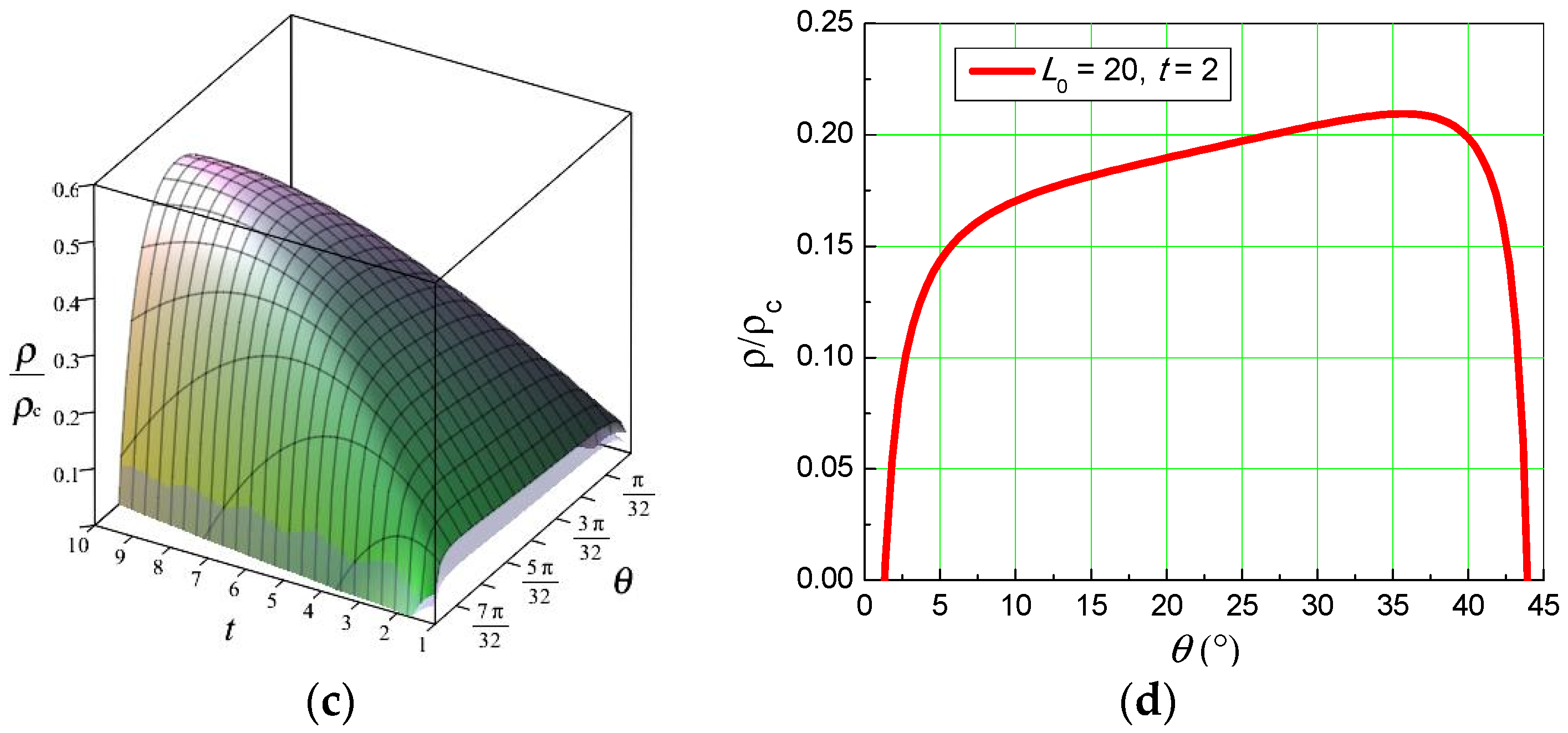
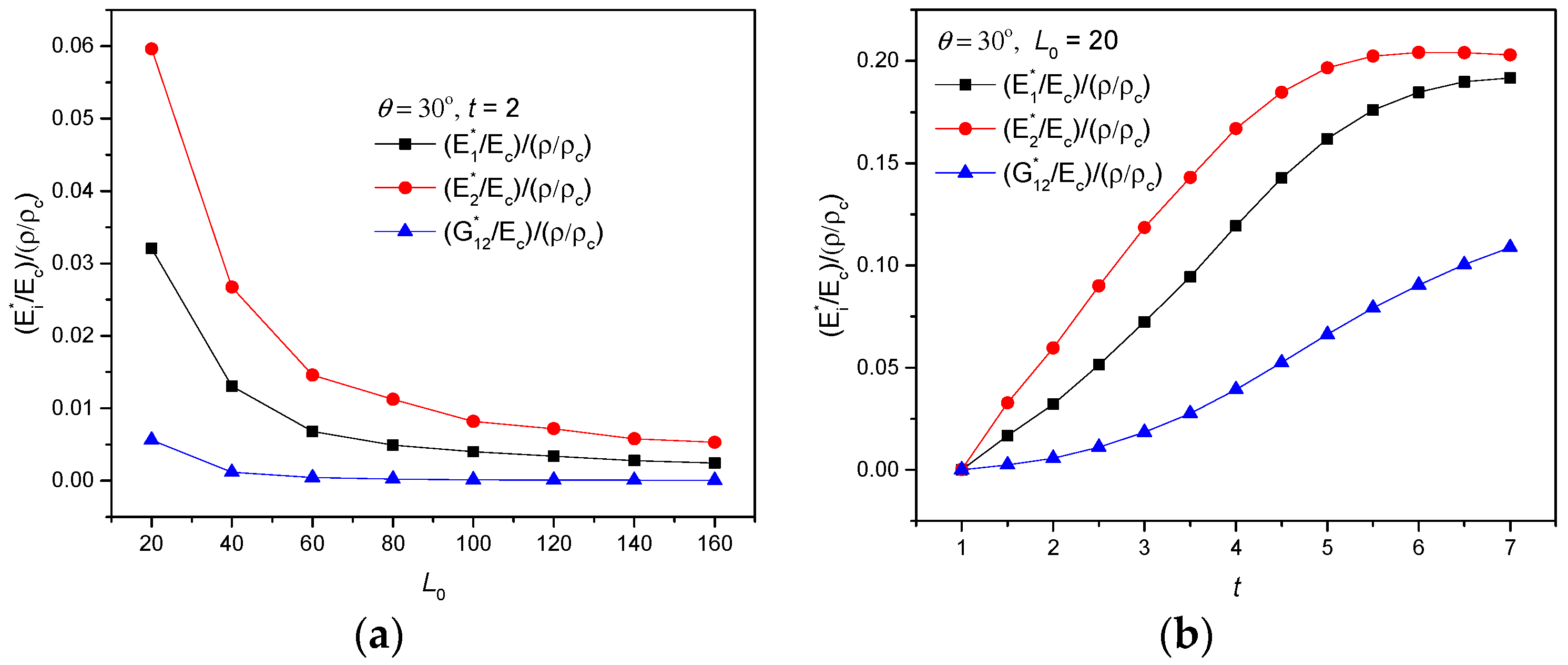
3.3. Relative Density Study
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Ashby, M.F. The properties of foams and lattices. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2006, 364, 15–30. [Google Scholar] [CrossRef] [PubMed]
- Harkati, E.; Daoudi, N.; Bezazi, A.; Haddad, F. Scarpa. In-plane elasticity of a multi re-entrant auxetic honeycomb. Compos. Struct. 2017, 180, 130–139. [Google Scholar] [CrossRef]
- Lira, C.; Innocenti, P.; Scarpa, F. Transverse elastic shear of auxetic multi re-entrant honeycombs. Compos. Struct. 2009, 90, 314–322. [Google Scholar] [CrossRef]
- Scarpa, F.; Tomlinson, G. Theoretical characteristics of the vibration of sandwich plates with in-plane negative Poisson’s ratio values. J. Sound Vib. 2000, 230, 45–67. [Google Scholar] [CrossRef]
- Liu, W.; Wang, N.; Luo, T.; Lin, Z. In-plane dynamic crushing of re-entrant auxetic cellular structure. Mater. Des. 2016, 100, 84–91. [Google Scholar] [CrossRef]
- Innocenti, P.; Scarpa, F. Thermal conductivity properties and heat transfer analysis of multi-re-entrant auxetic honeycomb structures. J. Compos. Mater. 2009, 43, 2419–2439. [Google Scholar] [CrossRef]
- Lakes, R. Materials with structural hierarchy. Nature 1983, 361, 511–515. [Google Scholar] [CrossRef]
- Oftadeh, R.; Haghpanah, B.; Papadopoulos, J.; Hamouda, A.M.S.; Nayeb-Hashemi, H.; Vaziri, A. Mechanics of anisotropic hierarchical honeycombs. Int. J. Mech. Sci. 2014, 81, 126–136. [Google Scholar] [CrossRef]
- Mousanezhad, D.; Ebrahimi, H.; Haghpanah, B.; Ghosh, R.; Ajdari, A.; Hamouda, A.M.S.; Vaziri, A. Spiderweb honeycombs. Int. J. Solids Struct. 2015, 66, 218–227. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Zega, V.; Ardito, R.; Corigliano, A. 3D auxetic single material periodic structure with ultra-wide tunable bandgap. Sci. Rep. 2018, 8, 2262. [Google Scholar] [CrossRef] [PubMed]
- Bruggi, M.; Corigliano, A. Optimal 2D auxetic micro-structures with band gap. Meccanica 2019. [Google Scholar] [CrossRef]
- Wang, Q.M.; Jackson, J.A.; Ge, Q.; Hopkins, J.B.; Spadaccini, C.M.; Fang, N.X. Lightweight mechanical metamaterials with tunable negative thermal expansion. Phys. Rev. Lett. 2016, 117, 175901. [Google Scholar] [CrossRef] [PubMed]
- Billon, K.; Zampetakis, I.; Scarpa, F.; Ouisse, M.; Hetherington, A. Mechanics and band gaps in hierarchical auxetic rectangular perforated composite metamaterials. Compos. Struct. 2017, 160, 1042–1050. [Google Scholar] [CrossRef] [Green Version]
- Qiao, J.; Chen, C. In-plane crushing of a hierarchical honeycomb. Int. J. Solids Struct. 2016, 85, 57–66. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Q.; Pugno, N. Elastic and transport properties of the tailorable multifunctional hierarchical honeycombs. Compos. Struct. 2014, 107, 698–710. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, B.; Pugno, N.; Wang, B.; Ding, Q. In-plane stiffness of the anisotropic multifunctional hierarchical honeycombs. Compos. Struct. 2015, 131, 616–624. [Google Scholar] [CrossRef]
- Taylor, C.M.; Smith, C.W.; Miller, W.; Evans, K.E. The effects of hierarchy on the in-plane elastic properties of honeycombs. Int. J. Solids Struct. 2011, 48, 1330–1339. [Google Scholar] [CrossRef] [Green Version]
- Mousanezhad, D.; Haghpanah, B.; Ghosh, R.; Hamouda, A.M.; Nayeb-Hashemi, H.; Vaziri, A. Elastic properties of chiral, anti-chiral, and hierarchical honeycombs: A simple energy-based approach. Theor. Appl. Mech. Lett. 2016, 6, 81–96. [Google Scholar] [CrossRef] [Green Version]
- Gatt, R.; Mizzi, L.; Azzopardi, J.I.; Azzopardi, K.M.; Attard, D.; Casha, A.; Briffa, J.; Grima, J.N. Hierarchical Auxetic Mechanical Metamaterials. Sci. Rep. 2015, 5, 8395. [Google Scholar] [CrossRef]
- Chen, Y.; Jia, Z.; Wang, L. Hierarchical honeycomb lattice metamaterials with improved thermal resistance and mechanical properties. Compos. Struct. 2016, 152, 395–402. [Google Scholar] [CrossRef] [Green Version]
- Yin, H.; Huang, X.; Scarpa, F.; Wen, G.; Chen, Y.; Zhang, C. In-plane crashworthiness of bio-inspired hierarchical honeycombs. Compos. Struct. 2018, 192, 516–527. [Google Scholar] [CrossRef] [Green Version]
- Wu, W.; Tao, Y.; Xia, Y.; Chen, J.; Lei, H.; Sun, L.; Fang, D. Mechanical properties of hierarchical anti-tetrachiral metamaterials. Extre. Mech. Lett. 2017, 16, 18–32. [Google Scholar] [CrossRef]
- Wu, W.; Song, X.; Liang, J.; Xia, R.; Qian, G.; Fang, D. Mechanical properties of anti-tetrachiral auxetic stents. Compos. Struct. 2018, 185, 381–392. [Google Scholar] [CrossRef]
- Gong, X.; Huang, J.; Scarpa, F.; Liu, Y.; Leng, J. Zero Poisson’s ratio cellular structure for two-dimensional morphing applications. Compos. Struct. 2015, 134, 384–392. [Google Scholar] [CrossRef]
- Lira, C.; Scarpa, F.; Olszewska, M.; Celuch, M. The SILICOMB cellular structure: Mechanical and dielectric properties. Phys. Status Solidi 2009, 246, 2055–2062. [Google Scholar] [CrossRef]
- Salit, V.; Weller, T. On the feasibility of introducing auxetic behavior into thin-walled structures. Acta Mater. 2009, 57, 125–135. [Google Scholar] [CrossRef]
- Zhang, W.; Neville, R.; Zhang, D.; Scarpa, F.; Wang, L.; Lakes, R. The two-dimensional elasticity of a chiral hinge lattice metamaterial. Int. J. Solids Struct. 2018, 141, 254–263. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Zhao, S.; Sun, R.; Scarpa, F.; Wang, J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers 2019, 11, 1132. https://doi.org/10.3390/polym11071132
Zhang W, Zhao S, Sun R, Scarpa F, Wang J. In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers. 2019; 11(7):1132. https://doi.org/10.3390/polym11071132
Chicago/Turabian StyleZhang, Wenjiao, Shuyuan Zhao, Rujie Sun, Fabrizio Scarpa, and Jinwu Wang. 2019. "In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial" Polymers 11, no. 7: 1132. https://doi.org/10.3390/polym11071132
APA StyleZhang, W., Zhao, S., Sun, R., Scarpa, F., & Wang, J. (2019). In-Plane Mechanical Behavior of a New Star-Re-Entrant Hierarchical Metamaterial. Polymers, 11(7), 1132. https://doi.org/10.3390/polym11071132







