Effects of Intrinsic Properties on Fracture Nucleation and Propagation in Swelling Hydrogels
Abstract
1. Introduction
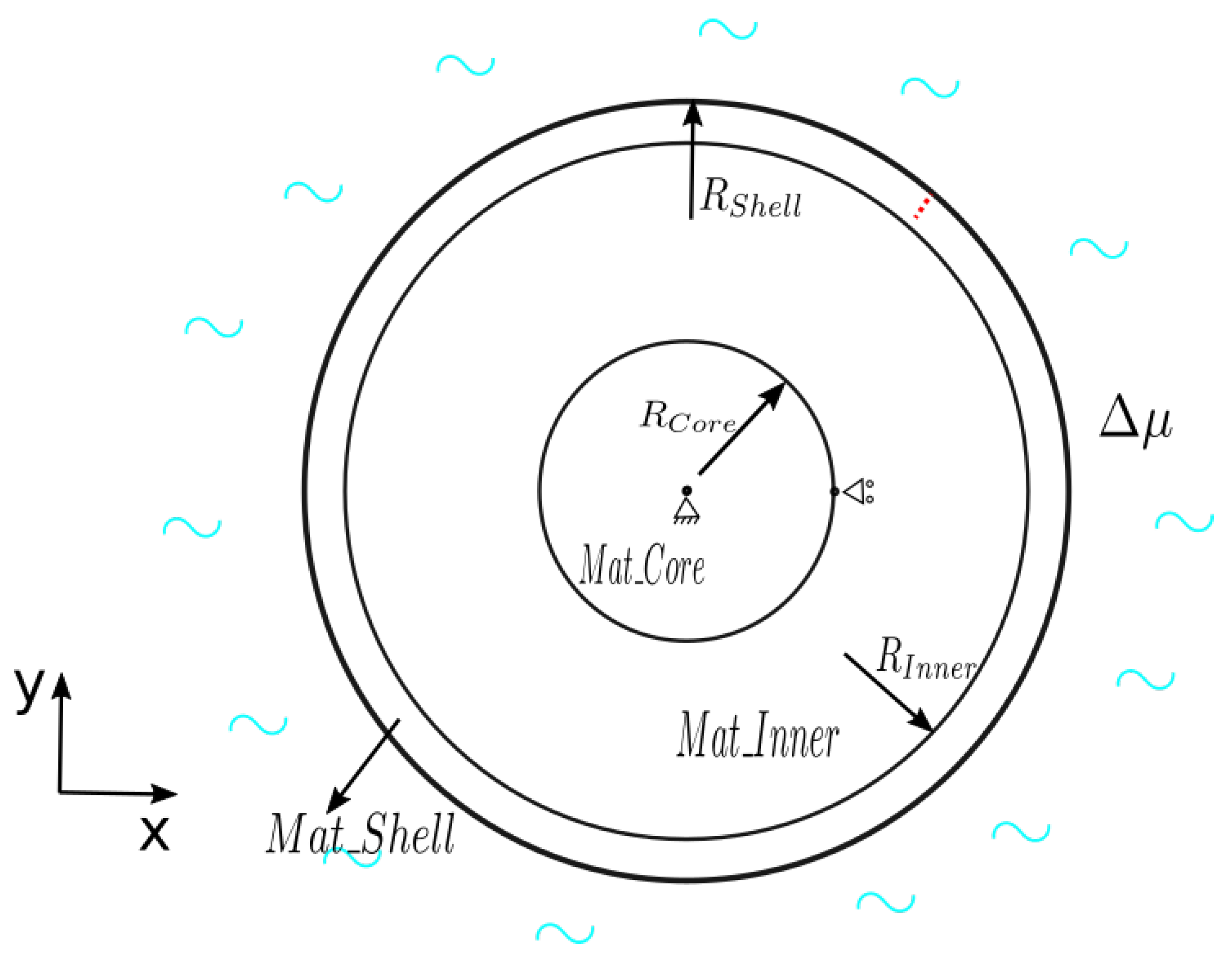
2. Results
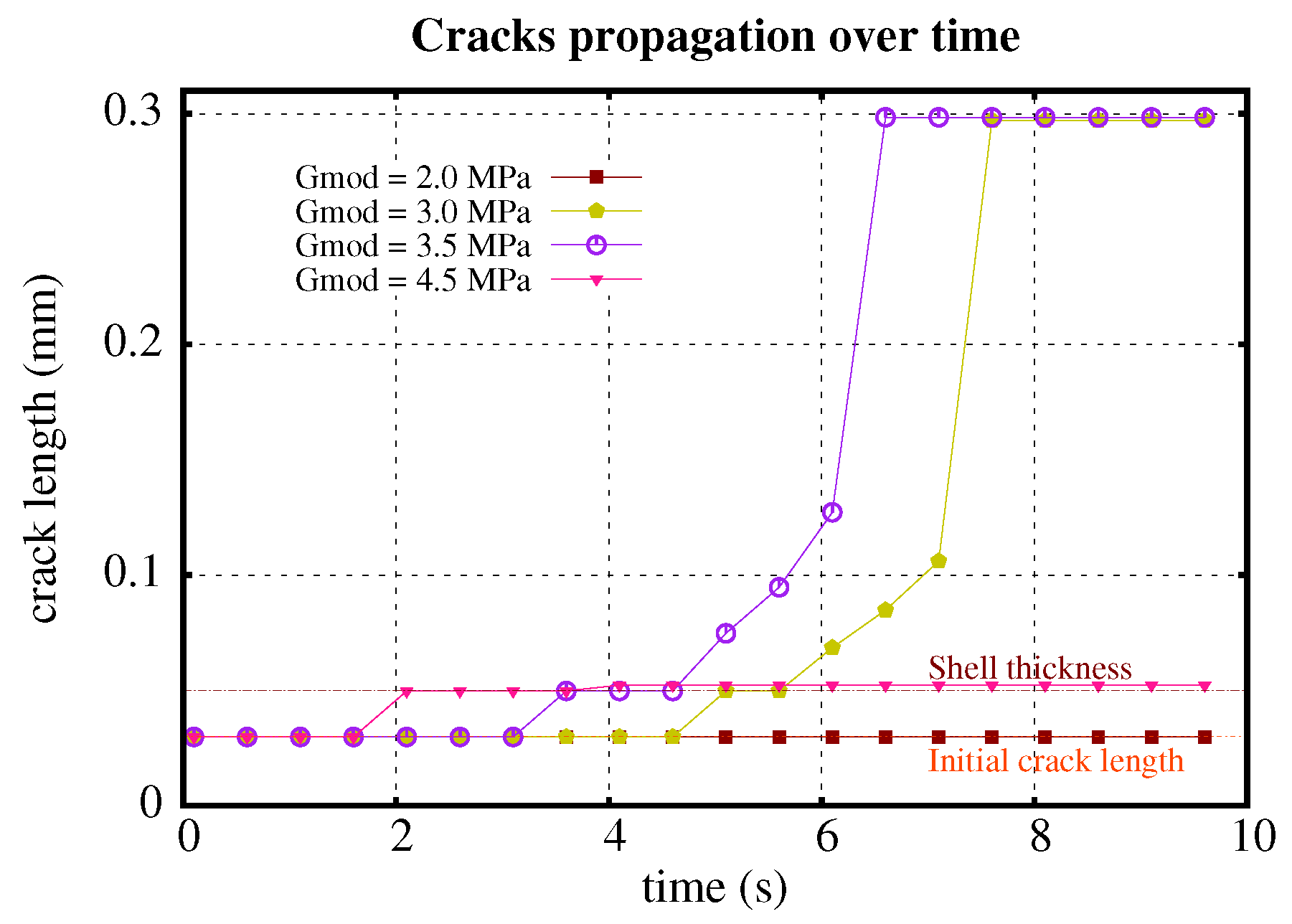
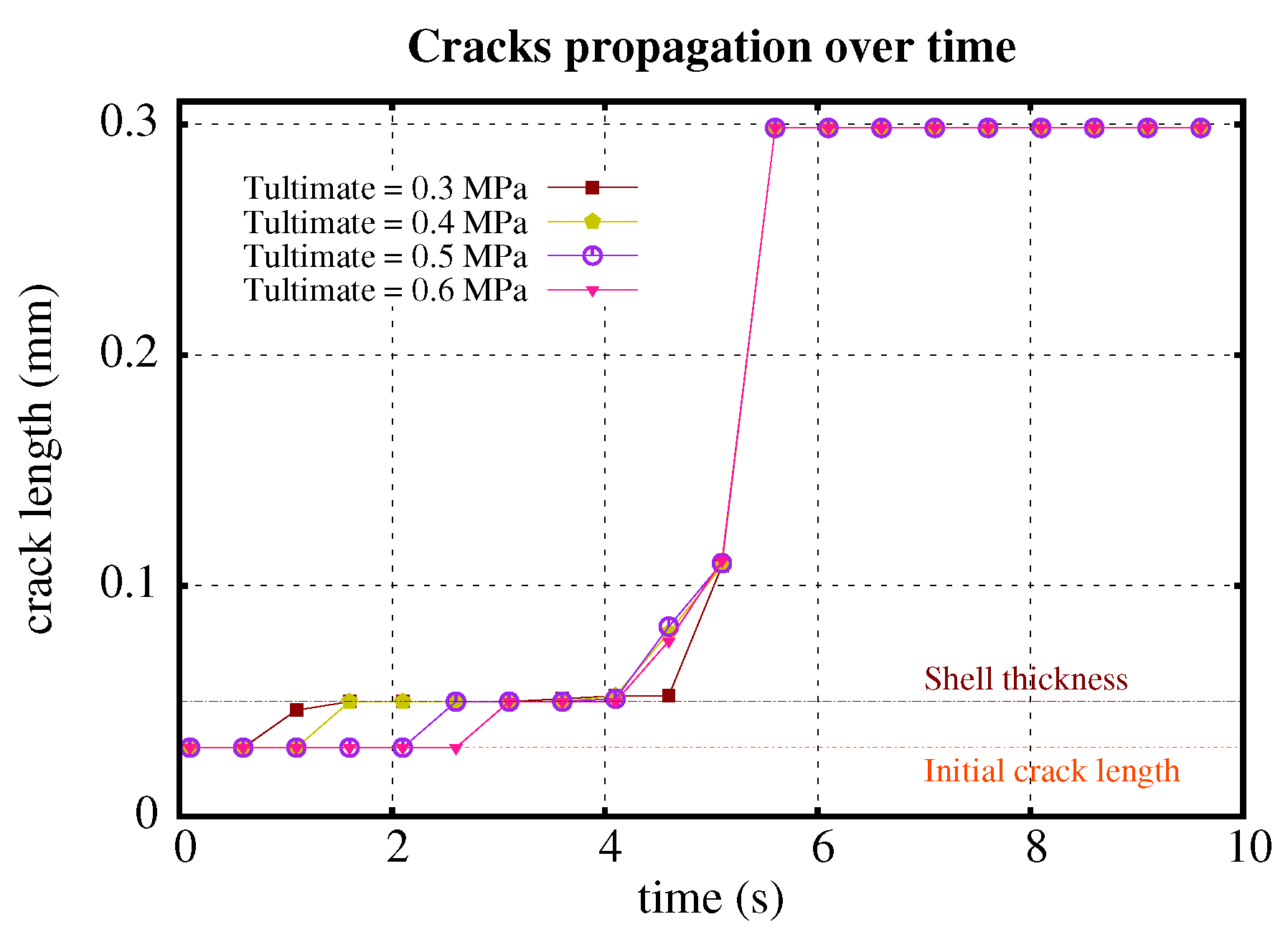
2.1. Crack Propagation
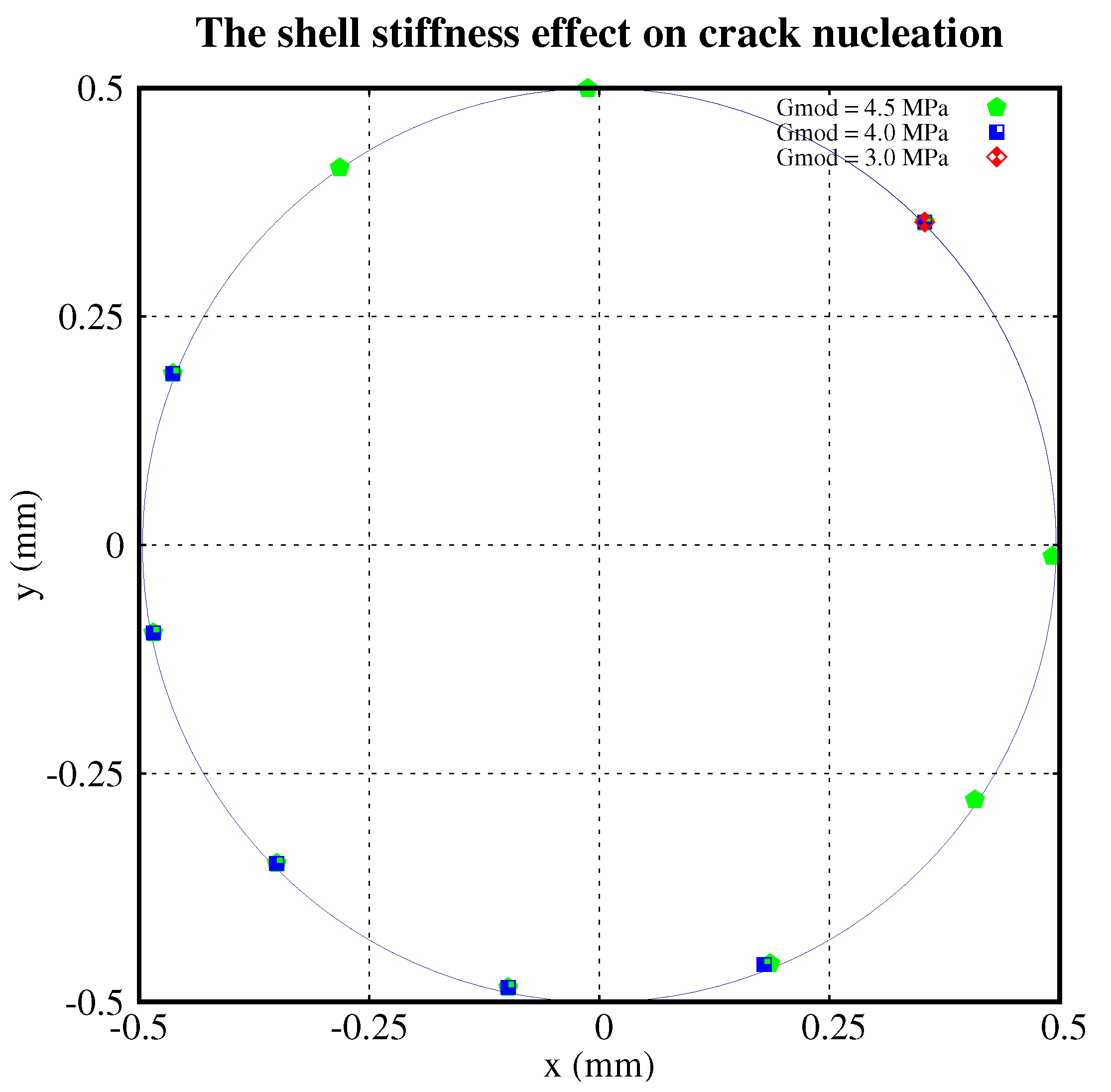
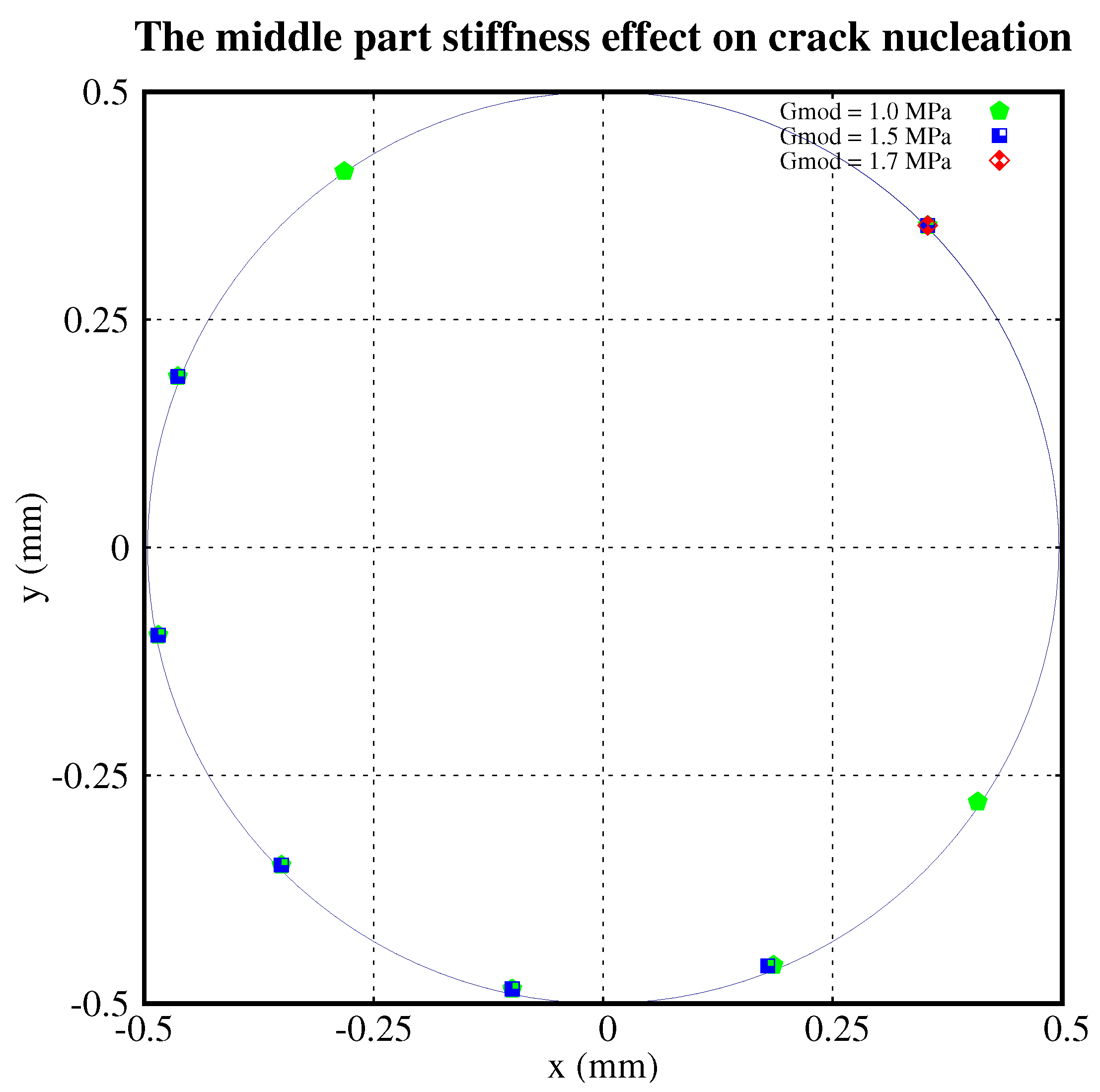
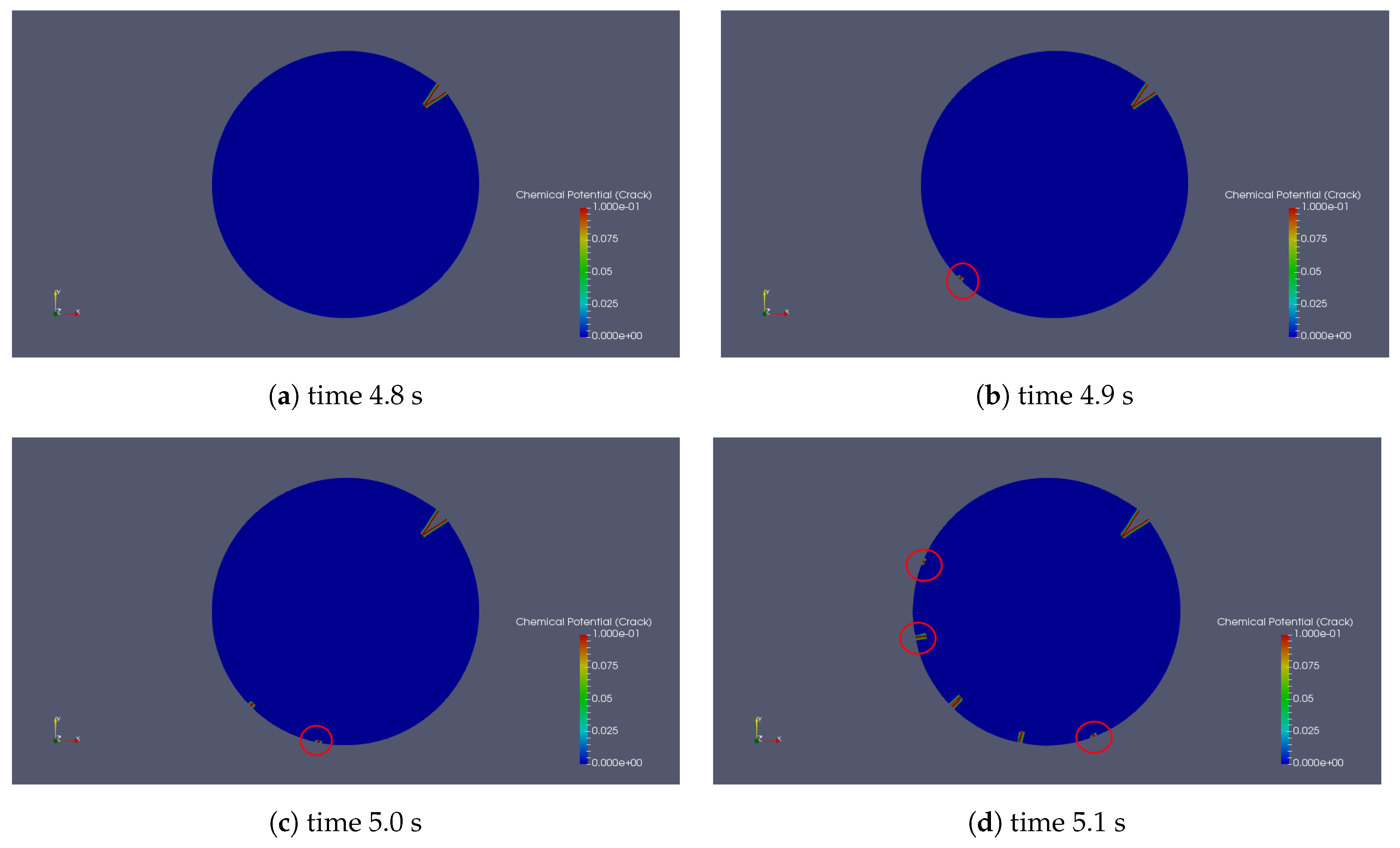
2.2. Crack Nucleation
3. Discussion
- The higher the ultimate strength of the shell, the fewer the cracks which nucleate.
- The higher the shear modulus of the shell, the more cracks which nucleate.
- The higher the shear modulus of the middle part of the particle, the fewer the cracks which nucleate.
- The distribution of nucleations is roughly symmetric about the diameter crossing the initial crack.
4. Methods
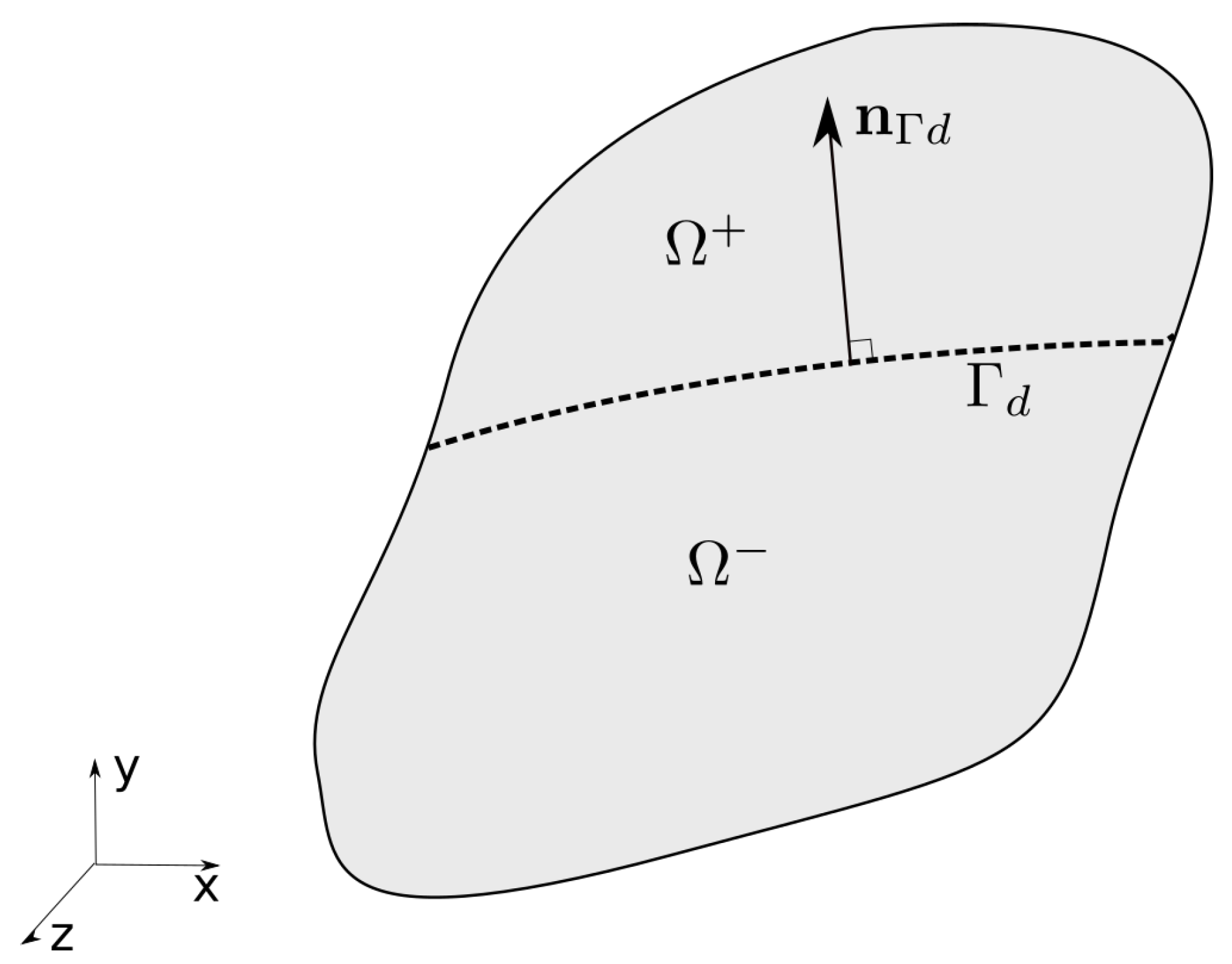
4.1. Kinematic Relations
4.2. Balance Equations
4.3. Swelling Behaviours
4.4. Nucleation Mechanism
4.5. Crack Propagation Mechanism
4.6. Constitutive Equation
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tanaka, T. Phase Transitions of Gels. In Polyelectrolyte Gels; American Chemical Society: Washington, WA, USA, 1992; Chapter 1; pp. 1–21. [Google Scholar]
- Ikeda-Fukazawa, T.; Ikeda, N.; Tabata, M.; Hattori, M.; Aizawa, M.; Yunoki, S.; Sekine, Y. Effects of crosslinker density on the polymer network structure in poly- N, N -dimethylacrylamide hydrogels. J. Polym. Sci. Pol. Phys. 2013, 51, 1017–1027. [Google Scholar] [CrossRef]
- Saunders, J.R.; Moussa, W. Dynamic mechanical properties and swelling of UV-photopolymerized anionic hydrogels. J. Polym. Sci. Pol. Phys. 2012, 50, 1198–1208. [Google Scholar] [CrossRef]
- Baumberger, T.; Caroli, C.; Martina, D. Solvent control of crack dynamics in a reversible hydrogel. Nat. Mater. 2006, 5, 552–555. [Google Scholar] [CrossRef]
- Tanaka, Y.; Shimazaki, R.; Yano, S.; Yoshida, G.; Yamaguchi, T. Solvent effects on the fracture of chemically crosslinked gels. Soft Matter 2016, 12, 8135–8142. [Google Scholar] [CrossRef]
- Fossum, R.D.; Schmidt, M.; Meyer, A. Absorbent Structures Comprising Coated Water-Swellable Material. U.S. Patent 7517586B2, 14 April 2009. [Google Scholar]
- Cervera, M.; Oliver, J.; Herrero, E.; Onate, E. A computational model for progressive cracking in large dams due to the swelling of concrete. Eng. Fract. Mech. 1990, 35, 573–585. [Google Scholar] [CrossRef]
- Zhang, J.; An, Y.; Yazzie, K.; Chawla, N.; Jiang, H. Finite element simulation of swelling-induced crack healing in gels. Soft Matter 2012, 8, 8107. [Google Scholar] [CrossRef]
- Guo, J.; Luo, J.; Xiao, Z. On the opening profile and near tip fields of an interface crack between a polymeric hydrogel and a rigid substrate. Eng. Fract. Mech. 2016, 153, 91–102. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Wells, G.; Sluys, L. A new method for modelling cohesive cracks using finite elements. Int. J. Numer. Meth. Eng. 2001, 50, 2667–2682. [Google Scholar] [CrossRef]
- Leonhart, D.; Meschke, G. Extended Finite Element Method for hygro-mechanical analysis of crack propagation in porous materials. Proc. Appl. Math. Mech. 2011, 11, 161–162. [Google Scholar] [CrossRef]
- Kraaijeveld, F.; Huyghe, J.M.; Remmers, J.J.C.; de Borst, R. Two-Dimensional Mode I Crack Propagation in Saturated Ionized Porous Media Using Partition of Unity Finite Elements. J. Appl. Mech. 2013, 80, 020907. [Google Scholar] [CrossRef]
- Irzal, F.; Remmers, J.J.; Huyghe, J.M.; De Borst, R. A large deformation formulation for fluid flow in a progressively fracturing porous material. Comput. Methods Appl. Mech. Eng. 2013, 256, 29–37. [Google Scholar] [CrossRef][Green Version]
- Remij, E.W.; Remmers, J.J.C.; Huyghe, J.M.; Smeulders, D.M.J. The enhanced local pressure model for the accurate analysis of fluid pressure driven fracture in porous materials. Comput. Methods Appl. Mech. Eng. 2015, 286, 293–312. [Google Scholar] [CrossRef]
- Stolarska, M.; Chopp, D.L.; Mos, N.; Belytschko, T. Modelling crack growth by level sets in the extended finite element method. Int. J. Numer. Meth. Eng. 2001, 51, 943–960. [Google Scholar] [CrossRef]
- Ding, J.; Remmers, J.; Leszczynski, S.; Huyghe, J. Swelling driven crack propagation in large deformation in ionized hydrogel. J. Appl. Mech. 2018, 85, 021007. [Google Scholar] [CrossRef]
- Remmers, J. Discontinuities in Materials and Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2006. [Google Scholar]
- Wilson, W.; Huyghe, J.M.; van Donkelaar, C.C. A composition-based cartilage model for the assessment of compositional changes during cartilage damage and adaptation. Osteoarthr. Cartil. 2006, 14, 554–560. [Google Scholar] [CrossRef] [PubMed]
- Wilson, W.; Huyghe, J.M.; Van Donkelaar, C.C. Depth-dependent compressive equilibrium properties of articular cartilage explained by its composition. Biomech. Model. Mech. 2007, 6, 43–53. [Google Scholar] [CrossRef] [PubMed]


| Name | Symbol | Value |
|---|---|---|
| Shear modulus (core) | G | MPa |
| Shear modulus (middle) | G | MPa |
| Shear modulus (shell) | G | MPa |
| Intrinsic permeability | 1.0 × 10 mm | |
| Fluid dynamic viscosity | 1.0 × 10 MPas | |
| Porosity | 0.83 | |
| Ultimate strength (core) | MPa | |
| Ultimate strength (middle) | MPa | |
| Ultimate strength (shell) | MPa | |
| Toughness | N/mm | |
| Gas constant | R | 8.3145 J·molK |
| Temperature | T | 293.0 K |
| Initial fixed charge density | 332.0 × 10 mmoleq/mm | |
| External salt concentration | 154.0 × 10 mmol/mm |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, J.; Remij, E.W.; Remmers, J.J.C.; Huyghe, J.M. Effects of Intrinsic Properties on Fracture Nucleation and Propagation in Swelling Hydrogels. Polymers 2019, 11, 926. https://doi.org/10.3390/polym11050926
Ding J, Remij EW, Remmers JJC, Huyghe JM. Effects of Intrinsic Properties on Fracture Nucleation and Propagation in Swelling Hydrogels. Polymers. 2019; 11(5):926. https://doi.org/10.3390/polym11050926
Chicago/Turabian StyleDing, Jingqian, Ernst W. Remij, Joris J. C. Remmers, and Jacques M. Huyghe. 2019. "Effects of Intrinsic Properties on Fracture Nucleation and Propagation in Swelling Hydrogels" Polymers 11, no. 5: 926. https://doi.org/10.3390/polym11050926
APA StyleDing, J., Remij, E. W., Remmers, J. J. C., & Huyghe, J. M. (2019). Effects of Intrinsic Properties on Fracture Nucleation and Propagation in Swelling Hydrogels. Polymers, 11(5), 926. https://doi.org/10.3390/polym11050926





