Copper and Nickel Coating of Carbon Fiber for Thermally and Electrically Conductive Fiber Reinforced Composites
Abstract
1. Introduction
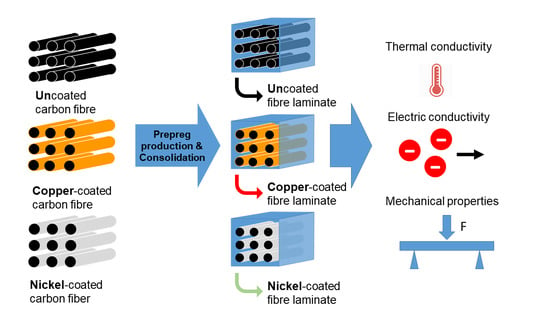
2. Production and Characterization Methods
2.1. Materials
2.2. Resin Preparation and Curing
2.3. Prepreg Production and Consolidation
2.4. Determination of Fiber Volume Content
2.5. Morphological Characterization
2.6. Thermal and Electrical Conductivity Measurements
2.7. Flexural Modulus and Strength
3. Results and Discussions
3.1. Morphology of Metal Coated Fibers and Laminates
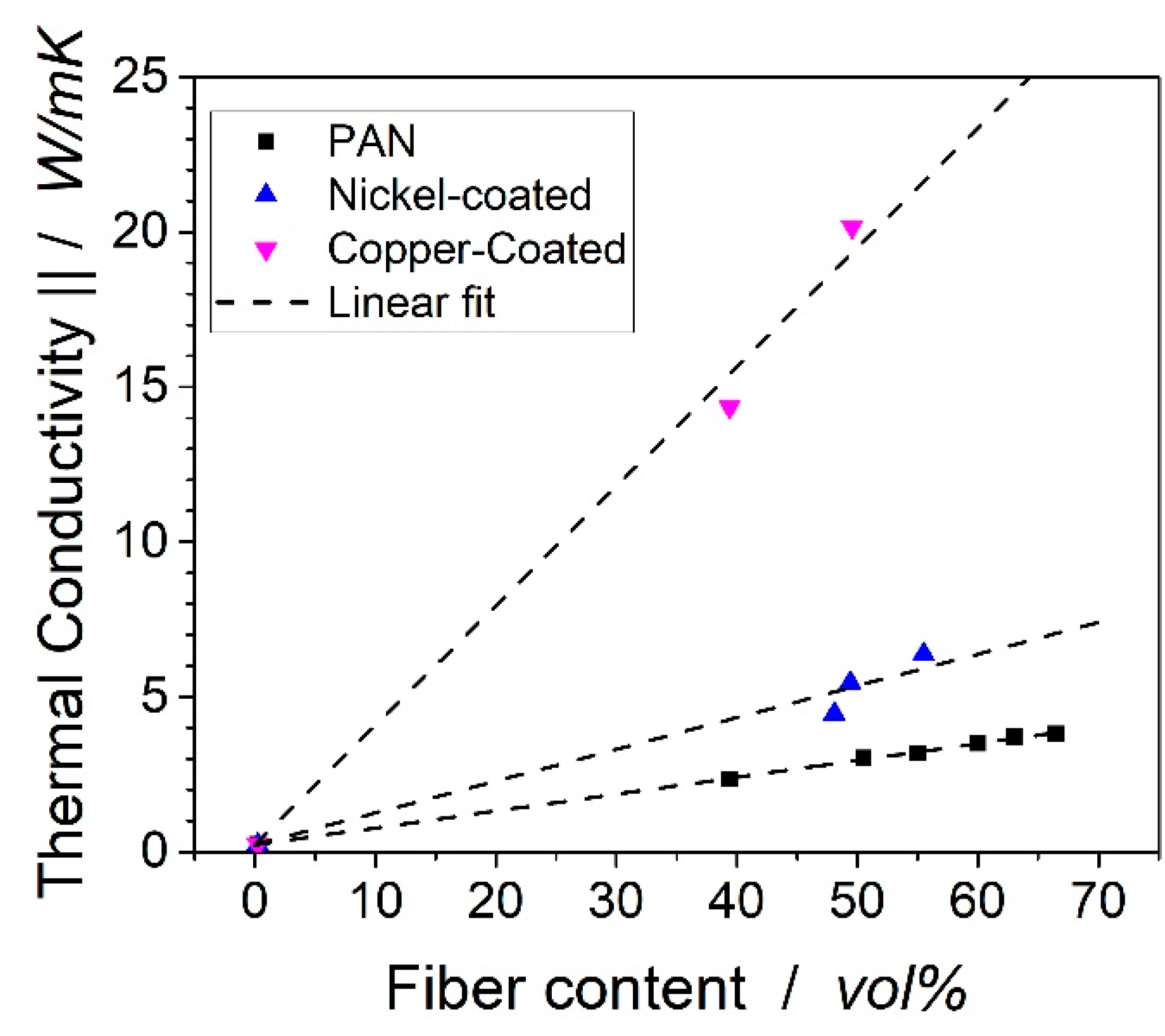
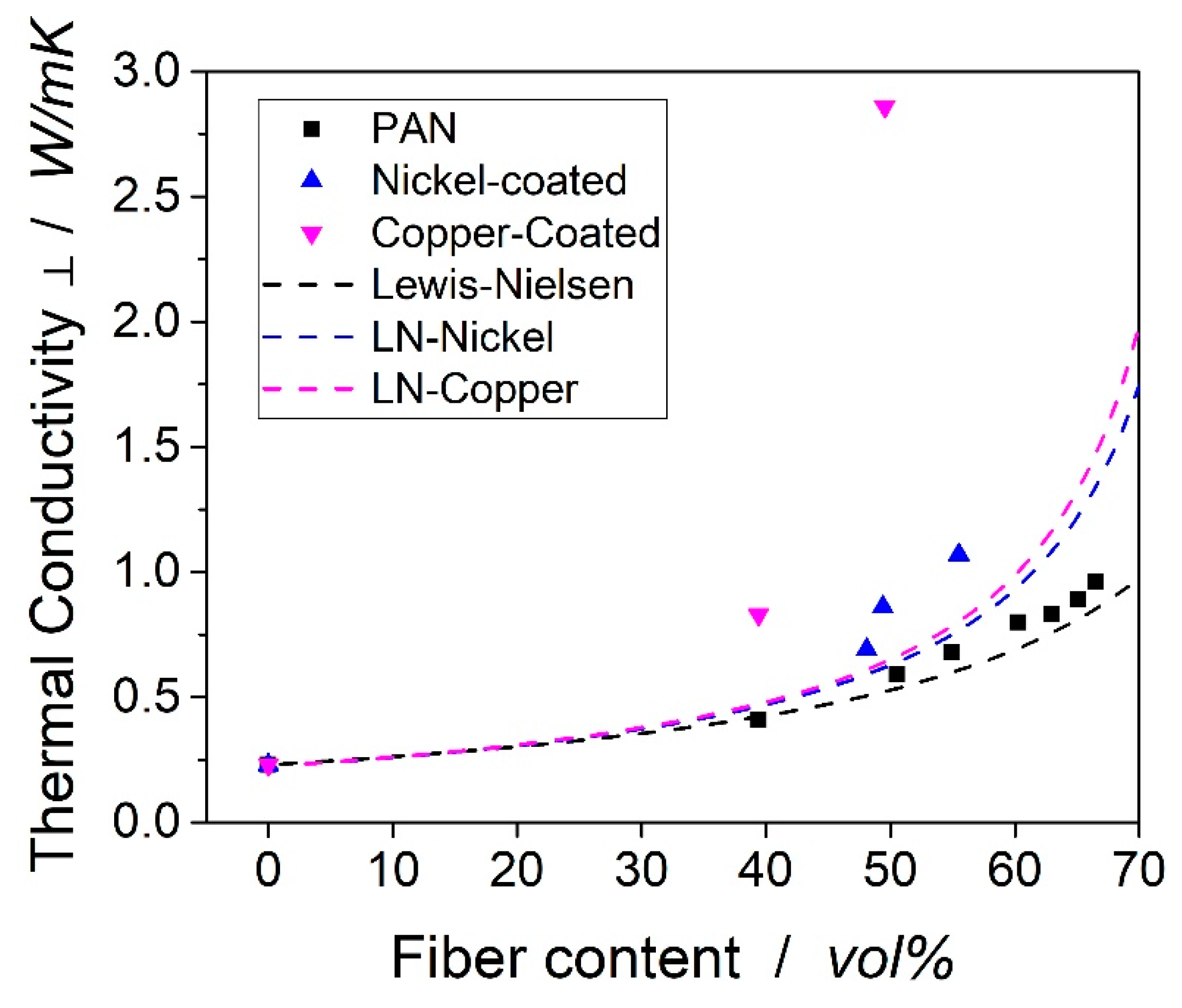
3.2. Thermal Conductivity of Laminates
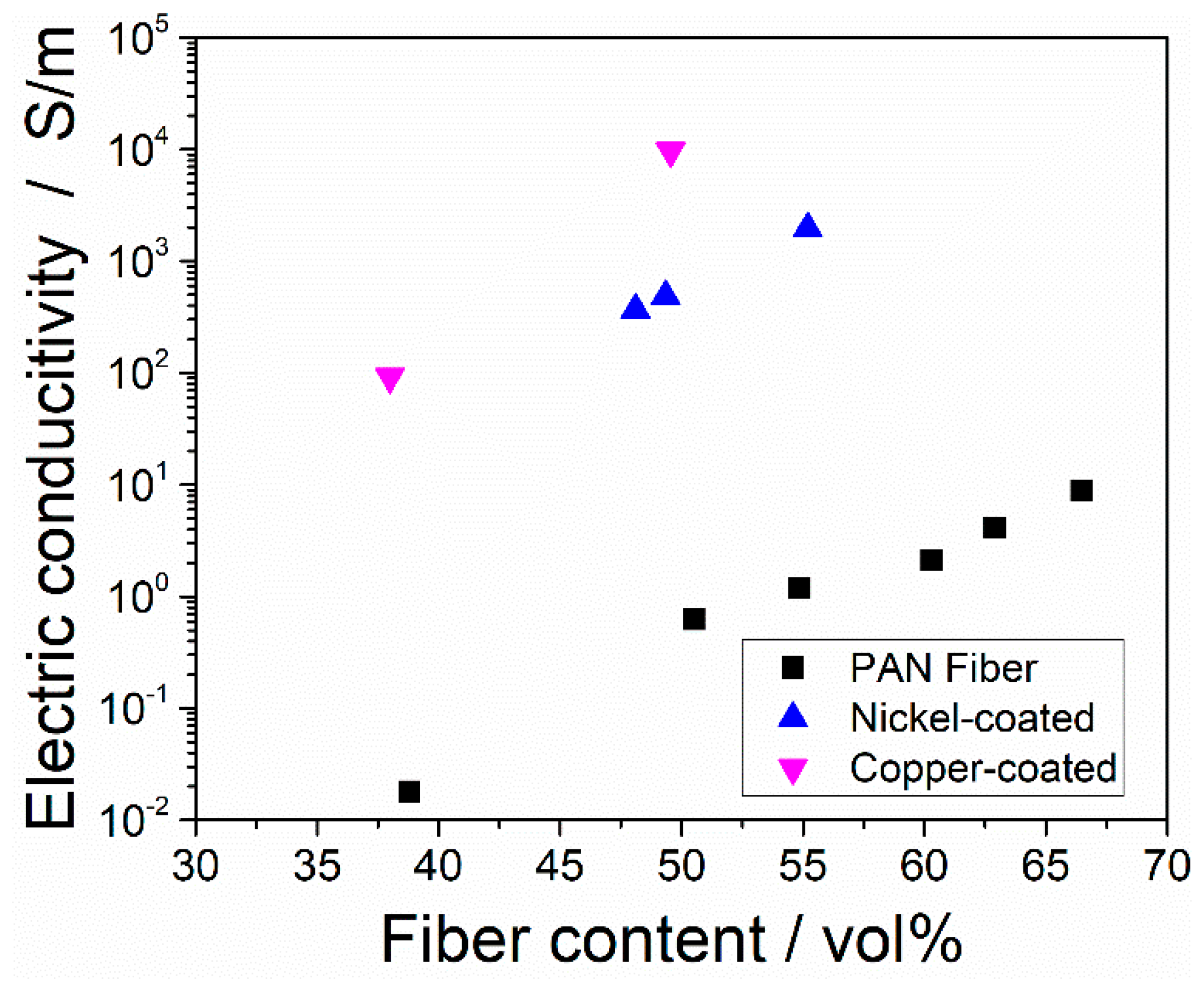
3.3. Electric Conductivity
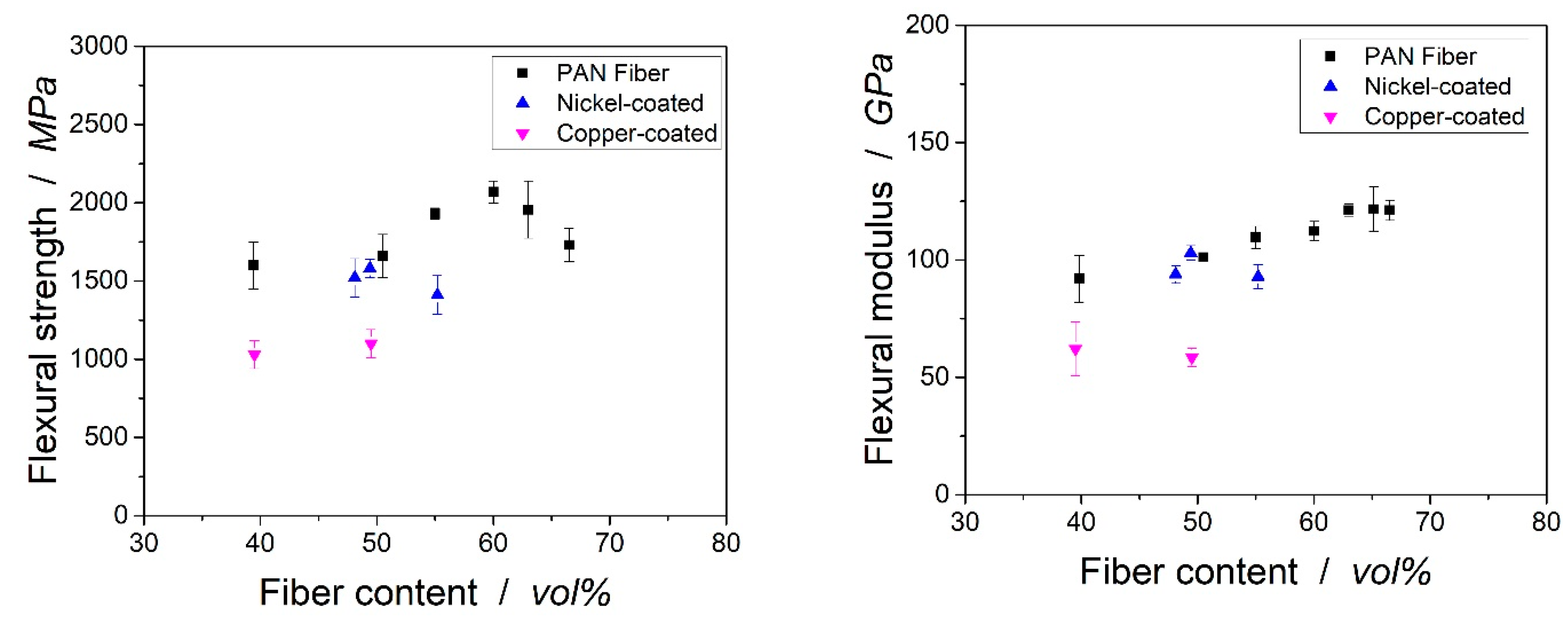
3.4. Mechanical Properties
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Balandin, A.A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Shahil, K.M.; Goyal, V.; Balandin, A. Thermal Properties of Graphene: Applications in Thermal Interface Materials. In The Electrochemical Society; ECS Transactions: Pennington, NJ, USA, 2011; pp. 193–199. [Google Scholar]
- Yan, H.; Tang, Y.; Long, W.; Li, Y. Enhanced thermal conductivity in polymer composites with aligned graphene nanosheets. J. Mater. Sci. 2014, 49, 5256–5264. [Google Scholar] [CrossRef]
- Guo, W.; Chen, G. Fabrication of graphene/epoxy resin composites with much enhanced thermal conductivity via ball milling technique. J. Appl. Polym. Sci. 2014, 131. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Nijenhuis, K. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Burger, N.; Laachachi, A.; Ferriol, M.; Lutz, M.; Toniazzo, V.; Ruch, D. Review of thermal conductivity in composites: Mechanisms, parameters and theory. Prog. Polym. Sci. 2016, 61, 1–28. [Google Scholar] [CrossRef]
- Ng, H.Y.; Lu, X.; Lau, S.K. Thermal conductivity of boron nitride-filled thermoplastics: Effect of filler characteristics and composite processing conditions. Polym. Compos. 2005, 26, 778–790. [Google Scholar] [CrossRef]
- Boudenne, A.; Ibos, L.; Fois, M.; Majesté, J.C.; Géhin, E. Electrical and thermal behavior of polypropylene filled with copper particles. Compos. Part A Appl. Sci. Manuf. 2005, 36, 1545–1554. [Google Scholar] [CrossRef]
- Pargi, M.N.F.; Chong, Y.T.; Teh, P.L.; Yeoh, C.K. The effect of particle size on the electrical and thermal properties of recycled copper filled polyester composites. Int. J. Mater. Eng. Innov. 2013, 4, 291–301. [Google Scholar] [CrossRef]
- Tekce, H.S.; Kumlutas, D.; Tavman, I.H. Effect of Particle Shape on Thermal Conductivity of Copper Reinforced Polymer Composites. J. Reinf. Plast. Compos. 2007, 26, 113–121. [Google Scholar] [CrossRef]
- Zhang, D.; Ye, L.; Deng, S.; Zhang, J.; Tang, Y.; Chen, Y. CF/EP composite laminates with carbon black and copper chloride for improved electrical conductivity and interlaminar fracture toughness. Compos. Sci. Technol. 2012, 72, 412–420. [Google Scholar] [CrossRef]
- Li, J.; Kim, J.-K.; Lung Sham, M. Conductive graphite nanoplatelet/epoxy nanocomposites: Effects of exfoliation and UV/ozone treatment of graphite. Scr. Mater. 2005, 53, 235–240. [Google Scholar] [CrossRef]
- Fu, Y.-X.; He, Z.-X.; Mo, D.-C.; Lu, S.-S. Thermal conductivity enhancement with different fillers for epoxy resin adhesives. Appl. Therm. Eng. 2014, 66, 493–498. [Google Scholar] [CrossRef]
- Debelak, B.; Lafdi, K. Use of exfoliated graphite filler to enhance polymer physical properties. Carbon 2007, 45, 1727–1734. [Google Scholar] [CrossRef]
- Raman, C.; Meneghetti, P. Boron nitride finds new applications in thermoplastic compounds. Plast. Addit. Compd. 2008, 10, 26–31. [Google Scholar] [CrossRef]
- Yuan, F.-Y.; Zhang, H.-B.; Li, X.; Li, X.-Z.; Yu, Z.-Z. Synergistic effect of boron nitride flakes and tetrapod-shaped ZnO whiskers on the thermal conductivity of electrically insulating phenol formaldehyde composites. Compos. Part A Appl. Sci. Manuf. 2013, 53, 137–144. [Google Scholar] [CrossRef]
- Zhou, W.; Qi, S.; An, Q.; Zhao, H.; Liu, N. Thermal conductivity of boron nitride reinforced polyethylene composites. Mater. Res. Bull. 2007, 42, 1863–1873. [Google Scholar] [CrossRef]
- Huang, H.S.; Ganguli, S.; Roy, A.K. Prediction of the transverse thermal conductivity of pitch-based carbon fibers. J. Compos. Mater. 2013, 48, 1383–1390. [Google Scholar] [CrossRef]
- Jiang, Z.; Ouyang, T.; Yao, X.; Fei, Y. The effect of the spinning conditions on the structure of mesophase pitch-based carbon fibers by Taguchi method. Carbon Lett. 2016, 19, 89–98. [Google Scholar] [CrossRef]
- Qin, X.; Lu, Y.; Xiao, H.; Wen, Y.; Yu, T. A comparison of the effect of graphitization on microstructures and properties of polyacrylonitrile and mesophase pitch-based carbon fibers. Carbon 2012, 50, 4459–4469. [Google Scholar] [CrossRef]
- Evans, R.E.; Hall, D.E.; Luxon, B.A. Nickel coated graphite fiber conductive composites. In Proceedings of the SAMPE Conference, München, Germany, 7–10 April 1986; p. 31. [Google Scholar]
- Yu, S.; Park, B.-I.; Park, C.; Hong, S.M.; Han, T.H.; Koo, C.M. RTA-treated carbon fiber/copper core/shell hybrid for thermally conductive composites. ACS Appl. Mater. Interfaces 2014, 6, 7498–7503. [Google Scholar] [CrossRef] [PubMed]
- Böttger-Hiller, F.; Kleiber, J.; Böttger, T.; Lampke, T. Multimetallic Electrodeposition on Carbon Fibers. IOP Conf. Ser. Mater. Sci. Eng. 2016, 118, 12027. [Google Scholar] [CrossRef]
- Böttger-Hiller, F.; Nestler, K.; Zeidler, H.; Glowa, G.; Lampke, T. Plasma electrolytic polishing of metalized carbon fibers. AIMS Mater. Sci. 2016, 3, 260–269. [Google Scholar] [CrossRef]
- Monkiewitsch, M. Faservolumengehaltsbestimmung mittels Thermogravimetrischer Analyse (TGA): Methodendarstellung und Ergebnisse eines Ringversuchs als Grundlage für einen Normentwurf; Industrievereinigung Verstärkte Kunststoffe e.V.: Frankfurt, Germany, 2018. [Google Scholar]
- Bard, S.; Schönl, F.; Demleitner, M.; Altstädt, V. Influence of Fiber Volume Content on Thermal Conductivity in Transverse and Fiber Direction of Carbon Fiber-Reinforced Epoxy Laminates. Materials 2019, 12, 1084. [Google Scholar] [CrossRef]
- Baller, J.; Becker, N.; Ziehmer, M.; Thomassey, M.; Zielinski, B.; Müller, U.; Sanctuary, R. Interactions between silica nanoparticles and an epoxy resin before and during network formation. Polymer 2009, 50, 3211–3219. [Google Scholar] [CrossRef]
- Rana, S.; Fangueiro, R. Fibrous and Textile Materials for Composite Applications; Springer: Singapore, 2016. [Google Scholar]
- Nielsen, L.E. Generalized Equation for the Elastic Moduli of Composite Materials. J. Appl. Phys. 1970, 41, 4626. [Google Scholar] [CrossRef]
- Hiroshi, H.; Minoru, T. Equivalent inclusion method for steady state heat conduction in composites. Int. J. Eng. Sci. 1986, 24, 1159–1172. [Google Scholar] [CrossRef]
- Springer, G.S.; Tsai, S.W. Thermal Conductivities of Unidirectional Materials. J. Compos. Mater. 1967, 1, 166–173. [Google Scholar] [CrossRef]
- Rolfes, R.; Hammerschmidt, U. Transverse thermal conductivity of CFRP laminates: A numerical and experimental validation of approximation formulae. Compos. Sci. Technol. 1995, 54, 45–54. [Google Scholar] [CrossRef]
- Zhang, G. Thermal Transport in Carbon-Based Nanomaterials; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Dong, K.; Liu, K.; Zhang, Q.; Gu, B.; Sun, B. Experimental and numerical analyses on the thermal conductive behaviors of carbon fiber/epoxy plain woven composites. Int. J. Heat Mass Transf. 2016, 102, 501–517. [Google Scholar] [CrossRef]
- Mottram, J.T.; Taylor, R. Thermal conductivity of fibre-phenolic resin composites. Part I: Thermal diffusivity measurements. Compos. Sci. Technol. 1987, 29, 189–210. [Google Scholar] [CrossRef]
- King, J.A.; Lopez Gaxiola, D.; Johnson, B.A.; Keith, J.M. Thermal Conductivity of Carbon-filled Polypropylene-based Resins. J. Compos. Mater. 2010, 44, 839–855. [Google Scholar] [CrossRef]
- Heinle, C.; Brocka, Z.; Hülder, G.; Ehrenstein, G.W.; Osswald, T.A. Thermal conductivity of polymers filled with non-isometric fillers: A process dependent, anisotropic property. In Proceedings of the 67th Annual Technical Conference of the Society of Plastics Engineers (ANTEC), Chicago, IL, USA, 22–24 June 2009. [Google Scholar]
- Progelhof, R.C.; Throne, J.L.; Ruetsch, R.R. Methods for predicting the thermal conductivity of composite systems: A review. Polym. Eng. Sci. 1976, 16, 615–625. [Google Scholar] [CrossRef]
- Pal, R. On the Lewis-Nielsen model for thermal/electrical conductivity of composites. Compos. Part A Appl. Sci. Manuf. 2008, 39, 718–726. [Google Scholar] [CrossRef]
- Corcione, C.E.; Frigione, M.; Acierno, D. Rheological characterization of UV-curable epoxy systems: Effects of o-Boehmite nanofillers and a hyperbranched polymeric modifier. J. Appl. Polym. Sci. 2009, 112, 1302–1310. [Google Scholar] [CrossRef]
- Boudenne, A.; Ibos, L.; Candau, Y.; Thomas, S. Handbook of Multiphase Polymer Systems, 1st ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mariani, E.; von Oppen, F. Flexural phonons in free-standing graphene. Phys. Rev. Lett. 2008, 100, 76801. [Google Scholar] [CrossRef]
- Minnich, A.J. Determining phonon mean free paths from observations of quasiballistic thermal transport. Phys. Rev. Lett. 2012, 109, 205901. [Google Scholar] [CrossRef]






| Fiber | Manufacturer | Tensile Strength | Tensile Modulus |
|---|---|---|---|
| - | - | MPa | GPa |
| HTS40 | TohoTenax | 4620 | 239 |
| HTS40_NC (Nickel coated) | TohoTenax | 2900 | 230 |
| Grafil_34700 (Copper-coated) | Inca-Fiber GmbH | n.a. | n.a. |
| Sample | Heat Capacity | Density | Diffusivity ⊥ | Diffusivity || |
|---|---|---|---|---|
| - | J/gK | g/cm³ | m²/s | m²/s |
| PAN_39.4 | 1.053 | 1.39 ± 0.010 | 0.29 ± 0.005 | 1.60 ± 0.005 |
| PAN_50.5 | 1.037 | 1.45 ± 0.012 | 0.39 ± 0.003 | 2.01 ± 0.004 |
| PAN_54.9 | 1.030 | 1.47 ± 0.009 | 0.45 ± 0.004 | 2.18 ± 0.006 |
| PAN_60.3 | 1.023 | 1.50 ± 0.014 | 0.51 ± 0.007 | 2.28 ± 0.007 |
| PAN_62.9 | 1.019 | 1.51 ± 0.008 | 0.54 ± 0.005 | 2.40 ± 0.003 |
| PAN_66.5 | 1.014 | 1.53 ± 0.011 | 0.61 ± 0.008 | 2.45 ± 0.004 |
| NC_48.1 | 0.992 | 1.90 ± 0.015 | 0.37 ± 0.003 | 2.36 ± 0.003 |
| NC_49.4 | 0.989 | 1.92 ± 0.090 | 0.45 ± 0.002 | 2.87 ± 0.005 |
| NC_55.2 | 0.974 | 2.01 ± 0.007 | 0.55 ± 0.003 | 3.26 ± 0.003 |
| CC_39.5 | 1.019 | 2.33 ± 0.012 | 0.35 ± 0.005 | 6.04 ± 0.004 |
| CC_49.5 | 0.991 | 2.67 ± 0.007 | 1.075 ± 0.003 | 7.62 ± 0.006 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bard, S.; Schönl, F.; Demleitner, M.; Altstädt, V. Copper and Nickel Coating of Carbon Fiber for Thermally and Electrically Conductive Fiber Reinforced Composites. Polymers 2019, 11, 823. https://doi.org/10.3390/polym11050823
Bard S, Schönl F, Demleitner M, Altstädt V. Copper and Nickel Coating of Carbon Fiber for Thermally and Electrically Conductive Fiber Reinforced Composites. Polymers. 2019; 11(5):823. https://doi.org/10.3390/polym11050823
Chicago/Turabian StyleBard, Simon, Florian Schönl, Martin Demleitner, and Volker Altstädt. 2019. "Copper and Nickel Coating of Carbon Fiber for Thermally and Electrically Conductive Fiber Reinforced Composites" Polymers 11, no. 5: 823. https://doi.org/10.3390/polym11050823
APA StyleBard, S., Schönl, F., Demleitner, M., & Altstädt, V. (2019). Copper and Nickel Coating of Carbon Fiber for Thermally and Electrically Conductive Fiber Reinforced Composites. Polymers, 11(5), 823. https://doi.org/10.3390/polym11050823