Slip-Spring and Kink Dynamics Models for Fast Extensional Flow of Entangled Polymeric Fluids
Abstract
1. Introduction
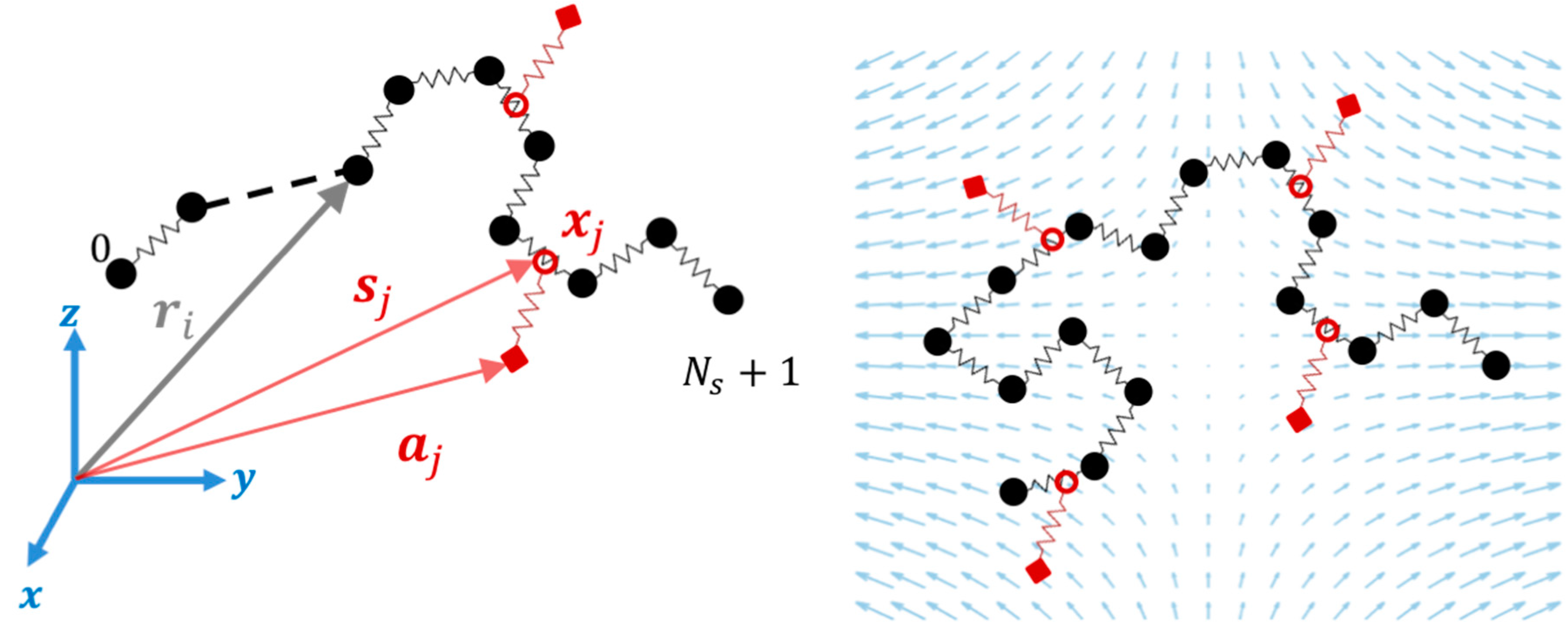
2. Model and Simulation Method
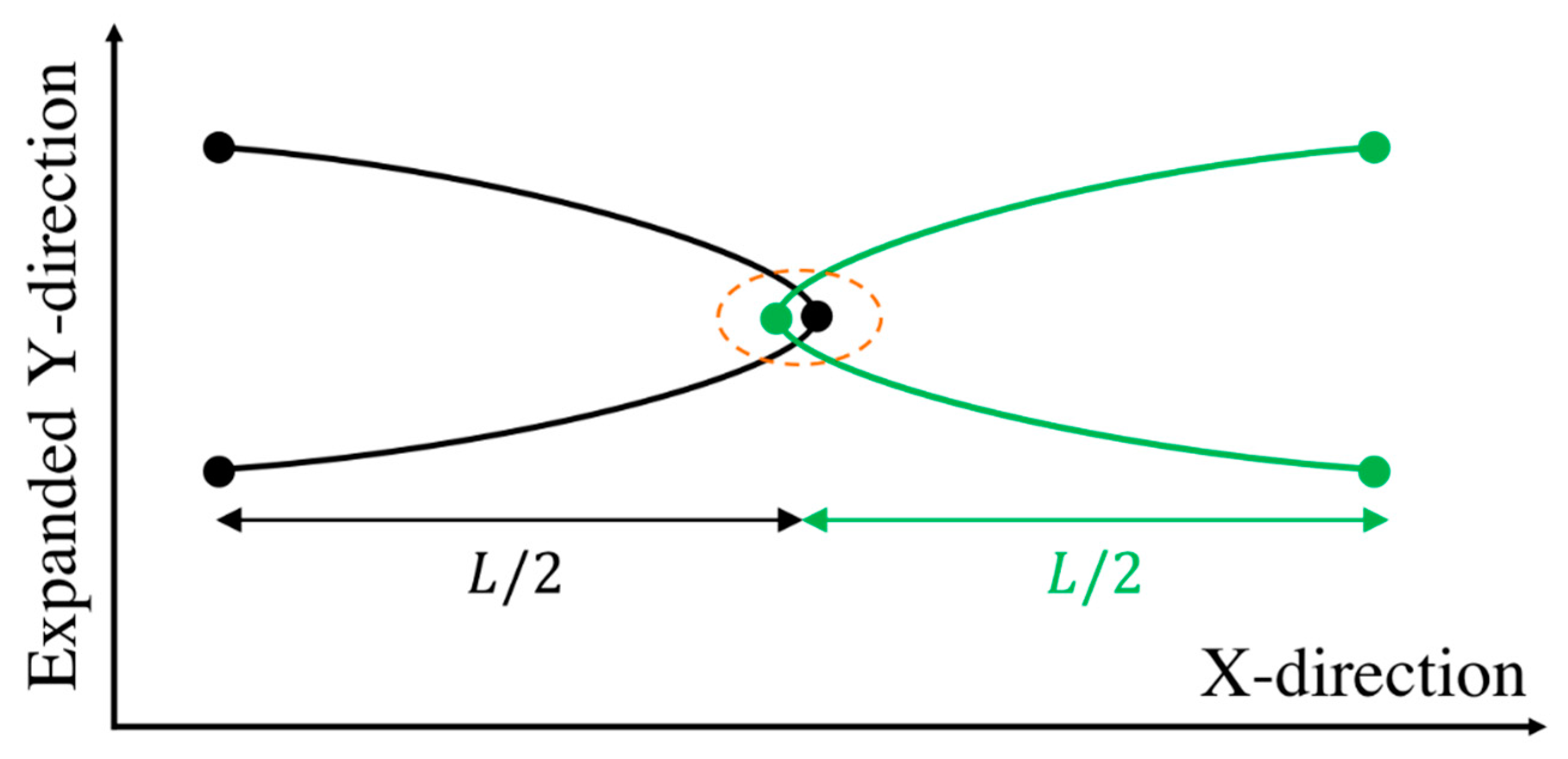
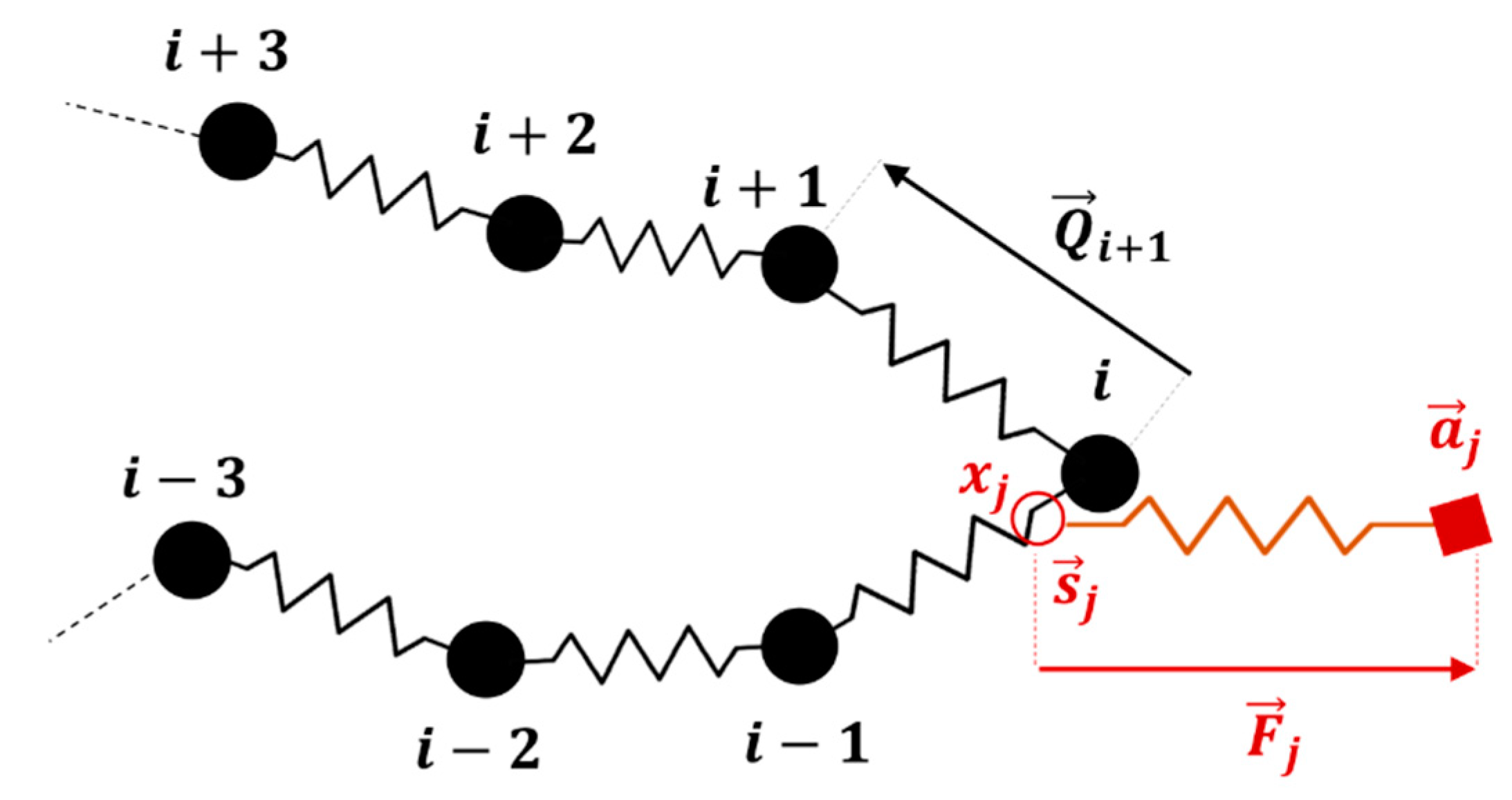
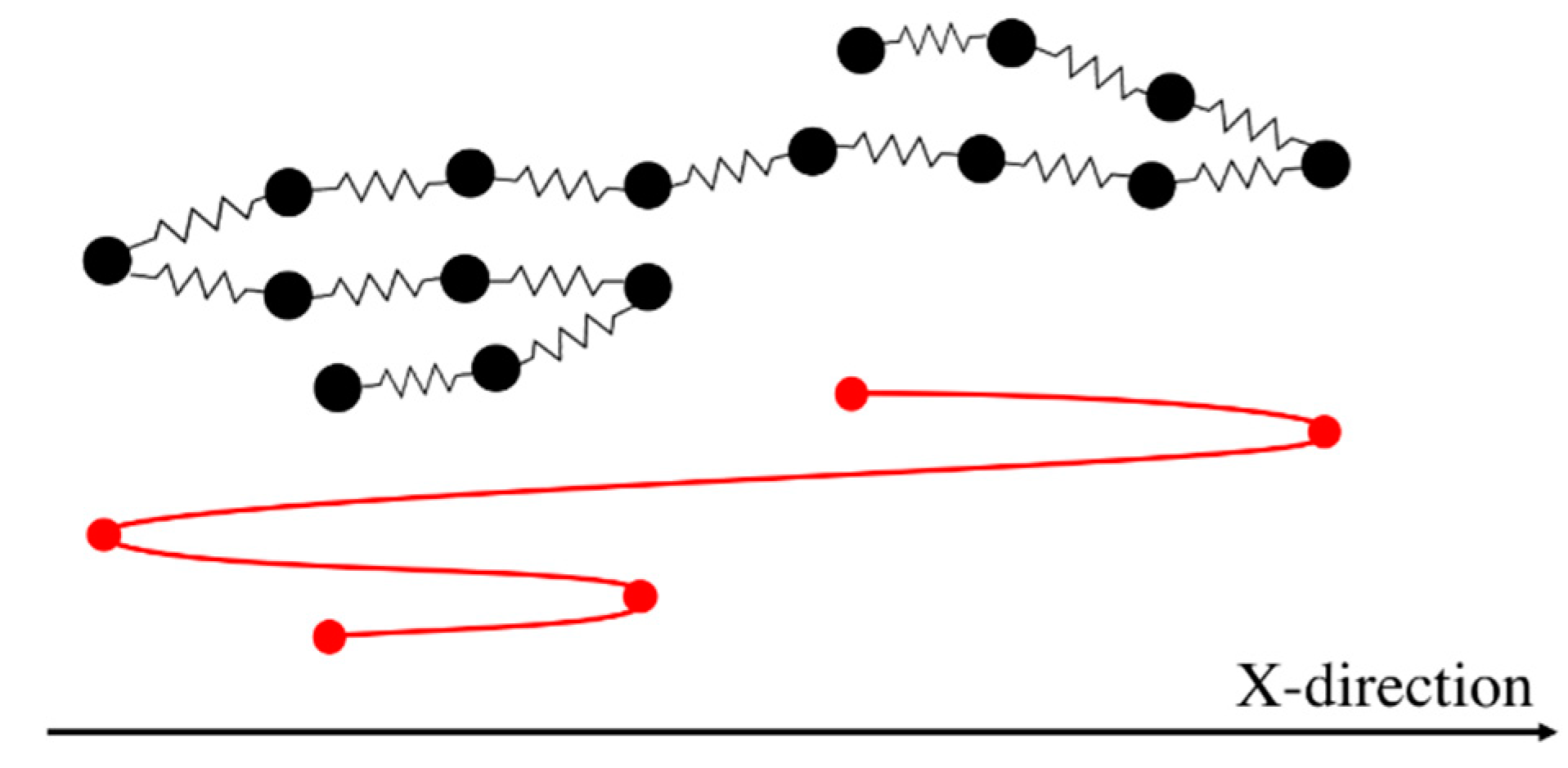
2.1. Kink Dynamics Algorithm
Kink Dynamics Predictions for Entanglement Force
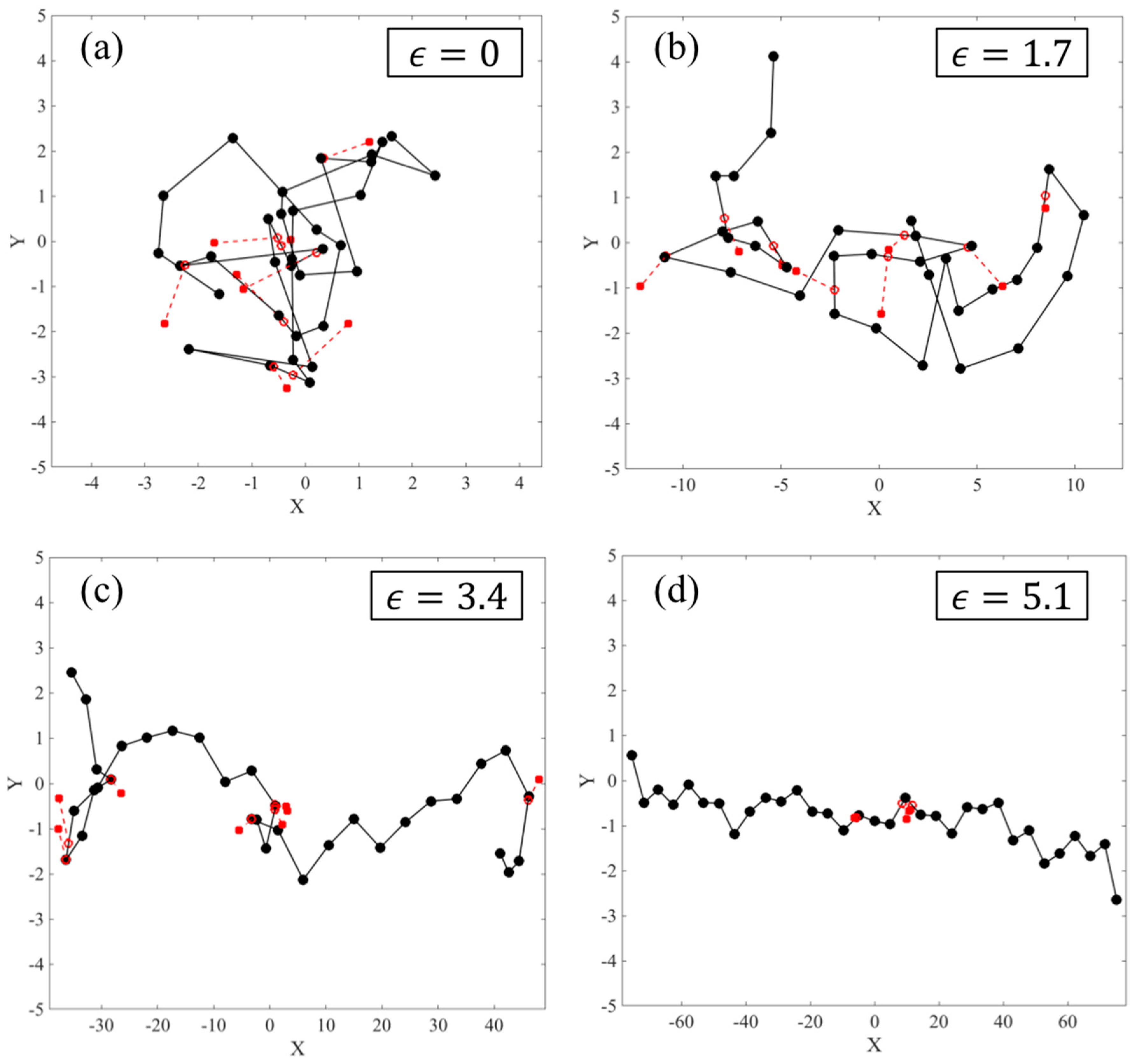
- Under affine motion, immediately after formation of the locally fully extended kinked state, the stress reaches at its final value which does not change during the unraveling of the kinked state to the fully extended state.
- The chain end-to-end distance evolves very similarly under dilute and entangled kink conditions for a specific chain length.
- Using the EKD model, when (a highly entangled system), the tension along the chain at the start of the folded state is almost flat and as the chain unravels, it becomes quadratic after a few Hencky strain units, depending on the length of the chain.
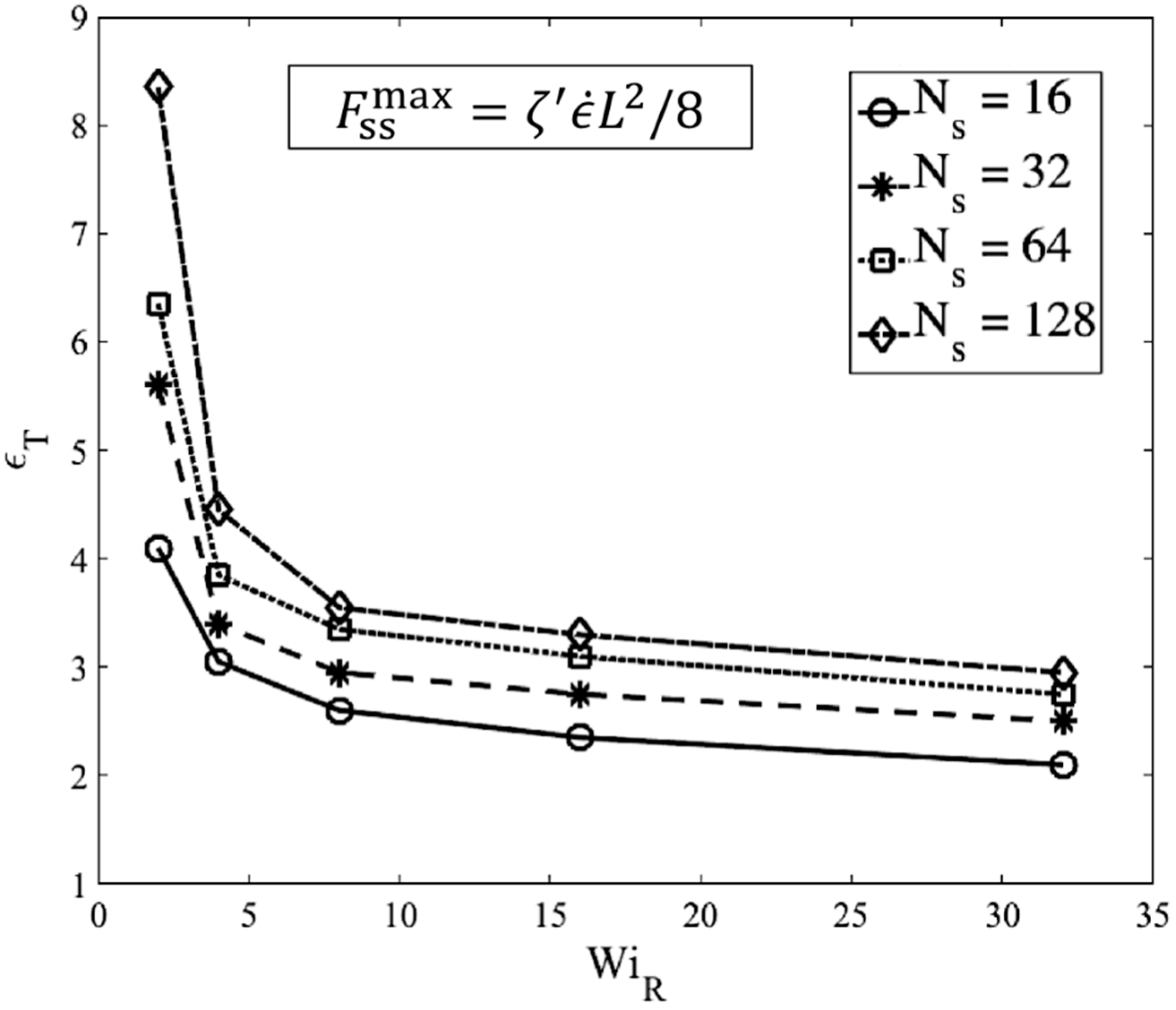
- What is the transition strain () beyond which the EKD results become valid?
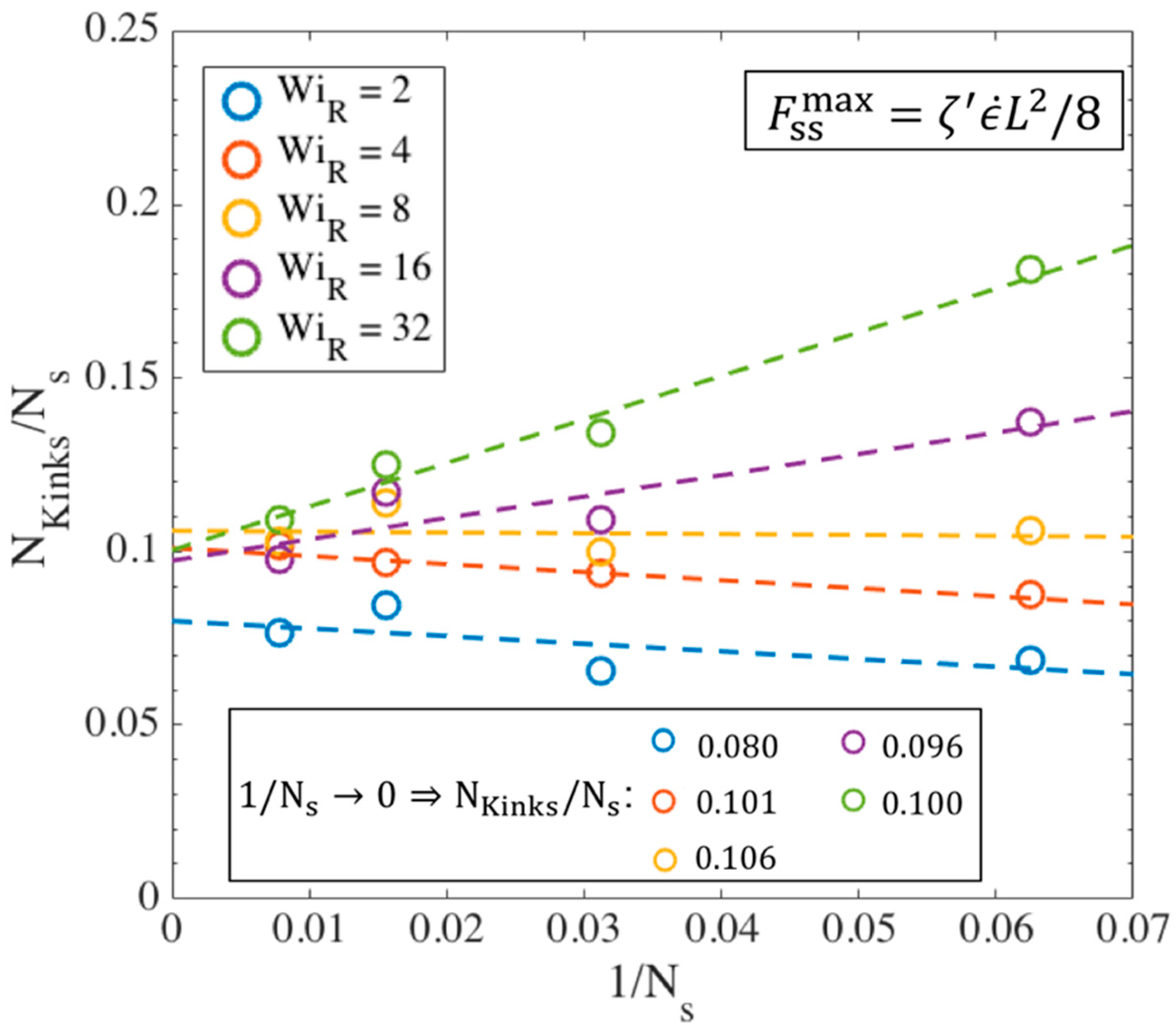
- What is the number of kinks for a chain of arbitrary chain length at the transition strain?
- What is the ratio of the number of entangled to free kinks in an entangled sample?
- What is the distribution of strand lengths between the kinks?
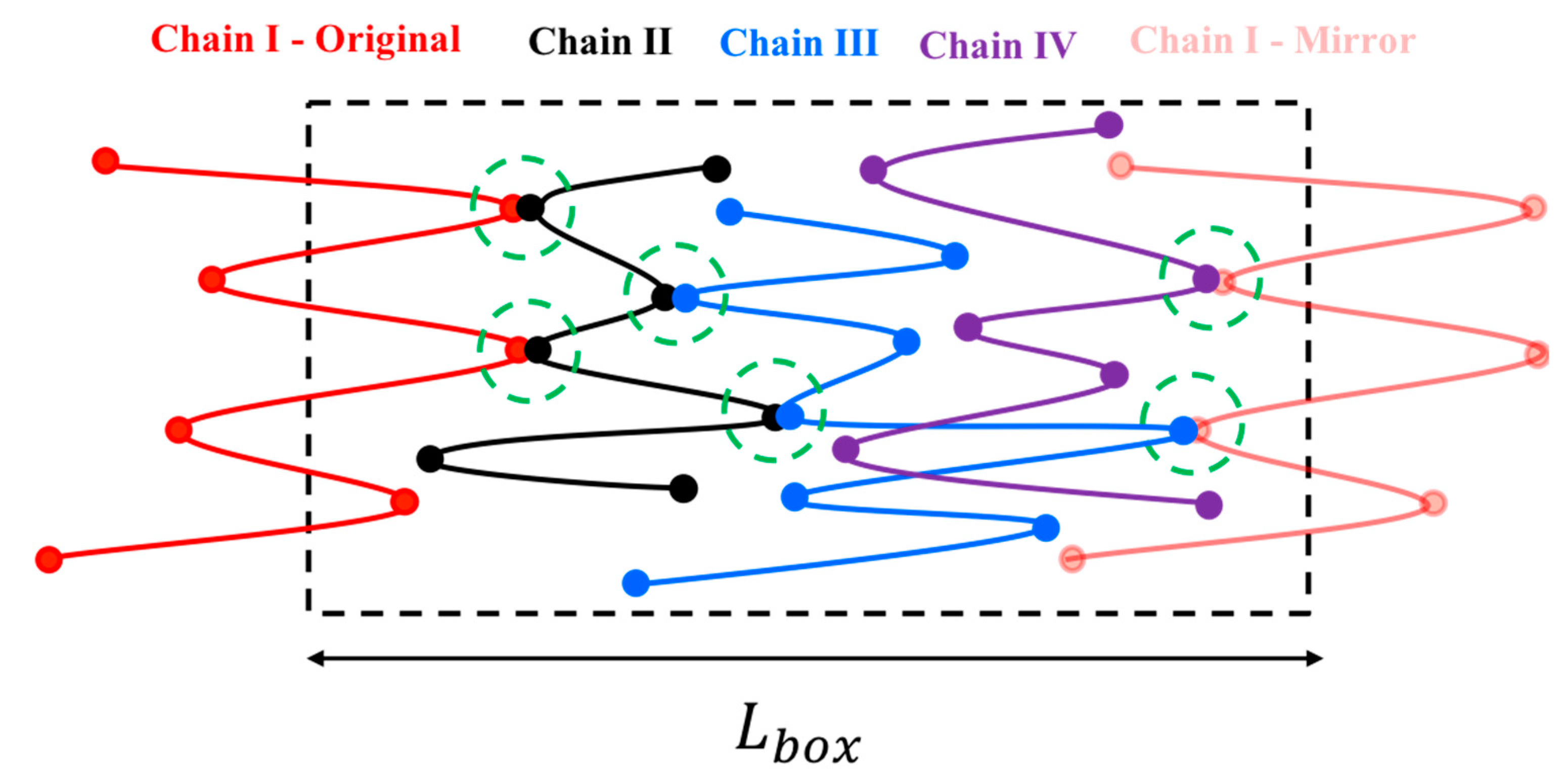
2.2. Slip-Spring Simulations
3. Simulation Results and Discussions
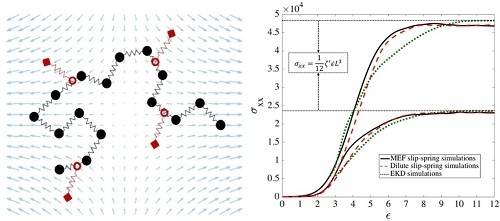
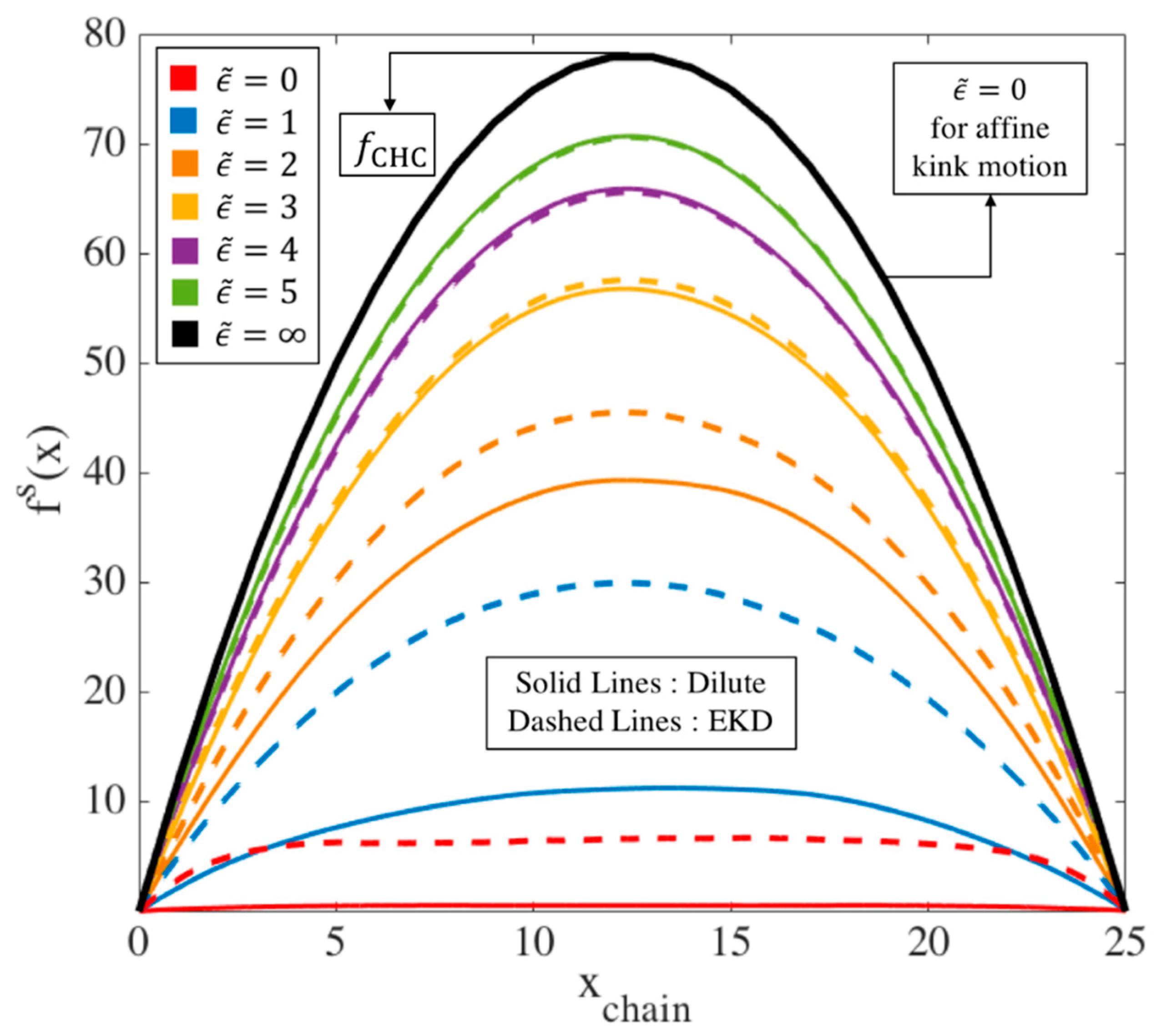
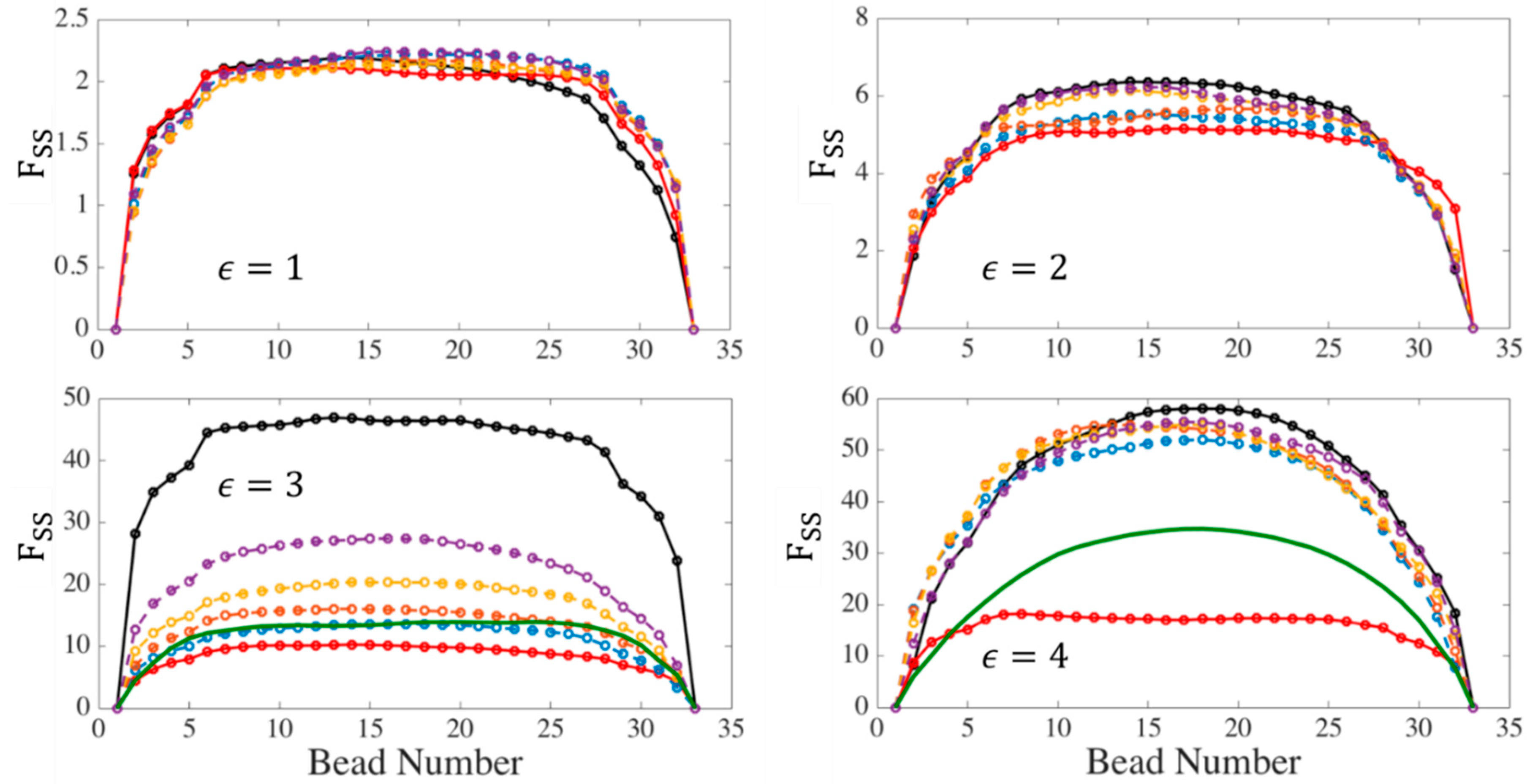
3.1. Comparison of Maximum Entanglement Force (MEF), Two-Chain (TC), Affine Motion (AM) Methods
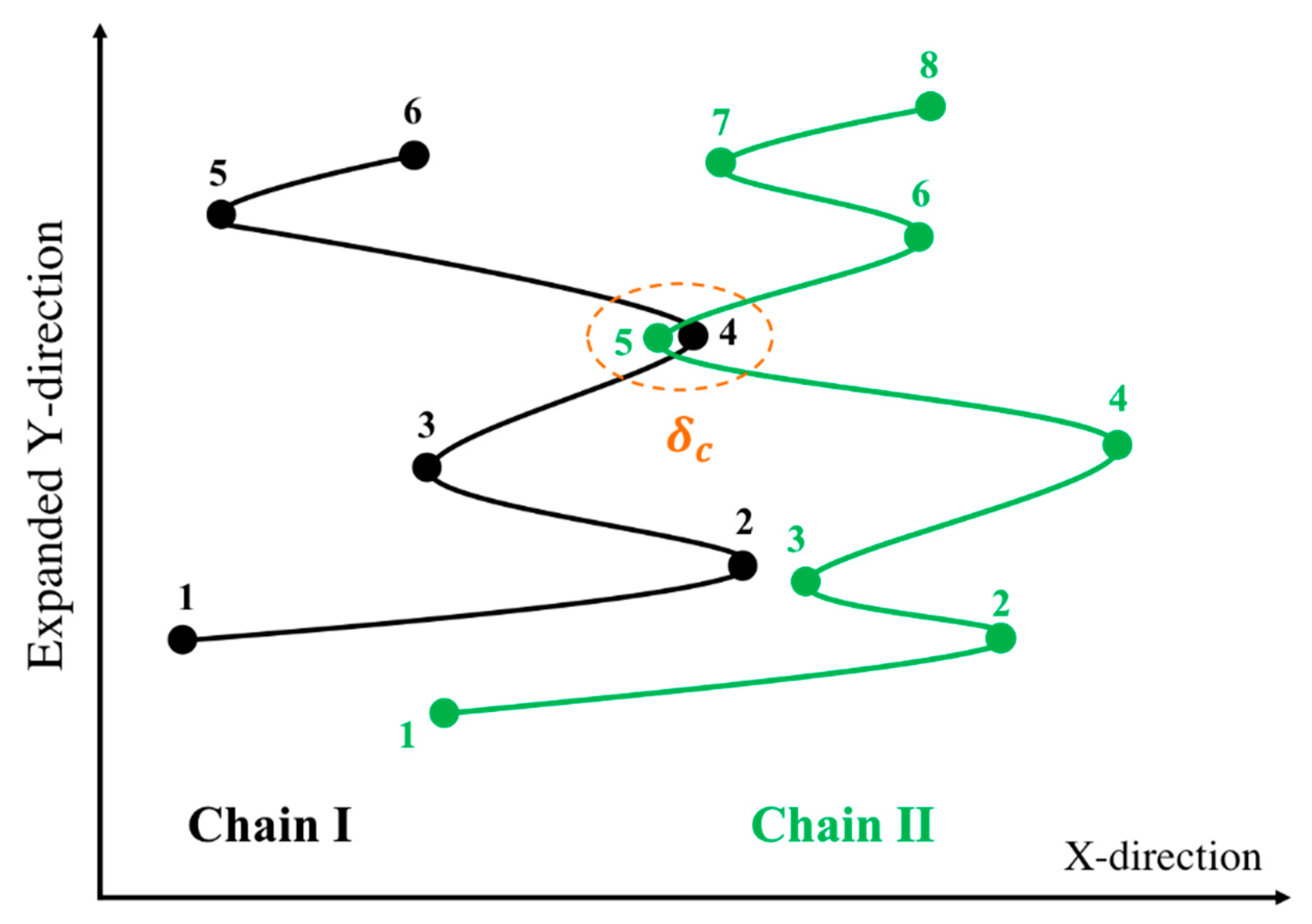
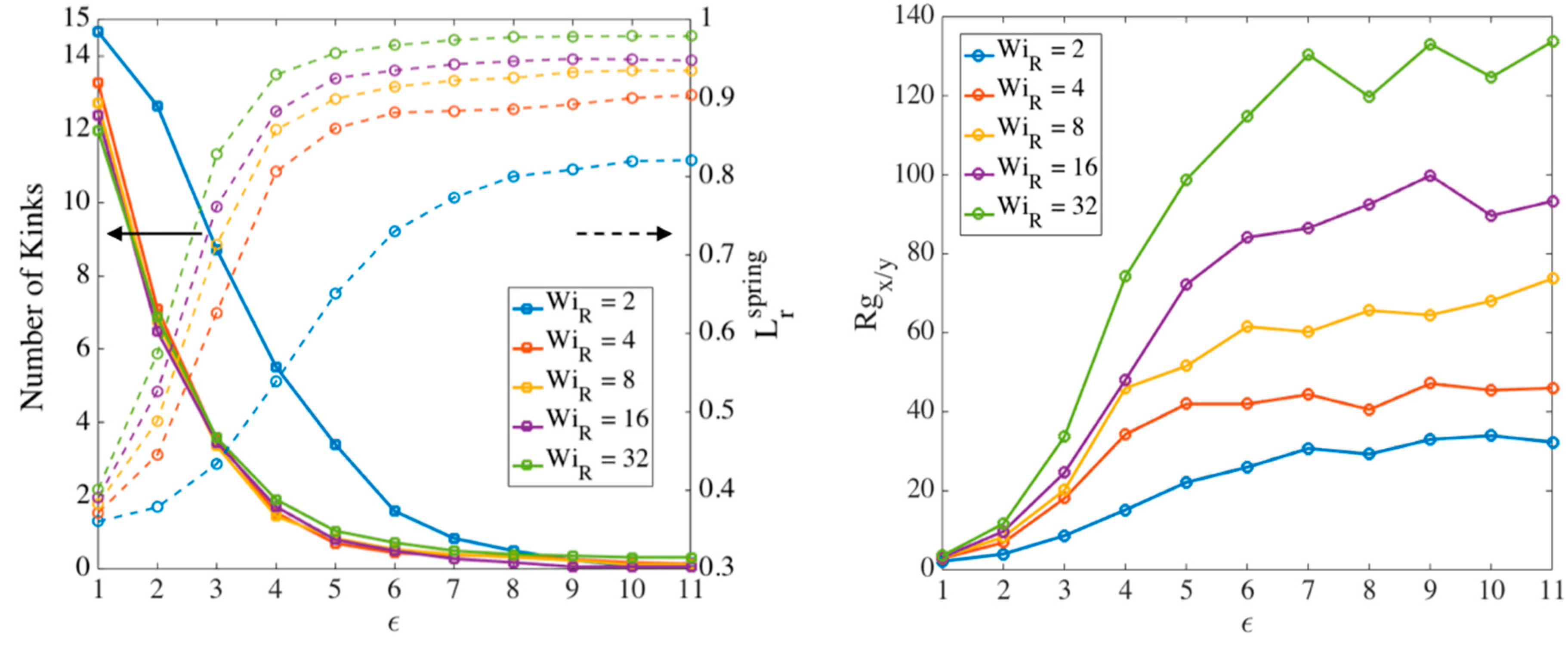
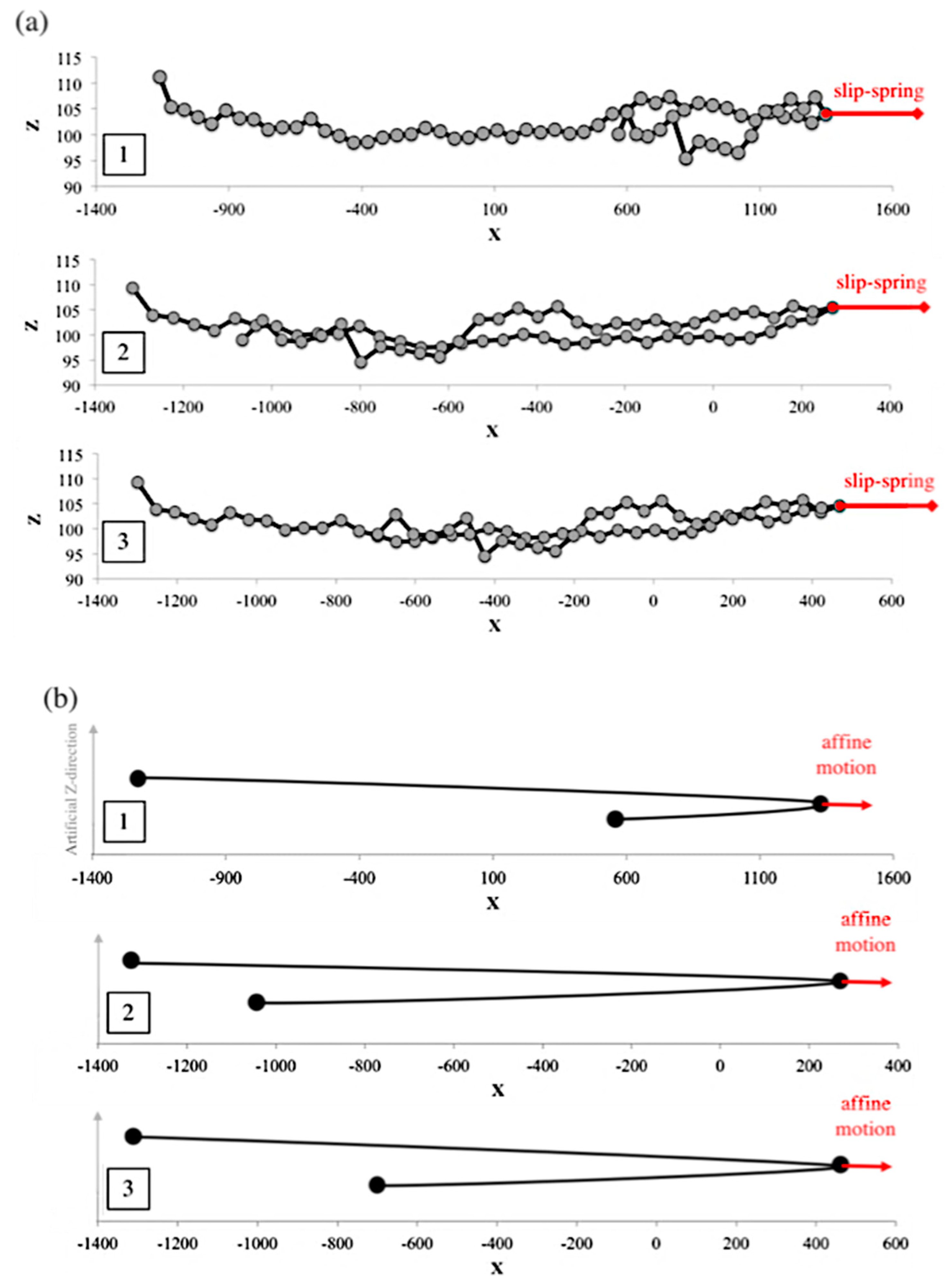
3.2. MEF Results for Chain Conformation
- [18]
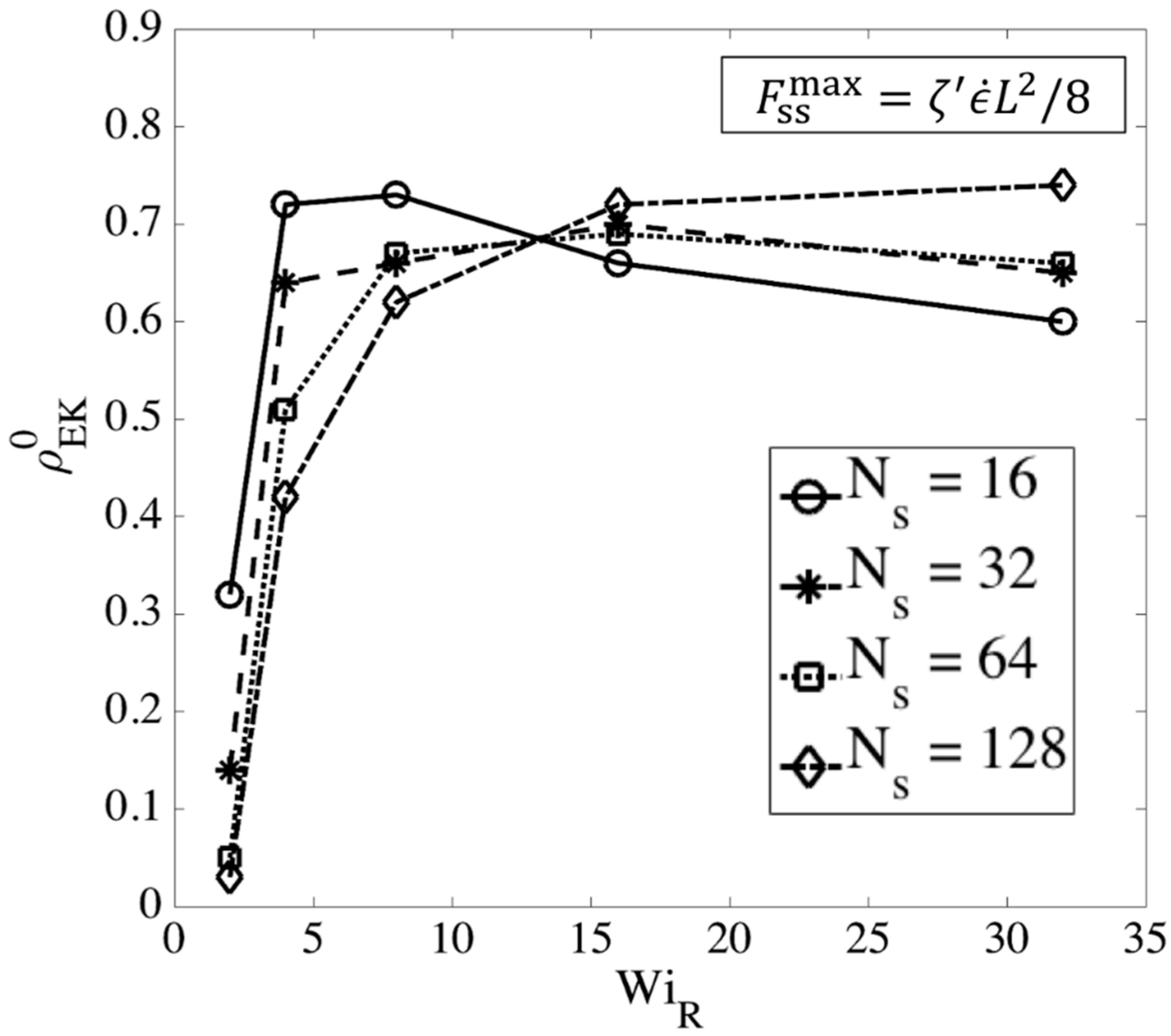
- Fraction of entangled kinks:
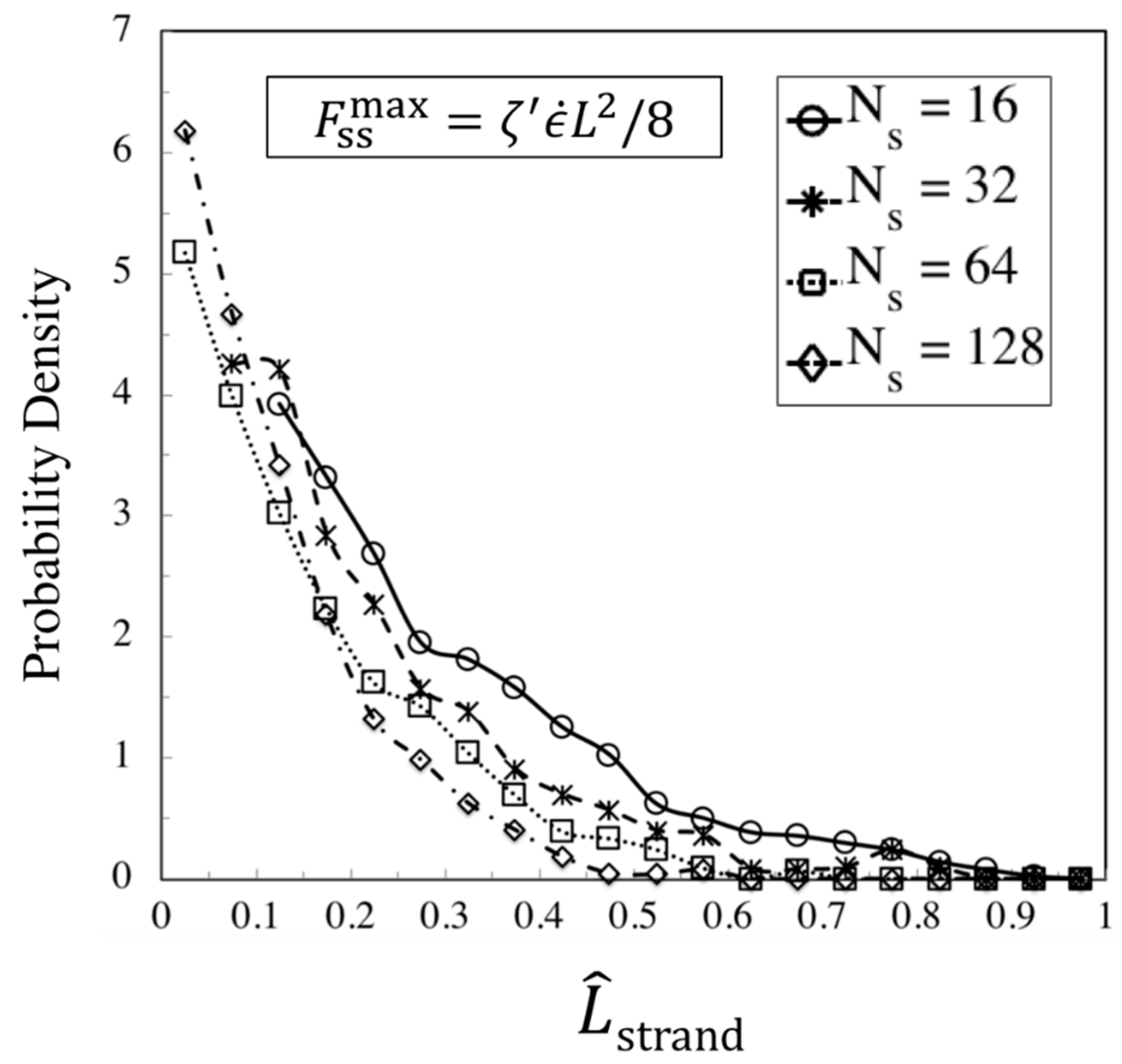
- Strand length probability distribution:
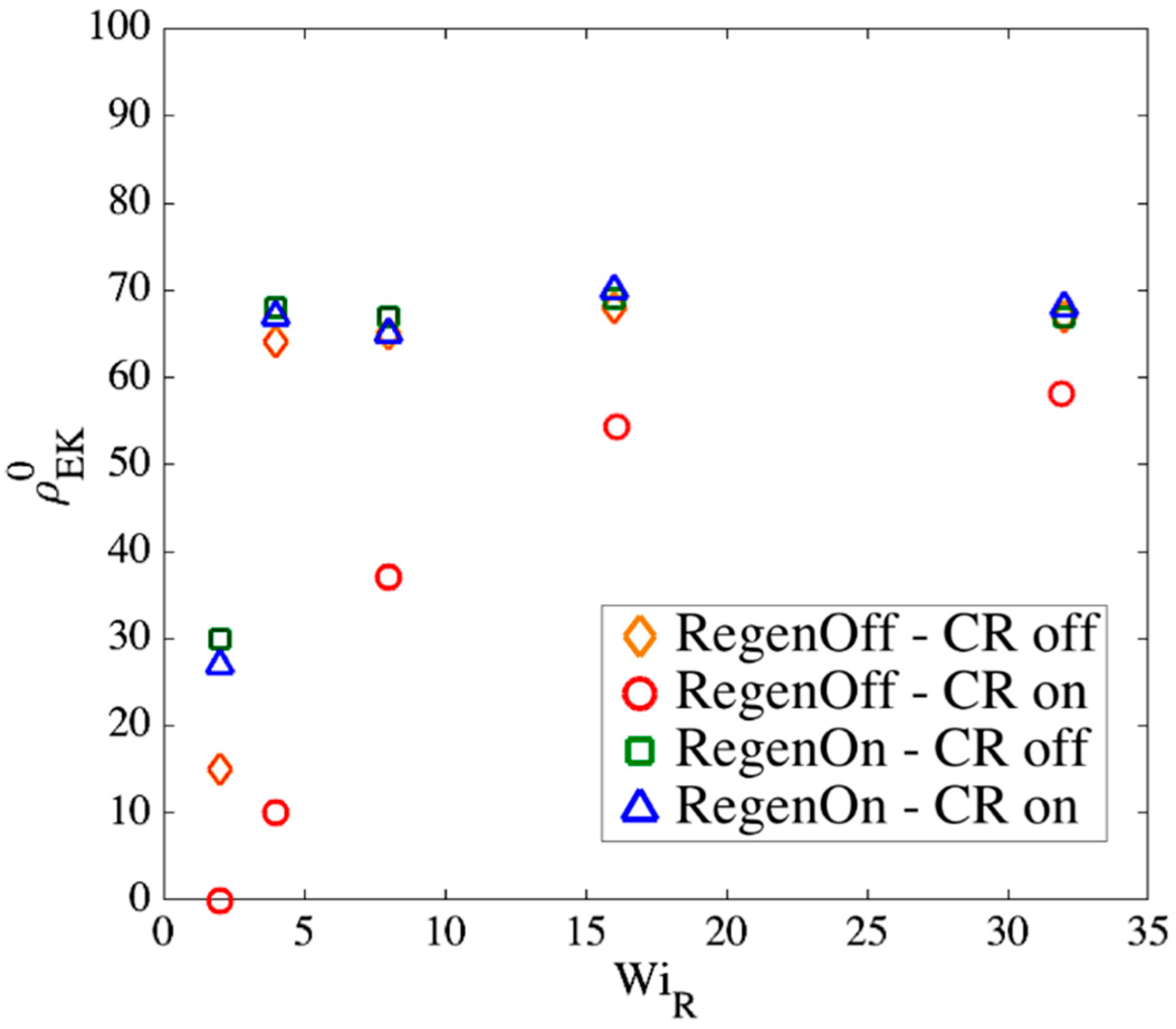
3.3. Addition of Slip-Link Regeneration and Constraint Release to Slip-Link Model
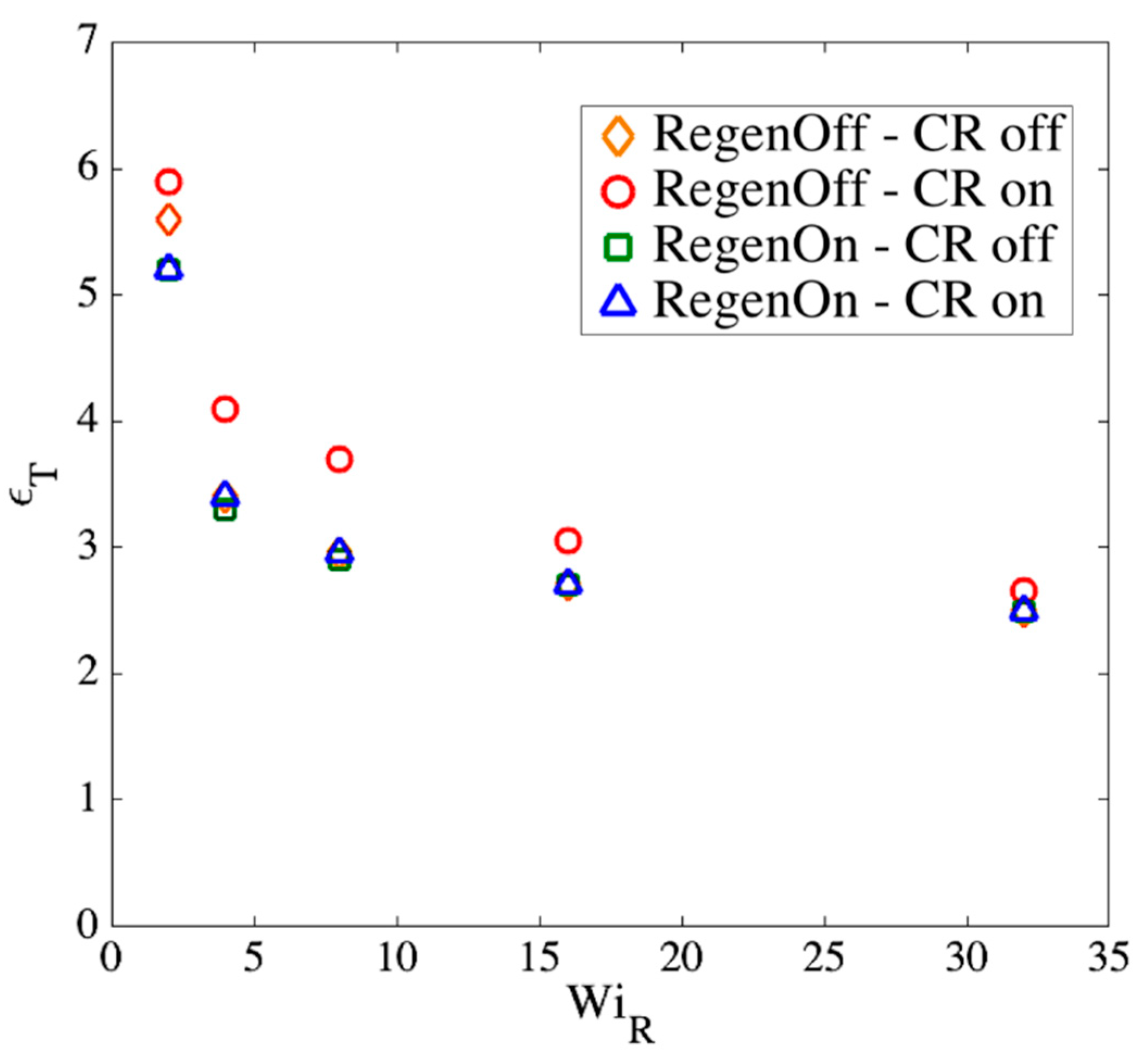
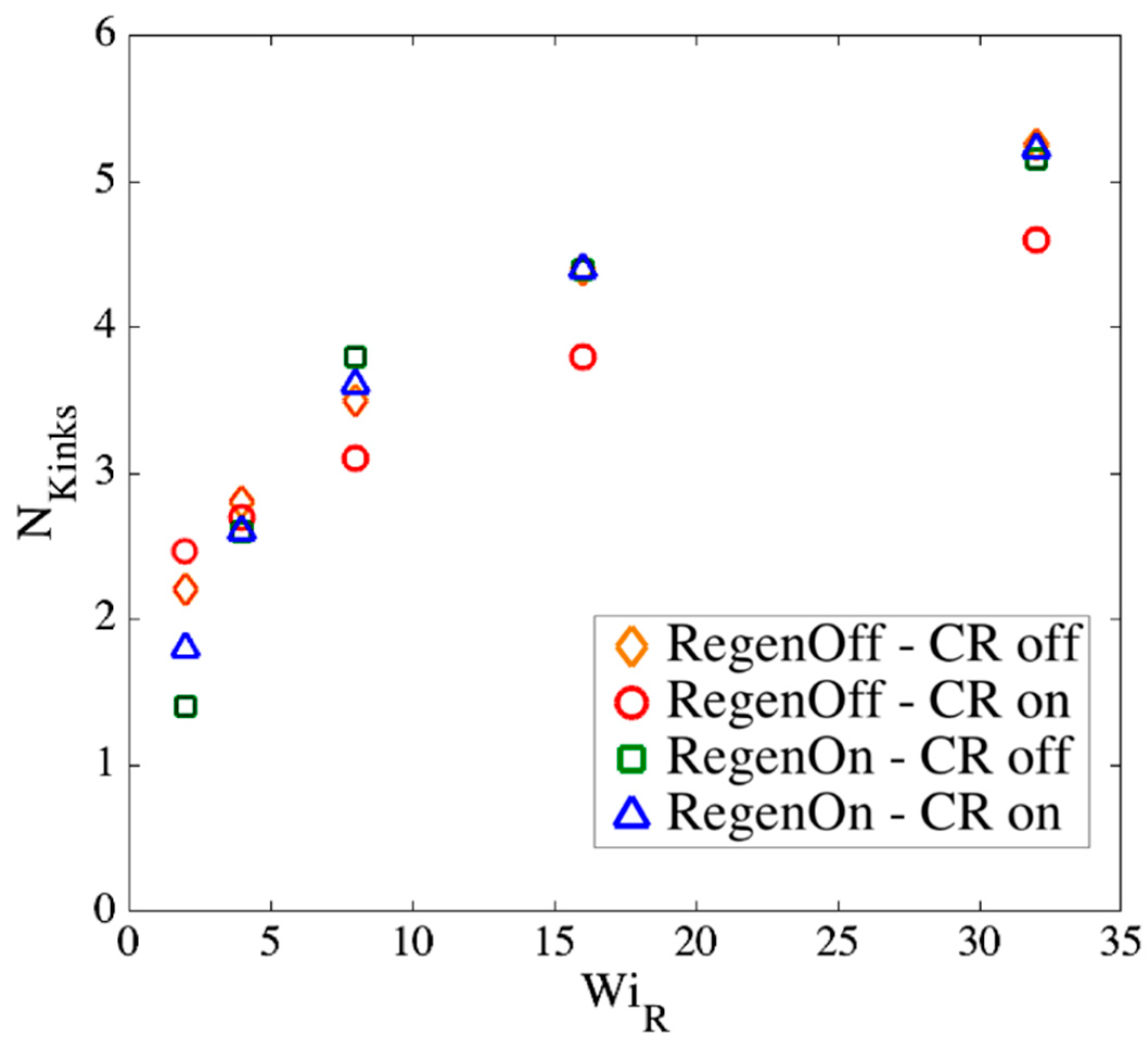
- Regeneration off—CR off: when a slip-link passes through its chain end, it is destroyed, and no further action is taken for other slip-links on the chain. This results in a continual reduction in the number of slip-links until all of them are gone. This condition has been used to obtain the results in Section 3.2.
- Regeneration off—CR on: when a slip-link passes through its chain end, it is destroyed. Simultaneously, another slip-link on the same chain is randomly chosen and removed to represent constraint release produced by other chains, which are not simulated directly. Since there is no regeneration, slip-springs disappear faster than in Condition 1 above.
- Regeneration on—CR off: If a slip-link passes by the chain end, it is removed and instantaneously recreated at a random location on the chain. Thus, the total number of entanglements stays constant under this condition.
- Regeneration on—CR on: If the chain end passes through a slip-link, the slip-link is destroyed and recreated at a random position on the same chain. Simultaneously, another randomly chosen slip-link is removed and recreated at a random position along the chain. Therefore, the number of slip-links stays constant.
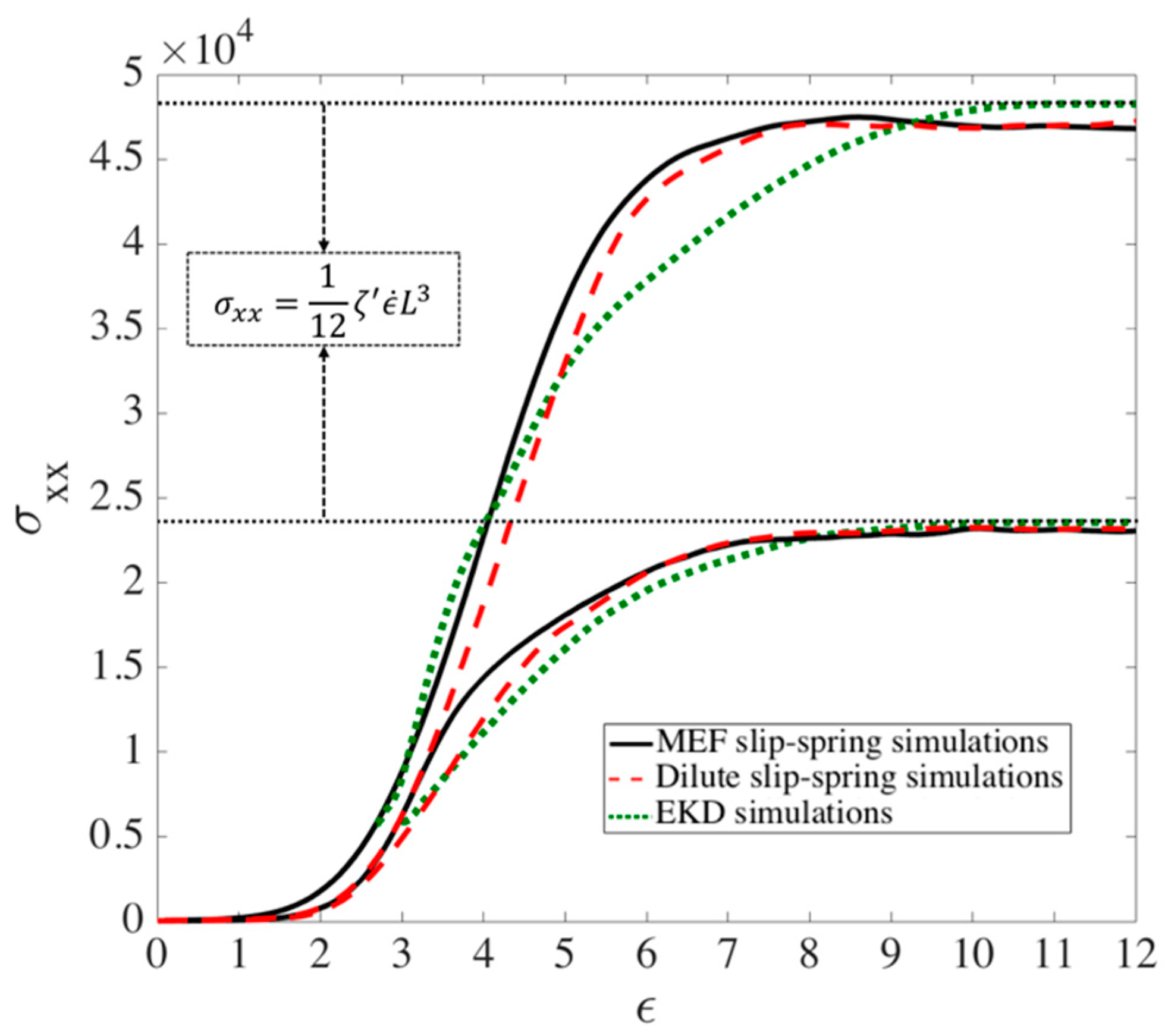
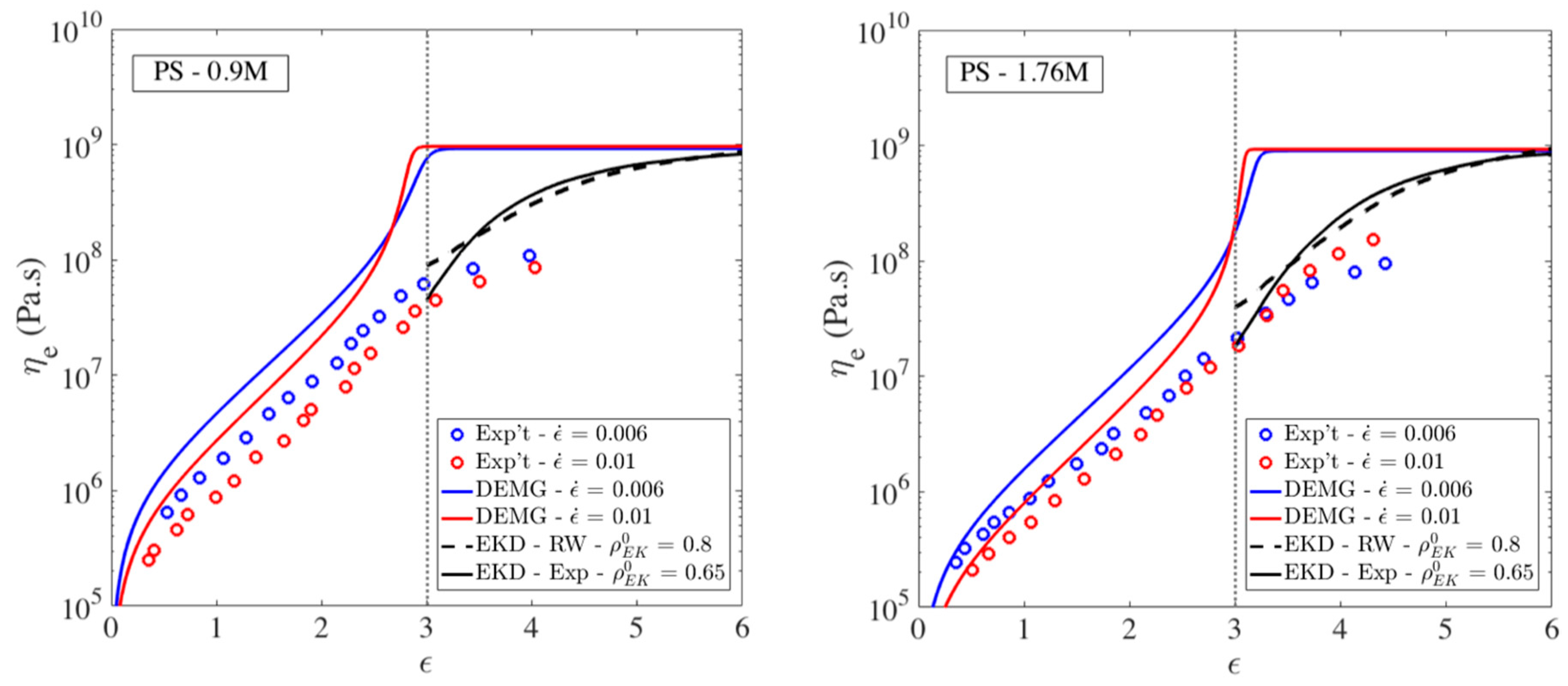
3.4. Comparison of Kink Dynamics Results with Experimental Data
4. Conclusions and Future Directions
Author Contributions
Funding
Conflicts of Interest
Appendix A
Time-Step Size in Slip-Spring Simulations
| Condition | Direction of Slip-Spring Jump | |
|---|---|---|
| i | 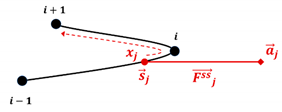 | |
| ii | 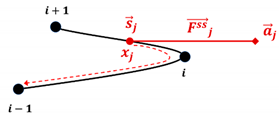 |
Appendix B
MEF Performance in Unraveling a Kinked Chain
| Conformation | |||
|---|---|---|---|
| 1 | 1.22 | 0.61 | 2.00 |
| 2 | 4.87 | 2.42 | 2.01 |
| 3 | 2.99 | 1.52 | 1.97 |
References
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 1.—Brownian motion in the equilibrium state. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 1789–1801. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. Dynamics of concentrated polymer systems. Part 2.—Molecular motion under flow. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1978, 74, 1802–1817. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative theory for linear dynamics of linear entangled polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Marrucci, G.; Grizzuti, N. Fast Flows of concentrated polymers: Predictions of the tube model on chain stretching. Gazz. Chim. Ital. 1988, 118, 179–185. [Google Scholar]
- Pearson, D.; Herbolzheimer, E.; Grizzuti, N.; Marrucci, G. Transient behavior of entangled polymers at high shear rates. J. Polym. Sci. Part B Polym. Phys. 1991, 29, 1589–1597. [Google Scholar] [CrossRef]
- Mead, D.W.; Yavich, D.; Leal, L.G. The reptation model with segmental stretch—I. Basic equations and general properties. Rheol. Acta 1995, 34, 360–383. [Google Scholar] [CrossRef]
- Mead, D.W.; Yavich, D.; Leal, L.G. The reptation model with segmental stretch—II. Steady flow properties. Rheol. Acta 1995, 34, 360–383. [Google Scholar] [CrossRef]
- Marrucci, G. Dynamics of entanglements: A nonlinear model consistent with the Cox-Merz rule. J. Nonnewton. Fluid Mech. 1996, 62, 279–289. [Google Scholar] [CrossRef]
- Mead, D.W.; Larson, R.G.; Doi, M. A molecular theory for fast flows of entangled polymers. Macromolecules 1998, 31, 7895–7914. [Google Scholar] [CrossRef]
- Ianniruberto, G.; Marrucci, G. A simple constitutive equation for entangled polymers with chain stretch. J. Nonnewton. Fluid Mech. 2002, 102, 383–395. [Google Scholar] [CrossRef]
- Graham, R.S.; Likhtman, A.E.; McLeish, T.C.B.; Milner, S.T. Microscopic theory of linear, entangled polymer chains under rapid deformation including chain stretch and convective constraint release. J. Rheol. 2003, 47, 1171–1200. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Graham, R.S. Simple constitutive equation for linear polymer melts derived from molecular theory: Rolie-Poly equation. J. Nonnewton. Fluid Mech. 2003, 114, 1–12. [Google Scholar] [CrossRef]
- McLeish, T.C.B.; Cates, M.E.; Higgins, J.E.; Olmsted, P.D.; Marrucci, G.; Ianniruberto, G. Flow-induced orientation and stretching of entangled polymers. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 361, 677–688. [Google Scholar]
- Bhattacharjee, P.K.; Nguyen, D.A.; McKinley, G.H.; Sridhar, T. Extensional stress growth and stress relaxation in entangled polymer solutions. J. Rheol. 2003, 47, 269–290. [Google Scholar] [CrossRef]
- Bhattacharjee, P.K.; Oberhauser, J.P.; Mckinley, G.H.; Leal, L.G.; Sridhar, T. Extensional Rheometry of Entangled Solutions. Macromolecules 2002, 35, 10131–10148. [Google Scholar] [CrossRef]
- Moghadam, S.; Saha Dalal, I.; Larson, R.G. Unraveling Dynamics of Entangled Polymers in Strong Extensional Flows. Macromolecules 2019, 53, 1296–1307. [Google Scholar] [CrossRef]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Marrucci, G. Primitive Chain Network Simulation of Elongational Flows of Entangled Linear Chains: Stretch/Orientation-induced Reduction of Monomeric Friction. Macromolecules 2012, 45, 2773–2782. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Yaoita, T.; Matsumiya, Y.; Watanabe, H.; Ianniruberto, G.; Marrucci, G. Stretch/orientation Induced Acceleration in Stress Relaxation in Coarse-grained Molecular Dynamics Simulations. Nihon Reoroji Gakkaishi 2013, 41, 35–37. [Google Scholar] [CrossRef]
- Matsumiya, Y.; Watanabe, H.; Masubuchi, Y.; Huang, Q.; Hassager, O. Nonlinear Elongational Rheology of Unentangled Polystyrene and Poly(p-tert-butylstyrene) Melts. Macromolecules 2018, 51, 9710–9729. [Google Scholar] [CrossRef]
- Ianniruberto, G. Extensional Flows of Solutions of Entangled Polymers Confirm Reduction of Friction Coefficient. Macromolecules 2015, 48, 6306–6312. [Google Scholar] [CrossRef]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Marrucci, G. Primitive Chain Network Simulation of Elongational Flows of Entangled Linear Chains: Role of Finite Chain Extensibility. Macromolecules 2011, 44, 9675–9682. [Google Scholar] [CrossRef]
- O’Connor, T.C.; Alvarez, N.J.; Robbins, M.O. Relating Chain Conformations to Extensional Stress in Entangled Polymer Melts. Phys. Rev. Lett. 2018, 121, 47801. [Google Scholar] [CrossRef] [PubMed]
- Hsu, H.; Kremer, K. Primitive Path Analysis and Stress Distribution in Highly Strained Macromolecules. ACS Macro Lett. 2018, 7, 107–111. [Google Scholar] [CrossRef] [PubMed]
- Murashima, T.; Hagita, K.; Kawakatsu, T. Elongational Viscosity of Weakly Entangled Polymer Melt via Coarse-Grained Molecular Dynamics Simulation. Nihon Reoroji Gakkaishi 2018, 46, 207–220. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular—Dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Daivis, P.J.; Matin, M.L.; Todd, B.D. Nonlinear shear and elongational rheology of model polymer melts by non-equilibrium molecular dynamics. J. Nonnewton. Fluid Mech. 2003, 111, 1–18. [Google Scholar]
- Xu, W.-S.; Carrillo, J.-M.Y.; Lam, C.N.; Sumpter, B.G.; Wang, Y. Molecular Dynamics Investigation of the Relaxation Mechanism of Entangled Polymers after a Large Step Deformation. ACS Macro Lett. 2018, 7, 190–195. [Google Scholar] [CrossRef]
- Kröger, M.; Luap, C.; Muller, R. Polymer Melts under Uniaxial Elongational Flow: Stress−Optical Behavior from Experiments and Nonequilibrium Molecular Dynamics Computer Simulations. Macromolecules 1997, 30, 526–539. [Google Scholar] [CrossRef]
- Doi, M.; Takimoto, J.I. Molecular modelling of entanglement. Philos. Trans. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 2003, 361, 641–652. [Google Scholar]
- Masubuchi, Y.; Takimoto, J.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Masubuchi, Y.; Takimoto, J.; Koyama, K.; Greco, F. Brownian simulations of a network of reptating primitive chains Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar]
- Uneyama, T. Single Chain Slip-Spring Model for Fast Rheology Simulations of Entangled Polymers on GPU. J. Soc. Rheol. Japan 2011, 39, 135–152. [Google Scholar]
- Yaoita, T.; Isaki, T.; Masubuchi, Y.; Watanabe, H.; Ianniruberto, G.; Greco, F.; Marrucci, G. Statics, linear, and nonlinear dynamics of entangled polystyrene melts simulated through the primitive chain network model. J. Chem. Phys. 2008, 128, 154901–154911. [Google Scholar] [PubMed]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902. [Google Scholar] [PubMed]
- Masubuchi, Y.; Ianniruberto, G.; Marrucci, G. Stress Undershoot of Entangled Polymers under Fast Startup Shear Flows in Primitive Chain Network Simulations. J. Soc. Rheol. Jpn. 2018, 46, 23–28. [Google Scholar]
- Schieber, J.D. Fluctuations in entanglements of polymer liquids. J. Chem. Phys. 2003, 118, 5162–5166. [Google Scholar]
- Nair, D.M.; Schieber, J.D. Linear viscoelastic predictions of a consistently unconstrained brownian slip-link model. Macromolecules 2006, 39, 3386–3397. [Google Scholar]
- Schieber, J.D.; Indei, T.; Steenbakkers, R.J.A. Fluctuating entanglements in single-chain mean-field models. Polymers 2013, 5, 643–678. [Google Scholar]
- Ramírez, J.; Sukumaran, S.K.; Likhtman, A.E. Hierarchical Modeling of Entangled Polymers. Macromol. Symp. 2007, 252, 119–129. [Google Scholar]
- Likhtman, A.E. Single-Chain Slip-Link Model of Entangled Polymers: Simultaneous Description of Neutron Spin—Echo, Rheology, and Diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar]
- Zamponi, M.; Wischnewski, A.; Monkenbusch, M.; Willner, L.; Richter, D.; Likhtman, A.E.; Kali, G.; Farago, B. Molecular observation of constraint release in polymer melts. Phys. Rev. Lett. 2006, 96, 1–4. [Google Scholar]
- Del Biondo, D.; Masnada, E.M.; Merabia, S.; Couty, M.; Barrat, J.-L. Numerical study of a slip-link model for polymer melts and nanocomposites. J. Chem. Phys. 2013, 138, 194902–194913. [Google Scholar] [PubMed]
- Pilyugina, E.; Andreev, M.; Schieber, J.D. Dielectric relaxation as an independent examination of relaxation mechanisms in entangled polymers using the discrete slip-link model. Macromolecules 2012, 45, 5728–5743. [Google Scholar]
- Andreev, M.; Khaliullin, R.N.; Steenbakkers, R.J.A.; Schieber, J.D. Approximations of the discrete slip-link model and their effect on nonlinear rheology predictions. J. Rheol. 2013, 57, 535–557. [Google Scholar]
- Khaliullin, R.N.; Schieber, J.D. Self-Consistent Modeling of Constraint Release in a Single-Chain Mean-Field Slip-Link Model. Macromolecules 2009, 42, 7504–7517. [Google Scholar]
- Schieber, J.D.; Nair, D.M.; Kitkrailard, T. Comprehensive comparisons with nonlinear flow data of a consistently unconstrained Brownian slip-link model. J. Rheol. 2007, 51, 1111–1141. [Google Scholar]
- Schieber, J.D.; Andreev, M. Entangled Polymer Dynamics in Equilibrium and Flow Modeled Through Slip Links. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 367–381. [Google Scholar] [PubMed]
- Huang, Q.; Hengeller, L.; Alvarez, N.J.; Hassager, O. Bridging the Gap between Polymer Melts and Solutions in Extensional Rheology. Macromolecules 2015, 48, 4158–4163. [Google Scholar]
- Larson, R.G. The unraveling of a polymer chain in a strong extensional flow. Rheol. Acta 1990, 29, 371–384. [Google Scholar]
- Hinch, E.J. Uncoiling a polymer molecule in a strong extensional flow. J. Nonnewton. Fluid Mech. 1994, 54, 209–230. [Google Scholar] [CrossRef]
- Rallison, J.M.; Hinch, E.J. Do we understand the physics in the constitutive equation? J. Nonnewton. Fluid Mech. 1988, 29, 37–55. [Google Scholar] [CrossRef]
- Hsiao, K.; Sasmal, C.; Prakash, J.R.; Schroeder, C.M.; Hsiao, K. Direct observation of DNA dynamics in semidilute solutions in extensional flow. 2017, 61, 151–167. [Google Scholar] [CrossRef]
- Cho, S.; Jeong, S.; Kim, J.M.; Baig, C. Molecular dynamics for linear polymer melts in bulk and confined systems under shear flow. Sci. Rep. 2017, 7, 9004. [Google Scholar] [CrossRef] [PubMed]
- Kirkwood, J.G.; Riseman, J. The intrinsic viscosities and diffusion constants of flexible macromolecules in solution. J. Chem. Phys. 1948, 16, 565–573. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine deformation and elasticity of polymer networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of polymer networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Likhtman, A.E.; Sukumaran, S.K.; Ramirez, J. Linear Viscoelasticity from Molecular Dynamics Simulation of Entangled Polymers. Macromolecules 2007, 40, 6748–6757. [Google Scholar] [CrossRef]
- Sukumaran, S.K.; Likhtman, A.E. Modeling Entangled Dynamics: Comparison between Stochastic Single-Chain and Multichain Models. Macromolecules 2009, 42, 4300–4309. [Google Scholar] [CrossRef]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions; Brenner, H., Ed.; Butterworth-Heinemann: Oxford, UK, 1988; ISBN 978-0-409-90110-1. [Google Scholar]
- Dealy, J.M.; Read, D.J.; Larson, R.G. Structure and Rheology of Molten Polymers. In Structure and Rheology of Molten Polymers; Carl Hanser Verlag GmbH & Co. KG: Munich, Germany, 2018; ISBN 978-1-56990-611-8. [Google Scholar]
- Glauber, R.J. Time-Dependent Statistics of the Ising Model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Kushwaha, A.; Shaqfeh, E.S.G. Slip-link simulations of entangled polymers in planar extensional flow: Disentanglement modified extensional thinning. J. Rheol. 2011, 55, 463–483. [Google Scholar] [CrossRef]

| Dilute | ||
| Affine |
| Input | ||||||
|---|---|---|---|---|---|---|
| Value |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moghadam, S.; Saha Dalal, I.; Larson, R.G. Slip-Spring and Kink Dynamics Models for Fast Extensional Flow of Entangled Polymeric Fluids. Polymers 2019, 11, 465. https://doi.org/10.3390/polym11030465
Moghadam S, Saha Dalal I, Larson RG. Slip-Spring and Kink Dynamics Models for Fast Extensional Flow of Entangled Polymeric Fluids. Polymers. 2019; 11(3):465. https://doi.org/10.3390/polym11030465
Chicago/Turabian StyleMoghadam, Soroush, Indranil Saha Dalal, and Ronald G. Larson. 2019. "Slip-Spring and Kink Dynamics Models for Fast Extensional Flow of Entangled Polymeric Fluids" Polymers 11, no. 3: 465. https://doi.org/10.3390/polym11030465
APA StyleMoghadam, S., Saha Dalal, I., & Larson, R. G. (2019). Slip-Spring and Kink Dynamics Models for Fast Extensional Flow of Entangled Polymeric Fluids. Polymers, 11(3), 465. https://doi.org/10.3390/polym11030465