Thermal Decomposition Mechanism and Kinetics Study of Plastic Waste Chlorinated Polyvinyl Chloride
Abstract
1. Introduction
2. Material and Methods
2.1. Elemental Analysis
2.2. Thermogravimetric Eexperiments
2.3. Kinetic Theory
2.3.1. Flynn-Wall-Ozawa Method
2.3.2. Coats-Redfern Method
2.3.3. Shuffled Complex Evolution Optimization Method
3. Results and Discussion
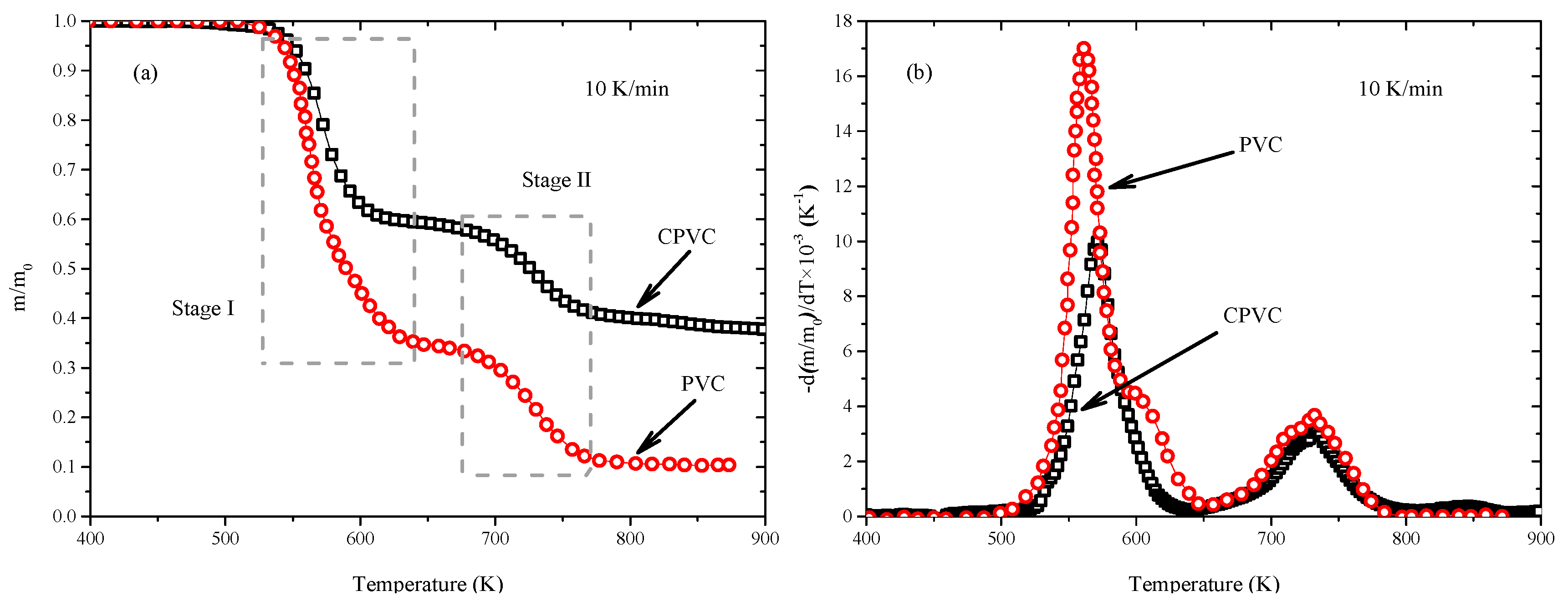
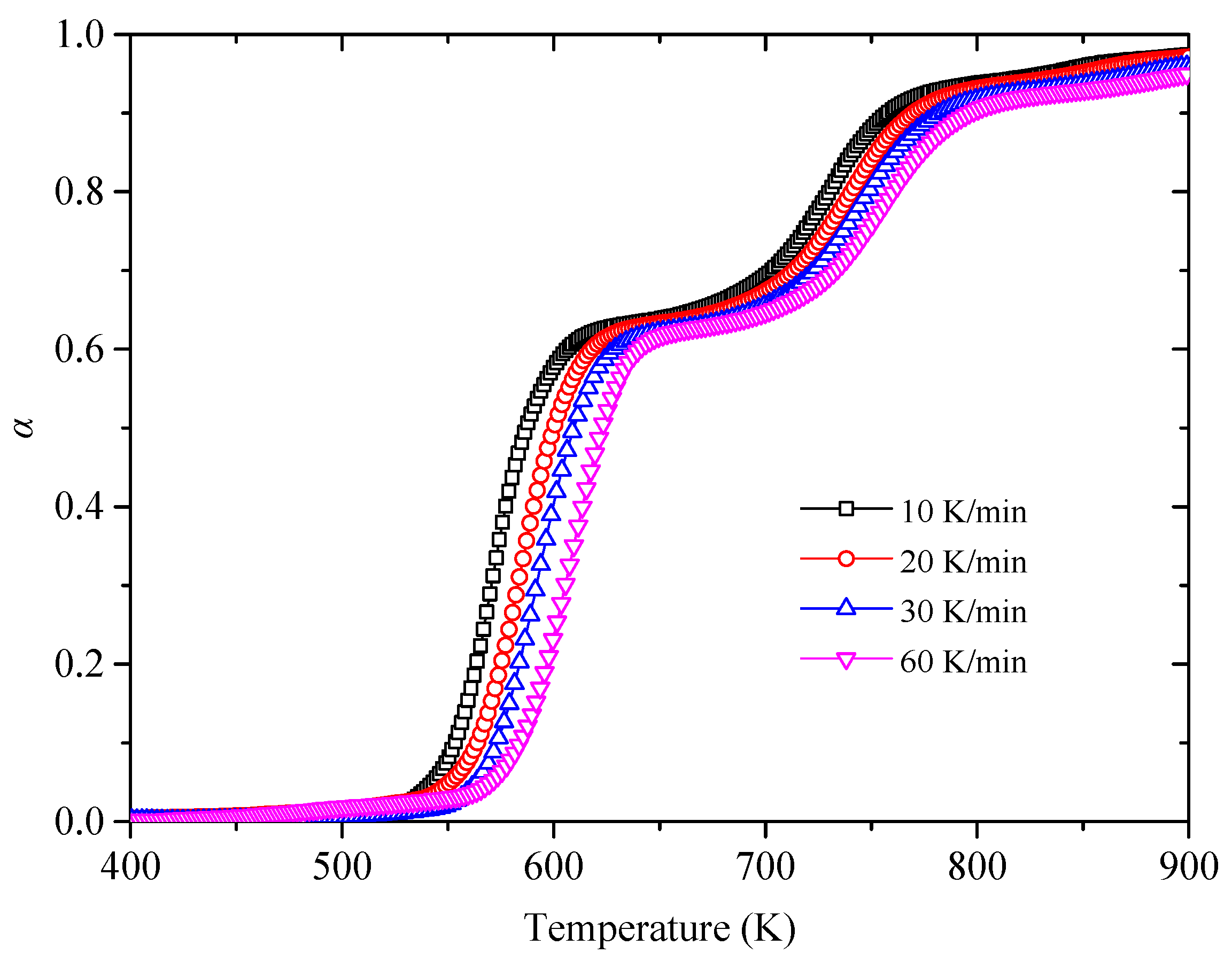
3.1. Thermogravimetric Analysis
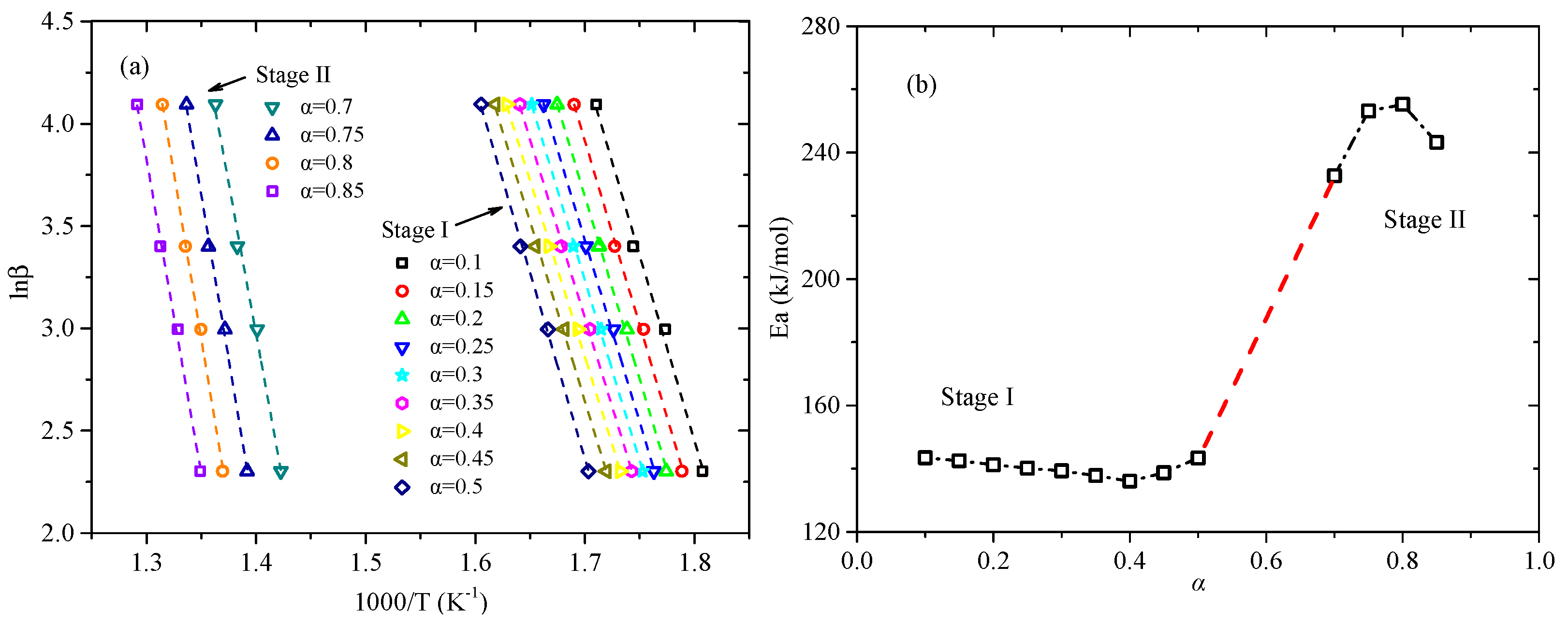
3.2. Kinetic Analysis Base on FWO Method
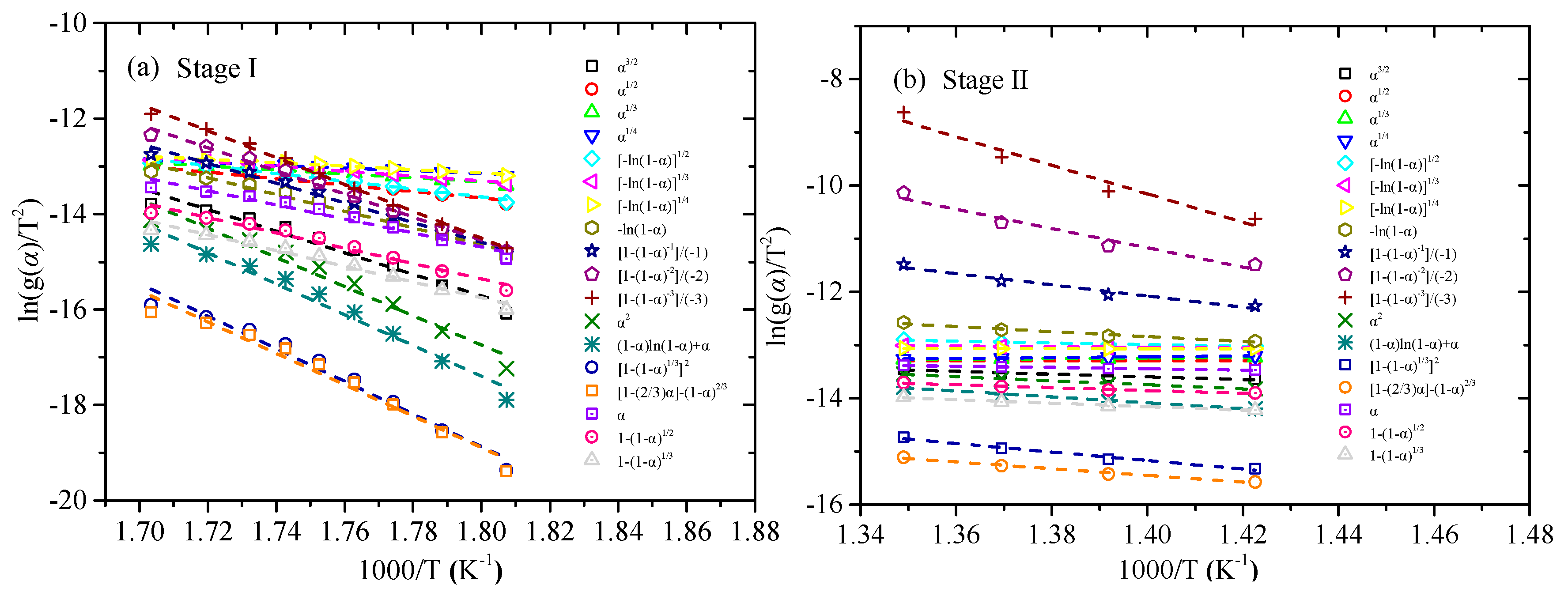
3.3. Estimation and Verification of Reaction Model
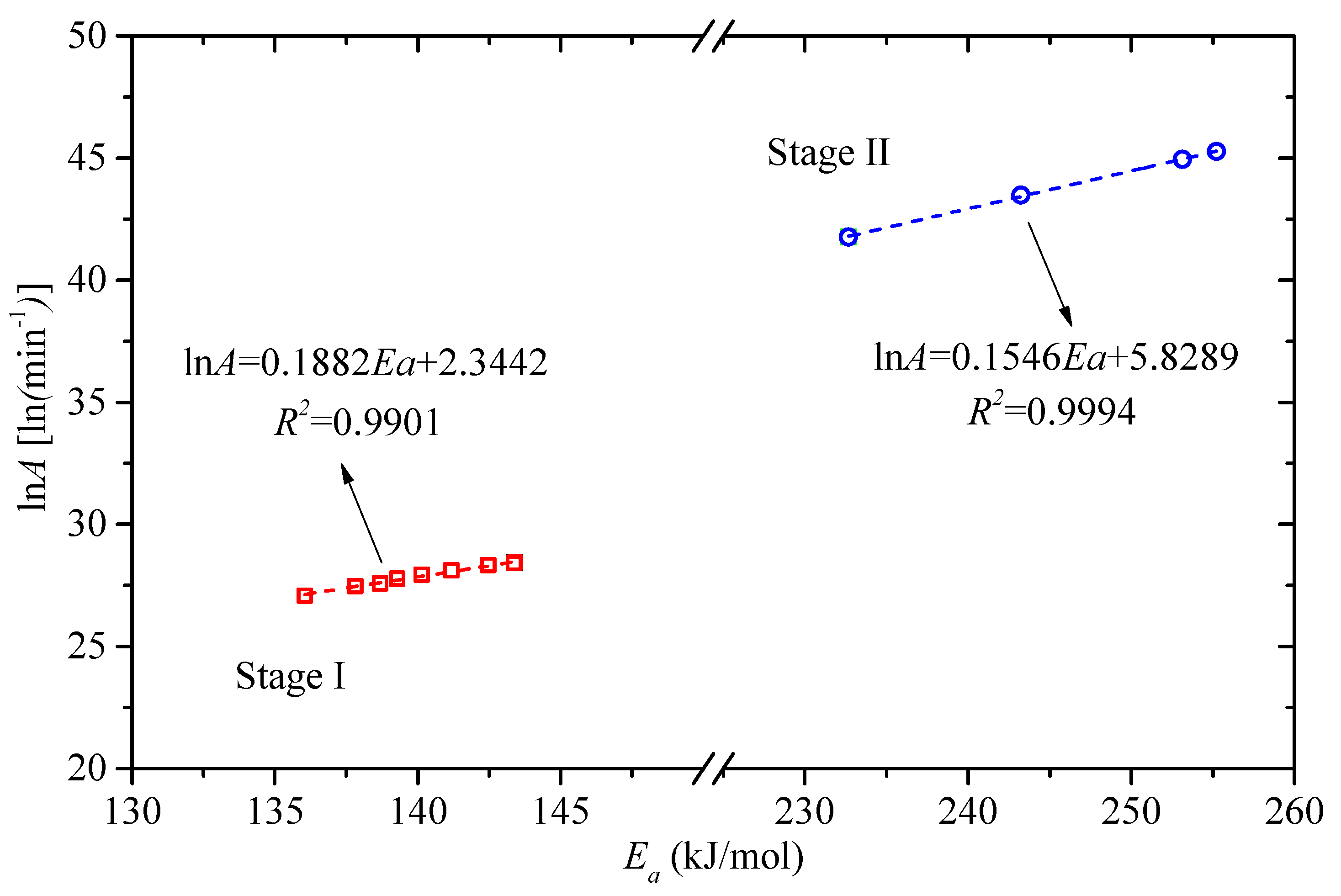
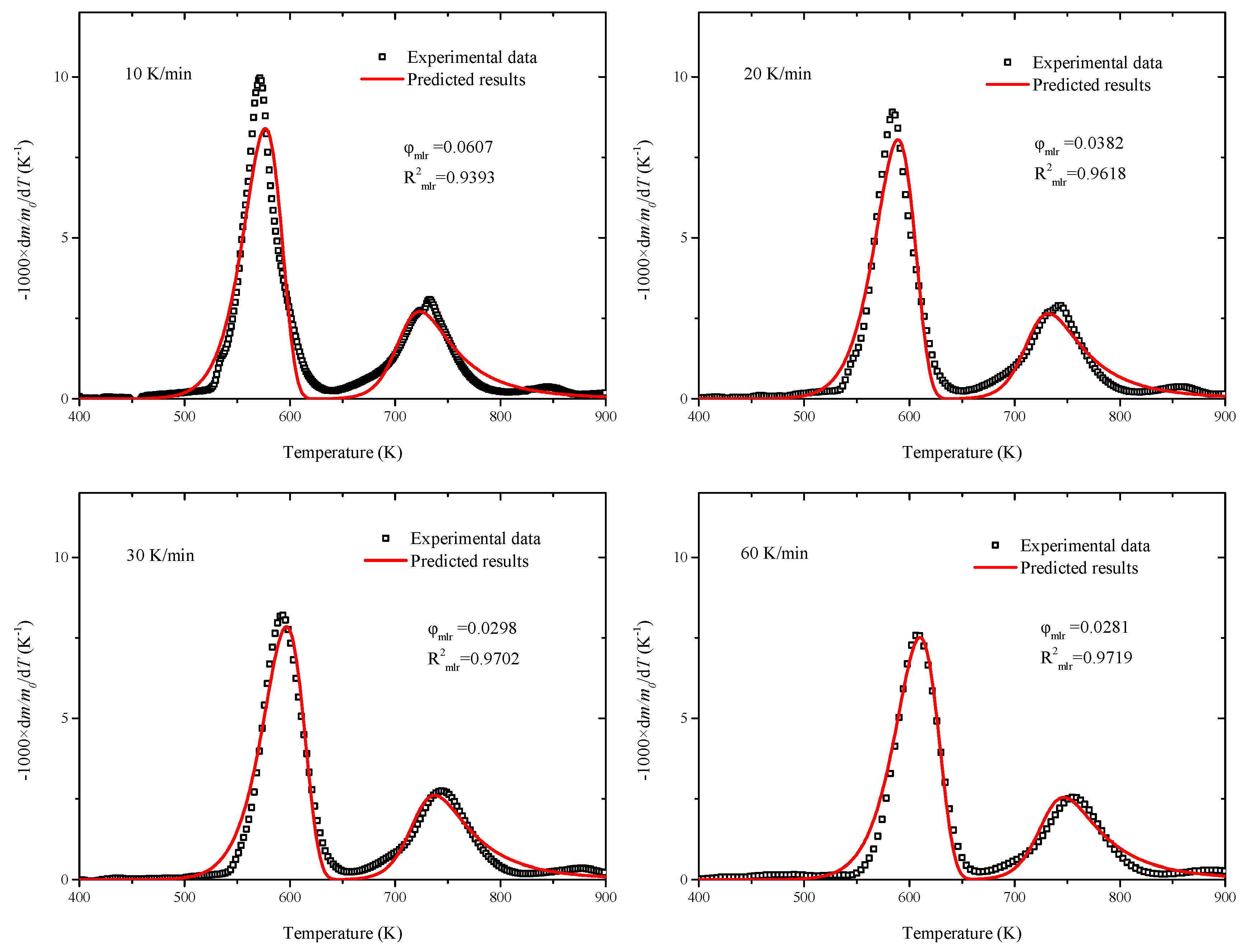
3.4. Kinetic Parameters Estimation by Shuffled Complex Evolution
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, R.; Li, Q.; Xu, X.; Zhang, D. Comparative pyrolysis characteristics of representative commercial thermosetting plastic waste in inert and oxygenous atmosphere. Fuel 2019, 246, 212–221. [Google Scholar] [CrossRef]
- Yang, Q.; Lu, W.; Bai, L.; Yan, B.; Cheng, Y. UV enhanced gas-solid synthesis of chlorinated poly vinyl chloride characterized by a UV-Vis online analysis method. Chin. J. Chem. Eng. 2015, 23, 1052–1059. [Google Scholar] [CrossRef]
- Chen, R.; Xu, X.; Lu, S.; Zhang, Y.; Lo, S. Pyrolysis study of waste phenolic fibre-reinforced plastic by thermogravimetry/Fourier transform infrared/mass spectrometry analysis. Energy Convers. Manag. 2018, 165, 555–566. [Google Scholar] [CrossRef]
- Jiang, L.; Zhang, D.; Li, M.; He, J.J.; Gao, Z.H.; Zhou, Y.; Sun, J.H. Pyrolytic behavior of waste extruded polystyrene and rigid polyurethane by multi kinetics methods and Py-GC/MS. Fuel 2018, 222, 11–20. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Lu, S.; Wang, C.; Zhou, R. Comparative pyrolysis behaviors and reaction mechanisms of hardwood and softwood. Energy Convers. Manag. 2017, 132, 102–109. [Google Scholar] [CrossRef]
- Huang, J.; Li, X.; Zeng, G.; Cheng, X.; Tong, H.; Wang, D. Thermal decomposition mechanisms of poly(vinyl chloride): A computational study. Waste Manag. 2018, 76, 483–496. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, W.; Yu, L.; Lu, K. The accuracy and efficiency of GA and PSO optimization schemes on estimating reaction kinetic parameters of biomass pyrolysis. Energy 2019, 176, 582–588. [Google Scholar] [CrossRef]
- Li, M.; Jiang, L.; He, J.J.; Sun, J.H. Kinetic triplet determination and modified mechanism function construction for thermo-oxidative degradation of waste polyurethane foam using conventional methods and distributed activation energy model method. Energy 2019, 175, 1–13. [Google Scholar] [CrossRef]
- Bach, Q.V.; Chen, W.H.; Eng, C.F.; Wang, C.W.; Liang, K.C.; Kuo, J.Y. Pyrolysis characteristics and non-isothermal torrefaction kinetics of industrial solid wastes. Fuel 2019, 251, 118–125. [Google Scholar] [CrossRef]
- Miranda, R.; Pakdel, H.; Roy, C.; Darmstadt, H.; Vasile, C. Vacuum pyrolysis of PVC II: Product analysis. Polym. Degrad. Stab. 1999, 66, 107–125. [Google Scholar] [CrossRef]
- Miranda, R.; Yang, J.; Roy, C.; Vasile, C. Vacuum pyrolysis of PVC I. Kinetic study. Polym. Degrad. Stab. 1999, 64, 127–144. [Google Scholar] [CrossRef]
- Gui, B.; Qiao, Y.; Wan, D.; Liu, S.; Han, Z.; Yao, H.; Xu, M. Nascent tar formation during polyvinylchloride (PVC) pyrolysis. Proc. Combustion Inst. 2013, 34, 2321–2329. [Google Scholar] [CrossRef]
- Al-Salem, S.M.; Lettieri, P. Kinetic study of high density polyethylene (HDPE) pyrolysis. Chem. Eng. Res. Des. 2010, 88, 1599–1606. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Liu, J.; Wang, Z.; Kong, B.; Gong, X.; Guo, L. Study of high density polyethylene (HDPE) pyrolysis with reactive molecular dynamics. Polym. Degrad. Stab. 2014, 104, 62–70. [Google Scholar] [CrossRef]
- Luyt, A.S.; Malik, S.S.; Gasmi, S.A.; Porfyris, A.; Andronopoulou, A.; Korres, D.; Papaspyrides, C. Halogen-free flame-retardant compounds. Thermal decomposition and flammability behavior for alternative polyethylene grades. Polymers 2019, 11, 1479. [Google Scholar] [CrossRef] [PubMed]
- Park, K.B.; Jeong, Y.S.; Guzelciftci, B.; Kim, J.S. Characteristics of a new type continuous two-stage pyrolysis of waste polyethylene. Energy 2019, 166, 343–351. [Google Scholar] [CrossRef]
- Swann, J.D.; Ding, Y.; Stoliarov, S.I. Characterization of pyrolysis and combustion of rigid poly(vinyl chloride) using two-dimensional modeling. Int. J. Heat Mass Transf. 2019, 132, 347–361. [Google Scholar] [CrossRef]
- Sun, Q.L.; Shi, X.G.; Lin, Y.L.; Zhu, H.; Wang, X.; Cheng, C.G.; Liu, J.H. Thermogravimetric-mass spectrometric study of the pyrolysis behavior of PVC. J. China Univ. Min. Technol. 2007, 17, 242–245. [Google Scholar] [CrossRef]
- Wu, J.; Chen, T.; Luo, X.; Han, D.; Wang, Z.; Wu, J. TG/FTIR analysis on co-pyrolysis behavior of PE, PVC and PS. Waste Manag. 2014, 34, 676–682. [Google Scholar] [CrossRef]
- Wang, Y.K.; Tsai, F.C.; Ma, C.C.; Wang, M.L.; Kuo, S.W. Using Methacryl-polyhedral oligomeric silsesquioxane as the thermal stabilizer and plasticizer in poly (vinyl chloride) nanocomposites. Polymers 2019, 11, 1711. [Google Scholar] [CrossRef]
- Elakesh, E.O.; Hull, T.R.; Price, D.; Carty, P. Effect of stabilisers and lubricant on the thermal decomposition of chlorinated poly(vinyl chloride) (CPVC). Poly. Degrad. Stab. 2005, 88, 41–45. [Google Scholar] [CrossRef]
- Elakesh, E.O.; Hull, T.R.; Price, D.; Carty, P. Thermal decomposition of chlorinated poly(vinyl chloride) (CPVC). J. Vinyl Additwe Tech. 2003, 9, 116–126. [Google Scholar]
- Carty, P.; Price, D.; Milnes, G.J. Chlorinated poly(vinyl chloride) and plasticized chlorinated poly(vinyl chloride)-thermal decomposition studies. J. Vinyl Additwe Tech. 2002, 8, 227–237. [Google Scholar]
- Ding, Y.; Wang, C.; Chaos, M.; Chen, R.; Lu, S. Estimation of beech pyrolysis kinetic parameters by shuffled complex evolution. Bioresour. Tech. 2016, 200, 658–665. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Zhang, J.; Wang, C.; Lu, S. The effect of chemical reaction kinetic parameters on the bench-scale pyrolysis of lignocellulosic biomass. Fuel 2018, 232, 147–153. [Google Scholar] [CrossRef]
- Ding, Y.; Fukumoto, K.; Ezekoye, O.A.; Lu, S.; Wang, C.; Li, C. Experimental and numerical simulation of multi-component combustion of typical charring material. Combust. Flame 2020, 211, 417–429. [Google Scholar] [CrossRef]
- Ding, Y.; Ezekoye, O.A.; Lu, S.; Wang, C. Thermal degradation of beech wood with thermogravimetry/fourier transform infrared analysis. Energy Convers. Manag. 2016, 120, 370–377. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Y.; Zhang, J.; Zhou, R.; Ren, Z.; Guo, H. Kinetic parameters estimation of pinus sylvestris pyrolysis by Kissinger-Kai method coupled with particle swarm optimization and global sensitivity analysis. Bioresour. Tech. 2019, 293, 122079. [Google Scholar] [CrossRef]
- Vyazovkin, S.; Burnham, A.K.; Criado, J.M.; Pérez-Maqueda, L.A.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Collazzo, G.C.; Broetto, C.C.; Perondi, D.; Junges, J.; Dettmer, A.; Dornelles Filho, A.A.; Godinho, M. A detailed non-isothermal kinetic study of elephant grass pyrolysis from different models. Appl. Therm. Eng. 2017, 110, 1200–1211. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Tariq, R.; Hameed, Z.; Ali, I.; Naqvi, M.; Chen, W.H.; Shahbaz, M. Pyrolysis of high ash sewage sludge: Kinetics and thermodynamic analysis using Coats-Redfern method. Renew. Energy 2019, 131, 854–860. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determintion of activtion energy from thermogravimetric data. Poly. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Ozawa, T. A new method of analyzing thermogravimetric data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Coats, A.W.; Redfern, J. Kinetic parameters from thermogravimetric data. Nature 1964, 201, 68–69. [Google Scholar] [CrossRef]
- Chen, R.; Li, Q.; Zhang, Y.; Xu, X.; Zhang, D. Pyrolysis kinetics and mechanism of typical industrial non-tyre rubber wastes by peak-differentiating analysis and multi kinetics methods. Fuel 2019, 235, 1224–1237. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V.K. Optimal use of the SCE-UA global optimization method for calibrating watershed models. J. Hydrol. 1994, 158, 265–284. [Google Scholar] [CrossRef]
- Chaos, M.; Khan, M.M.; Krishnamoorthy, N.; de Ris, J.L.; Dorofeev, S.B. Evaluation of optimization schemes and determination of solid fuel properties for CFD fire models using bench-scale pyrolysis tests. Proc. Combust. Inst. 2011, 33, 2599–2606. [Google Scholar] [CrossRef]
- Castro, A.; Soares, D.; Vilarinho, C.; Castro, F. Kinetics of thermal de-chlorination of PVC under pyrolytic conditions. Waste Manag. 2012, 32, 847–851. [Google Scholar] [CrossRef]
- Liebman, S.; Ahlstrom, D.; Quinn, E.; Geigley, A.; Meluskey, J. Thermal decomposition of poly (vinyl chloride) and chlorinated poly (vinyl chloride). II. Organic analysis. J. Poly. Sci. Part A-1 Poly. Chem. 1971, 9, 1921–1935. [Google Scholar] [CrossRef]
- Carty, P.; White, S. Anomalous flammability behaviour of CPVC (chlorinated poly vinylchloride) in blends with ABS (acrylonitrile-butadiene-styrene) containing flame-retarding/ smoke-suppressing compounds. Polymer 1997, 38, 1111–1119. [Google Scholar] [CrossRef]
- Kim, S. Pyrolysis kinetics of waste PVC pipe. Waste Manag. 2001, 21, 609–616. [Google Scholar] [CrossRef]
- Yu, J.; Sun, L.; Ma, C.; Qiao, Y.; Yao, H. Thermal degradation of PVC: A review. Waste Manag. 2016, 48, 300–314. [Google Scholar] [CrossRef] [PubMed]
- Aracil, I.; Font, R.; Conesa, J.A. Semivolatile and volatile compounds from the pyrolysis and combustion of polyvinyl chloride. J. Anal. Appl. Pyrolysis 2005, 74, 465–478. [Google Scholar] [CrossRef]
- Lattimer, R.P.; Pausch, J.B.; Meuzelaar, H.L.C. Pyrolysis studies of chlorinated poly(vinyl chloride). Macromolecules 1983, 16, 1896–1900. [Google Scholar] [CrossRef]

| Reaction Model | Differential Form f(α) | Integral Form g(α) |
|---|---|---|
| Power law models | ||
| Power law (P3/2) | 2/3α−1/2 | α3/2 |
| Power law (P2) | 2α1/2 | α1/2 |
| Power law (P3) | 3α2/3 | α1/3 |
| Power law (P4) | 4α3/4 | α1/4 |
| Nucleation models | ||
| Avrami-Erofeev (A2) | 2(1 − α)[−ln(1 − α)]1/2 | [−ln(1 − α)]1/2 |
| Avrami-Erofeev (A3) | 3(1 − α)[−ln(1 − α)]2/3 | [−ln(1 − α)]1/3 |
| Avrami-Erofeev (A4) | 4(1 − α)[−ln(1 − α)]3/4 | [−ln(1 − α)]1/4 |
| Reaction-order models | ||
| First order (F1) | 1 − α | −ln(1 − α) |
| Second order (F2) | (1 − α)2 | [1 − (1 − α)(−1)]/(−1) |
| Third order (F3) | (1 − α)3 | [1 − (1 − α)(−2)]/(−2) |
| Fourth order (F4) | (1 − α)4 | [1 − (1 − α)(−3)]/(−3) |
| Diffusion models | ||
| 1-D diffusion (D1) | (1/2)α−1 | α2 |
| 2-D diffusion−Valensi (D2) | [−ln(1 − α)]−1 | (1 − α)ln(1 − α) + α |
| 3-D diffusion-Jander (D3) | (3/2)[1 − (1 − α)1/3]−1(1 − α)2/3 | [1 − (1 − α)1/3]2 |
| 3-D diffusion-Ginstling (D4) | (3/2)[1 − (1 − α)1/3]−1 | [1 − (2/3)α]−(1 − α)2/3 |
| Geometrical contraction models | ||
| Prout-Tompkins (R1) | 1 | α |
| Contracting cylinder (R2) | 2(1 − α)1/2 | 1 − (1 − α)1/2 |
| Contracting sphere (R3) | 3(1 − α)2/3 | 1 − (1 − α)1/3 |
| Stage | α | Ea (kJ/mol) | R2 | lnA [ln(min−1)] |
|---|---|---|---|---|
| StageI | 0.10 | 143.41 | 0.9933 | 28.44 |
| 0.15 | 142.47 | 0.9973 | 28.33 | |
| 0.20 | 141.19 | 0.9981 | 28.11 | |
| 0.25 | 140.14 | 0.9991 | 27.93 | |
| 0.30 | 139.29 | 0.9993 | 27.77 | |
| 0.35 | 137.81 | 0.9988 | 27.47 | |
| 0.40 | 136.05 | 0.9990 | 27.08 | |
| 0.45 | 138.70 | 0.9982 | 27.57 | |
| 0.50 | 143.39 | 0.9988 | 28.42 | |
| Mean value | 140.27 | 0.9980 | 27.90 a | |
| StageII | 0.70 | 232.68 | 0.9915 | 41.77 |
| 0.75 | 253.13 | 0.9975 | 44.94 | |
| 0.80 | 255.24 | 0.9982 | 45.27 | |
| 0.85 | 243.24 | 0.9966 | 43.48 | |
| Mean value | 246.07 | 0.9959 | 43.87 b |
| Reaction Model | 10 K/min | 20 K/min | 30 K/min | 60 K/min | Average Value | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ea | R2 | Ea | R2 | Ea | R2 | Ea | R2 | Ea | R2 | |
| P3/2 | 187.94 | 0.9572 | 181.12 | 0.9671 | 184.78 | 0.9606 | 182.56 | 0.9755 | 184.10 | 0.9651 |
| P2 | 56.33 | 0.9471 | 53.92 | 0.9586 | 55.02 | 0.9504 | 54.61 | 0.9689 | 54.86 | 0.9562 |
| P3 | 34.40 | 0.9371 | 32.72 | 0.9500 | 33.39 | 0.9401 | 32.76 | 0.9621 | 33.32 | 0.9473 |
| P4 | 23.43 | 0.9241 | 22.12 | 0.9386 | 22.58 | 0.9264 | 22.06 | 0.9528 | 22.55 | 0.9355 |
| A2 | 67.93 | 0.9687 | 65.07 | 0.9778 | 66.45 | 0.9674 | 65.35 | 0.9853 | 66.20 | 0.9748 |
| A3 | 42.13 | 0.9637 | 40.15 | 0.9739 | 41.01 | 0.9723 | 40.22 | 0.9826 | 40.88 | 0.9731 |
| A4 | 29.23 | 0.9575 | 27.70 | 0.9690 | 28.29 | 0.9612 | 27.66 | 0.9791 | 28.22 | 0.9667 |
| F1 | 145.33 | 0.9727 | 139.81 | 0.9809 | 142.76 | 0.9762 | 140.73 | 0.9875 | 142.16 | 0.9793 |
| F2 | 171.71 | 0.9847 | 165.14 | 0.9909 | 168.74 | 0.9880 | 166.13 | 0.9953 | 167.93 | 0.9898 |
| F3 | 201.20 | 0.9920 | 193.44 | 0.9963 | 197.79 | 0.9951 | 194.50 | 0.9989 | 196.73 | 0.9956 |
| F4 | 233.61 | 0.9958 | 224.54 | 0.9985 | 229.71 | 0.9986 | 225.66 | 0.9993 | 228.38 | 0.9980 |
| D1 | 253.75 | 0.9583 | 244.71 | 0.9680 | 249.66 | 0.9617 | 246.76 | 0.9762 | 248.72 | 0.9661 |
| D2 | 268.18 | 0.9641 | 258.59 | 0.9731 | 263.89 | 0.9675 | 260.69 | 0.9807 | 262.84 | 0.9713 |
| D3 | 283.97 | 0.9697 | 273.75 | 0.9781 | 279.44 | 0.9731 | 275.91 | 0.9849 | 278.27 | 0.9764 |
| D4 | 273.44 | 0.9660 | 263.64 | 0.9749 | 269.07 | 0.9695 | 265.76 | 0.9822 | 267.97 | 0.9732 |
| R1 | 122.14 | 0.9550 | 117.52 | 0.9652 | 119.90 | 0.9584 | 118.36 | 0.9741 | 119.48 | 0.9632 |
| R2 | 133.34 | 0.9646 | 128.28 | 0.9738 | 130.94 | 0.9681 | 132.94 | 0.9837 | 131.37 | 0.9726 |
| R3 | 137.25 | 0.9675 | 132.04 | 0.9763 | 134.79 | 0.9710 | 129.17 | 0.9815 | 133.31 | 0.9741 |
| Reaction Model | 10 K/min | 20 K/min | 30 K/min | 60 K/min | Average Value | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ea | R2 | Ea | R2 | Ea | R2 | Ea | R2 | Ea | R2 | |
| P3/2 | 20.98 | 0.9836 | 21.42 | 0.9896 | 22.46 | 0.9973 | 21.55 | 0.9981 | 21.60 | 0.9922 |
| P2 | −1.01 | 0.5348 | −0.98 | 0.6524 | −0.74 | 0.7680 | −1.17 | 0.9317 | −0.97 | 0.7217 |
| P3 | −4.67 | 0.9880 | −4.71 | 0.9926 | −4.60 | 0.9967 | −4.96 | 0.9980 | −4.74 | 0.9939 |
| P4 | −6.50 | 0.9970 | −6.58 | 0.9982 | −6.54 | 0.9990 | −6.85 | 0.9943 | −6.62 | 0.9971 |
| A2 | 13.56 | 0.9188 | 13.89 | 0.9372 | 14.74 | 0.9763 | 13.99 | 0.9284 | 14.04 | 0.9402 |
| A3 | 5.04 | 0.7727 | 5.20 | 0.8229 | 5.72 | 0.9352 | 5.15 | 0.9284 | 5.28 | 0.8648 |
| A4 | 0.78 | −0.2026 | 0.85 | −0.0941 | 1.20 | 0.4707 | 0.73 | 0.1447 | 0.89 | 0.0709 |
| F1 | 39.12 | 0.9587 | 39.96 | 0.9680 | 41.82 | 0.9875 | 40.50 | 0.9879 | 40.35 | 0.9755 |
| F2 | 87.28 | 0.9469 | 89.15 | 0.9563 | 93.09 | 0.9777 | 90.70 | 0.9779 | 90.05 | 0.9647 |
| F3 | 150.74 | 0.9410 | 153.98 | 0.9506 | 160.68 | 0.9725 | 156.88 | 0.9727 | 155.57 | 0.9592 |
| F4 | 222.63 | 0.9394 | 227.40 | 0.9488 | 237.21 | 0.9708 | 231.81 | 0.9710 | 229.76 | 0.9575 |
| F5 | 298.04 | 0.9394 | 304.42 | 0.9487 | 317.47 | 0.9704 | 310.40 | 0.9707 | 307.58 | 0.9573 |
| D1 | 31.97 | 0.9871 | 32.62 | 0.9918 | 34.06 | 0.9979 | 32.91 | 0.9986 | 32.89 | 0.9939 |
| D2 | 45.87 | 0.9822 | 46.80 | 0.9877 | 48.81 | 0.9971 | 47.34 | 0.9976 | 47.21 | 0.9911 |
| D3 | 66.66 | 0.9746 | 68.03 | 0.9810 | 70.91 | 0.9938 | 68.98 | 0.9943 | 68.65 | 0.9859 |
| D4 | 52.62 | 0.9794 | 53.69 | 0.9853 | 55.98 | 0.9961 | 54.37 | 0.9966 | 54.16 | 0.9893 |
| R1 | 9.99 | 0.9694 | 10.22 | 0.9807 | 10.86 | 0.9950 | 10.19 | 0.9963 | 10.31 | 0.9854 |
| R2 | 22.25 | 0.9655 | 22.73 | 0.9751 | 23.88 | 0.9931 | 28.23 | 0.9918 | 24.27 | 0.9814 |
| R3 | 27.33 | 0.9633 | 27.92 | 0.9727 | 29.28 | 0.9913 | 22.93 | 0.9937 | 26.87 | 0.9803 |
| Parameters | Calculated Values | Search Range | Optimized Values |
|---|---|---|---|
| YA,0 | 0.50 a | [0, 1] | 0.61 |
| lnAA[ln (min−1)] | 27.90 | [13.95, 41.85] | 29.98 |
| Ea,A (kJ/mol) | 140.27 | [70.14, 210.41] | 146.75 |
| nA | 1.00 | - | - |
| vA | 0.50 a | [0, 1] | 0.35 |
| lnAB[ln (min−1)] | 43.87 | [21.935, 65.81] | 54.94 |
| Ea,B (kJ/mol) | 246.07 | [123.04, 369.11] | 332.81 |
| nB | 4.00 | - | - |
| vB | 0.50 a | [0, 1] | 0.44 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, R.; Huang, B.; Ding, Y.; Li, W.; Mu, J. Thermal Decomposition Mechanism and Kinetics Study of Plastic Waste Chlorinated Polyvinyl Chloride. Polymers 2019, 11, 2080. https://doi.org/10.3390/polym11122080
Zhou R, Huang B, Ding Y, Li W, Mu J. Thermal Decomposition Mechanism and Kinetics Study of Plastic Waste Chlorinated Polyvinyl Chloride. Polymers. 2019; 11(12):2080. https://doi.org/10.3390/polym11122080
Chicago/Turabian StyleZhou, Ru, Biqing Huang, Yanming Ding, Wenjuan Li, and Jingjing Mu. 2019. "Thermal Decomposition Mechanism and Kinetics Study of Plastic Waste Chlorinated Polyvinyl Chloride" Polymers 11, no. 12: 2080. https://doi.org/10.3390/polym11122080
APA StyleZhou, R., Huang, B., Ding, Y., Li, W., & Mu, J. (2019). Thermal Decomposition Mechanism and Kinetics Study of Plastic Waste Chlorinated Polyvinyl Chloride. Polymers, 11(12), 2080. https://doi.org/10.3390/polym11122080