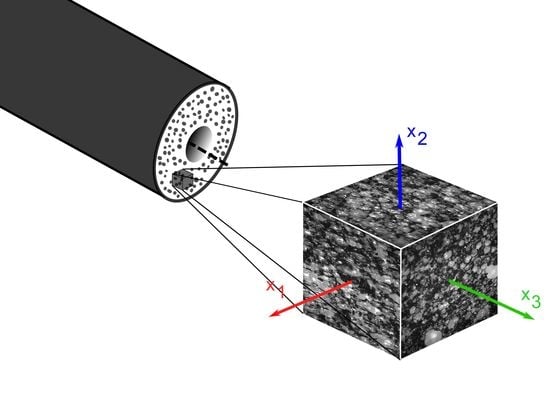
Anisotropy in Polyurethane Pre-Insulated Pipes
Abstract
1. Introduction
- The relative density.
- The degree to which cells are open or closed.
- The geometric anisotropy of the foams.
- ρf = density of the foam
- ρs = density of the basis solid material
- (a)
- The foam manufacturing process can have a great influence on the resulting microstructure of the foam [21]. All previous studies have been conducted with PU slabs foamed in rectangular moulds, where the distance between the mould walls is significantly larger than in pre-insulated pipes. Since cell anisotropy in foams is caused by the acting viscous forces between the liquid and the mould walls during the foaming process [7], it is expected that the narrower distance between mould walls in the case of the pre-insulated pipes will have a higher impact on the anisotropy of the cells. Moreover, the geometry of the mould, annular in the case of pipes, could have an influence on the cell’s microstructure. Furthermore, the effects of manufacturing in a continuous process remains to be explored.
- (b)
- (c)
- Not all studies cover the three orthogonal directions.
2. Materials and Methods
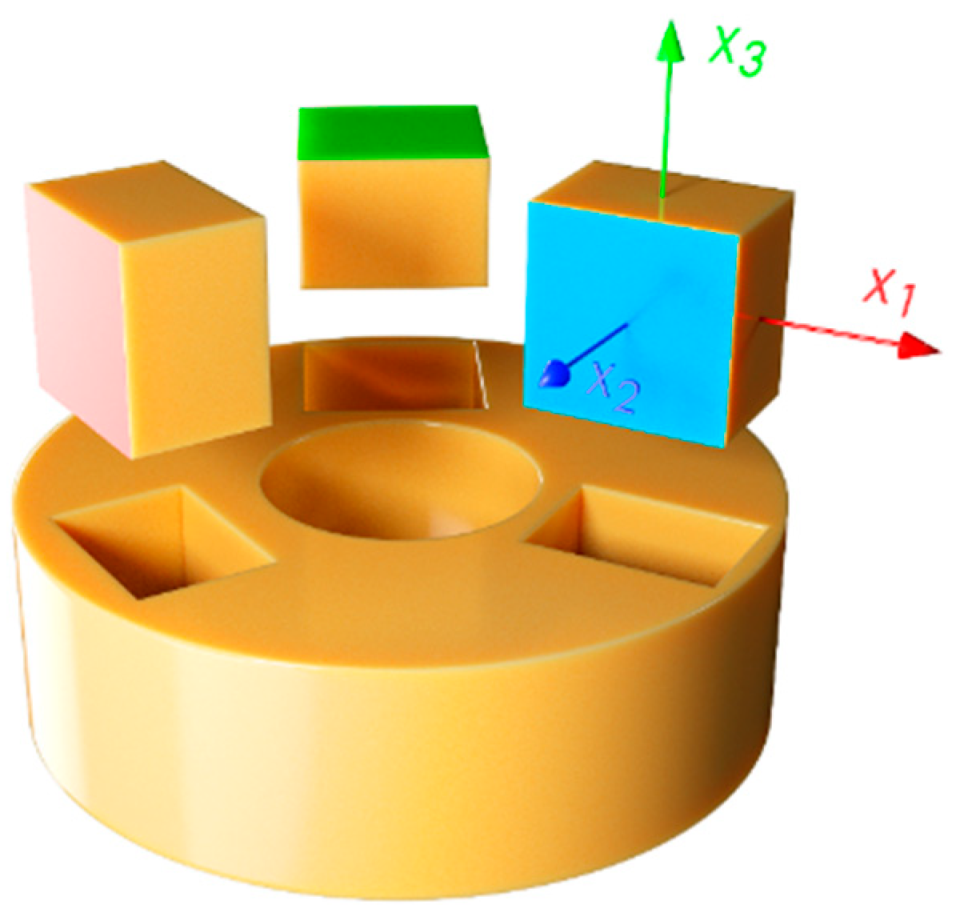
2.1. Sample Preparation
2.2. Microstructural Characterization
2.3. Mechanical Characterization
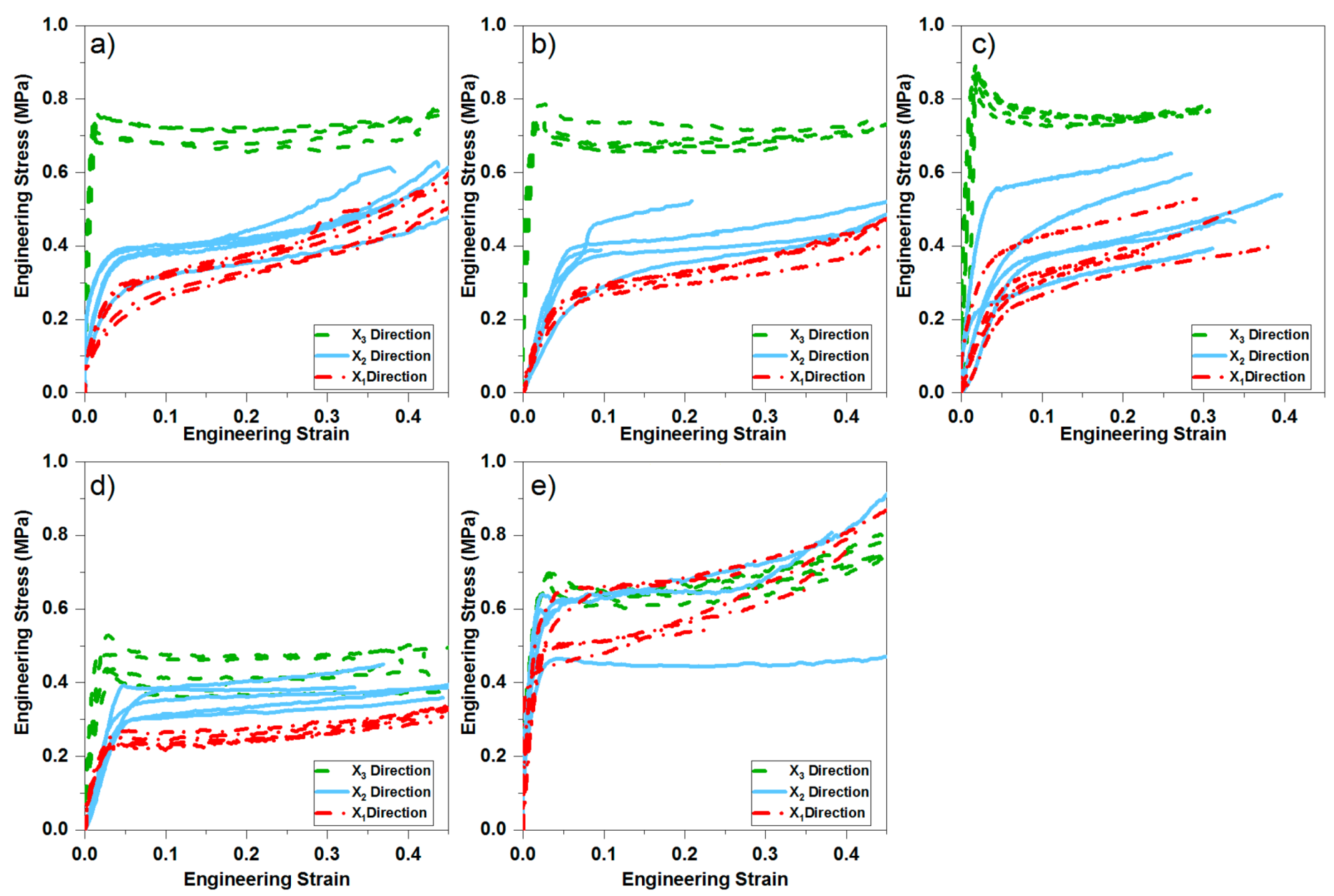
3. Results
3.1. Microstructure of the PU Foam
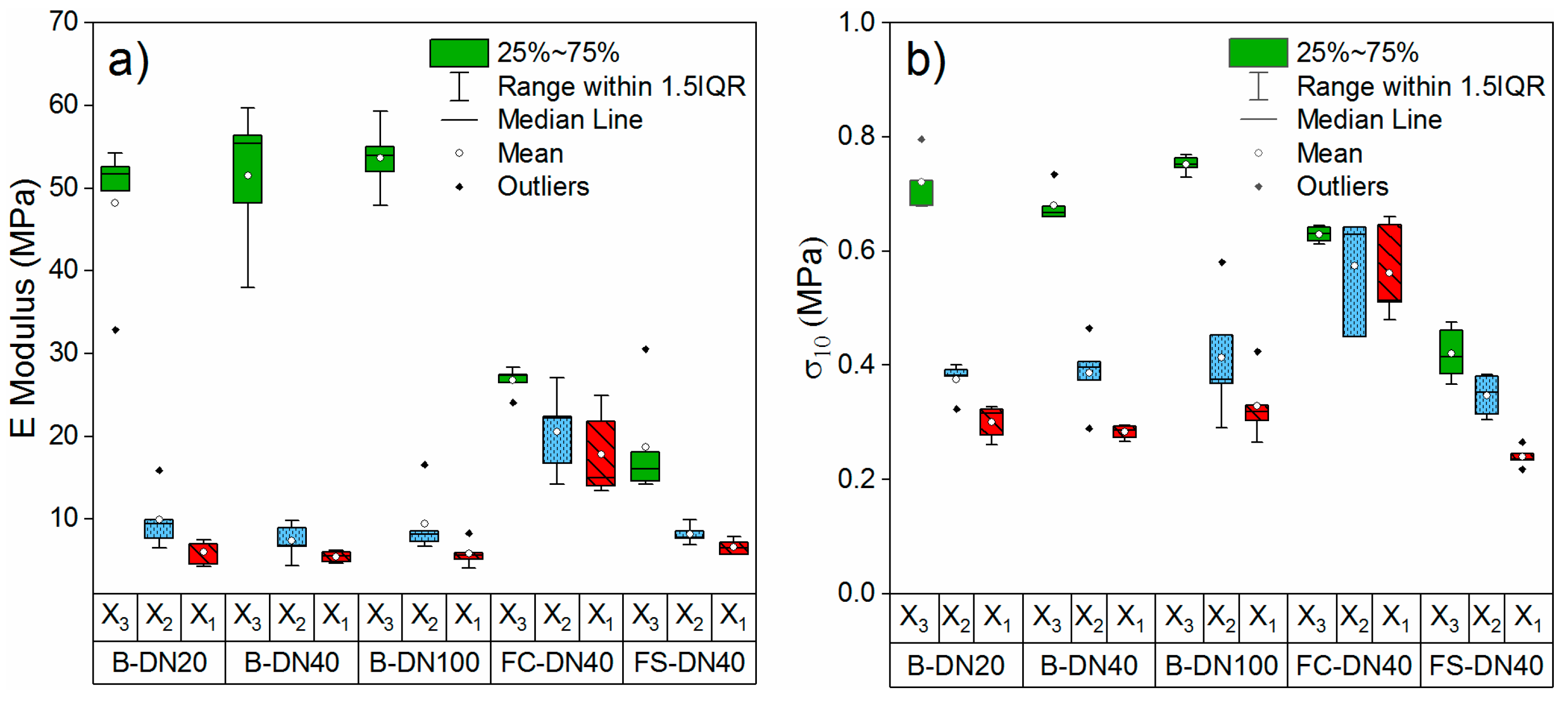
3.2. Mechanical Behaviour of the PU Foam
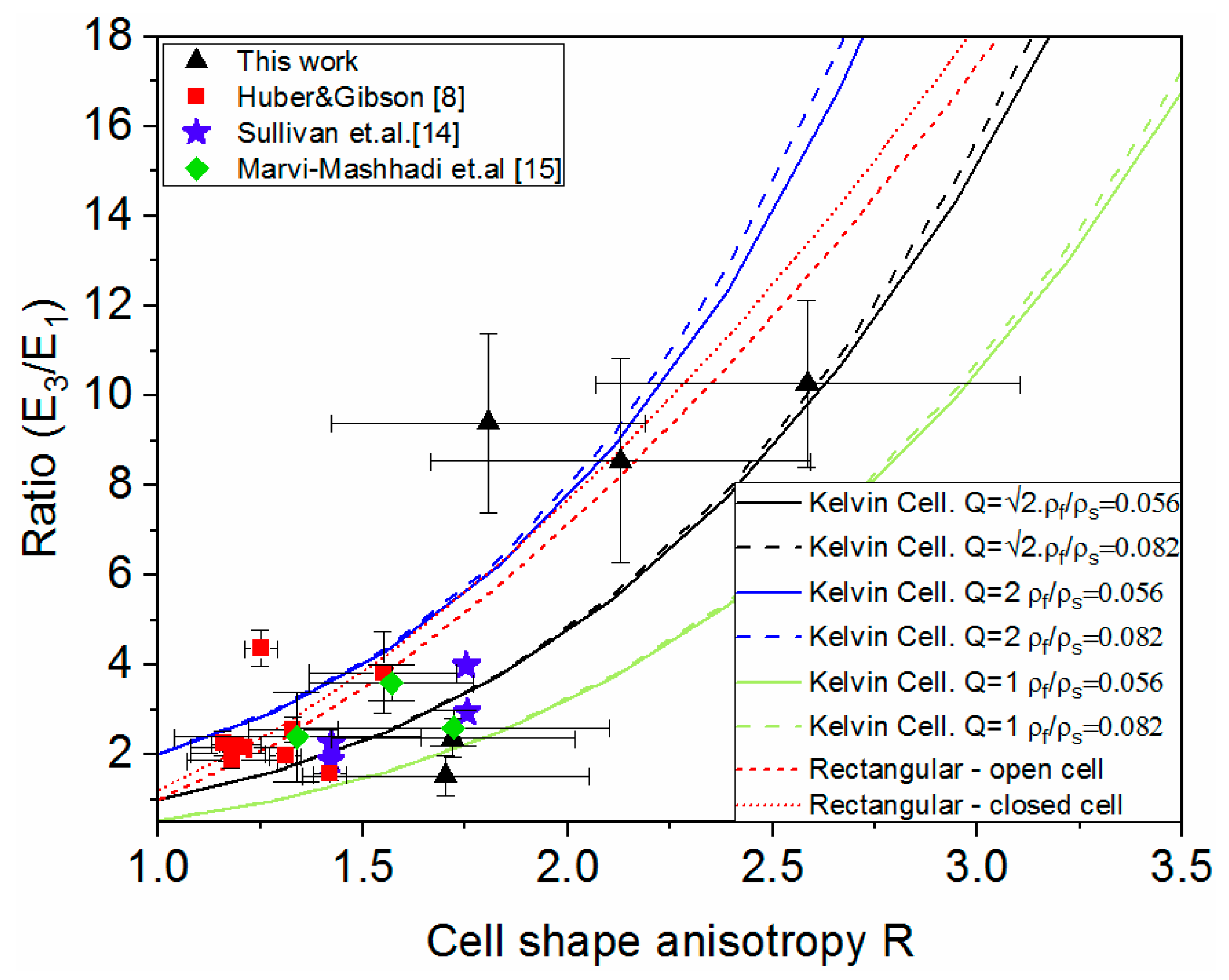
4. Discussion
4.1. Microstructure of the PU Foam
4.1.1. Effect of Pipe Diameter
4.1.2. Comparison between Smooth and Corrugated Flexible Pipes
4.2. Mechanical Behaviour of the PU Foam and Relation to the Cell Shape Anisotropy
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Logstor. New Standards for Production. Available online: https://www.logstor.com/about-us/hseq/production (accessed on 9 September 2019).
- Christensen, R. Fatigue Analysis of District Heating Systems. Neth. Agency Energy Environ. 1999, 7, 8. [Google Scholar]
- EN 13941-1: District Heating Pipes—Design and Installation of Thermal Insulated Bonded Single and Twin Pipe Systems for Directly Buried Hot Water Networks—Part 1: Design; European Committee for Standardization: Brussels, Belgium, 2016.
- Vega, A.; Yarahmadi, N.; Jakubowicz, I. Determination of the long-term performance of district heating pipes through accelerated ageing. Polym. Degrad. Stab. 2018, 153, 15–22. [Google Scholar] [CrossRef]
- Yarahmadi, N.; Vega, A.; Jakubowicz, I. Accelerated ageing and degradation characteristics of rigid polyurethane foam. Polym. Degrad. Stab. 2017, 138, 192–200. [Google Scholar] [CrossRef]
- Yarahmadi, N.; Vega, A.; Jakubowicz, I. Determination of essential parameters influencing service life time of polyurethane insulation in district heating pipes. Energy Procedia 2017, 116, 320–323. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids; Cambridge University Press: Cambridge, UK, 1997; ISBN 9781139878326. [Google Scholar]
- Huber, A.T.; Gibson, L.J. Anisotropy of foams. J. Mater. Sci. 1988, 23, 3031–3040. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. The Mechanics of Three-Dimensional Cellular Materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1982, 382, 43–59. [Google Scholar] [CrossRef]
- Chen, Y.; Das, R.; Battley, M. Effects of cell size and cell wall thickness variations on the stiffness of closed-cell foams. Int. J. Solids Struct. 2015, 52, 150–164. [Google Scholar] [CrossRef]
- Thomson, W. LXIII. On the division of space with minimum partitional area. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1887, 24, 503–514. [Google Scholar] [CrossRef]
- Gong, L.; Kyriakides, S.; Jang, W.-Y. Compressive response of open-cell foams. Part I: Morphology and elastic properties. Int. J. Solids Struct. 2005, 42, 1355–1379. [Google Scholar] [CrossRef]
- Ridha, M.; Shim, V.P.W.; Yang, L.M. An Elongated Tetrakaidecahedral Cell Model for Fracture in Rigid Polyurethane Foam. KEM 2006, 306, 43–48. [Google Scholar] [CrossRef]
- Sullivan, R.M.; Ghosn, L.J.; Lerch, B.A. A general tetrakaidecahedron model for open-celled foams. Int. J. Solids Struct. 2008, 45, 1754–1765. [Google Scholar] [CrossRef]
- Linul, E.; Marsavina, L.; Voiconi, T.; Sadowski, T. Study of factors influencing the mechanical properties of polyurethane foams under dynamic compression. J. Phys. Conf. Ser. 2013, 451, 012002. [Google Scholar] [CrossRef]
- Marsavina, L.; Constantinescu, D.M.; Linul, E.; Apostol, D.A.; Voiconi, T.; Sadowski, T. Refinements on fracture toughness of PUR foams. Eng. Fract. Mech. 2014, 129, 54–66. [Google Scholar] [CrossRef]
- Marsavina, L.; Constantinescu, D.M.; Linul, E.; Voiconi, T.; Apostol, D.A. Shear and mode II fracture of PUR foams. Eng. Fail. Anal. 2015, 58, 465–476. [Google Scholar] [CrossRef]
- Marsavina, L.; Linul, E.; Voiconi, T.; Sadowski, T. A comparison between dynamic and static fracture toughness of polyurethane foams. Polym. Test. 2013, 32, 673–680. [Google Scholar] [CrossRef]
- Hamilton, A.R.; Thomsen, O.T.; Madaleno, L.A.O.; Jensen, L.R.; Rauhe, J.C.M.; Pyrz, R. Evaluation of the anisotropic mechanical properties of reinforced polyurethane foams. Compos. Sci. Technol. 2013, 87, 210–217. [Google Scholar] [CrossRef]
- Marvi-Mashhadi, M.; Lopes, C.S.; LLorca, J. Effect of anisotropy on the mechanical properties of polyurethane foams: An experimental and numerical study. Mech. Mater. 2018, 124, 143–154. [Google Scholar] [CrossRef]
- Kurańska, M.; Prociak, A. Bio-Based Polyurethane Foams for Heat-Insulating Applications. In Nano and Biotech Based Materials for Energy Building Efficiency; Pacheco Torgal, F., Buratti, C., Kalaiselvam, S., Granqvist, C.-G., Ivanov, V., Eds.; Springer International Publishing: Cham, Switzerland, 2016; pp. 357–373. ISBN 978-3-319-27503-1. [Google Scholar]
- Akindoyo, J.O.; Beg, M.D.H.; Ghazali, S.; Islam, M.R.; Jeyaratnam, N.; Yuvaraj, A.R. Polyurethane types, synthesis and applications—A review. RSC Adv. 2016, 6, 114453–114482. [Google Scholar] [CrossRef]
- Gama, N.V.; Ferreira, A.; Barros-Timmons, A. Polyurethane Foams: Past, Present, and Future. Materials 2018, 11, 3390. [Google Scholar] [CrossRef]
- Orzel, R.A.; Womble, S.E.; Ahmed, F.; Brasted, H.S. Flexible Polyurethane Foam: A Literature Review of Thermal Decomposition Products and Toxicity. J. Am. Coll. Toxicol. 1989, 8, 1139–1175. [Google Scholar] [CrossRef]
- Logstor Product Catalogue; LOGSTOR: Løgstør, Denmark, 2019.
- EN 253: District Heating Pipes—Preinsulated Bonded Pipe Systems for Directly Buried Hot Water Networks—Pipe Assembly of Steel Service Pipe, Polyurethane Thermal Insulation and Outer Casing of Polyethylene; European Committee for Standardization: Brussels, Belgium, 2009.
- EN 15632-1: District Heating Pipes—Pre-Insulated Flexible Pipe Systems—Part 1: Classification; European Committee for Standardization: Brussels, Belgium, 2015.
- EN 15632-2: District Heating Pipes—Pre-Insulated Flexible Pipe Systems—Part 2: Bonded Plastic Service Pipes; European Committee for Standardization: Brussels, Belgium, 2015.
- Jin, H.; Lu, W.-Y.; Scheffel, S.; Hinnerichs, T.D.; Neilsen, M.K. Full-field characterization of mechanical behavior of polyurethane foams. Int. J. Solids Struct. 2007, 44, 6930–6944. [Google Scholar] [CrossRef][Green Version]
- Tekog˜lu, C.; Gibson, L.J.; Pardoen, T.; Onck, P.R. Size effects in foams: Experiments and modeling. Prog. Mater. Sci. 2011, 56, 109–138. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- ISO 844: Rigid Cellular Plastics—Determination of Compression Properties; International Organization for Standardization: Geneva, Switzerland, 2014.
- Peters, W.H.; Ranson, W.F. Digital Imaging Techniques in Experimental Stress Analysis. Opt. Eng. 1982, 21, 427–432. [Google Scholar] [CrossRef]
- Montminy, M.D.; Tannenbaum, A.R.; Macosko, C.W. The 3D structure of real polymer foams. J. Colloid Interface Sci. 2004, 280, 202–211. [Google Scholar] [CrossRef]
- Fischer, F.; Lim, G.T.; Handge, U.A.; Altstädt, V. Numerical Simulation of Mechanical Properties of Cellular Materials Using Computed Tomography Analysis. J. Cell. Plast. 2009, 45, 441–460. [Google Scholar] [CrossRef]
- Li, K.; Gao, X.-L.; Subhash, G. Effects of cell shape and strut cross-sectional area variations on the elastic properties of three-dimensional open-cell foams. J. Mech. Phys. Solids 2006, 54, 783–806. [Google Scholar] [CrossRef]

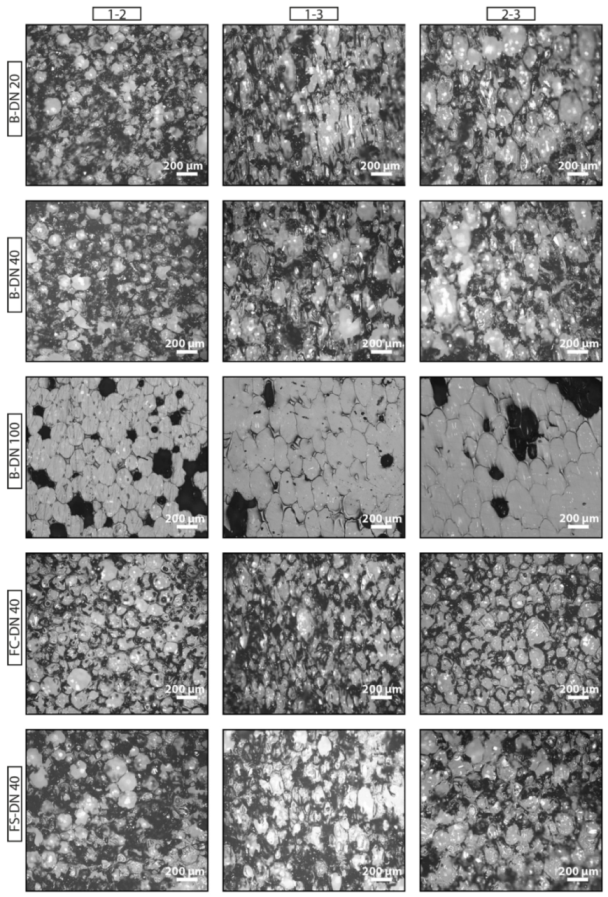
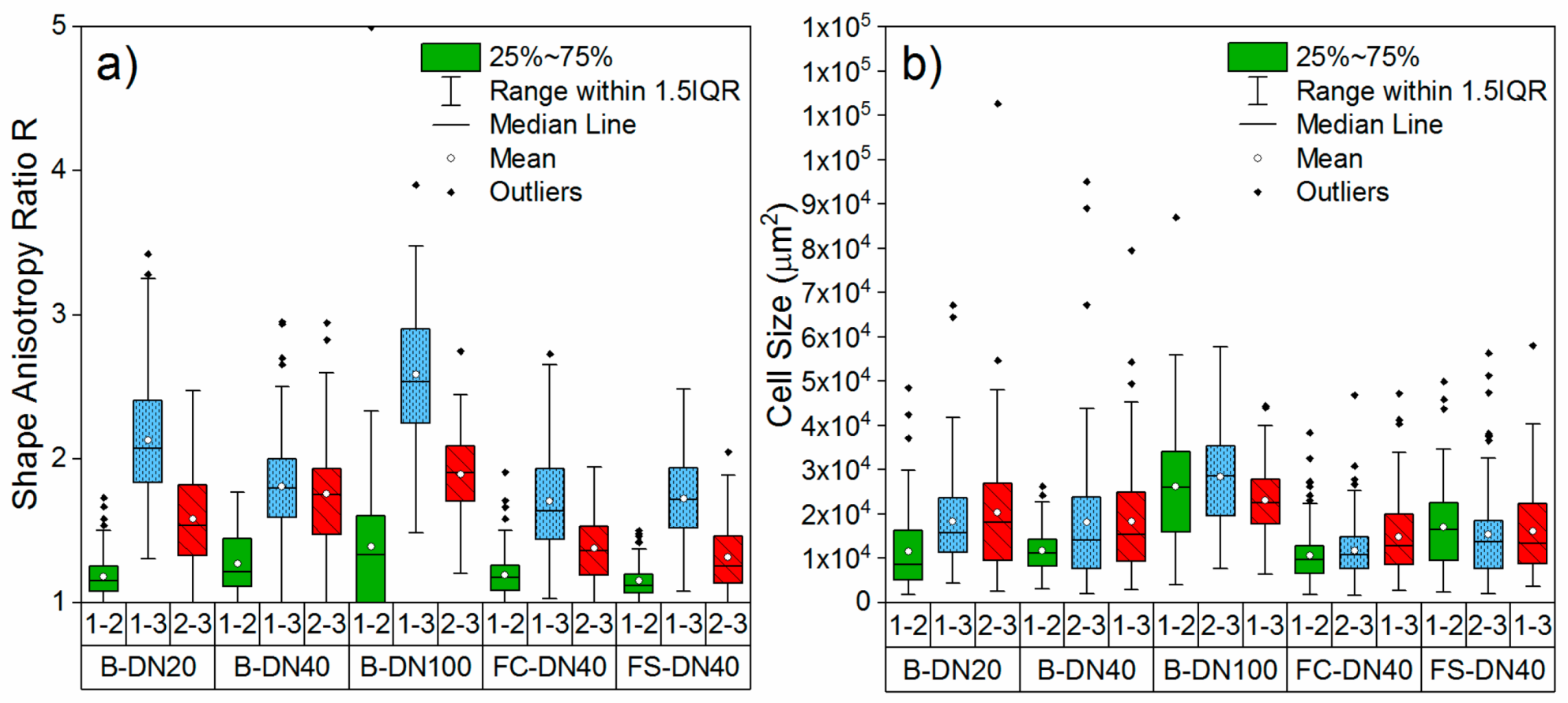
| Pipe | Plane | Number of Measured Cells | Mean Cell Area (mm2) | Cell Area Std. dev (mm2) | Mean R | R Standard Deviation | Symmetry |
|---|---|---|---|---|---|---|---|
| B-DN20 | 1-2 | 103 | 0.012 | 0.009 | 1.18 | 0.15 | orthotropic |
| 1-3 | 108 | 0.018 | 0.010 | 2.13 | 0.46 | ||
| 2-3 | 100 | 0.020 | 0.015 | 1.58 | 0.35 | ||
| B-DN40 | 1-2 | 114 | 0.012 | 0.005 | 1.27 | 0.19 | axisymmetric |
| 1-3 | 103 | 0.018 | 0.013 | 1.81 | 0.38 | ||
| 2-3 | 101 | 0.018 | 0.015 | 1.75 | 0.38 | ||
| B-DN100 | 1-2 | 79 | 0.026 | 0.013 | 1.39 | 0.54 | orthotropic |
| 1-3 | 81 | 0.023 | 0.008 | 2.58 | 0.52 | ||
| 2-3 | 74 | 0.028 | 0.011 | 1.89 | 0.31 | ||
| FC-DN40 | 1-2 | 130 | 0.011 | 0.006 | 1.19 | 0.15 | orthotropic |
| 1-3 | 107 | 0.015 | 0.008 | 1.70 | 0.35 | ||
| 2-3 | 137 | 0.012 | 0.007 | 1.37 | 0.23 | ||
| FS-DN40 | 1-2 | 100 | 0.017 | 0.010 | 1.15 | 0.12 | orthotropic |
| 1-3 | 100 | 0.016 | 0.010 | 1.72 | 0.30 | ||
| 2-3 | 101 | 0.015 | 0.010 | 1.32 | 0.24 |
| Pipe | (kg/m3) | Direction | E (MPa) | E Std dev (MPa) | σ10 (MPa) | σ10 St. dev (MPa) |
|---|---|---|---|---|---|---|
| B-DN20 | 76.2 | X3 | 52.1 | 1.9 | 0.72 | 0.05 |
| X2 | 8.4 | 1.6 | 0.38 | 0.03 | ||
| X1 | 6.1 | 1.5 | 0.30 | 0.03 | ||
| B-DN40 | 76.2 | X3 | 51.5 | 8.6 | 0.68 | 0.03 |
| X2 | 7.4 | 2.1 | 0.39 | 0.06 | ||
| X1 | 5.5 | 0.7 | 0.28 | 0.01 | ||
| B-DN100 | 75.6 | X3 | 53.6 | 4.2 | 0.75 | 0.02 |
| X2 | 7.7 | 0.8 | 0.41 | 0.11 | ||
| X1 | 5.2 | 0.8 | 0.33 | 0.06 | ||
| FS-DN40 | 67.9 | X3 | 15.7 | 1.8 | 0.63 | 0.01 |
| X2 | 8.2 | 1.1 | 0.57 | 0.11 | ||
| X1 | 6.6 | 1.0 | 0.56 | 0.08 | ||
| FC-DN40 | 99.2 | X3 | 27.4 | 0.8 | 0.42 | 0.05 |
| X2 | 20.5 | 5.1 | 0.35 | 0.04 | ||
| X1 | 17.9 | 5.2 | 0.24 | 0.02 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doyle, L.; Weidlich, I.; Illguth, M. Anisotropy in Polyurethane Pre-Insulated Pipes. Polymers 2019, 11, 2074. https://doi.org/10.3390/polym11122074
Doyle L, Weidlich I, Illguth M. Anisotropy in Polyurethane Pre-Insulated Pipes. Polymers. 2019; 11(12):2074. https://doi.org/10.3390/polym11122074
Chicago/Turabian StyleDoyle, Lucía, Ingo Weidlich, and Marcus Illguth. 2019. "Anisotropy in Polyurethane Pre-Insulated Pipes" Polymers 11, no. 12: 2074. https://doi.org/10.3390/polym11122074
APA StyleDoyle, L., Weidlich, I., & Illguth, M. (2019). Anisotropy in Polyurethane Pre-Insulated Pipes. Polymers, 11(12), 2074. https://doi.org/10.3390/polym11122074