Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy
Abstract
:1. Introduction
2. Theory
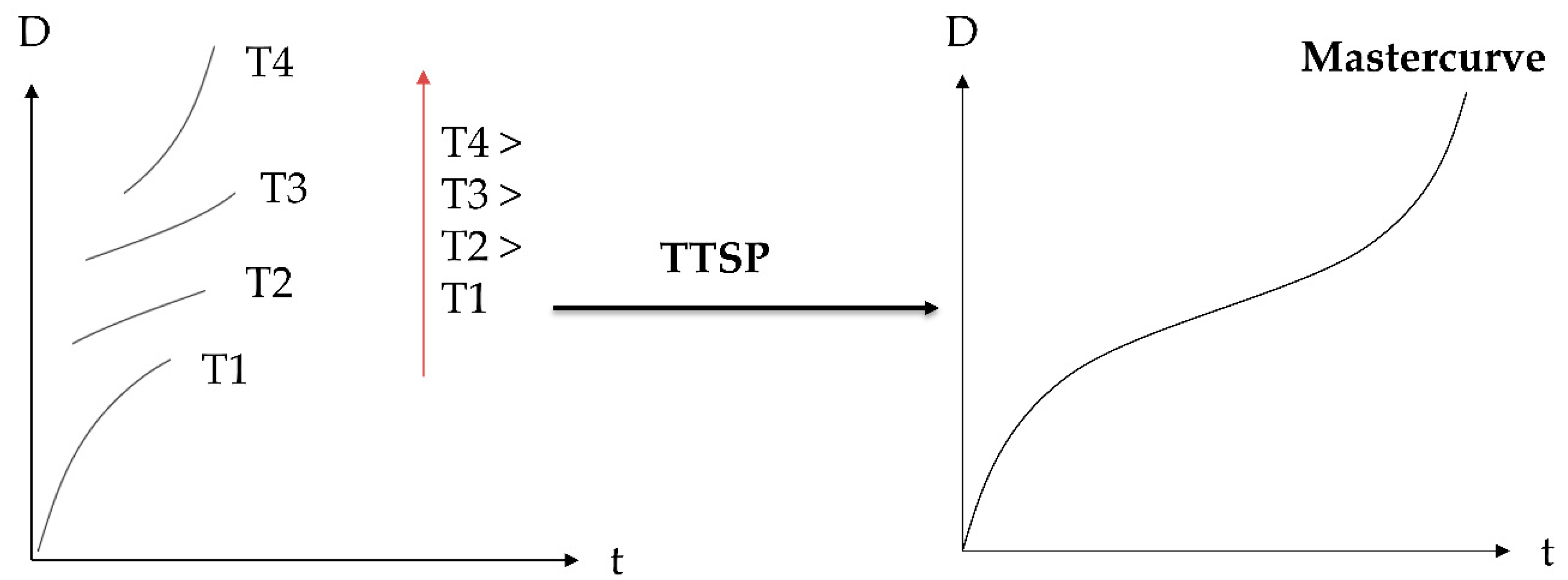
2.1. Time–Temperature Superposition
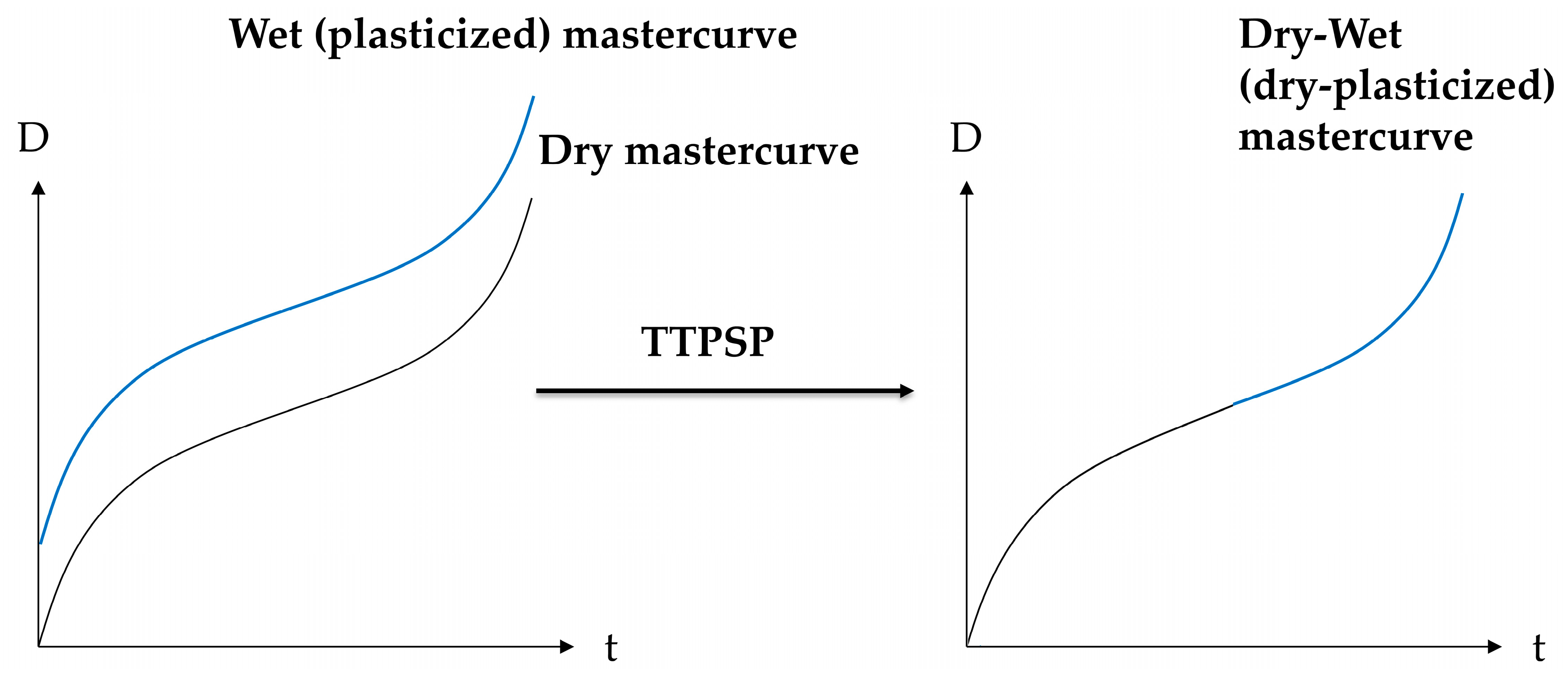
2.2. Proposed Principle: Time–Temperature–Plasticization Superposition
3. Materials and Methods
3.1. Epoxy Polymer
3.2. Conditioning in Water
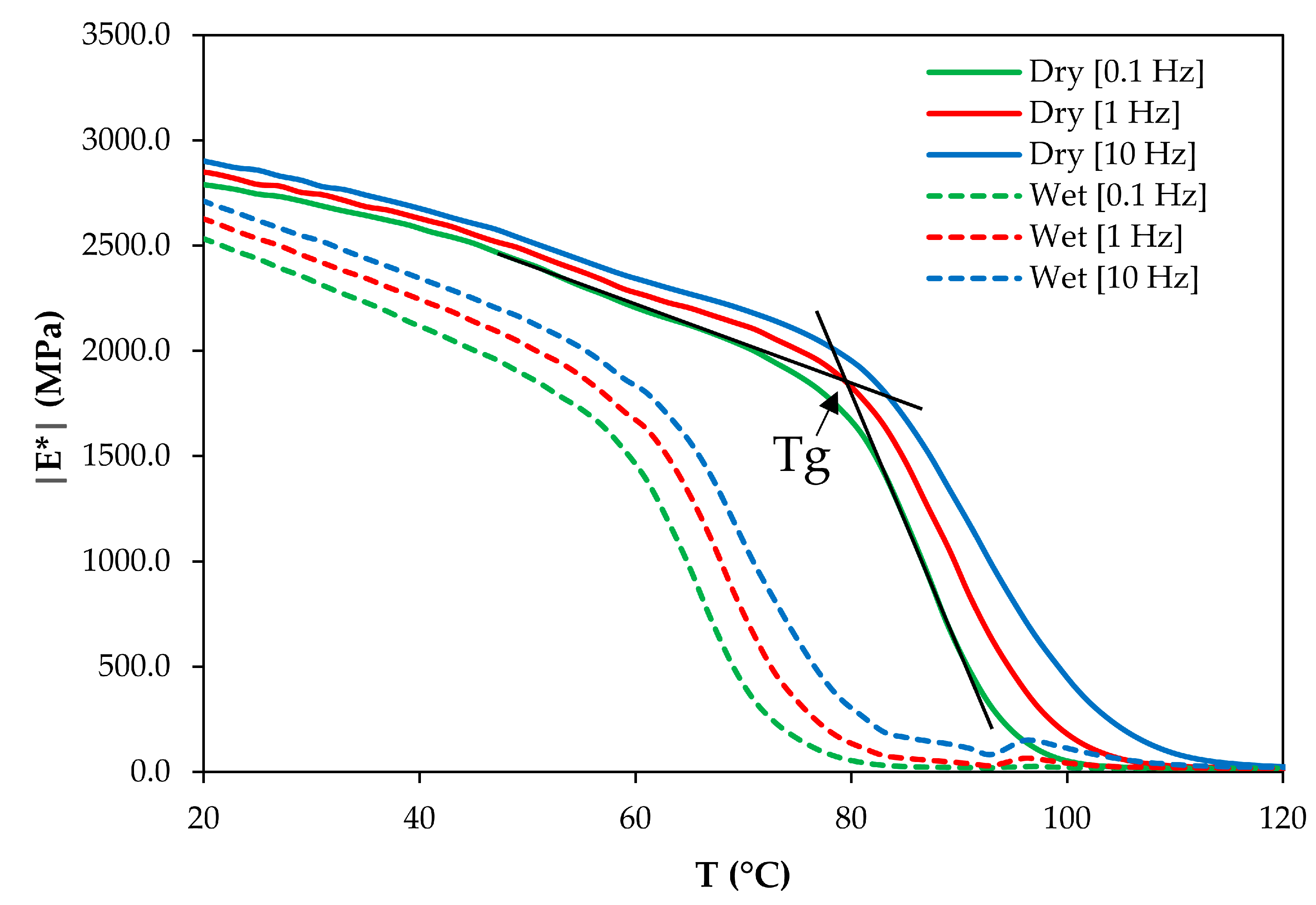
3.3. Glass Transition Measurements
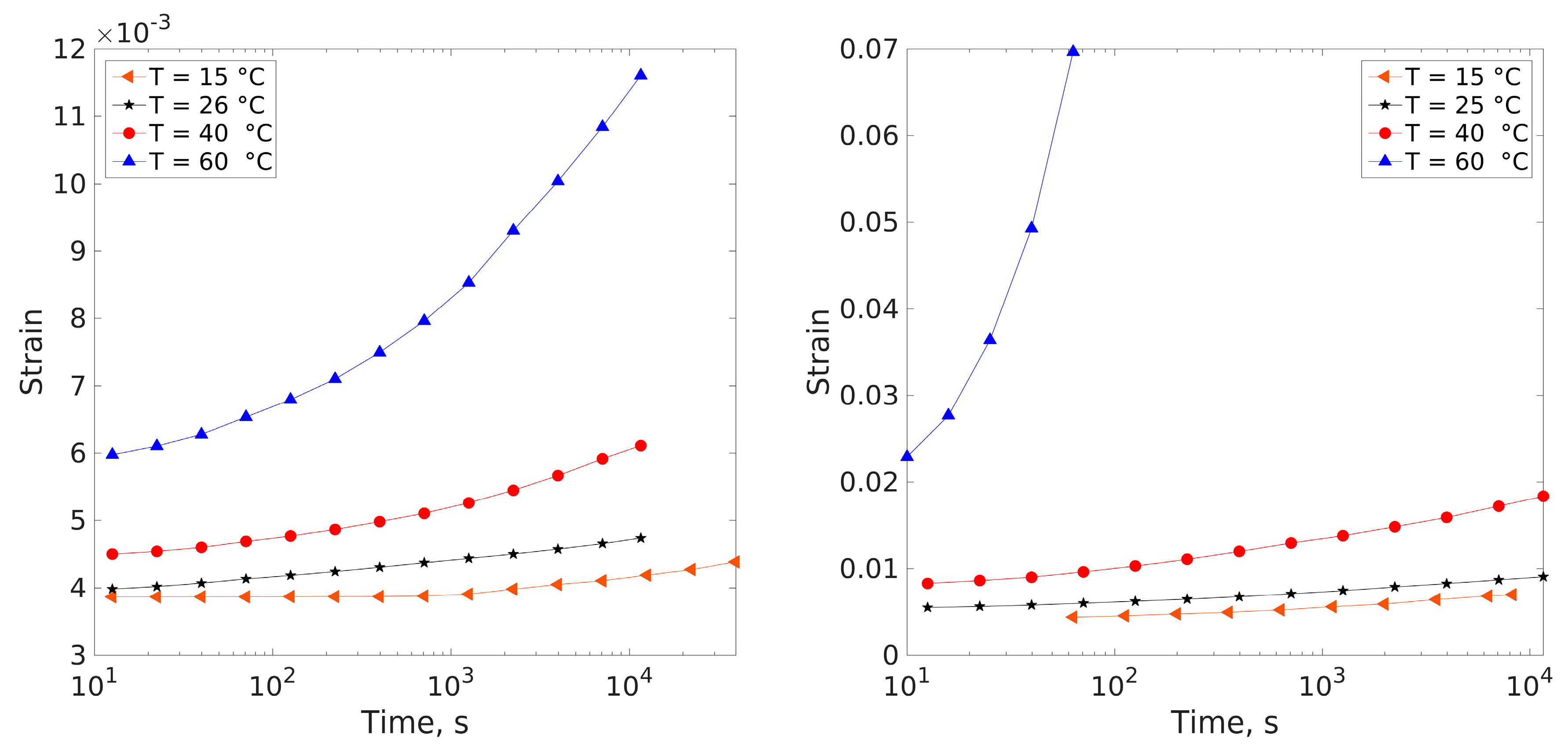
3.4. Creep Measurements
3.5. TTSP and TTPSP
4. Results and Discussion
4.1. Compliance Master Curves of Dry and Saturated Epoxy Time–Temperature Superposition Principle
4.2. Dry-Plasticized Compliance Master Curve Time–Temperature–Plasticization Superposition Principle
4.3. Predicting the Creep Characteristics of the Plastizised Epoxy from the Dry Data
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Xiao, G.Z.; Shanahan, M.E.R. Swelling of DGEBA/DDA epoxy resin during hygrothermal ageing. Polymer 1998, 39, 3253. [Google Scholar] [CrossRef]
- Toscano, A.; Pitarresi, G.; Scafidi, M.; Di Filippo, M.; Spadaro, G.; Alessi, S. Water diffusion and swelling stresses in highly crosslinked epoxy matrices. Polym. Degrad. Stab. 2016, 133, 255–263. [Google Scholar] [CrossRef] [Green Version]
- Pham, H.Q.; Marks, M.J. Epoxy resins. In Ullmann’s Encyclopedia of Industrial Chemistry; Wiley-VCH: Weinheim, Germany, 2005; ISBN 9783527303854. [Google Scholar]
- Startsev, V.O.; Lebedev, M.P.; Khrulev, K.A.; Molokov, M.V.; Frolov, A.S.; Nizina, T.A. Effect of outdoor exposure on the moisture diffusion and mechanical properties of epoxy polymers. Polym. Test. 2018, 65, 281–296. [Google Scholar] [CrossRef]
- Rocha, I.B.C.M.; Raijmaekers, S.; Nijssen, R.P.L.; van der Meer, F.P.; Sluys, L.J. Hygrothermal ageing behaviour of a glass/epoxy composite used in wind turbine blades. J. Compos. Struct. 2017, 174, 110–122. [Google Scholar] [CrossRef] [Green Version]
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Hygrothermal Aging of Amine Epoxy: Reversible Static and Fatigue Properties. Open Eng. 2018, 8, 447–454. [Google Scholar] [CrossRef]
- Krauklis, A.E. Environmental Aging of Constituent Materials in Fiber-Reinforced Polymer Composites. Ph.D. Thesis, NTNU, Trondheim, Norway, August 2019. [Google Scholar]
- Wang, M.; Xu, X.; Ji, J.; Yang, Y.; Shen, J.; Ye, M. The hygrothermal aging process and mechanism of the novolac epoxy resin. Compos. Part B Eng. 2016, 107, 1–8. [Google Scholar] [CrossRef]
- Clancy, T.C.; Frankland, S.J.V.; Hinkley, J.A.; Gates, T.S. Molecular modeling for calculation of mechanical properties of epoxies with moisture ingress. Polymer 2009, 50, 2736. [Google Scholar] [CrossRef]
- Krauklis, A.; Echtermeyer, A. Mechanism of Yellowing: Carbonyl Formation during Hygrothermal Aging in a Common Amine Epoxy. Polymers 2018, 10, 1017. [Google Scholar] [CrossRef] [PubMed]
- Cai, H.; Nakada, M.; Miyano, Y. Simplified determination of long-term viscoelastic behavior of amorphous resin. Mech. Time Depend. Mater. 2013, 17, 137–146. [Google Scholar] [CrossRef]
- Miyano, Y.; Nakada, M. Durability of Fiber-Reinforced Polymers; Wiley-VCH: Weinheim, Germany, 2018; ISBN 978-3527343560. [Google Scholar]
- Nakada, M.; Miyano, Y.; Cai, H.; Kasamori, M. Prediction of long-term viscoelastic behaviour of amorphous resin based on the time–temperature superposition principle. Mech. Time Depend. Mater. 2011, 15, 309–316. [Google Scholar] [CrossRef]
- Emri, I. Rheology of Solid Polymers. Rheol. Rev. 2005, 2005, 49. [Google Scholar]
- Brinson, H.F.; Brinson, L.C. Polymer Engineering Science and Viscoelasticity; Springer US: Boston, MA, USA, 2015; ISBN 978-1-4899-7768-7. [Google Scholar]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Hancock, B.C.; Zografi, G. The Relationship Between the Glass Transition Temperature and the Water Content of Amorphous Pharmaceutical Solids. Pharm. Res. 1994, 11, 471–477. [Google Scholar] [CrossRef] [PubMed]
- Simon, P.P.; Ploehn, H.J. Modeling the Effect of Plasticizer on the Viscoelastic Response of Crosslinked Polymers Using the Tube-Junction Model. J. Rheol. 2000, 44, 169–183. [Google Scholar] [CrossRef]
- Gagani, A.I.; Monsås, A.B.; Krauklis, A.E.; Echtermeyer, A.T. The effect of temperature and water immersion on the interlaminar shear fatigue of glass fiber epoxy composites using the I-beam method. Compos. Sci. Technol. 2019, 181, 107703. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Gagani, A.I.; Krauklis, A.E.; Moslemian, R. Long Term Fatigue Degradation—Superposition of Dry and Wet Properties. In Proceedings of the Twenty-Second International Conference on Composite Materials ICCM22, Melbourne, Australia, 11–16 August 2019. [Google Scholar]
- International Standard ISO 6721-11:2019(E). Plastics—Determination of Dynamic Mechanical Properties—Part 11: Glass Transition Temperature; International Organization for Standardization: Geneva, Switzerland, 2019. [Google Scholar]
- Standard Test Method for Assignment of the Glass Transition Temperature by Dynamic Mechanical Analysis; ASTM E1640-18; ASTM International: West Conshohocken, PA, USA, 2018. [CrossRef]
- Aerospace Series—Fibre Reinforced Plastics—Test Method—Determination of the Glass Transition Temperatures; NS-EN 6032:2015; Standard Norge: Oslo, Norway, 2016.
- Krauklis, A.E.; Gagani, A.I.; Echtermeyer, A.T. Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites. Materials 2018, 11, 586. [Google Scholar] [CrossRef] [PubMed]
- Honerkamp, J.; Weese, J. A note on estimating mastercurves. Rheol. Acta 1993, 32, 57–64. [Google Scholar] [CrossRef]
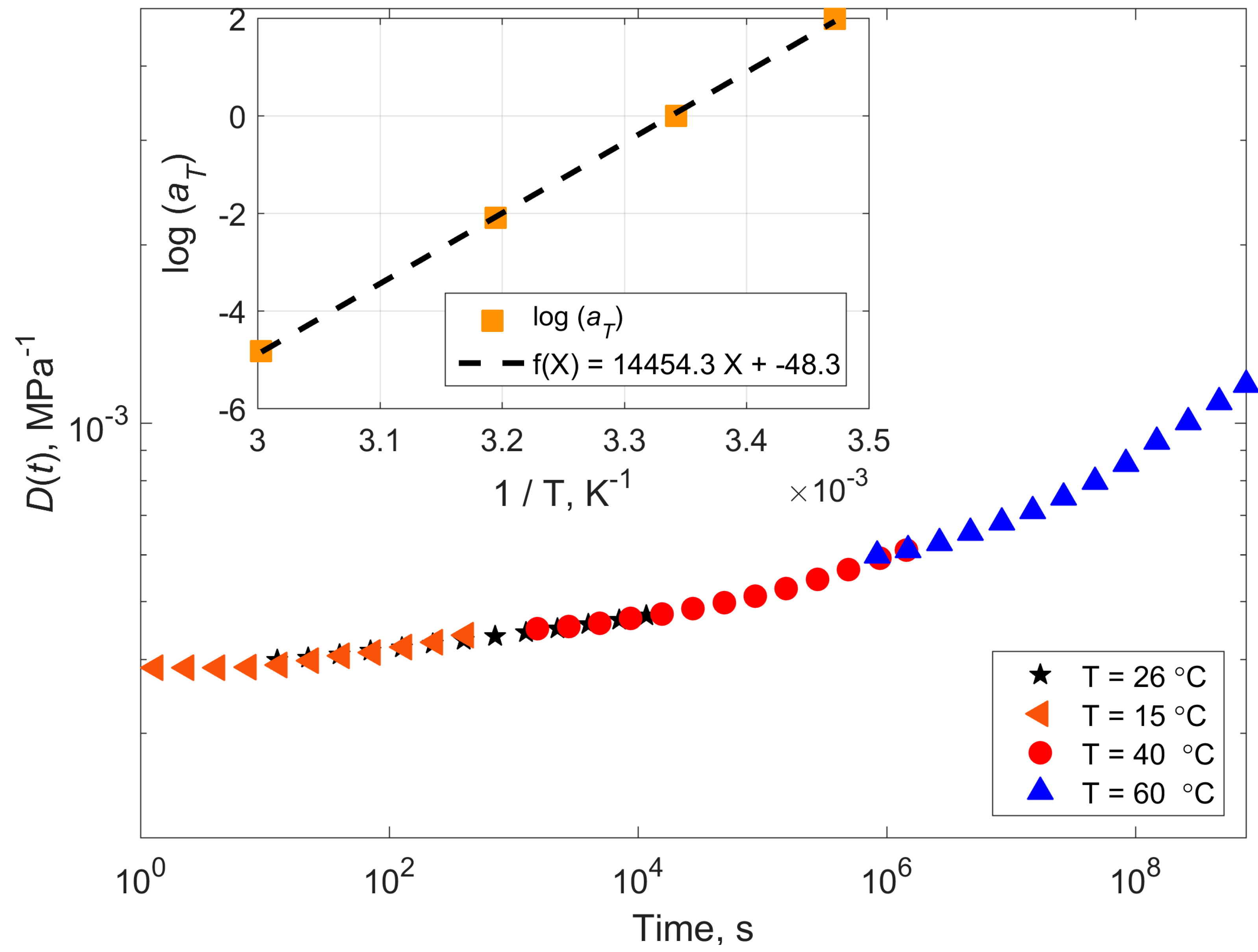
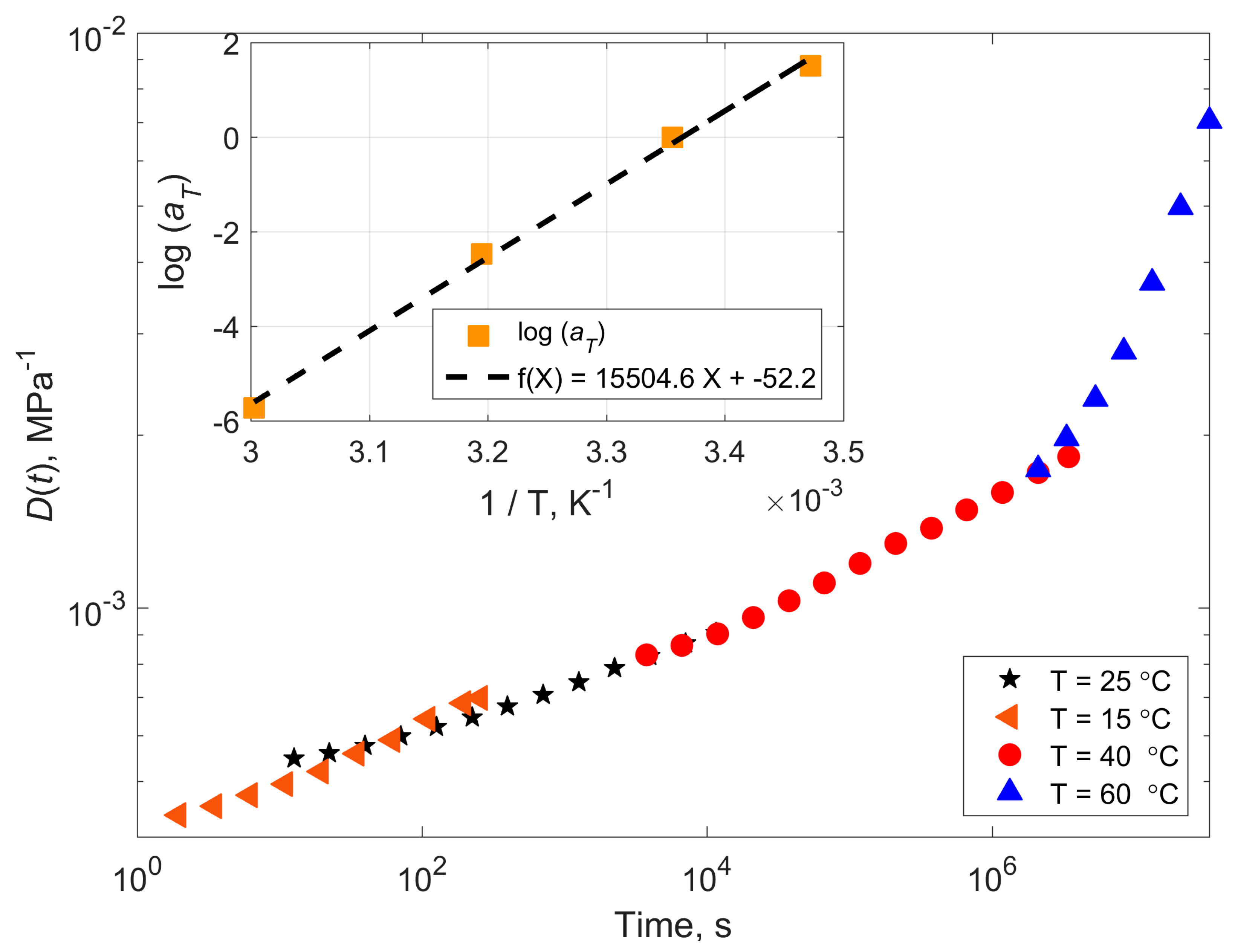
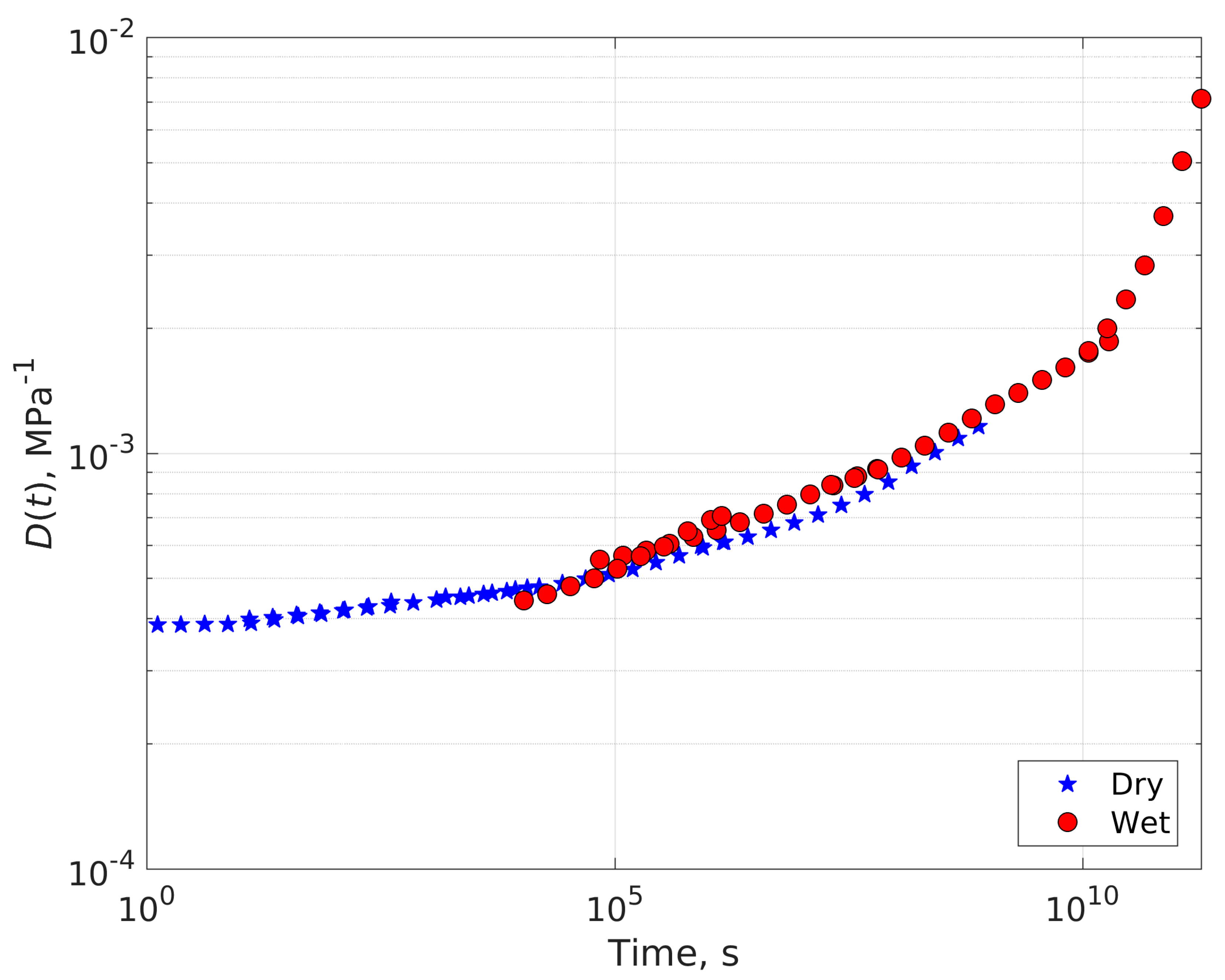
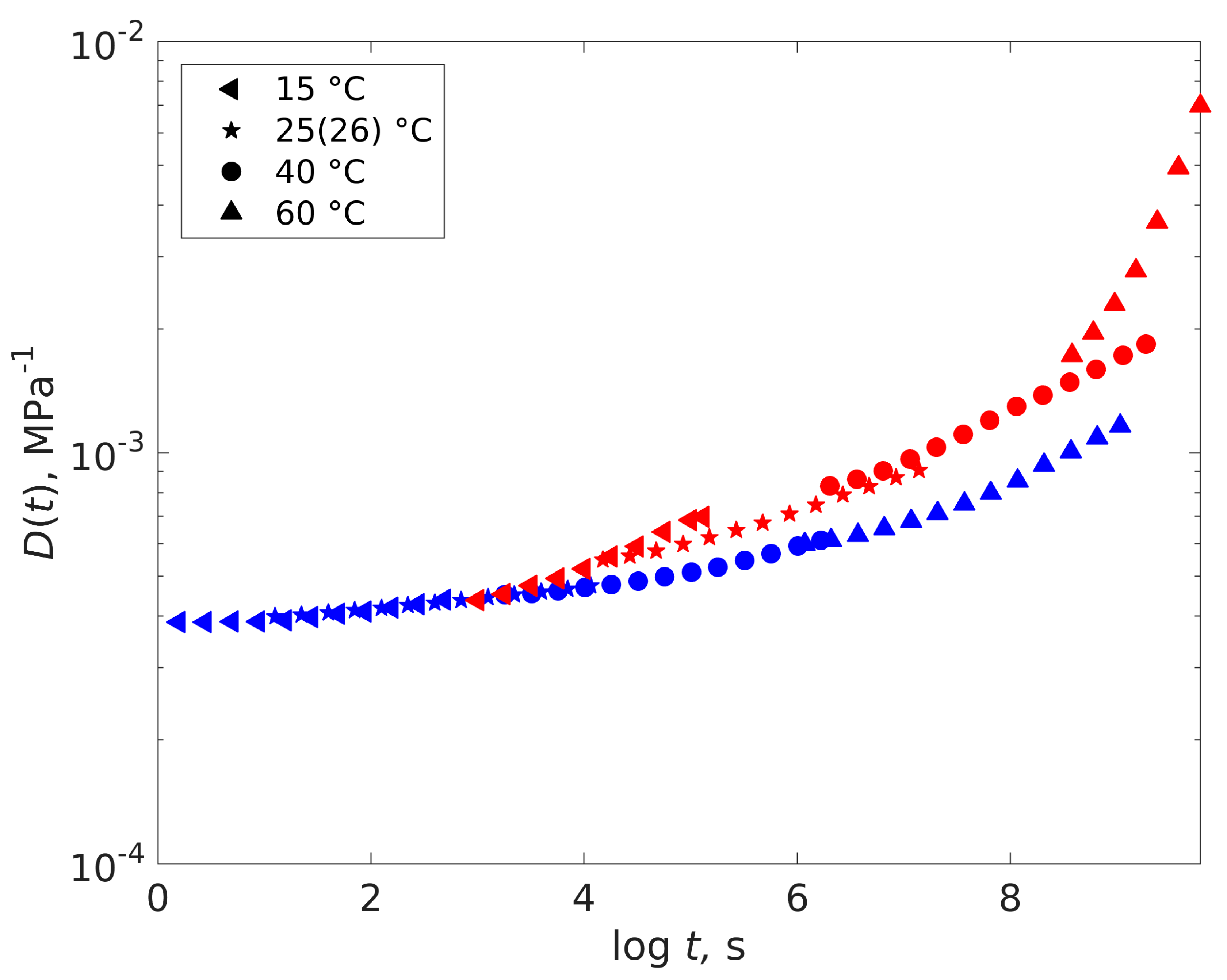
| Temperature (°C) | Shift Factor Log a(T) | Activation Energy (kJ/mol) | ||
|---|---|---|---|---|
| Dry Epoxy | Wet Epoxy | Dry Epoxy | Wet Epoxy | |
| 15 | 1.98 | 1.51 | 297 | 227 |
| 26 (Tref) | 0 | 0 | - | - |
| 40 | −2.09 | −2.47 | 268 | 316 |
| 60 | −4.82 | −5.72 | 271 | 321 |
| Mean | 277 | 297 | ||
| StDev | 16 | 53 | ||
| Tg Determination Frequency (Hz) | Glass Transition Temperature Tg (°C) | Dry-to-Plasticized Shift Factor log adry-to-plast | ||
|---|---|---|---|---|
| Dry Epoxy | Wet Epoxy | Predicted Using TTPSP, According to Equation (2) | Obtained Experimentally, According to Equation (3) | |
| 0.1 | 82 ± 2 | 57 ± 2 | −3.09 ± 0.70 | −3.74 |
| 1 | 83 ± 2 | 60 ± 2 | −2.81 ± 0.68 | |
| 10 | 84 ± 2 | 62 ± 2 | −2.66 ± 0.67 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krauklis, A.E.; Akulichev, A.G.; Gagani, A.I.; Echtermeyer, A.T. Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy. Polymers 2019, 11, 1848. https://doi.org/10.3390/polym11111848
Krauklis AE, Akulichev AG, Gagani AI, Echtermeyer AT. Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy. Polymers. 2019; 11(11):1848. https://doi.org/10.3390/polym11111848
Chicago/Turabian StyleKrauklis, Andrey E., Anton G. Akulichev, Abedin I. Gagani, and Andreas T. Echtermeyer. 2019. "Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy" Polymers 11, no. 11: 1848. https://doi.org/10.3390/polym11111848







