Mechanically Enhanced Electrical Conductivity of Polydimethylsiloxane-Based Composites by a Hot Embossing Process
Abstract
1. Introduction
2. Experimental
2.1. Materials
2.2. Composite Preparation and SCFNA Process
2.3. Characterization
3. Results and Discussion
3.1. Concentration-Induced Electrical Percolation of PDMS Composites
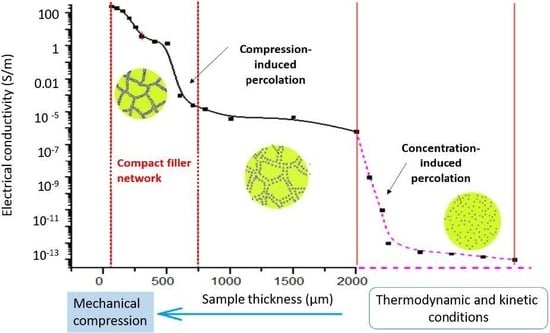
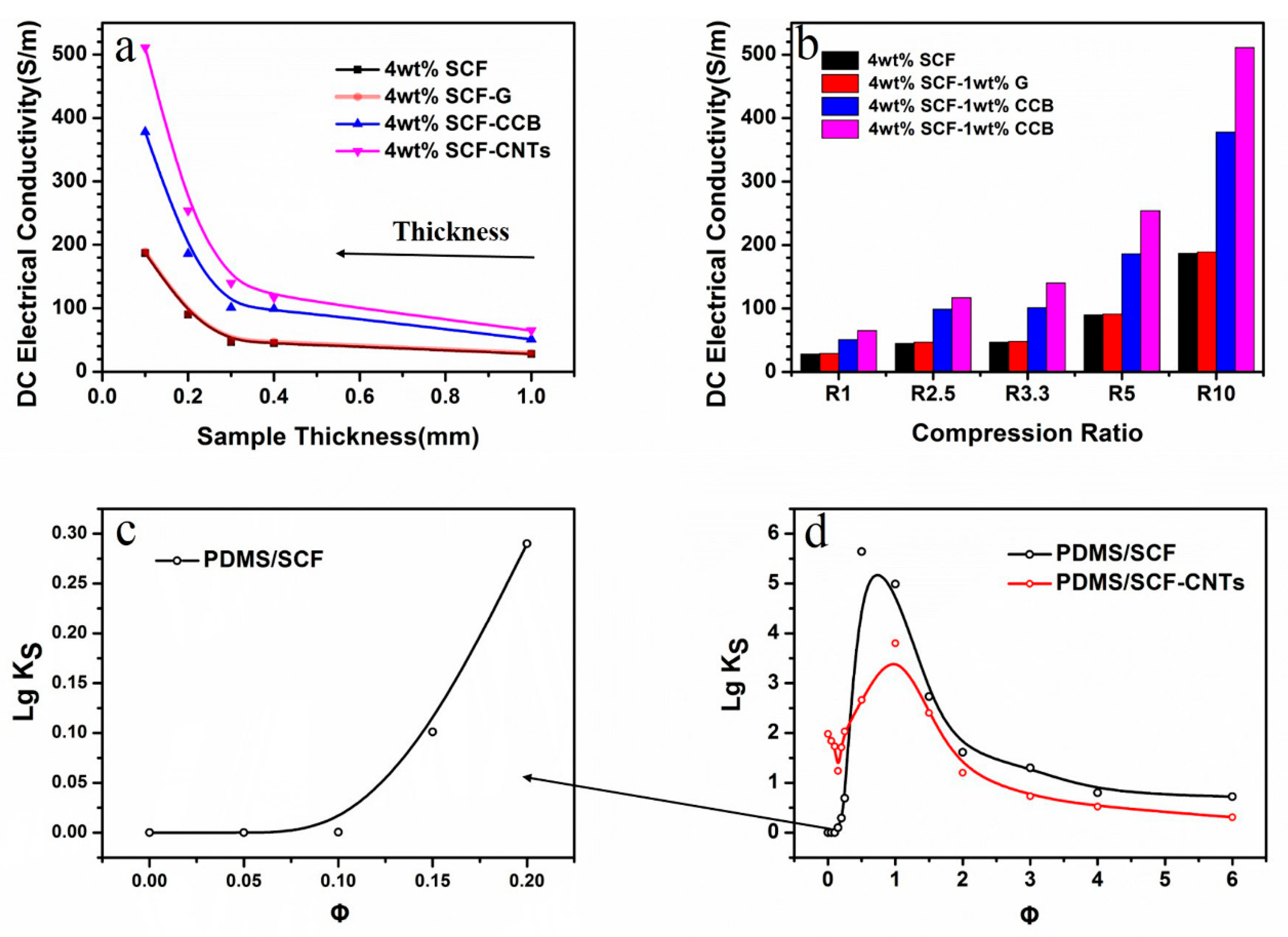
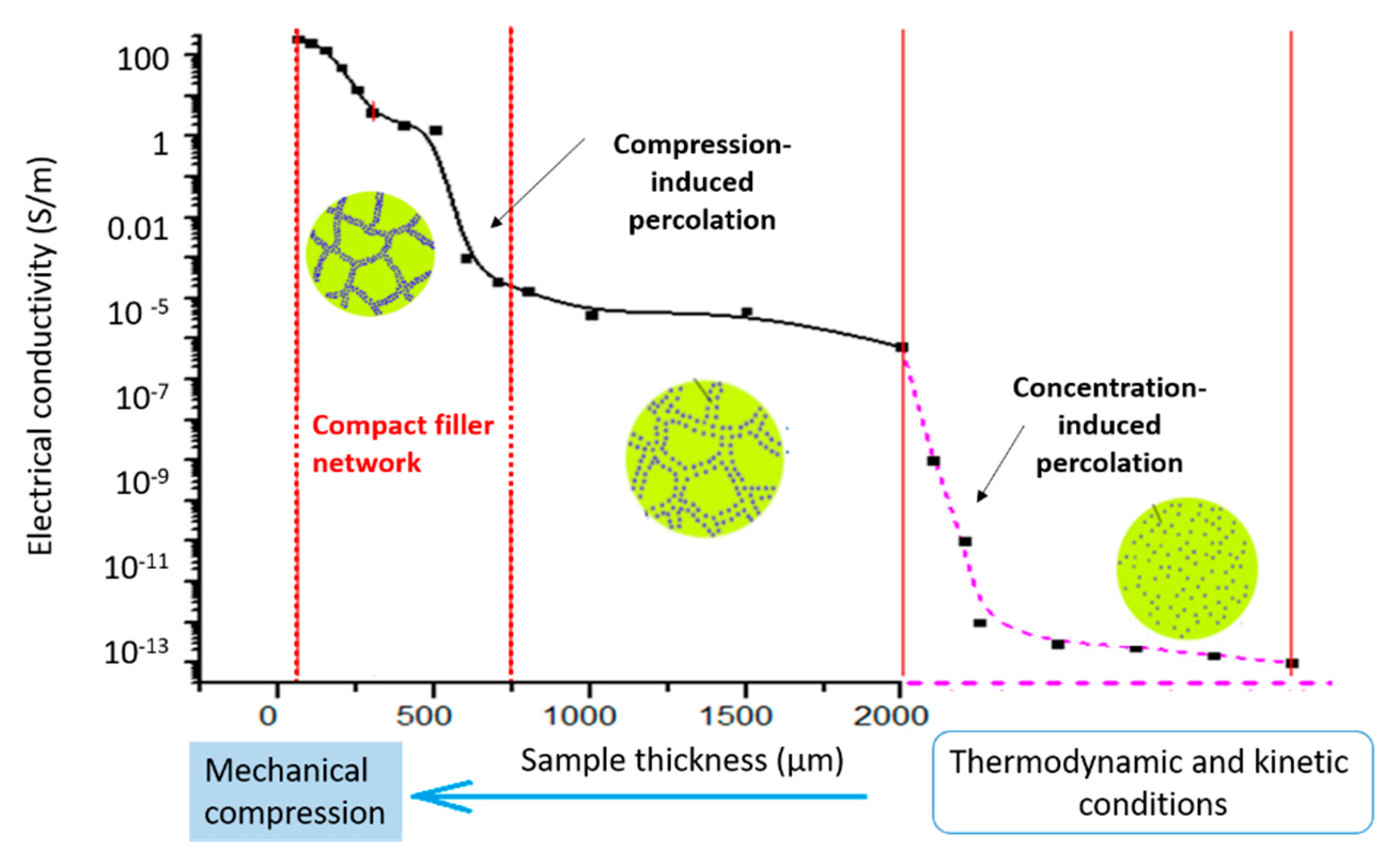
3.2. Compression-Induced Electrical Percolation of PDMS Composites
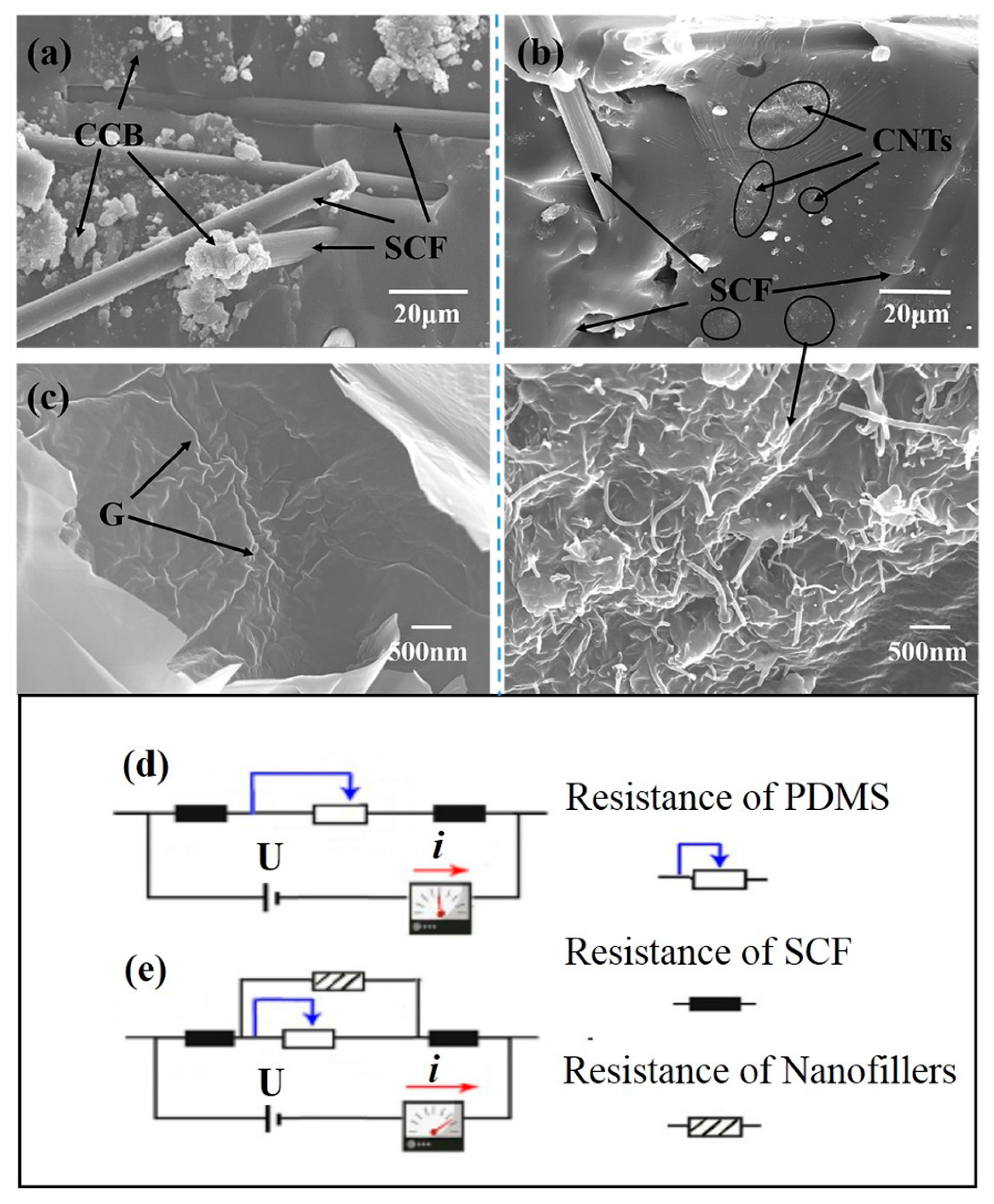
3.3. Characterization of the Conducting Filler Network in PDMS
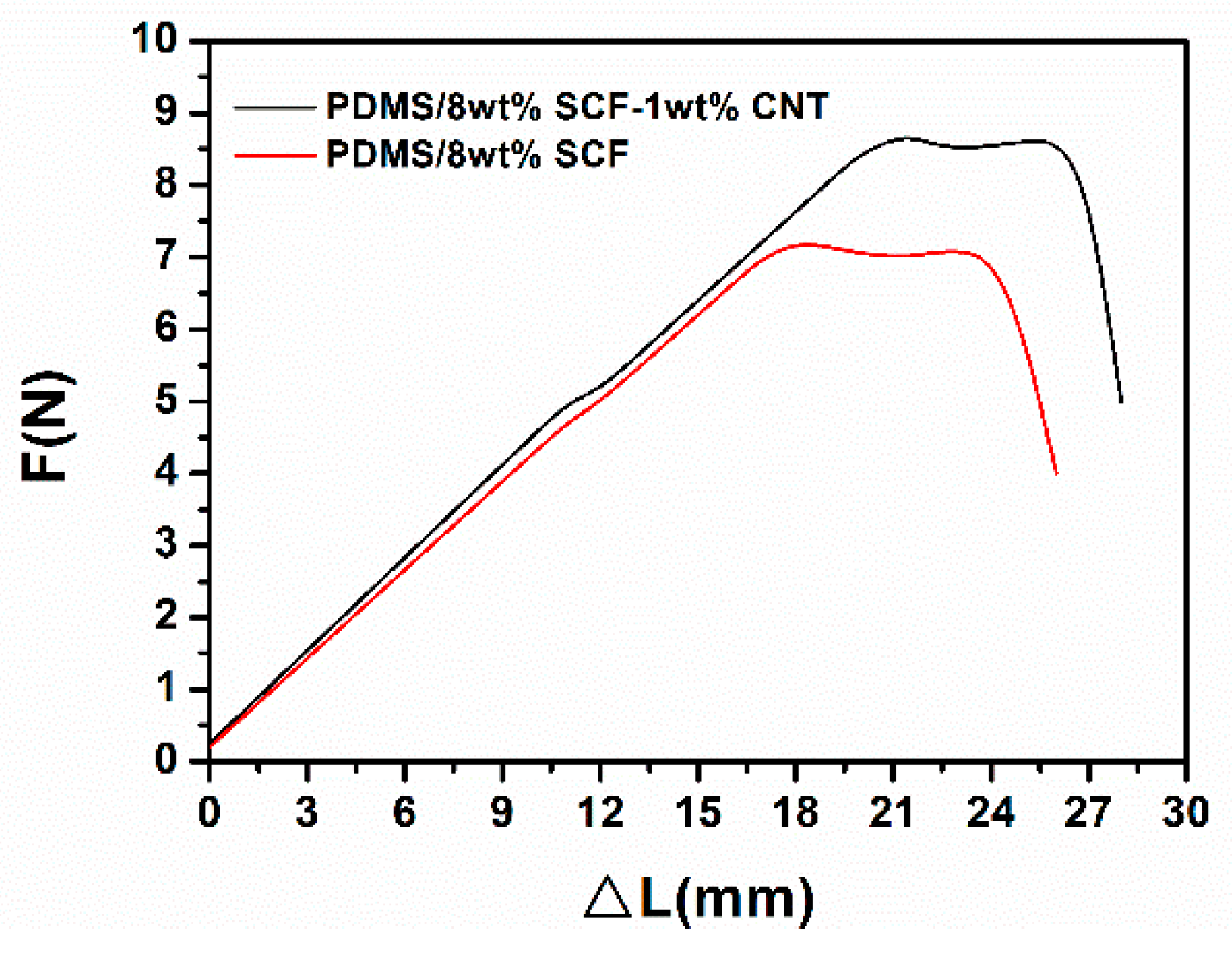
3.4. Mechanical Properties
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lu, Q.; Wang, X.; Cao, J.; Chen, C.; Chen, K.; Zhao, Z.; Niu, Z.; Chen, J. Freestanding carbon fiber cloth/sulfur composites for flexible room-temperature sodium-sulfur batteries. Energy Storage Mater. 2017, 8, 77–84. [Google Scholar] [CrossRef]
- Han, J.H.; Zhang, H.; Chen, M.J.; Wang, D.; Liu, Q.; Wu, Q.L.; Zhang, Z. The combination of carbon nanotube buckypaper and insulating adhesive for lightning strike protection of the carbon fiber/epoxy laminates. Carbon 2015, 94, 101–113. [Google Scholar] [CrossRef]
- Zeng, Z.; Jin, H.; Chen, M.J.; Li, W.W.; Zhou, L.C.; Zhang, Z. Lightweight and hierarchically porous MWCNT/WPU composites for ultra-high performance electromagnetic interference shielding. Adv. Funct. Mater. 2016, 26, 303–310. [Google Scholar] [CrossRef]
- Kuang, J.; Dai, Z.H.; Liu, L.Q.; Yang, Z.; Jin, M.; Zhang, Z. Synergistic effects from graphene and carbon nanotubes enable ordered hierarchical structure foams with combination of compressibility, super-elasticity and stability, and their potential application as pressure sensors. Nanoscale 2015, 7, 9252–9260. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Liu, L.Q.; Kuang, J.; Dai, Z.; Gao, Y.; Han, J.; Zhang, Z. Carbon nanomaterials based electrothermal air-pump actuators. Nanoscale 2014, 6, 6932–6938. [Google Scholar] [CrossRef] [PubMed]
- Gu, H.; Guo, J.; Wei, H.; Guo, S.; Liu, J.; Huang, Y.; Khan, M.A.; Wang, X.; Young, D.P.; Wei, S.; et al. Strengthened Magnetoresistive Epoxy Nanocomposite Papers Derived from Synergistic Nanomagnetite-Carbon Nanofiber Nanohybrids. Adv. Mater. 2015, 27, 6277–6282. [Google Scholar] [CrossRef] [PubMed]
- Deng, H.; Lin, L.; Ji, M.; Zhang, S.; Yang, M.; Fu, Q. Progress on the morphological control of conductive network in conductive polymer composites and the use as electroactive multifunctional materials. Prog. Polym. Sci. 2014, 39, 627–655. [Google Scholar] [CrossRef]
- Gao, X.; Huang, Y.; Liu, Y.; Kormakov, S.; Zheng, X.; Wu, D.; Wu, D. Improved electrical conductivity of PDMS/SCF composite sheets with bolting cloth prepared by a spatial confining forced network assembly method. RSC Adv. 2017, 7, 14761–14768. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, D.; Liu, Y.; Li, X.; Qiao, H.; Yu, Z.Z. Electrically conductive and super-tough polypropylene/carbon nanotube nanocomposites prepared by melt compounding. Compos. Part B 2014, 56, 384–391. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, J.; Ouyang, M.; Ma, C.A. Electric field controlled formation and dissociation of multiwalled carbon nanotube conductive pathways in a polymer melt. Appl. Phys. Lett. 2009, 94, 111915. [Google Scholar] [CrossRef]
- Zhang, K.; Yu, H.-O.; Shi, Y.-D.; Chen, Y.-F.; Zeng, J.-B.; Guo, J.; Wang, B.; Guo, Z.; Wang, M. Morphological regulation improved electrical conductivity and electromagnetic interference shielding in poly (l-lactide)/poly (ε-caprolactone)/carbon nanotube nanocomposites via constructing stereocomplex crystallites. J. Mater. Chem. C 2017, 5, 2807–2817. [Google Scholar] [CrossRef]
- Xiang, M.; Li, C.; Ye, L. Structure and conformation of polyetheramine in confined space of graphene oxide and its enhancement on the electrically conductive properties of monomer casting nylon-6. Compos. Part A 2017, 95, 1–11. [Google Scholar] [CrossRef]
- Yoo, T.J.; Hwang, E.B.; Jeong, Y.G. Thermal and electrical properties of poly(phenylene sulfide)/carbon nanotube nanocomposite films with a segregated structure. Compos. Part A 2016, 91, 77–84. [Google Scholar] [CrossRef]
- Chiu, F.C.; Chen, Y.J. Evaluation of thermal, mechanical, and electrical properties of PVDF/GNP binary and PVDF/PMMA/GNP ternary nanocomposites. Compos. Part A 2015, 68, 62–71. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.; Wang, J.; Ma, C.A. Self-assembly and conductive net-work formation of vapor-grown carbon fiber in a poly(vinylidenefluoride) melt. Carbon 2008, 46, 2053–2058. [Google Scholar] [CrossRef]
- Lan, Y.; Liu, H.; Cao, X.; Zhao, S.; Dai, K.; Yan, X.; Zheng, G.; Liu, C.; Shen, C.; Guo, Z. Electrically conductive thermoplastic polyurethane/polypropylene nanocomposites with selectively distributed graphene. Polymer 2016, 97, 11–19. [Google Scholar] [CrossRef]
- Zhu, J.; Wei, S.; Ryu, J.; Budhathoki, M.; Liang, G.; Guo, Z. In situ stabilized carbon nanofiber (CNF) reinforced epoxy nanocomposites. J. Mater. Chem. 2010, 20, 4937–4948. [Google Scholar] [CrossRef]
- Zhang, H.; Xu, X. Improving the transesterification and electrical conductivity of vitrimers by doping with conductive polymer wrapped carbon nanotubes. Compos. Part A 2017, 99, 15–22. [Google Scholar] [CrossRef]
- Jo, Y.; Kim, J.Y.; Kim, S.-Y.; Seo, Y.-H.; Jang, K.-S.; Lee, S.Y.; Jung, S.; Ryu, B.-H.; Kim, H.S.; Park, J.-U.; et al. 3D-printable, highly conductive hybrid composites employing chemically-reinforced, complex dimensional fillers and thermoplastic triblock copolymers. Nanoscale 2017, 9, 5072–5084. [Google Scholar] [CrossRef]
- Zhang, L.; Wan, C.; Zhang, Y. Morphology and electrical properties of polyamide 6/polypropylene/multi-walled carbon nanotubes composites. Compos. Sci. Technol. 2009, 69, 2212–2217. [Google Scholar] [CrossRef]
- Liu, H.; Gao, J.; Huang, W.; Dai, K.; Zheng, G.; Liu, C.; Shen, C.; Yan, X.; Guo, J.; Guo, Z. Electrically conductive strain sensing polyurethane nanocomposites with synergistic carbon nanotubes and graphene bifillers. Nanoscale 2016, 8, 12977–12989. [Google Scholar] [CrossRef] [PubMed]
- Sethi, D.; Ram, R.; Khastgir, D. Electrical conductivity and dynamic mechanical properties of silicon rubber-based conducting composites: Effect of cyclic deformation, pressure and temperature. Polym. Int. 2017, 66, 1295–1305. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, J.; Ladani, R.B.; Ravindran, A.R.; Mouritz, A.P.; Kinloch, A.J.; Wang, C.H. Novel Electrically Conductive Porous PDMS/Carbon Nanofiber Composites for Deformable Strain Sensors and Conductors. ACS Appl. Mater. Interfaces 2017, 9, 14207–14215. [Google Scholar] [CrossRef]
- Fisher, S.C.L.; Levy, O.; Kroner, E.; Hensel, R.; Karp, J.M.; Arzt, E. Bioinspired polydimethylsiloxane-based composites with high shear resistance against wet tissue. J. Mech. Behav. Biomed. Mater. 2016, 61, 87–95. [Google Scholar] [CrossRef] [PubMed]
- Christopher, J.B. Recent advances in materials and flexible electronics for peripheral nerve interfaces. Bioelectron. Med. 2018, 4, 6. [Google Scholar]
- Joshi, N.; Saxena, V.; Singh, A.; Koiry, S.P.; Debnath, A.K.; Chehimi, M.M.; Aswal, D.K.; Guptaa, S.K. Flexible H2S sensor based on gold modified polycarbazole films. Sensors Actuators B Chem. 2014, 200, 227–234. [Google Scholar] [CrossRef]
- Khosla, A.; Shah, S.; Shiblee, M.D.N.I.; Mir, S.H.; Nagahara, L.A.; Thundat, T.; Shekar, P.K.; Kawakami, M.; Furukawa, H. Carbon fiber doped thermosetting elastomer for flexible sensors: Physical properties and microfabrication. Sci. Rep. 2018, 8, 12313. [Google Scholar] [CrossRef]
- Kim, J.H.; Hwang, J.-Y.; Hwang, H.R.; Kim, H.S.; Lee, J.H.; Seo, J.; Shin, U.S.; Lee, S.-H. Simple and cost-effective method of highly conductive and elastic carbon nanotube/polydimethylsiloxane composite for wearable electronics. Sci. Rep. 2018, 8, 1375. [Google Scholar] [CrossRef]
- Park, O.K.; Lee, W.; Hwang, J.Y.; You, N.-H.; Jeong, Y.; Kim, S.M.; Ku, N.-C. Mechanical and electrical properties of thermochemically cross-linked polymer carbon nanotube fibers. Compos. Part A 2016, 91, 222–228. [Google Scholar] [CrossRef]
- Kong, K.T.S.; Mariatti, M.; Rashid, A.A.; Busfield, J.J.C. Enhanced conductivity behavior of polydimethylsiloxane (PDMS) hybrid composites containing exfoliated graphite nanoplatelets and carbon nanotubes. Compos. Part B 2014, 58, 457–462. [Google Scholar] [CrossRef]
- Zhang, S.; Deng, H.; Zhang, Q.; Fu, Q. Formation of conductive networks with both segregated and double-percolated characteristic in conductive polymer composites with balanced properties. ACS Appl. Mater. Interfaces 2014, 6, 6835–6844. [Google Scholar] [CrossRef] [PubMed]
- Thongruang, W.; Spontak, R.J.; Balik, C.M. Bridged double percolation in conductive polymer composites: An electrical conductivity, morphology and mechanical property study. Polymer 2002, 43, 3717–3725. [Google Scholar] [CrossRef]
- Wu, D.; Gao, X.; Sun, J.; Wu, D.; Liu, Y.; Kormakov, S.; Zheng, X.; Wu, L.; Huang, Y.; Guo, Z. Spatial Confining Forced Network Assembly for preparation of high-performance conductive polymeric composites. Compos. Part A 2017, 102, 88–95. [Google Scholar] [CrossRef]
- He, X.X.; Huang, Y.; Liu, Y.; Zheng, X.T.; Kormakov, S.; Sun, J.Y.; Zhuang, J.; Gao, X.L.; Wu, D.M. Improved thermal conductivity of polydimethylsiloxane/short carbon fibre composites prepared by spatial confining forced network assembly. J. Mater. Sci. 2018. [Google Scholar] [CrossRef]
- Essam, J.W. Percolation theory. Rep. Prog. Phys. 1980, 43, 833. [Google Scholar] [CrossRef]
- Shtein, M.; Nadiv, R.; Buzaglo, M.; Kahil, K.; Regev, O. Thermally Conductive Graphene-Polymer Composites: Size, Percolation, and Synergy Effects. Chem. Mater. 2015, 27, 2100–2106. [Google Scholar] [CrossRef]
- Badard, M.; Combessis, A.; Allais, A.; Flandin, L. Modeling the dynamic percolation of carbon nanotubes and revisiting critical exponents. Mater. Chem. Phys. 2017, 191, 89–95. [Google Scholar] [CrossRef]
- Saberi, A.A. Recent advances in percolation theory and its applications. Phys. Rep. 2015, 578, 1–32. [Google Scholar] [CrossRef]
- Chelidze, T.; Gueguen, Y. Pressure-induced percolation transitions in composites. J. Phys. D Appl. Phys. 1998, 31, 2877–2885. [Google Scholar] [CrossRef]
- Chen, Y.; Pan, F.; Wang, S.; Liu, B.; Zhang, J. Theoretical estimation on the percolation threshold for polymer matrix composites with hybrid fillers. Compos. Struct. 2015, 124, 292–299. [Google Scholar] [CrossRef]
- Rahatekar, S.S.; Shaffer, M.S.P.; Elliott, J.A. Modelling percolation in fibre and sphere mixtures: Routes to more efficient network formation. Compos. Sci. Technol. 2010, 70, 356–362. [Google Scholar] [CrossRef]
- Rajagopal, C.; Satyam, M. Studies on electrical conductivity of insulator-conductor composites. J. Appl. Phys. 1978, 49, 5536–5542. [Google Scholar] [CrossRef]


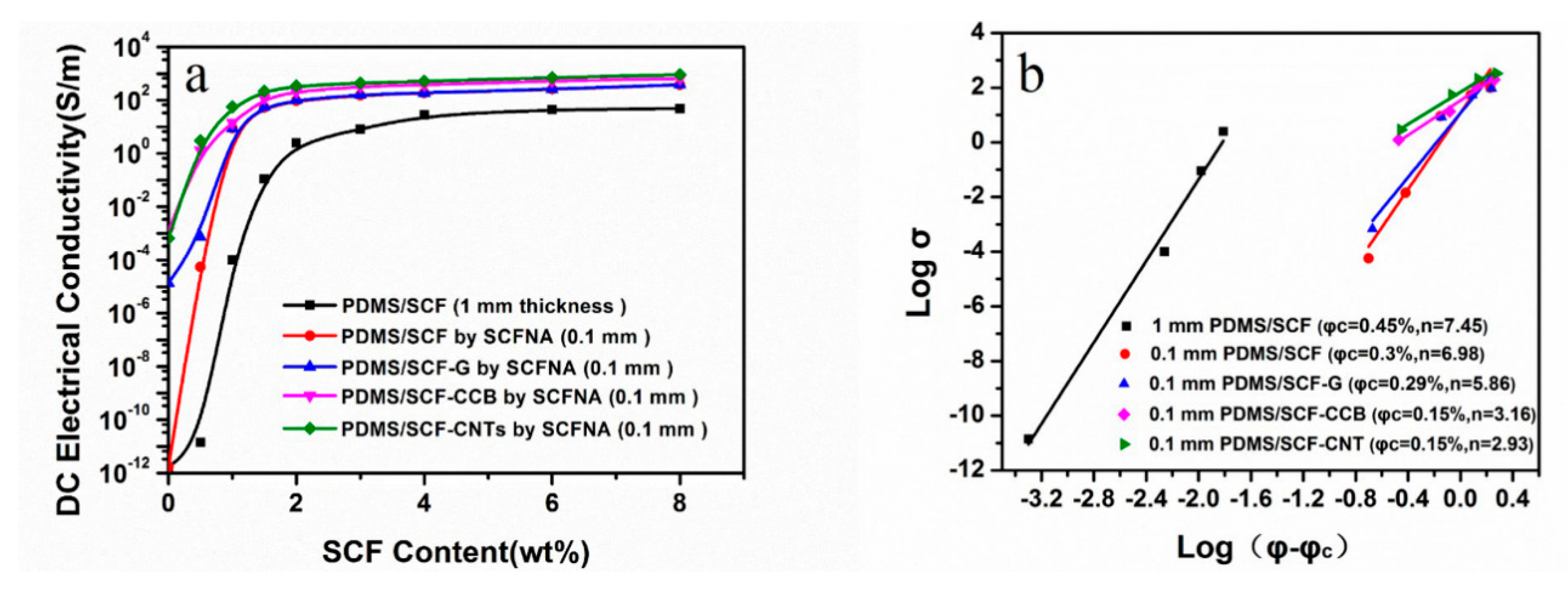


| SCF (wt %) | DC Electrical Conductivity (S/m) | ||||
|---|---|---|---|---|---|
| 1 mm | 0.1 mm | SCF-G (0.1 mm) | SCF-CCB (0.1 mm) | SCF-CNTs (0.1 mm) | |
| 0 | 1.71 × 10−12 | 1.71 × 10−12 | 1.38 × 10−5 | 1.21 × 10−3 | 6.51 × 10−4 |
| 0.5 | 1.40 × 10−11 | 5.50 × 10−5 | 7.21 × 10−4 | 1.31 | 3.02 |
| 1 | 1.01 × 10−4 | 8.81 | 8.84 | 14.5 | 56.8 |
| 1.5 | 0.11 | 53.2 | 56.7 | 120 | 221 |
| 2 | 2.51 | 95.2 | 100 | 211 | 343 |
| 3 | 8.11 | 154 | 161 | 333 | 443 |
| 4 | 27.7 | 187 | 189 | 378 | 511 |
| 6 | 44.6 | 257 | 261 | 533 | 702 |
| 8 | 48.6 | 378 | 383 | 657 | 909 |
| PDMS Composite | Maximum Tensile Strength (MPa) | Elongation at Break (%) | |
|---|---|---|---|
| SCF (wt %) | Nanofiller | ||
| 0 | 0 | 4.5 ± 0.1 | 110 ± 2 |
| 1 | 0 | 3.9 ± 0.2 | 96 ± 4 |
| 0 | 1 wt % CCB | 4.0 ± 0.1 | 98 ± 1 |
| 0 | 1 wt % CNT | 4.2 ± 0.1 | 105 ± 1 |
| 0 | 1 wt % G | 5.1 ± 0.1 | 125 ± 1 |
| 2 | 0 | 3.6 ± 0.2 | 91 ± 4 |
| 3 | 0 | 3.2 ± 0.2 | 83 ± 4 |
| 4 | 0 | 2.8 ± 0.2 | 72 ± 4 |
| 8 | 0 | 2.4 ± 0.1 | 60 ± 3 |
| 4 | 1 wt % CCB | 2.9 ± 0.2 | 73 ± 3 |
| 8 | 1 wt % CCB | 2.7 ± 0.2 | 64 ± 4 |
| 4 | 1 wt % CNT | 3.1 ± 0.2 | 77 ± 3 |
| 8 | 1 wt % CNT | 2.9 ± 0.2 | 71 ± 3 |
| 4 | 1 wt % G | 3.8 ± 0.2 | 94 ± 3 |
| 8 | 1 wt % G | 3.5 ± 0.2 | 84 ± 3 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Huang, Y.; He, X.; Fan, X.; Liu, Y.; Xu, H.; Wu, D.; Wan, C. Mechanically Enhanced Electrical Conductivity of Polydimethylsiloxane-Based Composites by a Hot Embossing Process. Polymers 2019, 11, 56. https://doi.org/10.3390/polym11010056
Gao X, Huang Y, He X, Fan X, Liu Y, Xu H, Wu D, Wan C. Mechanically Enhanced Electrical Conductivity of Polydimethylsiloxane-Based Composites by a Hot Embossing Process. Polymers. 2019; 11(1):56. https://doi.org/10.3390/polym11010056
Chicago/Turabian StyleGao, Xiaolong, Yao Huang, Xiaoxiang He, Xiaojing Fan, Ying Liu, Hong Xu, Daming Wu, and Chaoying Wan. 2019. "Mechanically Enhanced Electrical Conductivity of Polydimethylsiloxane-Based Composites by a Hot Embossing Process" Polymers 11, no. 1: 56. https://doi.org/10.3390/polym11010056
APA StyleGao, X., Huang, Y., He, X., Fan, X., Liu, Y., Xu, H., Wu, D., & Wan, C. (2019). Mechanically Enhanced Electrical Conductivity of Polydimethylsiloxane-Based Composites by a Hot Embossing Process. Polymers, 11(1), 56. https://doi.org/10.3390/polym11010056