Explicit Ion Effects on the Charge and Conformation of Weak Polyelectrolytes
Abstract
1. Introduction
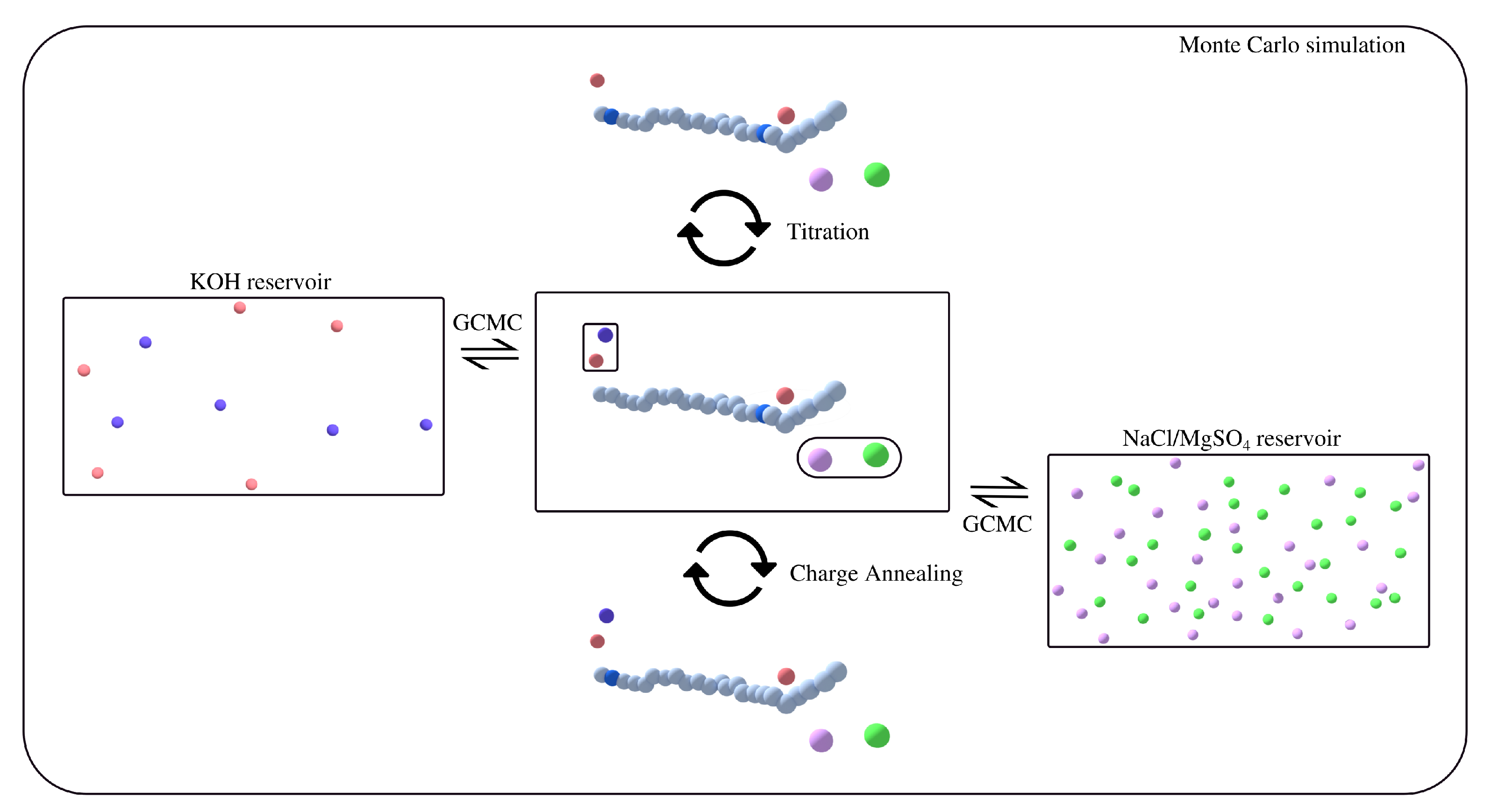
2. Methods
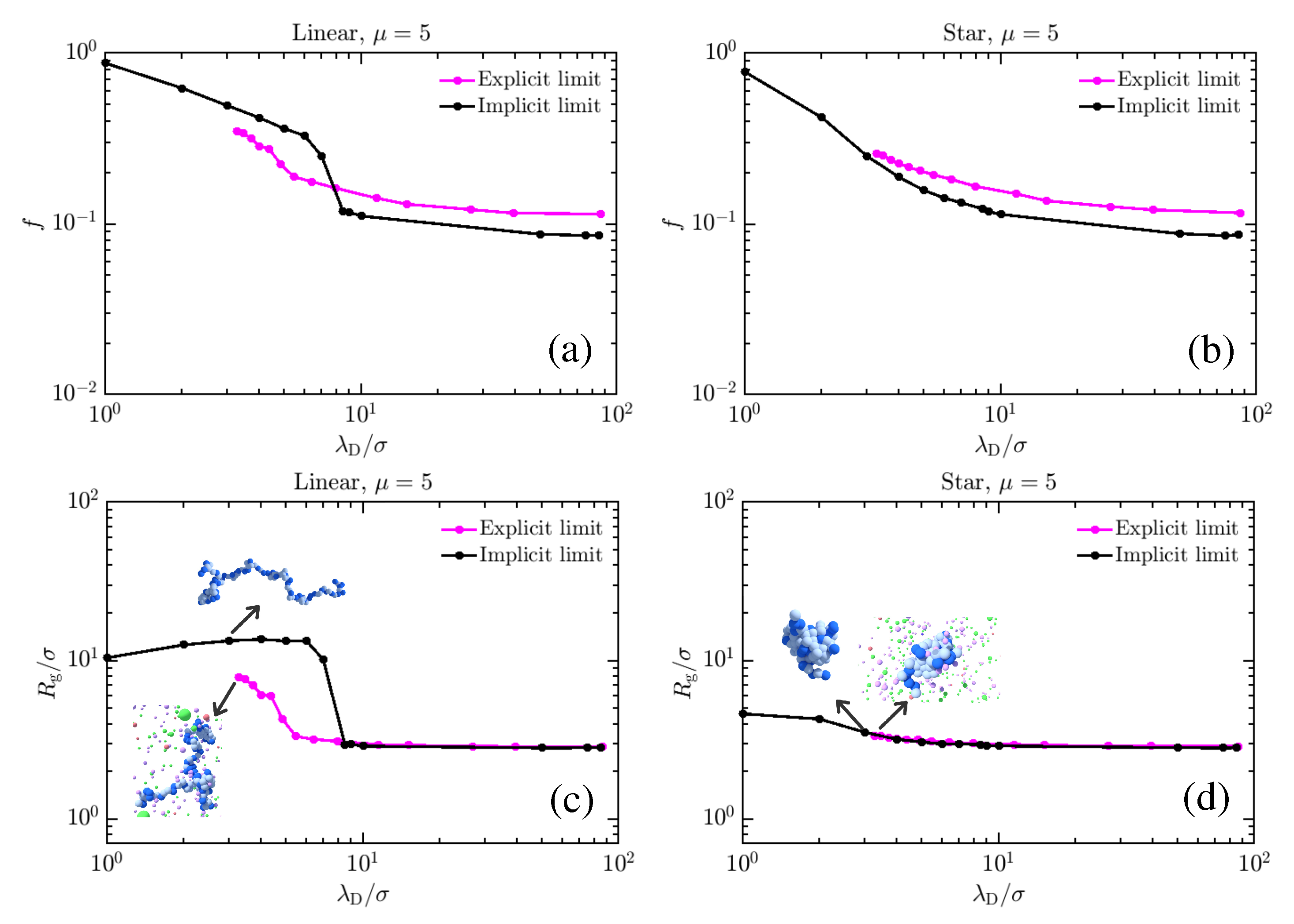
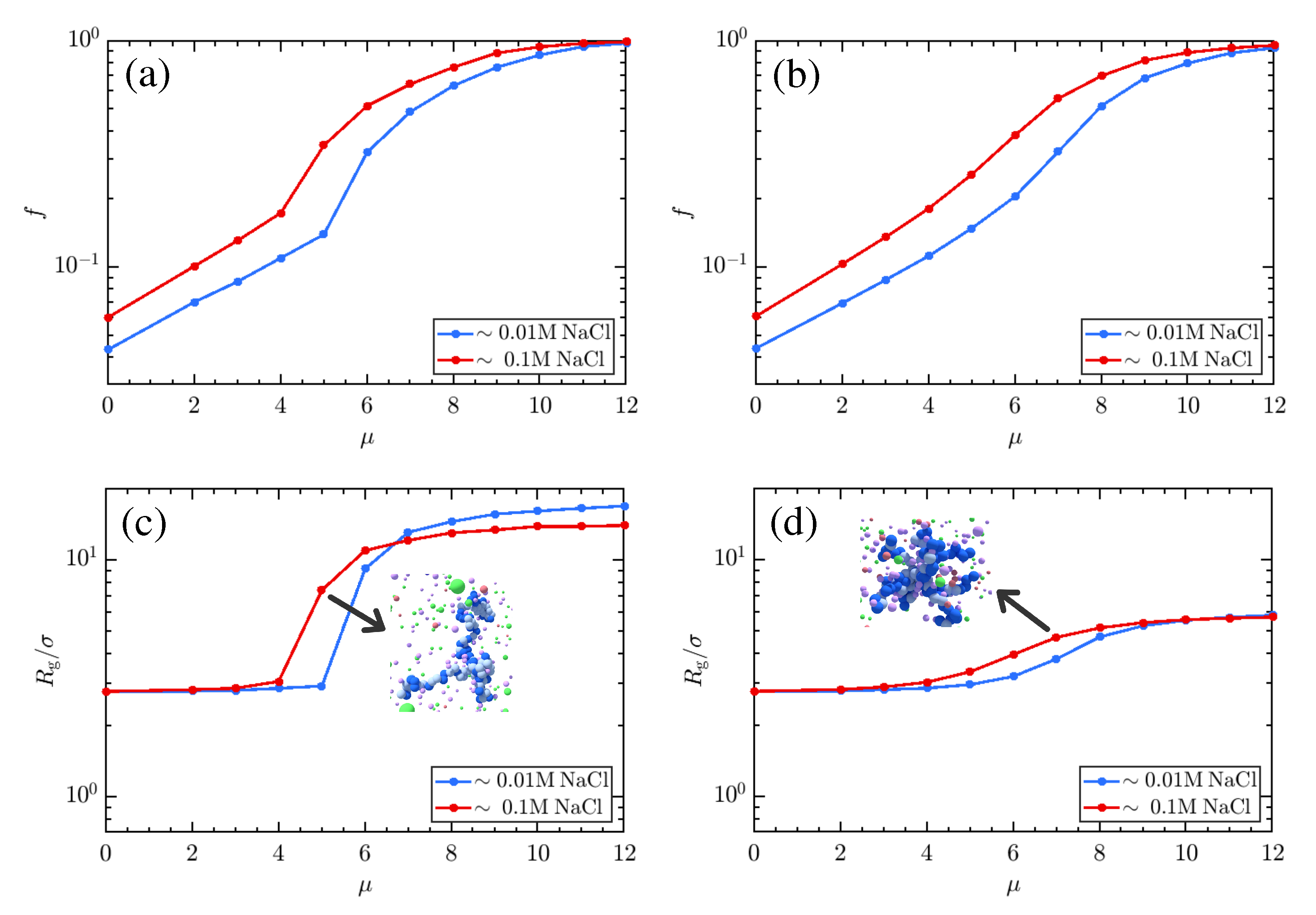
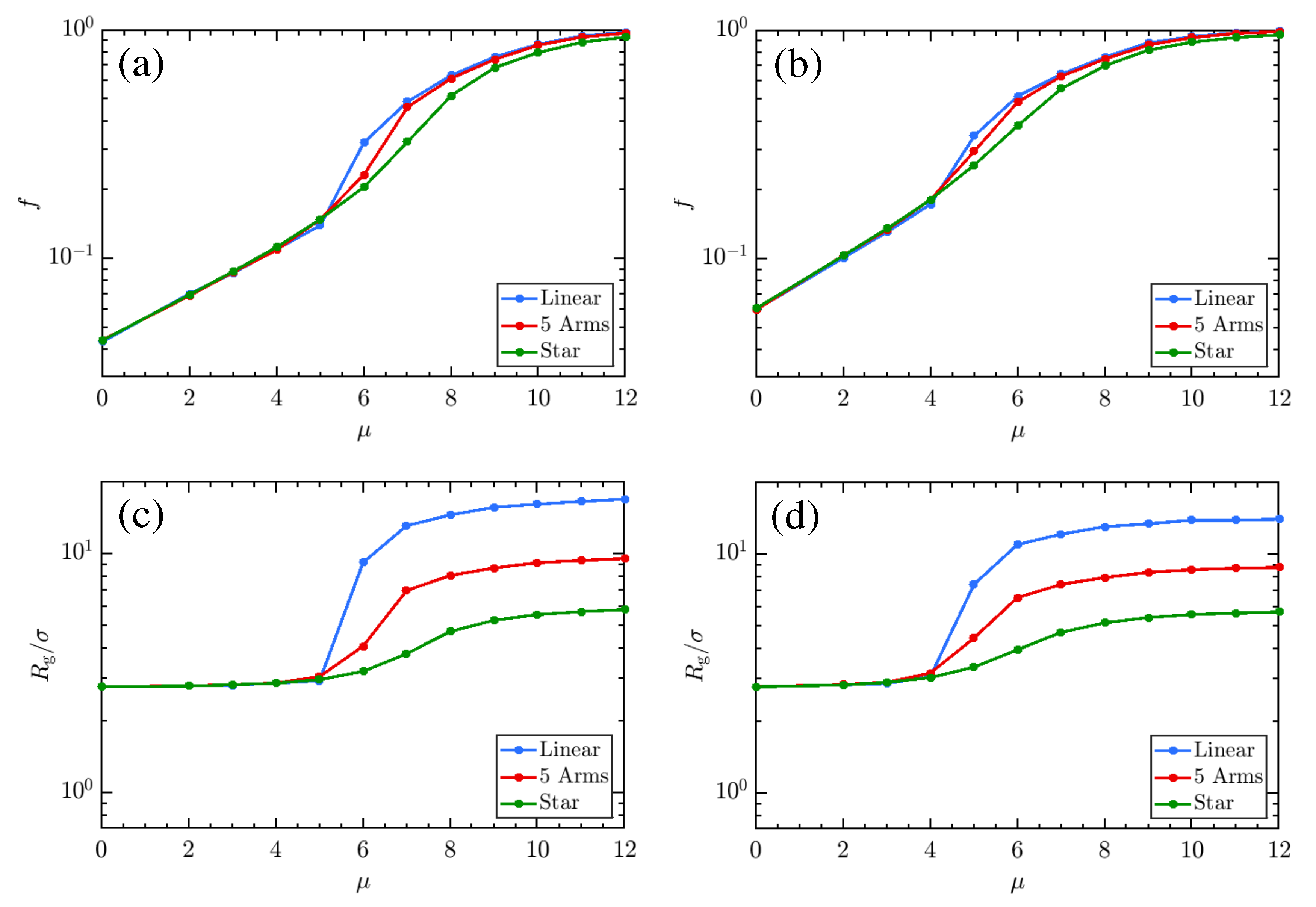
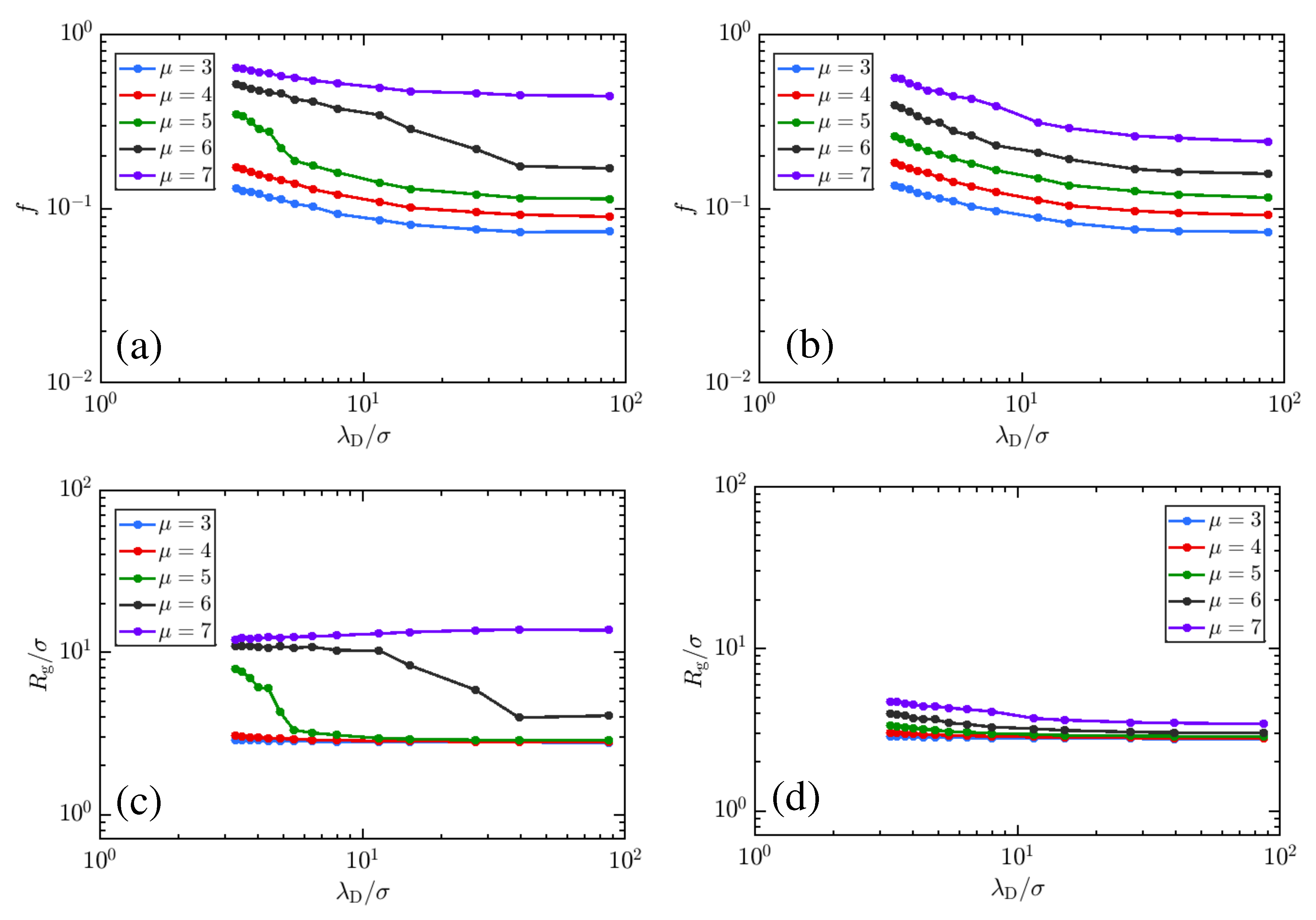
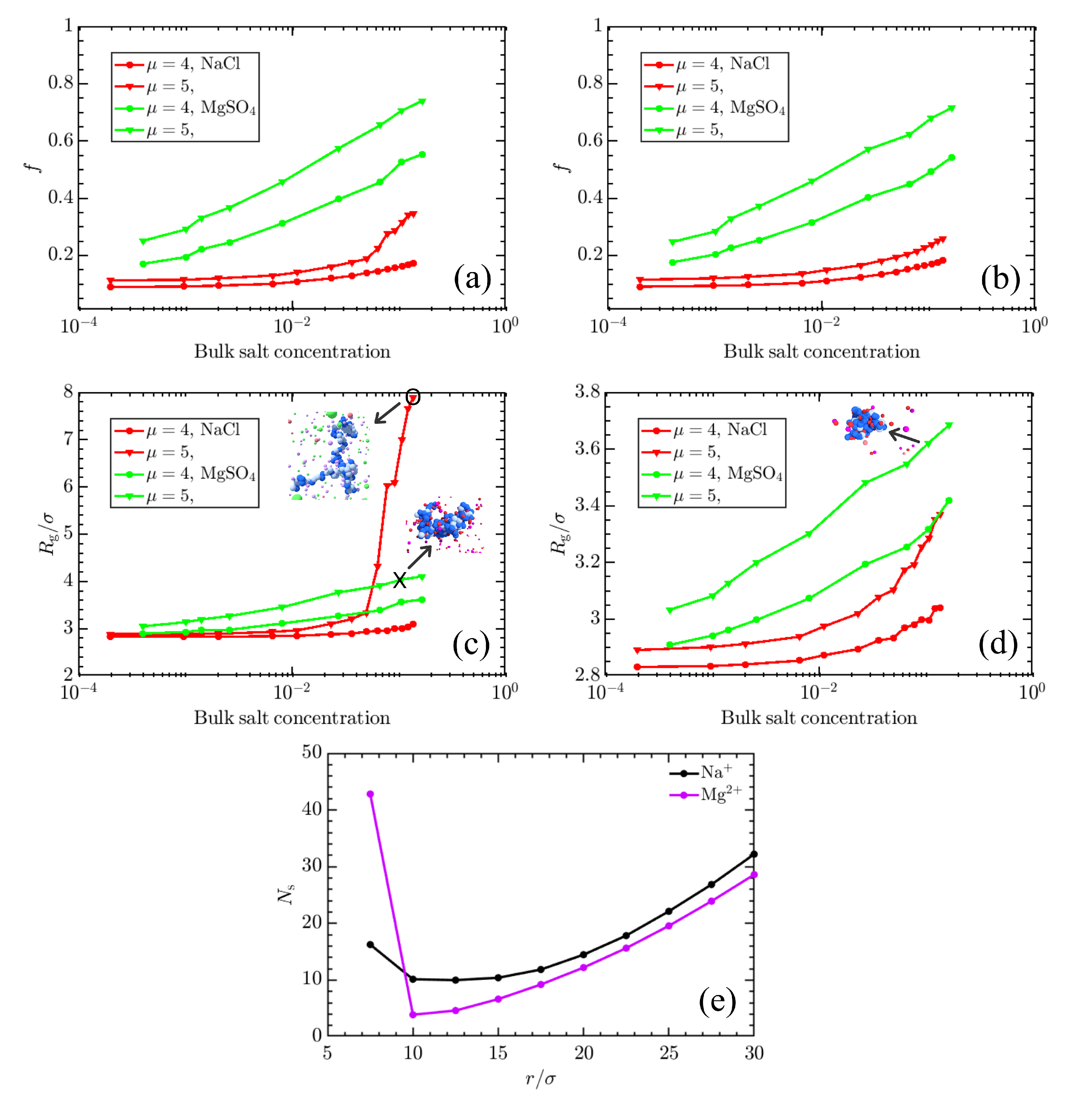
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Hoare, T.; Pelton, R. Highly pH and Temperature Responsive Microgels Functionalized with Vinylacetic Acid. Macromolecules 2004, 37, 2544–2550. [Google Scholar] [CrossRef]
- Song, X.; Zambare, R.S.; Qi, S.; Sowrirajalu, B.N.; James Selvaraj, A.P.; Tang, C.Y.; Gao, C. Charge-Gated Ion Transport through Polyelectrolyte Intercalated Amine Reduced Graphene Oxide Membranes. ACS Appl. Mater. Interfaces 2017, 9, 41482–41995. [Google Scholar] [CrossRef] [PubMed]
- Marcombe, R.; Cai, S.; Hong, W.; Zhao, X.; Lapusta, Y.; Suo, Z. A theory of constrained swelling of a pH-sensitive hydrogel. Soft Matter 2010, 6, 784. [Google Scholar] [CrossRef]
- Cheng, C.; White, N.; Shi, H.; Robson, M.; Bruening, M.L. Cation separations in electrodialysis through membranes coated with polyelectrolyte multilayers. Polymer 2014, 55, 1397–1403. [Google Scholar] [CrossRef]
- Zhao, Q.; Ji, Y.L.; Wu, J.K.; Shao, L.L.; An, Q.F.; Gao, C.J. Polyelectrolyte complex nanofiltration membranes: performance modulation via casting solution pH. RSC Adv. 2014, 4, 52808–52814. [Google Scholar] [CrossRef]
- Bromberg, L.; Temchenko, M.; Hatton, T.A. Smart Microgel Studies. Polyelectrolyte and Drug-Absorbing Properties of Microgels from Polyether-Modified Poly(acrylic acid). Langmuir 2003, 19, 8675–8684. [Google Scholar] [CrossRef]
- McGrath, A.J.; Dolan, C.; Cheong, S.; Herman, D.A.; Naysmith, B.; Zong, F.; Galvosas, P.; Farrand, K.J.; Hermans, I.F.; Brimble, M.; et al. Stability of polyelectrolyte-coated iron nanoparticles for T2-weighted magnetic resonance imaging. J. Magn. Magn. Mater. 2017, 439, 251–258. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Q.; Qu, Y.; Chen, M.; Soyekwo, F.; Lin, C.; Zhu, A.; Liu, Q. LBL assembled polyelectrolyte nanofiltration membranes with tunable surface charges and high permeation by employing a nanosheet sacrificial layer. J. Mater. Chem. A 2017, 5, 14819–14827. [Google Scholar] [CrossRef]
- Paltrinieri, L.; Wang, M.; Sachdeva, S.; Besseling, N.A.M.; Sudhölter, E.J.R.; de Smet, L.C.P.M. Fe3O4 nanoparticles coated with a guanidinium-functionalized polyelectrolyte extend the pH range for phosphate binding. J. Mater. Chem. A 2017, 5, 18476–18485. [Google Scholar] [CrossRef]
- Rathee, V.S.; Qu, S.; Phillip, W.A.; Whitmer, J.K. A coarse-grained thermodynamic model for the predictive engineering of valence-selective membranes. Mol. Syst. Des. Eng. 2016, 1, 301–312. [Google Scholar] [CrossRef]
- Rizwan, M.; Yahya, R.; Hassan, A.; Yar, M.; Azzahari, A.D.; Selvanathan, V.; Sonsudin, F.; Abouloula, C.N. pH sensitive hydrogels in drug delivery: Brief history, properties, swelling, and release mechanism, material selection and applications. Polymers 2017, 9, 137. [Google Scholar] [CrossRef]
- Zhang, L.; Zheng, M.; Liu, X.; Sun, J. Layer-by-layer assembly of salt-containing polyelectrolyte complexes for the fabrication of dewetting-induced porous coatings. Langmuir 2011, 27, 1346–1352. [Google Scholar] [CrossRef] [PubMed]
- Dübner, M.; Naoum, M.E.; Spencer, N.D.; Padeste, C. From pH- to Light-Response: Postpolymerization Modification of Polymer Brushes Grafted onto Microporous Polymeric Membranes. ACS Omega 2017, 2, 455–461. [Google Scholar] [CrossRef]
- Mahato, K.; Baranwal, A.; Srivastava, A.; Maurya, P.K.; Chandra, P. Smart Materials for Biosensing Applications. In Proceedings of the Techno-Societal 2016, International Conference on Advanced Technologies for Societal Applications, Pandharpur, India, 20–21 December 2016; pp. 421–431. [Google Scholar]
- Weidman, J.L.; Mulvenna, R.A.; Boudouris, B.W.; Phillip, W.A. Unusually Stable Hysteresis in the pH-Response of Poly(Acrylic Acid) Brushes Confined within Nanoporous Block Polymer Thin Films. J. Am. Chem. Soc. 2016, 138, 7030–7039. [Google Scholar] [CrossRef] [PubMed]
- Rydzek, G.; Pakdel, A.; Witecka, A.; Awang Shri, D.N.; Gaudière, F.; Nicolosi, V.; Mokarian-Tabari, P.; Schaaf, P.; Boulmedais, F.; Ariga, K. pH-Responsive Saloplastics Based on Weak Polyelectrolytes: From Molecular Processes to Material Scale Properties. Macromolecules 2018, 51, 4424–4434. [Google Scholar] [CrossRef]
- Hariri, H.H.; Schlenoff, J.B. Saloplastic macroporous polyelectrolyte complexes: Cartilage mimics. Macromolecules 2010, 43, 8656–8663. [Google Scholar] [CrossRef] [PubMed]
- Verma, G.; Hassan, P.A. Self assembled materials: design strategies and drug delivery perspectives. Phys. Chem. Chem. Phys. 2013, 15, 17016–17028. [Google Scholar] [CrossRef]
- Shen, H.J.; Shi, H.; Ma, K.; Xie, M.; Tang, L.L.; Shen, S.; Li, B.; Wang, X.S.; Jin, Y. Polyelectrolyte capsules packaging BSA gels for pH-controlled drug loading and release and their antitumor activity. Acta Biomater. 2013, 9, 6123–6133. [Google Scholar] [CrossRef]
- Anandhakumar, S.; Gokul, P.; Raichur, A.M. Stimuli-responsive weak polyelectrolyte multilayer films: A thin film platform for self triggered multi-drug delivery. Mater. Sci. Eng. C 2016, 58, 622–628. [Google Scholar] [CrossRef]
- Gaonkar, A.G.; Vasisht, N.; Khare, A.R.; Sobel, R. Microencapsulation in the Food Industry A Practical Implementation Guide; Academic Press: Cambridge, MA, USA, 2014; Volume 53, p. 590. [Google Scholar]
- Xiao, Z.; Liu, W.; Zhu, G.; Zhou, R.; Niu, Y. A review of the preparation and application of flavour and essential oils microcapsules based on complex coacervation technology. J. Sci. Food Agric. 2014, 94, 1482–1494. [Google Scholar] [CrossRef]
- Stewart, R.J.; Wang, C.; Shao, H. Complex coacervates as a foundation for synthetic underwater adhesives. Adv. Colloid Interface Sci. 2010, 167, 85–93. [Google Scholar] [CrossRef] [PubMed]
- Gao, H. Development of star polymers as unimolecular containers for nanomaterials. Macromol. Rapid Commun. 2012, 33, 722–734. [Google Scholar] [CrossRef] [PubMed]
- Qin, J.; Priftis, D.; Farina, R.; Perry, S.L.; Leon, L.; Whitmer, J.; Hoffmann, K.; Tirrell, M.; De Pablo, J.J. Interfacial tension of polyelectrolyte complex coacervate phases. ACS Macro Lett. 2014, 3, 565–568. [Google Scholar] [CrossRef]
- Kim, S.; Huang, J.; Lee, Y.; Dutta, S.; Yoo, H.Y.; Jung, Y.M.; Jho, Y.; Zeng, H.; Hwang, D.S. Complexation and coacervation of like-charged polyelectrolytes inspired by mussels. Proc. Natl. Acad. Sci. USA 2016, 113, E847–E853. [Google Scholar] [CrossRef] [PubMed]
- Jha, P.K.; Desai, P.S.; Li, J.; Larson, R.G. pH and salt effects on the associative phase separation of oppositely charged polyelectrolytes. Polymers 2014, 6, 1414–1436. [Google Scholar] [CrossRef]
- Chang, L.W.; Lytle, T.K.; Radhakrishna, M.; Madinya, J.J.; Vélez, J.; Sing, C.E.; Perry, S.L. Sequence and entropy-based control of complex coacervates. Nat. Commun. 2017, 8, 1273. [Google Scholar] [CrossRef]
- Lytle, T.K.; Sing, C.E. Transfer matrix theory of polymer complex coacervation. Soft Matter 2017. [Google Scholar] [CrossRef] [PubMed]
- Perry, S.L.; Li, Y.; Priftis, D.; Leon, L.; Tirrell, M. The effect of salt on the complex coacervation of vinyl polyelectrolytes. Polymers 2014, 6, 1756–1772. [Google Scholar] [CrossRef]
- Perry, S.L.; Sing, C.E. PRISM-Based Theory of Complex Coacervation: Excluded Volume versus Chain Correlation. Macromolecules 2015, 48, 5040–5053. [Google Scholar] [CrossRef]
- Hoda, N.; Larson, R.G. Explicit- and Implicit-Solvent Molecular Dynamics Simulations of Complex Formation between Polycations and Polyanions RID G-2511-2010. Macromolecules 2009, 42, 8851–8863. [Google Scholar] [CrossRef]
- Rathee, V.S.; Sidky, H.; Sikora, B.J.; Whitmer, J.K. Role of Associative Charging in the Entropy–Energy Balance of Polyelectrolyte Complexes. J. Am. Chem. Soc. 2018, 140, 15319–15328. [Google Scholar] [CrossRef] [PubMed]
- Murmiliuk, A.; Košovan, P.; Janata, M.; Procházka, K.; Uhlík, F.; Štěpánek, M. Local pH and Effective pK of a Polyelectrolyte Chain: Two Names for One Quantity? ACS Macro Lett. 2018, 7, 1243–1247. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, F.; Valenzuela, L.D.; Sammalkorpi, M.; Lutkenhaus, J.L. Effect of Water on the Thermal Transition Observed in Poly(allylamine hydrochloride)–Poly(acrylic acid) Complexes. Macromolecules 2016, 49, 7563–7570. [Google Scholar] [CrossRef]
- Longo, G.S.; Olvera De La Cruz, M.; Szleifer, I. Molecular theory of weak polyelectrolyte gels: The role of pH and salt concentration. Macromolecules 2011, 44, 147–158. [Google Scholar] [CrossRef]
- Willott, J.D.; Murdoch, T.J.; Leermakers, F.A.M.; de Vos, W.M. Behavior of Weak Polyelectrolyte Brushes in Mixed Salt Solutions. Macromolecules 2018, 51, 1198–1206. [Google Scholar] [CrossRef]
- Tagliazucchi, M.; de la Cruz, M.O.; Szleifer, I. Self-organization of grafted polyelectrolyte layers via the coupling of chemical equilibrium and physical interactions. Proc. Natl. Acad. Sci. USA 2010, 107, 5300–5305. [Google Scholar] [CrossRef]
- Lu, Y.; Zhuk, A.; Xu, L.; Liang, X.; Kharlampieva, E.; Sukhishvili, S.A. Tunable pH and temperature response of weak polyelectrolyte brushes: role of hydrogen bonding and monomer hydrophobicity. Soft Matter 2013, 9, 5464. [Google Scholar] [CrossRef]
- Mauser, T.; Déjugnat, C.; Möhwald, H.; Sukhorukov, G.B. Microcapsules made of weak polyelectrolytes: Templating and stimuli-responsive properties. Langmuir 2006, 22, 5888–5893. [Google Scholar] [CrossRef]
- Christau, S.; Thurandt, S.; Yenice, Z.; von Klitzing, R. Stimuli-responsive polyelectrolyte brushes as a matrix for the attachment of gold nanoparticles: The effect of brush thickness on particle distribution. Polymers 2014, 6, 1877–1896. [Google Scholar] [CrossRef]
- Dong, R.; Lindau, M.; Ober, C.K. Dissociation behavior of weak polyelectrolyte brushes on a planar surface. Langmuir 2009, 25, 4774–4779. [Google Scholar] [CrossRef]
- Choi, J.; Rubner, M.F. Influence of the degree of ionization on weak polyelectrolyte multilayer assembly. Macromolecules 2005, 38, 116–124. [Google Scholar] [CrossRef]
- Rathee, V.S.; Zervoudakis, A.J.; Sidky, H.; Sikora, B.J.; Whitmer, J.K. Weak polyelectrolyte complexation driven by associative charging. J. Chem. Phys. 2018, 148, 114901. [Google Scholar] [CrossRef]
- Rathee, V.S.; Sikora, B.J.; Sidky, H.; Whitmer, J.K. Simulating the thermodynamics of charging in weak polyelectrolytes: the Debye–Hückel limit. Mater. Res. Express 2018, 5, 014010. [Google Scholar] [CrossRef]
- Uyaver, S.; Seidel, C. Effect of varying salt concentration on the behavior of weak polyelectrolytes in a poor solvent. Macromolecules 2009, 42, 1352–1361. [Google Scholar] [CrossRef]
- Uyaver, S.; Seidel, C. First-order conformational transition of annealed polyelectrolytes in a poor solvent. Europhys. Lett. 2003, 64, 536–542. [Google Scholar] [CrossRef]
- Uyaver, S.; Seidel, C. Pearl-necklace structures in annealed polyelectrolytes. J. Phys. Chem. B 2004, 108, 18804–18814. [Google Scholar] [CrossRef]
- Qu, C.; Shi, Y.; Jing, B.; Gao, H.; Zhu, Y. Probing the Inhomogeneous Charge Distribution on Annealed Polyelectrolyte Star Polymers in Dilute Aqueous Solutions. ACS Macro Lett. 2016, 5, 402–406. [Google Scholar] [CrossRef]
- Sherman, E.; Haran, G. Coil-globule transition in the denatured state of a small protein. Proc. Natl. Acad. Sci. USA 2006, 103, 11539–11543. [Google Scholar] [CrossRef]
- Kirwan, L.J.; Papastavrou, G.; Borkovec, M.; Behrens, S.H. Imaging the Coil-to-Globule Conformational Transition of a Weak Polyelectrolyte by Tuning the Polyelectrolyte Charge Density. Nano Lett. 2004, 4, 149–152. [Google Scholar] [CrossRef]
- Wang, X.; Qiu, X.; Wu, C. Comparison of the Coil-to-Globule and the Globule-to-Coil Transitions of a Single Poly(N-isopropylacrylamide) Homopolymer Chain in Water. Macromolecules 1998, 31, 2972–2976. [Google Scholar] [CrossRef]
- Kundagrami, A.; Muthukumar, M. Effective charge and coil-globule transition of a polyelectrolyte chain. Macromolecules 2010, 43, 2574–2581. [Google Scholar] [CrossRef]
- Stevens, M.J.; Kremer, K. Structure of salt-free linear polyelectrolytes. Phys. Rev. Lett. 1993, 71, 2228–2231. [Google Scholar] [CrossRef]
- Ulrich, S.; Laguecir, A.; Stoll, S. Titration of hydrophobic polyelectrolytes using Monte Carlo simulations. J. Chem. Phys. 2005, 122. [Google Scholar] [CrossRef]
- Uhlík, F.; Košovan, P.; Limpouchová, Z.; Procházka, K.; Borisov, O.V.; Leermakers, F.A. Modeling of ionization and conformations of starlike weak polyelectrolytes. Macromolecules 2014, 47, 4004–4016. [Google Scholar] [CrossRef]
- Barr, S.A.; Panagiotopoulos, A.Z. Conformational transitions of weak polyacids grafted to nanoparticles. J. Chem. Phys. 2012, 137. [Google Scholar] [CrossRef]
- Panagiotopoulos, A.Z. Charge correlation effects on ionization of weak polyelectrolytes. J. Phys. Condens. Matter 2009, 21, 424113. [Google Scholar] [CrossRef]
- Léonforte, F.; Welling, U.; Müller, M. Single-chain-in-mean-field simulations of weak polyelectrolyte brushes. J. Chem. Phys. 2016, 145. [Google Scholar] [CrossRef]
- Nap, R.; Gong, P.; Szleifer, I. Weak polyelectrolytes tethered to surfaces: Effect of geometry, acid-base equilibrium and electrical permittivity. J. Polym. Sci. Part B Polym. Phys. 2006, 44, 2638–2662. [Google Scholar] [CrossRef]
- Brettmann, B.K.; Laugel, N.; Hoffmann, N.; Pincus, P.; Tirrell, M. Bridging contributions to polyelectrolyte brush collapse in multivalent salt solutions. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 284–291. [Google Scholar] [CrossRef]
- Stornes, M.; Linse, P.; Dias, R.S. Monte Carlo Simulations of Complexation between Weak Polyelectrolytes and a Charged Nanoparticle. Influence of Polyelectrolyte Chain Length and Concentration. Macromolecules 2017, 50, 5978–5988. [Google Scholar] [CrossRef]
- Heyes, D.M. Molecular dynamics simulations of restricted primitive model 1:1 electrolytes. Chem. Phys. 1982, 69, 155–163. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Sidky, H.; Sikora, B.; Rathee, V.S. SAPHRON.
- Qu, C.; Jing, B.; Wang, S.; Zhu, Y. Distinct Effects of Multivalent Macroion and Simple Ion on the Structure and Local Electric Environment of a Weak Polyelectrolyte in Aqueous Solution. J. Phys. Chem. B 2017, 121, 8829–8837. [Google Scholar] [CrossRef]
- Swift, T.; Swanson, L.; Geoghegan, M.; Rimmer, S. The pH-responsive behaviour of poly(acrylic acid) in aqueous solution is dependent on molar mass. Soft Matter 2016, 12, 2542–2549. [Google Scholar] [CrossRef]
- Lavrenko, P.N.; Kolomiets, I.P.; Ratnikova, O.V.; Vinogradova, L.V. Hydrodynamic, electrooptical, and conformational properties of fullerene-containing poly(2-vinylpyridines) in solutions. Polym. Sci. Ser. A 2006, 48, 981–988. [Google Scholar] [CrossRef]
- Huglin, M.B.; Rego, J.M. Study of polymer blends based on poly(vinylpyridines) and acidic polymers. Polymer 1990, 31, 1269–1276. [Google Scholar] [CrossRef]
- Pelton, R. Polyvinylamine: A tool for engineering interfaces. Langmuir 2014, 30, 15373–15382. [Google Scholar] [CrossRef]
- Romero Nieto, D.; Lindbråthen, A.; Hägg, M.B. Effect of Water Interactions on Polyvinylamine at Different pHs for Membrane Gas Separation. ACS Omega 2017, 2, 8388–8400. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: New York, NY, USA, 2002; p. 638. [Google Scholar]
- Kremer, K.; Grest, G.S. Molecular dynamics (MD) simulations for polymers. J. Phys. Condens. Matter 1990, 2, SA295–SA298. [Google Scholar] [CrossRef]
- Zhou, Q.; Akhavan, R. Cost-effective multi-mode FENE bead-spring models for dilute polymer solutions. J. Non-Newtonian Fluid Mech. 2004, 116, 269–300. [Google Scholar] [CrossRef]
- Bazant, M.Z.; Storey, B.D.; Kornyshev, A.A. Double Layer in Ionic Liquids: Overscreening versus Crowding. Phys. Rev. Lett. 2011, 106, 046102. [Google Scholar] [CrossRef]
- Israelachvili, J. Intermolecular and Surface Forces, 3rd ed.; Academic Press Inc.: San Diego, CA, USA, 2010; p. 704. [Google Scholar]
- Brennan, J.K. Cavity-bias sampling in reaction ensemble Monte Carlo simulations. Mol. Phys. 2005, 103, 2647–2654. [Google Scholar] [CrossRef]
- Smith, W.; Triska, B. The reaction ensemble method for the computer simulation of chemical and phase equilibria. I. Theory and basic examples. J. Chem. Phys. 1994, 100. [Google Scholar] [CrossRef]
- Johnson, J.K.; Panagiotopoulos, A.Z.; Gubbins, K.E. Reactive canonical Monte Carlo. Mol. Phys. 1994, 81, 717–733. [Google Scholar] [CrossRef]
- Sing, C.E. Development of the modern theory of polymeric complex coacervation. Adv. Colloid Interface Sci. 2017, 239, 2–16. [Google Scholar] [CrossRef]
- Radhakrishna, M.; Basu, K.; Liu, Y.; Shamsi, R.; Perry, S.L.; Sing, C.E. Molecular Connectivity and Correlation Effects on Polymer Coacervation. Macromolecules 2017, 50, 3030–3037. [Google Scholar] [CrossRef]
- Marciel, A.B.; Srivastava, S.; Tirrell, M.V. Structure and rheology of polyelectrolyte complex coacervates. Soft Matter 2018, 14, 2454–2464. [Google Scholar] [CrossRef]
- Johnston, B.M.; Johnston, C.W.; Letteri, R.A.; Lytle, T.K.; Sing, C.E.; Emrick, T.; Perry, S.L. The effect of comb architecture on complex coacervation. Org. Biomol. Chem. 2017. [Google Scholar] [CrossRef]
- Li, L.; Srivastava, S.; Andreev, M.; Marciel, A.B.; de Pablo, J.J.; Tirrell, M.V. Phase Behavior and Salt Partitioning in Polyelectrolyte Complex Coacervates. Macromolecules 2018, 51, 2988–2995. [Google Scholar] [CrossRef]
- Ou, Z.; Muthukumar, M. Entropy and enthalpy of polyelectrolyte complexation: Langevin dynamics simulations. J. Chem. Phys. 2006, 124, 154902. [Google Scholar] [CrossRef]
- Solis, F.J.; de la Cruz, M.O. Collapse of flexible polyelectrolytes in multivalent salt solutions. J. Chem. Phys. 2000, 112, 2030–2035. [Google Scholar] [CrossRef]
- González-Mozuelos, P.; de la Cruz, M.O. Ion condensation in salt-free dilute polyelectrolyte solutions. J. Chem. Phys. 1995, 103, 3145–3157. [Google Scholar] [CrossRef]
- De la Cruz, M.O.; Belloni, L.; Delsanti, M.; Dalbiez, J.P.; Spalla, O.; Drifford, M. Precipitation of highly charged polyelectrolyte solutions in the presence of multivalent salts. J. Chem. Phys. 1995, 103, 5781–5791. [Google Scholar] [CrossRef]
- Qu, C. Structural Dynamics of Weak Polyelectrolytes in Aqueous Solution. Ph.D. Thesis, University of Notre Dame, Notre Dame, IN, USA, 2016. [Google Scholar]
- Hsiao, P.Y. Overcharging, charge inversion, and reentrant condensation: Using highly charged polyelectrolytes in tetravalent salt solutions as an example of study. J. Phys. Chem. B 2008, 112, 7347–7350. [Google Scholar] [CrossRef]
- Hsiao, P.Y.; Luijten, E. Salt-induced collapse and reexpansion of highly charged flexible polyelectrolytes. Phys. Rev. Lett. 2006, 97. [Google Scholar] [CrossRef]
- Chremos, A.; Douglas, J.F. Influence of higher valent ions on flexible polyelectrolyte stiffness and counter-ion distribution. J. Chem. Phys. 2016, 144. [Google Scholar] [CrossRef]
- Nap, R.J.; Park, S.H.; Szleifer, I. Competitive calcium ion binding to end-tethered weak polyelectrolytes. Soft Matter 2018, 14, 2365–2378. [Google Scholar] [CrossRef]
- Liu, S.; Ghosh, K.; Muthukumar, M. Polyelectrolyte solutions with added salt: A simulation study. J. Chem. Phys. 2003, 119, 1813–1823. [Google Scholar] [CrossRef]
- Wei, J.; Hoagland, D.A.; Zhang, G.; Su, Z. Effect of Divalent Counterions on Polyelectrolyte Multilayer Properties. Macromolecules 2016, 49, 1790–1797. [Google Scholar] [CrossRef]
- Yin, D.W.; Horkay, F.; Douglas, J.F.; De Pablo, J.J. Molecular simulation of the swelling of polyelectrolyte gels by monovalent and divalent counterions. J. Chem. Phys. 2008, 129. [Google Scholar] [CrossRef]
- Yu, J.; Mao, J.; Yuan, G.; Satija, S.; Jiang, Z.; Chen, W.; Tirrell, M. Structure of Polyelectrolyte Brushes in the Presence of Multivalent Counterions. Macromolecules 2016, 49, 5609–5617. [Google Scholar] [CrossRef]
- Drozdov, A.D.; DeClaville Christiansen, J. Modeling the effects of pH and ionic strength on swelling of anionic polyelectrolyte gels. Model. Simul. Mater. Sci. Eng. 2015, 23. [Google Scholar] [CrossRef]
- Sircar, S.; Keener, J.P.; Fogelson, A.L. The effect of divalent vs. monovalent ions on the swelling of Mucin-like polyelectrolyte gels: Governing equations and equilibrium analysis. J. Chem. Phys. 2013, 138. [Google Scholar] [CrossRef]
- Horkay, F.; Tasaki, I.; Basser, P.J. Osmotic Swelling of Polyacrylate Hydrogels in Physiological Salt Solutions. Biomacromolecules 2000, 1, 84–90. [Google Scholar] [CrossRef]
- Horkay, F.; Tasaki, I.; Basser, P.J. Effect of monovalent-divalent cation exchange on the swelling of polyacrylate hydrogels in physiological salt solutions. Biomacromolecules 2001, 2, 195–199. [Google Scholar] [CrossRef]
- Deepika, R.; Girigoswami, K.; Murugesan, R.; Girigoswami, A. Influence of Divalent Cation on Morphology and Drug Delivery Efficiency of Mixed Polymer Nanoparticles. Curr. Drug Deliv. 2017, 14. [Google Scholar] [CrossRef]
- Ulrich, S.; Seijo, M.; Laguecir, A.; Stoll, S. Nanoparticle Adsorption on a Weak Polyelectrolyte. Stiffness, pH, Charge Mobility, and Ionic Concentration Effects Investigated by Monte Carlo Simulations. J. Phys. Chem. B 2006, 110, 20954–20964. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rathee, V.S.; Sidky, H.; Sikora, B.J.; Whitmer, J.K. Explicit Ion Effects on the Charge and Conformation of Weak Polyelectrolytes. Polymers 2019, 11, 183. https://doi.org/10.3390/polym11010183
Rathee VS, Sidky H, Sikora BJ, Whitmer JK. Explicit Ion Effects on the Charge and Conformation of Weak Polyelectrolytes. Polymers. 2019; 11(1):183. https://doi.org/10.3390/polym11010183
Chicago/Turabian StyleRathee, Vikramjit S., Hythem Sidky, Benjamin J. Sikora, and Jonathan K. Whitmer. 2019. "Explicit Ion Effects on the Charge and Conformation of Weak Polyelectrolytes" Polymers 11, no. 1: 183. https://doi.org/10.3390/polym11010183
APA StyleRathee, V. S., Sidky, H., Sikora, B. J., & Whitmer, J. K. (2019). Explicit Ion Effects on the Charge and Conformation of Weak Polyelectrolytes. Polymers, 11(1), 183. https://doi.org/10.3390/polym11010183





