Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts
Abstract
1. Introduction
2. Experiments
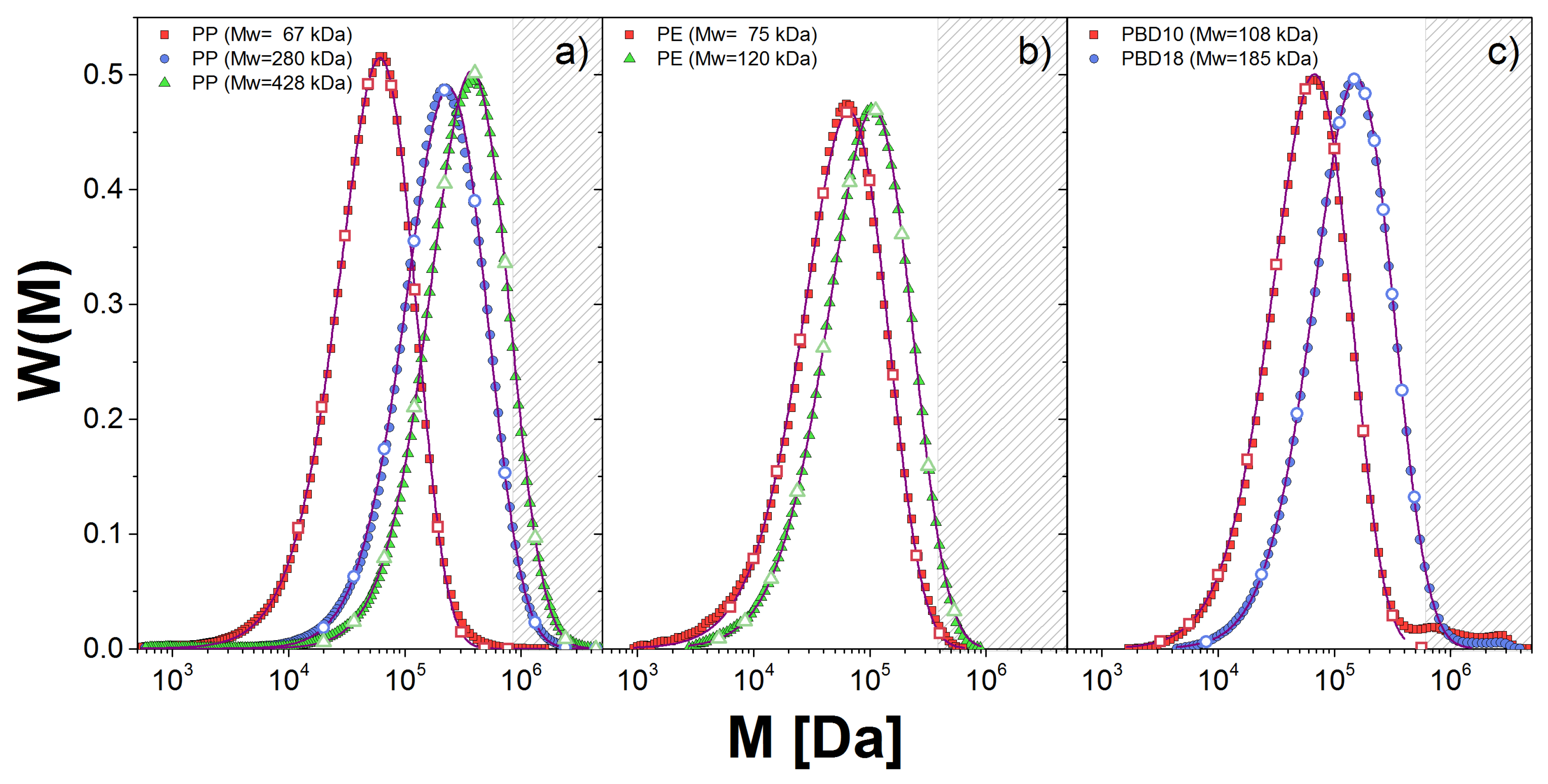
2.1. Samples
2.2. Characterization
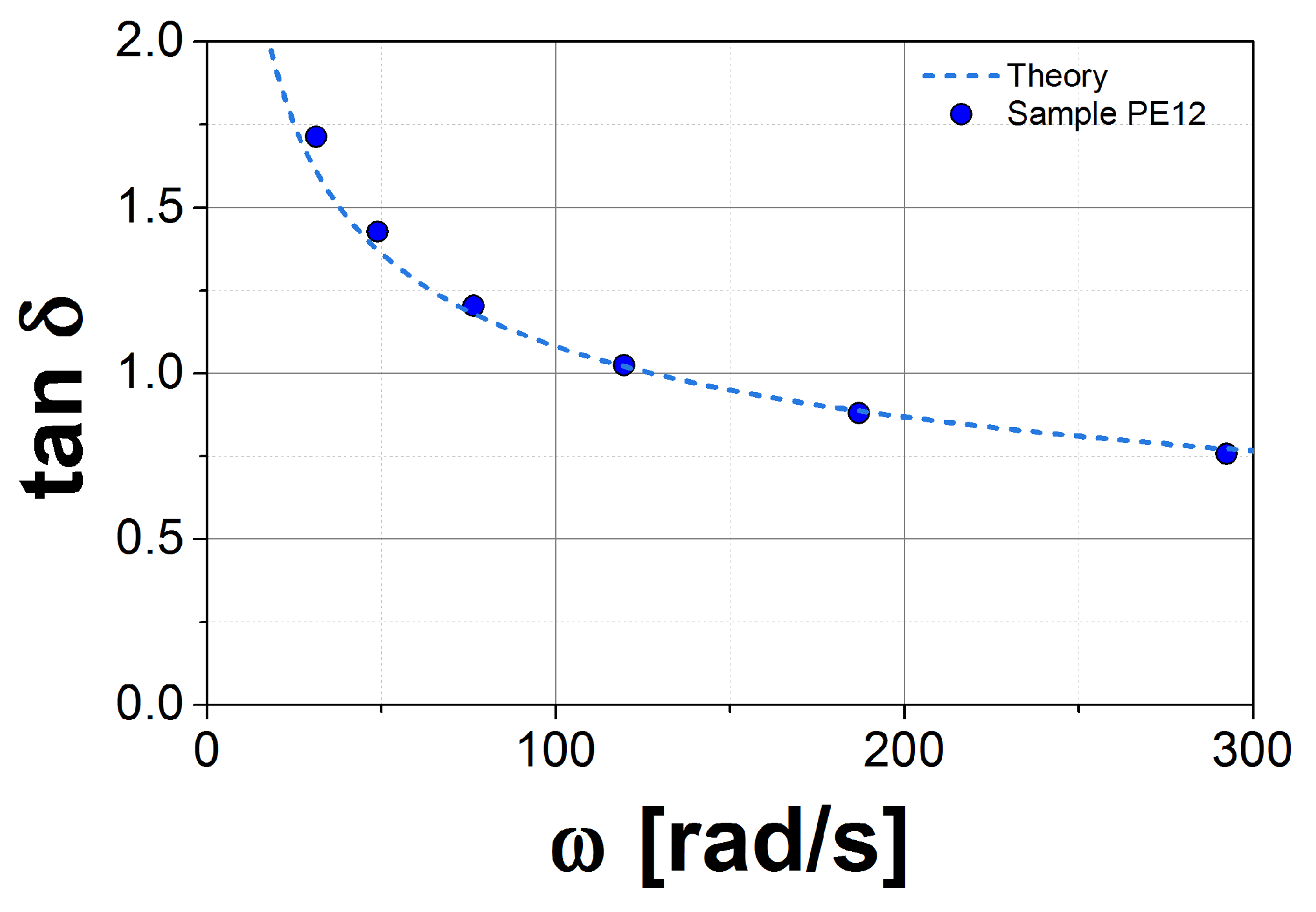
2.3. Rheological Measurements
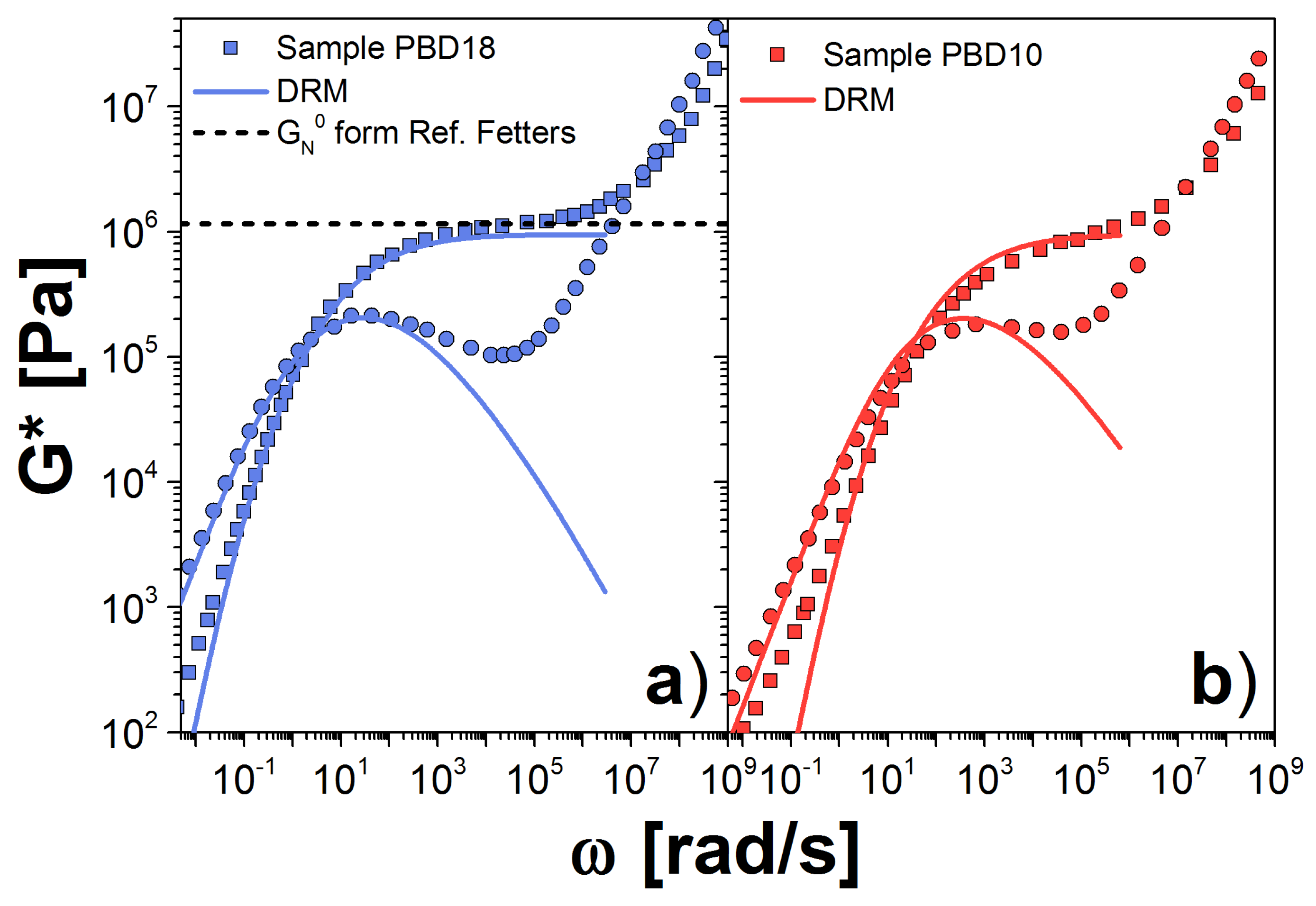
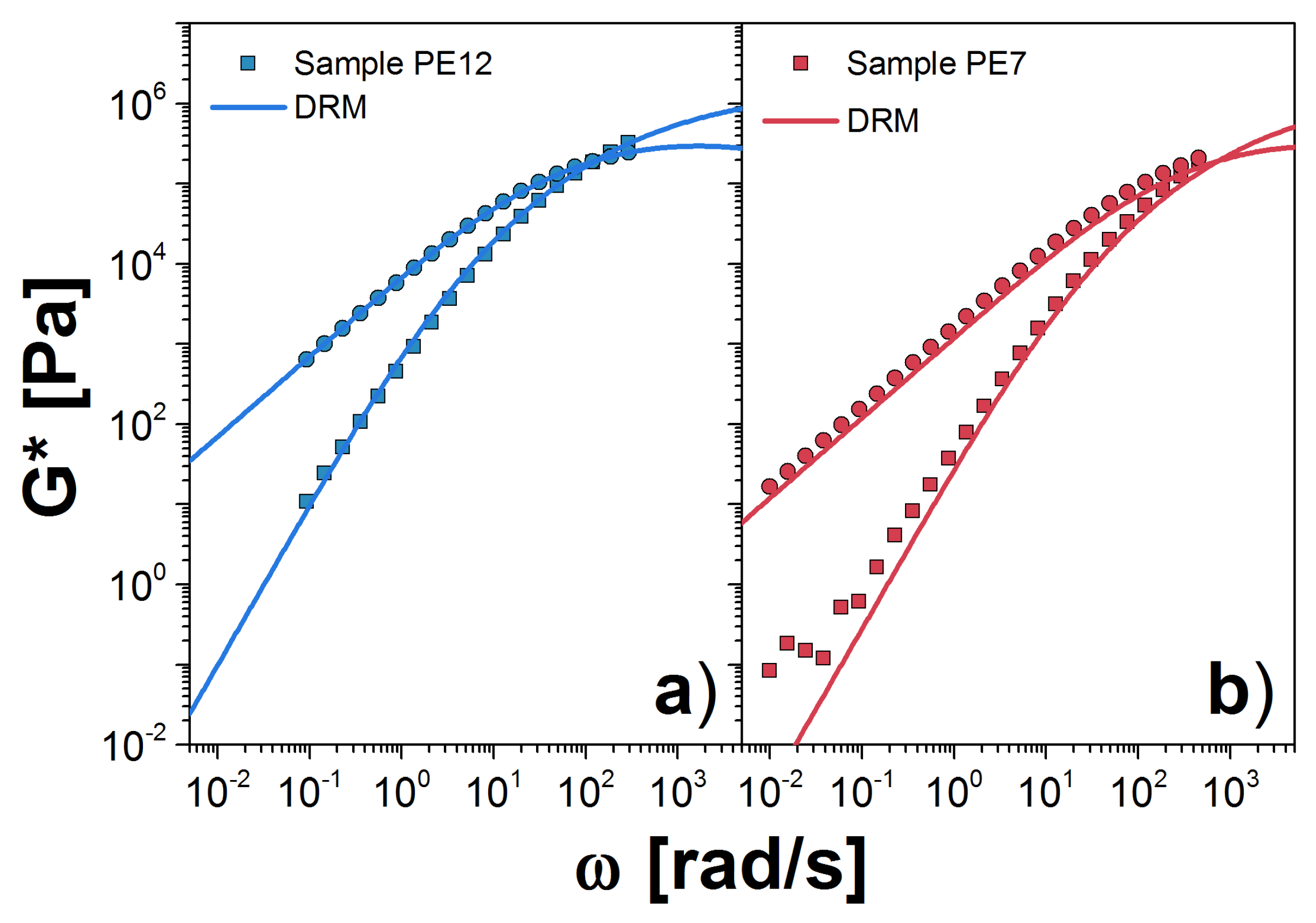
3. Double Reptation Model
3.1. Results for the DRM
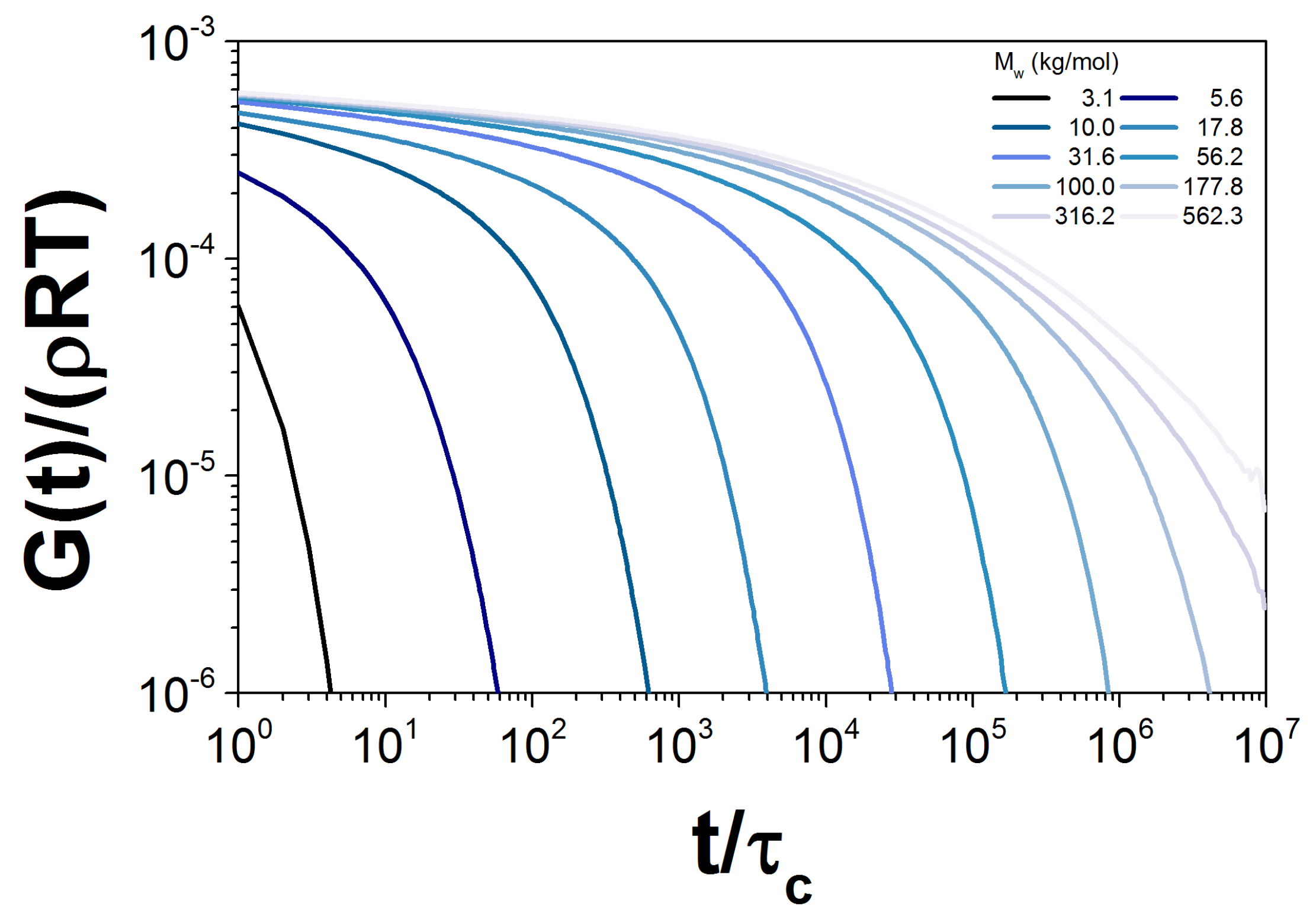
4. Clustered Fixed-Slip-Link Model
4.1. The Parameters
4.2. Implementation
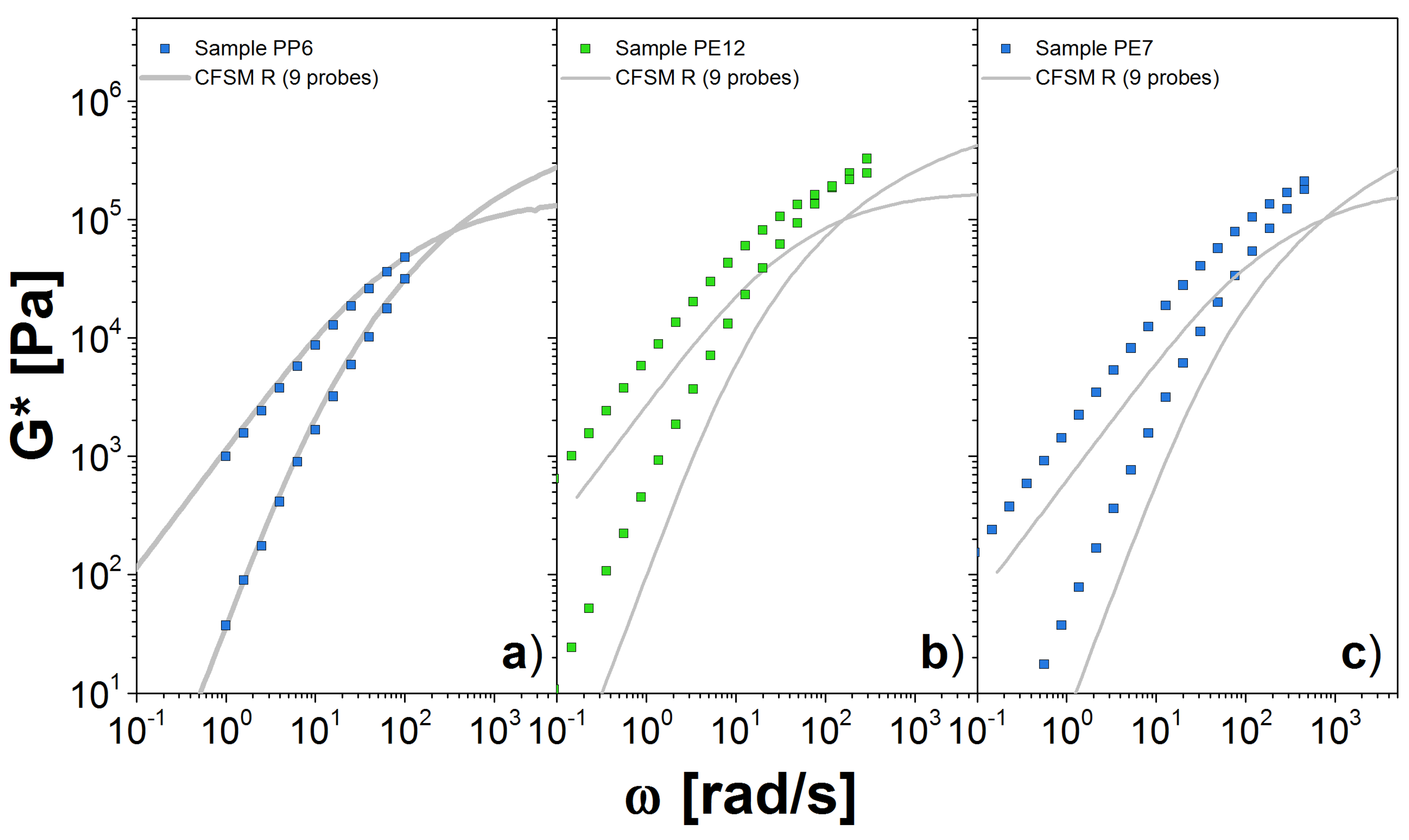
4.3. Results for the DSM
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DSM | discrete slip-link model |
| DRM | double-reptation model |
| PBD | polybutadiene |
| PP | polypropilene |
| PE | polyethylene |
| GEX | generalized exponential |
| PDI | polydisperse index |
| GPC | gel permeation chromatography |
| SAOS | small amplitude oscillatory shear |
| MWD | molecular weight distribution |
| CP | crossover point |
| CD | constraint dynamics |
| SD | sliding dynamics |
| CFSM | cluster fixed slip-link model |
References
- Ferry, J. Viscoelastic Properties of Polymers; Wiley: Hoboken, NJ, USA, 1980. [Google Scholar]
- Desai, P.S.; Kang, B.G.; Katzarova, M.; Hall, R.; Huang, Q.; Lee, S.; Shivokhin, M.; Chang, T.; Venerus, D.C.; Mays, J.; et al. Challenging Tube and Slip-Link Models: Predicting the Linear Rheology of Blends of Well-Characterized Star and Linear 1,4-Polybutadienes. Macromolecules 2016, 49, 4964–4977. [Google Scholar] [CrossRef]
- De Gennes, P. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Doi, M.; Edwards, S. The Theory of Polymer Dynamics; International Series of Monographs on Physics; Clarendon Press: Oxford, UK, 1988. [Google Scholar]
- Rubinstein, M.; Colby, R.H. Self-consistent theory of polydisperse entangled polymers: Linear viscoelasticity of binary blends. J. Chem. Phys. 1988, 89, 5291–5306. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4 power law of viscosity of polymeric liquids on the basis of the tube model. J. Polym. Sci. Polym. Lett. Ed. 1981, 19, 265–273. [Google Scholar] [CrossRef]
- Tuminello, W.H. Molecular weight and molecular weight distribution from dynamic measurements of polymer melts. Polym. Eng. Sci. 1986, 26, 1339–1347. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Double Reptation vs. Simple Reptation in Polymer Melts. EPL (Europhys. Lett.) 1988, 5, 437. [Google Scholar] [CrossRef]
- Des Cloizeaux, J. Relaxation of entangled polymers in melts. Macromolecules 1990, 23, 3992–4006. [Google Scholar] [CrossRef]
- Tsenoglou, C. Molecular weight polydispersity effects on the viscoelasticity of entangled linear polymers. Macromolecules 1991, 24, 1762–1767. [Google Scholar] [CrossRef]
- Léonardi, F.; Majesté, J.C.; Allal, A.; Marin, G. Rheological models based on the double reptation mixing rule: The effects of a polydisperse environment. J. Rheol. 2000, 44, 675–692. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Liu, C.Y.; Bailly, C. Quantitative Tube Model Predictions for the Linear Viscoelasticity of Linear Polymers. In Rheology Reviews; The British Society of Rheology: Swansea, UK, 2007; pp. 53–134. [Google Scholar]
- Kremer, K.; Grest, G.S.; Carmesin, I. Crossover from Rouse to Reptation Dynamics: A Molecular-Dynamics Simulation. Phys. Rev. Lett. 1988, 61, 566–569. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M.; Hess, S. Rheological Evidence for a Dynamical Crossover in Polymer Melts via Nonequilibrium Molecular Dynamics. Phys. Rev. Lett. 2000, 85, 1128–1131. [Google Scholar] [CrossRef] [PubMed]
- Auhl, R.; Everaers, R.; Grest, G.S.; Kremer, K.; Plimpton, S.J. Equilibration of long chain polymer melts in computer simulations. J. Chem. Phys. 2003, 119, 12718–12728. [Google Scholar] [CrossRef]
- Schieber, J.D.; Neergaard, J.; Gupta, S. A full-chain, temporary network model with sliplinks, chain-length fluctuations, chain connectivity and chain stretching. J. Rheol. 2003, 47, 213–233. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Self-Consistent Modeling of Constraint Release in a Single-Chain Mean-Field Slip-Link Model. Macromolecules 2009, 42, 7504–7517. [Google Scholar] [CrossRef]
- Khaliullin, R.N.; Schieber, J.D. Application of the Slip-Link Model to Bidisperse Systems. Macromolecules 2010, 43, 6202–6212. [Google Scholar] [CrossRef]
- Schieber, J.D.; Andreev, M. Entangled Polymer Dynamics in Equilibrium and Flow Modeled Through Slip Links. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Andreev, M.; Feng, H.; Yang, L.; Schieber, J.D. Universality and speedup in equilibrium and nonlinear rheology predictions of the fixed slip-link model. J. Rheol. 2014, 58, 723–736. [Google Scholar] [CrossRef]
- Katzarova, M.; Yang, L.; Andreev, M.; Córdoba, A.; Schieber, J.D. Analytic slip-link expressions for universal dynamic modulus predictions of linear monodisperse polymer melts. Rheol. Acta 2015, 54, 169–183. [Google Scholar] [CrossRef]
- Andreev, M.; Schieber, J.D. Accessible and Quantitative Entangled Polymer Rheology Predictions, Suitable for Complex Flow Calculations. Macromolecules 2015, 48, 1606–1613. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Coppola, S.; Balacca, L.; Righi, S.; Vlassopoulos, D. Decoding the viscoelastic response of polydisperse star/linear polymer blends. J. Rheol. 2010, 54, 507–538. [Google Scholar] [CrossRef]
- Fetters, L.J.; Lohse, D.J.; Colby, R.H. Chain Dimensions and Entanglement Spacings. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007; pp. 447–454. [Google Scholar]
- Guzmán, J.D.; Schieber, J.D.; Pollard, R. A regularization-free method for the calculation of molecular weight distributions from dynamic moduli data. Rheol. Acta 2005, 44, 342–351. [Google Scholar] [CrossRef]
- Thimm, W.; Friedrich, C.; Marth, M.; Honerkamp, J. An analytical relation between relaxation time spectrum and molecular weight distribution. J. Rheol. 1999, 43, 1663–1672. [Google Scholar] [CrossRef]
- Liu, C.; He, J.; van Ruymbeke, E.; Keunings, R.; Bailly, C. Evaluation of different methods for the determination of the plateau modulus and the entanglement molecular weight. Polymer 2006, 47, 4461–4479. [Google Scholar] [CrossRef]
- Struglinski, M.J.; Graessley, W.W. Effects of polydispersity on the linear viscoelastic properties of entangled polymers. 1. Experimental observations for binary mixtures of linear polybutadiene. Macromolecules 1985, 18, 2630–2643. [Google Scholar] [CrossRef]
- Santangelo, P.G.; Roland, C.M.; Puskas, J.E. Rheology of Star-Branched Polyisobutylene. Macromolecules 1999, 32, 1972–1977. [Google Scholar] [CrossRef]
- Aguilar, M.; Vega, J.; Na, B.P.; Martínez-Salazar, J. Novel features of the rheological behaviour of metallocene catalysed atactic polypropylene. Polymer 2003, 44, 1401–1407. [Google Scholar] [CrossRef]
- Van Ruymbeke, E.; Keunings, R.; Bailly, C. Prediction of linear viscoelastic properties for polydisperse mixtures of entangled star and linear polymers: Modified tube-based model and comparison with experimental results. J. Non-Newtonian Fluid Mech. 2005, 128, 7–22. [Google Scholar] [CrossRef]
- Stephanou, P.S.; Mavrantzas, V.G. Quantitative predictions of the linear viscoelastic properties of entangled polyethylene and polybutadiene melts via modified versions of modern tube models on the basis of atomistic simulation data. J. Non-Newtonian Fluid Mech. 2013, 200, 111–130. [Google Scholar] [CrossRef]
- Shivokhin, M.E.; Read, D.J.; Kouloumasis, D.; Kocen, R.; Zhuge, F.; Bailly, C.; Hadjichristidis, N.; Likhtman, A.E. Understanding Effect of Constraint Release Environment on End-to-End Vector Relaxation of Linear Polymer Chains. Macromolecules 2017, 50, 4501–4523. [Google Scholar] [CrossRef]
- Eckstein, A.; Suhm, J.; Friedrich, C.; Maier, R.D.; Sassmannshausen, J.; Bochmann, M.; Mülhaupt, R. Determination of Plateau Moduli and Entanglement Molecular Weights of Isotactic, Syndiotactic, and Atactic Polypropylenes Synthesized with Metallocene Catalysts. Macromolecules 1998, 31, 1335–1340. [Google Scholar] [CrossRef]
- Katzarova, M.; Andreev, M.; Sliozberg, Y.R.; Mrozek, R.A.; Lenhart, J.L.; Andzelm, J.W.; Schieber, J.D. Rheological predictions of network systems swollen with entangled solvent. AIChE J. 2014, 60, 1372–1380. [Google Scholar] [CrossRef]
- Kubo, R. Statistical-Mechanical Theory of Irreversible Processes. I. General Theory and Simple Applications to Magnetic and Conduction Problems. J. Phys. Soc. Jpn. 1957, 12, 570–586. [Google Scholar] [CrossRef]
- Baumgaertel, M.; Schausberger, A.; Winter, H.H. The relaxation of polymers with linear flexible chains of uniform length. Rheol. Acta 1990, 29, 400–408. [Google Scholar] [CrossRef]


| Polymer Name | T | |||||
|---|---|---|---|---|---|---|
| (g/mol) | (C) | (MPa) | (g/mL) | (g/mol) | ||
| PP6 | 0.67 | 2.02 | 120 | 0.47 | 0.791 | 183.4 |
| PP28 | 2.80 | 2.05 | 120 | 0.47 | 0.791 | 183.4 |
| PP42 | 4.28 | 1.98 | 120 | 0.47 | 0.791 | 183.4 |
| PP42 | 4.28 | 1.98 | 80 | 0.48 | 0.825 | 183.4 |
| PE7 | 0.75 | 2.20 | 190 | 2.6 | 0.785 | 150.4 |
| PE12 | 1.20 | 2.27 | 190 | 2.6 | 0.785 | 150.4 |
| PBD10 | 1.08 | 2.7 | 30 | 1.15 | 0.895 | 112.5 |
| PBD18 | 1.85 | 2.1 | 30 | 1.15 | 0.895 | 112.5 |
| PBD20 | 2.04 | 1.1 | 30 | 1.15 | 0.895 | 112.5 |
| Polymer Code | a | b | k | |||
|---|---|---|---|---|---|---|
| (g/mol) | (MPa) | (s(mol/g)) | () | |||
| PP6 | 1.33 (3) | 0.75 (1) | 13.7 (9) | 0.497 | 3.99 | 12.02 |
| PP28 | 2.2 (2) | 0.48 (4) | 5 (3) | 0.918 | 4.54 | 0.363 |
| PP42 * | 2.04 (8) | 0.54 (2) | 15 (4) | 1.000 | 4.51 | 19.05 |
| PP42 * | 2.04 (8) | 0.54 (2) | 15 (4) | 1.025 | 59.42 | 251.19 |
| PE7 | 1.26 (4) | 0.64 (1) | 9.1 (9) | 1.89 | 0.958 | 0.69 |
| PE12 * | 1.36 (2) | 0.61 (1) | 11.8 (6) | 1.44 | 1.02 | 1.82 |
| PBD10 | 1.48 (4) | 0.66 (1) | 9.3 (9) | 0.690 | 20.4 | 15.90 |
| PBD18 * | 1.96 (4) | 0.54 (1) | 6.7 (8) | 0.948 | 14.4 | 5.47 |
| PBD20 | - | - | - | - | - | - |
| Polymer Code | |||||
|---|---|---|---|---|---|
| (MPa) | (g/mol) | (g/mol) | (s) | ||
| PBD10 | 1.26 | 791.302 | 5.54 | 12.6 | 0.4 |
| PBD18 | 1.26 | 791.302 | 5.54 | 12.6 | 0.4 |
| PBD20 | 1.26 | 791.302 | – | 12.6 | 0.4 |
| PP6 | 1.00 | 1282.71 | 8.97 | 11.5 | 0.3 |
| PE12 | 1.44 | 1089.12 | 7.62 | 11.9 | 0.15 |
| PE7 | 1.44 | 1089.12 | 7.62 | 11.9 | 0.15 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Valadez-Pérez, N.E.; Taletskiy, K.; Schieber, J.D.; Shivokhin, M. Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers 2018, 10, 908. https://doi.org/10.3390/polym10080908
Valadez-Pérez NE, Taletskiy K, Schieber JD, Shivokhin M. Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers. 2018; 10(8):908. https://doi.org/10.3390/polym10080908
Chicago/Turabian StyleValadez-Pérez, Néstor E., Konstantin Taletskiy, Jay D. Schieber, and Maksim Shivokhin. 2018. "Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts" Polymers 10, no. 8: 908. https://doi.org/10.3390/polym10080908
APA StyleValadez-Pérez, N. E., Taletskiy, K., Schieber, J. D., & Shivokhin, M. (2018). Efficient Determination of Slip-Link Parameters from Broadly Polydisperse Linear Melts. Polymers, 10(8), 908. https://doi.org/10.3390/polym10080908





