Rotation Dynamics of Star Block Copolymers under Shear Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Model and Simulation Method
2.1.1. Coarse-Grained Model for the Star Block Copolymer
2.1.2. Multiparticle Collision Dynamics and Molecular Dynamics
2.2. Rotational Dynamics
2.2.1. Laboratory Frame
2.2.2. Eckart Frame
2.2.3. Hybrid Frame
2.2.4. Geometrical Approach
3. Results and Discussion
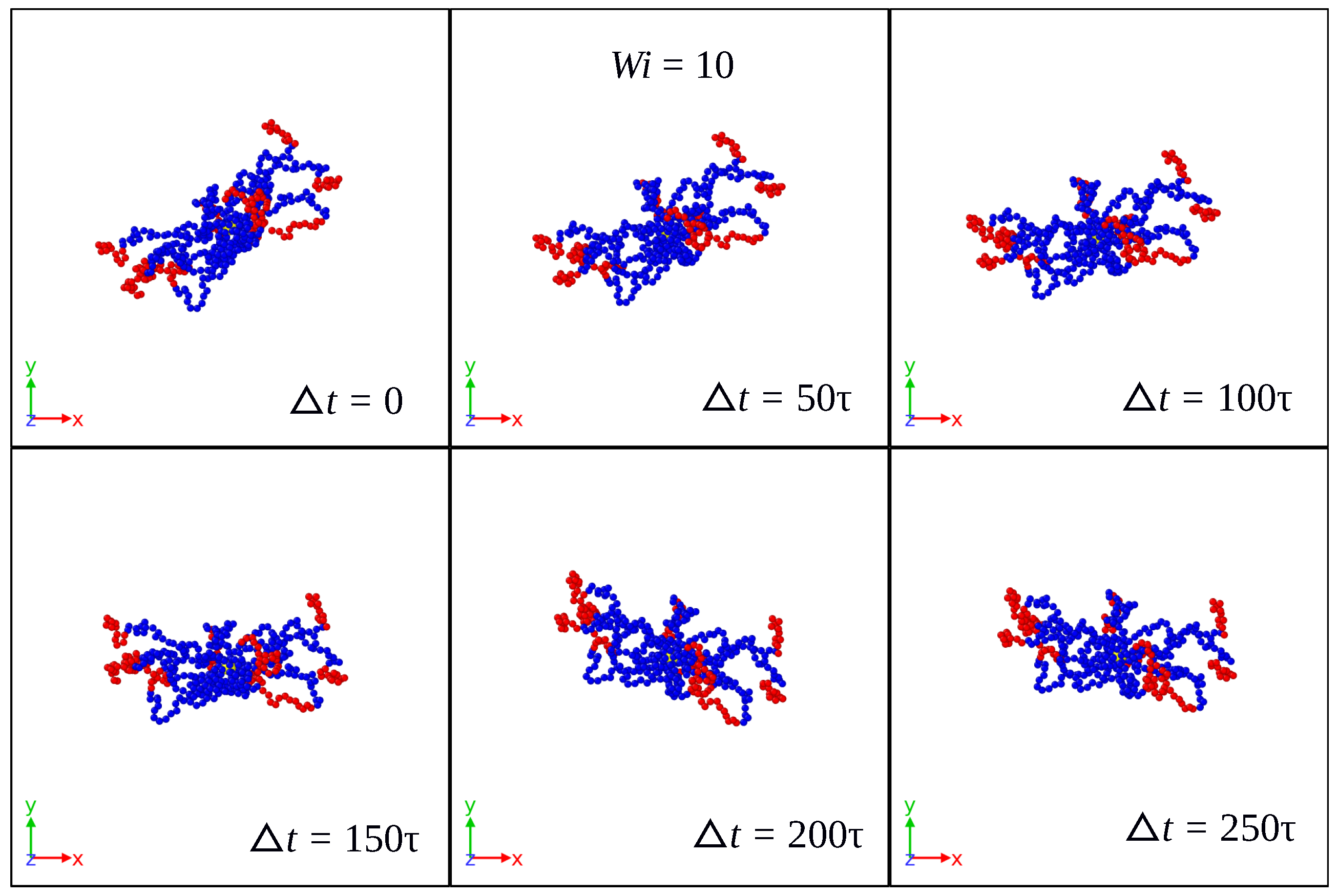
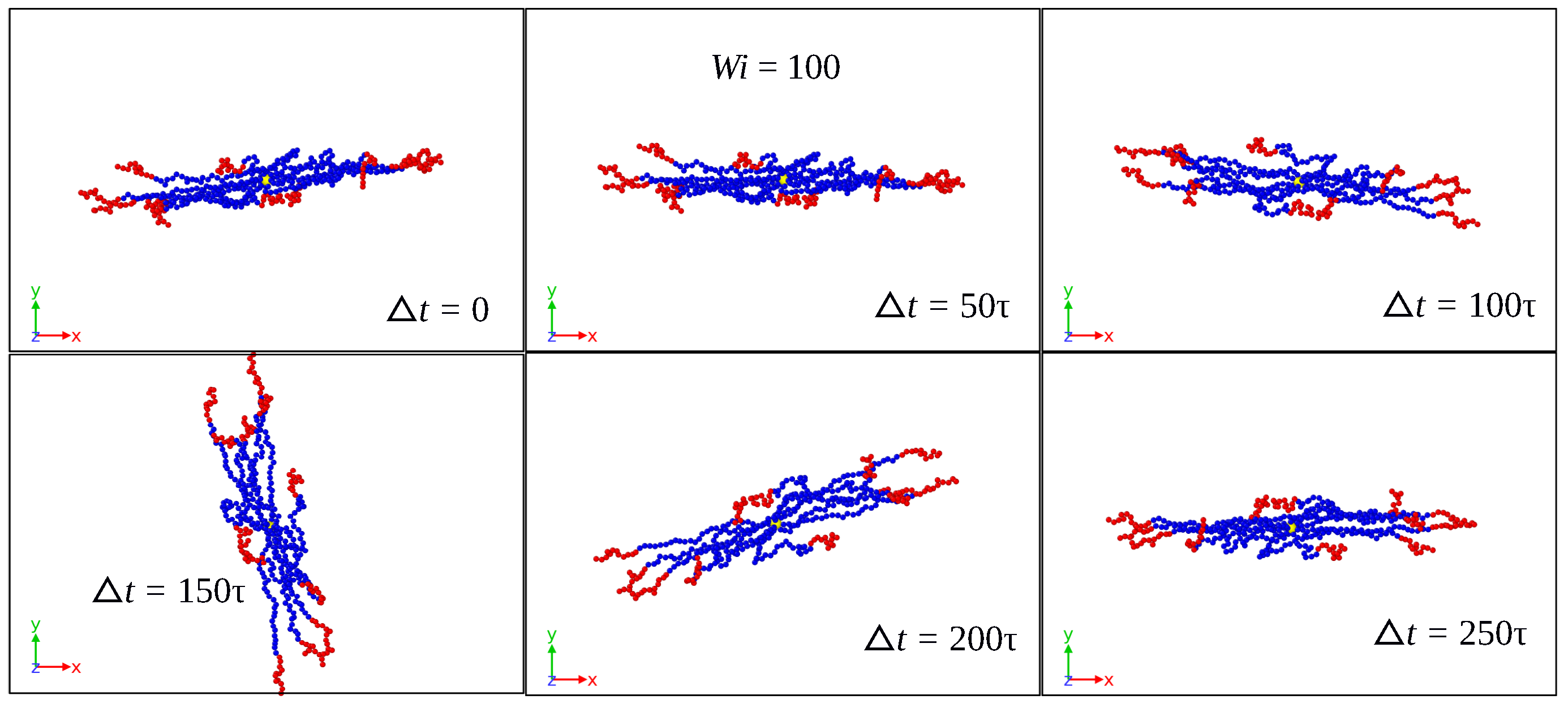
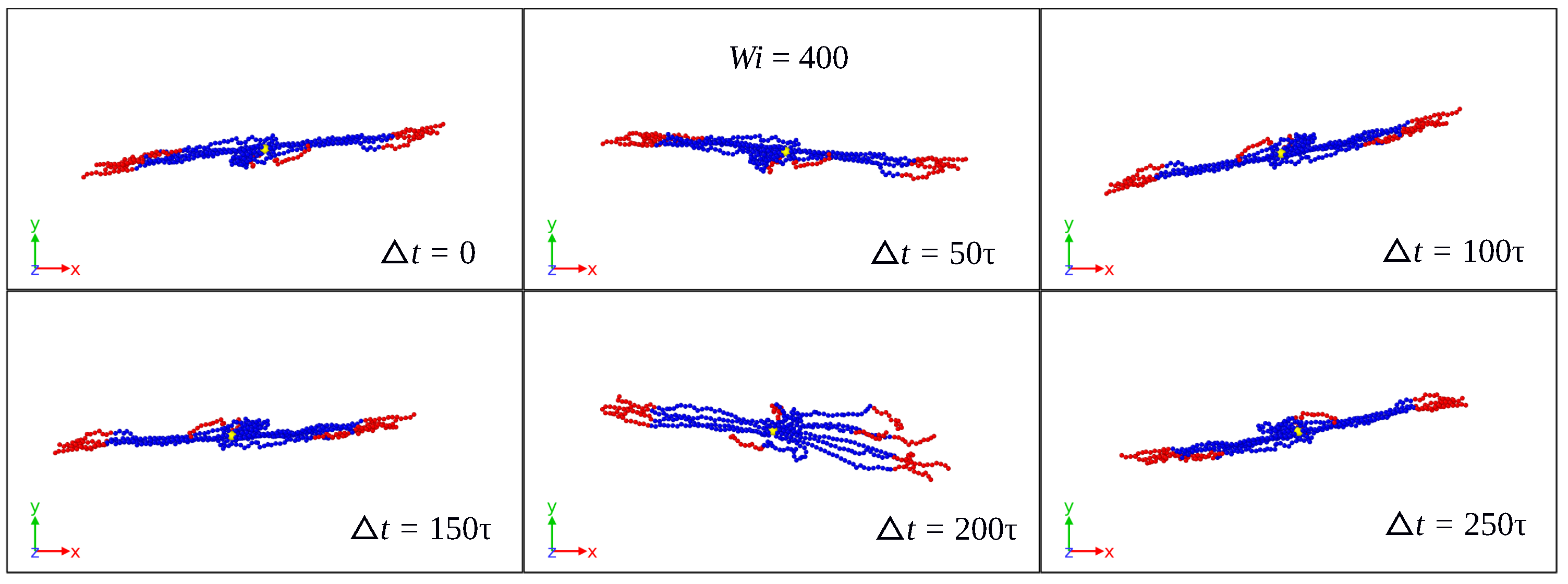
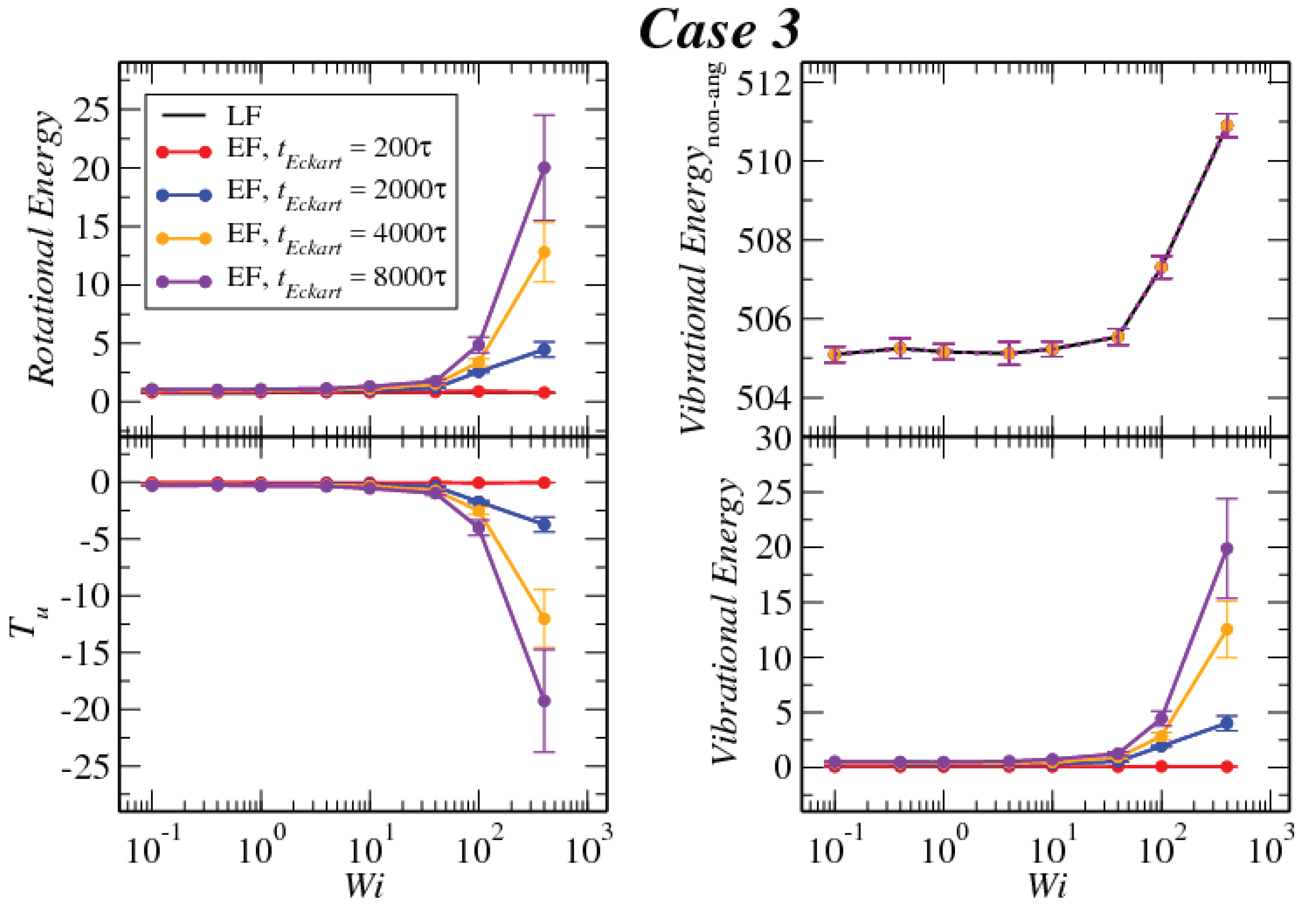
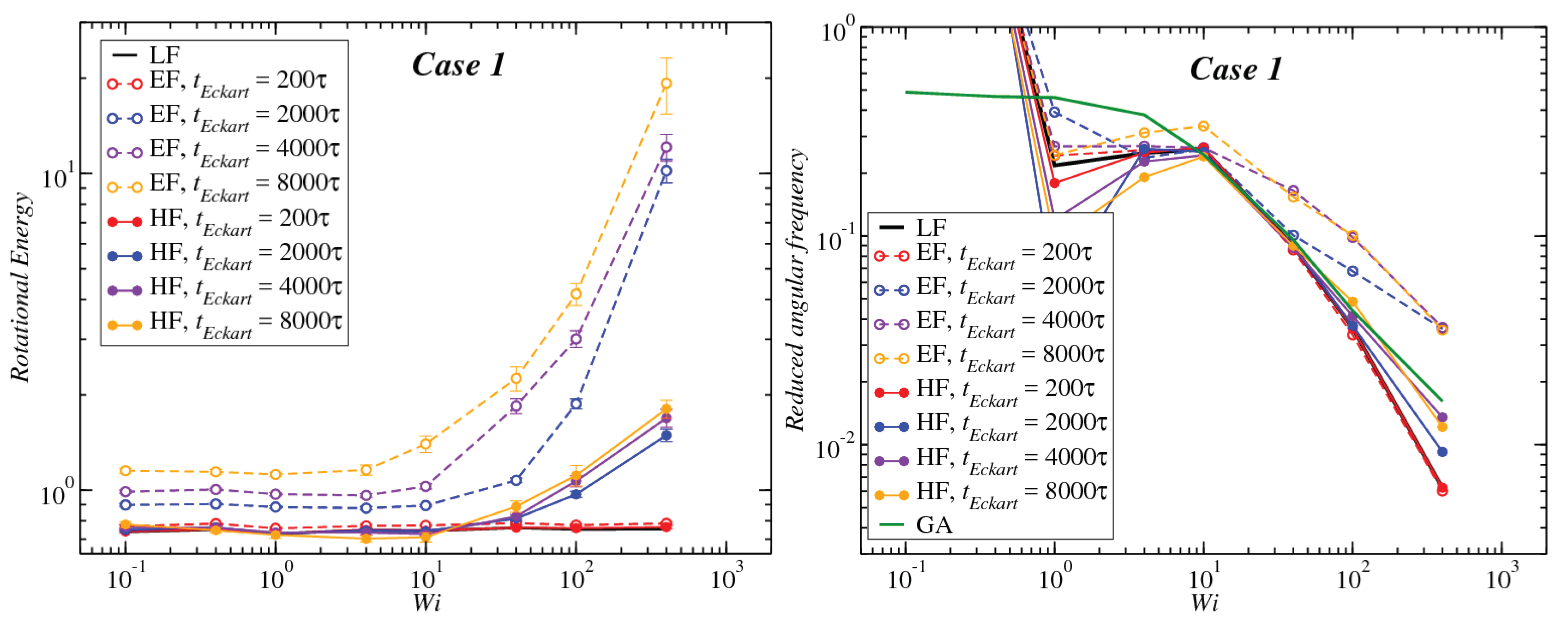
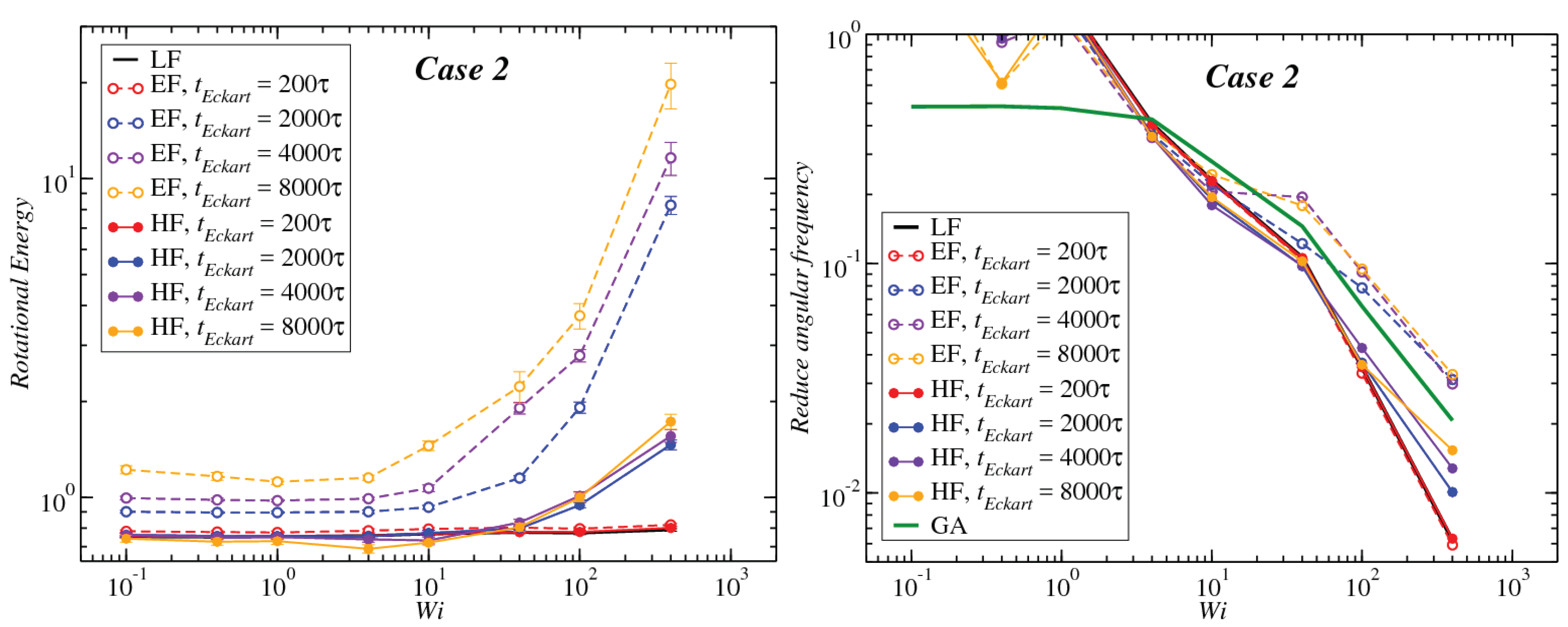
3.1. Global Conformation and Dynamics
3.2. Reference Configuration Update
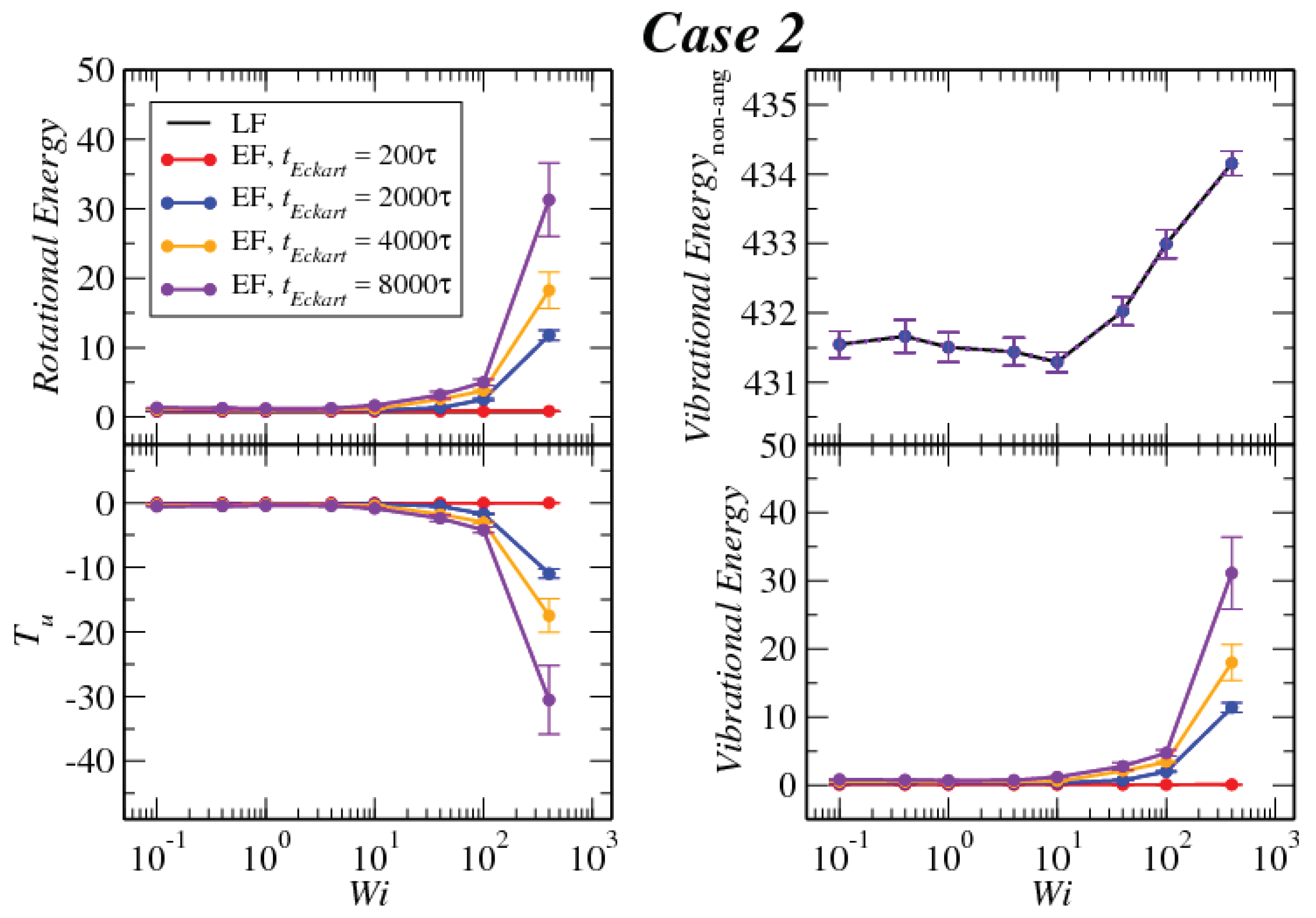
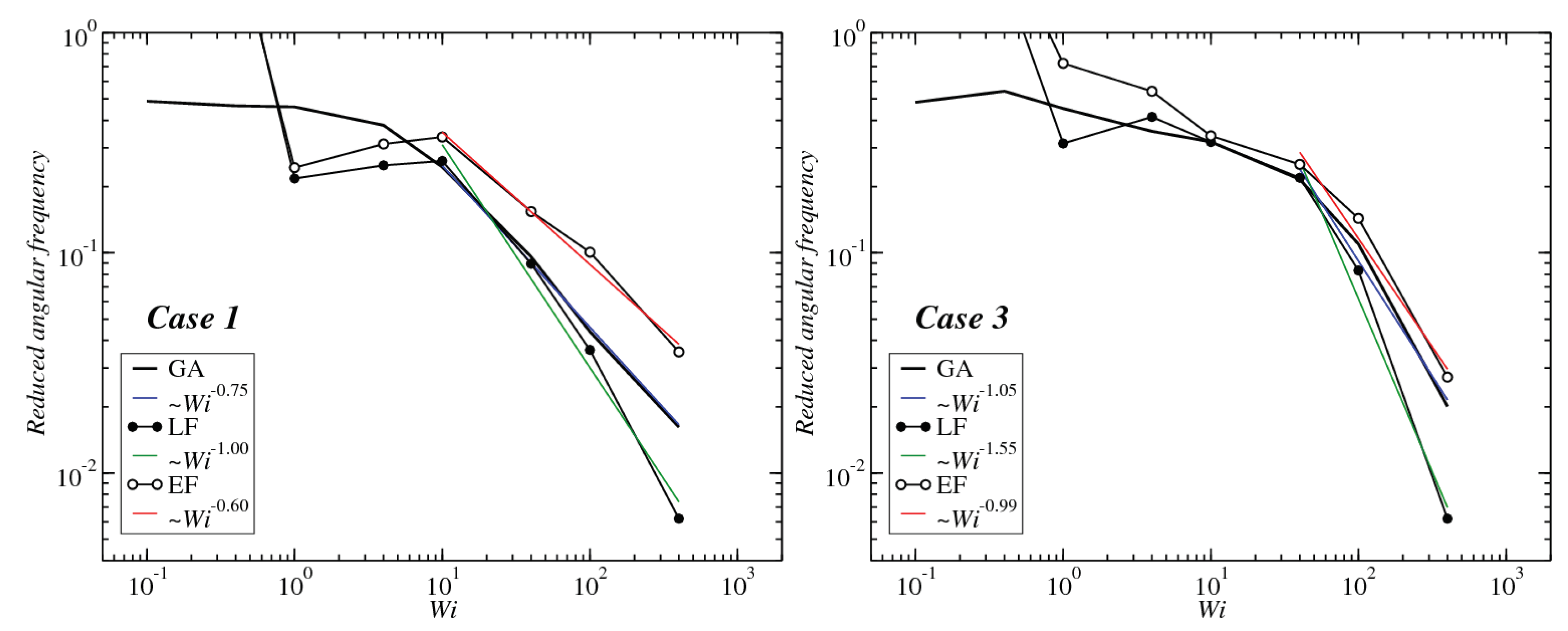
3.3. Angular Momentum and Angular Frequency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Rotation Frequencies


Appendix B. Kinetic Energy in the Eckart Frame
Appendix C. Explicit Calculation of Tu
References
- Winkler, R.G.; Fedosov, D.A.; Gompper, G. Dynamical and rheological properties of soft colloid suspensions. Curr. Opin. Colloid Interface Sci. 2014, 19, 594–610. [Google Scholar] [CrossRef]
- Vlassopoulos, D.; Cloitre, M. Tunable rheology of dense soft deformable colloid. Curr. Opin. Colloid Interface Sci. 2014, 19, 561–574. [Google Scholar] [CrossRef]
- Winkler, R. Semiflexible polymers in shear flow. Phys. Rev. Lett. 2006, 97, 128301. [Google Scholar] [CrossRef] [PubMed]
- Dalal, I.S.; Albaugh, A.; Hoda, N.; Larson, R.G. Tumbling and deformation of isolated polymer chains in shearing flow. Macromolecules 2012, 45, 9493–9499. [Google Scholar] [CrossRef]
- Kim, J.; Baig, C. Precise analysis of polymer rotational dynamics. Sci. Rep. 2016, 6, 19127. [Google Scholar] [CrossRef] [PubMed]
- Ripoll, M.; Winkler, R.G.; Gompper, G. Star polymers in shear flow. Phys. Rev. Lett. 2006, 96, 188302. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, T.; Masaoka, N. Numerical simulation of star polymers under shear flow using a coupling method of multi-particle collision dynamics and molecular dynamics. Rheol. Acta 2015, 54, 139–147. [Google Scholar] [CrossRef]
- Nikoubashman, A.; Likos, C.N. Branched polymers under shear. Macromolecules 2010, 43, 1610–1620. [Google Scholar] [CrossRef][Green Version]
- Chen, W.; Li, Y.; Zhao, H.; Liu, L.; Chen, J.; An, L. Conformations and dynamics of single flexible ring polymers in simple shear flow. Polymer 2015, 64, 93–99. [Google Scholar] [CrossRef]
- Capone, B.; Coluzza, I.; Lo Verso, F.; Likos, C.N.; Blaak, R. Telechelic star polymers as self-assembling units from the molecular to the macroscopic scale. Phys. Rev. Lett. 2012, 109, 238301. [Google Scholar] [CrossRef] [PubMed]
- Rovigatti, L.; Capone, B.; Likos, C.N. Soft self-assembled nanoparticles with temperature-dependent properties. Nanoscale 2016, 8, 3288–3295. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo-Cano, D.; Formanek, M.; Likos, C.; Camargo, M. Star block-copolymers in shear flow. J. Phys. Chem. B 2018, 122, 4149–4158. [Google Scholar] [CrossRef] [PubMed]
- Sablic, J.; Praprotnik, M.; Delgado-Buscalioni, R. Deciphering the dynamics of star molecules in shear flow. Soft Matter 2017, 13, 4971–4987. [Google Scholar] [CrossRef] [PubMed]
- Sablić, J.; Delgado-Buscalioni, R.; Praprotnik, M. Application of the Eckart frame to soft matter: Rotation of star polymers under shear flow. Soft Matter 2017, 13, 6988–7000. [Google Scholar] [CrossRef] [PubMed]
- Malevanets, A.; Kapral, R. Mesoscopic model for solvent dynamics. J. Chem. Phys. 1999, 110, 8605–8613. [Google Scholar] [CrossRef]
- Malevanets, A.; Kapral, R. Solute molecular dynamics in a mesoscale solvent. J. Chem. Phys. 2000, 112, 7260–7269. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation: From Algorithms to Applications; Academic Press: London, UK, 2001. [Google Scholar]
- Huang, C.C.; Chatterji, A.; Sutmann, G.; Gompper, G.; Winkler, R.G. Cell-level canonical sampling by velocity scaling for multiparticle collision dynamics simulations. J. Comput. Phys. 2010, 229, 168–177. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1986. [Google Scholar]
- Park, S.; Moon, J.; Kim, M. Rotational energy analysis for rotating–vibrating linear molecules in classical trajectory simulation. J. Chem. Phys. 1997, 107, 9899–9906. [Google Scholar] [CrossRef][Green Version]
- Rhee, Y.; Kim, M. Mode-specific energy analysis for rotating-vibrating triatomic molecules in classical trajectory simulation. J. Chem. Phys. 1997, 107, 1394–1402. [Google Scholar] [CrossRef]
- Eckart, C. Some studies concerning rotating axes and polyatomic molecules. Phys. Rev. 1935, 47, 552. [Google Scholar] [CrossRef]
- Louck, J.; Galbraith, H. Eckart vectors, Eckart frames, and polyatomic molecules. Rev. Mod. Phys. 1976, 48, 69. [Google Scholar] [CrossRef]
- Janešič, D.; Praprotnik, M.; Merzel, F. Molecular dynamics integration and molecular vibrational theory. I. New symplectic integrators. J. Chem. Phys. 2005, 122, 174101. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Janešič, D. Molecular dynamics integration and molecular vibrational theory. II. Simulation of nonlinear molecules. J. Chem. Phys. 2005, 122, 174102. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Janešič, D. Molecular dynamics integration and molecular vibrational theory. III. The infrared spectrum of water. J. Chem. Phys. 2005, 122, 174103. [Google Scholar] [CrossRef] [PubMed]
- Praprotnik, M.; Janešič, D. Molecular Dynamics Integration Meets Standard Theory of Molecular Vibrations. J. Chem. Inf. Model 2005, 45, 1571–1579. [Google Scholar] [CrossRef] [PubMed]
- Aust, C.; Hess, S.; Kröger, M. Rotation and deformation of a finitely extendable flexible polymer molecule in a steady shear flow. Macromolecules 2002, 35, 8621–8630. [Google Scholar] [CrossRef]
- Singh, S.; Fedosov, D.; Chatterji, A.; Winkler, R.; Gompper, G. Conformational and dynamical properties of ultra-soft colloids in semi-dilute solutions under shear flow. J. Phys. Condens. Matter 2012, 24, 464103. [Google Scholar] [CrossRef] [PubMed]








| Abbreviation | Meaning |
|---|---|
| Case 1 | |
| Case 2 | |
| Case 3 | |
| LF | Laboratory frame |
| EF | Eckart frame |
| HF | Hybrid frame |
| GA | Geometric approximation |
| Rotational | Vibrational without Angular Momentum | = Vibrational with Angular Momentum + Coriolis Coupling | |
|---|---|---|---|
| Laboratory Frame | – | ||
| Eckart frame | |||
| Hybrid frame | – |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaramillo-Cano, D.; Likos, C.N.; Camargo, M. Rotation Dynamics of Star Block Copolymers under Shear Flow. Polymers 2018, 10, 860. https://doi.org/10.3390/polym10080860
Jaramillo-Cano D, Likos CN, Camargo M. Rotation Dynamics of Star Block Copolymers under Shear Flow. Polymers. 2018; 10(8):860. https://doi.org/10.3390/polym10080860
Chicago/Turabian StyleJaramillo-Cano, Diego, Christos N. Likos, and Manuel Camargo. 2018. "Rotation Dynamics of Star Block Copolymers under Shear Flow" Polymers 10, no. 8: 860. https://doi.org/10.3390/polym10080860
APA StyleJaramillo-Cano, D., Likos, C. N., & Camargo, M. (2018). Rotation Dynamics of Star Block Copolymers under Shear Flow. Polymers, 10(8), 860. https://doi.org/10.3390/polym10080860





