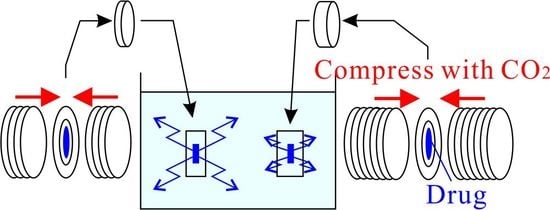
1. Introduction
Plastics are used in various applications because of their lightness and strength [
1]. The form of the plastic, such as board, bead, and fiber, varies depending on its usage. In addition, porous plastics are used as cushioning, heat insulators, sound-absorbing materials, and filters, among others. Further, a porous material with a through-hole is also used as a support for holding a drug [
2]. Methods of manufacturing such porous polymer materials include foam injection molding [
3] and molding with supercritical CO
2 followed by foaming [
4,
5].
There are several plastic molding methods such as injection molding, melt spinning, electrospinning, solidification by mixing main and curing agents, and photo formation. In recent years, 3D printers have also been put to practical use in the creation of plastic structures. To bond plastics, the use of adhesives and hot pressing have been proposed. In recent years, Aizawa has developed a CO
2-assisted polymer compression (CAPC) method, in which plastic fibers are attached by pressing in the presence of CO
2 at room temperature [
6]. The protocol of this method is that the polymer is impregnated with CO
2, plasticized, and compressed. CO
2 is known to be easily soluble in polymers [
7,
8,
9] and cause a decrease in the glass transition point and melting point [
10,
11,
12]. Because CO
2 impregnation does not lower the glass transition point to room temperature, it is possible to plasticize certain polymers to such a degree that they can be compressed. CAPC is a very convenient method of fabricating porous polymer materials because it can be conducted at room temperature, uses only CO
2, and achieves adhesion without using an adhesive. CO
2 is released from the fabricated material into the atmosphere to yield an uncontaminated porous body. Moreover, it is possible to control the porosity and pore size distribution by controlling the compression process [
13]. The absence of heat and contamination in the process is expected to be most suitable for medicine, especially because the drug-containing sample will not undergo heat denaturation.
An application of plastics in the medical field is drug loading, which uses a water-absorbent polymer and various kinds of tapes such as poultice and bandage [
14]. Recently, drug delivery has been extremely important to increasing the added value of a medicine [
15]; it is a technique for delivering a designated medicine to a specified location, as well as for continuously supplying a specified medicine in a specified amount. Regarding the loading of the drug on a porous material, control of sustained release is expected because of the nature of the material [
16,
17,
18].
CAPC enables a drug to be easily placed inside a porous material, and when the sample is used as medicine, control of sustained release is expected. This possibility is suggested by the controllability of porosity and pore size, although there have been no reports actually verifying this. In this study, we performed a quantitative analysis of the properties of sustained release of a drug, specifically methylene blue, from samples prepared using nonwoven fabrics.
Methylene blue has extremely low toxicity and is used as a fungicide in aquariums where tropical fish are bred [
19,
20,
21]. If the tablet can gradually supply methylene blue to an aquarium, it would be possible to leave the tablet in a filter when the fish becomes sick. Therefore, using methylene blue for evaluation is meaningful from the point of view of further application.
First, we investigated the effect of thickness on the elution rate by using samples with different thickness but with the same porosity. Subsequently, the influence of porosity on the elution rate was investigated by fixing the thickness and varying the porosity. Finally, the effect of temperature on the elution rate was investigated by performing the experiment at temperatures between 10 and 60 °C. For these set of experiments, the elution rate was analyzed using a diffusion model, and the influences of the porosity and tortuosity on the diffusion rate in the porous material were discussed.
3. Results and Discussion
First, validation of the concentration measurement and calibration of the absorbance against concentration were carried out. The observed spectra of methylene blue in the MES buffer solution at steady-state condition are shown in
Figure 3a. The linear relationship between the absorbance at 664 nm and methylene blue concentration was maintained up to a concentration of 12 μM (
Figure 3b).
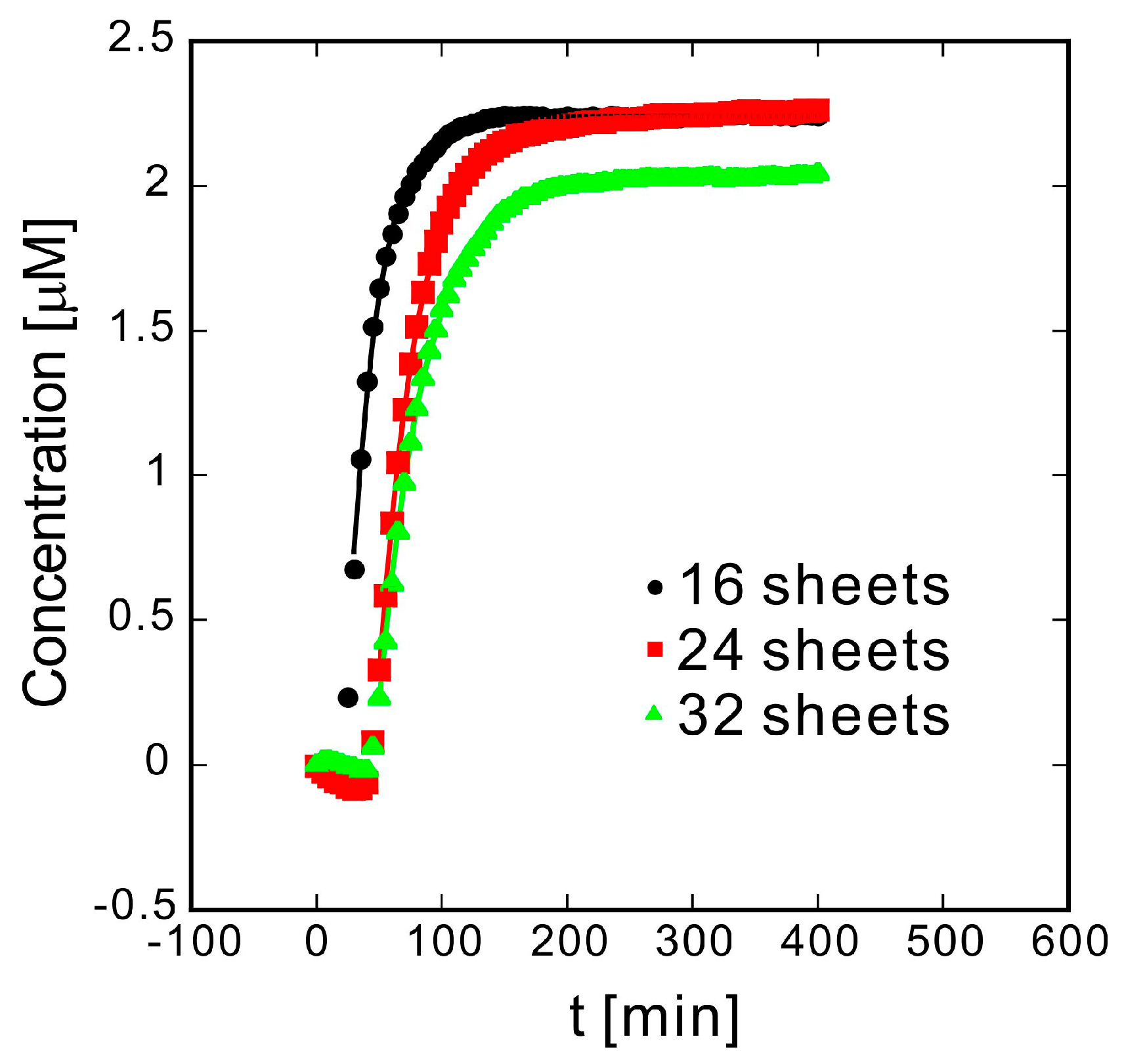
The correlation between elution distance and elution rate was investigated using samples prepared by changing the number of sheets and sample thickness simultaneously to obtain similar porosities. The absorbance is converted to solution concentration,
Cbulk, which is fitted to an exponential increase equation (
Figure 4). The range of the best-fit line (solid line) is the range of the fitted data, which matches the experimental results well. The fitting equation is as follows:
where
m1 is the equilibrium concentration,
m2 is the apparent elution rate,
m3 is the apparent delay time, and
t is the time. The delay time is the time taken by the buffer solution to penetrate the sample and reach the methylene-blue-loaded fabric and for methylene blue to diffuse from the sample.
Because methylene blue did not remain in the sample after the elution test, it was assumed that all of it diffused into the bulk. This suggests that there is no special interaction between methylene blue and the nonwoven fabric.
Cbulk rises exponentially at rate
m2 after a certain time
m3 and eventually approaches
m1. As the number of sheets
n increases and the elution distance lengthens,
m2 becomes slower (
Table 1). Although the samples were prepared similarly, there is a slight variation in
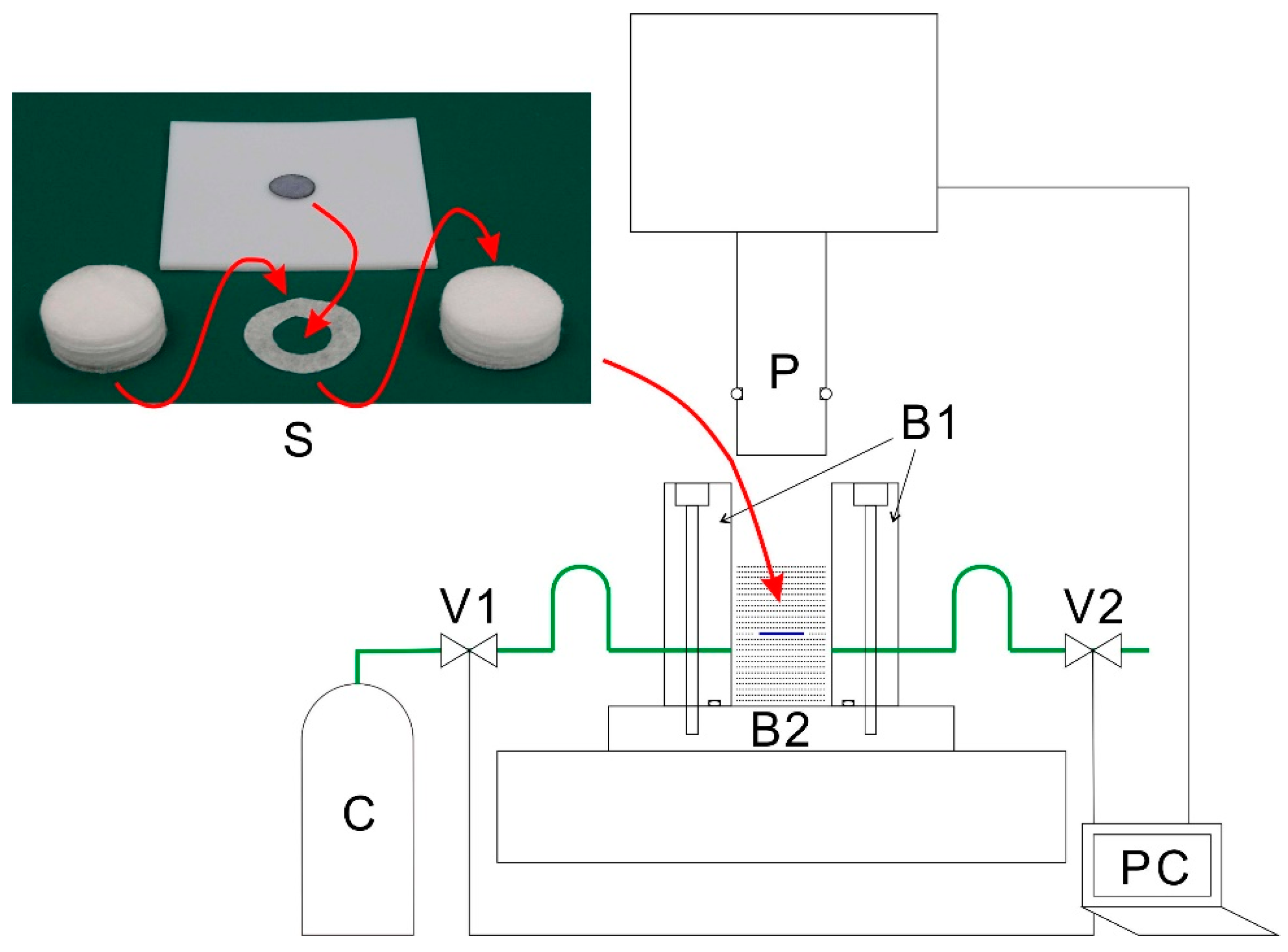
m1. This is because while methylene blue is placed on the nonwoven fabric, part of it remains on the PTFE sheet (
Figure 1) depending on the sample, leading to a difference in the amount of methylene blue loaded.
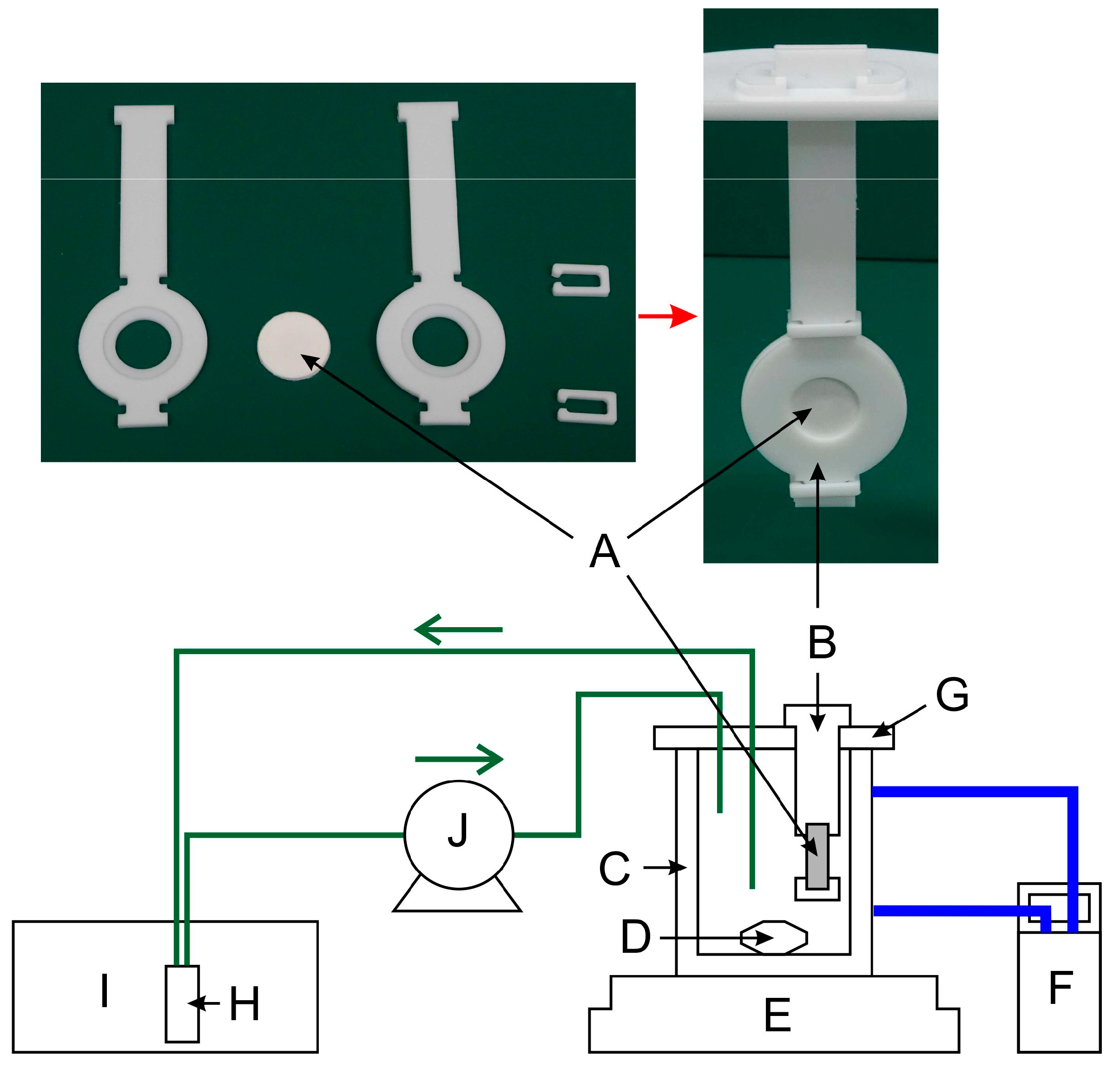
In this experiment, samples are slowly circulated between the beaker and optical cell by the peristaltic pump (8.8 mL h
−1), and a time difference occurs between the change in concentration in the beaker and reflection for the optical cell. Therefore, the time constant of the experimental set-up was estimated. After methylene blue was dropped in the beaker, the time dependence of the absorbance was measured with the dropping time set to 0, and the response of the optical cell due to the instantaneous rise of the concentration in the beaker, as well as an exponential rise in delay time, was observed. The delay time at this time was
m3′ = 6.73 min and elution rate
m2′ was 0.1623 min
−1. When both the behavior of elution and observed reflection are exponential, there is a difference between the true elution rate,
m2″, and
m2, and true delay time,
m3″, and
m3. The differences are described as follows:
When the observed delay time is short (
m3′ <<
m3″) and the reflection rate is high (
m2′ >>
m2″),
m3″ and
m3, and
m2″ and
m2 are in agreement. However, in this experiment, these conditions were not satisfied. Thus, it was necessary to calculate
m2″ and
m3″ from Equations (4) and (5).
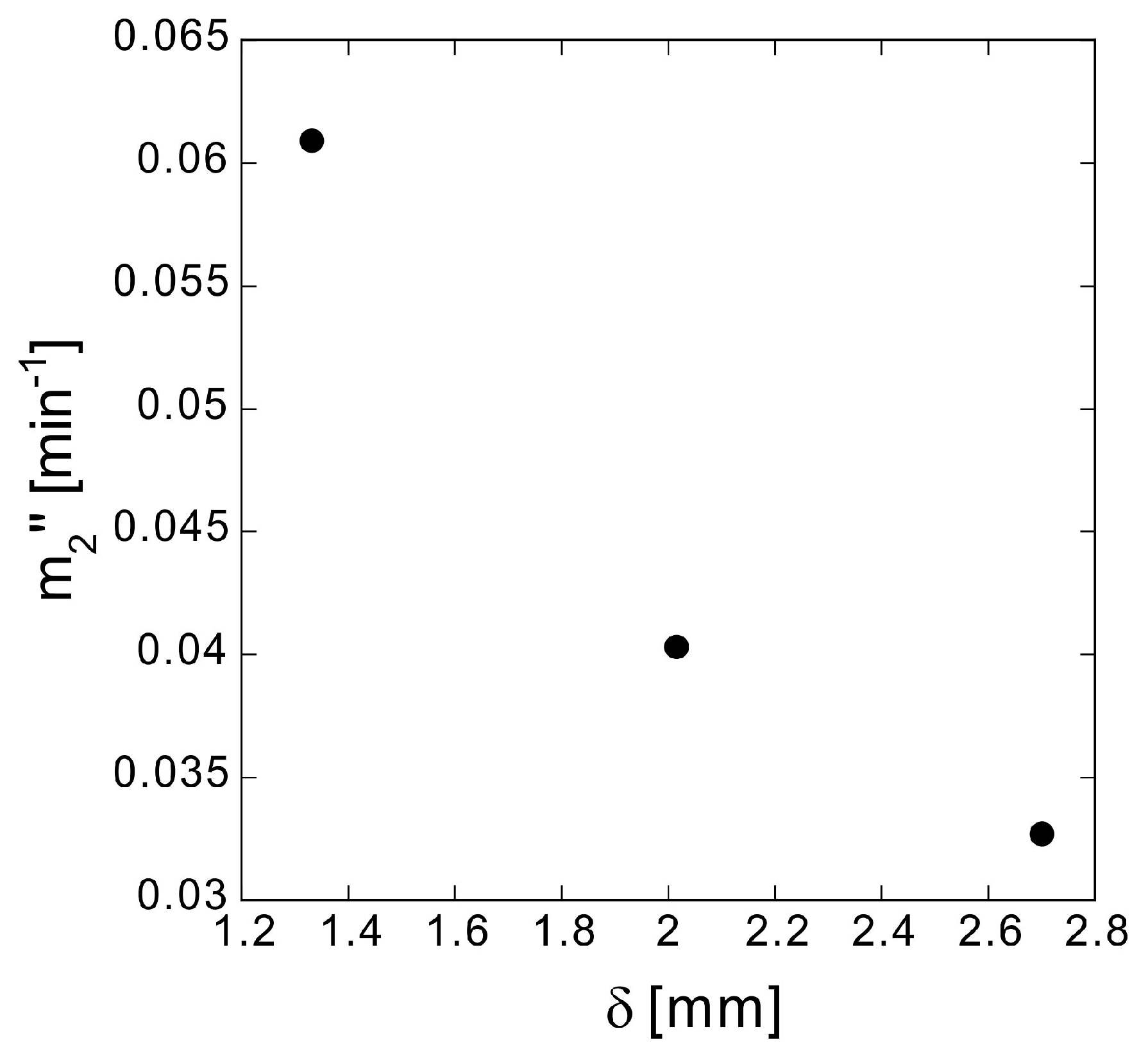
The plot of the derived values in
Figure 5 show that
m2″ decreases as
δ increases.
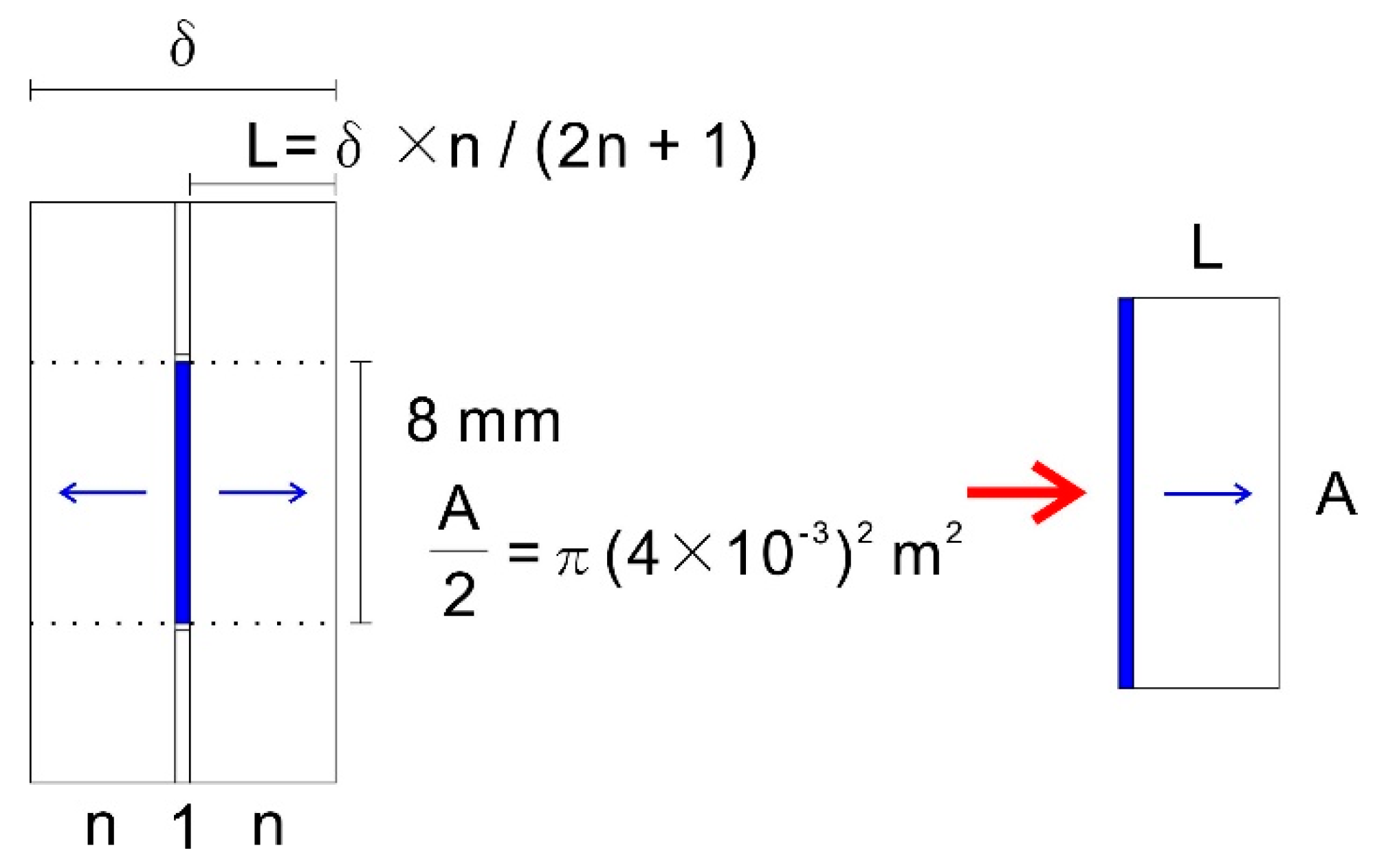
The effective diffusion coefficient in the porous material (
Deff) of the tablet was investigated by constructing a diffusion model. In this model, the state after delay time
m3″ associated with the initial penetration of water, as seen in the experiment, was set to time 0. In addition, to simplify the model, unidirectional diffusion behavior in a porous material with an area twice the elution cross-section was assumed instead of gradual release of the drug at the center from both sides of the tablet (
Figure 6). The thickness of the diffusion layer (
L) was calculated from the number of sheets (
n) on each side, total number of sheets (2
n + 1), and sample thickness
δ, assuming that the overlapping nonwoven fabrics are evenly compressed (
Figure 6).
The driving force for the diffusion of solute in solution is the concentration difference, and in describing the diffusion behavior in the tablet, estimation of the concentration inside the tablet (
Cdrug) is indispensable. Experimental results showed that the concentration outside the tablet is
Cbulk, which is 0 at time 0 and
m1 at time ∞. As shown above,
Cbulk rose exponentially. On the basis of this information, we attempted to formulate a model. First, it was assumed that
Cdrug at time 0, which is unknown, is
C0. At time ∞,
Cdrug coincides with
Cbulk, and the release of the drug, with concentration as the driving force, stops. When the amount of solute introduced into the porous material and the amount of solute discharged from the porous material are equivalent, the decay of
Cdrug should be exponential, since the change in
Cbulk after passing through the porous material is also exponential. Thus, it is necessary to link
Cdrug(0) =
C0 and
Cdrug(∞) =
m1 exponentially. Then, under the condition that the amount of solute introduced into the porous material is equal to the amount of solute discharged from the porous material, the rate constant for the decrease in
Cdrug must match the rate constant for the increase in
Cbulk. Based on this hypothesis, the following equation was derived:
Table 2 summarizes the concentration difference between the interior of the tablet and the bulk, which is the driving force for diffusion.
The change in diffusion flow rate
J was calculated from the amount of solute eluted from the tablet. If the bulk amount of water is
Vbulk and the pores in the tablet are
Vvoid, the bulk amount of water after the water has seeped into the pores is (
Vbulk –
Vvoid). Sample c in
Table 1 has the largest
Vvoid among the samples;
Vvoid is about 0.3 mL (0.9 × 0.9 × 3.14 × 0.2701 × 0.453), which is negligible compared to
Vbulk in the beaker (200 mL). That is, the space inside the tablet is very small relative to
Vbulk (
Vbulk >>
Vvoid); thus, in this experiment,
Vbulk can be considered constant at 200 mL. Under this condition, by multiplying the
Cbulk (mol m
−3) by
Vbulk (200 mL = 2 × 10
−4 m
3), the amount of methylene blue eluted from the tablet into bulk water can be obtained. Under the condition that the concentration gradient in the porous material can be approximated linearly,
J is given by
Thus,
Deff can be calculated using the equation
On the other hand, since the elution rate is obtained by differentiating the amount eluted into bulk water (2 × 10
−4 Cbulk) by
t, J is given by
From Equations (8) and (9),
Deff is derived as follows:
Normally, since the unit of
Deff is m
2 s
−1, it is necessary to convert the units of
m1 to mol m
−3,
m2″ to s
−1,
L to m,
A to m
2, and
C0 to mol m
−3. Usually, elution from solid drugs is indicated by elution of the surface of the drug into the solvent and diffusion after elution. For the concentration near the surface of the drug, the saturation solubility should be used as
C0. The solubility
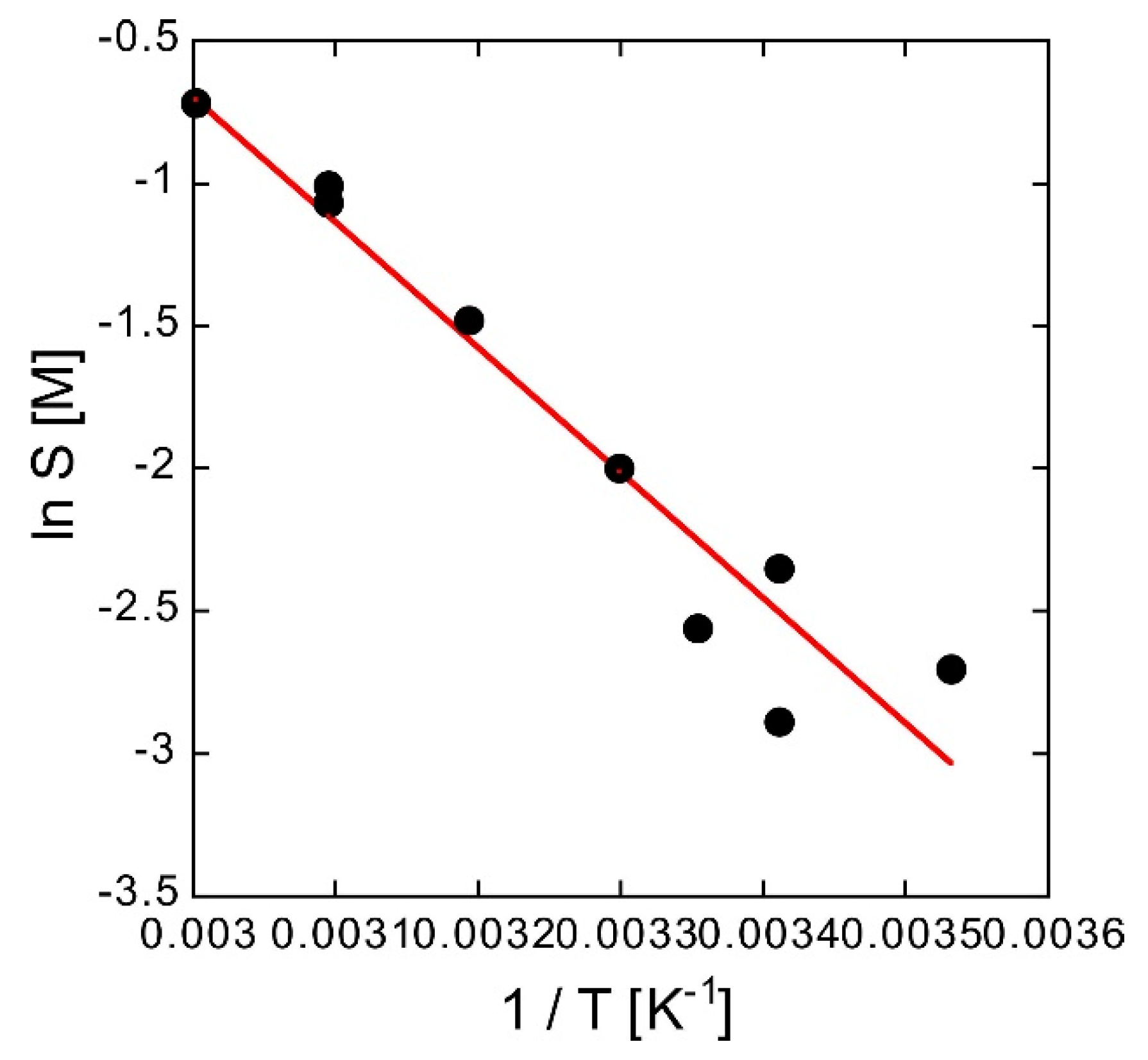
S was determined using a van’t Hoff plot with 1/
T on the abscissa and ln
S on the ordinate. In
Figure 7, the markers are the measured values and the solid line is the linear fitting obtained by the least squares method. To suppress fluctuations in the experiments, subsequent analysis was performed using the
S obtained from the fitting of the van’t Hoff plot. Data fitting using the least squares method yields the following equation:
The S in the aqueous solution containing 1 mM MES buffer at 25 °C, calculated from Equation (11), was 0.105 M. This is close to the solubility in water at 25 °C stated in the SDS sheet of the methylene blue reagent, which is 0.136 M.
The results of the calculation of
Deff in the porous body are shown in
Table 3. It is known that
Deff in a porous body filled with solvent is smaller than the bulk diffusion coefficient. This is because the diffusion path is narrower if the solvent exists only in the gap of the porous material (effect of porosity). Furthermore, the path in the gap of the porous body is bent and the diffusion path is longer than
L (effect of tortuosity). Assuming that the bulk diffusion coefficient is
Dbulk,
Deff is given by the following equation [
22].
where
τ is the tortuosity factor. For one-dimensional diffusion,
τ is defined as the square of
Leff/
L, where
Leff is the actual diffusion distance. The diffusion coefficient of methylene blue in water at 23 °C is 4.6 × 10
−10 m
2 s
−1 according to Miložič et al. [
23]. The arbitrary temperature can be estimated in proportion to the absolute temperature using the Einstein-Stokes equation.
Dbulk at 25 °C is 4.6 × 10
−10 m
2 s
−1, and the calculated
τ values using this and Equation (12) are shown in
Table 3. The
Deff and
τ values of samples a, b, and c are same; thus, the decrease in
m2″ with increasing
δ is caused by the expansion of the diffusion distance.
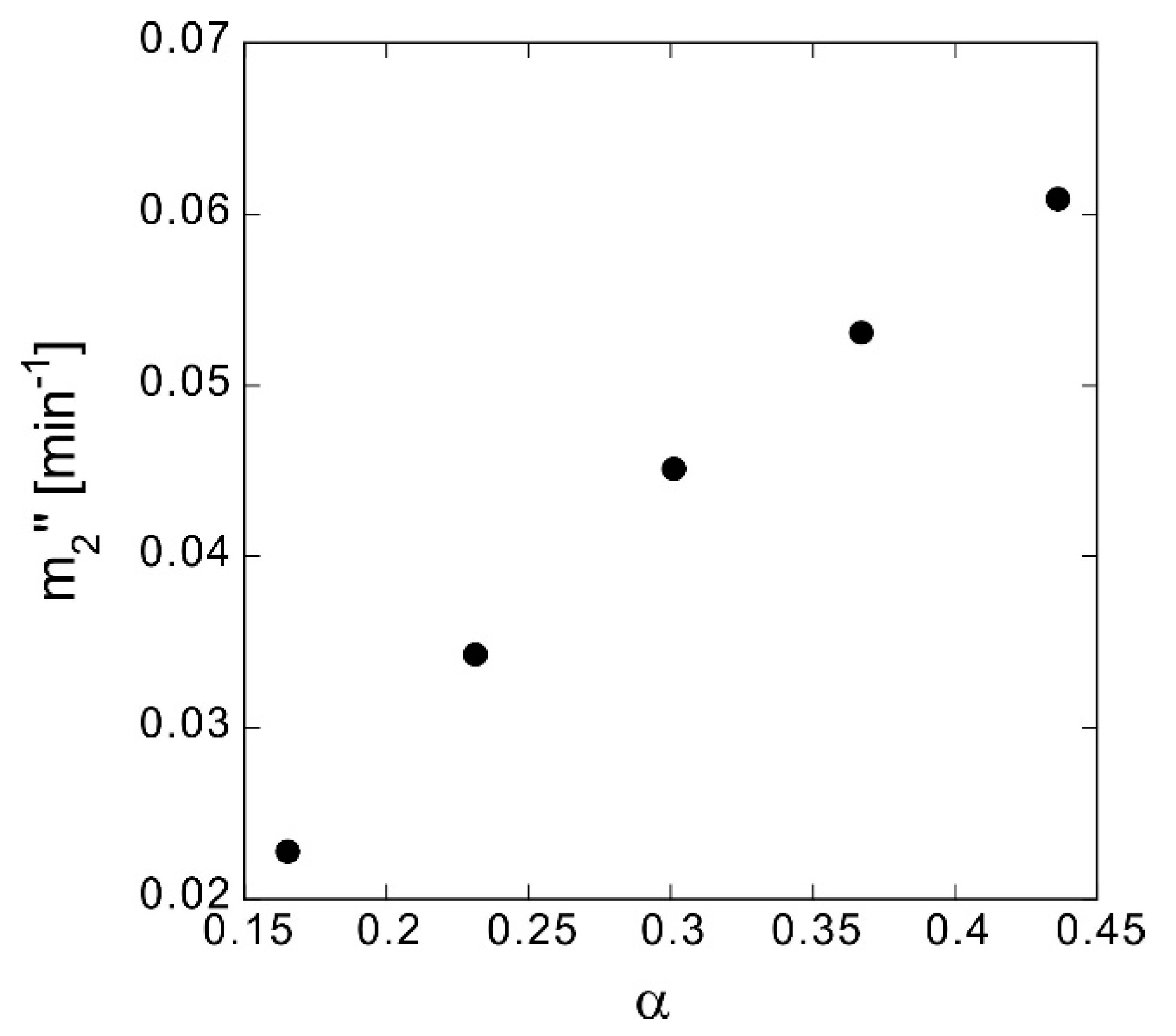
Subsequently, without changing
δ, samples with different compression ratios and associated
α were produced by increasing the number of overlapping sheets. From samples a to g in
Table 4, the number of sheets on one side (
n) increases by two and
α decreases.
m2″ increases as
α increases (
Figure 8) and since
δ is almost the same,
Deff also decreases (
Table 4). The calculated
τ values of samples a, d, e, and f are almost the same, but that of sample g is higher; this may be due to the influence of sample fluctuation. It is natural that
α decreases as the compression ratio increases and that
τ shows a tendency to increase. Nevertheless, the difference in
Deff is considerably larger than the difference in
τ, and the former is dominated by the decrease in the volume involved in elution caused by the decrease in
α.
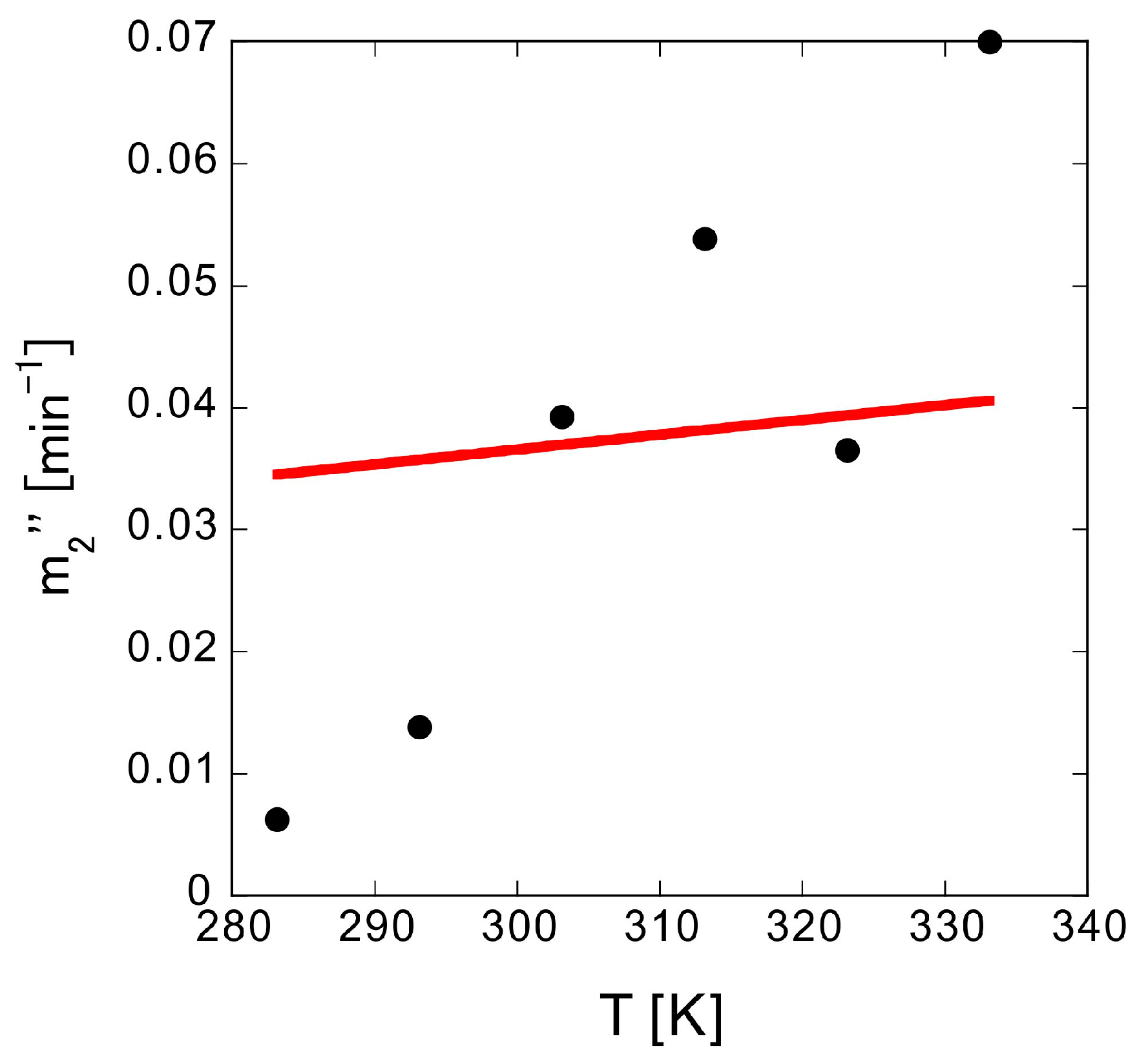
Finally, the temperature dependence of
m2″ was measured. The
m2″ values of samples h to m, prepared with 20 sheets pressed on one side, were measured from 10 to 60 °C. If the diffusion coefficient follows the Einstein-Stokes equation, it is proportional to the absolute temperature; however, the temperature dependence of
m2″ is not proportional to the absolute temperature (
Figure 9). Thus, factors other than the diffusion coefficient should dominate the trend observed for
m2″. Analysis based on the tablet elution model was consequently carried out.
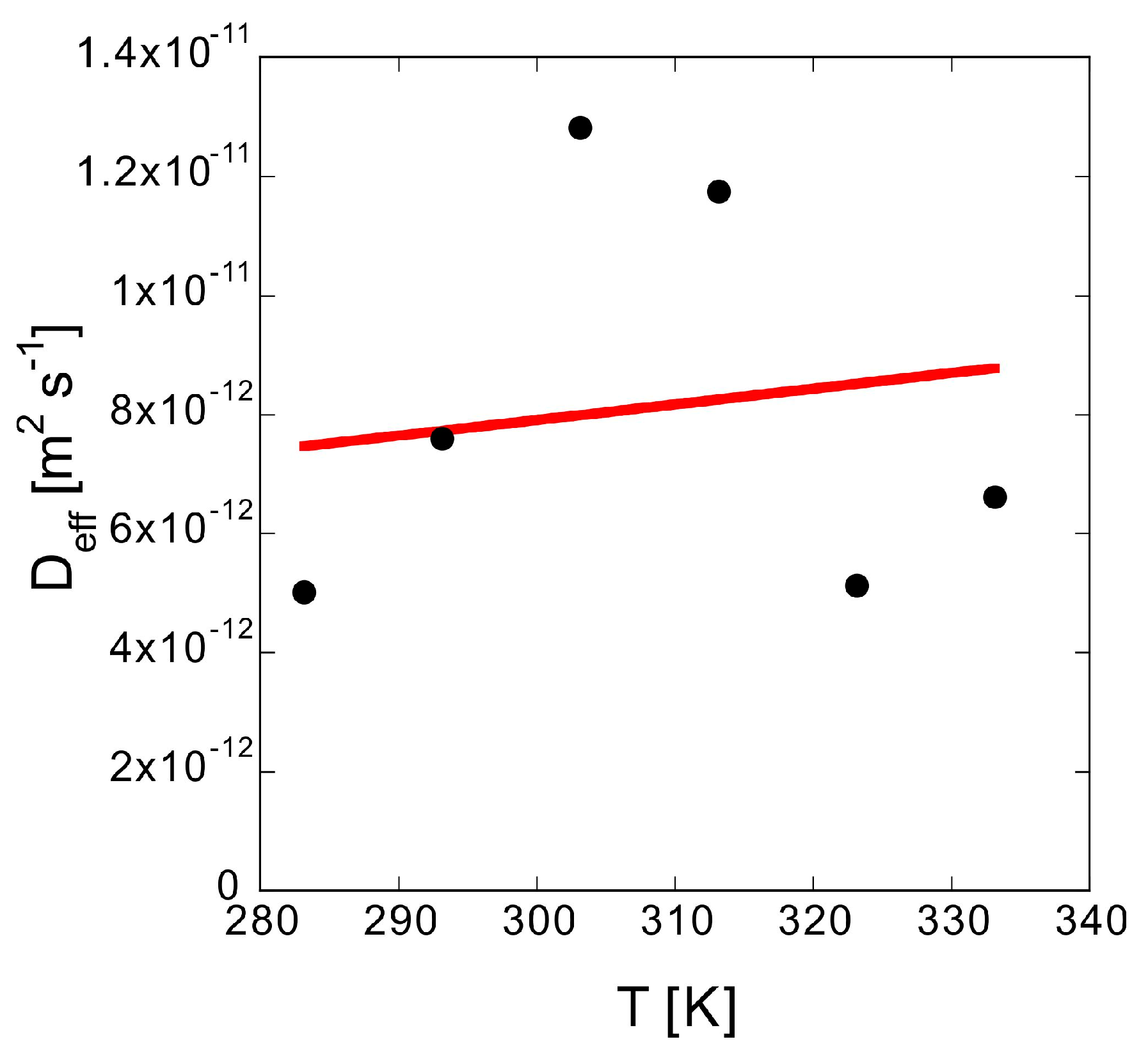
Figure 10 shows that
Deff gradually increases with
T. According to the Einstein-Stokes equation,
Dbulk is proportional to
T. For a porous material with the same
α and degree of flexion,
Deff should also be proportional to
T; thus, the solid line from the least squares approximation shows proportionality. Although the data fluctuation is large, the trends generally agree.
m2″ varies significantly with
T despite the moderate change in
Deff. This is because the
S of methylene blue varies significantly with
T (
Table 5). With the concentration difference as the driving force,
J increases, leading to an increase in
m2″.