Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code
Abstract
1. Introduction
2. Model and Methods
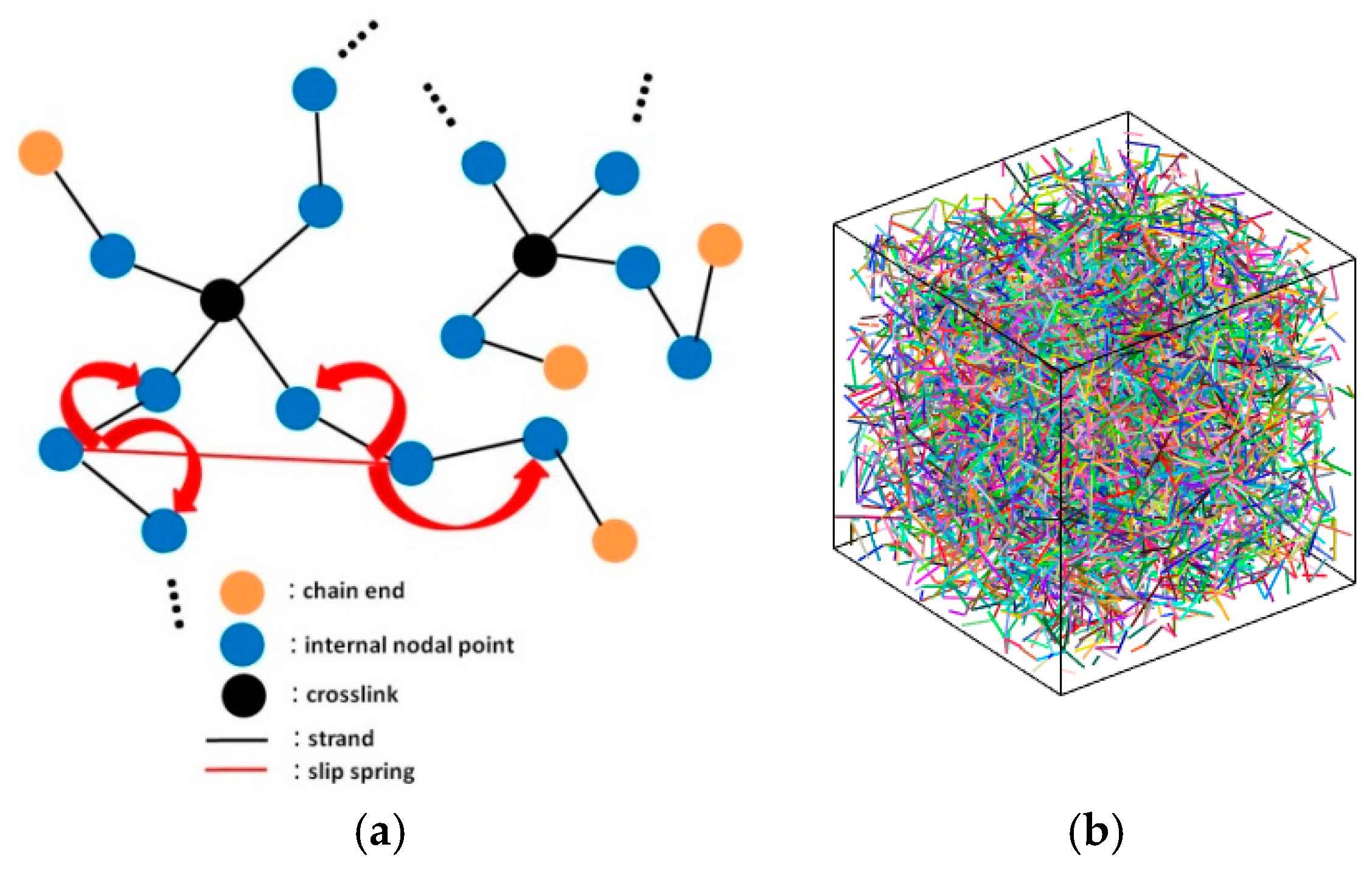
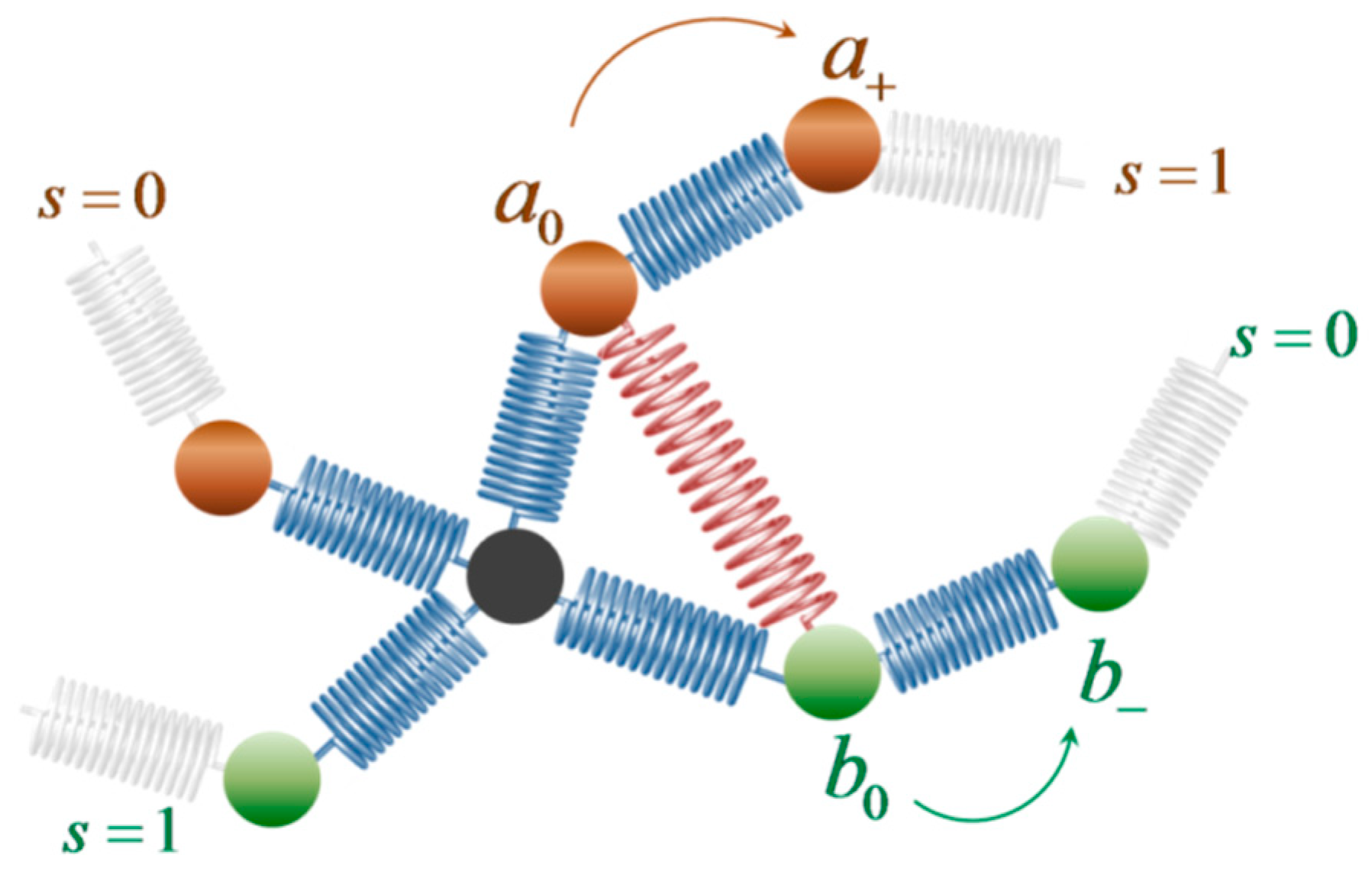
2.1. Model and Free Energy Function
- b: Kuhn length, indicative of the conformational stiffness of the polymer and dependent on the chain chemical constitution. In the case of cis-PI, b is equal to 9.58 Å [79].
- kB: Boltzmann constant;
- : Length of end-to-end vector of the strand;
- : Number of Kuhn segments in the strand;
- ij: Strand connecting beads i and j.
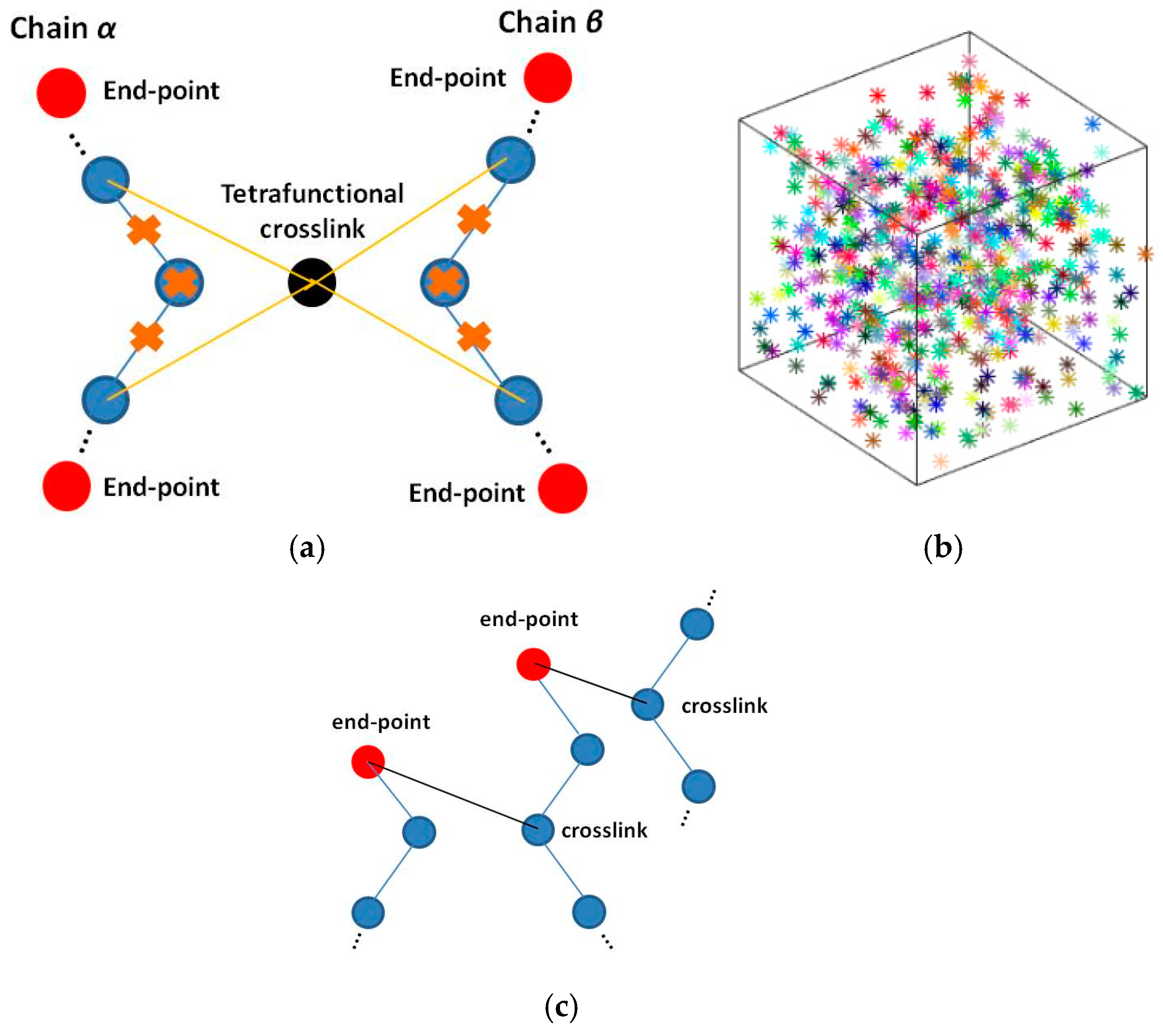
2.2. Crosslinking
2.3. Brownian Dynamics and Kinetic Monte Carlo (BD/kMC) Scheme
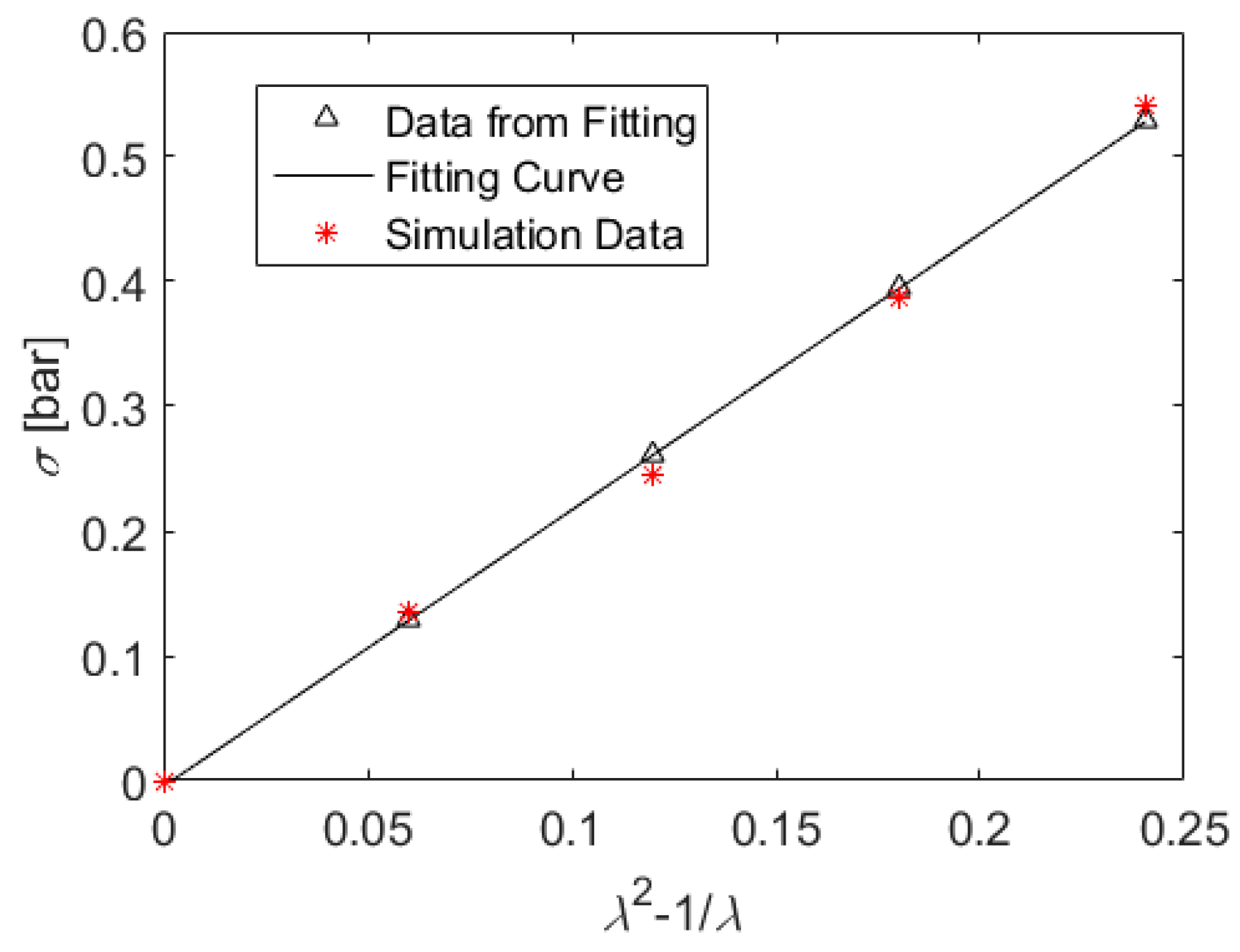
2.4. Stress Tensor and Deformations
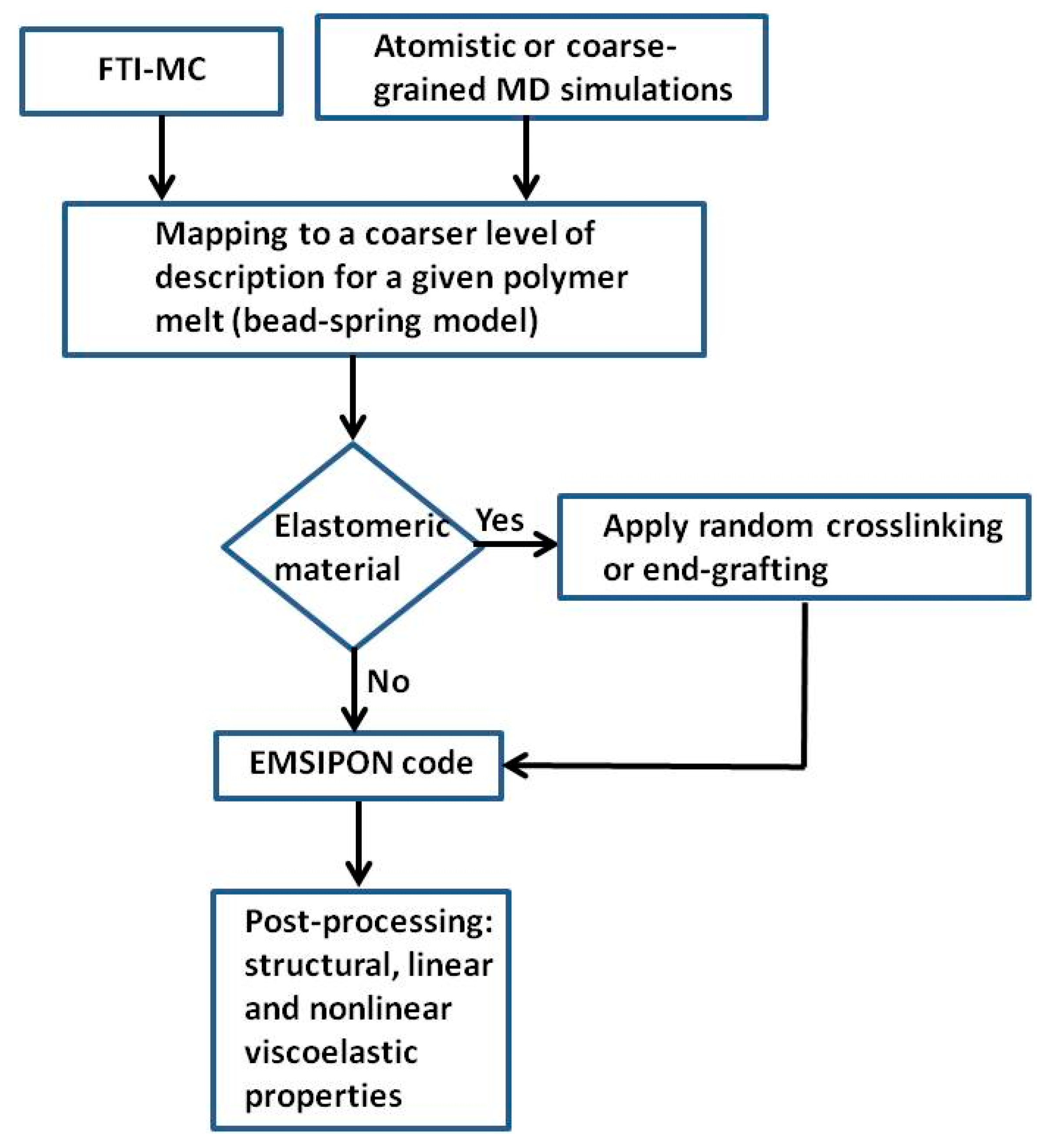
3. Details about the Engine for Mesoscopic Simulations for Polymer Networks (EMSIPON) Code
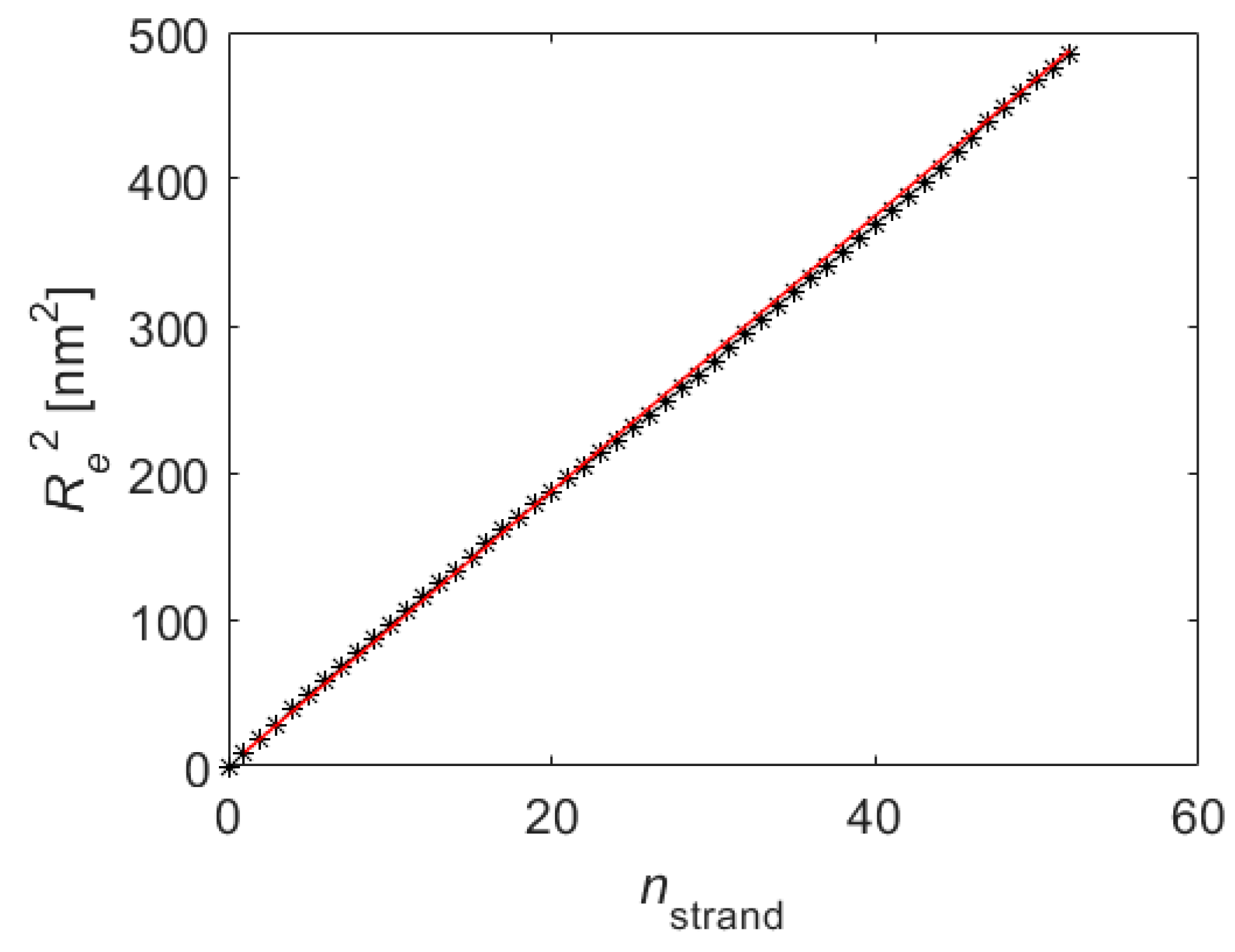
4. Simulations
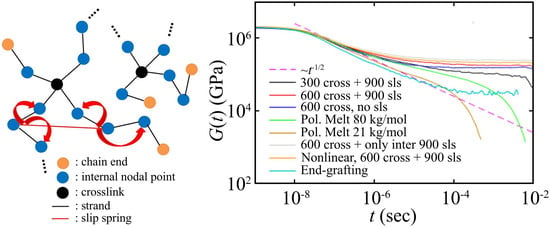
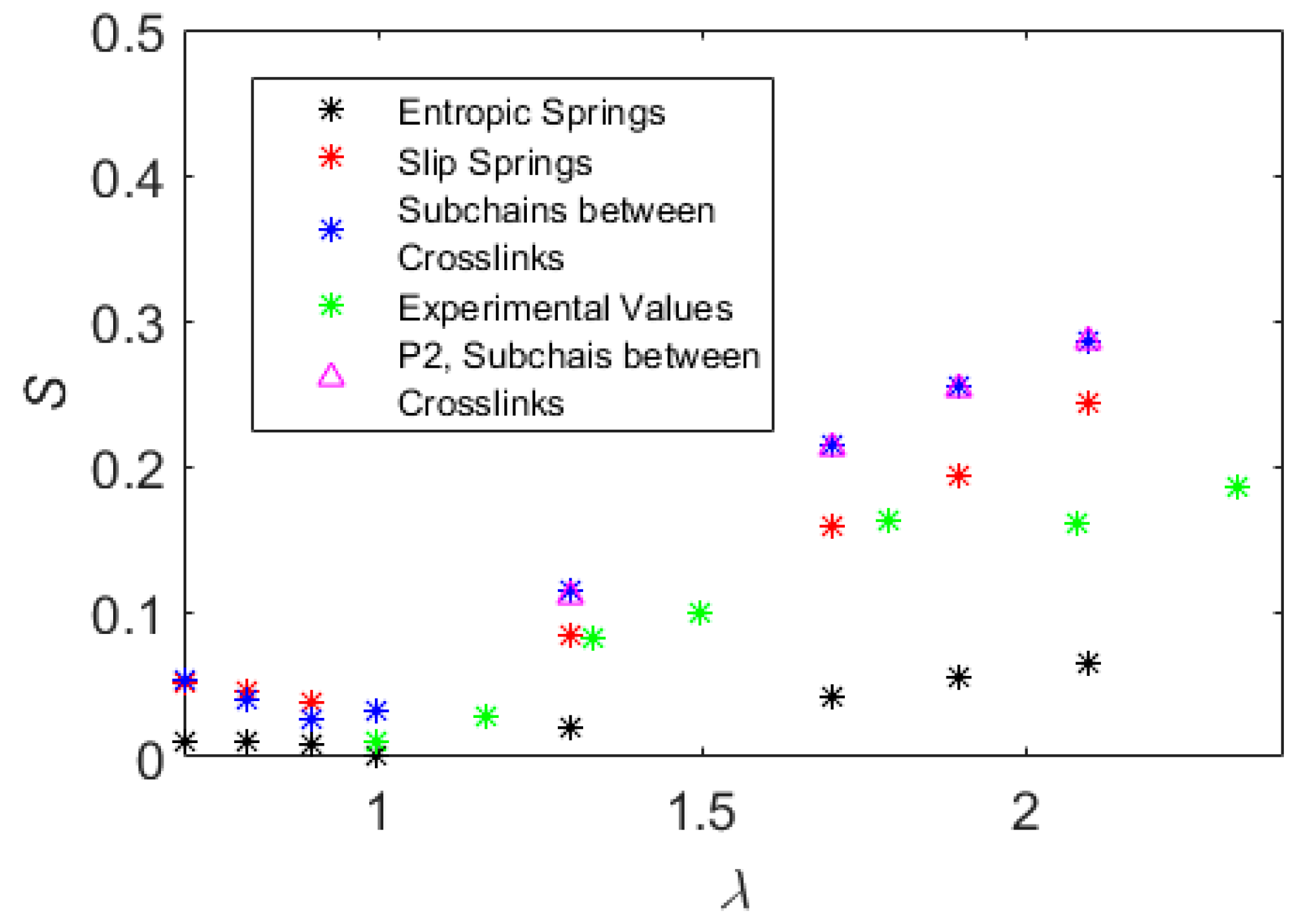
5. Results
6. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Theodorou, D.N. Hierarchical Modelling of Polymeric Materials. Chem. Eng. Sci. 2007, 62, 5697–5714. [Google Scholar] [CrossRef]
- Masubuchi, Y. Simulating the Flow of Entangled Polymers. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 11–13. [Google Scholar] [CrossRef] [PubMed]
- Kremer, K.; Grest, G.S. Dynamics of Entangled Linear Polymer Melts: A Molecular Dynamics Simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Müller-Plathe, F. Coarse-graining in Polymer Simulation: From Atomistic to Mesoscopic Scale and Back. Chem. Phys. Chem. 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Reith, D.; Pütz, M.; Müller-Plathe, F. Deriving Effective Mesoscale Potentials from Atomistic Simulations. J. Comput. Chem. 2003, 24, 1624–1636. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Faller, R. Systematic Coarse-graining of Atomistic Models for Simulation of Polymer Systems. Comput. Chem. Eng. 2005, 29, 2380–2385. [Google Scholar] [CrossRef]
- Milano, G.; Müller-Plathe, F. Mapping Atomistic Simulations to Mesoscopic Models: A Systematic Coarse-Graining Procedure for Vinyl Polymer Chains. J. Phys. Chem. B 2005, 109, 18609–18619. [Google Scholar] [CrossRef] [PubMed]
- Spyriouni, T.; Tzoumanekas, C.; Theodorou, D.N.; Müller-Plathe, F.; Milano, G. Coarse-Grained and Reverse-Mapped United-Atom Simulations of Long-Chain Atactic Polystyrene Melts: Structure, Thermodynamic Properties, Chain Conformation and Entanglements. Macromolecules 2007, 40, 3876–3885. [Google Scholar] [CrossRef]
- Kamio, K.; Moothi, K.; Theodorou, D.N. Coarse Grained End Bridging Monte Carlo Simulations of Poly(ethylene terephelate) Melt. Macromolecules 2007, 40, 710–722. [Google Scholar] [CrossRef]
- Dinpajooh, M.; Guenza, M.G. On the Density Dependence of the Integral Equation Coarse-Graining Effective Potential. J. Phys. Chem. B 2018, 122, 3426–3440. [Google Scholar] [CrossRef] [PubMed]
- Xia, W.; Song, J.; Jeong, C.; Hsu, D.D.; Phelan, F.R.; Douglas, J.F.; Keten, S. Energy-Renormalization for Achieving Temperature Transferable Coarse-Graining of Polymer Dynamics. Macromolecules 2017, 50, 8787–8796. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics, 1st ed.; Clarendon Press: Oxford, UK, 1986; ISBN 0198520336. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980; ISBN 978-0-471-04894-7. [Google Scholar]
- Tzoumanekas, C.; Theodorou, D.N. Topological Analysis of Linear Polymer Melts: A Statistical Approach. Macromolecules 2006, 39, 4592–4604. [Google Scholar] [CrossRef]
- Anogiannakis, S.F.; Tzoumanekas, C.; Theodorou, D.N. Microscopic Description of Entanglements in Polyethylene Networks and Melts: Strong, Weak, Pairwise, and Collective Attributes. Macromolecules 2012, 45, 9475–9492. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube Theory of Entangled Polymer Dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Rouse, P.E. A Theory of the Linear Viscoelastic Properties of Dilute Solutions of Coiling Polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Zimm, B.H. Dynamics of Polymer Molecules in Dilute Solution: Viscoelasticity, Flow Birefringence and Dielectric Loss. J. Chem. Phys. 1956, 24, 269–278. [Google Scholar] [CrossRef]
- Edwards, S.F. The Statistical Mechanics of Polymerized Material. Proc. Soc. Lond. 1967, 92, 9–16. [Google Scholar] [CrossRef]
- De Gennes, P.G. Reptation of a Polymer Chain in Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- De Gennes, P.G. Scaling Concepts in Polymer Physics, 1st ed.; Cornell University Press: Ithaca, NY, USA, 1979; ISBN 080141203X. [Google Scholar]
- Edwards, S.F.; Vilgis, T.A. The Tube Model Theory of Rubber Elasticity. Rep. Prog. Phys. 1988, 51, 243–297. [Google Scholar] [CrossRef]
- Doi, M. Explanation for the 3.4-power Law for Viscosity of Polymeric Liquids on the Basis of the Tube Model. J. Polym. Sci. Polym. Phys. 1983, 21, 667–684. [Google Scholar] [CrossRef]
- Milner, S.T.; McLeish, T.C.B. Reptation and Contour-Length Fluctuations in Melts of Linear Polymers. Phys. Rev. Lett. 1998, 81, 725–728. [Google Scholar] [CrossRef]
- Likhtman, A.E.; McLeish, T.C.B. Quantitative Theory for Linear Dynamics of Linear Entangled Polymers. Macromolecules 2002, 35, 6332–6343. [Google Scholar] [CrossRef]
- Ball, R.C.; Doi, M.; Edwards, S.F. Elasticity of Entangled Networks. Polymer 1981, 22, 1010–1018. [Google Scholar] [CrossRef]
- Edwards, D.; Vilgis, T. The Effect of Entanglements in Rubber Elasticity. Polymer 1986, 27, 483–492. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D. Segment Connectivity, Chain-length Breathing, Segmental Stretch and Constraint Release in Reptation Models. I. Theory and Single-step Strain Predictions. J. Chem. Phys. 1998, 109, 10018–10027. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerus, D.C. Segment Connectivity, Chain-length Breathing, Segmental Stretch and Constraint Release in Reptation Models. II. Double-step Strain Predictions. J. Chem. Phys. 1998, 109, 10028–10032. [Google Scholar] [CrossRef]
- Hua, C.C.; Schieber, J.D.; Venerous, D.C. Segment Connectivity, Chain-length Breathing, Segmental Stretch, and Constraint Release in Reptation Models. III. Shear Flows. J. Rheol. 1999, 43, 701–717. [Google Scholar] [CrossRef]
- Schieber, J.D.; Andreev, M. Entangled Polymer Dynamics in Equilibrium and Flow Modelled Through Slip Links. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 367–381. [Google Scholar] [CrossRef] [PubMed]
- Likhtman, A.E. Single-Chain Slip-Link Model of Entangled Polymers: Simultaneous Description of Neutron Spin-Echo, Rheology, and Diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Takimoto, J.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian Simulations of a Network of Reptating Primitive Chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Ianniruberto, G.; Greco, F.; Marrucci, G. Entanglement Molecular Weight and Frequency Response of Sliplink Networks. J. Chem. Phys. 2003, 119, 6925–6930. [Google Scholar] [CrossRef]
- Oberdisse, J.; Ianniruberto, G.; Greco, F.; Marrucci, G. Primitive-chain Brownian Simulations of Entangled Rubbers. Europhys. Lett. 2002, 58, 530–536. [Google Scholar] [CrossRef]
- Oberdisse, J.; Ianniruberto, G.; Greco, F.; Marrucci, G. Mechanical Properties of End-crosslinked Entangled Polymer Networks Using Sliplink Brownian Dynamics Simulations. Rheol. Acta 2006, 46, 95–109. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Uneyama, T.; Watanable, H.; Ianniruberto, G.; Greco, F.; Marrucci, G. Structure of Entangled Polymer Network from Primitive Chain Network Simulations. J. Chem. Phys. 2010, 132, 134902. [Google Scholar] [CrossRef] [PubMed]
- Kushwaha, A.; Shaqfeh, E.S.G. Slip-link Simulations of Entangled Polymers in Planar Extensional Flow: Disentanglement Modified Extensional Thinning. J. Rheol. 2011, 55, 463–483. [Google Scholar] [CrossRef]
- Uneyama, T.; Masubuchi, Y. Detailed Balance Condition and Effective Free Energy in the Primitive Chain Network Model. J. Chem. Phys. 2011, 135, 184904. [Google Scholar] [CrossRef] [PubMed]
- Ramirez-Hernández, A.; Müller, M.; de Pablo, J.J. Theoretically Informed Entangled Polymer Simulations: Linear and Non-linear Rheology of Melts. Soft Matter 2013, 9, 2030–2036. [Google Scholar] [CrossRef]
- Ramírez-Hernández, A.; Detcheverry, F.A.; Peters, B.L.; Chappa, V.C.; Schweizer, K.S.; Müller, M.; de Pablo, J.J. Dynamical Simulations of Coarse Grain Polymeric Systems: Rouse and Entangled Dynamics. Macromolecules 2013, 46, 6287–6299. [Google Scholar] [CrossRef]
- Uneyama, T.; Masubuchi, Y. Mutli-chain Slip-spring Model for Entangled Polymer Dynamics. J. Chem. Phys. 2012, 137, 154902. [Google Scholar] [CrossRef] [PubMed]
- Chappa, V.C.; Morse, D.C.; Zippelius, A.; Müller, M. Translationally Invariant Slip-spring Model for Entangled Polymer Dynamics. Phys. Rev. Lett. 2012, 109, 148302. [Google Scholar] [CrossRef] [PubMed]
- Langeloth, M.; Masubuchi, Y.; Böhm, M.C.; Müller-Plathe, F.H. Recovering the Reptation Dynamics of Polymer Melts in Dissipative Particle Dynamics Simulations via Slip-springs. J. Chem. Phys. 2013, 138, 104907. [Google Scholar] [CrossRef] [PubMed]
- Ramírez-Hernández, A.; Peters, B.L.; Andreev, M.; Schieber, J.D.; de Pablo, J.J. A Multichain Polymer Slip-spring Model with Fluctuating Number of Entanglements for Linear and Nonlinear Rheology. J. Chem. Phys. 2015, 143, 243147. [Google Scholar] [CrossRef] [PubMed]
- Masubuchi, Y. Effects of Degree of Freedom below Entanglement Segment on Relaxation of Polymer Configuration under Fast Shear in Multi-chain Slip-spring Simulations. J. Chem. Phys. 2015, 143, 224905. [Google Scholar] [CrossRef] [PubMed]
- Masubuchi, Y.; Langeloth, M.; Böhm, M.C.; Inoue, T.; Müller-Plathe, F. A Multichain Slip-spring Dissipative Particle Dynamics Simulation Method for Entangled Polymer Solutions. Macromolecules 2016, 49, 9186–9191. [Google Scholar] [CrossRef]
- Megariotis, G.; Vogiatzis, G.G.; Schneider, L.; Müller, M.; Theodorou, D.N. Mesoscopic Simulations of Crosslinked Polymer Networks. J. Phys. Conf. Ser. 2016, 738, 012063. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Megariotis, G.; Theodorou, D.N. Equation of State Based Slip Spring Model for Entangled Polymer Dynamics. Macromolecules 2017, 50, 3004–3029. [Google Scholar] [CrossRef]
- Sgouros, A.; Megariotis, G.; Theodorou, D.N. Slip-spring Model for the Linear and Nonlinear Viscoelastic Properties of Molten Polyethylene Derived from Atomistic Simulations. Macromolecules 2017, 50, 4524–4541. [Google Scholar] [CrossRef]
- Ramírez-Hernández, A.; Brandon, L.P.; Schneider, L.; Andreev, M.; Schieber, J.D.; Müller, M.; de Pablo, J.J. A Multi-chain Polymer Slip-spring Model with Fluctuating Number of Entanglements: Density Fluctuations, Confinement, and Phase Separation. J. Chem. Phys. 2017, 146, 014903. [Google Scholar] [CrossRef] [PubMed]
- Mark, J.E.; Erman, B. Rubberlike Elasticity: A Molecular Primer, 2nd ed.; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-81425-6. [Google Scholar]
- Roberts, A.D. Natural Rubber Science and Technology, 1st ed.; Oxford University Press: Oxford, UK, 1988; ISBN 0-19-855225-4. [Google Scholar]
- Wall, F.T. Statistical Thermodynamics of Rubber. J. Chem. Phys. 1942, 10, 132–134. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Elasticity of a Network of Long-chain Molecules. I. Trans. Faraday Soc. 1943, 39, 36–41. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Elasticity of a Network of Long-chain Molecules-II. Trans. Faraday Soc. 1943, 39, 241–246. [Google Scholar] [CrossRef]
- Wall, F.T.; Flory, P.J. Statistical Thermodynamics of Rubber Elasticity. J. Chem. Phys. 1951, 19, 1435–1439. [Google Scholar] [CrossRef]
- Kuhn, W. Dependence of the Average Transversal on the Longitudinal Dimensions of Statistical Coils Formed by Chain Molecules. J. Polym. Sci. 1946, 1, 380–388. [Google Scholar] [CrossRef]
- Flory, P.J.; Gordon, M.; McCrum, N.G. Statistical Thermodynamics of Random Networks. Proc. R. Soc. Lond. 1976, 351, 351–380. [Google Scholar] [CrossRef]
- James, H.M. Statistical Properties of Networks of Flexible Chains. J. Chem. Phys. 1947, 15, 651–668. [Google Scholar] [CrossRef]
- James, H.M.; Guth, E. Theory of Elastic Properties of Rubber. J. Chem. Phys. 1948, 11, 455–481. [Google Scholar] [CrossRef]
- Ronca, G.; Allerga, G. An Approach to Rubber Elasticity with Internal Constraints. J. Chem. Phys. 1975, 63, 4990–4997. [Google Scholar] [CrossRef]
- Flory, P.J. Theory of Elasticity of Polymer Networks. The Effect of Local Constraints on Junctions. J. Phys. Chem. 1977, 66, 5720–5729. [Google Scholar] [CrossRef]
- Kloczkowski, A.; Mark, J.E.; Erman, B. A Diffused-constraint Theory for the Elasticity of Amorphous Polymer Networks. 1. Fundamentals and Stress-strain Isotherms in Elongation. Macromolecules 1995, 28, 5089–5096. [Google Scholar] [CrossRef]
- Treloar, L.R.G. The Physics of Rubber Elasticity, 3rd ed.; Oxford Clarendon Press: Oxford, UK, 1975; ISBN 0198570279. [Google Scholar]
- Erman, B.; Flory, P.J. Relationships between Stress, Strain, and Molecular Constitution of Polymers Networks. Comparison of Theory with Experiments. Macromolecules 1982, 15, 806–811. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Nonaffine Deformation and Elasticity of Polymer Networks. Macromolecules 1997, 30, 8036–8044. [Google Scholar] [CrossRef]
- Rubinstein, M.; Panyukov, S. Elasticity of Polymer Networks. Macromolecules 2002, 35, 6670–6686. [Google Scholar] [CrossRef]
- Moller, J.C.; Barr, S.A.; Schultz, E.J.; Breitzman, T.D.; Berry, R.J. Simulation of Fracture Nucleation in Cross-Linked Polymer Networks. JOM 2012, 65, 147–167. [Google Scholar] [CrossRef]
- Yang, S.; Qu, J. Computing Thermomechanical Properties of Crosslinked Epoxy by Molecular Dynamics Simulation. Polymer 2012, 53, 4806–4817. [Google Scholar] [CrossRef]
- Morozinis, A. Molecular Simulation of Cavitation in Elastomers and Polymer Melts. Ph.D. Thesis, School of Chemical Engineering, National Technical University of Athens, Athens, Greece, 2013. [Google Scholar]
- Morozinis, A.K.; Tzoumanekas, C.; Anogiannakis, S.D.; Theodorou, D.N. Atomistic Simulations of Cavitation in a Model Polyethylene Network. Polym. Sci. Ser. C 2013, 55, 212–218. [Google Scholar] [CrossRef]
- Varshney, V.; Patnaik, S.S.; Roy, A.K.; Farmer, B.L. A Molecular Dynamics Study of Epoxy-Based Networks: Cross-Linking Procedure and Prediction of Molecular and Material Properties. Macromolecules 2008, 41, 6837–6842. [Google Scholar] [CrossRef]
- Everaers, R.; Kremer, K. Entanglement Effects in Model Polymer Networks. Lect. Notes Phys. 2007, 519, 221–234. [Google Scholar] [CrossRef]
- Li, Y.; Kröger, M.; Liu, W.K. Primitive Chain Network Study on Uncrosslinked and Crosslinked cis-Polyisoprene Polymers. Polymer 2011, 52, 5867–5878. [Google Scholar] [CrossRef]
- Gavrilov, A.A.; Komarov, P.V.; Khalatur, P.G. Thermal Properties and Topology of Epoxy Networks: A Multiscale Simulation Methodology. Macromolecules 2015, 48, 206–212. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Voyiatzis, E.; Theodorou, D.N. Monte Carlo Simulations of a Coarse-grained Model for an Athermal All-polystyrene Nanocomposite System. Eur. Polym. J. 2011, 47, 699–712. [Google Scholar] [CrossRef]
- Vogiatzis, G.G.; Theodorou, D.N. Structure of Polymer Layers Grafted to Nanoparticles in Silica-Polystyrene Nanocomposites. Macromolecules 2013, 46, 4670–4683. [Google Scholar] [CrossRef]
- Hanson, D.E. The Distributions of Chain Lengths in a Crosslinked Polyisoprene Network. J. Chem. Phys. 2011, 134, 064906. [Google Scholar] [CrossRef] [PubMed]
- Kröger, M. Simple, Admissible, and Accurate Approximants of the Inverse Langevin and Brillouin Functions, Relevant for Strong Polymer Deformations and Flows. J. Non-Newton. Fluid Mech. 2015, 223, 77–87. [Google Scholar] [CrossRef]
- Vogiatzis, G.G. Multiscale Simulations of Polymer-Matrix Nanocomposites. Ph.D. Thesis, School of Chemical Engineering, National Technical University of Athens, Athens, Greece, 2015. [Google Scholar]
- Sanchez, I.C.; Lacombe, R.H. An Elementary Molecular Theory of Classical Fluids. Pure Fluids. J. Phys. Chem. 1976, 80, 2352–2362. [Google Scholar] [CrossRef]
- Van Gunsteren, W.F.; Berendsen, H.J.C. Algorithms for Brownian Dynamics. Mol. Phys. 1982, 45, 637–647. [Google Scholar] [CrossRef]
- Leimkuhler, B.; Matthews, C.; Tretyakov, M.V. On the Long-time Integration of Stochastic Gradient Systems. Proc. R. Soc. A 2015, 470, 20140120. [Google Scholar] [CrossRef]
- Mavrantzas, V.G.; Theodorou, D.N. Atomistic Simulation of Polymer Melt elasticity: Calculation of the Free Energy of an Oriented Polymer Melt. Macromolecules 1998, 31, 6310–6332. [Google Scholar] [CrossRef]
- Lustig, S.R.; Shay, R.M.; Caruthers, J.M. Thermodynamic Constitutive Equations for Materials with Memory on a Material Time Scale. J. Rheol. 1996, 40, 69–106. [Google Scholar] [CrossRef]
- Astarita, G.; Marruci, G. Principles of Non-Newtonian Fluid Mechanics, 1st ed.; McGraw Hill: London, UK, 1974; ISBN 0070840229. [Google Scholar]
- Ramirez, J.; Sukumaran, S.K.; Vorselaars, B.; Likhtman, A.E. Efficient on the Fly Calculation of Time Correlation Functions in Computer Simulations. J. Chem. Phys. 2010, 133, 154103. [Google Scholar] [CrossRef] [PubMed]
- Likhtman, A. Polymer Science: A Comprehensive Reference; Matyjaszewski, K., Möller, M., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2012; pp. 133–179. ISBN 9780444533494. [Google Scholar]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s Ratio and Modern Materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef] [PubMed]
- Rubinstein, M.; Colby, R.H. Polymer Physics, 1st ed.; Oxford University Press: Oxford, UK, 2003; ISBN 019852059X. [Google Scholar]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Lees, A.W.; Edwards, S.F. The Computer Study of Transport Processes under Extreme Conditions. J. Phys. C Solid State Phys. 1972, 5, 1921–1928. [Google Scholar] [CrossRef]
- Ercolessi, F.; Adams, J.B. Interatomic Potentials from 1st-principles Calculations—The Force Matching Method. Europhys. Lett. 1994, 26, 583–588. [Google Scholar] [CrossRef]
- Izvekov, S.; Voth, G.A. Multiscale Coarse-graining of Liquid-state Systems. J. Chem. Phys. 2005, 123, 134105. [Google Scholar] [CrossRef] [PubMed]
- Noid, W.G.; Chu, J.W.; Ayton, G.S.; Voth, G.A. Multiscale Coarse-graining and Structural Correlations: Connections to Liquid-state Theory. J. Phys. Chem. B 2007, 111, 4116–4127. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Doxastakis, M.; Mavrantzas, V.G.; Theodorou, D.N. Detailed Molecular Dynamics Simulation of the Self-diffusion of n-Alkane and cis-1,4-Polyisoprene Oligomer Melts. J. Chem. Phys. 2002, 116, 436–446. [Google Scholar] [CrossRef]
- Kojima, M.; Tosaka, M.; Funani, E.; Nitta, K.; Ohsima, M.; Kohjyia, S. Phase Behavior of Crosslinked Polyisoprene Rubber and Supercritical Carbon Dioxide. J. Supercrit. Fluids 2005, 35, 175–181. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Molecular Simulation of Liquids, 1st ed.; Oxford Science Publications: Oxford, UK, 1987; ISBN 0198556454. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 1st ed.; Academic Press: New York, NY, USA, 1996; ISBN 9780122673511. [Google Scholar]
- De Gennes, P.G. The Physics of Liquid Crystals, 1st ed.; Clarendon: Oxford, UK, 1974; ISBN 0198517858. [Google Scholar]
- Megariotis, G.; Vyrkou, A.; Leygue, A.; Theodorou, D.N. Systematic Coarse Graining of 4-Cyano-4’-Pentylbiphenyl. Ind. Eng. Chem. Res. 2011, 50, 546–556. [Google Scholar] [CrossRef]
- Amram, B.; Bokobza, L.; Queslel, J.P.; Monnerie, L. Fourier-transform Infra-red Dichroism Study of Molecular Orientation in Synthetic High cis-1,4-Polyisoprene and in Natural Rubber. Polymer 1986, 27, 877–882. [Google Scholar] [CrossRef]
- Kanberoglou, C.; Bahar, I.; Erman, B. Stress-strain Relations and Molecular Orientation in Highly Crosslinked cis-Polyisoprene Networks. Polymer 1993, 34, 4997–4999. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic Simulations of Hard-Sphere Suspensions under Steady Shear. Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
- Espanol, P.; Warren, P.B. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]



| 172 | |
| 53 | |
| 52 | |
| 300 (pc = 3.4%), 600 (pc = 7.0%) | |
| 900, 1200 | |
| B | 0.958 nm |
| 3.06 nm | |
| 10.0 s−1 | |
| 400 K | |
| 30 nm | |
| 50 ps | |
| 0.5 | |
| 649.4 K | |
| 955 kg/m3 |
| , 10−4 bar−1 | , deg | |
| pc = 7.0%, nslip-springs = 900 | ||
| pc = 3.5%, nslip-springs = 1200 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megariotis, G.; Vogiatzis, G.G.; Sgouros, A.P.; Theodorou, D.N. Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code. Polymers 2018, 10, 1156. https://doi.org/10.3390/polym10101156
Megariotis G, Vogiatzis GG, Sgouros AP, Theodorou DN. Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code. Polymers. 2018; 10(10):1156. https://doi.org/10.3390/polym10101156
Chicago/Turabian StyleMegariotis, Grigorios, Georgios G. Vogiatzis, Aristotelis P. Sgouros, and Doros N. Theodorou. 2018. "Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code" Polymers 10, no. 10: 1156. https://doi.org/10.3390/polym10101156
APA StyleMegariotis, G., Vogiatzis, G. G., Sgouros, A. P., & Theodorou, D. N. (2018). Slip Spring-Based Mesoscopic Simulations of Polymer Networks: Methodology and the Corresponding Computational Code. Polymers, 10(10), 1156. https://doi.org/10.3390/polym10101156