Mechanisms of the Complex Thermo-Mechanical Behavior of Polymer Glass Across a Wide Range of Temperature Variations
Abstract
:1. Introduction
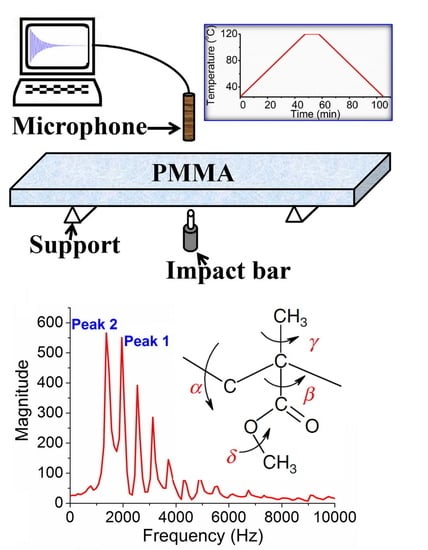
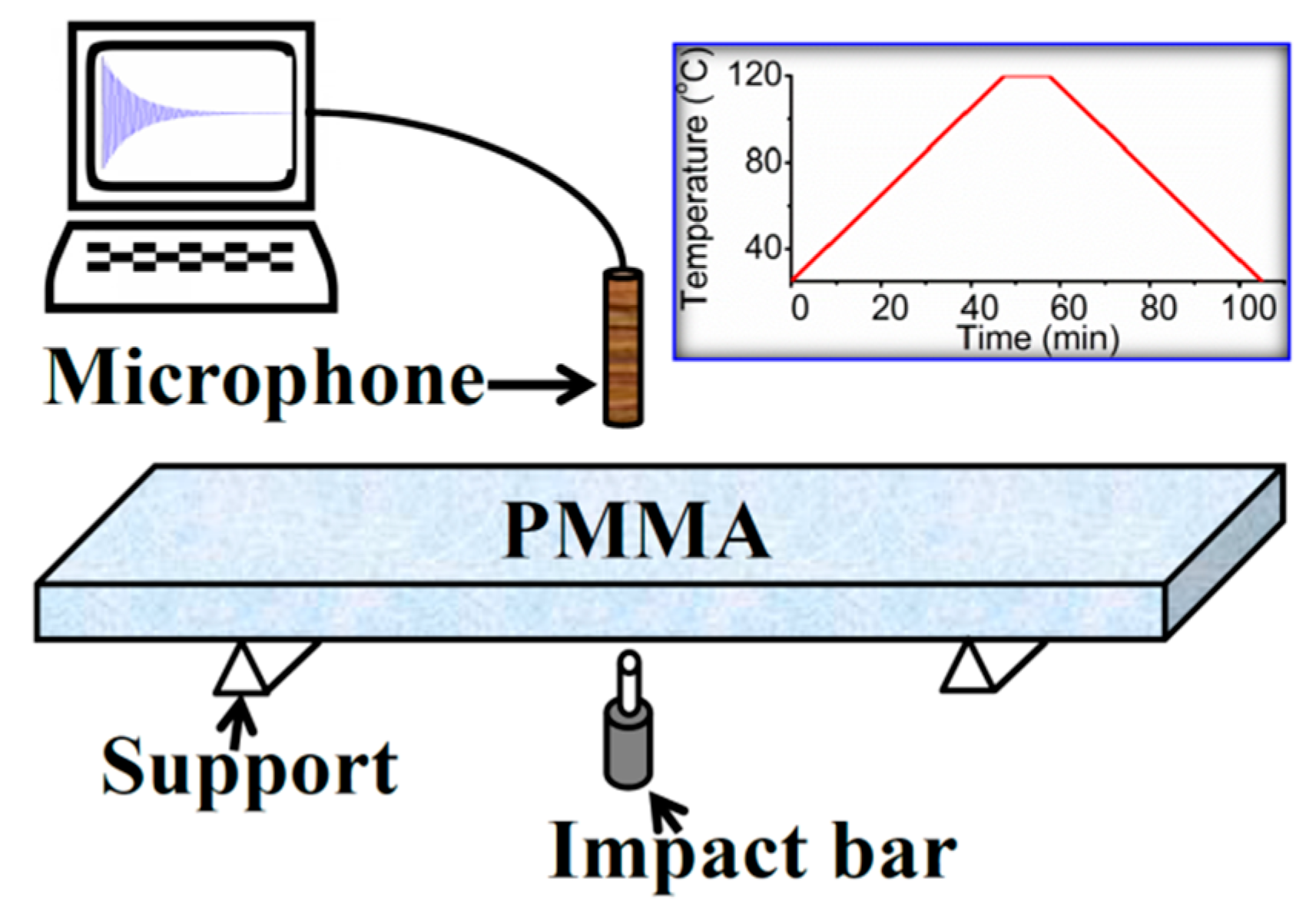
2. Materials and Methods
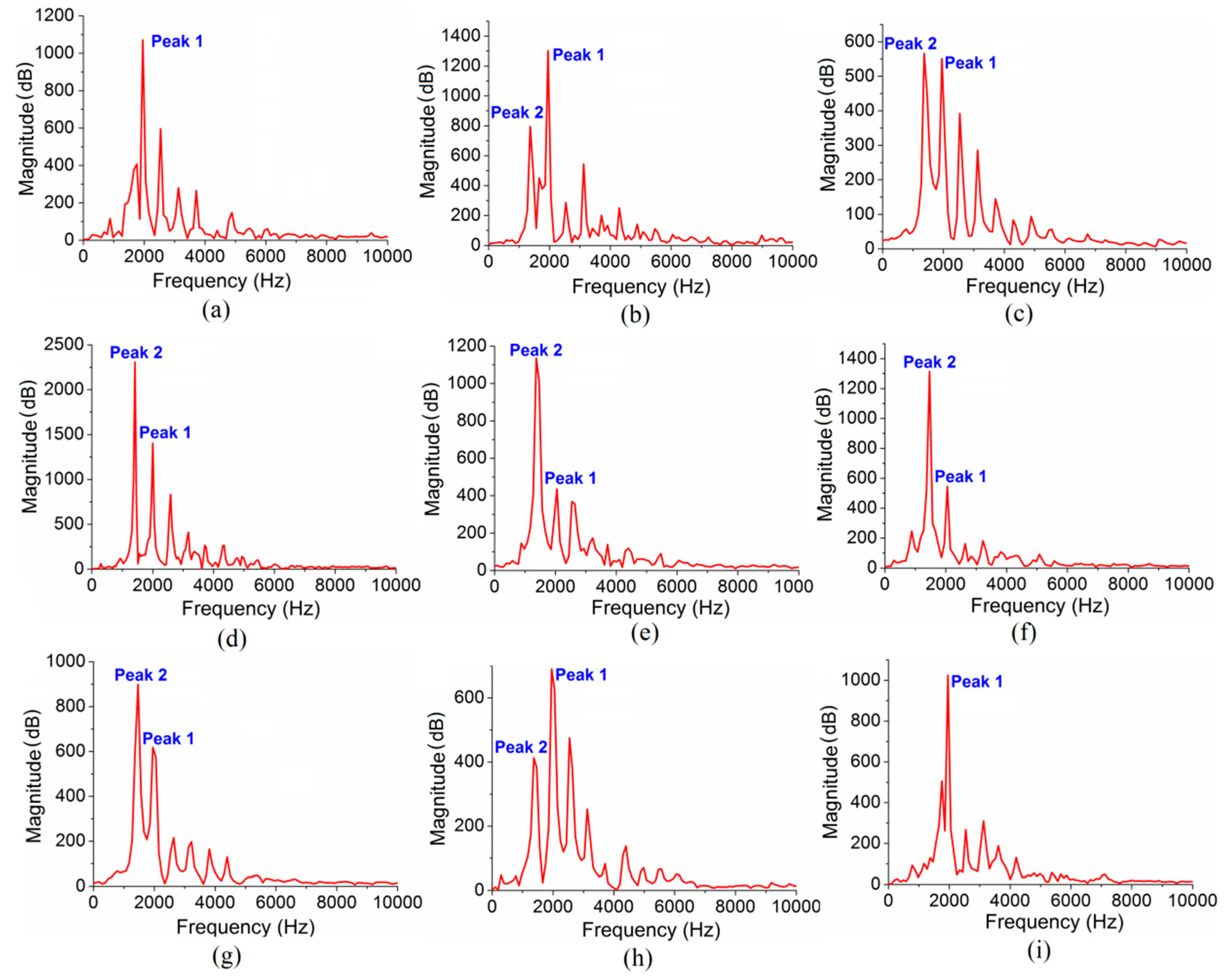
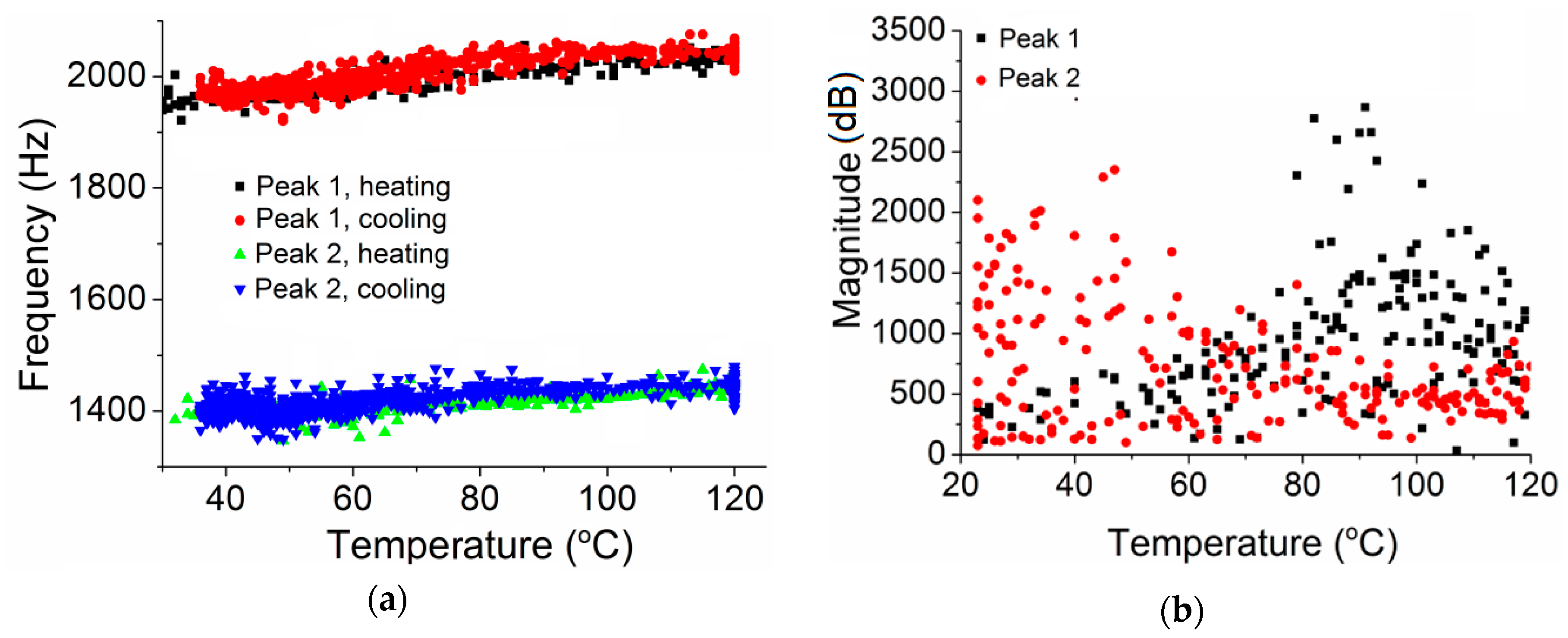
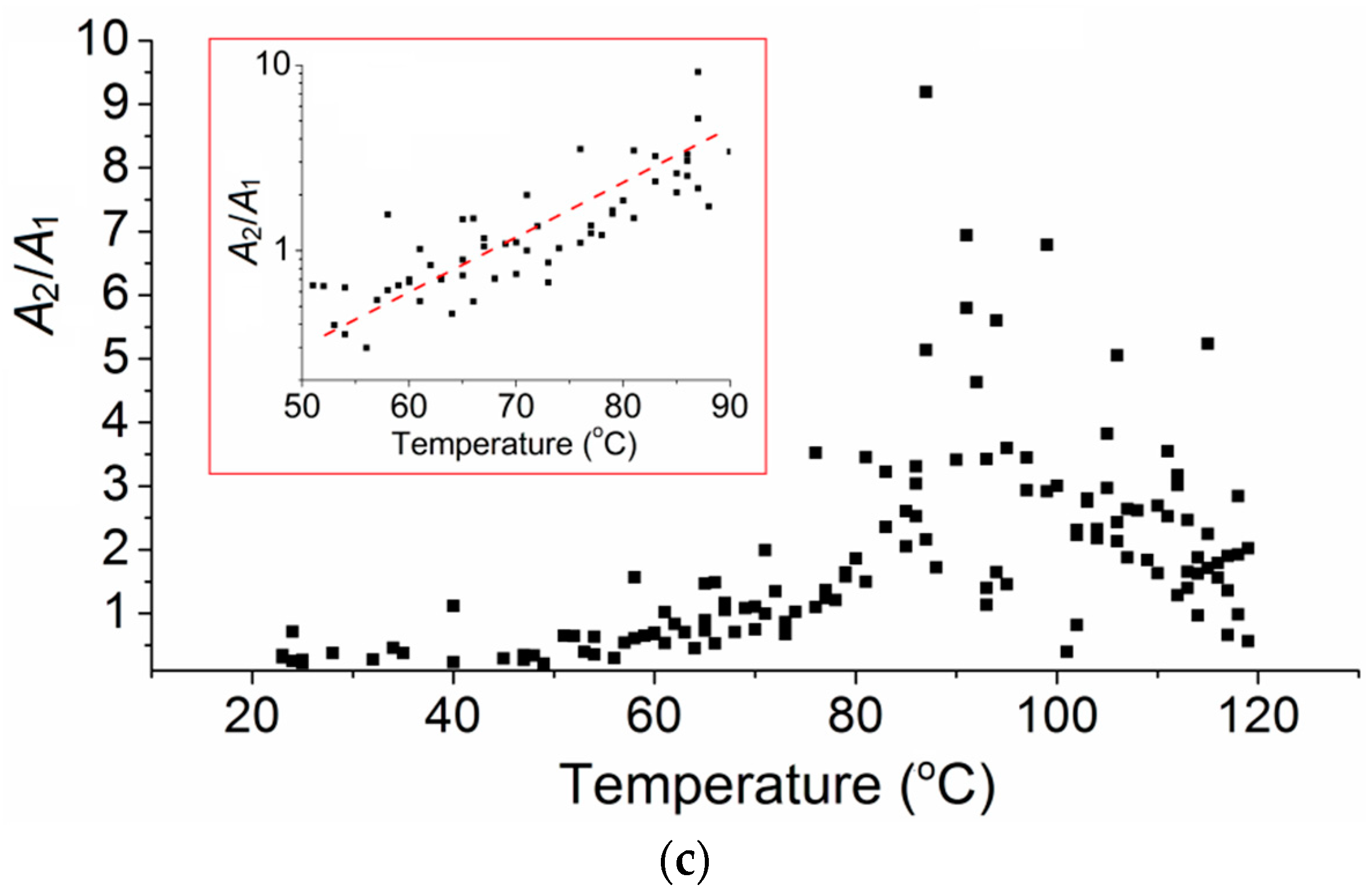
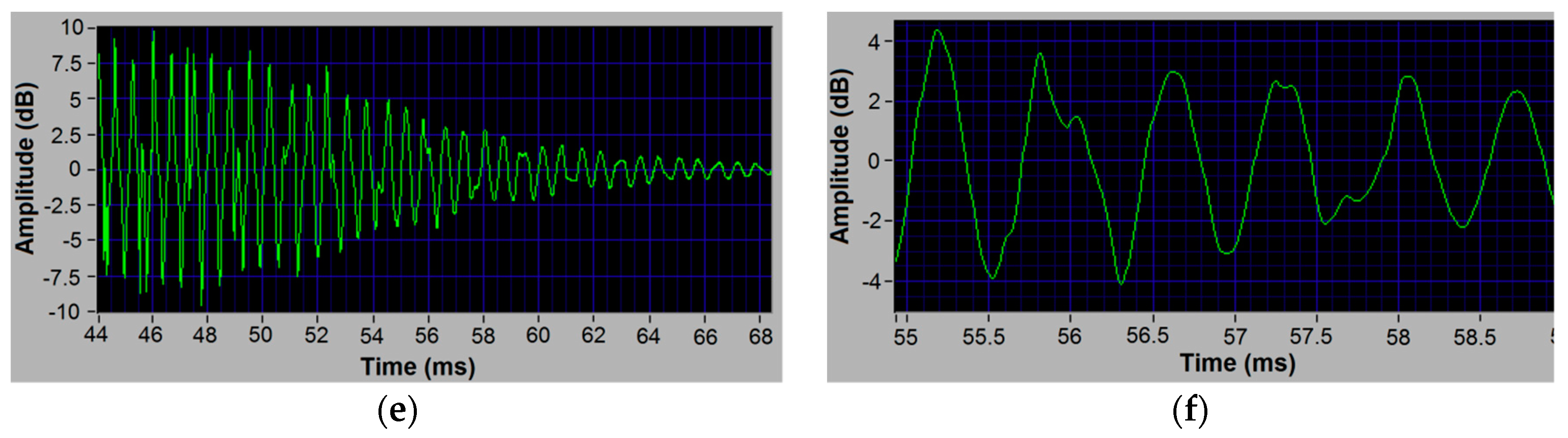
3. Results
4. Discussion
- (1)
- What are these vibrational modes and why do they change with temperature?
- (2)
- Can one still obtain the elastic properties of the material from the dominant peaks?
4.1. Possible Vibrational Mode of Peak 2
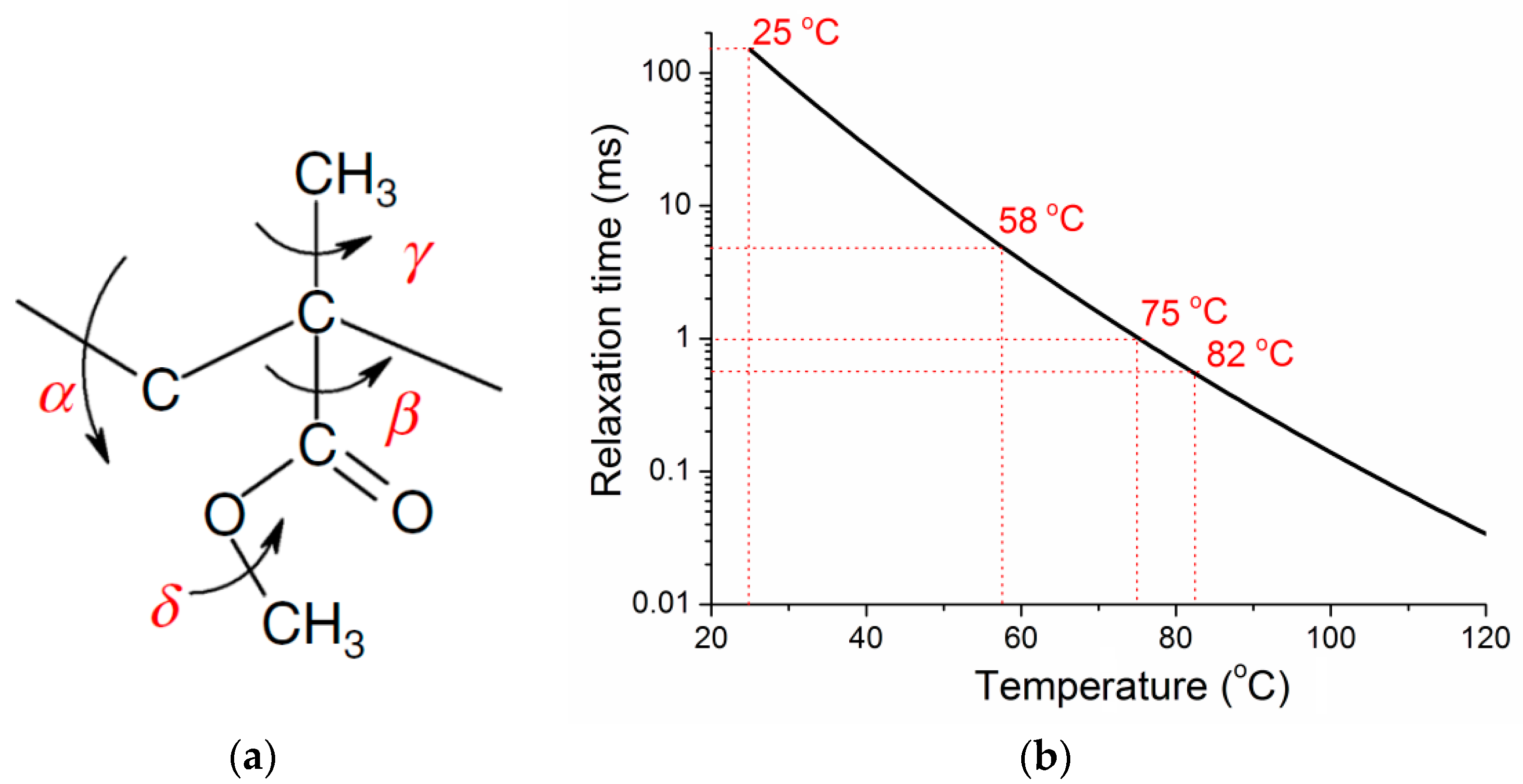
4.2. Structure Relaxation of PMMA
4.3. The Modulus of PMMA Network
4.4. Young’s Modulus of Bulk PMMA Material
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Richeton, J.; Ahzi, S.; Vecchio, K.S.; Jiang, F.C.; Adharapurapu, R.R. Influence of temperature and strain rate on the mechanical behavior of three amorphous polymers: Characterization and modeling of the compressive yield stress. Int. J. Solids Struct. 2006, 43, 2318–2335. [Google Scholar] [CrossRef]
- Smith, K.E.; Parks, S.S.; Hyjek, M.A.; Downey, S.E.; Gall, K. The effect of the glass transition temperature on the toughness of photopolymerizable (meth)acrylate networks under physiological conditions. Polymer 2009, 50, 5112–5123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hoy, R.S. Why is understanding glassy polymer mechanics so difficult? J. Polym. Sci. 2011, 49, 979–984. [Google Scholar] [CrossRef] [Green Version]
- Fleischhauer, R.; Dal, H.; Kaliske, M.; Schneider, K. A constitutive model for finite deformation of amorphous polymers. Int. J. Mech. Sci. 2012, 65, 48–63. [Google Scholar] [CrossRef]
- Berdichevsky, V.L.; Herman, J.N. On rheology of cross-linked polymers: 1. Slippage of polymer chains and its macroscopic modeling. Int. J. Eng. Sci. 2016, 100, 183–198. [Google Scholar] [CrossRef]
- Mahieux, C.A.; Reifsnider, K.L. Property modeling across transition temperatures in polymers: Application to thermoplastic systems. J. Mater. Sci. 2002, 37, 911–920. [Google Scholar] [CrossRef]
- Sujithra, R.; Srinivasan, S.M.; Arockiarajan, A. Modeling memory effects in amorphous polymers. Int. J. Eng. Sci. 2014, 84, 95–112. [Google Scholar] [CrossRef]
- Schmidt-Rohr, K.; Kulik, A.S.; Beckham, H.W.; Ohlemacher, A.; Pawelzik, U.; Boeffel, C.; Spiess, H.W. Molecular nature of the beta-relaxation in poly(methyl methacrylate) investigated by multidimensional NMR. Macromolecules 1994, 27, 4733–4745. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D. Relationship between the alpha- and beta-relaxation processes in amorphous polymers: Insight from atomistic molecular dynamics simulations of 1,4-polybutadiene melts and blends. J. Polym. Sci. 2007, 45, 627–643. [Google Scholar] [CrossRef]
- Fytas, G.; Wang, C.H.; Fischer, E.W.; Mehler, K. Evidence of two relaxation processes in the photon-correlation spectra of poly(methyl methacrylate) above Tg. J. Polym. Sci. 1986, 24, 1859–1867. [Google Scholar] [CrossRef]
- Garwe, F.; Schonhals, A.; Lockwenz, H.; Beiner, M.; Schroter, K.; Donth, E. Influence of cooperative alpha dynamics on local beta relaxation during the development of the dynamic glass transition in poly(n-alkyl methacrylate)s. Macromolecules 1996, 29, 247–253. [Google Scholar] [CrossRef]
- Muzeau, E.; Perez, J.; Johari, G.P. Mechanical spectrometry of the beta-relaxation in poly(methyl methacrylate). Macromolecules 1991, 24, 4713–4723. [Google Scholar] [CrossRef]
- Anand, L.; Ames, N.M.; Srivastava, V.; Chester, S.A. A thermo-mechanically coupled theory for large deformations of amorphous polymers. Part I: Formulation. Int. J. Plast. 2009, 25, 1474–1494. [Google Scholar] [CrossRef]
- Deng, Y.J.; Peng, L.F.; Lai, X.M.; Fu, M.W.; Lin, Z.Q. Constitutive modeling of size effect on deformation behaviors of amorphous polymers in micro-scaled deformation. Int. J. Plast. 2017, 89, 197–222. [Google Scholar] [CrossRef]
- Srivastava, V.; Chester, S.A.; Ames, N.M.; Anand, L. A thermo-mechanically-coupled large-deformation theory for amorphous polymers in a temperature range which spans their glass transition. Int. J. Plast. 2010, 26, 1138–1182. [Google Scholar] [CrossRef] [Green Version]
- Basterra-Beroiz, B.; Rommel, R.; Kayser, F.; Westermann, S.; Valentin, J.L.; Heinrich, G. Swelling of polymer networks with topological constraints: Application of the Helmis-Heinrich-Straube model. Express Polym. Lett. 2018, 12, 731–739. [Google Scholar] [CrossRef]
- Heidemann, K.M.; Sharma, A.; Rehfeldt, F.; Schmidt, C.F.; Wardetzky, M. Elasticity of 3D networks with rigid filaments and compliant crosslinks. Soft Matter 2015, 11, 343–354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Meng, F.L.; Terentjev, E.M. Theory of semiflexible filaments and networks. Polymers 2017, 9, 52. [Google Scholar] [CrossRef]
- Chen, W.; Lu, F.; Cheng, M. Tension and compression tests of two polymers under quasistatic and dynamic loading. Polym. Test. 2002, 21, 113–121. [Google Scholar] [CrossRef]
- Narva, K.K.; Lassila, L.V.; Vallittu, P.K. The static strength and modulus of fiber reinforced denture base polymer. Dent. Mater. 2005, 21, 421–428. [Google Scholar] [CrossRef] [PubMed]
- Davis, W.M.; Macosko, C.W. Non-linear dynamic mechanical moduli for polycarbonate and pmma. J. Rheol. 1978, 22, 53–71. [Google Scholar] [CrossRef]
- Ornaghi, H.L.; Bolner, A.S.; Fiorio, R.; Zattera, A.J.; Amico, S.C. Mechanical and dynamic mechanical analysis of hybrid composites molded by resin transfer molding. J. Appl. Polym. Sci. 2010, 118, 887–896. [Google Scholar] [CrossRef]
- Montecinos, S.; Tognana, S.; Salgueiro, W. Determination of the Young’s modulus in CuAlBe shape memory alloys with different microstructures by impulse excitation technique. Mater. Sci. Eng. 2016, 676, 121–127. [Google Scholar] [CrossRef]
- Tognana, S.; Salgueiro, W.; Somoza, A.; Marzocca, A. Measurement of the Young’s modulus in particulate epoxy composites using the impulse excitation technique. Mater. Sci. Eng. 2010, 527, 4619–4623. [Google Scholar] [CrossRef]
- Liu, W.D.; Liu, M.; Zhang, L.Z. Oxidation-induced mechanical deterioration and hierarchical cracks in glassy carbon. Carbon 2016, 100, 178–186. [Google Scholar] [CrossRef]
- Liu, W.D.; Ruan, H.H.; Zhang, L.Z. Revealing structural relaxation of optical glass through the temperature dependence of Young’s Modulus. J. Am. Ceram. Soc. 2014, 97, 3475–3482. [Google Scholar] [CrossRef]
- Lei, Y.; Adhikari, S.; Friswell, M.I. Vibration of nonlocal Kelvin-Voigt viscoelastic damped Timoshenko beams. Int. J. Eng. Sci. 2013, 66–67, 1–13. [Google Scholar] [CrossRef]
- Anderson, O.L. Derivation of wachtmans equation for temperature dependence of elastic moduli of oxide compounds. Phys. Rev. 1966, 144, 553–557. [Google Scholar] [CrossRef]
- Wachtman, J.B.; Tefft, W.E.; Lam, D.G.; Apstein, C.S. Exponential temperature dependence of Young’s modulus for several oxides. Phys. Rev. 1961, 122, 1754–1759. [Google Scholar] [CrossRef]
- Jones, D.R.H.; Ashby, M.F. Engineering Materials 1—An Introduction to Properties, Applications and Design; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Bergman, R.; Alvarez, F.; Alegria, A.; Colmenero, J. The merging of the dielectric alpha- and beta-relaxations in poly(methyl methacrylate). J. Chem. Phys. 1998, 109, 7546–7555. [Google Scholar] [CrossRef]
- Casalini, R.; Snow, A.W.; Roland, C.M. Temperature dependence of the Johari-Goldstein relaxation in poly(methyl methacrylate) and poly(thiomethyl methacrylate). Macromolecules 2013, 46, 330–334. [Google Scholar] [CrossRef]
- Weiner, J.H. Statistical Mechanics of Elasticity; Dover Publications: Mineola, NY, USA, 2002. [Google Scholar]
- Mahieux, C.A.; Reifsnider, K.L. Property modeling across transition temperatures in polymers: A robust stiffness-temperature model. Polymer 2001, 42, 3281–3291. [Google Scholar] [CrossRef]
- Richeton, J.; Schlatter, G.; Vecchio, K.S.; Remond, Y.; Ahzi, S. A unified model for stiffness modulus of amorphous polymers across transition temperatures and strain rates. Polymer 2005, 46, 8194–8201. [Google Scholar] [CrossRef]
- Jurjiu, A.; Biter, T.L.; Turcu, F. Dynamics of a polymer network based on dual sierpinski gasket and dendrimer: A theoretical approach. Polymers 2017, 9, 245. [Google Scholar] [CrossRef]
- Jurjiu, A.; Galiceanu, M. Dynamics of a polymer network modeled by a fractal cactus. Polymers 2018, 10, 787. [Google Scholar] [CrossRef]

| Modulus | DMA (Tensile) | Uniaxial Compressive | IET (Bending) |
|---|---|---|---|
| E1 at 2000 Hz | 11.14 GPa | 5.9 GPa | 6.43 GPa |
| E2 at 1500 Hz | 4.6 GPa | 3.14 GPa | 3.5 GPa |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, W.; Zhang, L. Mechanisms of the Complex Thermo-Mechanical Behavior of Polymer Glass Across a Wide Range of Temperature Variations. Polymers 2018, 10, 1153. https://doi.org/10.3390/polym10101153
Liu W, Zhang L. Mechanisms of the Complex Thermo-Mechanical Behavior of Polymer Glass Across a Wide Range of Temperature Variations. Polymers. 2018; 10(10):1153. https://doi.org/10.3390/polym10101153
Chicago/Turabian StyleLiu, Weidong, and Liangchi Zhang. 2018. "Mechanisms of the Complex Thermo-Mechanical Behavior of Polymer Glass Across a Wide Range of Temperature Variations" Polymers 10, no. 10: 1153. https://doi.org/10.3390/polym10101153
APA StyleLiu, W., & Zhang, L. (2018). Mechanisms of the Complex Thermo-Mechanical Behavior of Polymer Glass Across a Wide Range of Temperature Variations. Polymers, 10(10), 1153. https://doi.org/10.3390/polym10101153