Two Orders of Magnitude Variation of Diffusion-Enhanced Förster Resonance Energy Transfer in Polypeptide Chains
Abstract
:1. Introduction
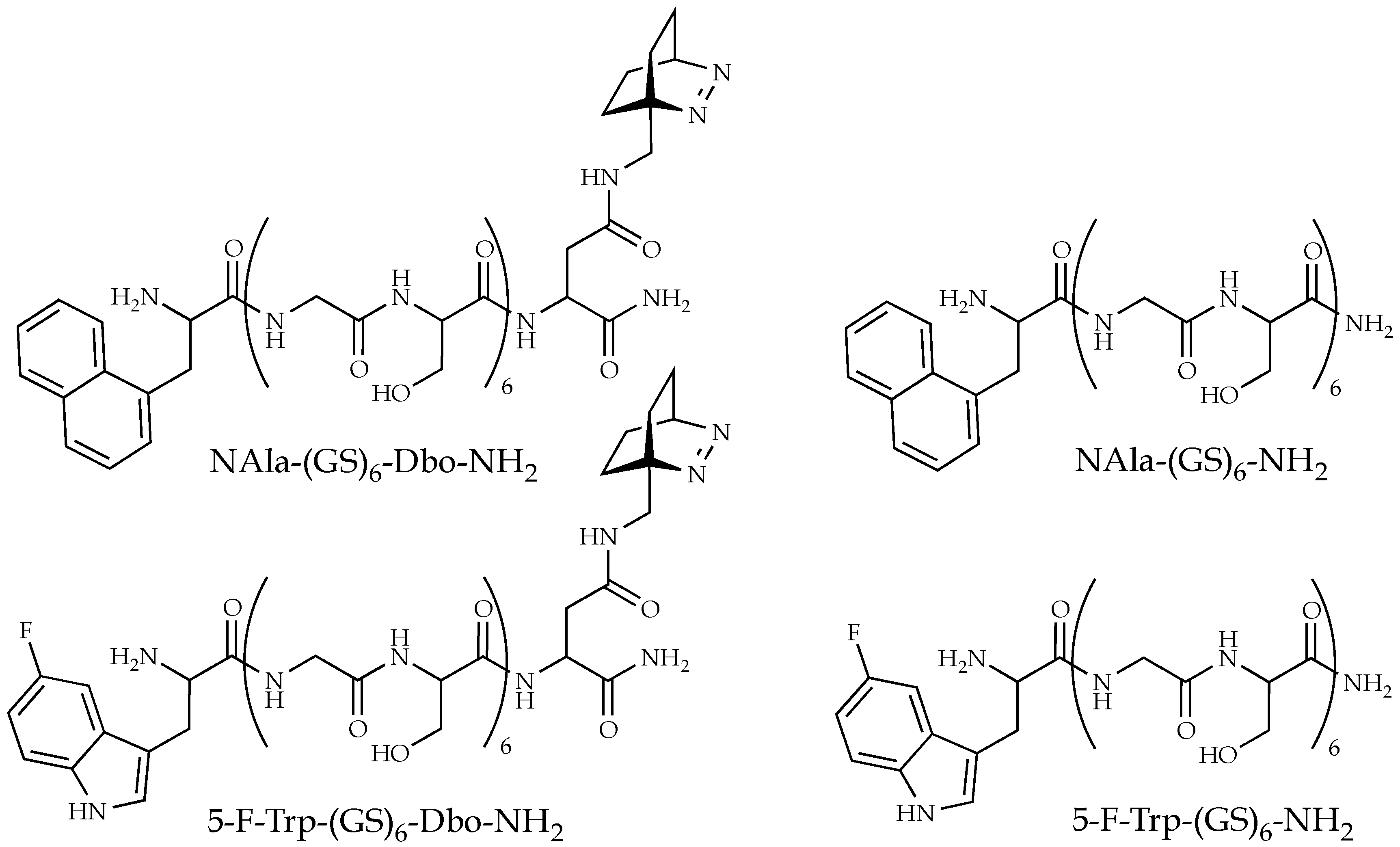
2. Materials and Methods
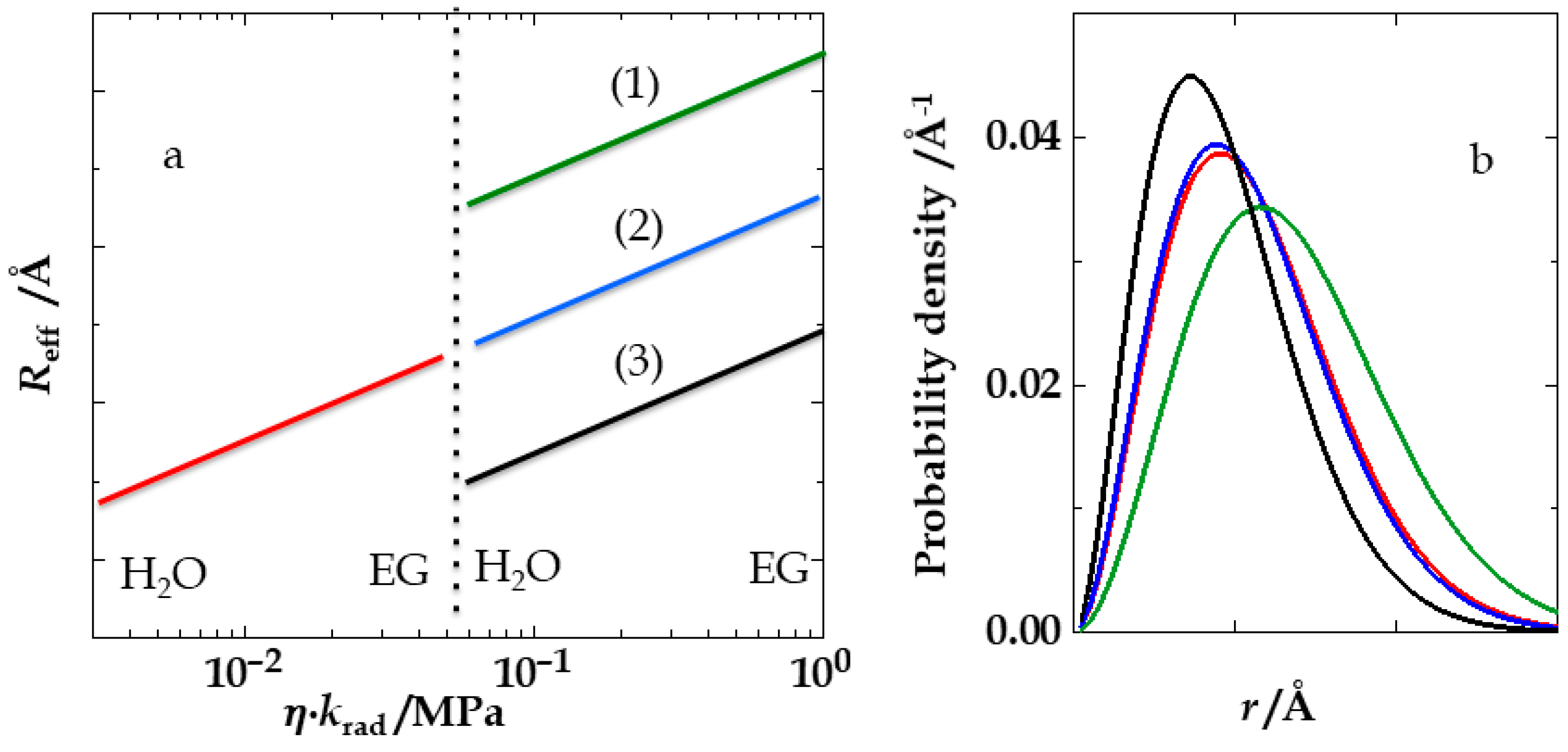
3. Theoretical Analysis
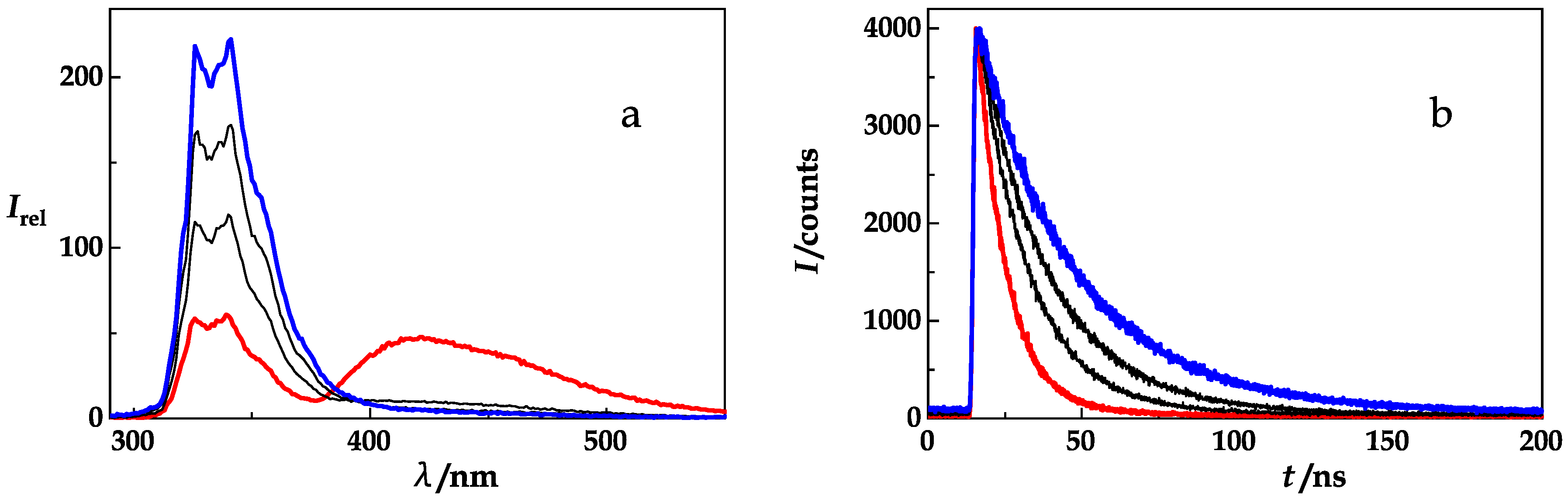
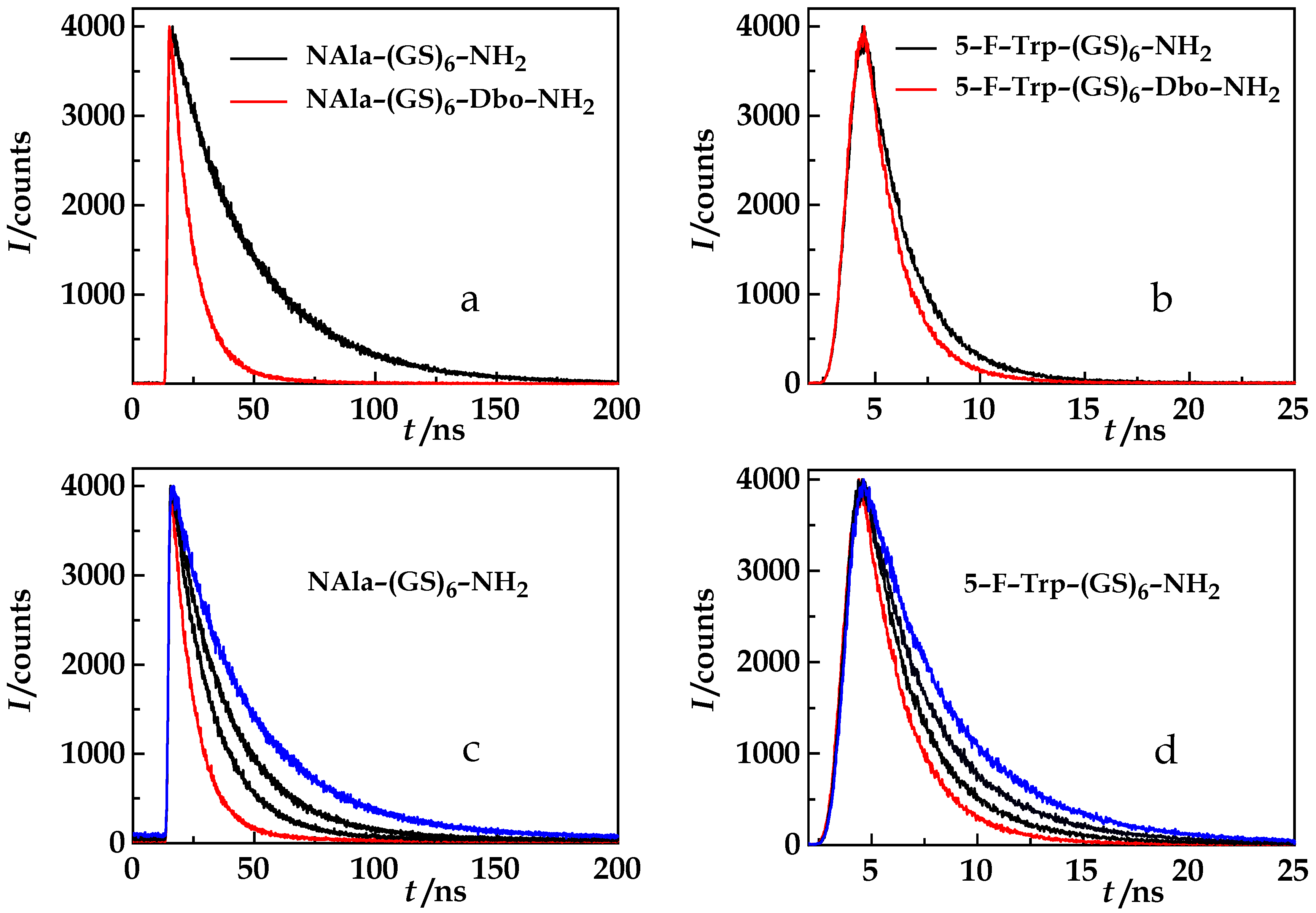
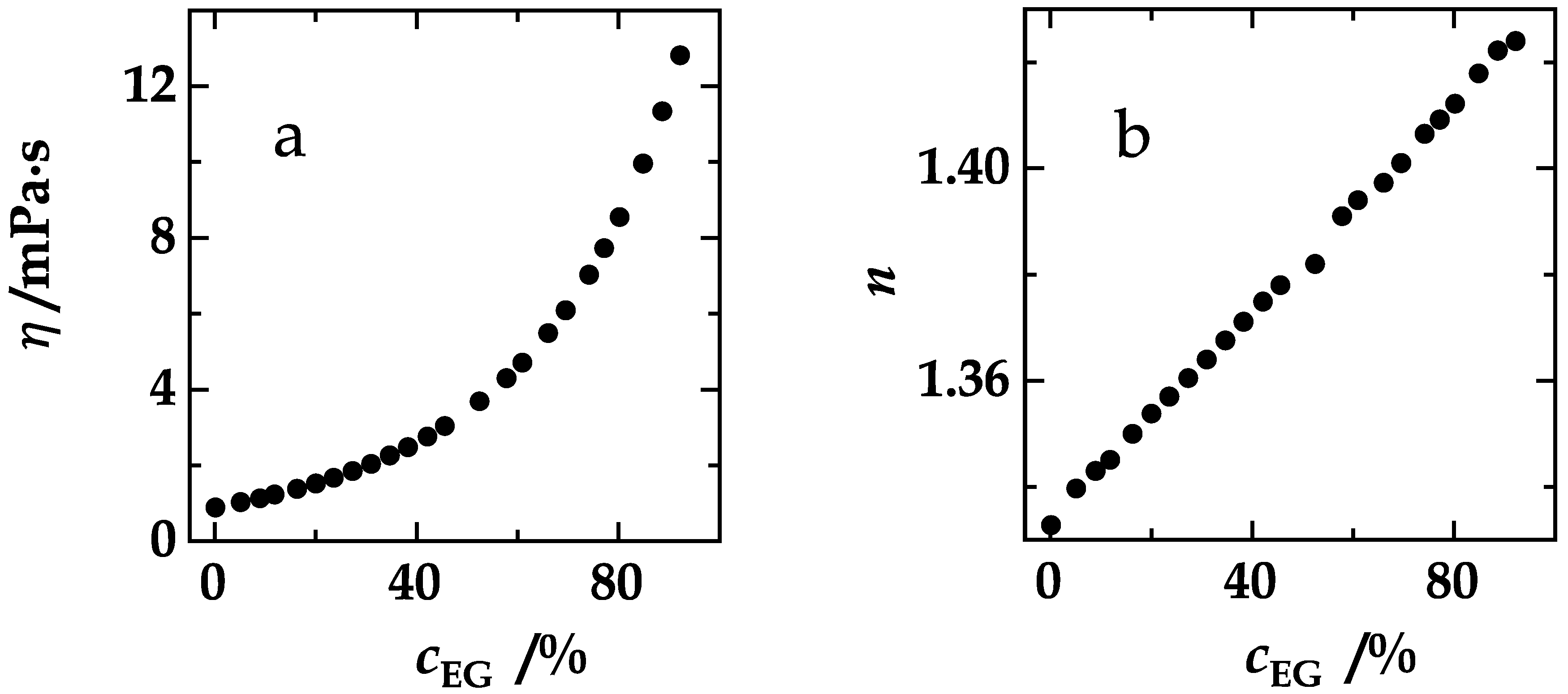
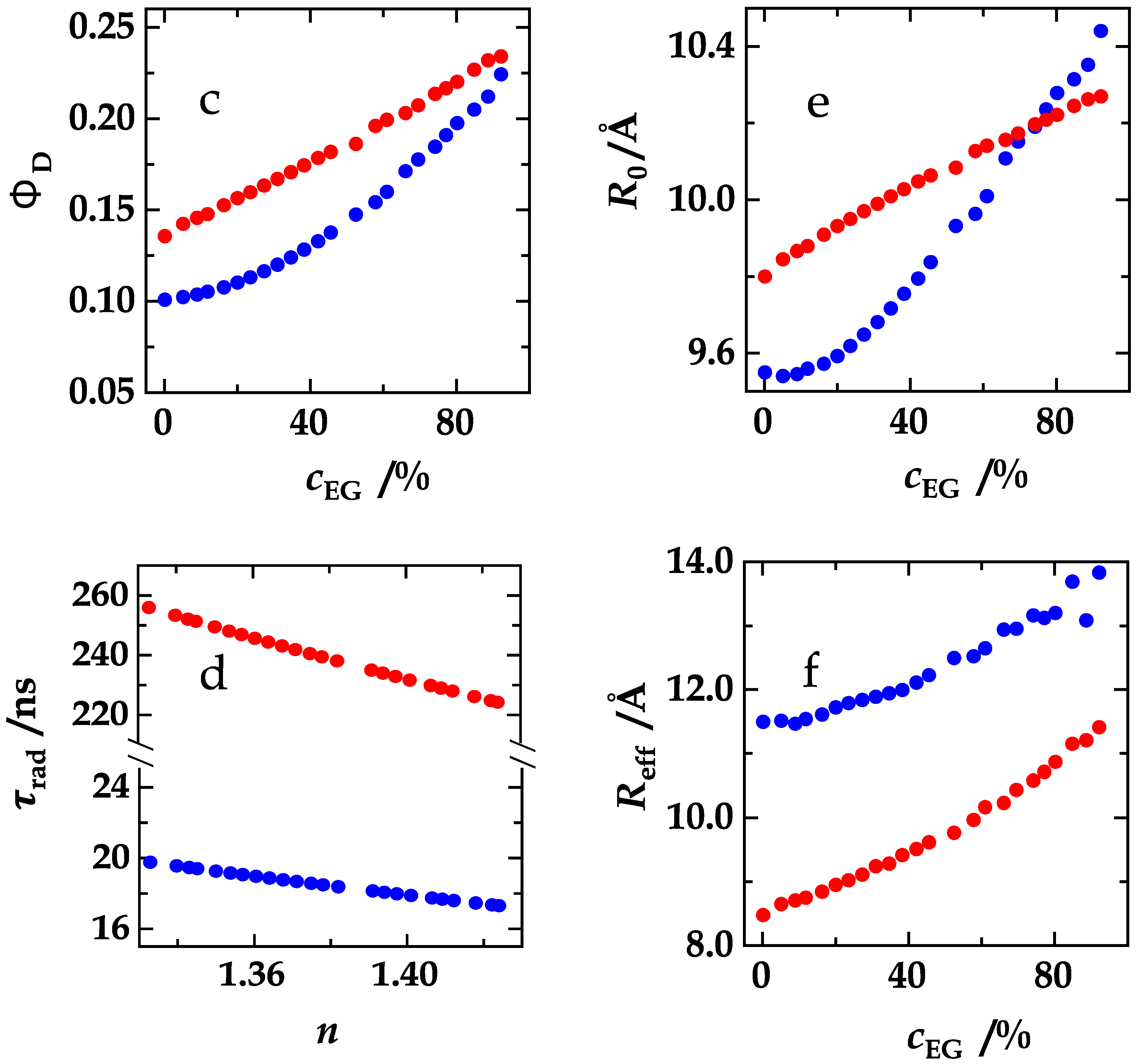
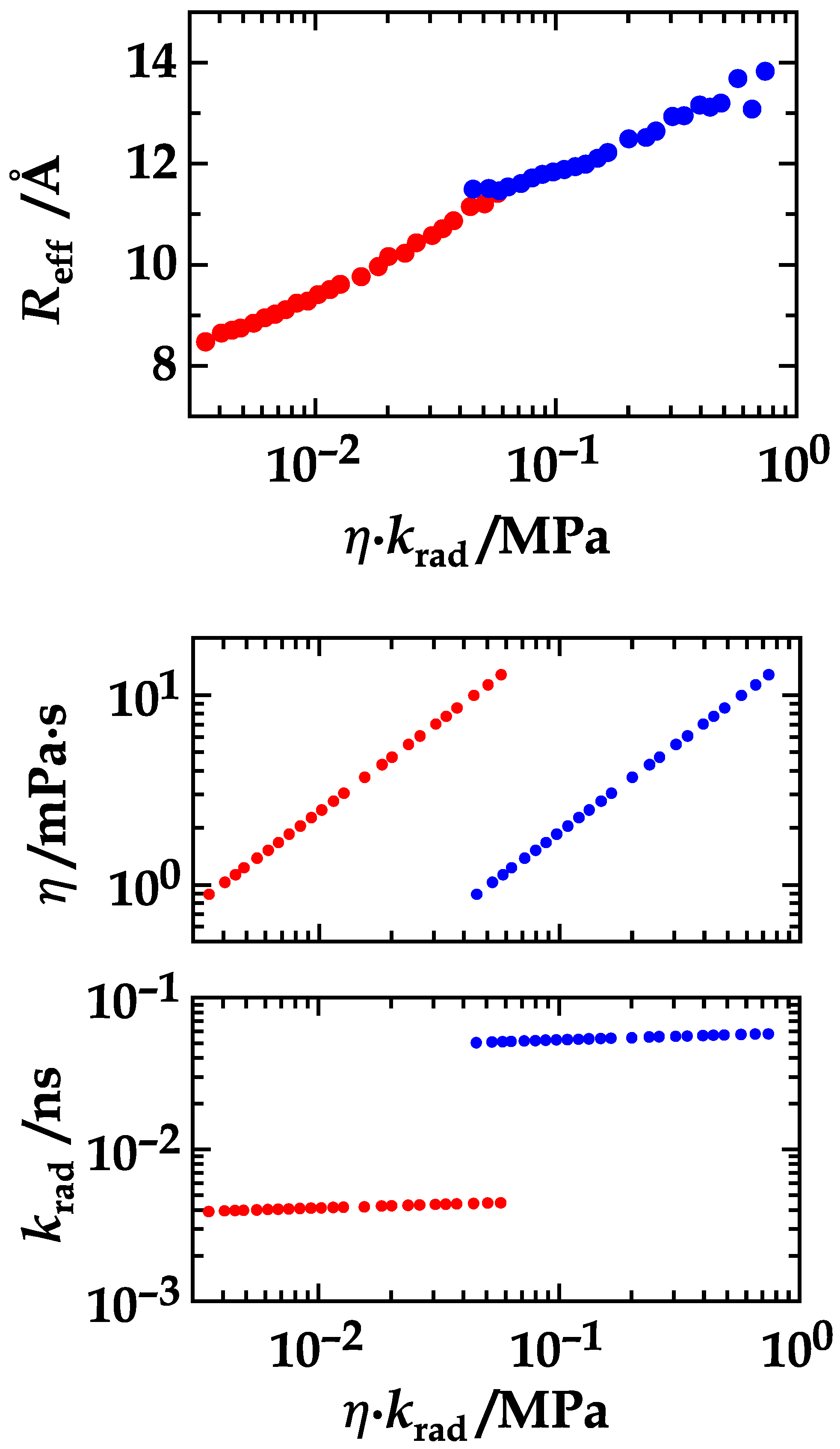
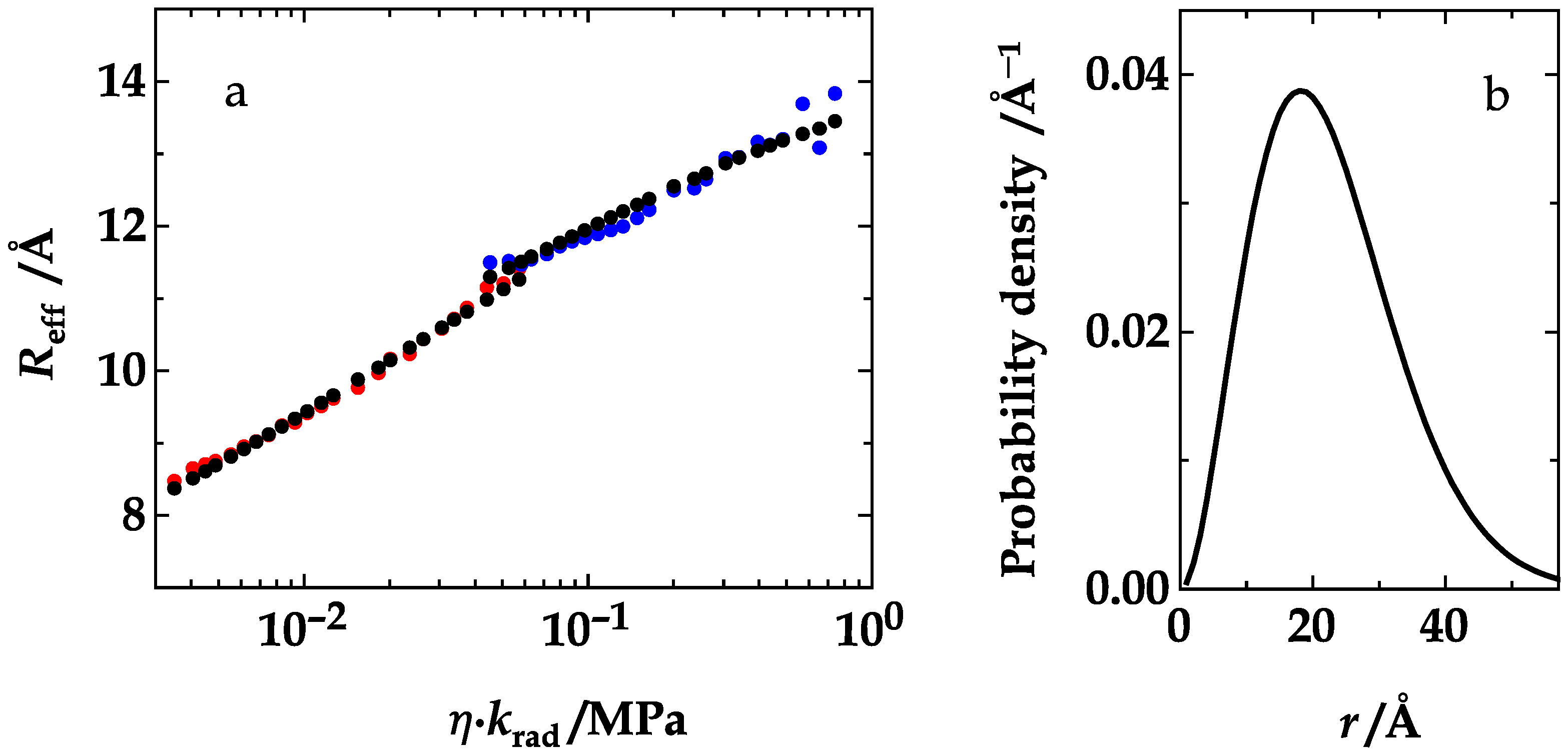
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References and Note
- Förster, T. Zwischenmolekulare Energiewanderung und Fluoreszenz. Ann. Phys. 1948, 2, 55–75. [Google Scholar] [CrossRef]
- Stryer, L.; Haugland, R.P. Energy Transfer: A Spectroscopic Ruler. Proc. Natl. Acad. Sci. USA 1967, 58, 719–726. [Google Scholar] [CrossRef] [PubMed]
- Haas, E. Fluorescence Resonance Energy Transfer (FRET) and Single Fluorescence Detection Studies of the Mechanism of Protein Folding and Unfolding. In Protein Folding Handbook; Buchner, K., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lakowicz, J.R. Principles of Fluorescence Spectroscopy, 3rd ed.; Kluwer Academic/Plenum: New York, NY, USA, 2006. [Google Scholar]
- Stryer, L. Fluorescence Energy Transfer as a Spectroscopic Ruler. Annu. Rev. Biochem. 1978, 47, 819–846. [Google Scholar] [CrossRef] [PubMed]
- Stryer, L.; Thomas, D.D.; Meares, C.F. Diffusion-Enhanced Fluorescence Energy Transfer. Annu. Rev. Biophys. Bioeng. 1982, 11, 203–222. [Google Scholar] [CrossRef] [PubMed]
- Ha, T. Single-Molecule Fluorescence Resonance Energy Transfer. Methods 2001, 25, 78–86. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B. Single-Molecule Fluorescence Spectroscopy of Protein Folding. ChemPhysChem 2005, 6, 1206–1220. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B. Application of Single Molecule Förster Resonance Energy Transfer to Protein Folding. Methods Mol. Biol. 2007, 350, 115–138. [Google Scholar] [PubMed]
- Sahoo, H.; Roccatano, D.; Hennig, A.; Nau, W.M. A 10-Å Spectroscopic Ruler Applied to Short Polyprolines. J. Am. Chem. Soc. 2007, 129, 9762–9772. [Google Scholar] [CrossRef] [PubMed]
- Sahoo, H.; Nau, W.M. Phosphorylation-Induced Conformational Changes in Short Peptides Probed by Fluorescence Resonance Energy Transfer in the 10-Å Domain. ChemBioChem 2007, 8, 567–573. [Google Scholar] [CrossRef] [PubMed]
- Jacob, M.H.; Nau, W.M. Short-Distance FRET Applied to the Polypeptide Chain. In Folding, Misfolding and Nonfolding of Peptides and Small Proteins; Schweitzer-Stenner, R., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Jacob, M.H.; Dsouza, R.N.; Ghosh, I.; Norouzy, A.; Schwarzlose, T.; Nau, W.M. Diffusion-Enhanced Förster Resonance Energy Transfer and the Effects of External Quenchers and the Donor Quantum Yield. J. Phys. Chem. B 2013, 117, 185–198. [Google Scholar] [CrossRef] [PubMed]
- Haas, E.; Katchalski-Katzir, E.; Steinberg, I.Z. Brownian Motion of the Ends of Oligopeptides Chains in Solution as Estimated by Energy Transfer Between the Chain Ends. Biopolymers 1978, 17, 11–31. [Google Scholar] [CrossRef]
- Lakowicz, J.R.; Kusba, J.; Gryczynski, I.; Wiczk, W.; Szmacinski, H.; Johnson, M.L. End-to-End Diffusion and Distance Distributions of Flexible Donor-Acceptor Systems Observed by Intramolecular Energy-Transfer and Frequency-Domain Fluorometry—Enhanced Resolution by Global Analysis of Externally Quenched and Nonquenched Samples. J. Phys. Chem. 1991, 95, 9654–9660. [Google Scholar] [CrossRef]
- Jacob, M.; Schindler, T.; Balbach, J.; Schmid, F.X. Diffusion Control in an Elementary Protein Folding Reaction. Proc. Natl. Acad. Sci. USA 1997, 94, 5622–5627. [Google Scholar] [CrossRef] [PubMed]
- Jacob, M.; Geeves, M.; Holtermann, G.; Schmid, F.X. Diffusional Barrier Crossing in a Two-State Protein Folding reaction. Nat. Struct. Biol. 1999, 6, 923–926. [Google Scholar] [PubMed]
- Jacob, M.; Schmid, F.X. Protein folding as a diffusional process. Biochemistry 1999, 38, 13773–13779. [Google Scholar] [CrossRef] [PubMed]
- Zeeb, M.; Jacob, M.H.; Schindler, T.; Balbach, J. 15N Relaxation Study of the Cold Shock Protein CspB at Various Solvent Viscosities. J. Biomol. NMR 2003, 27, 221–234. [Google Scholar] [CrossRef] [PubMed]
- Strickler, S.J.; Berg, R.A. Relationship Between Absorption Intensity and Fluorescence Lifetime of Molecules. J. Chem. Phys. 1962, 37, 814–822. [Google Scholar] [CrossRef]
- Hudgins, R.R.; Huang, F.; Gramlich, G.; Nau, W.M. A Fluorescence-Based Method for Direct Measurement of Submicrosecond Intramolecular Contact Formation in Biopolymers: An Exploratory Study with Polypeptides. J. Am. Chem. Soc. 2002, 124, 556–564. [Google Scholar] [CrossRef] [PubMed]
- Nau, W.M.; Huang, F.; Wang, X.J.; Bakirci, H.; Gramlich, G.; Marquez, C. Exploiting Long-Lived Molecular Fluorescence. Chimia 2003, 57, 161–167. [Google Scholar] [CrossRef]
- Sahoo, H.; Roccatano, D.; Zacharias, M.; Nau, W.M. Distance Distributions of Short Polypeptides Recovered by Fluorescence Resonance Energy Transfer in the 10 A Domain. J. Am. Chem. Soc. 2006, 128, 8118–8119. [Google Scholar] [CrossRef] [PubMed]
- Eftink, M.R.; Jia, Y.; Hu, D.; Ghiron, C.A. Fluorescence Studies with Tryptophan Analogues: Excited State Interactions Involving the Side Chain Amino Group. J. Phys. Chem. 1995, 99, 5713–5723. [Google Scholar] [CrossRef]
- Joshi, S.; Ghosh, I.; Pokhrel, S.; Madler, L.; Nau, W.M. Interactions of Amino Acids and Polypeptides with Metal Oxide Nanoparticles Probed by Fluorescent Indicator Adsorption and Displacement. ACS Nano 2012, 6, 5668–5679. [Google Scholar] [CrossRef] [PubMed]
- Lampert, R.A.; Meech, S.R.; Metcalfe, J.; Phillips, D.; Schaap, A.P. The Refractive Index Correction to the Radiative Rate Constant in Fluorescence Lifetime Measurements. Chem. Phys. Lett. 1983, 94, 137–140. [Google Scholar] [CrossRef]
- Wallace, B.; Atzberger, P.J. Förster Resonance Energy Transfer: Role of Diffusion of Fluorophore Orientation and Separation in Observed Shifts of FRET Efficiency. PLoS ONE 2017, 12, e0177122. [Google Scholar] [CrossRef] [PubMed]
- Haas, E.; Katchalski-Katzir, E.; Steinberg, I.Z. Effect of the Orientation of Donor and Acceptor on the Probability of Energy Transfer Involving Electronic Transitions of Mixed Polarization. Biochemistry 1978, 17, 5064–5070. [Google Scholar] [CrossRef] [PubMed]
- Steinberg, I.Z. Long-Range Nonradiative Transfer of Electronic Excitation Energy in Proteins and Polypeptides. Annu. Rev. Biochem. 1971, 40, 83–114. [Google Scholar] [CrossRef] [PubMed]
- We also tried to expose the peptides to conditions of extremely high viscosity, to achieve frozen conformations, by creating gels on the basis of sucrose and trehalose. Although the results reported herein were qualitatively supported (very low energy transer efficienicy values in gels) we did not succeed in a direct comparison of these glassy-matrix conditions due to several unknown parameters, such as the refractive indices.
- Dutt, G.B.; Doraiswamy, S.; Periasamy, N.; Venkataraman, B. Rotational reorientation dynamics of polar dye molecular probes by picosecond laser spectroscopic technique. J. Chem. Phys. 1990, 93, 8498–8513. [Google Scholar] [CrossRef]
- Bohne, D.; Fischer, S.; Obermeier, E. Thermal Conductivity, Density, Viscosity, and Prandtl-Numbers of Ethylene Glycol-Water Mixtures. Berichte der Bunsengesellschaft für Physikalische Chemie 1984, 88, 739–742. [Google Scholar] [CrossRef]
- Nau, W.M.; Greiner, G.; Rau, H.; Wall, J.; Olivucci, M.; Scaiano, J.C. Fluorescence of 2,3-diazabicyclo[2.2.2]oct-2-ene revisited: Solvent-induced quenching of the n,pi*-excited state by an aborted hydrogen atom transfer. J. Phys. Chem. A 1999, 103, 1579–1584. [Google Scholar] [CrossRef]
- Möglich, A.; Joder, K.; Kiefhaber, T. End-To-End Distance Distributions and Intrachain Diffusion Constants in Unfolded Polypeptide Chains Indicate Intramolecular Hydrogen Bond Formation. Proc. Natl. Acad. Sci. USA 2006, 103, 12394–12399. [Google Scholar] [CrossRef] [PubMed]
- Norouzy, A.; Assaf, K.I.; Zhang, S.; Jacob, M.H.; Nau, W.M. Coulomb Repulsion in Short Polypeptides. J. Phys. Chem. B 2015, 119, 33–43. [Google Scholar] [CrossRef] [PubMed]
- Jacob, M.H.; D’Souza, R.N.; Schwarzlose, T.; Wang, X.; Huang, F.; Haas, E.; Nau, W.M. Method-Unifying View of Loop-Formation Kinetics in Peptide and Protein Folding. J. Phys. Chem. B 2018, 122, 4445–4456. [Google Scholar] [CrossRef] [PubMed]
- Nettels, D.; Gopich, I.V.; Hoffmann, A.; Schuler, B. Ultrafast Dynamics of Protein Collapse from Single-Molecule Photon Statistics. Proc. Natl. Acad. Sci. USA 2007, 104, 2655–2660. [Google Scholar] [CrossRef] [PubMed]
- Nettels, D.; Hoffmann, A.; Schuler, B. Unfolded Protein and Peptide Dynamics Investigated with Single-Molecule FRET and Correlation Spectroscopy from Picoseconds to Seconds. J. Phys. Chem. B 2008, 112, 6137–6146. [Google Scholar] [CrossRef] [PubMed]
- Grupi, A.; Haas, E. Time-Resolved FRET Detection of Subtle Temperature-Induced Conformational Biases in Ensembles of Alpha-Synuclein Molecules. J. Mol. Biol. 2011, 411, 234–247. [Google Scholar] [CrossRef] [PubMed]
- Grupi, A.; Haas, E. Segmental Conformational Disorder and Dynamics in the Intrinsically Disordered Protein Alpha-Synuclein and Its Chain Length Dependence. J. Mol. Biol. 2011, 405, 1267–1283. [Google Scholar] [CrossRef] [PubMed]
- Buscaglia, M.; Lapidus, L.J.; Eaton, W.A.; Hofrichter, J. Effects of Denaturants on the Dynamics of Loop Formation in Polypeptides. Biophys. J. 2006, 91, 276–288. [Google Scholar] [CrossRef] [PubMed]
- Beechem, J.M.; Haas, E. Simultaneous Determination of Intramolecular Distance Distributions and Conformational Dynamics by Global Analysis of Energy Transfer Measurements. Biophys. J. 1989, 55, 1225–1236. [Google Scholar] [CrossRef]
- Ratner, V.; Amir, D.; Kahana, E.; Haas, E. Fast Collapse but Slow Formation of Secondary Structure Elements in the Refolding Transition of E. coli Adenylate Kinase. J. Mol. Biol. 2005, 352, 683–699. [Google Scholar] [CrossRef] [PubMed]
- Orevi, T.; Ben Ishay, E.; Pirchi, M.; Jacob, M.H.; Amir, D.; Haas, E. Early Closure of a Long Loop in the Refolding of Adenylate Kinase: A Possible Key Role of Non-Local Interactions in the Initial Folding Steps. J. Mol. Biol. 2009, 385, 1230–1242. [Google Scholar] [CrossRef] [PubMed]
- Orevi, T.; Ben Ishay, E.; Gershanov, S.L.; Dalak, M.B.; Amir, D.; Haas, E. Fast Closure of N-Terminal Long Loops but Slow Formation of Beta Strands Precedes the Folding Transition State of Escherichia coli Adenylate Kinase. Biochemistry 2014, 53, 3169–3178. [Google Scholar] [CrossRef] [PubMed]
- Lerner, E.; Orevi, T.; Ben Ishay, E.; Amir, D.; Haas, E. Kinetics of Fast Changing Intramolecular Distance Distributions Obtained by Combined Analysis of FRET Efficiency Kinetics and Time-Resolved FRET Equilibrium Measurements. Biophys. J. 2014, 106, 667–676. [Google Scholar] [CrossRef] [PubMed]
- Orevi, T.; Rahamim, G.; Amir, D.; Kathuria, S.; Bilsel, O.; Matthews, C.R.; Haas, E. Sequential Closure of Loop Structures Forms the Folding Nucleus During the Refolding Transition of the Escherichia coli Adenylate Kinase Molecule. Biochemistry 2016, 55, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Duhamel, J.; Yekta, A.; Winnik, M.A.; Jao, T.C.; Mishra, M.K.; Rubin, I.D. A Blob Model to Study Polymer Chain Dynamics in Solution. J. Phys. Chem. 1993, 97, 13708–13712. [Google Scholar] [CrossRef]
- Duhamel, J. Polymer Chain Dynamics in Solution Probed with a Fluorescence Blob Model. Acc. Chem. Res. 2006, 39, 953–960. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Duhamel, J.; Winnik, M.A. Probing End-to-End Cyclization Beyond Willemski and Fixman. J. Phys. Chem. B 2011, 115, 3289–3302. [Google Scholar] [CrossRef] [PubMed]
- Casier, R.; Duhamel, J. Pyrene Excimer Fluorescence as a Direct and Easy Experimental Means to Characterize the Length Scale and Internal Dynamics of Polypeptide Foldons. Macromolecules 2018, 51, 3450–3457. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacob, M.H.; Ghosh, I.; D’Souza, R.N.; Nau, W.M. Two Orders of Magnitude Variation of Diffusion-Enhanced Förster Resonance Energy Transfer in Polypeptide Chains. Polymers 2018, 10, 1079. https://doi.org/10.3390/polym10101079
Jacob MH, Ghosh I, D’Souza RN, Nau WM. Two Orders of Magnitude Variation of Diffusion-Enhanced Förster Resonance Energy Transfer in Polypeptide Chains. Polymers. 2018; 10(10):1079. https://doi.org/10.3390/polym10101079
Chicago/Turabian StyleJacob, Maik H., Indrajit Ghosh, Roy N. D’Souza, and Werner M. Nau. 2018. "Two Orders of Magnitude Variation of Diffusion-Enhanced Förster Resonance Energy Transfer in Polypeptide Chains" Polymers 10, no. 10: 1079. https://doi.org/10.3390/polym10101079
APA StyleJacob, M. H., Ghosh, I., D’Souza, R. N., & Nau, W. M. (2018). Two Orders of Magnitude Variation of Diffusion-Enhanced Förster Resonance Energy Transfer in Polypeptide Chains. Polymers, 10(10), 1079. https://doi.org/10.3390/polym10101079





