Designing High-Refractive Index Polymers Using Materials Informatics †
Abstract
:1. Introduction
2. Materials and Methods
2.1. Polymer Properties
2.2. Machine Learning
2.3. Computational Details
3. Results and Discussion
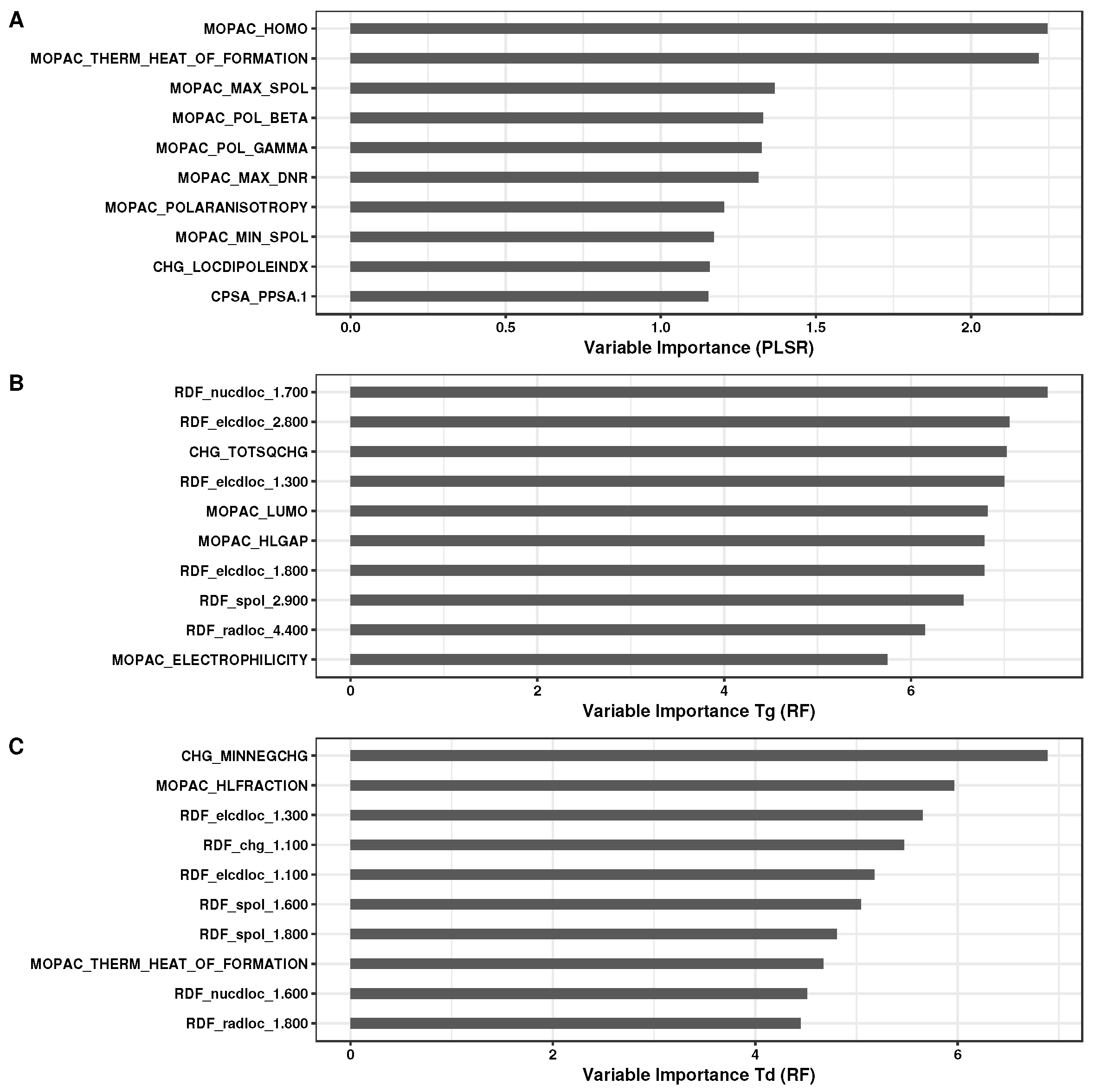
3.1. Analysis of Regression Models
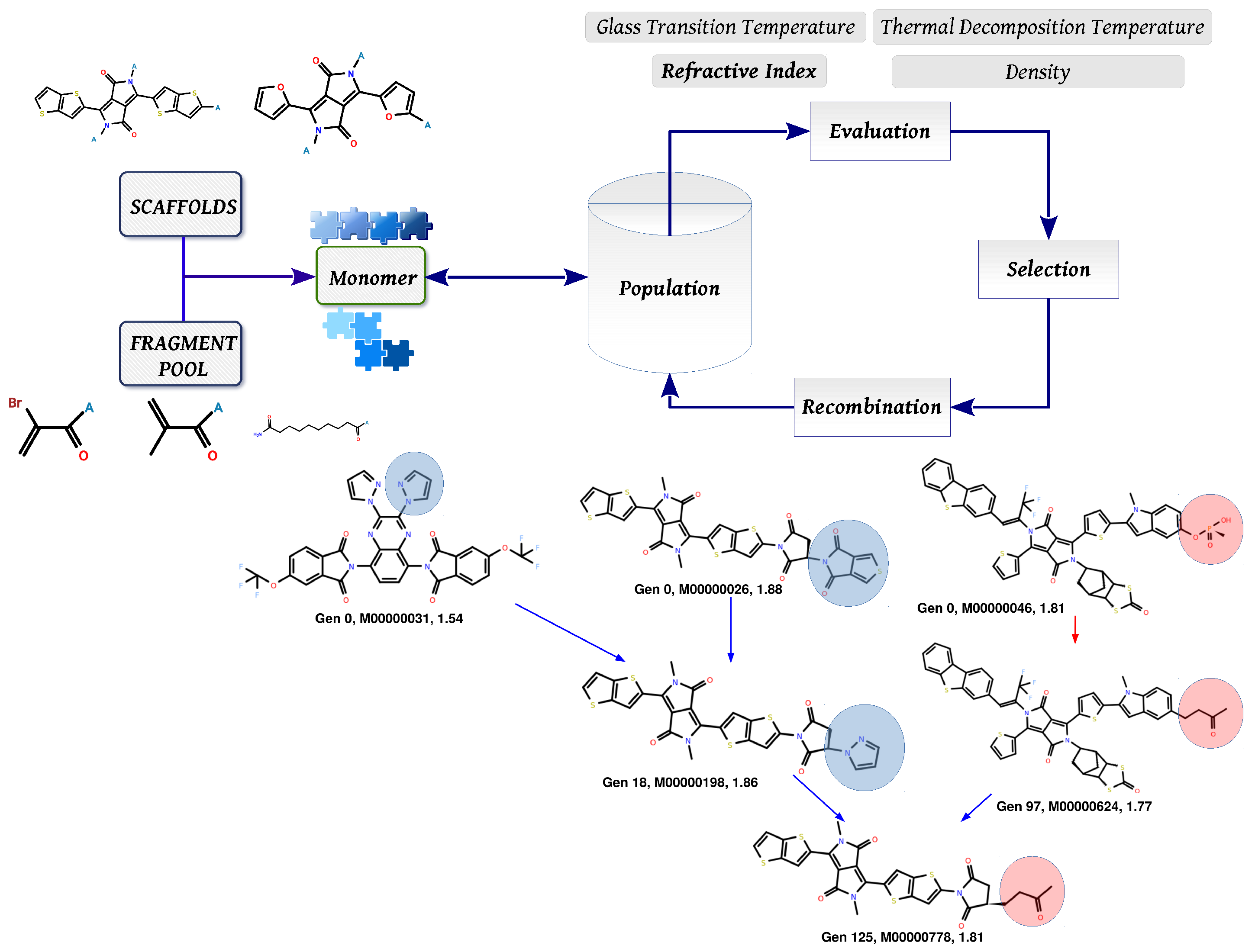
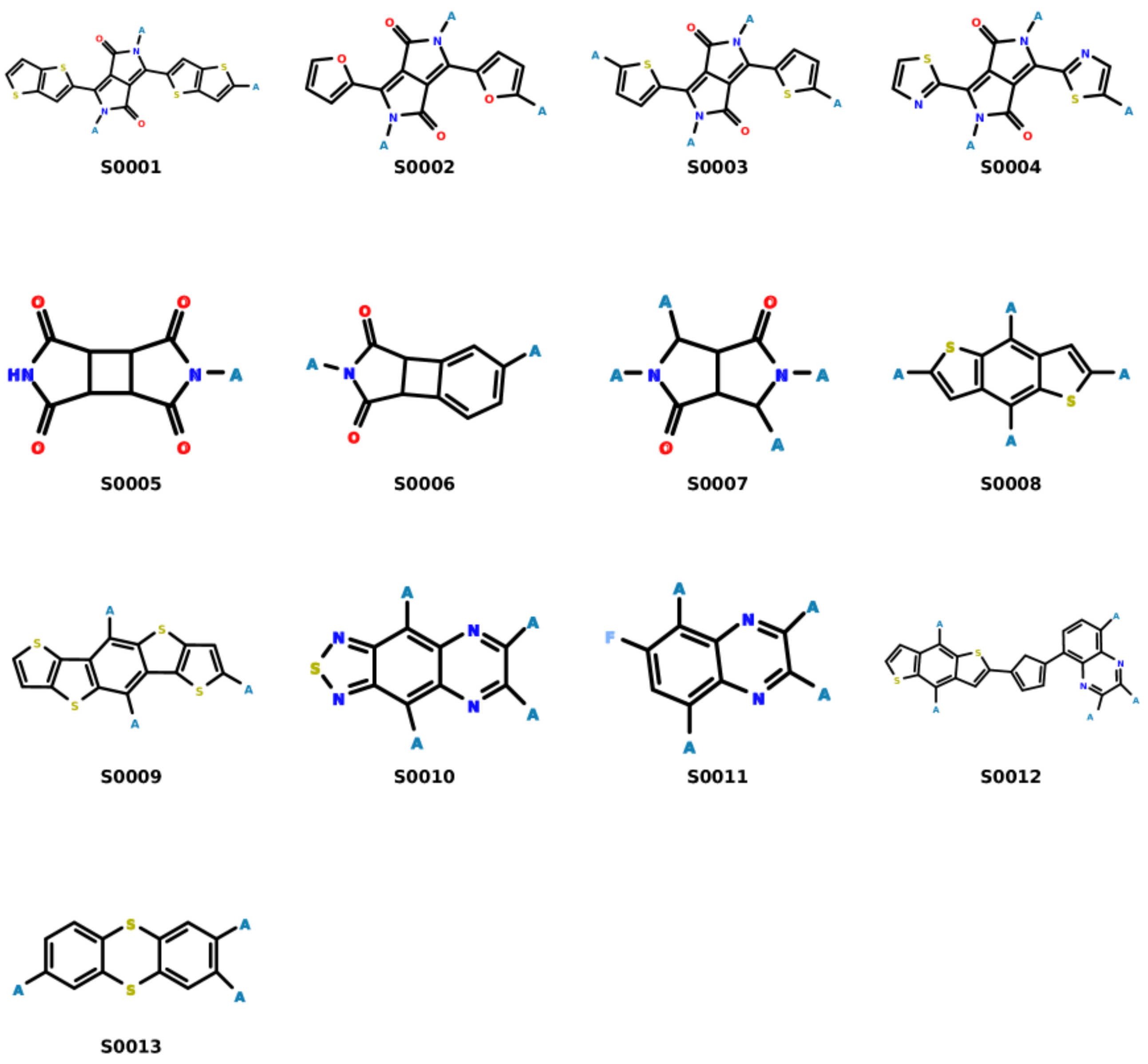
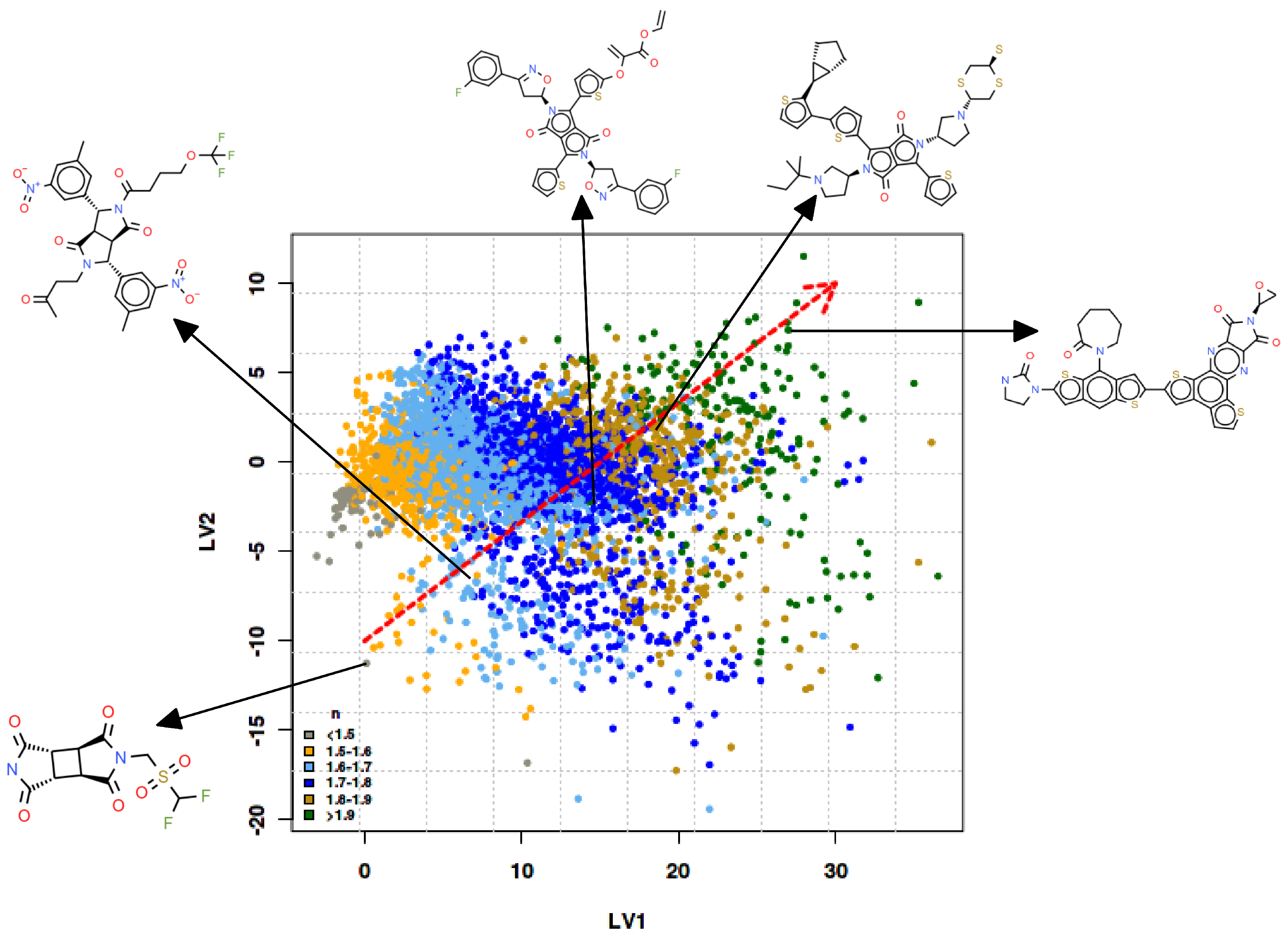
3.2. Molecular Evolution Analysis
3.3. Comparison with DFT
3.4. Analysis of Selected Monomers
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| QC | Quantum Chemistry |
| QSPR | Quantitative Structure Property Relationship |
| ML | Machine Learning |
| DFT | Density Functional Theory |
| TD-DFT | Time-Dependent Density Functional Theory |
References
- Yetisen, A.K.; Montelongo, Y.; Butt, H. Rewritable three-dimensional holographic data storage via optical forces. Appl. Phys. Lett. 2016, 109, 061106. [Google Scholar] [CrossRef]
- Kim, K.C. Effective graded refractive-index anti-reflection coating for high refractive-index polymer ophthalmic lenses. Mater. Lett. 2015, 160, 158–161. [Google Scholar] [CrossRef]
- Li, X.; Yu, X.; Han, Y. Polymer thin films for antireflection coatings. J. Mater. Chem. C 2013, 1, 2266–2285. [Google Scholar] [CrossRef]
- Sanders, D.P. Advances in Patterning Materials for 193 nm Immersion Lithography. Chem. Rev. 2010, 110, 321–360. [Google Scholar] [CrossRef] [PubMed]
- Suwa, M.; Niwa, H.; Tomikawa, M. High Refractive Index Positive Tone Photo-sensitive Coating. J. Photopolym. Sci. Technol. 2006, 19, 275–276. [Google Scholar] [CrossRef]
- Macdonald, E.K.; Shaver, M.P. Intrinsic high refractive index polymers. Polym. Int. 2014, 64, 6–14. [Google Scholar] [CrossRef]
- Higashihara, T.; Ueda, M. Recent Progress in High Refractive Index Polymers. Macromolecules 2015, 48, 1915–1929. [Google Scholar] [CrossRef]
- Suzuki, Y.; Higashihara, T.; Ando, S.; Ueda, M. Synthesis and Characterization of High Refractive Index and High Abbe’s Number Poly(thioether sulfone)s based on Tricyclo[5.2.1.02,6]decane Moiety. Macromolecules 2012, 45, 3402–3408. [Google Scholar] [CrossRef]
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle Polymer Composites: Where Two Small Worlds Meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef] [PubMed]
- Martin, R.L.; Simon, C.M.; Smit, B.; Haranczyk, M. In Silico Design of Porous Polymer Networks: High-Throughput Screening for Methane Storage Materials. J. Am. Chem. Soc. 2014, 136, 5006–5022. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Wang, C.; Lorenzini, R.G.; Ma, R.; Zhu, Q.; Sinkovits, D.W.; Pilania, G.; Oganov, A.R.; Kumar, S.; Sotzing, G.A.; et al. Rational design of all organic polymer dielectrics. Nat. Commun. 2014, 5, 4845. [Google Scholar] [CrossRef] [PubMed]
- Bérubé, N.; Gosselin, V.; Gaudreau, J.; Côté, M. Designing Polymers for Photovoltaic Applications Using ab Initio Calculations. J. Phys. Chem. C 2013, 117, 7964–7972. [Google Scholar] [CrossRef]
- Martin, S. Lattice Enumeration for Inverse Molecular Design Using the Signature Descriptor. J. Chem. Inf. Model. 2012, 52, 1787–1797. [Google Scholar] [CrossRef] [PubMed]
- Le, T.; Epa, V.C.; Burden, F.R.; Winkler, D.A. Quantitative Structure-Property Relationship Modeling of Diverse Materials Properties. Chem. Rev. 2012, 112, 2889–2919. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Foscato, M.; Jensen, V.R.; Alsberg, B.K. Evolutionary de novo design of phenothiazine derivatives for dye-sensitized solar cells. J. Mater. Chem. A 2015, 3, 9851–9860. [Google Scholar] [CrossRef]
- Wang, C.; Pilania, G.; Boggs, S.; Kumar, S.; Breneman, C.; Ramprasad, R. Computational strategies for polymer dielectrics design. Polymer 2014, 55, 979–988. [Google Scholar] [CrossRef]
- Venkatraman, V.; Alsberg, B.K. A quantitative structure–property relationship study of the photovoltaic performance of phenothiazine dyes. Dyes Pigments 2015, 114, 69–77. [Google Scholar] [CrossRef]
- Lameijer, E.W.; Kok, J.N.; Bäck, T.; IJzerman, A.P. The Molecule Evoluator. An Interactive Evolutionary Algorithm for the Design of Drug-Like Molecules. J. Chem. Inf. Model. 2006, 46, 545–552. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Heyndrickx, W.; Occhipinti, G.; Jensen, V.R.; Alsberg, B.K. An Evolutionary Algorithm for de Novo Optimization of Functional Transition Metal Compounds. J. Am. Chem. Soc. 2012, 134, 8885–8895. [Google Scholar] [CrossRef] [PubMed]
- Duchowicz, P.R.; Fioressi, S.E.; Bacelo, D.E.; Saavedra, L.M.; Toropova, A.P.; Toropov, A.A. QSPR studies on refractive indices of structurally heterogeneous polymers. Chemom. Intell. Lab. Syst. 2015, 140, 86–91. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Lobanov, V.S.; Karelson, M. QSPR: The correlation and quantitative prediction of chemical and physical properties from structure. Chem. Soc. Rev. 1995, 24, 279–287. [Google Scholar] [CrossRef]
- Astray, G.; Cid, A.; Moldes, O.; Ferreiro-Lage, J.A.; Gaĺvez, J.F.; Mejuto, J.C. Prediction of Refractive Index of Polymers Using Artificial Neural Networks. J. Chem. Eng. Data 2010, 55, 5388–5393. [Google Scholar] [CrossRef]
- Liu, W.; Cao, C. Artificial neural network prediction of glass transition temperature of polymers. Colloid Polym. Sci. 2009, 287, 811–818. [Google Scholar] [CrossRef]
- Toropova, A.P.; Toropov, A.A.; Kudyshkin, V.O.; Leszczynska, D.; Leszczynski, J. Optimal descriptors as a tool to predict the thermal decomposition of polymers. J. Math. Chem. 2014, 52, 1171–1181. [Google Scholar] [CrossRef]
- Bicerano, J. Prediction of Polymer Properties, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Maekawa, S.; Moorthi, K. Polymer Optical Constants from Long-Range Corrected DFT Calculations. J. Phys. Chem. B 2016, 120, 2507–2516. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Gupta, M.; Foscato, M.; Svendsen, H.F.; Jensen, V.R.; Alsberg, B.K. Computer-aided molecular design of imidazole-based absorbents for CO2 capture. Int. J Greenh. Gas Control. 2016, 49, 55–63. [Google Scholar] [CrossRef]
- Venkatraman, V.; Abburu, S.; Alsberg, B.K. Artificial evolution of coumarin dyes for dye sensitized solar cells. Phys. Chem. Chem. Phys. 2015, 17, 27672–27682. [Google Scholar] [CrossRef] [PubMed]
- Foscato, M.; Occhipinti, G.; Venkatraman, V.; Alsberg, B.K.; Jensen, V.R. Automated Design of Realistic Organometallic Molecules from Fragments. J. Chem. Inf. Model. 2014, 54, 767–780. [Google Scholar] [CrossRef] [PubMed]
- Foscato, M.; Venkatraman, V.; Occhipinti, G.; Alsberg, B.K.; Jensen, V.R. Automated Building of Organometallic Complexes from 3D Fragments. J. Chem. Inf. Model. 2014, 54, 1919–1931. [Google Scholar] [CrossRef] [PubMed]
- Degen, J.; Wegscheid-Gerlach, C.; Zaliani, A.; Rarey, M. On the Art of Compiling and Using ‘Drug-Like’ Chemical Fragment Spaces. Chem. Med. Chem. 2008, 3, 1503–1507. [Google Scholar] [CrossRef] [PubMed]
- Lorentz, H.A. Ueber die Beziehung zwischen der Fortpflanzungsgeschwindigkeit des Lichtes und der Körperdichte. Ann. Phys. Chem. 1880, 245, 641–665. [Google Scholar] [CrossRef]
- Lorenz, L. Ueber die Refractionsconstante. Ann. Phys. Chem. 1880, 247, 70–103. [Google Scholar] [CrossRef]
- Terui, Y.; Ando, S. Coefficients of molecular packing and intrinsic birefringence of aromatic polyimides estimated using refractive indices and molecular polarizabilities. J. Polym. Sci. Polym. Phys. 2004, 42, 2354–2366. [Google Scholar] [CrossRef]
- Nakabayashi, K.; Imai, T.; Fu, M.C.; Ando, S.; Higashihara, T.; Ueda, M. Poly(phenylene thioether)s with Fluorene-Based Cardo Structure toward High Transparency, High Refractive Index, and Low Birefringence. Macromolecules 2016, 49, 5849–5856. [Google Scholar] [CrossRef]
- Xiao, X.; Qiu, X.; Kong, D.; Zhang, W.; Liu, Y.; Leng, J. Optically transparent high temperature shape memory polymers. Soft Matter 2016, 12, 2894–2900. [Google Scholar] [CrossRef] [PubMed]
- Mark, J.E. The Polymer Data Handbook, 2nd ed.; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Otsuka, S.; Kuwajima, I.; Hosoya, J.; Xu, Y.; Yamazaki, M. PoLyInfo: Polymer Database for Polymeric Materials Design. In Proceedings of the 2011 International Conference on Emerging Intelligent Data and Web Technologies, Institute of Electrical and Electronics Engineers, Tirana, Albania, 7–9 September 2011. [Google Scholar]
- Katritzky, A.R.; Sild, S.; Karelson, M. Correlation and Prediction of the Refractive Indices of Polymers by QSPR. J. Chem. Inf. Model. 1998, 38, 1171–1176. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Sild, S.; Lobanov, V.; Karelson, M. Quantitative Structure-Property Relationship (QSPR) Correlation of Glass Transition Temperatures of High Molecular Weight Polymers. J. Chem. Inf. Model. 1998, 38, 300–304. [Google Scholar] [CrossRef]
- Yu, X.; Yi, B.; Wang, X. Prediction of refractive index of vinyl polymers by using density functional theory. J. Comput. Chem. 2007, 28, 2336–2341. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Alsberg, B.K. KRAKENX: Software for the generation of alignment-independent 3D descriptors. J. Mol. Model. 2016, 22, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Åstrand, P.O.; Alsberg, B.K. Quantitative structure–property relationship modeling of Grätzel solar cell dyes. J. Comput. Chem. 2013, 35, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Alsberg, B.K. Quantitative structure–property relationship modelling of thermal decomposition temperatures of ionic liquids. J. Mol. Liq. 2016, 223, 60–67. [Google Scholar] [CrossRef]
- Abdi, H. Partial least squares regression and projection on latent structure regression (PLS Regression). Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 97–106. [Google Scholar] [CrossRef]
- Ziegler, A.; König, I.R. Mining data with random forests: Current options for real-world applications. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2013, 4, 55–63. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Meinshausen, N. quantregForest: Quantile Regression Forests, R package version 1.3-5. 2016.
- ChemAxon Marvin 5.9.3. 2012. Available online: http://www.chemaxon.com/products/marvin/marvinsketch (accessed on 22 January 2018).
- O’Boyle, N.M.; Banck, M.; James, C.A.; Morley, C.; Vandermeersch, T.; Hutchison, G.R. Open Babel: An open chemical toolbox. J. Chem. 2011, 3, 33. [Google Scholar] [CrossRef] [PubMed]
- Rappe, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Stewart, J.J.P. MOPAC2016; Stewart Computational Chemistry: Colorado Springs, CO, USA, 2016; Available online: http://OpenMOPAC.net (accessed on 22 January 2018).
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Yanai, T.; Tew, D.P.; Handy, N.C. A new hybrid exchange-correlation functional using the Coulomb-attenuating method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Reish, M.E.; Nam, S.; Lee, W.; Woo, H.Y.; Gordon, K.C. A Spectroscopic and DFT Study of the Electronic Properties of Carbazole-Based D-A Type Copolymers. J. Phys. Chem. C 2012, 116, 21255–21266. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09 Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing; R Core Team: Vienna, Austria, 2016. [Google Scholar]
- Mevik, B.H.; Wehrens, R. The pls Package: Principal Component and Partial Least Squares Regression in R. J. Stat. Softw. 2007, 18, 1–24. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Chong, I.G.; Jun, C.H. Performance of some variable selection methods when multicollinearity is present. Chemom. Intell. Lab. Syst. 2005, 78, 103–112. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Jang, S.H.; Jen, A.Y. Structured Organic Non-Linear Optics. In Comprehensive Nanoscience and Technology; Elsevier: Amsterdam, The Netherlands, 2011; pp. 143–187. [Google Scholar]
- Vleeschouwer, F.D.; Speybroeck, V.V.; Waroquier, M.; Geerlings, P.; Proft, F.D. Electrophilicity and Nucleophilicity Index for Radicals. Org. Lett. 2007, 9, 2721–2724. [Google Scholar] [CrossRef] [PubMed]
- Groh, W.; Zimmermann, A. What is the lowest refractive index of an organic polymer? Macromolecules 1991, 24, 6660–6663. [Google Scholar] [CrossRef]
- Javadi, A.; Shockravi, A.; Koohgard, M.; Malek, A.; Shourkaei, F.A.; Ando, S. Nitro-substituted polyamides: A new class of transparent and highly refractive materials. Eur. Polym. J. 2015, 66, 328–341. [Google Scholar] [CrossRef]
- Liu, J.; Ueda, M. High refractive index polymers: fundamental research and practical applications. J. Mater. Chem. 2009, 19, 8907–8919. [Google Scholar] [CrossRef]
- Ertl, P.; Schuffenhauer, A. Estimation of synthetic accessibility score of drug-like molecules based on molecular complexity and fragment contributions. J. Chem. 2009, 1, 8. [Google Scholar] [CrossRef] [PubMed]
- Ertl, P.; Schuffenhauer, A. SA_Score. Available online: https://github.com/rdkit/rdkit/tree/master/Contrib/SA_Score (accessed on 01 March 2017).
- Miller-Chou, B.A.; Koenig, J.L. A review of polymer dissolution. Prog. Polym. Sci. 2003, 28, 1223–1270. [Google Scholar] [CrossRef]
- Viera, A.; Garrett, J. Understanding interobserver agreement: The kappa statistic. Fam. Med. 2005, 37, 360–363. [Google Scholar]
- You, N.H.; Higashihara, T.; Yasuo, S.; Ando, S.; Ueda, M. Synthesis of sulfur-containing poly(thioester)s with high refractive indices and high Abbe numbers. Polym. Chem. 2010, 1, 480–484. [Google Scholar] [CrossRef]
- Zhang, G.; Ren, H.H.; Li, D.S.; Long, S.R.; Yang, J. Synthesis of highly refractive and transparent poly(arylene sulfide sulfone) based on 4,6-dichloropyrimidine and 3,6-dichloropyridazine. Polymer 2013, 54, 601–606. [Google Scholar] [CrossRef]
- Song, Y.; Wang, J.; Li, G.; Sun, Q.; Jian, X.; Teng, J.; Zhang, H. Synthesis, characterization and optical properties of fluorinated poly(aryl ether)s containing phthalazinone moieties. Polymer 2008, 49, 4995–5001. [Google Scholar] [CrossRef]
- Tagaya, A.; Koike, Y. Compensation and control of the birefringence of polymers for photonics. Polym. J 2012, 44, 306–314. [Google Scholar] [CrossRef]
- Rosipal, R. Kernel Partial Least Squares for Nonlinear Regression and Discrimination. Neural Netw. World 2003, 13, 291–300. [Google Scholar]
- Levatić, J.; Ceci, M.; Kocev, D.; Džeroski, S. Semi-supervised Learning for Multi-target Regression. In New Frontiers in Mining Complex Patterns: Third International Workshop, NFMCP 2014, Held in Conjunction with ECML-PKDD 2014, Nancy, France, 19 September 2014, Revised Selected Papers; Appice, A., Ceci, M., Loglisci, C., Manco, G., Masciari, E., Ras, Z.W., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 3–18. [Google Scholar]
- Smith, J.S.; Isayev, O.; Roitberg, A.E. ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192–3203. [Google Scholar] [CrossRef] [PubMed]
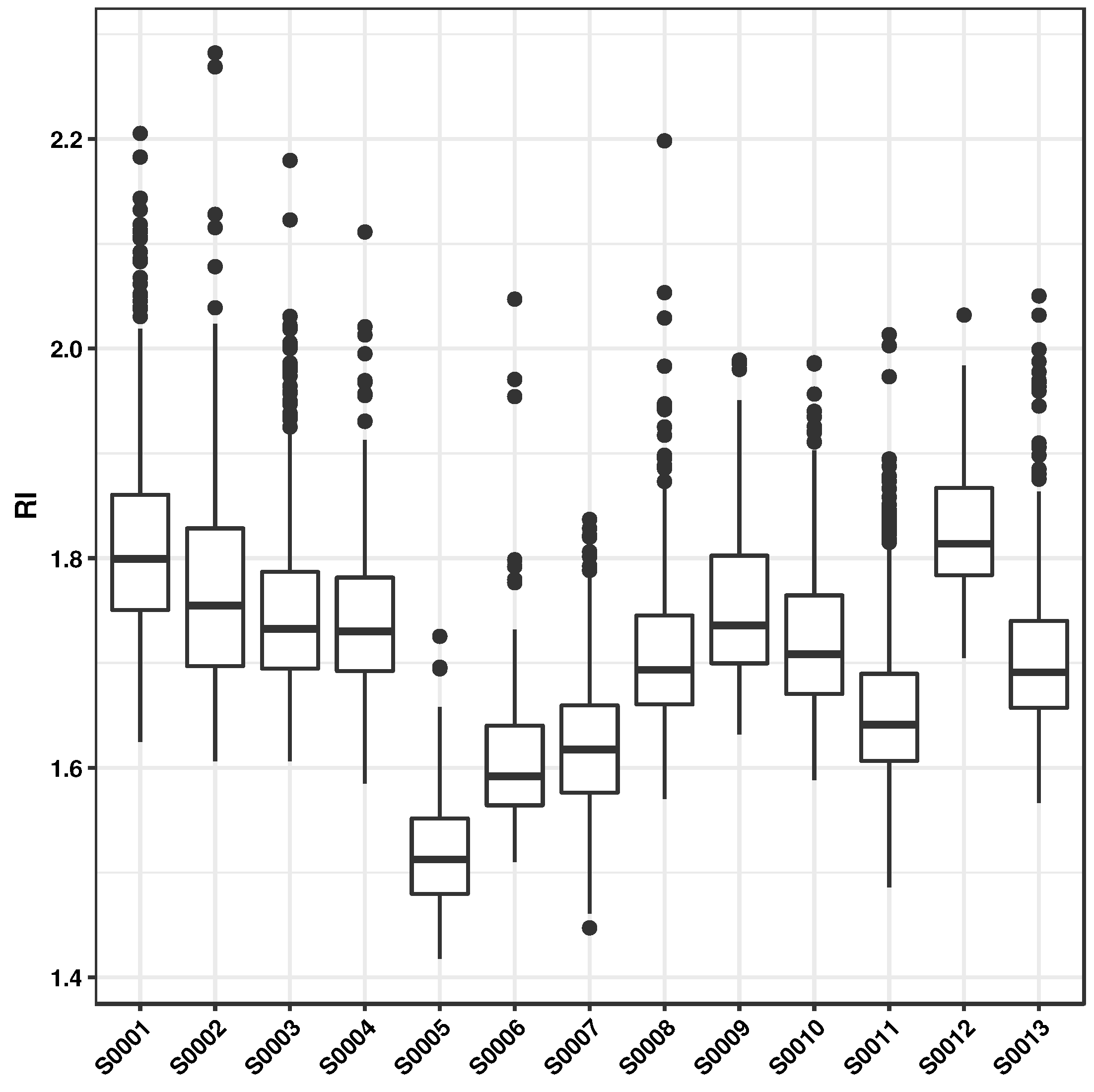
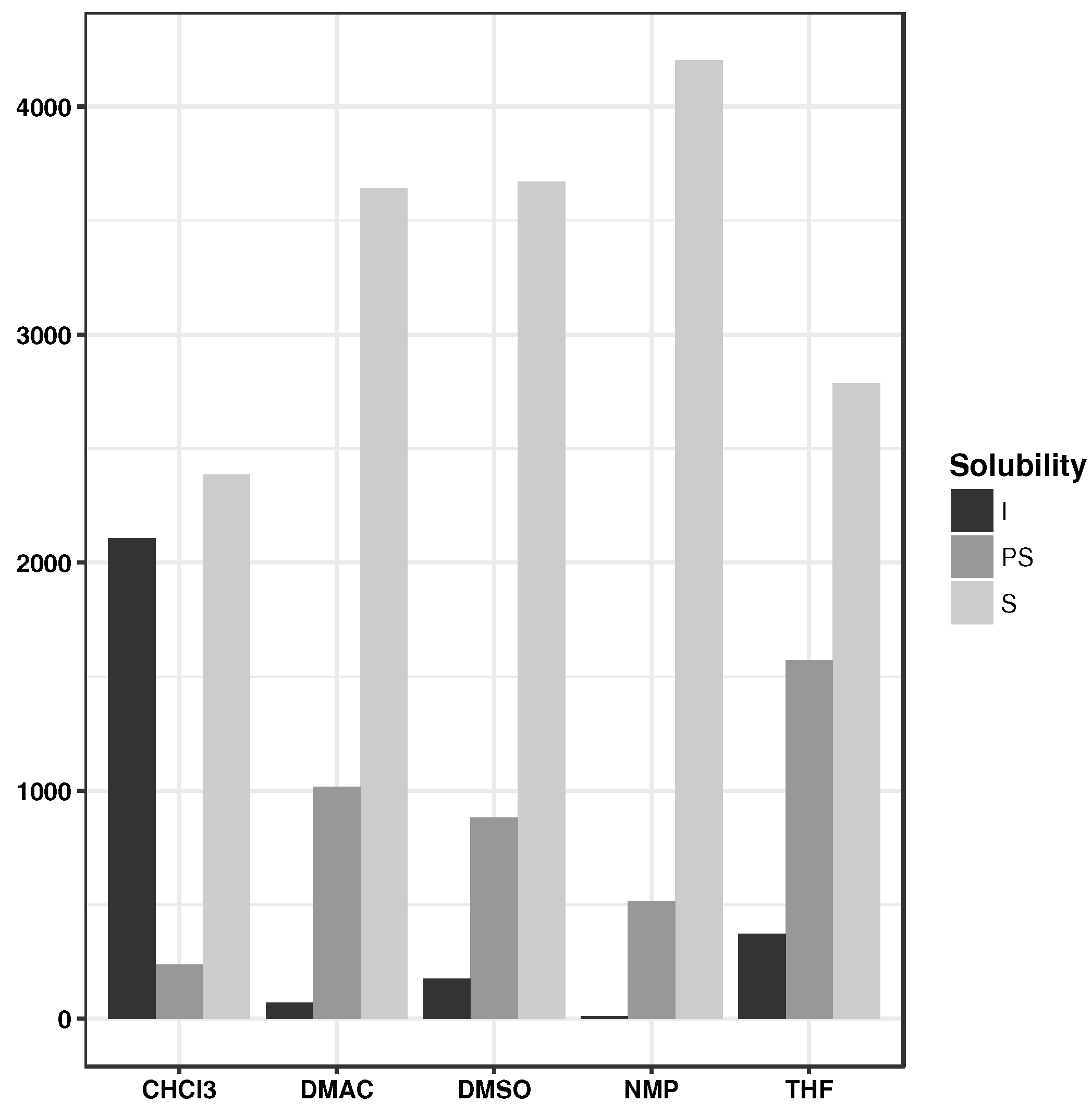
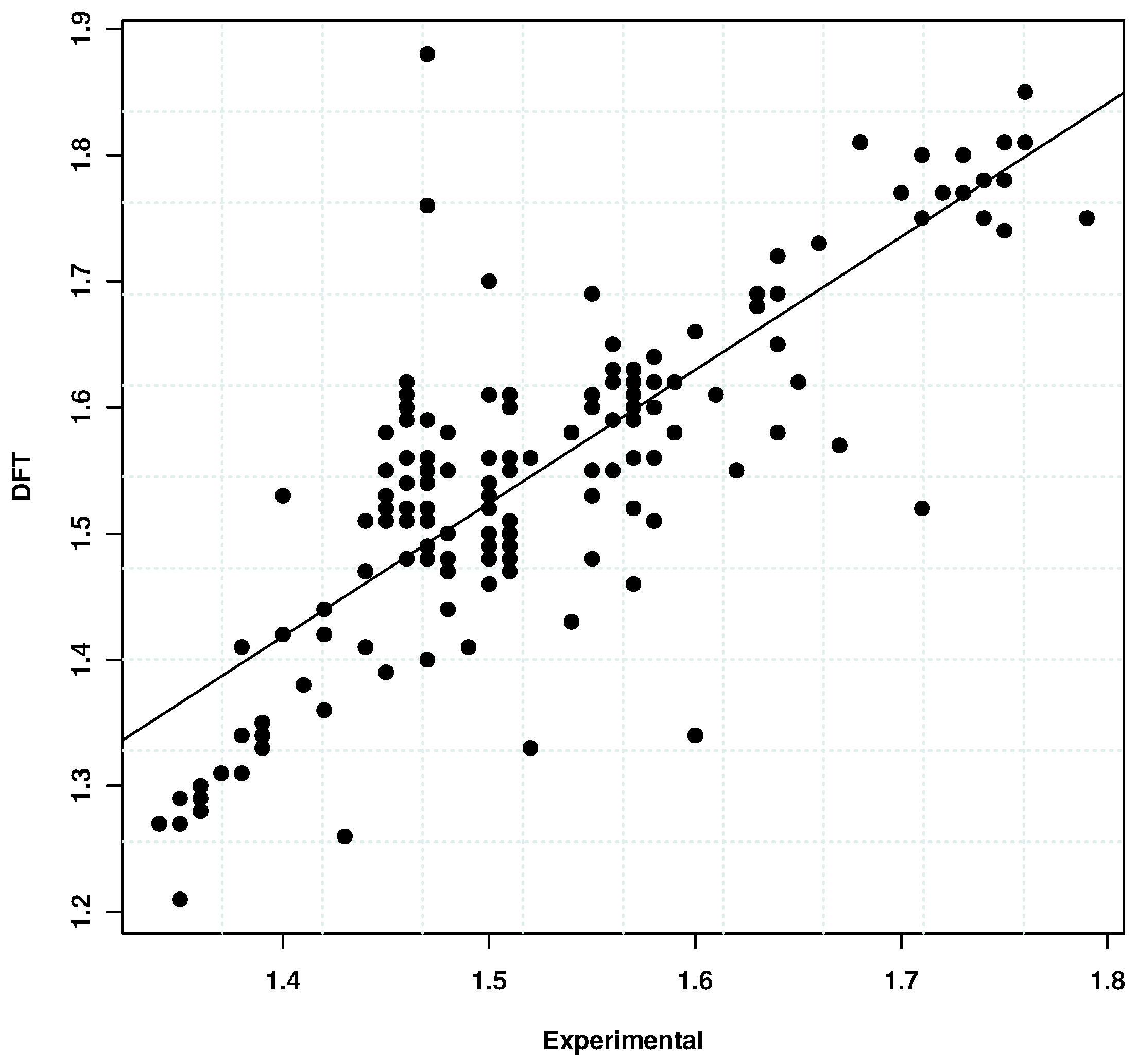
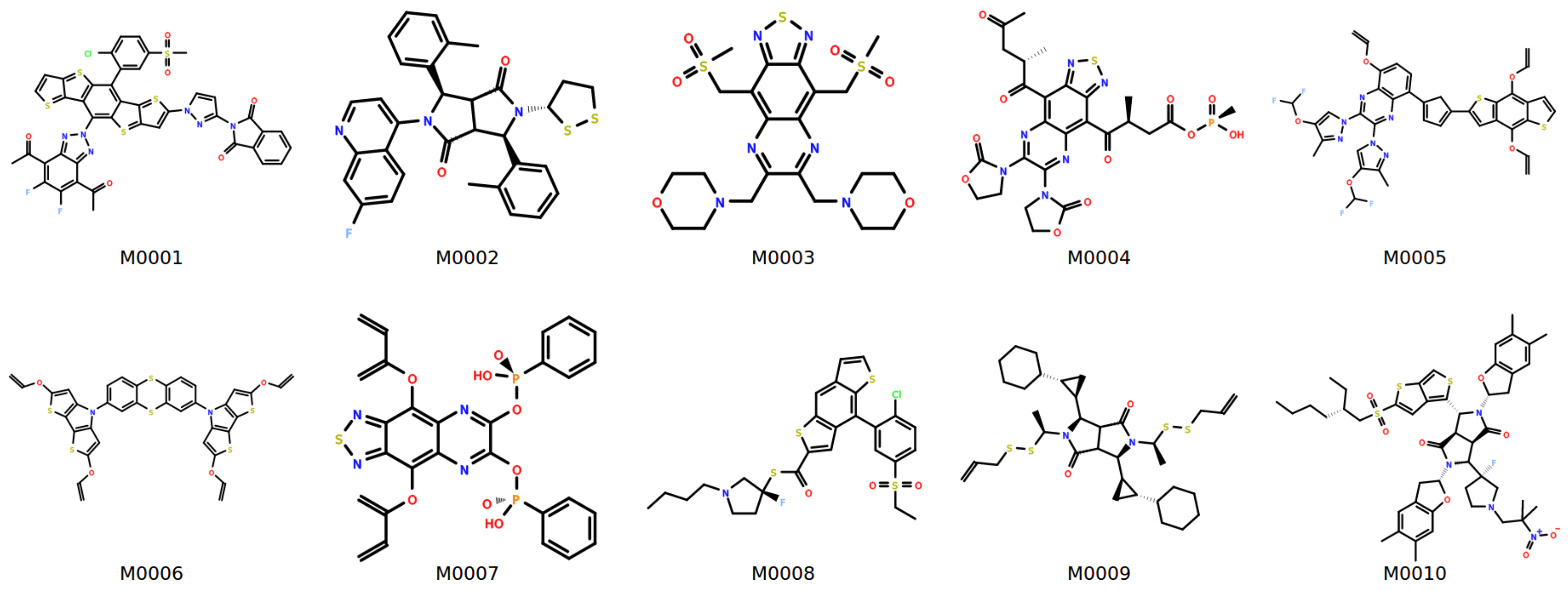
| Property | Range | |||
|---|---|---|---|---|
| n | 237 | 1.34–1.71 | 120 | 117 |
| 195 | 0.84–2.1 | 99 | 96 | |
| (C) | 601 | −143–399 | 304 | 297 |
| (C) | 175 | 125–563 | 90 | 85 |
| Model | Property | Calibration | Testing | ||
|---|---|---|---|---|---|
| PLSR | n | 0.79 | 0.04 (0.03) | 0.79 | 0.04 (0.03) |
| (C) | 0.81 | 52 (34) | 0.83 | 49 (38) | |
| (C) | 0.61 | 49 (24) | 0.62 | 51 (41) | |
| RF | n | 0.83 | 0.03 (0.01) | 0.88 | 0.03 (0.02) |
| (C) | 0.86 | 44 (14) | 0.88 | 40 (30) | |
| (C) | 0.80 | 35 (12) | 0.72 | 45 (30) | |
| 0.64 | 0.13 (0.04) | 0.66 | 0.14 (0.08) | ||
| Solvent | #Samples | I | PS | S | ||
|---|---|---|---|---|---|---|
| CHCl | 136 | 53 | 34 | 48 | 0.56 | 0.50 |
| NMP | 145 | 10 | 42 | 93 | 0.62 | 0.36 |
| DMAc | 105 | 8 | 41 | 56 | 0.52 | 0.48 |
| DMSO | 154 | 19 | 56 | 79 | 0.53 | 0.58 |
| THF | 120 | 15 | 59 | 46 | 0.49 | 0.62 |
| Structure | MW | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| M0001 | 927 | 1.98 ± 0.11 | 256 ± 27 | 438 ± 65 | 1.35 ± 0.23 | 1.79 | 7.79 | 0.09 | 367 |
| M0002 | 570 | 1.75 ± 0.05 | 226 ± 62 | 456 ± 56 | 1.37 ± 0.32 | 1.72 | 22.85 | 0.07 | 356 |
| M0003 | 571 | 1.74 ± 0.15 | 210 ± 51 | 398 ± 84 | 1.29 ± 0.16 | 1.67 | 5.85 | 0.09 | 420 |
| M0004 | 663 | 1.79 ± 0.10 | 242 ± 50 | 408 ± 65 | 1.36 ± 0.31 | 1.65 | 7.45 | 0.38 | 411 |
| M0005 | 801 | 1.80 ± 0.04 | 222 ± 47 | 466 ± 50 | 1.36 ± 0.22 | 1.98 | 1.98 | 0.05 | 429 |
| M0006 | 716 | 1.84 ± 0.06 | 206 ± 41 | 396 ± 74 | 1.27 ± 0.16 | 1.80 | 10.88 | −0.12 | 299 |
| M0007 | 637 | 1.78 ± 0.14 | 223 ± 42 | 439 ± 81 | 1.37 ± 0.25 | 1.76 | 3.49 | −0.05 | 455 |
| M0008 | 596 | 1.78 ± 0.09 | 180 ± 64 | 370 ± 87 | 1.33 ± 0.32 | 1.70 | 13.13 | −0.03 | 347 |
| M0009 | 649 | 1.72 ± 0.04 | 198 ± 85 | 387 ± 79 | 1.63 ± 0.44 | 1.90 | 33.36 | 0.03 | 257 |
| M0010 | 935 | 1.77 ± 0.11 | 226 ± 38 | 428 ± 60 | 1.44 ± 0.35 | 1.73 | 24.80 | −0.13 | 305 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Venkatraman, V.; Alsberg, B.K. Designing High-Refractive Index Polymers Using Materials Informatics. Polymers 2018, 10, 103. https://doi.org/10.3390/polym10010103
Venkatraman V, Alsberg BK. Designing High-Refractive Index Polymers Using Materials Informatics. Polymers. 2018; 10(1):103. https://doi.org/10.3390/polym10010103
Chicago/Turabian StyleVenkatraman, Vishwesh, and Bjørn Kåre Alsberg. 2018. "Designing High-Refractive Index Polymers Using Materials Informatics" Polymers 10, no. 1: 103. https://doi.org/10.3390/polym10010103
APA StyleVenkatraman, V., & Alsberg, B. K. (2018). Designing High-Refractive Index Polymers Using Materials Informatics. Polymers, 10(1), 103. https://doi.org/10.3390/polym10010103






