Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics
Abstract
1. Introduction
2. Methods
Gibbs Free Energy Calculation
3. Results and Discussion
3.1. Crystal Structure Comparison between Forms I and II
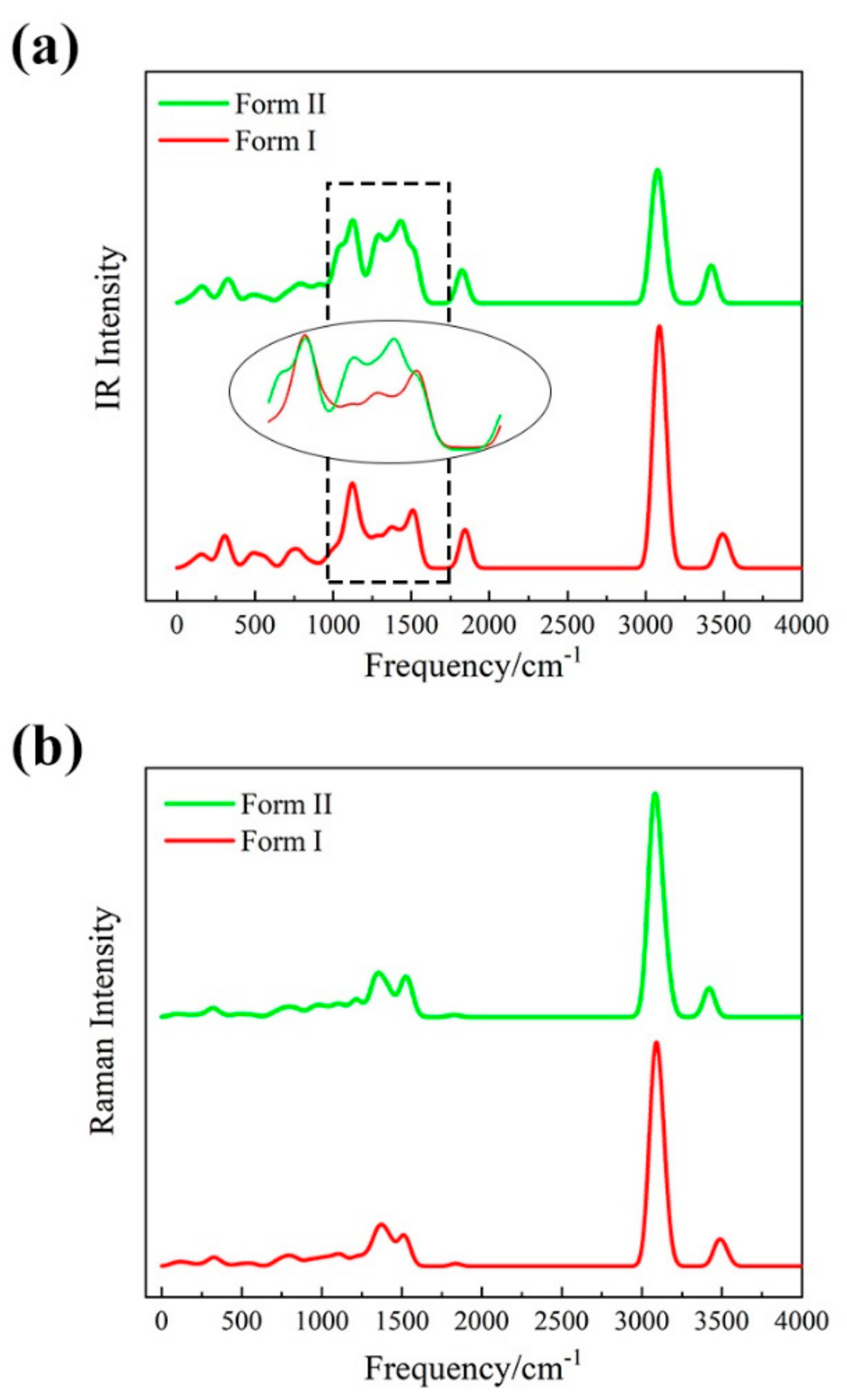
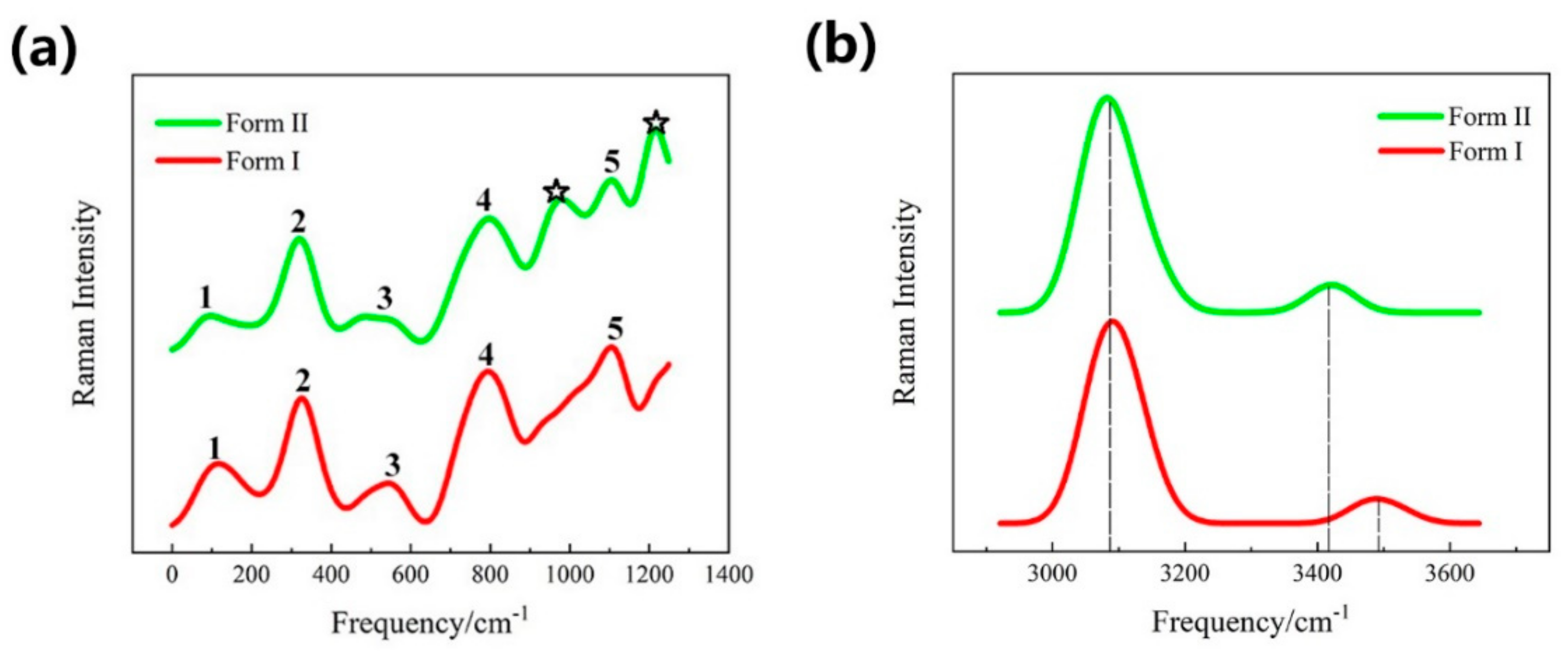
3.2. Vibrational Spectra
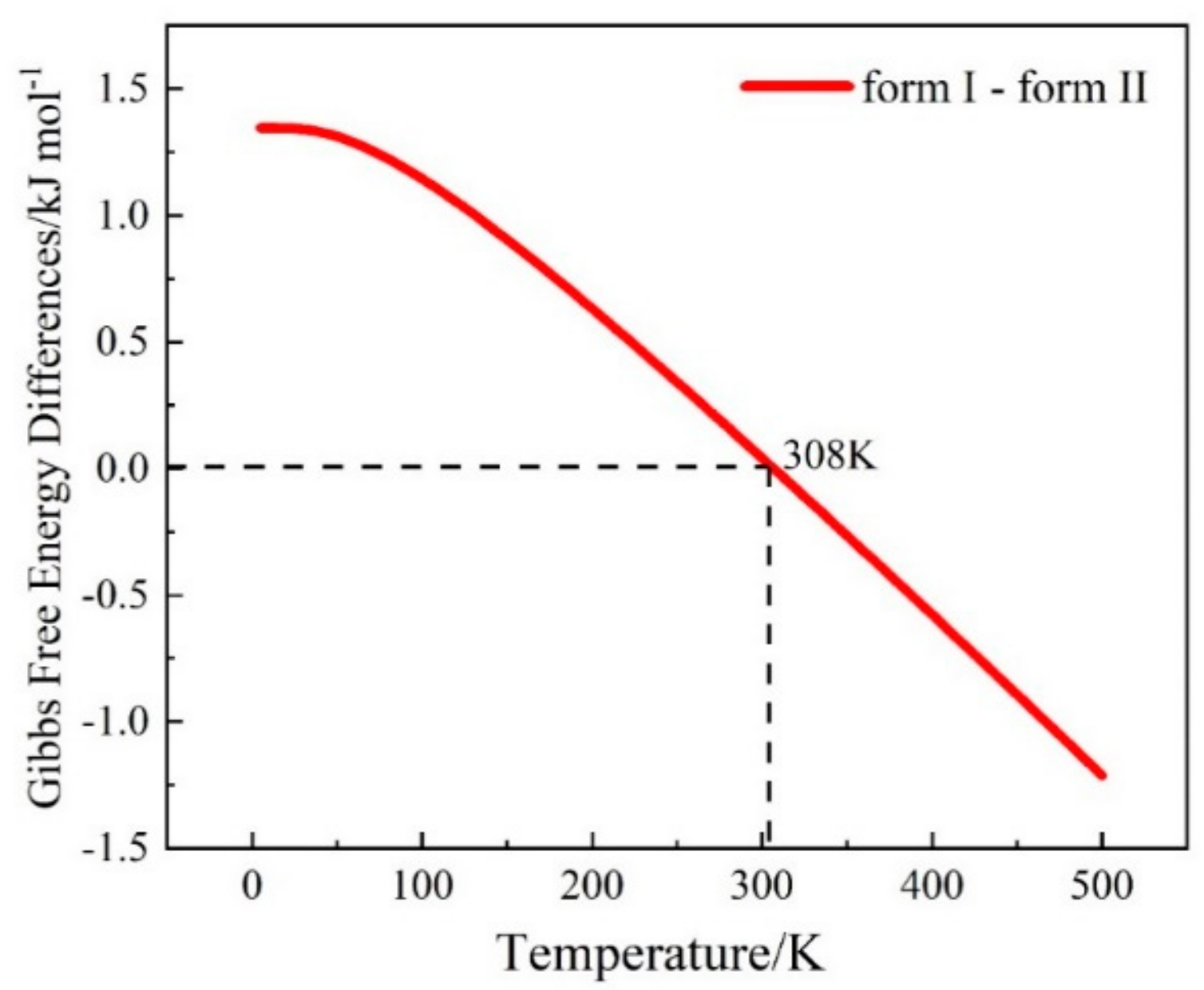
3.3. The Calculation of Gibbs Free Energy Difference
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ryan, K.; Lengyel, J.; Shatruk, M. Crystal structure prediction via deep learning. J. Am. Chem. Soc. 2018, 140, 10158–10168. [Google Scholar] [CrossRef] [PubMed]
- Neumann, M.A.; van de Streek, J.; Fabbiani, F.P.A.; Hidber, P.; Grassmann, O. Combined crystal structure prediction and high-pressure crystallization in rational pharmaceutical polymorph screening. Nat. Commun. 2015, 6, 7793. [Google Scholar] [CrossRef] [PubMed]
- Woodley, S.M.; Catlow, R. Crystal structure prediction from first principles. Nat. Mater. 2008, 7, 937–946. [Google Scholar] [CrossRef] [PubMed]
- Price, S.L. The computational prediction of pharmaceutical crystal structures and polymorphism. Adv. Drug Deliv. Rev. 2004, 56, 301–319. [Google Scholar] [CrossRef] [PubMed]
- Braga, D.; Grepioni, F.; Maini, L. The growing world of crystal forms. Chem. Commun. 2010, 46, 6232–6242. [Google Scholar] [CrossRef]
- Verwer, P.; Leusen, F.J.J. Computer simulation to predict possible crystal polymorphs. Rev. Comput. Chem. 1998, 12, 327–365. [Google Scholar]
- Luo, H.Y.; Hao, X.; Gong, Y.Q.; Zhou, J.H.; He, X.; Li, J.J. Rational crystal polymorph design of olanzapine. Cryst. Growth Des. 2019, 19, 2388–2395. [Google Scholar] [CrossRef]
- Fábián, L.; Kálmán, A. Volumetric measure of isostructurality. Acta. Cryst. 2010, B55, 1099–1108. [Google Scholar] [CrossRef]
- László, F.; Alajos, K. Isostructurality in one and two dimensions: Isostructurality of polymorphs. Acta. Cryst. 2004, B60, 547–558. [Google Scholar]
- Elander, R.P. Industrial production of β-lactam antibiotics. Appl. Microbiol. Biotechnol. 2003, 61, 385–392. [Google Scholar] [CrossRef]
- Fábián, L.; Kalman, A.; Argay, G.; Bernath, G.; Gyarmati, Z.C. Two polymorphs of a beta-lactam (trans-13-azabicyclo[10.2.0]tetradecan-14-one). Concomitant crystal polymorphism and isostructurality. Chem. Commun. 2004, 18, 2114–2115. [Google Scholar] [CrossRef] [PubMed]
- Jeng-Da, C.; Martin, H.G. Long-Range corrected hybrid density functionals with damped atom-atom dispersion corrections. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar]
- Maddox, J. Crystals from first principles. Nature 1988, 335, 201. [Google Scholar] [CrossRef]
- He, X.; Zhu, T.; Wei, X.W.; Liu, J.F.; Zhang, J.Z.H. Fragment quantum mechanical calculation of proteins and its applications. Acc. Chem. Res. 2014, 47, 2748. [Google Scholar] [CrossRef]
- Liu, J.F.; He, X. Accurate prediction of energetic properties of ionic liquid clusters using a fragment-based quantum mechanical method. Chem. Phys. 2017, 19, 20657–20666. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.F.; He, X.; Zhang, J.Z.H. Structure of liquid water—A dynamical mixture of tetrahedral and ‘ring-and-chain’ like structures. Chem. Phys. 2017, 19, 11931–11936. [Google Scholar]
- Li, J.J.; Sode, O.; Voth, G.A.; Hirata, S. A solid-solid phase transition in carbon dioxide at high pressures and intermediate temperatures. Nat. Commun. 2013, 4, 141–155. [Google Scholar] [CrossRef]
- Liu, J.F.; He, X.; Zhang, J.Z.H.; Qi, L.W. Hydrogen-bond structure dynamics in bulk water: Insights from ab initio simulations with coupled cluster theory. Chem. Sci. 2017, 9, 2065–2073. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.F.; Qi, L.W.; Zhang, J.Z.H.; He, X. Fragment quantum mechanical method for large-sized ion-water clusters. J. Chem. Theory Comput. 2017, 13, 2021–2034. [Google Scholar] [CrossRef]
- He, X.; Sode, O.; Xantheas, S.S.; Hirata, S. Second-order many-body perturbation study of ice Ih. J. Chem. Phys. 2012, 137, 15864–18468. [Google Scholar] [CrossRef]
- Hirata, S.; Gilliard, K.; He, X.; Li, J.J.; Sode, O. Ab initio molecular crystal structures, spectra, and phase diagrams. Acc. Chem. Res. 2014, 47, 2721–2730. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.Y.; Tilbury, C.J.; Reutzel-Edens, S.M.; Bhardwaj, R.M.; Li, J.J.; Doherty, M.F. Modeling olanzapine solution growth morphologies. Cryst. Growth Des. 2018, 18, 905–911. [Google Scholar] [CrossRef]
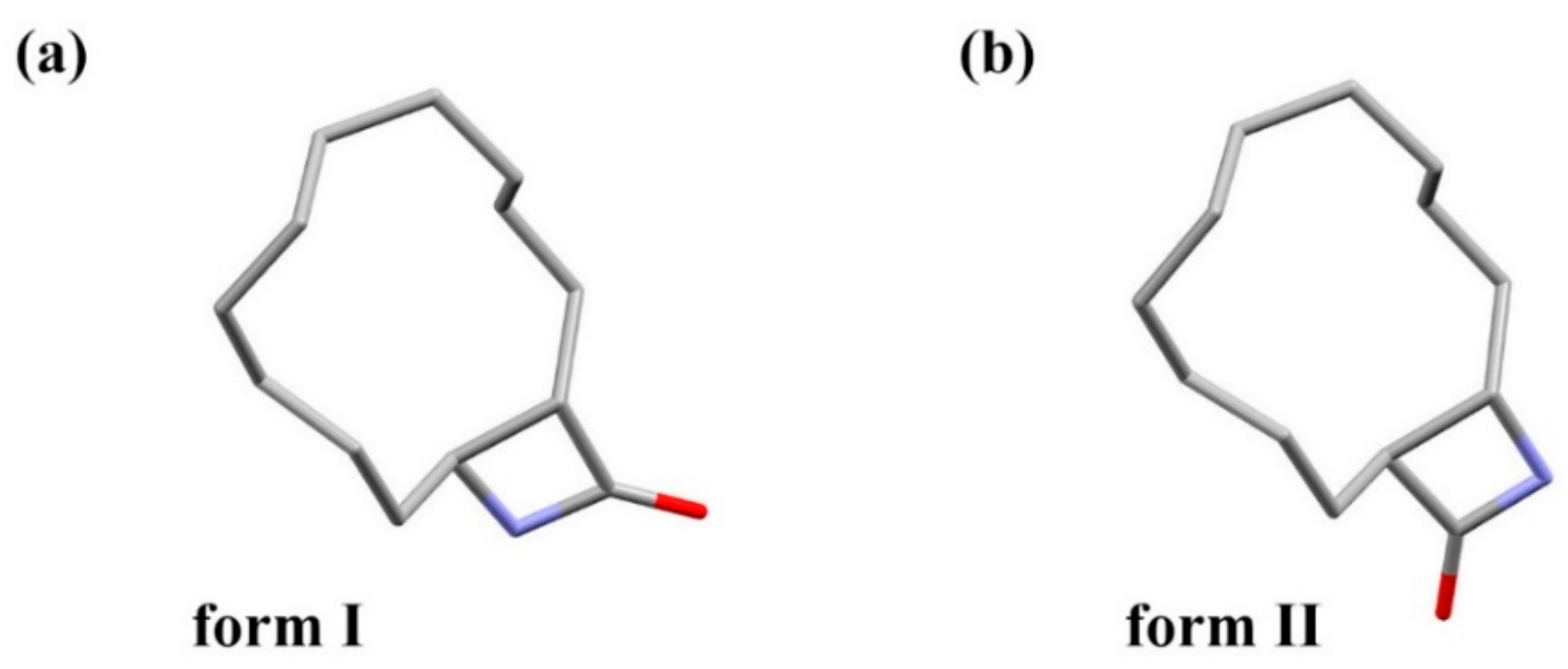
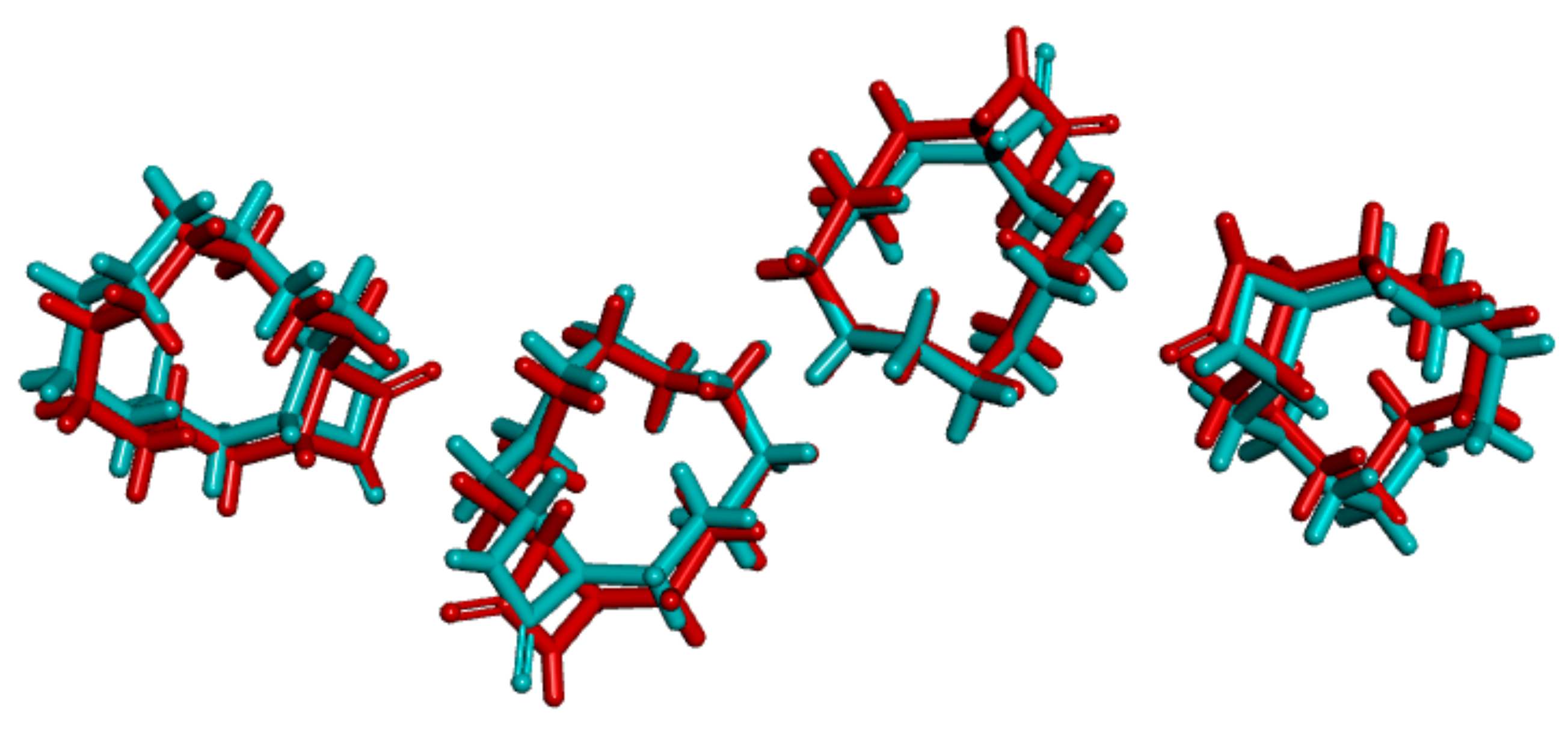
| Formula | Space Group | a (Å) | b (Å) | c (Å) | α (deg) | β (deg) | γ (deg) | V (Å3) | Z | |
|---|---|---|---|---|---|---|---|---|---|---|
| Form I | C13H23NO | P21/c | 5.858 | 7.629 | 28.237 | 90 | 97.97 | 90 | 1249.7 | 4 |
| Form II | C13H23NO | P21/c | 5.962 | 7.267 | 28.689 | 90 | 94.90 | 90 | 1238.4 | 4 |
| Parameters | Expt. Form I | DFT Form I | Expt. Form II | DFT Form II |
|---|---|---|---|---|
| a/Å | 5.858 | 5.645 | 5.962 | 5.781 |
| b/Å | 7.629 | 7.451 | 7.267 | 7.327 |
| c/Å | 28.237 | 28.519 | 28.689 | 28.402 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Liu, J.; He, X.; Li, J. Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics. Crystals 2019, 9, 460. https://doi.org/10.3390/cryst9090460
Luo H, Liu J, He X, Li J. Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics. Crystals. 2019; 9(9):460. https://doi.org/10.3390/cryst9090460
Chicago/Turabian StyleLuo, Hongyuan, Jinyun Liu, Xiao He, and Jinjin Li. 2019. "Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics" Crystals 9, no. 9: 460. https://doi.org/10.3390/cryst9090460
APA StyleLuo, H., Liu, J., He, X., & Li, J. (2019). Low-Temperature Polymorphic Transformation of β-Lactam Antibiotics. Crystals, 9(9), 460. https://doi.org/10.3390/cryst9090460





