1. Introduction
Metamaterials are usually manmade structures designed to have some exotic properties that are rarely or never seen in natural materials. The split-ring resonators (SRRs) array is a well-studied structure that responds to incident electromagnetic waves in a range of frequencies like a negative-permeability material [
1]. Similarly, the structure of periodically arranged rubber-shelled metal spheres embedded in an epoxy background is an acoustic metamaterial with negative mass density for low frequency sound [
2]. In both cases, the exotic wave properties are caused by the coupling of the propagating wave in the background medium to the local resonance mechanism in each cell. The negativity of the material parameters in these two cases also implies the existence of a frequency gap [
3]. No wave with frequency in the gap can propagate in this metamaterial if it occupies the whole space. If the metamaterial is distributed in a finite region, waves get attenuated before they penetrate through the medium.
Frequency gap and wave attenuation effects can also be achieved using the Bragg scattering [
3] mechanism instead of local resonance. The bandgap of a usual photonic [
4] or sonic crystal [
5,
6] is caused by the destructive interference between different ‘component waves’ in the Fourier series expansion of the Bloch mode. To make such a bandgap large, a high contrast of material parameters between the periodically distributed inclusions and the background material is required [
7]. In addition, the center of the gap usually corresponds to a wavelength of about two to three times the lattice constant (spatial period) of the structure. This fact means that in order to isolate waves using non-resonant structures, the entire structure has to be bulky. Therefore, resonant structure is the better choice in this respect.
Recently, some researchers have noticed that bubble phononic crystals can attenuate sound very effectively, so they designed bubble phononic screens to isolate acoustic waves [
8,
9,
10,
11]. Similar to the negative-density metamaterial mentioned above, the high attenuation ability of the bubble phononic crystal is caused by the resonance coupling of elastic waves and bubble pulsation. In fact, a similar effect of bubble pulsation resonance in water is a well-known phenomenon and has been studied for decades [
12]. The sound attenuation ability of bubbly water has also been discovered theoretically for about two decades [
13,
14]. To the best of our knowledge, the sound attenuation effect has been explained so far by the multiple scattering theory of waves when the bubble positions and bubble sizes are randomly distributed, whereas the concept of phononic bandgap was used if the bubbles were periodically arranged. We will show in this paper that bubbly water can be treated as a natural metamaterial, and the resonance coupling of the pressure wave with the bubble pulsation results in a negative modulus of the medium, giving a low frequency gap.
Acoustic gaps and dispersion effects in a short wavelength regime for sound waves propagating in liquid have also been studied recently and attracted much attention [
15,
16]. The phononic gaps at elevated frequencies emerge due to symmetry breaking in phonon interactions. These theoretical predictions bear a general character shared among soft and biological (non-crystalline) materials/metamaterials, as have been verified through inelastic X-ray scattering (IXS) experiments.
The metamaterial theory of bubbly water we developed in this paper is based on an oscillator model for a pulsating bubble in water. According to this model, the pulsating bubble can be regarded as a radially vibrating oscillator. The spherical bubble (the air region) acts as a spring, and a shell of water around the bubble is the mass connected to the spring. To derive the effective bulk modulus of the bubbly water, it is assumed that all the bubbles have the same size and are periodically distributed in the water background. For the sake of simplicity, we only consider simple cubic (SC) structures. Therefore, a cubic unit cell contains three regions: the air sphere, the mass shell (water), and the water outside the shell. We treat the material in each region as a lump material. We then derive the dynamical modulus by considering the radial oscillator motion and the pressure–volume (P–V) relation of the air region.
The purpose of this paper is to provide a simple theory to study the acoustic properties of bubbly water at low filling fraction and long wavelengths. The scattering function of a single air bubble in water and the corresponding oscillator model are derived in
Section 2. We then use this model to derive the bulk modulus of the bubbly water in
Section 3 and briefly discuss the effects of absorption and the possibility of generalizing this theory. Numerical results are presented in
Section 4. Finally, we conclude this paper in
Section 5.
2. Scattering Function and the Oscillator Model for a Single Bubble
In this section, we derive the acoustic scattering function of a small air bubble for the incident plane wave. The resonance frequency of the radial vibrating motion of the bubble can be read out directly from the scattering function. On the other hand, the radial stiffness constant C of the bubble can be derived by analyze the relation between the inner pressure and the radial displacement of the bubble. We then use the relation to derive the effective mass m of the oscillator. The result obtained in this section will be used in the next section for constructing the dynamic model we mentioned in the last section.
2.1. Scattering Function of a Bubble
Suppose a spherical air bubble of radius
is surrounded by water, and the pulsation of the bubble is driven by a plane incident wave
of wavelength much larger than the bubble size (
); here
is the wave number. In this limit the bubble scatters the incident wave isotropically, leading to the scattering wave of the form
Here, represents the spherical wave solution of the Helmholtz equation (with source) , and is the scattering function to be determined later.
Although the bubble is assumed to be small, we also assume that the acoustic process is fast enough to avoid heat conduction between the bubble and the environment, thus the pulsation of the bubble can be approximated as an adiabatic process in the thermodynamics sense, satisfying the adiabatic
P–
V relation
. Here
P is the interior pressure of the bubble,
V is the bubble volume, and
is the specific heat ratio for air. Under this assumption, the radial motion of the bubble satisfies
where
,
, and
are the variation of the pressure, the volume, and the radius of the bubble, respectively, and
R is the instantaneous radius of the bubble, respectively. Denote
as
,
as
, and assume both of them are small comparing to the static value of
P and
R. We can therefore rewrite Equation (2) as
Here is the hydrostatic ambient pressure when the incident wave is absent, and is the bulk modulus of the air.
The pressure across the bubble surface must be continuous, therefore
. In addition, both
and
get a time factor
under the influence of the incident wave. Differentiate Equation (3) twice with respect to time, we get
However, the radial acceleration
is related to the pressure gradient via
Here
is density of the water, and the second equality is approximately correct under the long wavelength assumption. Combine Equations (1), (4), and (5) and use the fact
, we find
Here
is the Minnaert frequency, which is the resonance frequency of the ‘bubble oscillator’, given by
As can be easily observed, the strongest scattering happens at a frequency very close to the resonance frequency . Therefore, the effective medium properties might be modified by the resonance. We will derive the effective bulk modulus in the next section.
2.2. The Stiffness Constant and the Mass of the Oscillator Model
The mechanism of this low frequency resonance can be understood intuitively. When the wavelength is much longer than the bubble radius, the pressure difference across the bubble itself is negligible, thus we can think of the bubble as a perfect spring. However, even under the long wavelength condition, the scattered wave rapidly drops in the radial direction, so there is a pressure difference between the bubble surface and an imaginary “outer surface” that surrounds the bubble and a water shell around the bubble. These two effects together cause the bubble to vibrate radially like an oscillator that is driven by a driving force. The bubble itself acts as a spring, the water shell is the mass, and the radial pressure difference is the driving force. The detailed derivation of this oscillator model can be found in [
12]. Here we just derive the stiffness constant and the mass of the water shell for later use.
We denote the surface area
of the bubble as
, and rewrite the bubble pressure
in Equation (3) as
, then according to Equation (3), the radial restoring force
is
The radial stiffness constant is related to the oscillator mass through the relation
3. Effective Bulk Modulus and Dispersion Relation
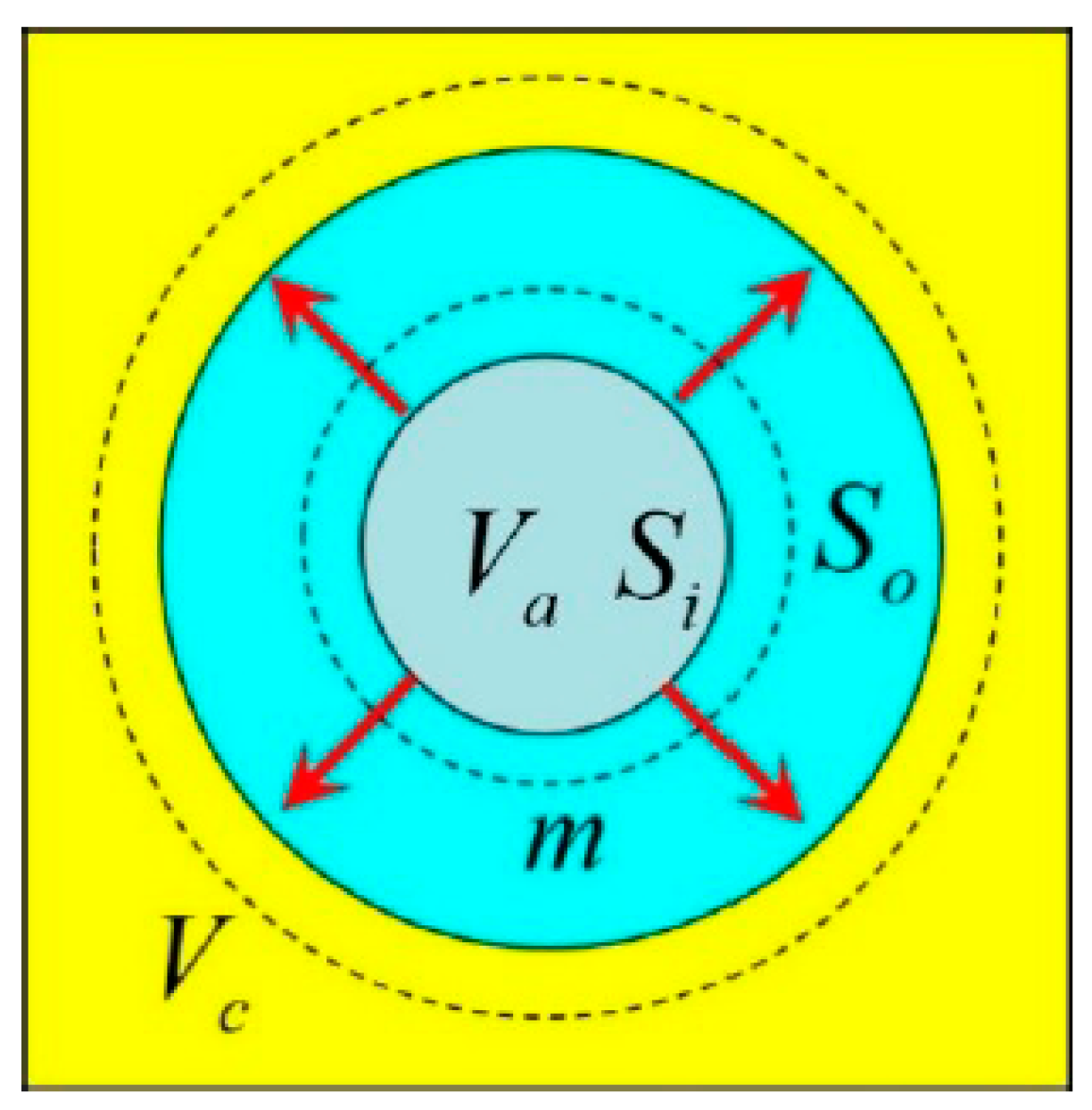
In this section, we derive the effective bulk modulus of the bubbly water. For the sake of simplicity, we assume all bubbles are of the same size, and their centers are located periodically on the cites of a simple cubic lattice. We denote the bubble volume and the cell volume as
and
, and the water volume
in one unit cell as
. The volume filling fraction of the bubbles is denoted as
(do not confuse it with the scattering function
). Thus, we have
and
. We also denote the bulk modulus for air and water as
and
, respectively. Similar notation rules also apply to the densities
,, the vibration displacements
,
, and the vibration velocities
. In addition, the bubble surface is denoted either as
or
, and the outer surface of the ‘mass shell’ is denoted as
Since the volume enclosed by
is four times of the bubble volume, and the ‘outer radius’
corresponding to
is related to the bubble radius
as
. Our goal is to derive the effective density of the medium
and the effective bulk modulus
for use in the following two equations
The left equation is Newton’s second law expressed in density form. Here
is the effective momentum density of the vibrating medium, and
plays the role of the force density. Any component of
is calculated from the pressure difference between the corresponding two boundaries of the cell, divided by the lattice constant. The right equation is in fact the time derivative of the equation
, which describes the relation between the volume variation rate
and the corresponding pressure variation
(see
Figure 1). With these two equations we can derive the wave equation for monochromatic (single frequency) waves in this sound-bubble coupling system and the dispersion relations of the propagating modes. The results provide simple explanation of some dramatic wave phenomena such as the very high attenuation rate of sound and Anderson localization, both of which have not yet been explained using the simple concept of frequency-dependent effective bulk modulus.
3.1. The Pressure–Volume Relations and the Effective Bulk Modulus
We begin with the following relation about the volumes:
Now replace the volume variation rates by the corresponding divergence of the displacements, and apply the relations
, for them, we find
Comparing Equation (12) with Equation (10), and making use of the equality
, we get
The ratio will be derived in the next subsection using the oscillator model.
3.2. The Dynamics Equation of the Radial Vibrating Oscillator
We now study the radial motion of the bubble. The mass of the oscillator can be thought of as a water shell of constant density
between the inner surface
and the outer surface
. The total radial force
drives the radial motion of the mass shell, satisfying the equation of motion:
Applying the sinusoidal condition to
has a time factor
), we get
Substitute Equation (15) into Equation (14), we find
here we have used the alternative expression of the Minnaert frequency
which can be derived from Equation (7), Equation (9), and the relation
.
3.3. The Effective Bulk Modulus as a Function of Frequency
Now it is straightforward to derive the frequency-dependent bulk modulus. Substitute Equation (16) into Equation (13), we get
which can be written as
where the parameters
,
, and
are given by
It is clear from Equation (19) that the inverse bulk modulus as a function of frequency has the same form as the dielectric function in the Lorentz model, or that for the polariton wave in the polar medium. According to this observation we learn immediately that the effective bulk modulus for the bubbly water medium becomes negative in the frequency range . This frequency interval is also the frequency gap or forbidden band of the propagating modes.
The bulk modulus of air is given by
, where
is the sound speed in air. Similarly,
gives the bulk modulus of the water. Substitute these two relations and
into Equation (20), we get
The bulk modulus ratio between water and air is about , thus according to Equation (21) even a low filling fraction will give a large , corresponding to a wide gap. We will derive in the next section the dispersion relation of the propagating modes and discuss the effect of the frequency gap.
3.4. Dispersion Relation of Acoustic Modes
To determine the dispersion relation, besides the bulk modulus, we should know the effective mass density. Since we assume the wavelength is long enough, it is reasonable to assume that the bubble moves together (in phase) with the surrounding water in the same cell. This consideration leads us to the simple average result
The correctness of this expression will be tested later.
The wave equation for a monochromatic (single frequency) wave can be derived by substituting Equation (19) and Equation (22) into Equation (10). The result is
Here the ratio
before the double time derivative is the inverse square speed of sound in the bubbly water medium. Adopting water as the standard medium or reference ‘wave vacuum’, we can define the refractive index of this medium as
Here is a reference index at high frequency. This refractive index becomes imaginary in the frequency gap, which indicates that waves cannot propagate in the medium if its frequency is within the gap.
We can deepen our understanding of the refractive index function by studying the dispersion relation of the propagating modes. Substitute the plane wave form
into Equation (23), we get
This dispersion relation is of the same form as that for the phonon-polariton waves. According to Equation (25), propagating modes can exist with frequency below or above . Within the interval , the wave vector becomes imaginary, thus the wave amplitude decays along the wave vector direction. If the bubbly water medium is filled in a slab region of finite thickness, an incident wave having a frequency within the gap would get attenuated before it penetrates through the slab. Furthermore, if a pulsating source of sound surrounded by the ‘bubble cloud’ radiates sound waves of frequency in the gap, the sound wave would be trapped by the bubble cloud, leading to the phenomena such like the Anderson localization of acoustic waves.
The negative modulus of the bubbly water is caused by the dynamical coupling of the sound field in water and the local resonance of every bubble oscillator. Similar mechanism for polar crystal also leads to the negative dielectric function in the polariton gap. The main difference between these two systems is that in the bubbly water case the oscillators vibrate radially so they couple with the scalar pressure field, whereas in the polar crystal case the local dipoles (for example, the pairs) are coupled with the electric vector field.
3.5. Absorption Effect and the Possibility of Generalization
In the derivation of the effective bulk modulus, we never considered any absorption or loss effects. For real bubbles, the damping effect caused by thermal conductivity (non-adiabatic correction), shear viscosity absorption at the bubble surface, and the radiation loss due to scattering must be considered. These corrections will cause the resonance frequency of the bubble to change slightly, reducing the peak of the scattering function and widening its width. These corrections will also introduce a damping force on the radial motion of the bubble oscillator and change the bulk modulus such that it does not acquire an unphysical infinite value. Since the absorption effect is a very cumbersome effect, and our aim in this study is not to study this effect, we will not further address this issue. We follow the spirit of [
13,
14] to choose the proper bubble size so that we can avoid the effects of the absorption.
Another question is how to generalize our theory to elastic solid media containing bubbles. As the authors have demonstrated in [
8,
9,
10,
11], for elastic media with very low shear stress, the primary mechanism of the first band gap is still caused by the resonance of the bubble. Therefore, we believe that our theory can be generalized and applied to such a system without much difficulty.
4. Numerical Results
In this section we discuss some numerical results based on our theory. Hereafter we assume
,
,
, and
. These parameters give us the bulk modulus
and
. If the radius of a bubble is measured in mm, the Minnaert frequency measured in kHz and we get a simple formula
or
. To avoid high absorption, we assume the bubbles have radius larger than
[
12,
13].
The scattering function
as a function of dimensionless frequency
is plotted in
Figure 2. Here we replaced the
function by its dimensionless correspondence
because here the information of the size is irrelevant. According to
Figure 1, the absolute value as well as the imaginary part of
goes to the maximum value
at
, and behaves like an even function with respect to this peak location. The real part of
, on the other hand, first raises to
, and then drops to zero at this place, and continually goes downwards to
, then approaches the horizontal axis without crossing the zero value. Resonance of this kind belongs to the Lorentz dispersion, which is responsible for the negative bulk modulus and the low frequency gap of this bubbly water medium.
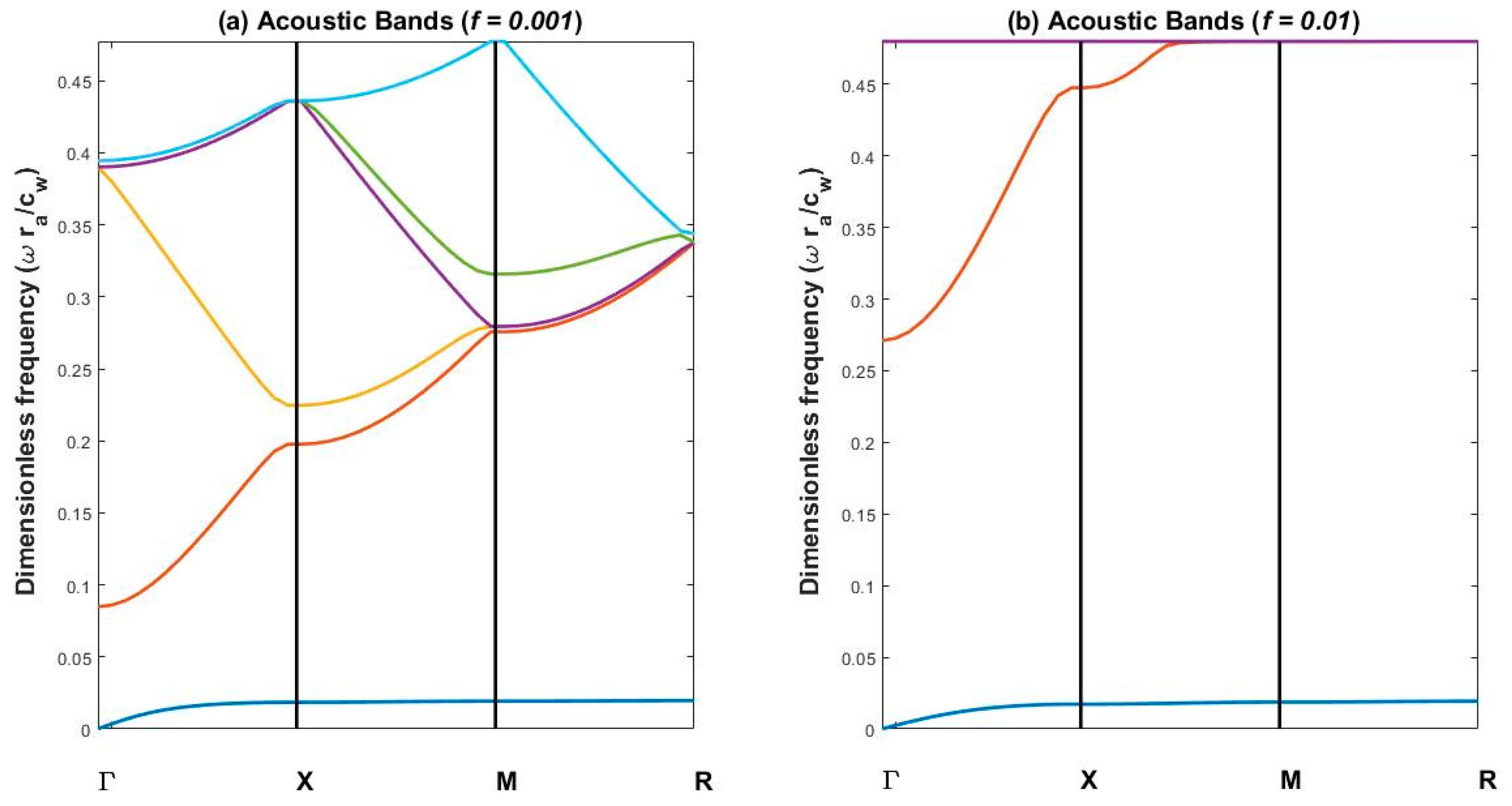
We now study the characteristics of the acoustic band structures of the bubbly-water sonic crystals. Plane wave expansion method (PWEM) were implemented for the calculations. Results for filling fraction
and
are shown in
Figure 3. These results indicate that bubbly-water sonic crystal is an ideal structure to open large gap at low frequency. For the case with filling fraction
, the gap is opened between
(at X) and
(at
). Comparing them with the gap boundaries
and
predicted by the effective metamaterial theory, we find excellent agreement between them. The low frequency limit of the gap in
Figure 3 is a little higher than the prediction. We believe this discrepancy is due to the bad convergence of the PWEM at low filling fraction. Similarly for the
case, we have the gap opened from
(at X) to
(at ¡). The gap
boundaries provided by the effective theory are
and
, also in very good agreement with the band structure result. We noticed that the agreement between
and
in this case is better than in the former case. This fact is consistent with our judgement about the PWEM.
The metamaterial theory developed in this paper not only can provide the range of the gap, but also can give us the attenuation rate of the wave, which is directly related to the imaginary part of the effective wave number that determined by Equation (25). In addition, absorption or loss effect can be easily included by a simple replacement of the frequency:
[
12]. Here
is a positive number smaller than 0.1 if we assume the that the bubble radius is larger then 100
1 m. For the purpose of demonstration, in the simulation of lossy media, we take
.
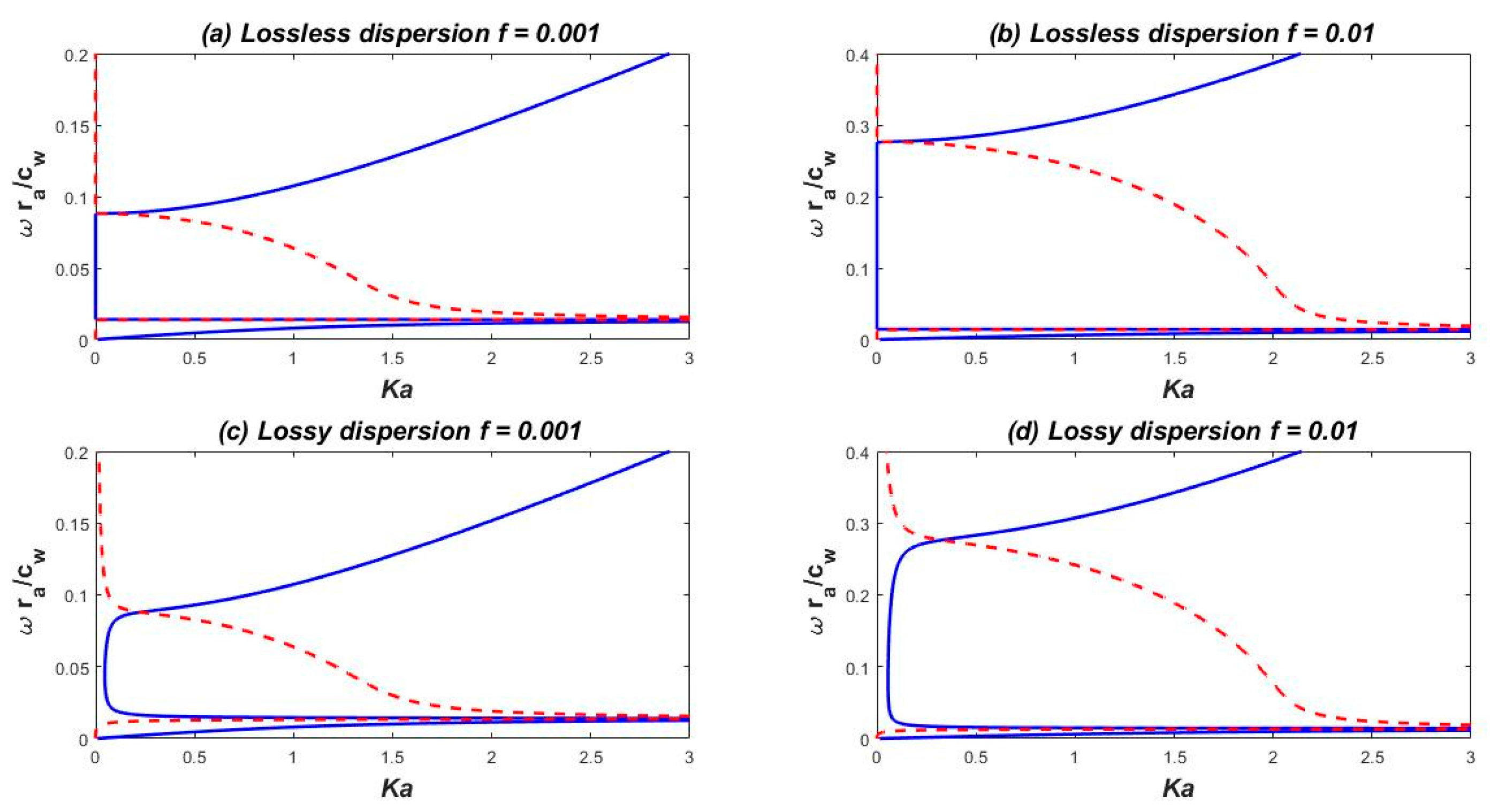
Figure 4a,b is the results for the lossless media, while
Figure 4c,d is the results for the lossy media. Here the dimensionless variable
Ka is the product of the wavenumber
K in Equation (25) times the lattice constant
a of the SC structure. the lattice constant in the SC structure. The real part of the wave number (wave vector) of the mode waves are represented by the blue solid curves, and the red broken lines represent the imaginary part of the wave vector. These dispersion relations are similar to the dispersion relations of the phonon-polariton that mentioned in the previous section. We noticed that the presence of loss or absorption does not destroy the attenuation effect because it is so large.
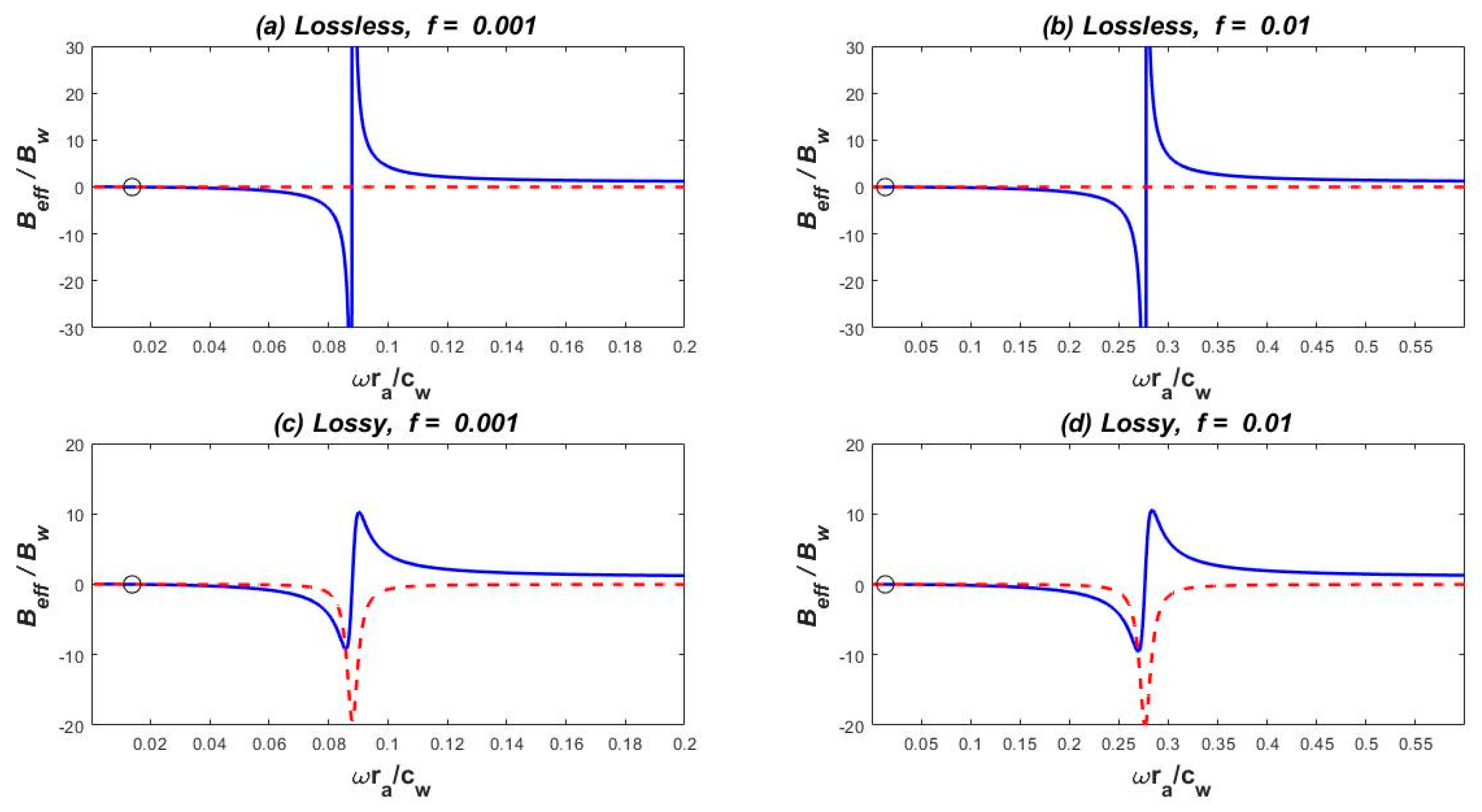
Now we discuss the effective bulk modulus according to Equation (19) and its modified form when loss cannot be ignored. As before, four cases are studied, and their results (
) are shown in
Figure 5. The parameters used in the calculations are the same as those used in
Figure 4. The small circles in the four subplots indicate the starting frequencies (changes from positive to negative) of the negative bulk modulus. For the lossless cases, the starting points and the resonance points (infinite effective modulus) are the same as the gap boundaries of the metamaterial. The loss effect seemed not to change the effective bulk modulus much if the frequency is not very close to the resonance point. However, the effective modulus at the resonance frequency no longer goes to the unphysical value of infinity, as expected.
Finally, we discuss the valid range of the theory developed in this paper. Based on our numerical simulations, we found that the gap range given by the effective theory is in good agreement with that obtained from the band structure calculation (the discrepancy is less than 3%) if the filling fraction
f of the bubbles is within the range 0.0005 to 0.02. Beyond this range, we are not sure about the accuracy, and need further investigation. In addition, the bubble radius must not be less than
, otherwise high absorption effects must be considered [
12].