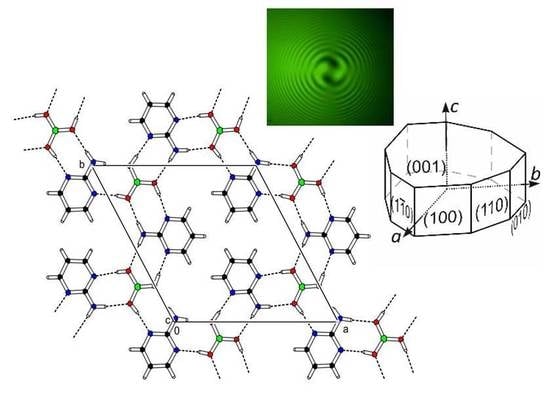
Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal
Abstract
:1. Introduction
2. Experimental Setup
2.1. Materials and Methods
2.2. Syntheses
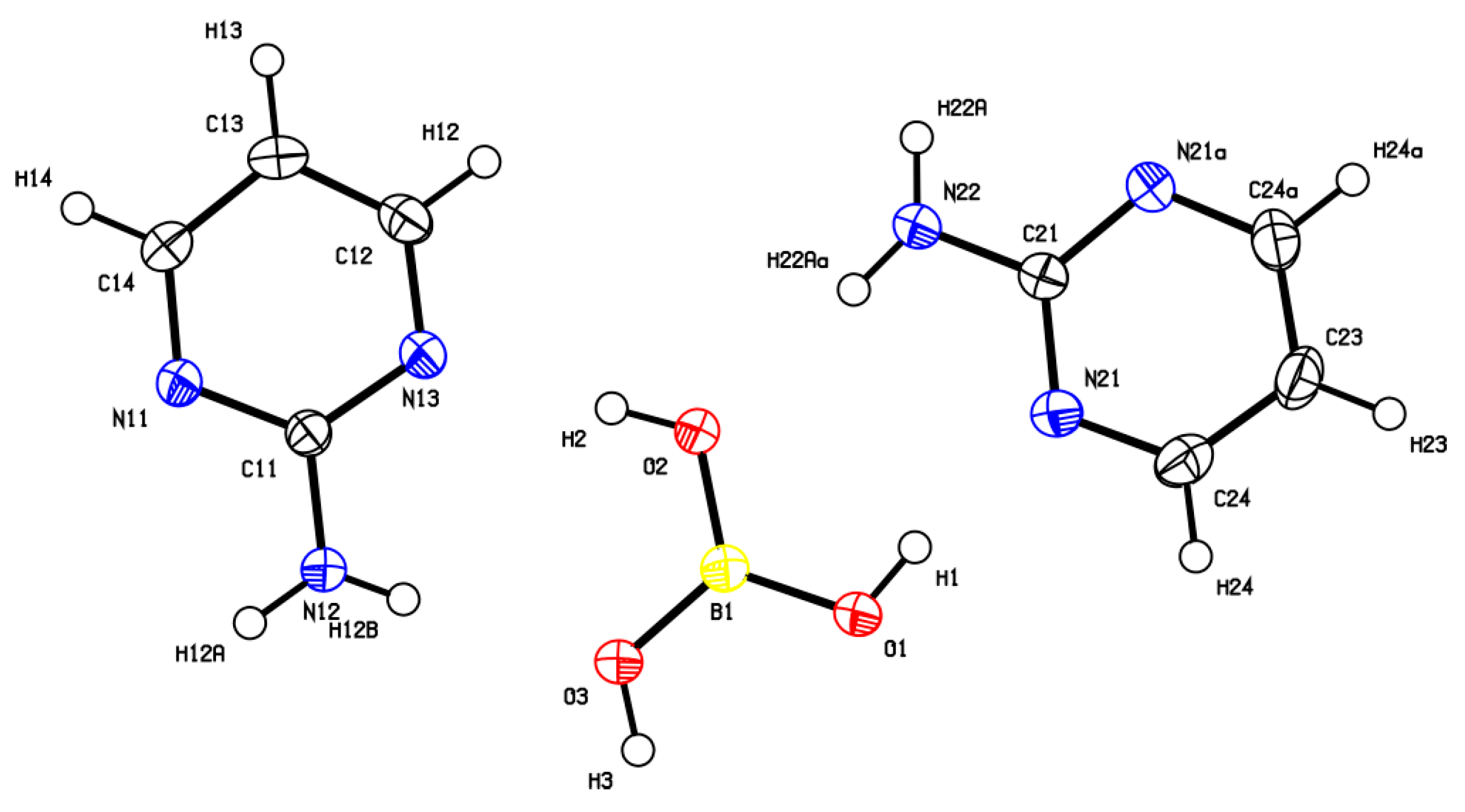
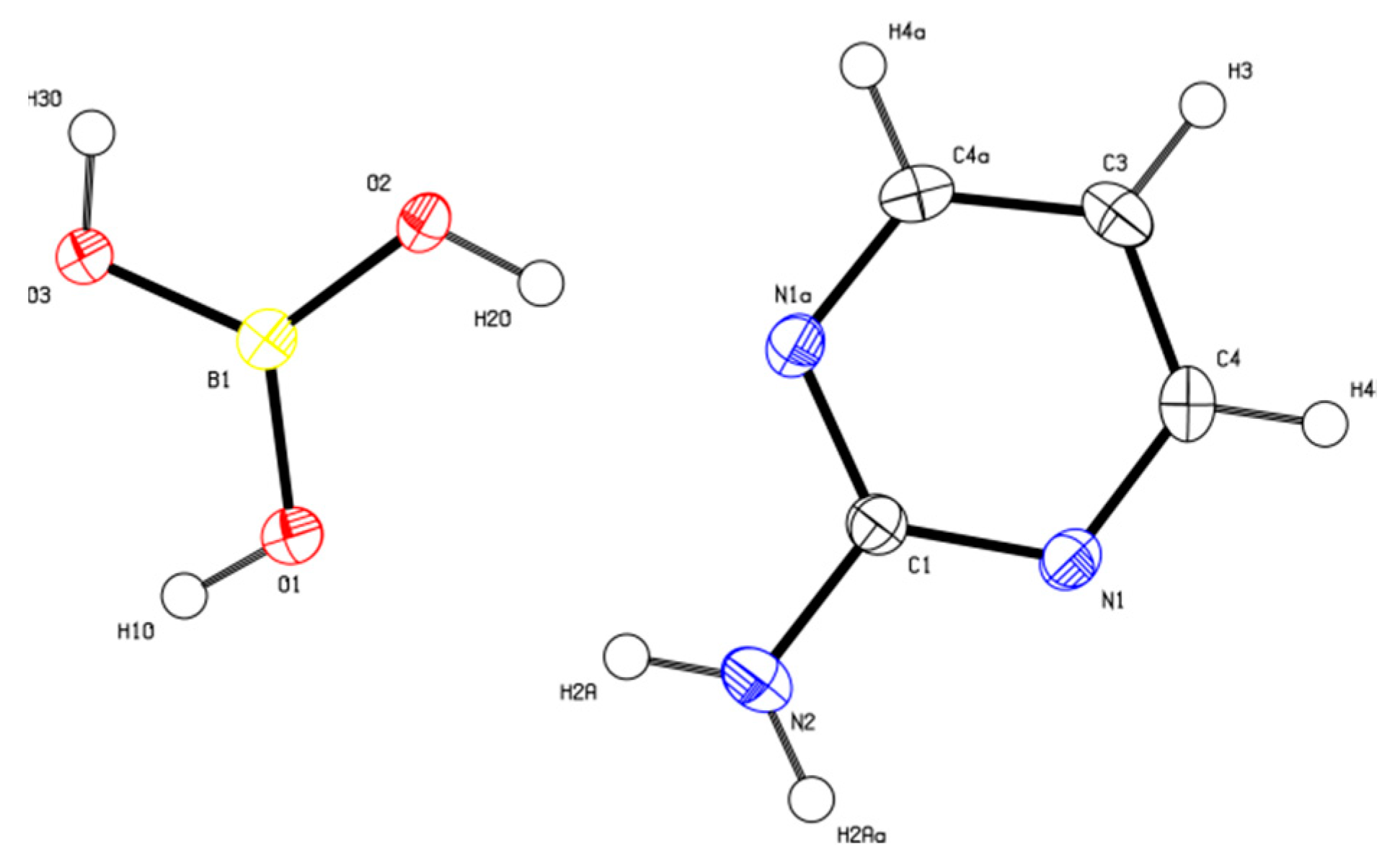
2.3. Crystal Structure Determination
2.4. Crystal Growth
2.5. Quantum Chemical Computations
2.6. Optical Properties
3. Results and Discussion
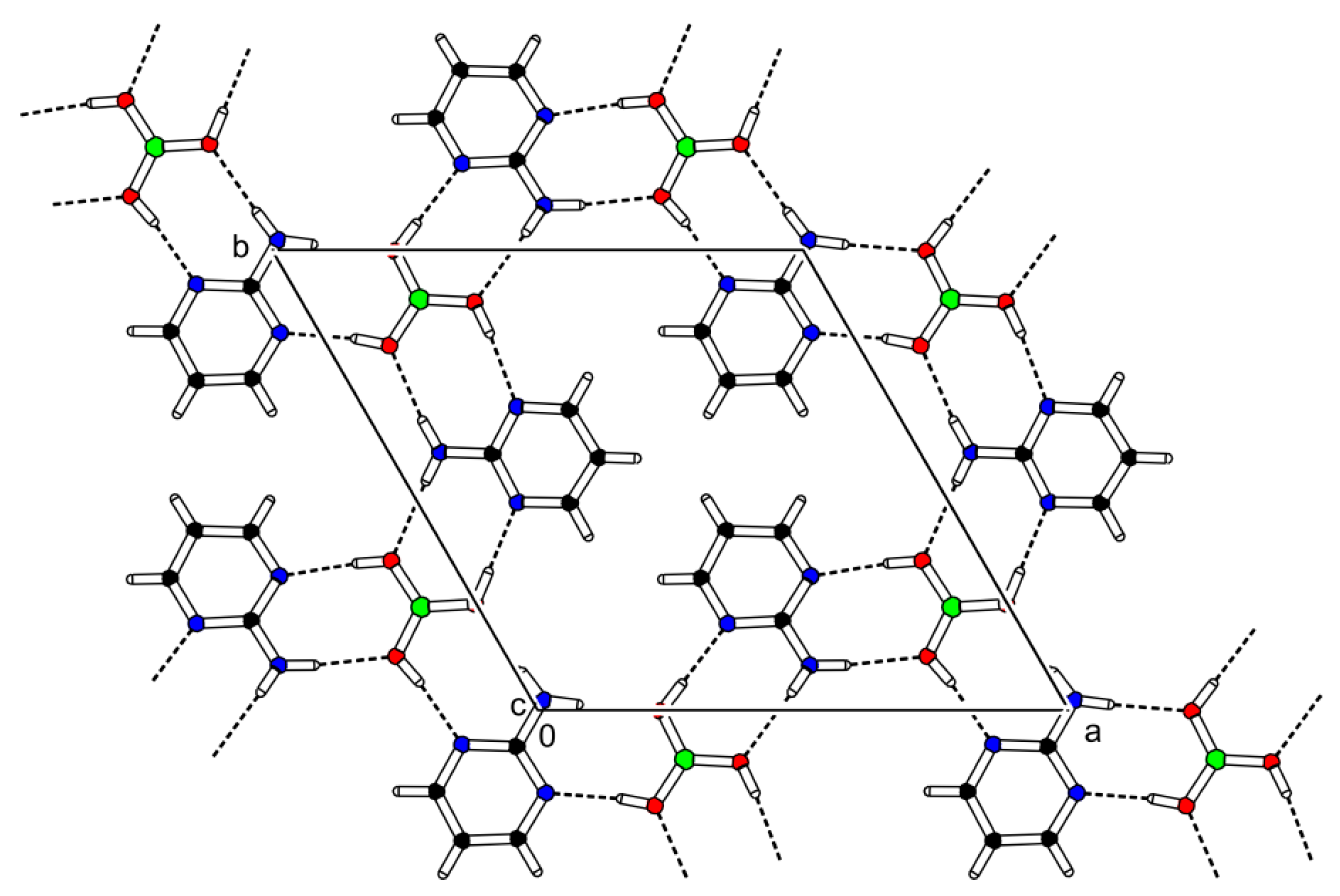
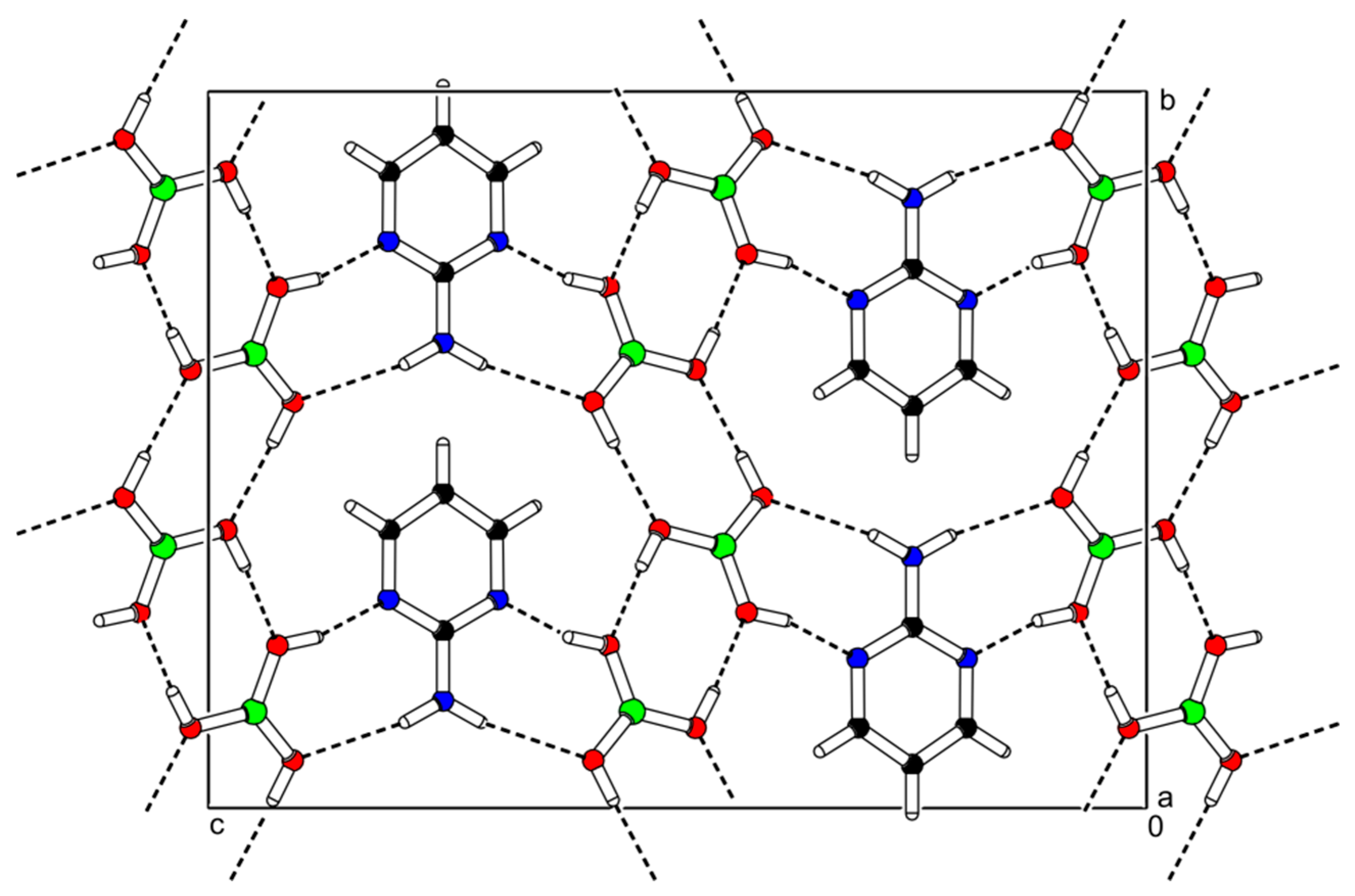
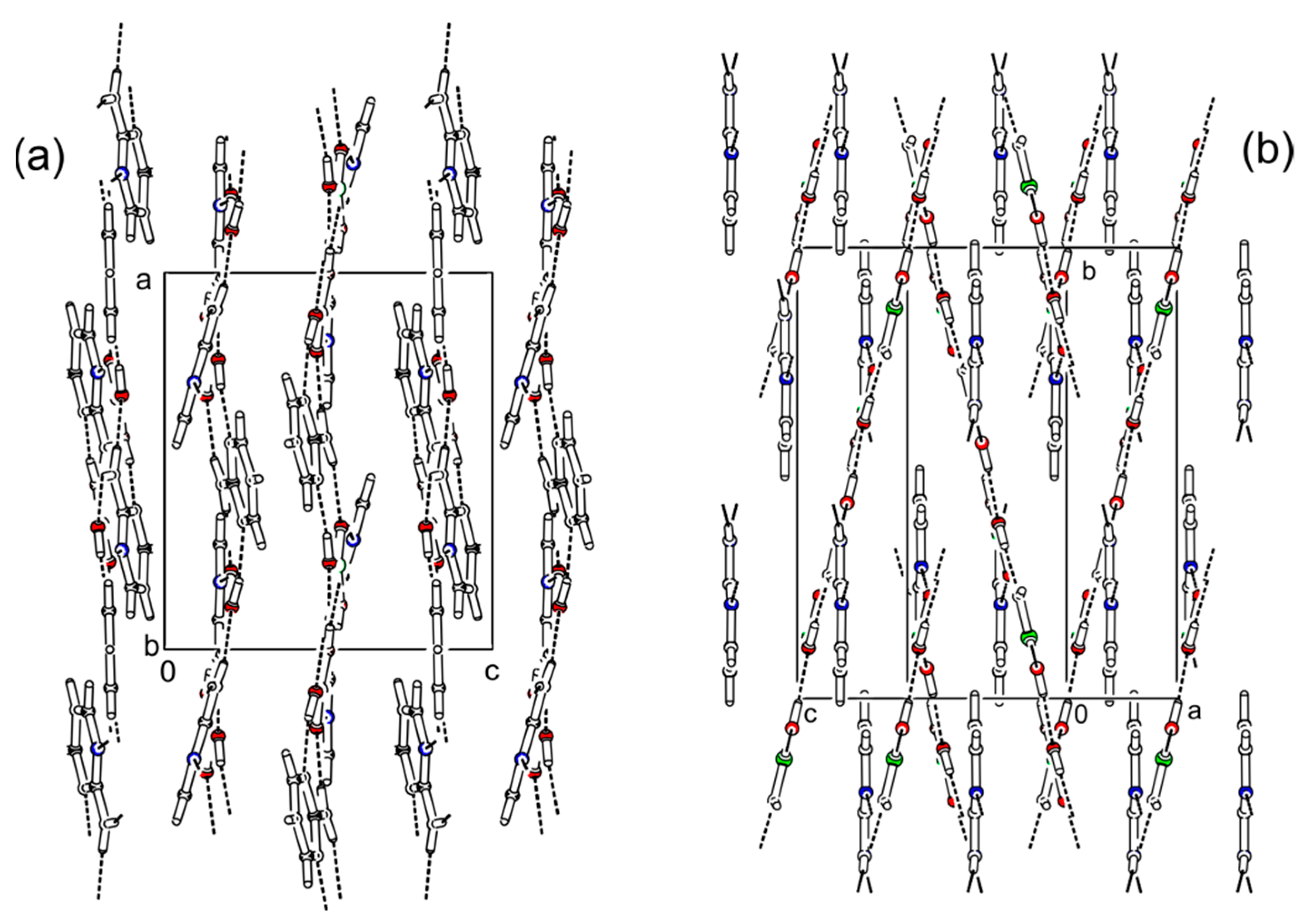
3.1. Crystal Structure Description
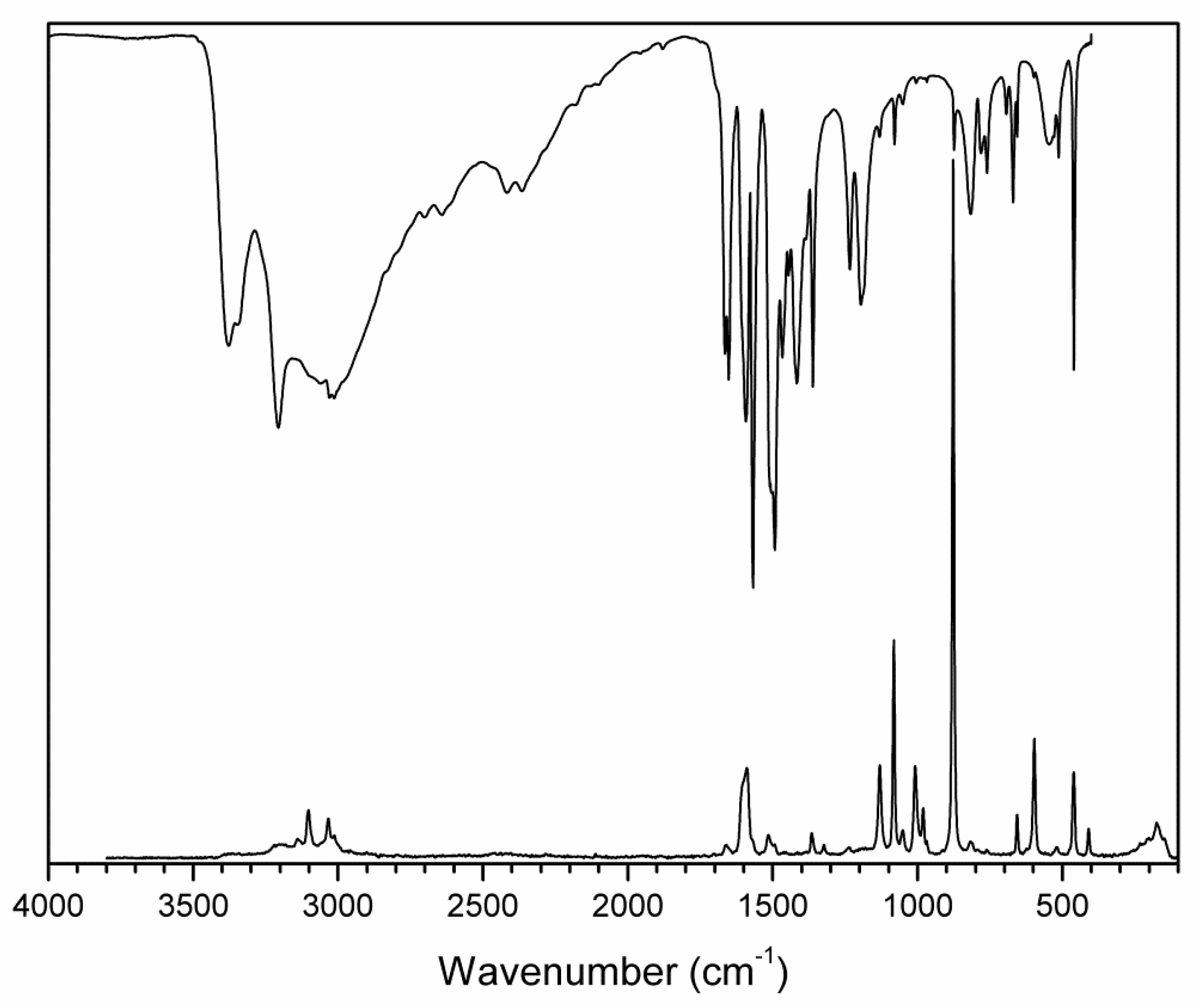
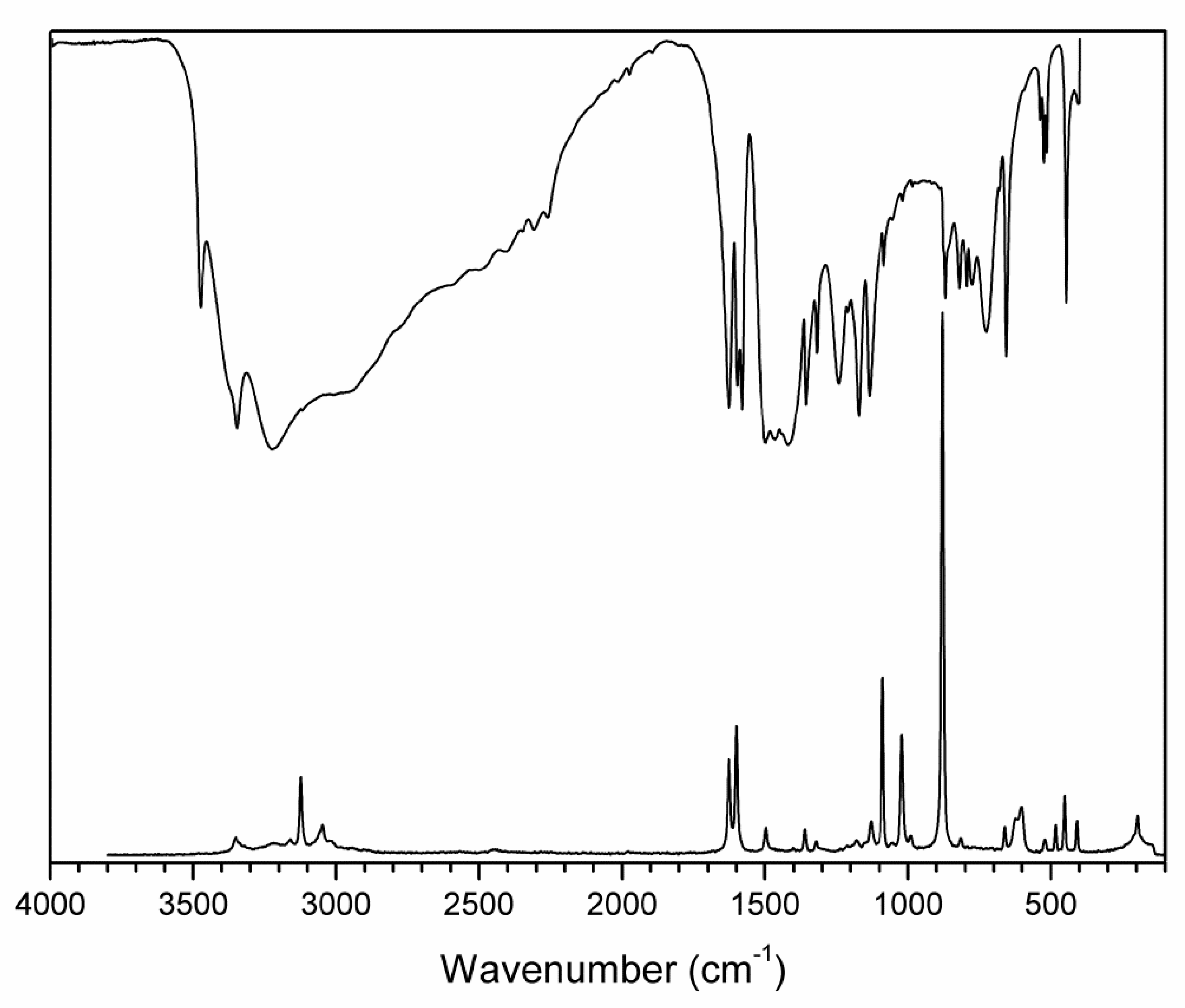
3.2. Vibrational and UV-Vis Spectra
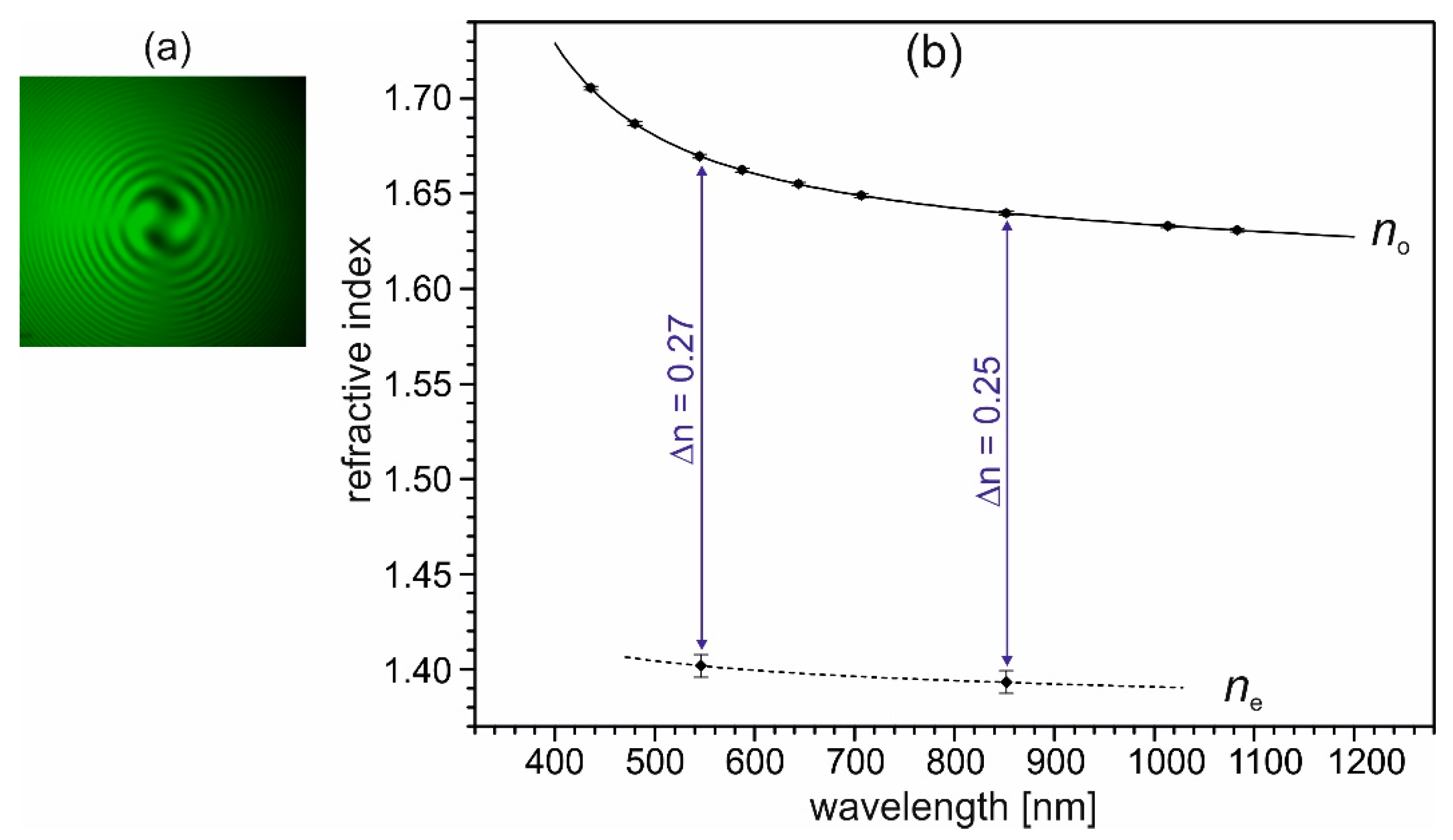
3.3. Optical Properties of (2-AMP)3(H3BO3)2
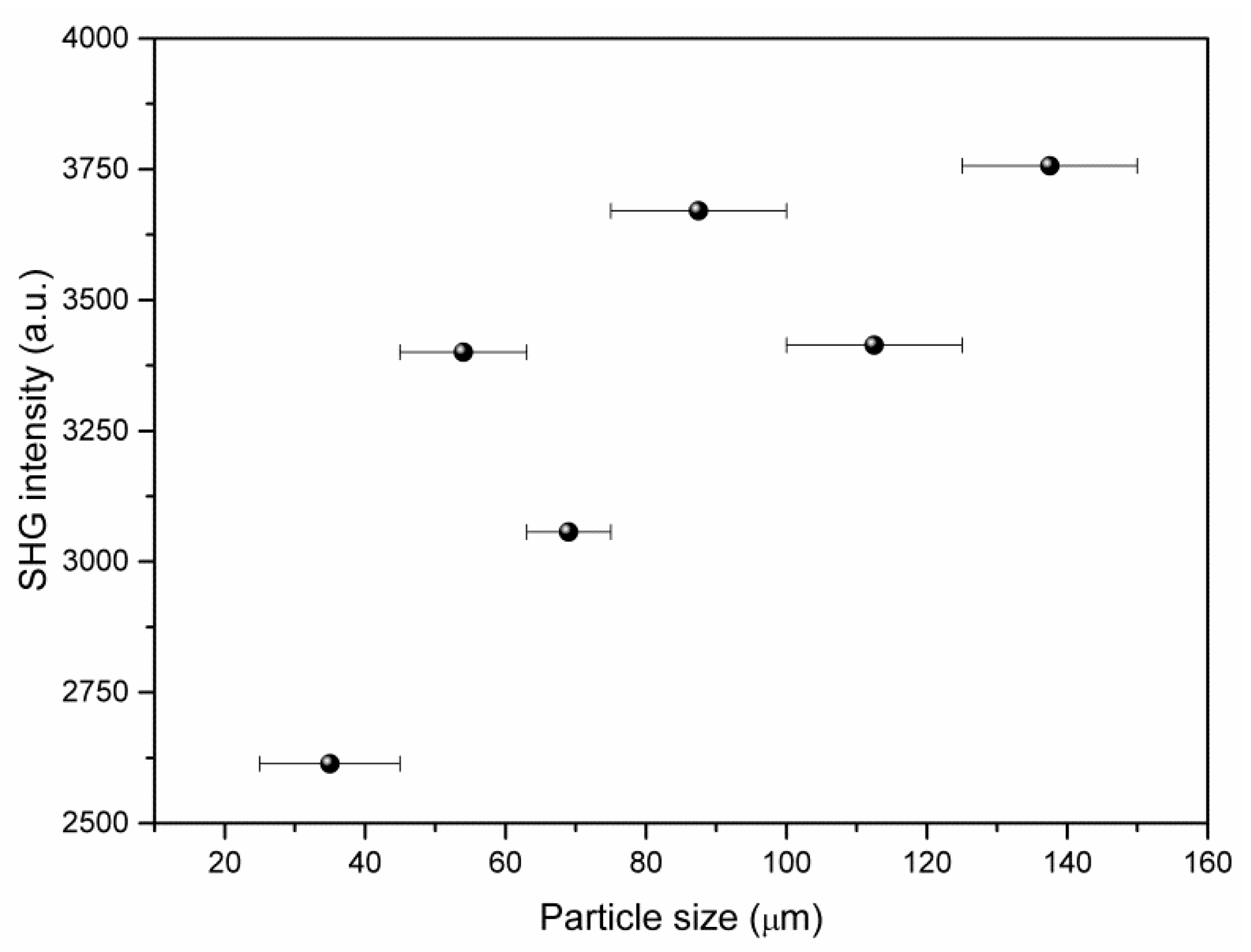
3.4. Second Harmonic Generation (SHG) Measurements of (2-AMP)3(H3BO3)2
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Němec, P.; Pasztor, F.; Brajer, M.; Němec, I. Spectrally- and polarization-resolved hyper-Rayleigh scattering measurements with polarization-insensitive detection. Opt. Commun. 2017, 388, 21–28. [Google Scholar] [CrossRef]
- Kaminskii, A.A.; Becker, P.; Rhee, H.; Lux, O.; Kaltenbach, A.; Eichler, H.J.; Shirakawa, A.; Yoneda, H.; Němec, I.; Fridrichová, M.; et al. Stimulated Raman scattering in monoclinic non-centrosymmetric guanylurea(1+) hydrogen phosphite (GUHP). Phys. Status Solidi (B) 2013, 250, 1837–1856. [Google Scholar] [CrossRef]
- Kaminskii, A.A.; Rhee, H.; Eichler, H.J.; Lux, O.; Němec, I.; Yoneda, H.; Shirakawa, A.; Becker, P.; Bohatý, L. Observation of stimulated Raman scattering in polar tetragonal crystals of barium antimony tartrate trihydrate, Ba[Sb2((+)C4H2O6)2]·3H2O. Ann. Phys. 2017, 529. [Google Scholar] [CrossRef]
- Chen, C.; Sasaki, T.; Li, R.; Wu, Y.; Lin, Z.; Mori, Y.; Hu, Z.; Wang, J.; Aka, G.; Yoshimura, M.; et al. Nonlinear Optical Borate Crystals; Wiley-VCH Verlag&Co. KGaA: Weinheim, Germany, 2012. [Google Scholar]
- Ilczyszyn, M.M. Vibrational studies of the ferroelastic crystal—Betaine borate. Part I. Vibrational investigation of the paraelastic phase. J. Mol. Struct. 2000, 519, 257–274. [Google Scholar] [CrossRef]
- Ilczyszyn, M.M. Vibrational studies of the ferroelastic crystal—Betaine borate. Part II. Vibrational investigations of the paraelastic-ferroelastic phase transition. J. Mol. Struct. 2000, 519, 275–296. [Google Scholar] [CrossRef]
- Panicker, C.Y.; Varghese, H.T.; John, A.; Philip, D.; Nogueira, H.I.S. Vibrational spectra of melamine diborate, C3N6H62H3BO3. Spectrochim. Acta A 2002, 58, 1545–1551. [Google Scholar] [CrossRef]
- Wang, K.; Duan, D.F.; Wang, R.; Lin, A.L.; Cui, Q.L.; Liu, B.B.; Cui, T.; Zou, B.; Zhang, X.; Hu, J.Z.; et al. Stability of Hydrogen-Bonded Supramolecular Architecture under High Pressure Conditions: Pressure-Induced Amorphization in Melamine-Boric Acid Adduct. Langmuir 2009, 25, 4787–4791. [Google Scholar] [CrossRef] [PubMed]
- Aarthi, J.; Gowri, S.; Dilip, C.S. A new metal-organic hybrid crystal with excellent transparency in the visible spectrum: Growth, structure and properties of sodium fumarate—Boric acid tetrahydrate. J. Mol. Struct. 2019, 1181, 660–667. [Google Scholar] [CrossRef]
- Rajasekar, G.; Dhatchaiyini, M.K.; Vinitha, G.; Bhaskaran, A. Structural, optical, dielectric, second and third-order nonlinear properties of new semiorganic crystal: Sodium (bis) boro succinate. J. Mol. Struct. 2019, 1177, 594–602. [Google Scholar] [CrossRef]
- Bharthasarathi, T.; Arulmozhichelvan, P.; Murugakoothan, P. Crystal growth, thermal and optical studies on a metalorganic nonlinear optical material dipotassium boro maleate (DKBM). Mat. Lett. 2010, 64, 1506–1509. [Google Scholar] [CrossRef]
- Dhanuskodi, S.; Mary, P.A.A. Growth and characterization of a new nonlinear optical crystal-ammonium borodilactate. J. Cryst. Growth 2003, 253, 424–428. [Google Scholar] [CrossRef]
- Dhanuskodi, S.; Vasantha, K. X-ray diffraction, spectroscopic and thermal studies on a potential semiorganic NLO material: Lithium bis-L-malato borate. Spectrochim. Acta A 2005, 61, 1777–1782. [Google Scholar] [CrossRef] [PubMed]
- Mary, S.S.; Kirupavathy, S.S.; Gopalakrishnan, R. Theoretical and experimental analysis on spectral, hyperpolarizibility and dielectric properties of semi-organic nonlinear optical crystal: Potassium boromalate hydrate (PBH). Optik 2014, 125, 3837–3843. [Google Scholar] [CrossRef]
- Kurtz, S.K.; Perry, T.T. A powder technique for evaluation of nonlinear optical materials. J. Appl. Phys. 1968, 39, 3798–3814. [Google Scholar] [CrossRef]
- Rodrigues-Carvajal, J.; Roisnel, T. FullProf. 98 and WinPLOTR New Windows 95/NT Applications for Diffraction; International Union for Crystallography: Chester, UK, 1998; pp. 35–36. [Google Scholar]
- Spek, A.L. Single-crystal structure validation with the program PLATON. J. Appl. Crystallogr. 2003, 36, 7–13. [Google Scholar] [CrossRef]
- Blessing, R.H. An empirical correction for absorption anisotropy. Acta Crystallogr. A 1995, 51, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Sheldrick, G.M. A short history of SHELX. Acta Crystallogr. A 2008, 64, 112–122. [Google Scholar] [CrossRef]
- Sheldrick, G.M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 2015, 71, 3–8. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09W, Revision D.01; Gaussian Inc.: Wallingford, CT, USA, 2013. [Google Scholar]
- Michalska, D.; Wysokinski, R. The prediction of Raman spectra of platinum(II) anticancer drugs by density functional theory. Chem. Phys. Lett. 2005, 403, 211–217. [Google Scholar] [CrossRef]
- Dennington, R.; Keith, T.; Millam, J. GaussView Version 5.0.8; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
- Merrick, J.P.; Moran, D.; Radom, L. An evaluation of harmonic vibrational frequency scale factors. J. Phys. Chem. A 2007, 111, 11683–11700. [Google Scholar] [CrossRef]
- Yoshida, H.; Ehara, A.; Matsuura, H. Density functional vibrational analysis using wavenumber-linear scale factors. Chem. Phys. Lett. 2000, 325, 477–483. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; De La Pierre, M.; D’Arco, P.; et al. CRYSTAL14: A Program for the Ab Initio Investigation of Crystalline Solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Valenzano, L.; Torres, F.J.; Doll, K.; Pascale, F.; Zicovich-Wilson, C.M.; Dovesi, R. Ab Initio study of the vibrational spectrum and related properties of crystalline compounds; the case of CaCO3 calcite. Z. Phys. Chem. 2006, 220, 893–912. [Google Scholar] [CrossRef]
- Ferrero, M.; Rerat, M.; Orlando, R.; Dovesi, R. Coupled perturbed Hartree-Fock for periodic systems: The role of symmetry and related computational aspects. J. Chem. Phys. 2008, 128. [Google Scholar] [CrossRef]
- Ferrero, M.; Rerat, M.; Orlando, R.; Dovesi, R. The calculation of static polarizabilities of 1–3D periodic compounds. The implementation in the CRYSTAL code. J. Comput. Chem. 2008, 29, 1450–1459. [Google Scholar] [CrossRef]
- Becker, P.; Held, P.; Liebertz, J.; Bohatý, L. Optical properties of the germanate melilites Sr2MgGe2O7, Sr2ZnGe2O7 and Ba2ZnGe2O7. Cryst. Res. Technol. 2009, 44, 603–612. [Google Scholar] [CrossRef]
- Rousseau, D.L.; Bauman, R.P.; Porto, S.P.S. Normal mode determination in crystals. J. Raman Spectr. 1981, 10, 253–290. [Google Scholar] [CrossRef]
- Da Silva, M.B.; Santos, R.C.R.; Hernandez, J.S.R.; Caetano, E.W.S.; Freire, V.N. Vibrational modes and phonon and thermodynamic properties of the metaboric acid polymorphs alpha-, beta-, and gamma-(BOH)(3)O-3 within a density functional theory framework. J. Phys. Chem. A 2018, 122, 7628–7645. [Google Scholar] [CrossRef]
- Novak, A. Hydrogen bonding in solids correlation of spectroscopic and crystallographic data. In Large Molecules. Structure and Bonding; Springer: Berlin, Germany, 1974; Volume 18, pp. 177–216. [Google Scholar]
- Lautie, A.; Froment, F.; Novak, A. Relationship between NH stretching frequencies and N...O distances of crystals containing NH...O hydrogen-bonds. Spectrosc. Lett. 1976, 9, 289–299. [Google Scholar] [CrossRef]
- Ghosh, G. Dispersion-equation coefficients for the refractive index and birefringence of calcite and quartz crystals. Opt. Commun. 1990, 163, 95–102. [Google Scholar] [CrossRef]
- Albert, A.; Goldacre, R.; Phillips, J. The strength of heterocyclic bases. J. Chem. Soc. 1948, 2240–2249. [Google Scholar] [CrossRef]
- Smith, R.M.; Martell, A.E. Critical Stability Constants; Plenum Press: New York, NY, USA, 1976; Volume 4, p. 25. [Google Scholar]
- Cruz-Cabeza, A.J. Acid–base crystalline complexes and the pKa rule. CrystEngComm 2012, 14, 6362–6365. [Google Scholar] [CrossRef]

| Identification code | (2-AMP)3(H3BO3)2 | 2-AMP(H3BO3)2 |
|---|---|---|
| Empirical formula | C12H21B2N9O6 | C4H11B2N3O6 |
| Formula weight | 409.00 | 218.78 |
| Temperature (K) | 150(2) | 150(2) |
| a (Å) | 13.1632(4) | 3.7634(2) |
| b (Å) | 13.1632(4) | 13.8978(7) |
| c (Å) | 9.9288(3) | 18.2041(8) |
| α (°) | 90 | 90 |
| β (°) | 90 | 91.757(2) |
| γ (°) | 120 | 90 |
| Volume (Å3) | 1489.88(10) | 951.68(8) |
| Z | 3 | 4 |
| Calculated density (Mg/m3) | 1.368 | 1.527 |
| Crystal system | Trigonal | Monoclinic |
| Space group | P3221 | C2/c |
| Absoption coefficient (mm-1) | 0.108 mm−1 | 0.134 mm−1 |
| F(000) | 642 | 456 |
| Crystal size (mm) | 0.60 × 0.57 × 0.31 | 0.58 × 0.17 × 0.16 |
| Diffractometer and radiation | Nonius Kappa CCD, Mo λ = 0.71073 Å | |
| Scan technique | ω and ψ scans to fill the Ewald sphere | |
| Completeness to θ | 99.9% | 99.9% |
| Range of h, k and l | −17→17, −17→17, −12→12 | −4→3, −18→18, −20→23 |
| θ Range for data collection (°) | 1.79–27.47° | 2.24–27.48° |
| Refl. collected/unique (Rint) | 26047/2287 (0.022) | 7829/1097 (0.019) |
| No. of observed reflections | 2216 | 997 |
| Criterion for observed reflections | I > 2σ(I) | |
| Absorption correction | multi-scan | multi-scan |
| Function minimized | Σ w(Fo2 - Fc2)2 | |
| Parameters refined | 134 | 70 |
| R; wR(F2) (I>2σ(I)) | 0.0267; 0.0752 | 0.0293; 0.0769 |
| R; wR(F2) (all data) | 0.0280; 0.0764 | 0.0326; 0.0791 |
| Value of S | 1.074 | 1.080 |
| Absolut struct. param. (Flack) | -0.1(2) | |
| Δρmax and Δρmin (eÅ−3) | 0.17 and −0.16 | 0.18 and –0.19 |
| Weighting scheme | W = [σ2(Fo2) + aP2 + bP]−1 | |
| P = (Fo2 + 2Fc2)/3 | ||
| a = 0.0491 | a = 0.0418 | |
| b = 0.1274 | b = 0.4767 | |
| Compound | (2-AMP)3(H3BO3)2 | 2-AMP(H3BO3)2 | ||||||
|---|---|---|---|---|---|---|---|---|
| Representations | A1 | A2 | E | Ag | Au | Bg | Bu | |
| Acoustic | 1 | 1 | 1 | 2 | ||||
| External modes | Translational | 7 | 7 | 14 | 4 | 3 | 5 | 3 |
| Librational | 7 | 8 | 15 | 4 | 4 | 5 | 5 | |
| Internal modes | 59 | 61 | 120 | 29 | 29 | 31 | 31 | |
| Total | 73 | 77 | 150 | 37 | 37 | 41 | 41 | |
| Activity | IR | z | x, y | x | y, z | |||
| Raman | αxx+αyy, αzz | (αxxx-αyyx,αxyy), (αxzy,αyzx) | αxx,αyy,αzz, αxy | αxz,αyz | ||||
| IR | Raman | Assignment | IR | Raman | Assignment |
|---|---|---|---|---|---|
| 174w | γrg, γC-NH2 | 1416m | νBO, δBOH | ||
| 409w | δNCN | 1446w | δCH, νrg, δNCN | ||
| 460m | 460w | γrg | 1467m | νC-NH2, δNH2, δNCN, νBO, | |
| 513w | 518w | τNH2, δOBO, δBOH | 1493s | δBOH | |
| 546w | γCH, γrg, δOBO, δBOH | 1510sh | |||
| 597w | δrg, δNCN | 1568s | νrg, δrg, δNCN, ρNH2, δCH | ||
| 657w | 657w | 1592m | 1589w | δNH2, νC-NH2, νrg | |
| 670w | γBO3 | 1652m | |||
| 693w | ? | 1664m | 1660w | ||
| 760w | γBO3, γXH(…X) | 2364w | ? | ||
| 779w | γCH, γBO3, γXH(…X) | 2418w | |||
| 817w | 818w | γrg, γCN3, γBO3 | 2641w | ||
| 874w | 877vs | δBO3, γBO3, νsrg, δsrg | 2700w | ||
| 981w | γCH | 3012s | 3012w | νOH(…N), νCH | |
| 1008w | νrg, δrg | 3030s | 3033w | ||
| 1050w | 1050w | ρNH2, δCH | 3060sb | νOH(…N) | |
| 1080w | 1081s | δCH, νrg | 3100sh | 3102w | νOH(…N), νCH |
| 1131w | 1131w | δCH, ρNH2 | 3140w | ||
| 1185sh | ? | 3205s | 3200wb | νNH(…O) | |
| 1196m | νBO, δBOH | 3345s | |||
| 1233m | νrg, δrg, ρNH2 | 3378m | |||
| 1362m | 1365w | δCH, νC-NH2 |
| IR | Raman | Assignment | IR | Raman | Assignment |
|---|---|---|---|---|---|
| 195w | external mode | 1212m | νrg, δrg, ρNH2 | ||
| 406w | 408w | δNCN | 1244m | νrg, δrg, ρNH2, νBO, δBOH | |
| 446m | 451w | γrg | 1319m | 1319w | δCH, ρNH2 |
| 482w | δOBO, δBOH | 1359m | 1360w | δCH, νC-NH2 | |
| 515w | τNH2, δOBO, δBOH | 1421s | νBO, δBOH | ||
| 524w | 520w | 1468s | νC-NH2, δNH2, δNCN, νBO, | ||
| 537w | γCH, γrg, δOBO, δBOH | 1501s | 1496w | δBOH | |
| 601w | δrg, δNCN | 1582s | νrg, δrg, δNCN, ρNH2, δCH | ||
| 623w | 1599m | 1600m | δNH2, νC-NH2, νrg | ||
| 658m | 661w | δrg, δNCN, γBO3 | 1629s | 1626m | |
| 726m | γBO3, γXH(…X) | 2263m | ? | ||
| 777m | γCH, γBO3 | 2313m | |||
| 794m | 2410m | ||||
| 821m | 816w | γrg, γCN3, γBO3 | 3000sb | 3020w | νOH(…N), νCH |
| 870m | 879vs | δBO3, γBO3, νsrg, δsrg | 3047w | νCH | |
| 990w | γCH | 3124sh | 3124m | ||
| 1022m | νrg, δrg | 3159w | νOH(…O) | ||
| 1087m | 1089m | δCH, νrg | 3230sb | 3220w | |
| 1135m | 1128w | δCH, ρNH2 | 3350s | νOH(…N), νNH(…O) | |
| 1174s | 1180w | δCH, ρNH2, νBO, δBOH | 3480m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kloda, M.; Matulková, I.; Císařová, I.; Becker, P.; Bohatý, L.; Němec, P.; Gyepes, R.; Němec, I. Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal. Crystals 2019, 9, 403. https://doi.org/10.3390/cryst9080403
Kloda M, Matulková I, Císařová I, Becker P, Bohatý L, Němec P, Gyepes R, Němec I. Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal. Crystals. 2019; 9(8):403. https://doi.org/10.3390/cryst9080403
Chicago/Turabian StyleKloda, Matouš, Irena Matulková, Ivana Císařová, Petra Becker, Ladislav Bohatý, Petr Němec, Róbert Gyepes, and Ivan Němec. 2019. "Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal" Crystals 9, no. 8: 403. https://doi.org/10.3390/cryst9080403
APA StyleKloda, M., Matulková, I., Císařová, I., Becker, P., Bohatý, L., Němec, P., Gyepes, R., & Němec, I. (2019). Cocrystals of 2-Aminopyrimidine with Boric Acid—Crystal Engineering of a Novel Nonlinear Optically (NLO) Active Crystal. Crystals, 9(8), 403. https://doi.org/10.3390/cryst9080403