Dissociation Behavior of Dislocations in Ice
Abstract
1. Introduction
1.1. Burgers Vectors of Dislocations in Ice
1.2. Extended Dislocations in Ice
1.3. Basal Slip System in Ice
1.4. Equilibrium Widths of Extended Dislocations in Ice
2. Formation of a Glissile Extended Dislocation
2.1. Driving Force for Dissociation of Perfect Dislocation <a>
2.2. Dissociation-Completing Time
2.3. Dissociation-Beginning Time
2.4. Shuffle-Glide Transformation and Nucleation of Shockley Partials in Ice
2.5. Extended Width Changing under a Shear Stress
3. Formation of a Sessile Extended Dislocation
3.1. Driving Force for Dissociation of Perfect Dislocations <c> and <c + a>
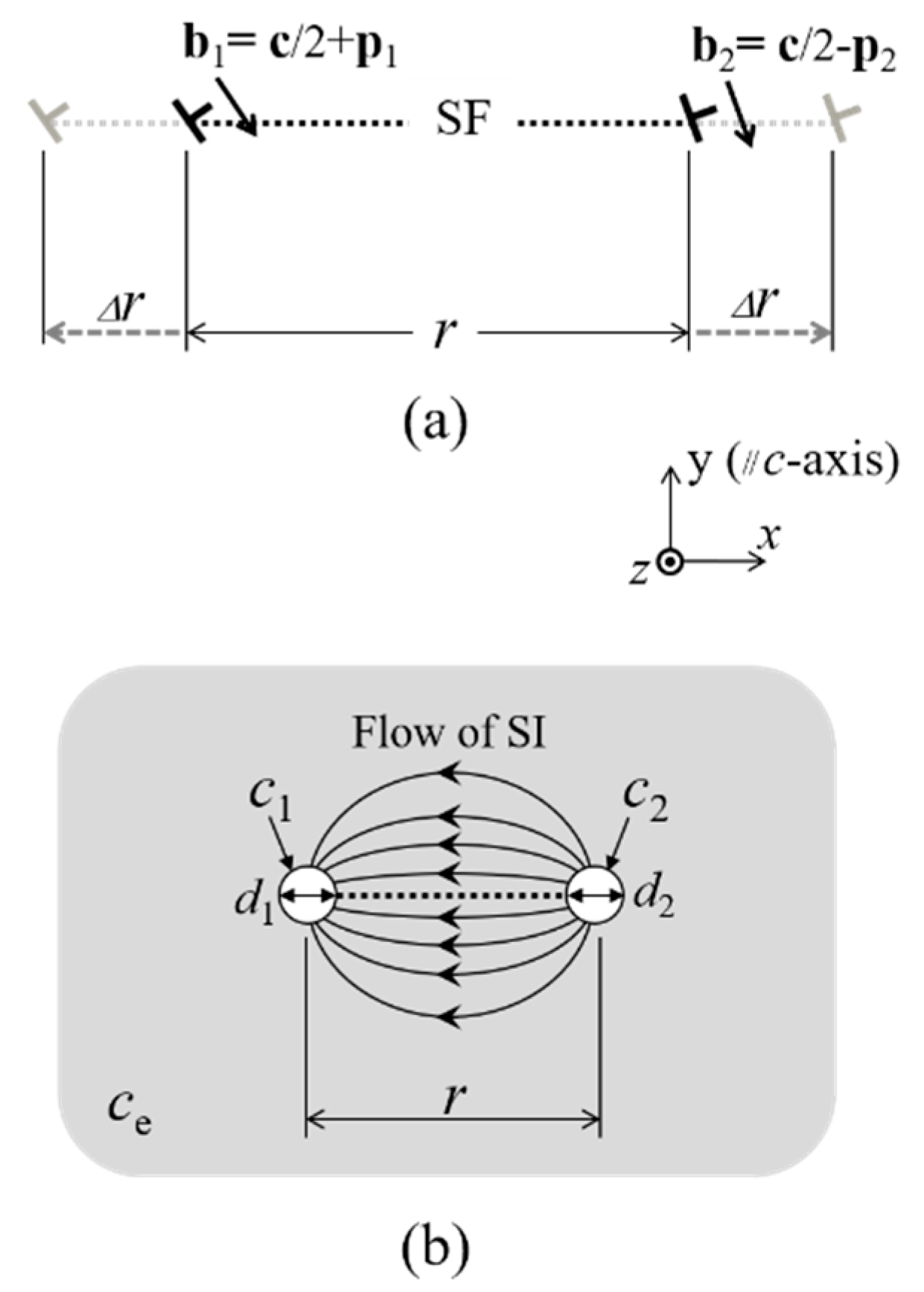
3.2. Diffusive Flow of Self-Interstitials between Two Partial Dislocations
4. Summary
Funding
Conflicts of Interest
References
- Petrenko, V.F.; Whitworth, R.W. Physics of Ice; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Hondoh, T. Nature and behavior of dislocations in ice. In Physics of Ice Core Records; Hondoh, T., Ed.; Hokkaido University Press: Sapporo, Japan, 2000; pp. 3–24. [Google Scholar]
- Hondoh, T. An overview of microphysical processes in ice sheets: Toward Nanoglaciology. Low Temp. Sci. 2009, 68, 1–23. [Google Scholar]
- Hondoh, T. Dislocation mechanism for transformation between cubic ice Ic and hexagonal ice Ih. Philos. Mag. 2015, 95, 3590–3620. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Chemical Physics of Ice; Cambridge University Press: London, UK, 1970. [Google Scholar]
- Hobbs, P.V. Ice Physics; Oxford University Press: Oxford, UK, 1974. [Google Scholar]
- Kuhs, W.F.; Sippel, C.; Falenty, A.; Hansen, T.C. Extent and relevance of stacking disorder in “ice Ic”. Proc. Natl. Acad. Sci. USA 2012, 109, 21259–21264. [Google Scholar] [CrossRef]
- Fukuda, A.; Hondoh, T.; Higashi, A. Dislocation mechanisms of plastic deformation of ice. J. Phys. Paris 1987, 48, 163–173. [Google Scholar] [CrossRef]
- Hirth, J.P.; Lothe, J. Theory of Dislocations; McGraw-Hill book Inc.: New York, NY, USA, 1968. [Google Scholar]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Alexander, H. Dislocations in covalent crystals. In Dislocations in Solids; Nabarro, F.R.N., Ed.; Elsevier Science Publishers, B.V.: Amsterdam, The Netherlands, 1986; Volume 7, pp. 113–234. [Google Scholar]
- Holt, D.B.; Yacobi, B.G. Extended Defects in Semiconductors; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Pizzagalli, L.; Beauchamp, P. Dislocation motion in silicon: The shuffle-glide controversy revisited. Philos. Mag. Lett. 2008, 88, 421–427. [Google Scholar] [CrossRef]
- Hondoh, T.; Itoh, T.; Amakai, S.; Goto, K.; Higashi, A. Formation and annihilation of stacking faults in pure ice. J. Phys. Chem. 1983, 87, 4040–4044. [Google Scholar] [CrossRef]
- Hudait, A.; Qiu, S.; Lupi, L.; Molinero, V. Free energy contributions and structural characterization of stacking disordered ices. Phys. Chem. Chem. Phys. 2016, 18, 9544–9553. [Google Scholar] [CrossRef]
- Lupi, L.; Hudait, A.; Peters, B.; Gründwald, M.; Mullen, R.G.; Nguyen, A.H.; Molinero, V. Role of stacking disorder in ice nucleation. Nature 2017, 551, 218–222. [Google Scholar] [CrossRef]
- Rӧttger, K.; Endriss, A.; Ihringer, J.; Doyle, S.; Kuhs, W.F. Lattice constants and thermal expansion of H2O and D2O ice Ih between 10 and 265 K. Addendum. Acta Cryst. 2012, B68, 91. [Google Scholar] [CrossRef]
- Gammon, P.H.; Kiefte, H.; Clouter, M.J. Elastic constants of ice samples by Brillouin spectroscopy. J. Phys. Chem. 1983, 87, 4025–4029. [Google Scholar] [CrossRef]
- Shearwood, C.; Whitworth, R.W. The velocity of dislocations in ice. Philos. Mag. 1991, A64, 289–302. [Google Scholar] [CrossRef]
- Okada, Y.; Hondoh, T.; Mae, S. Basal glide of dislocations in ice observed by synchrotron radiation topography. Philos. Mag. 1999, A79, 2853–2868. [Google Scholar] [CrossRef]
- Wessel, K.; Alexander, H. On the mobility of partial dislocations in silicon. Philos. Mag. 1977, 35, 1523–1536. [Google Scholar] [CrossRef]
- Silva Junior, D.L.; de Koning, M. Structure and energetics of extended defects in ice Ih. Phys. Rev. 2012, B85, 024119. [Google Scholar] [CrossRef]
- Schulson, E.M.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Tan, J.J.; Li, Y. High-pressure phase transitions and thermodynamic behaviors of cadmium sulfide. Acta Phys. Pol. 2011, A120, 501–506. [Google Scholar] [CrossRef]
- Cullity, B.D. Elements of X-Ray Diffraction; Addison-Wesley Pub. Co. Inc.: Reading, MA, USA, 1956; (Japanese Edition). [Google Scholar]
- Hondoh, T.; Itoh, T.; Higashi, A. Formation of stacking faults in pure ice single crystals by cooling. Jpn. J. Appl. Phys. 1981, 20, L737–L740. [Google Scholar] [CrossRef]
- Higashi, A. (Ed.) Lattice Defects in Ice Crystals: X-Ray Topographic Observations; Hokkaido University Press: Sapporo, Japan, 1988. [Google Scholar]
- Goto, K.; Hondoh, T.; Higashi, A. Experimental determinations of the concentration and the mobility of interstitials in pure ice crystals. In Point Defects and Defect Interactions in Metals; Takamura, J., Doyama, M., Kiritani, M., Eds.; University of Tokyo Press: Tokyo, Japan, 1982; pp. 174–176. [Google Scholar]
- Goto, K.; Hondoh, T.; Higashi, A. Determination of diffusion coefficients of self-interstitials in ice with a new method of observing climb of dislocations by x-ray topography. Jpn. J. Appl. Phys. 1986, 25, 351–357. [Google Scholar] [CrossRef]
- Hondoh, T.; Hoshi, R.; Goto, A.; Yamagami, H. A new method using synchrotron-radiation topography for determining point-defect diffusivity under hydrostatic pressure. Philos. Mag. 1991, 63, 1–5. [Google Scholar] [CrossRef]
- Ramseier, R.O. Self-diffusion of tritium in natural and synthetic ice monocrystals. J. Appl. Phys. 1967, 38, 2553–2556. [Google Scholar] [CrossRef]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Principles of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Singapore, 2003. [Google Scholar]
- Wei, Y.; Dempsey, J.P. The motion of non-basal dislocations in ice crystals. Philos. Mag. 1994, 69, 1–10. [Google Scholar] [CrossRef]
- Weikusat, I.; Kuiper, E.N.; Pennock, G.M.; Kipfstuhl, S.; Drury, M.R. EBSD analysis of subgrain boundaries and dislocation slip systems in Antarctic and Greenland ice. Solid Earth 2017, 8, 883–898. [Google Scholar] [CrossRef]
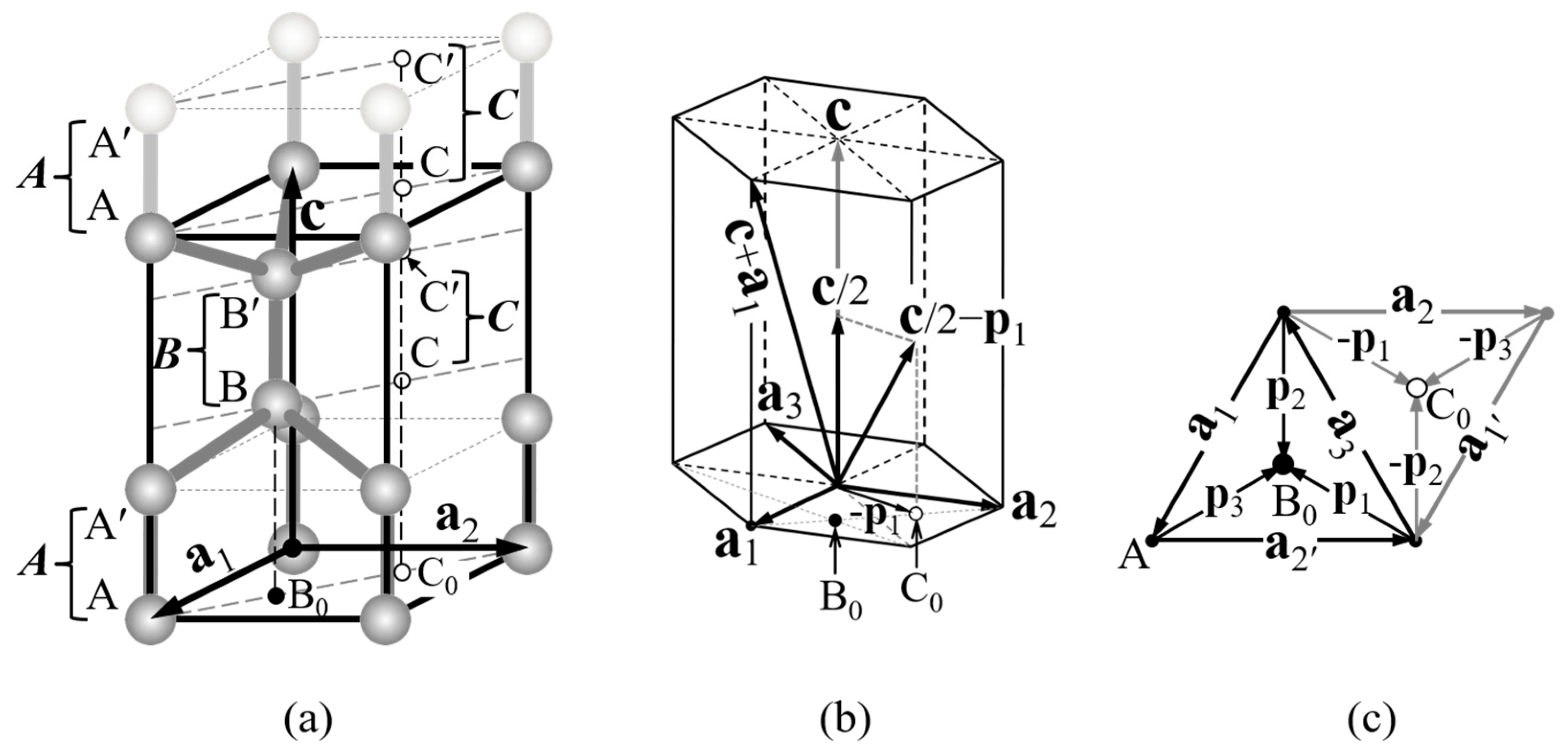
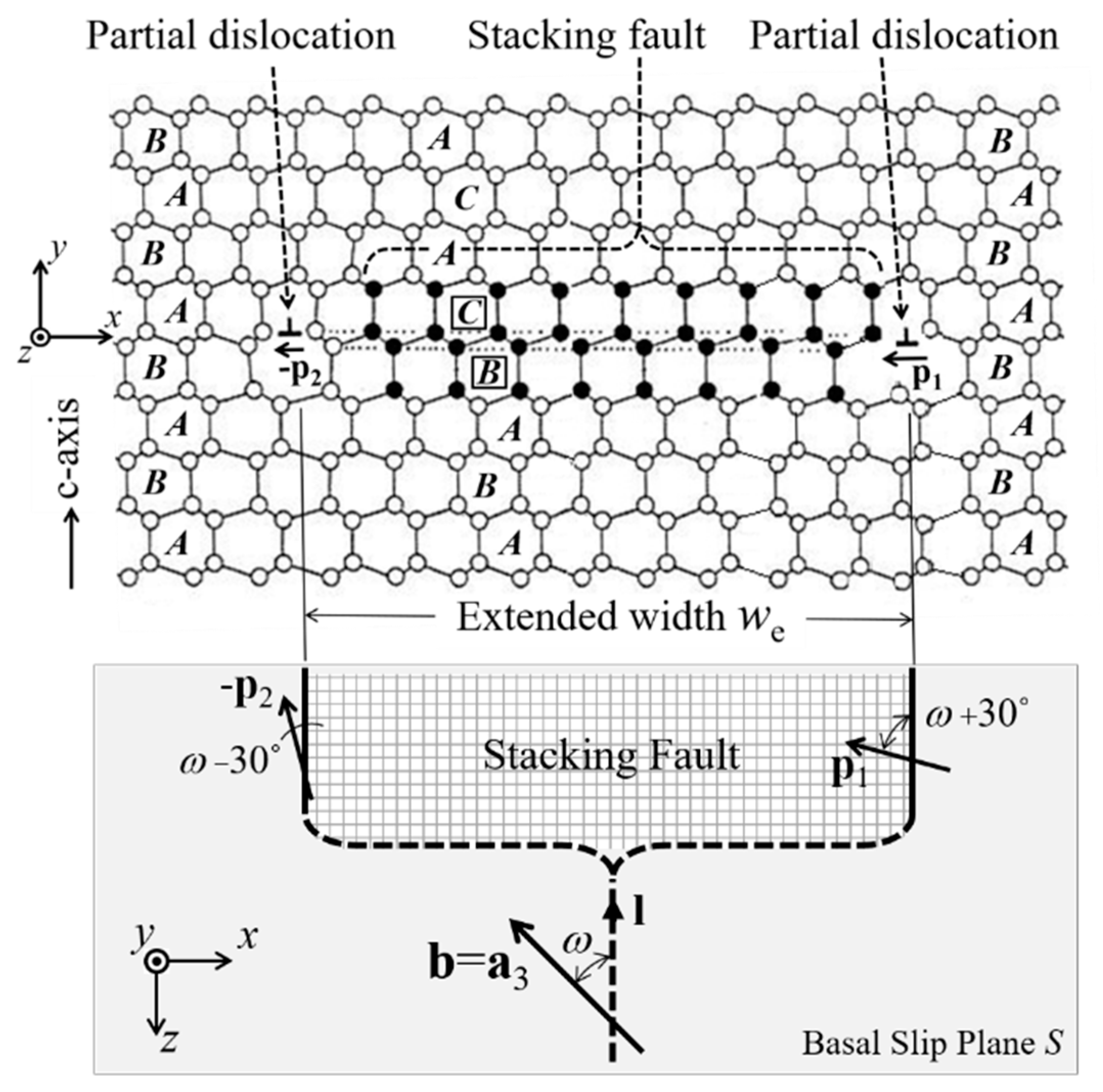
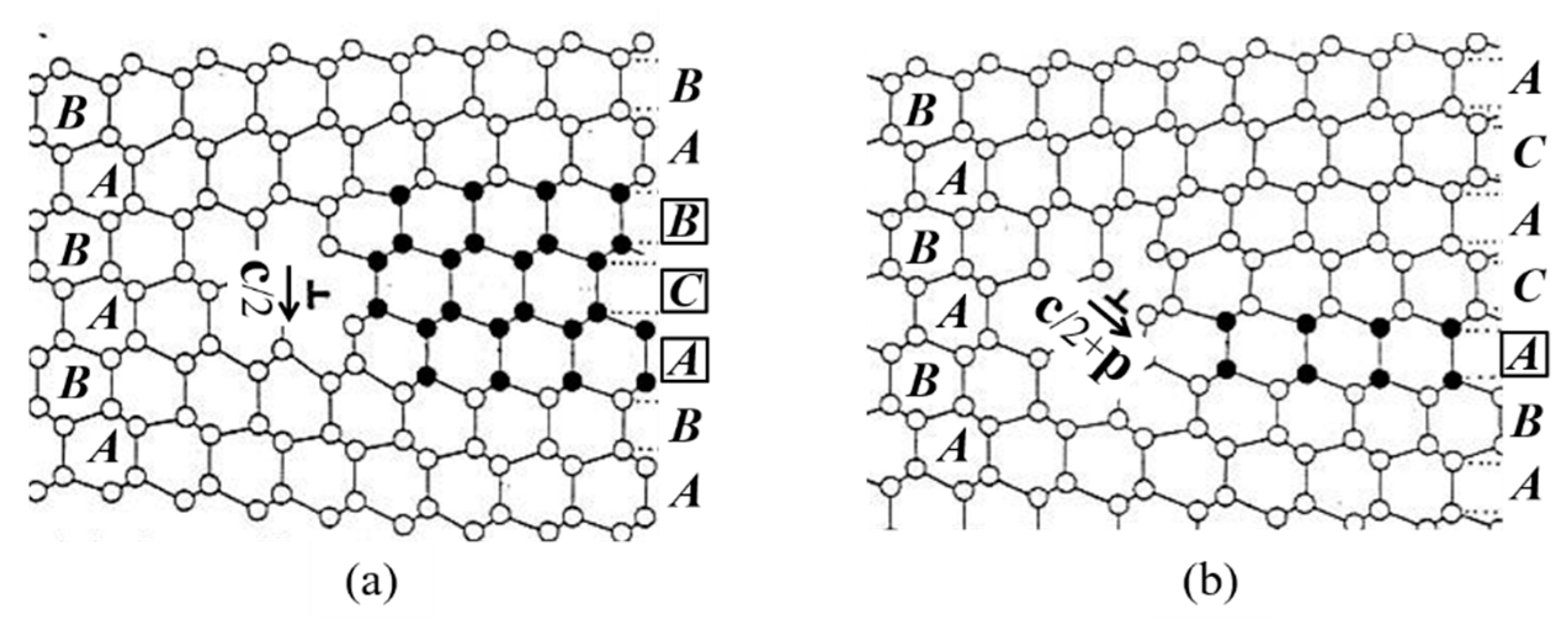
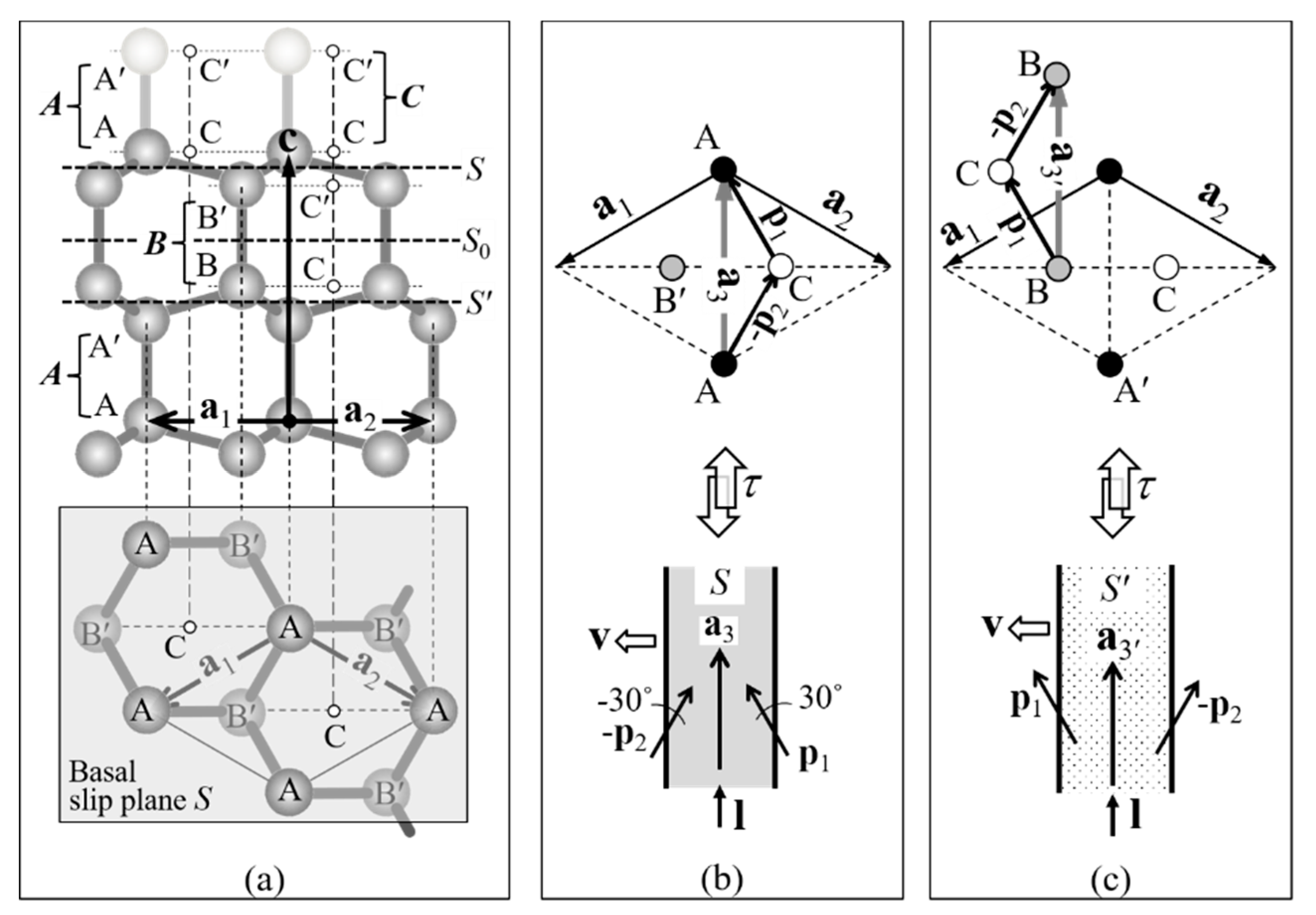

| Plane | Perfect Dislocation | Dissociation Reaction | Extended Width *1 we |
|---|---|---|---|
| (0001) | <a> | pj + (−pk) | 25 nm (<a>: screw) 49 nm (<a>: 60°) 57 nm (<a>: edge) |
| (0001) | <c> | c/2 + c/2 | 129 nm |
| (c/2 + pi) + (c/2 − pi) | 256 nm (<p>: screw) 193 nm (<p>: edge) | ||
| (0001) | <c + a> | (c/2 + pj) + (c/2 − pk) | 437 nm (<a>: screw) 501 nm (<a>: edge) |
| Case | Temperature | |||||
|---|---|---|---|---|---|---|
| 253 K (−20 °C) | 223 K (−50 °C) | 193 K (−80 °C) | 173 K (−100 °C) | 123 K (−150 °C) | ||
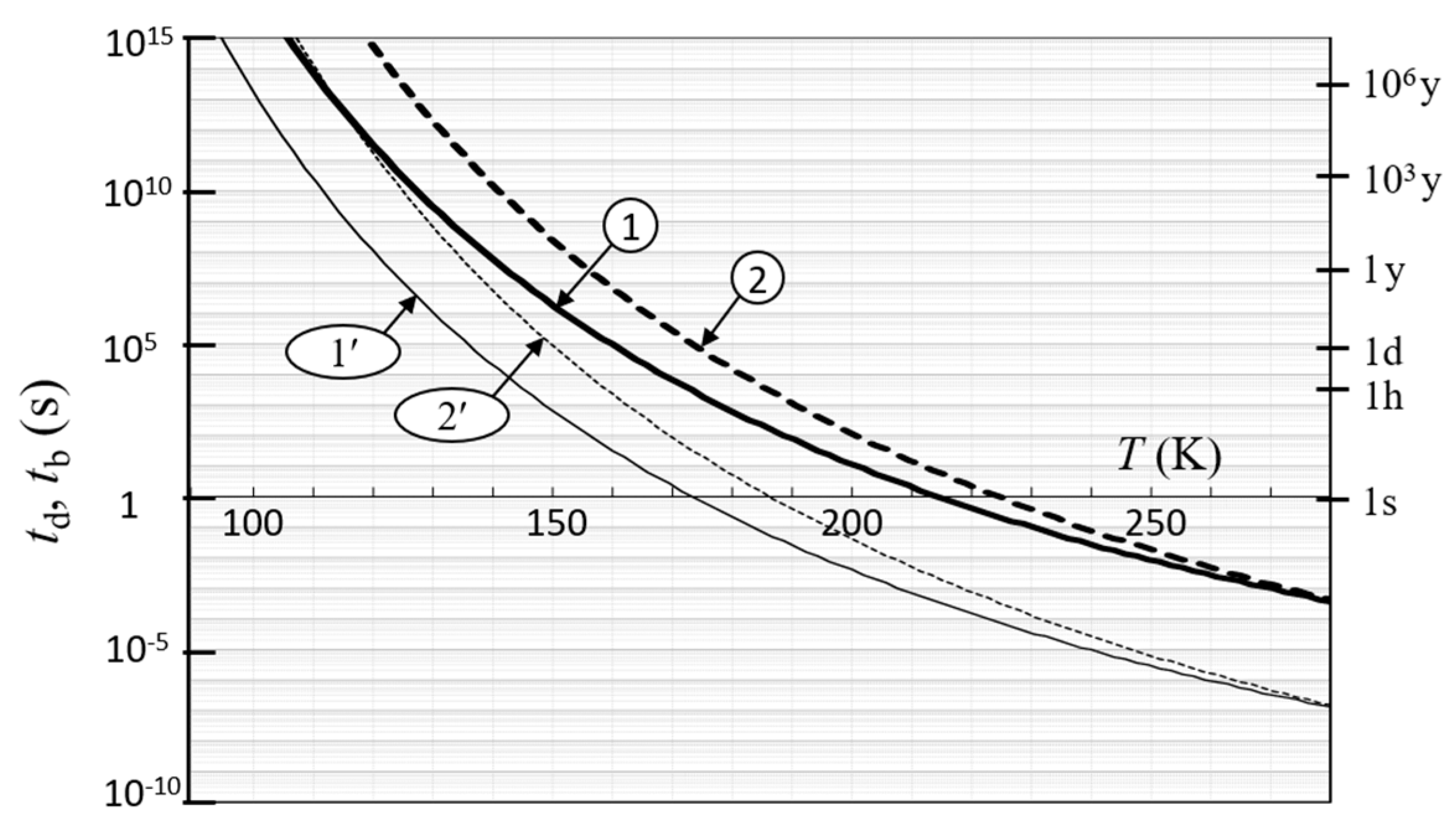
| td *1 | 1 | 5.8 × 10−3 s (5.8 ms) | 2.7 × 10−1 s (0.27 s) | 4.2 × 10 s (42 s) | 3.2 × 103 s (0.89 h) | 7.9 × 1010 s (2.5 Ky) |
| 2 | 1.2 × 10−2 s (12 ms) | 9.7 × 10−1 s (0.97 s) | 5.7 × 102 s (570 s) | 1.1 × 104 s (4 h) | 9.8 × 1013 s (3.1 My) | |
| tb *2 | 1′ | 2.0 × 10−6 s (2.0 μs) | 2.0 × 10−4 s (0.2 ms) | 1.5 × 10−2 s (15 ms) | 1.1 s (1.1 s) | 2.7 × 107 s (0.86 y) |
| 2′ | 4.1 × 10−6 s (4.1 μs) | 9.2 × 10−4 s (0.92 ms) | 0.20 s (0.20 s) | 3.8 × 101 s (38 s) | 3.4×1010 s (1.1 Ky) | |
| Material | Shear Modulus μ (GPa) *1 | Poisson’s Ratio ν *1 | Burgers Vector bp (nm) *2 | SF Energy γp (mJ/m2) *3 | Extended Width we (nm) | 2γp/bp (MPa) |
|---|---|---|---|---|---|---|
| Ice ( Ih ) | 3.55 | 0.325 | 0.261 | 0.62 | 25 | 4.8 |
| Si (diamond) | 68.1 | 0.218 | 0.222 | 55 | 4.2 | 500 |
| Ge (diamond) | 56.4 | 0.200 | 0.231 | 60 | 3.5 | 520 |
| CdS (wurzite) | 18.5 | 0.378 | 0.239 | 8.7 | 6.7 | 73 |
| Cu (fcc) | 54.6 | 0.324 | 0.148 | 45 | 1.6 | 610 |
| Zn (hcp) | 43.4 | 0.249 | 0.154 | 140 | 0.5 | 1800 |
| Cylinder Diameter d (nm) (=R0) | Final Distance R (nm) | Dissociation-Beginning and -Completing Times tb, td (s) | ||||
|---|---|---|---|---|---|---|
| T = 273 (K) (0 °C) | 253 (K) (−20 °C) | 223 (K) (−50 °C) | 183 (K) (−90 °C) | |||
| td | 2.94 (=4c) | 495 (=0.99we) *1 | 5.5 × 106 (64 d) | 1.3 × 108 (4.1 y) | 4.2 × 1010 (1.3 Ky) | 1.9 × 1015 (61 My) |
| 1.47 (=2c) | 6.2 × 106 (72 d) | 1.4 × 108 (4.6 y) | 4.8 × 1010 (1.5 Ky) | 2.2 × 1015 (68 My) | ||
| tb | 0.734 (=c) | 1.35 (=3a) | 0.15 | 3.0 | 720 | 1.7 × 107 (200 d) |
| 1.47 (=2c) | 2.25 (=5a) | 0.63 | 13.5 | 3840 | 1.3 × 108 (4.1 y) | |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hondoh, T. Dissociation Behavior of Dislocations in Ice. Crystals 2019, 9, 386. https://doi.org/10.3390/cryst9080386
Hondoh T. Dissociation Behavior of Dislocations in Ice. Crystals. 2019; 9(8):386. https://doi.org/10.3390/cryst9080386
Chicago/Turabian StyleHondoh, Takeo. 2019. "Dissociation Behavior of Dislocations in Ice" Crystals 9, no. 8: 386. https://doi.org/10.3390/cryst9080386
APA StyleHondoh, T. (2019). Dissociation Behavior of Dislocations in Ice. Crystals, 9(8), 386. https://doi.org/10.3390/cryst9080386





