Anomalous Behaviors of Spin Waves Studied by Inelastic Light Scattering
Abstract
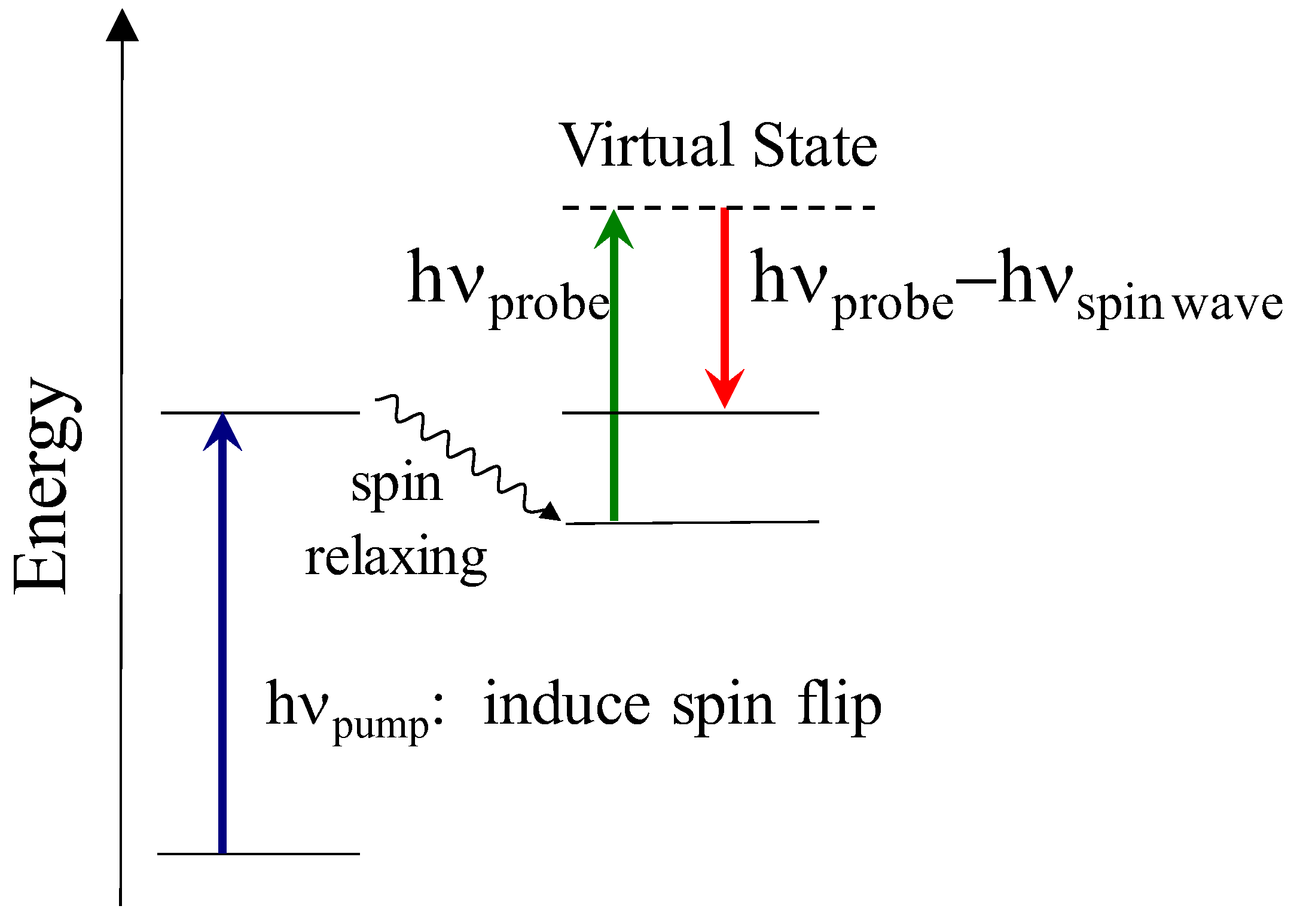
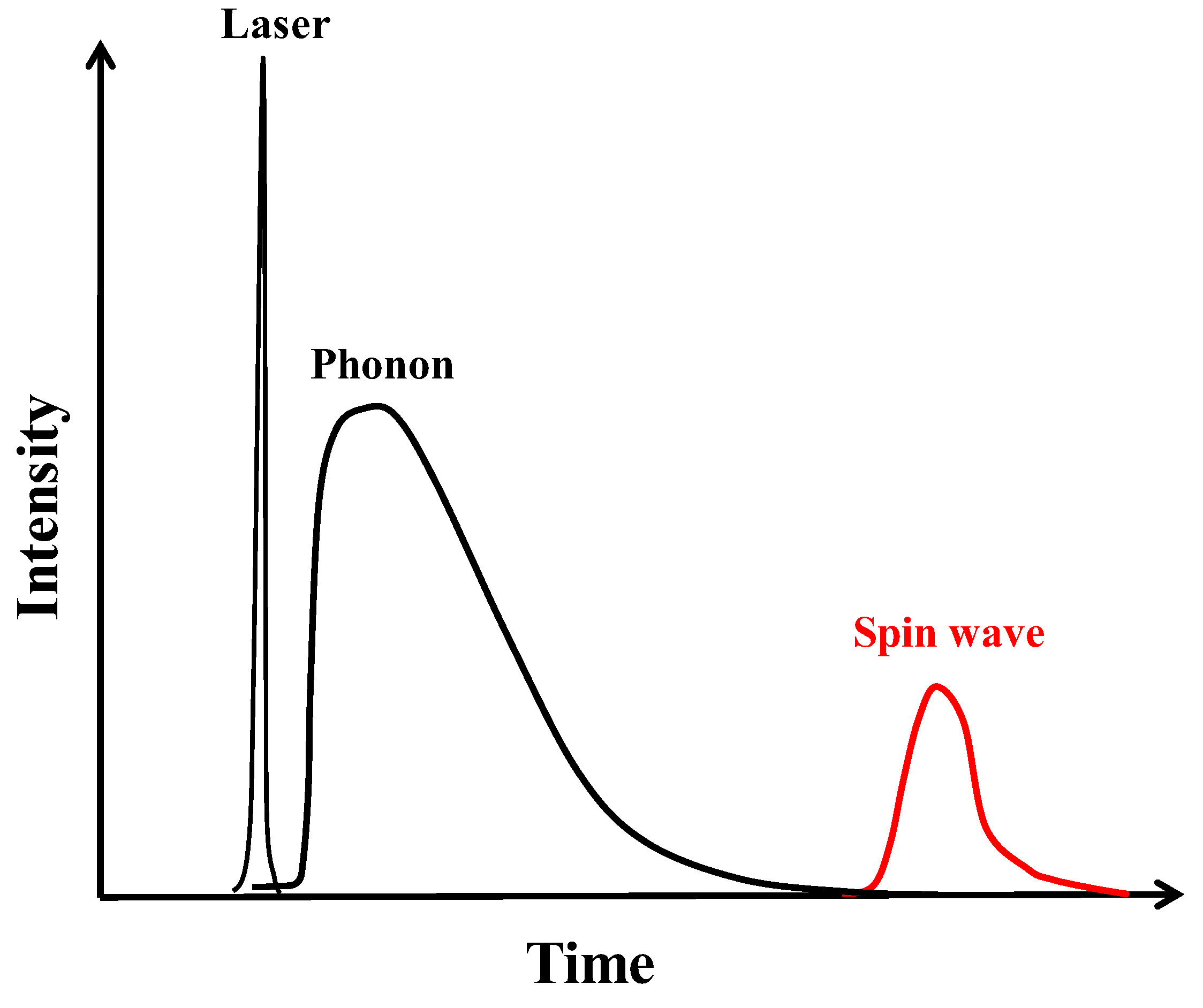
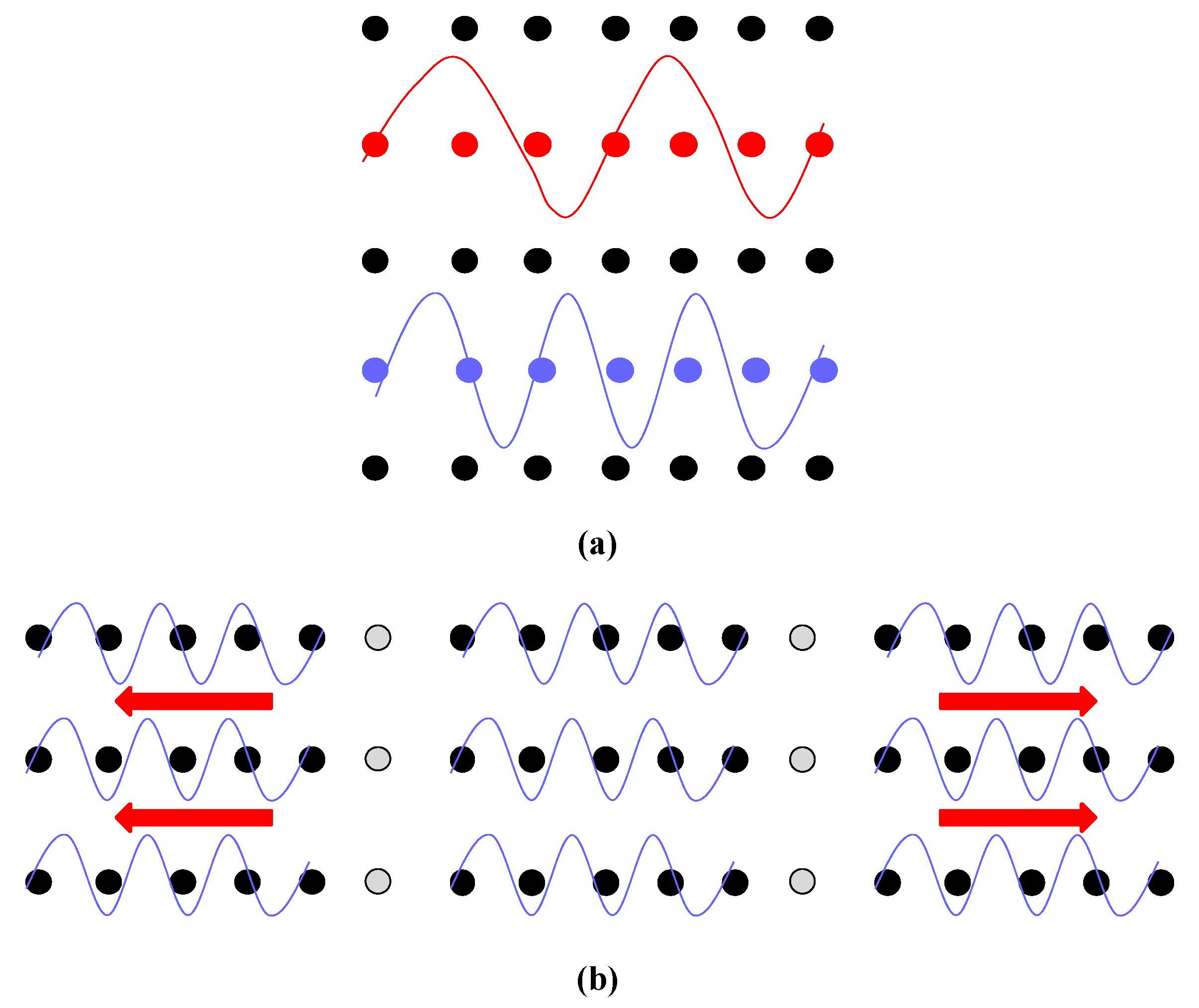
1. Introduction
2. Anti-Stokes to Stokes Intensity Ratio
3. Broad Linewidth
4. Resonance Effect
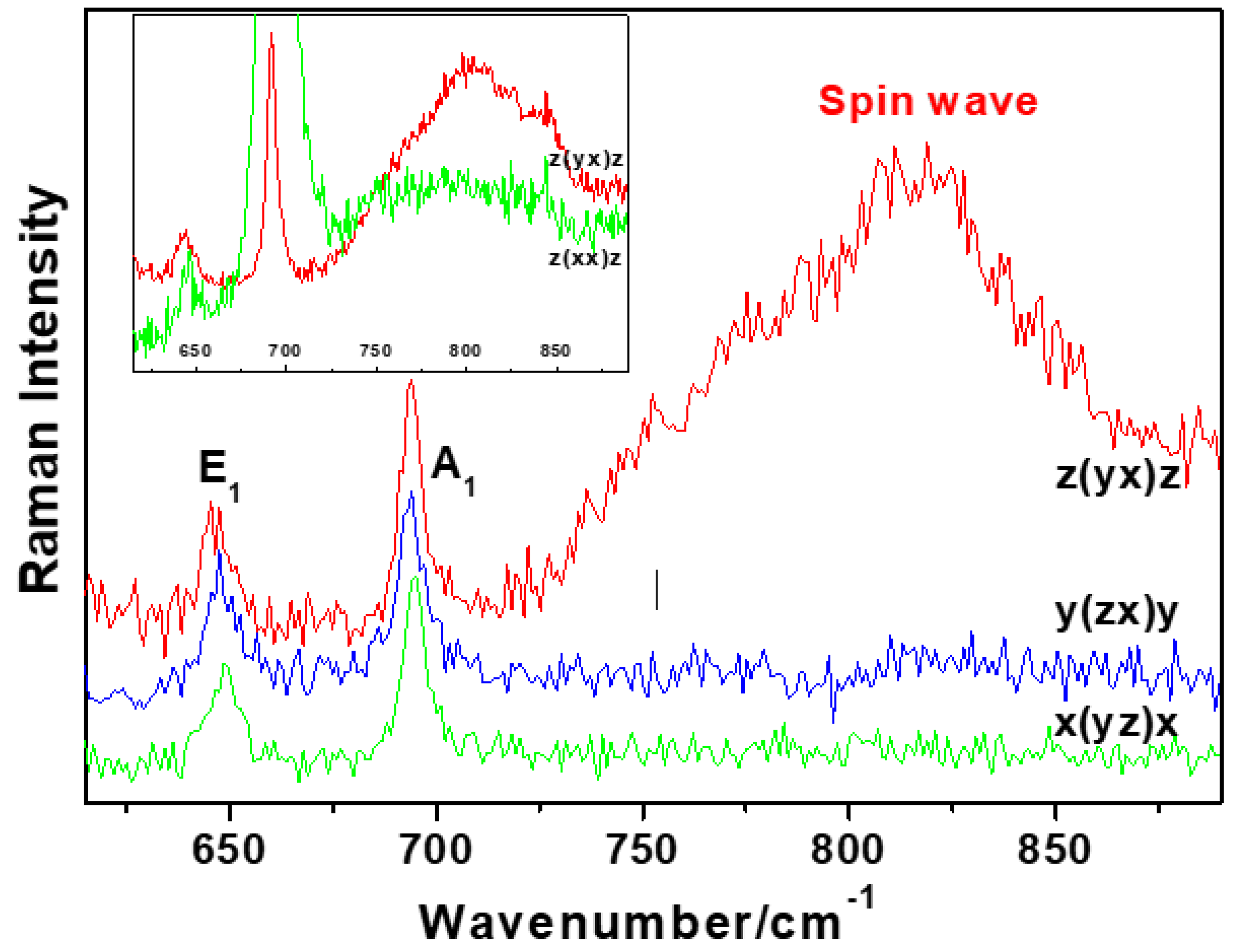
5. Polarization Selection
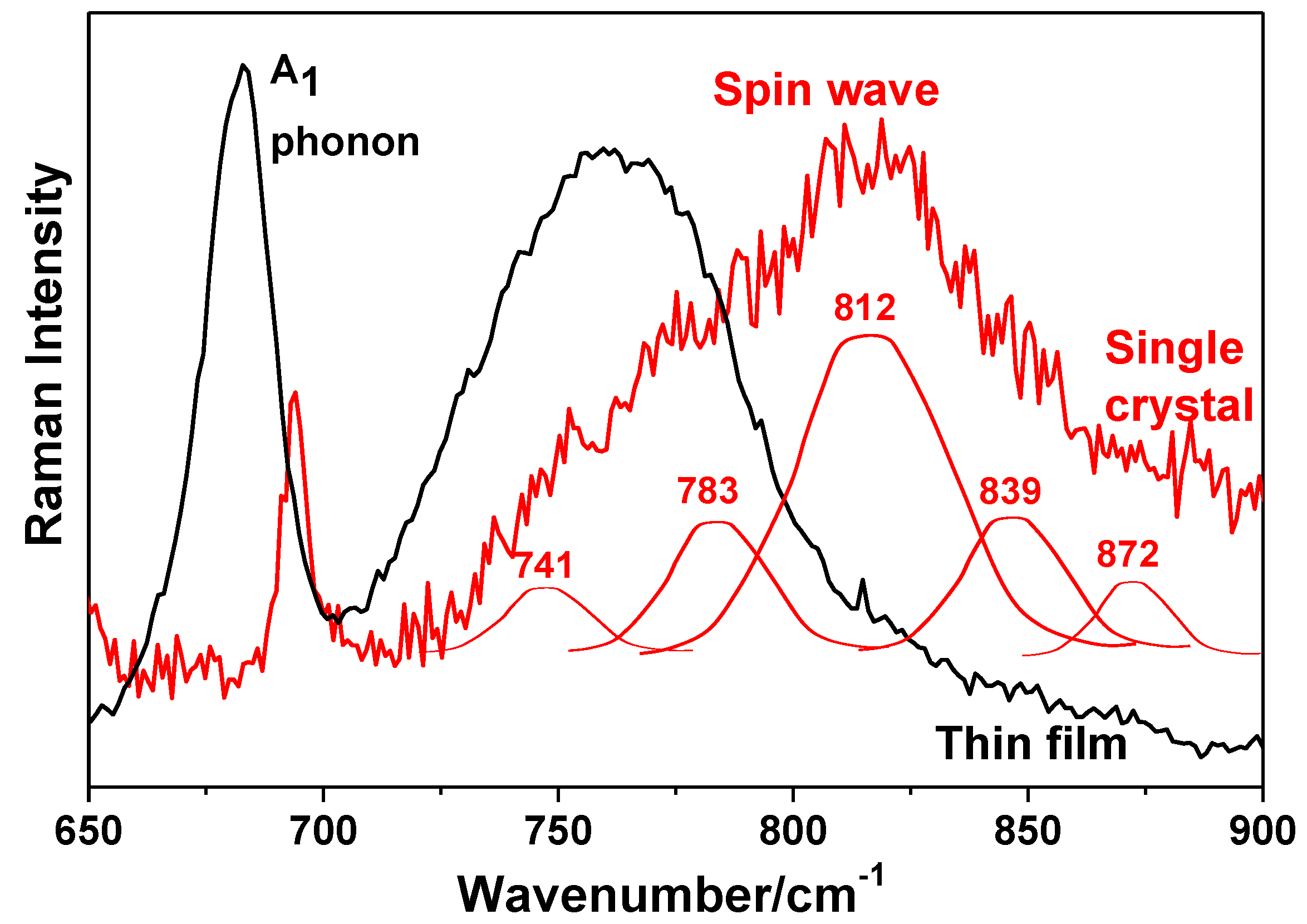
6. Impurity Dependence
7. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Kruglyak, V.V.; Demokritov, S.O.; Grundler, D. Magnonics. J. Phys. D Appl. Phys. 2010, 43, 264001. [Google Scholar] [CrossRef]
- Neusser, S.; Grundler, D. Magnonics: Spin waves on the nanoscale. Adv. Mater. 2009, 21, 2927. [Google Scholar] [CrossRef]
- Rovillain, P.; De Sousa, R.; Gallais, Y.; Sacuto, A.; Méasson, M.A.; Colson, D.; Forget, A.; Bibes, M.; Barthélémy, A.; Cazayous, M. Electric-field control of spin waves at room temperature in multiferroic BiFeO3. Nat. Mater. 2010, 9, 975–979. [Google Scholar] [CrossRef] [PubMed]
- Lenk, B.; Ulrichs, H.; Garbs, F.; Münzenberg, M. The building blocks of magnonics. Phys. Rep. 2011, 507, 107–136. [Google Scholar] [CrossRef]
- Demokritov, S.O.; Slavin, A.N. Magnonics, from Fundamental to Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Stamps, R.L.; Breitkreutz, S.; Åkerman, J.; Chumak, A.V.; Otani, Y.C.; Bauer, G.E.W.; Thiele, J.U.; Bowen, M.; Majetich, S.A.; Mathias Kläui, M.; et al. The 2014 magnetism roadmap. J. Phys. D Appl. Phys. 2014, 47, 333001. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnon transistor for all-magnon data processing. Nat. Commun. 2014, 5, 4700. [Google Scholar] [CrossRef]
- Chumak, A.V.; Vasyuchka, V.I.; Serga, A.A.; Hillebrands, B. Magnon spintronics. Nat. Phys. 2015, 11, 453. [Google Scholar] [CrossRef]
- Chen, W.; Sigrist, M. Dissipationless multiferroic magnonics. Phys. Rev. Lett. 2015, 114, 157203. [Google Scholar] [CrossRef]
- Oh, J.; Le, M.D.; Nahm, H.H.; Sim, H.; Jeong, J.; Perring, T.G.; Woo, H.; Nakajima, K.; Ohira-Kawamura, S.; Yamani, Z.; et al. Spontaneous decays of magneto-elastic excitations in non-collinear antiferromagnet (Y, Lu)MnO3. Nat. Commun. 2016, 7, 13146. [Google Scholar] [CrossRef]
- Grundler, D. Nanomagnonics around the corner. Nat. Nanotech. 2016, 11, 407. [Google Scholar] [CrossRef]
- Chumak, A.V.; Schultheiss, H. Magnonics: Spin waves connecting charges, spins and photons. J. Phys. D Appl. Phys. 2017, 50, 300201. [Google Scholar] [CrossRef]
- Garst, M.; Waizner, J.; Grundler, D. Collective spin excitations of helices and magnetic skyrmions: Review and perspectives of magnonics in non-centrosymmetric magnets. J. Phys. D Appl. Phys. 2017, 50, 293002. [Google Scholar] [CrossRef]
- Yu, H.; Xiao, J.; Pirro, P. Magnonspintronics. J. Magn. Magn. Mater. 2018, 450, 1–2. [Google Scholar] [CrossRef]
- Wang, X.S.; Zhang, H.W.; Wang, X.R. Topological Magnonics: A Paradigm for Spin-Wave Manipulation and Device Design. Phys. Rev. Appl. 2018, 9, 024029. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Odintsov, S.A.; Beginin, E.N.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Toward nonlinear magnonics: Intensity-dependent spin-wave switching in insulating side-coupled magnetic stripes. Phys. Rev. B 2017, 96, 144428. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Grachev, A.A.; Sheshukova, S.E.; Sharaevskii, Y.P.; Serdobintsev, A.A.; Mitin, D.M.; Nikitov, S.A. Magnon straintronics: Reconfigurable spin-wave routing in strain-controlled bilateral magnetic stripes. Phys. Rev. Lett. 2018, 120, 257203. [Google Scholar] [CrossRef] [PubMed]
- Sadovnikov, A.V.; Grachev, A.A.; Beginin, E.N.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Voltage-controlled spin-wave coupling in adjacent ferromagnetic-ferroelectric heterostructures. Phys. Rev. Appl. 2017, 7, 014013. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Gubanov, V.A.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Spin-wave drop filter based on asymmetric side-coupled magnonic crystals. Phys. Rev. Appl. 2018, 9, 051002. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Grachev, A.A.; Gubanov, V.A.; Odintsov, S.A.; Martyshkin, A.A.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Spin-wave intermodal coupling in the interconnection of magnonic units. Appl. Phys. Lett. 2018, 112, 142402. [Google Scholar] [CrossRef]
- Vaz, C.A.F. Electric field control of magnetism in multiferroic heterostructures. J. Phys. Condens. Matter. 2012, 24, 333201. [Google Scholar] [CrossRef]
- De Sousa, R.; Moore, J.E. Electrical control of magnon propagation in multiferroic BiFeO3 films. Appl. Phys. Lett. 2008, 92, 022514. [Google Scholar] [CrossRef]
- Matsukura, F.; Tokura, Y.; Ohno, H. Control of magnetism by electric fields. Nat. Nanotechnol. 2015, 10, 209–220. [Google Scholar] [CrossRef] [PubMed]
- De Sousa, R.; Allen, M.; Cazayous, M. Theory of Spin-Orbit Enhanced Electric-Field Control of Magnetism in Multiferroic BiFeO3. Phys. Rev. Lett. 2013, 110, 267202. [Google Scholar] [CrossRef] [PubMed]
- Cherepov, S.; Amiri, P.K.; Alzate, J.G.; Wong, K.; Lewis, M.; Upadhyaya, P.; Nath, J.; Bao, M.; Bur, A.; Wu, T.; et al. Electric-field-induced spin wave generation using multiferroicmagnetoelectric cells. Appl. Phys. Lett. 2014, 104, 082403. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Beginin, E.N.; Bublikov, K.V.; Grishin, S.V.; Sheshukova, S.E.; Sharaevskii, Y.P.; Nikitov, S.A. Brillouin light scattering study of transverse mode coupling in confined yttrium iron garnet/barium strontium titanate multiferroic. J. Appl. Phys. 2015, 118, 203906. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Beginin, E.N.; Sheshukova, S.E.; Sharaevskii, Y.P.; Stognij, A.I.; Novitski, N.N.; Sakharov, V.K.; Khivintsev, Y.V.; Nikitov, S.A. Route toward semiconductor magnonics: Light-induced spin-wave nonreciprocity in a YIG/GaAs structure. Phys. Rev. B 2019, 99, 054424. [Google Scholar] [CrossRef]
- Sadovnikov, A.V.; Bublikov, K.V.; Beginin, E.N.; Nikitov, S.A. The electrodynamic characteristics of a finite-width metal/dielectric/ferroelectric/dielectric/metal layer structure. J. Commun. Technol. Electron. 2014, 59, 914–919. [Google Scholar] [CrossRef]
- Kuzmenko, A.M.; Szaller, D.; Kain, T.; Dziom, V.; Weymann, L.; Shuvaev, A.; Pimenov, A.; Mukhin, A.A.; Ivanov, V.U.; Gudim, I.A.; et al. Switching of magnons by electric and magnetic fields in multiferroic borates. Phys. Rev. Lett. 2018, 120, 027203. [Google Scholar] [CrossRef]
- Rado, G.T.; Weertman, J.R. Spin-wave resonance in a ferromagnetic metal. J. Phys. Chem. Solids 1959, 11, 315–333. [Google Scholar] [CrossRef]
- Flovik, V.; Pettersen, B.H.; Wahlström, E. Eddy-current effects on ferromagnetic resonance: Spin wave excitations and microwave screening effects. J. Appl. Phys. 2016, 119, 163903. [Google Scholar] [CrossRef]
- Vazhenina, I.G.; Iskhakov, R.S.; Chekanova, L.A. Spin-wave resonance in chemically deposited Fe-Ni films: Measuring the spin-wave stiffness and surface anisotropy constant. Phys. Solid State 2018, 60, 292–298. [Google Scholar] [CrossRef]
- Liu, X.; Li, X.; Bac, S.K.; Zhang, X.; Dong, S.; Lee, S.; Dobrowolska, M.; Furdyna, J.K. Ferromagnetic resonance and spin-wave resonances in GaMnAsP films. AIP Adv. 2018, 8, 056402. [Google Scholar] [CrossRef]
- Gopman, D.B.; Lau, J.W.; Mohanchandra, K.P.; Wetzlar, K.; Carman, G.P. Determination of the exchange constant of Tb0.3Dy0.7Fe2 by broadband ferromagnetic resonance spectroscopy. Phys. Rev. B 2016, 93, 064425. [Google Scholar] [CrossRef] [PubMed]
- Gokhale, M.P.; Mills, D.L. Spin excitations of a model itinerant ferromagnetic film: Spin waves, Stoner excitations, and spin-polarized electron-energy-loss spectroscopy. Phys. Rev. B 1994, 49, 3880–3893. [Google Scholar] [CrossRef] [PubMed]
- Plihal, M.; Mills, D.L.; Kirschner, J. Spin wave signature in the spin polarized electron energy loss spectrum of ultrathin Fe films: Theory and experiment. Phys. Rev. Lett. 1999, 82, 2579–2582. [Google Scholar] [CrossRef]
- Vollmer, R.; Etzkorn, M.; Kumar, P.S.A.; Ibach, H.; Kirschner, J. Spin-polarized electron energy loss spectroscopy of high energy, large wave vector spin waves in ultrathin FCC Co films on Cu (001). Phys. Rev. Lett. 2003, 91, 147201. [Google Scholar] [CrossRef] [PubMed]
- Prokop, J.; Tang, W.X.; Zhang, Y.; Tudosa, I.; Peixoto, T.R.F.; Zakeri, K.; Kirschner, J. Magnons in a ferromagnetic monolayer. Phys. Rev. Lett. 2009, 102, 177206. [Google Scholar] [CrossRef] [PubMed]
- Zakeri, K.; Zhang, Y.; Kirschner, J. Surface magnons probed by spin-polarized electron energy loss spectroscopy. J. Electron Spectrosc. Relat. Phenom. 2013, 189, 157–163. [Google Scholar] [CrossRef]
- Hutchings, M.T.; Samuelsen, E.J. Measurement of spin-wave dispersion in NiO by inelastic neutron scattering and its relation to magnetic properties. Phys. Rev. B 1972, 6, 3447–3461. [Google Scholar] [CrossRef]
- Bohn, H.G.; Zinn, W.; Dorner, B.; Kollmar, A. Neutron scattering study of spin waves and exchange interactions in ferromagnetic EuS. Phys. Rev. B 1980, 22, 5447. [Google Scholar] [CrossRef]
- Mook, H.A.; Paul, D.M.K. Neutron-scattering measurement of the spin-wave spectra for nickel. Phys. Rev. Lett. 1985, 54, 227–229. [Google Scholar] [CrossRef] [PubMed]
- Rossat-Mignod, J.; Regnault, L.P.; Vettier, C.; Bourges, P.; Burlet, P.; Bossy, J.; Henry, J.Y.; Lapertot, G. Neutron scattering study of the YBa2Cu3O6+x system. Physica C 1991, 185–189, 86–92. [Google Scholar] [CrossRef]
- Huberman, T.; Coldea, R.; Cowley, R.A.; Tennant, D.A.; Leheny, R.L.; Christianson, R.J.; Frost, C.D. Two-magnon excitations observed by neutron scattering in the two-dimensional spin-5/2 Heisenberg antiferromagnet Rb2MnF4. Phys. Rev. B 2005, 72, 014413. [Google Scholar] [CrossRef]
- Ran, K.; Wang, J.; Wang, W.; Dong, Z.; Ren, X.; Bao, S.; Li, S.; Ma, Z.; Gan, Y.; Zhang, Y.; et al. Spin-Wave Excitations Evidencing the Kitaev Interaction in Single Crystalline a-RuCl3. Phys. Rev. Lett. 2017, 118, 107203. [Google Scholar] [CrossRef] [PubMed]
- Golosovsky, I.V.; Ovsyanikov, A.K.; Aristov, D.N.; Matveeva, P.G.; Mukhin, A.A.; Boehm, M.; Regnault, L.P.; Bezmaternykh, L.N. Spin-wave dynamics and exchange interactions in multiferroicNdFe3(BO3)4explored by inelastic neutron scattering. J. Magn. Magn. Mater. 2018, 451, 443–449. [Google Scholar] [CrossRef]
- Fleury, P.A.; Porto, S.P.S.; Cheesman, L.E.; Guggenheim, H.J. Light Scattering by Spin Waves in FeF2. Phys. Rev. Lett. 1966, 17, 84–87. [Google Scholar] [CrossRef]
- Fleury, P.A.; Porto, S.P.S.; Loudon, R. Two-Magnon Light Scattering in Antiferromagnetic. Phys. Rev. Lett. 1967, 18, 658–662. [Google Scholar] [CrossRef]
- Fleury, P.A. Evidence for Magnon-Magnon Interactions in RbMnF3. Phys. Rev. Lett. 1968, 21, 151. [Google Scholar] [CrossRef]
- Fleury, P.A.; Guggenheim, H.J. Magnon-Pair Modes in Two Dimensions. Phys. Rev. Lett. 1970, 25, 197. [Google Scholar] [CrossRef]
- Cottam, M.G. On the temperature dependence of one-magnon light scattering in antiferromagnets. J. Phys. C Solid State Phys. 1975, 8, 1933–1949. [Google Scholar] [CrossRef]
- Bates, P.A.; Cottam, M.G.; Smith, S.R.P. “Anomalous” behaviour of the anti-Stokes-Stokes intensity ratio for one-magnon Raman scattering in FeF2. Solid State Commun. 1980, 33, 129–132. [Google Scholar] [CrossRef]
- Petrou, A.; Peterson, D.L.; Venugopalan, S.; Galazka, R.R.; Ramdas, A.K.; Rodriguez, S. Zeeman Effect of the Magnetic Excitations in a Diluted Magnetic Semiconductor: A Raman Scattering Study of Cd1-xMnxTe. Phys. Rev. Lett. 1982, 48, 1036–1039. [Google Scholar] [CrossRef]
- Rezende, S.M.; De Aguiar, F.M.; Lucena, M.A.; Azevedo, A. Magnon Excitation by Spin Injection in Thin Fe/Cr/Fe Films. Phys. Rev. Lett. 2000, 84, 4212–4215. [Google Scholar] [CrossRef] [PubMed]
- Cazzanelli, E.; Kuzmin, A.; Mironova-Ulmane, N.; Mariotto, G. Behavior of one-magnon frequency in antiferromagnetic NicMg1-cO solid solutions. Phys. Rev. B 2005, 71, 134415. [Google Scholar] [CrossRef]
- Meloche, E.; Cottam, M.G.; Gnezdilov, V.P.; Lockwood, D.J. One-magnon inelastic light scattering in the canted antiferromagnetNiF2. Phys. Rev. B 2010, 81, 024426. [Google Scholar] [CrossRef]
- Di, K.; Zhang, V.L.; Lim, H.S.; Ng, S.C.; Kuok, M.H.; Yu, J.; Yoon, J.; Qiu, X.; Yang, H. Direct observation of the Dzyaloshinskii-Moriya interaction in a Pt/Co/Ni film. Phys. Rev. Lett. 2015, 114, 047201. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.M.H.; Sandilands, L.J.; Sohn, C.H.; Kim, C.H.; Wysocki, A.L.; Yang, I.S.; Moon, S.J.; Ko, J.H.; Yamaura, J.; Hiroi, Z.; et al. Two-magnon scattering in the 5d all-in-all-out pyrochlore magnet Cd2Os2O7. Nat. Commun. 2015, 8, 251. [Google Scholar] [CrossRef]
- Gretarsson, H.; Sung, N.H.; Höppner, M.; Kim, B.J.; Keimer, B.; Tacon, M.L. Two-Magnon Raman Scattering and Pseudospin-Lattice Interactions in Sr2IrO4 and Sr3Ir2O7. Phys. Rev. Lett. 2016, 116, 136401. [Google Scholar] [CrossRef]
- Odintsov, S.A.; Sadovnikov, A.V.; Grachev, A.A.; Beginin, E.N.; Sharaevskii, Y.P.; Nikitov, S.A. Spatial–frequency selection of magnetostatic waves in a two-dimensional magnonic crystal lattice. JETP Lett. 2016, 104, 563–567. [Google Scholar] [CrossRef]
- Wettling, W.; Cottam, M.G.; Sandercock, J.R. The relation between one-magnon light scattering and the complex magneto-optic effects in YIG. J. Phys. C Solid State Phys. 1975, 8, 211. [Google Scholar] [CrossRef]
- White, R.M.; Nemanich, R.J.; Herring, C. Light scattering from magnetic excitations in orthoferrites. Phys. Rev. B 1982, 25, 1822–1836. [Google Scholar] [CrossRef]
- Camley, R.E.; Grünberg, P.; Mayr, C.M. Stokes—Anti-Stokes asymmetry in Brillouin scattering from magnons in thin ferromagnetic films. Phys. Rev. B 1982, 26, 2609–2614. [Google Scholar] [CrossRef]
- Petrou, A.; Peterson, D.L.; Venugopalan, S.; Galazka, R.R.; Ramdas, A.K.; Rodriguez, S. Raman scattering study of the magnetic excitations in diluted magnetic semiconductors in the presence of an external magnetic field. Phys. Rev. B 1983, 27, 3471–3482. [Google Scholar] [CrossRef]
- Lockwood, D.J.; Cottam, M.G.; So, V.C.Y.; Katiyar, R.S. Raman scattering from one-magnon excitations in FeF2. J. Phys. C Solid State Phys. 1984, 17, 6009–6026. [Google Scholar] [CrossRef]
- Zivieri, R.; Vavassori, P.; Giovannini, L.; Nizzoli, F.; Fullerton, E.E.; Grimsditch, M.; Metlushko, V. Stokes–Anti-Stokes Brillouin intensity asymmetry of spin-wave modes in ferromagnetic films and multilayers. Phys. Rev. B 2002, 65, 165406. [Google Scholar] [CrossRef]
- Crew, D.C.; Stamps, R.L.; Liu, H.Y.; Wang, Z.K.; Kuok, M.H.; Ng, S.C.; Barmak, K.; Kim, J.; Lewis, L.H. Light scattering from spin wave excitations in a Co/CoPt exchange spring. J. Magn. Magn. Mater. 2005, 290, 530–532. [Google Scholar] [CrossRef]
- Stashkevich, A.A.; Roussigné, Y.; Djemia, P.; Chérif, S.M.; Evans, P.R.; Murphy, A.P.; Hendren, W.R.; Atkinson, R.; Pollard, R.J.; Zayats, A.V.; et al. Spin-wave modes in Ni nanorod arrays studied by Brillouin light scattering. Phys. Rev. B 2009, 80, 144406. [Google Scholar] [CrossRef]
- Jantzt, W.; Sandercock, J.R.; Wettling, W. Determination of magnetic and elastic properties of FeBO3 by light scattering. J. Phys. C Solid State Phys. 1976, 9, 2229–2240. [Google Scholar] [CrossRef]
- Venugopalan, S.; Becker, M.M. Raman scattering study of LuFeO3. J. Chem. Phys. 1990, 93, 3833–3836. [Google Scholar] [CrossRef]
- Grünberg, P.; Metawe, F. Light scattering from bulk and surface spin waves in EuO. Phys. Rev. Lett. 1977, 39, 1561–1565. [Google Scholar] [CrossRef]
- Sandercock, J.; Wettling, W. Light scattering from thermal magnons in iron and nickel. IEEE Trans. Magn. 1978, 14, 442–444. [Google Scholar] [CrossRef]
- Sandercock, J.R.; Wettling, W. Light scattering from surface and bulk thermal magnons in iron and nickel. J. Appl. Phys. 1979, 50, 7784. [Google Scholar] [CrossRef]
- Grimsditch, M.; Malozemoff, A.; Brunsch, A. Standing Spin Waves Observed by Brillouin Scattering in Amorphous Metallic Films. Phys. Rev. Lett. 1979, 43, 711. [Google Scholar] [CrossRef]
- Malozemoff, A.P.; Grimsditch, M.; Aboaf, J.; Brunsch, A. Brillouin-scattering studies of polycrystalline and amorphous sputtered films of Fe1−xBx and Co1−xBx. J. Appl. Phys. 1979, 50, 5885. [Google Scholar] [CrossRef]
- Basistyy, R.; Stanislavchuk, T.N.; Sirenko, A.A.; Litvinchuk, A.P.; Kotelyanskii, M.; Carr, G.L.; Lee, N.; Wang, X.; Cheong, S.W. Infrared-active optical phonons and magnetic excitations in the hexagonal manganitesRMnO3 (R = Ho, Er, Tm, Yb, and Lu). Phys. Rev. B 2014, 90, 024307. [Google Scholar] [CrossRef]
- Stanislavchuk, T.N.; Wang, Y.; Janssen, Y.; Carr, G.L.; Cheong, S.W.; Sirenko, A.A. Magnon and electromagnon excitations in multiferroic DyFeO3. Phys. Rev. B 2016, 93, 094403. [Google Scholar] [CrossRef]
- Nakajima, T.; Tokunaga, Y.; Matsuda, M.; Dissanayake, S.; Fernandez-Baca, J.; Kakurai, K.; Taguchi, Y.; Tokura, Y.; Arima, T. Magnetic structures and excitations in a multiferroic Y-type hexaferrite BaSrCo2Fe11AlO22. Phys. Rev. B 2016, 94, 195154. [Google Scholar] [CrossRef]
- Soda, M.; Chang, L.J.; Matsumoto, M.; Garlea, V.O.; Roessli, B.; White, J.S.; Kawano-Furukawa, H.; Masuda, T. Polarization analysis of magnetic excitation in multiferroicBa2CoGe2O7. Phys. Rev. B 2018, 97, 214437. [Google Scholar] [CrossRef]
- Leiner, J.C.; Kim, T.; Park, K.; Oh, J.; Perring, T.G.; Walker, H.C.; Xu, X.; Wang, Y.; Cheong, S.W.; Park, J.G. Magnetic excitations in the bulk multiferroic two-dimensional triangular lattice antiferromagnet (Lu,Sc)FeO3. Phys. Rev. B 2018, 98, 134412. [Google Scholar] [CrossRef]
- Hien, N.T.M.; Chen, X.B.; Hoang, L.H.; Lee, D.; Jang, S.Y.; Noh, T.W.; Yang, I.S. Raman scattering studies of the magnetic ordering in hexagonal HoMnO3 thin films. J. Raman Spectrosc. 2010, 41, 983–988. [Google Scholar] [CrossRef]
- Chen, X.B.; Hien, N.T.M.; Lee, D.; Jang, S.Y.; Noh, T.W.; Yang, I.S. Resonant A1 phonon and four-magnon Raman scattering in hexagonal HoMnO3 thin film. New J. Phys. 2010, 12, 073046. [Google Scholar] [CrossRef]
- Hien, N.T.M.; Oh, S.Y.; Chen, X.B.; Lee, D.; Jang, S.Y.; Noh, T.W.; Yang, I.S. Raman scattering studies of hexagonal rare-earth RMnO3 (R = Tb, Dy, Ho, Er) thin films. J. Raman Spectrosc. 2011, 42, 1774–1779. [Google Scholar] [CrossRef]
- Chen, X.B.; Hien, N.T.M.; Lee, D.; Jang, S.Y.; Noh, T.W.; Yang, I.S. Spin exchange interactions in hexagonal manganites RMnO3 (R = Tb, Dy, Ho, Er) epitaxial thin films. Appl. Phys. Lett. 2011, 99, 052506. [Google Scholar] [CrossRef]
- Chen, X.B.; Hien, N.T.M.; Yang, I.S.; Lee, D.; Noh, T.W. A Raman Study of the Origin of Oxygen Defects in Hexagonal Manganite Thin Films. Chin. Phys. Lett. 2012, 29, 126103. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Hien, N.T.M.; Chen, X.B.; Yang, I.S.; Park, Y.; Jung, Y.M. 2D correlation analysis of the magnetic excitations in Raman spectra of HoMnO3. J. Mol. Struct. 2014, 1069, 280–283. [Google Scholar] [CrossRef]
- Chen, X.B.; Hien, N.T.M.; Han, K.; Nam, J.Y.; Huyen, N.T.; Shin, S.; Wang, X.; Cheong, S.W.; Lee, D.; Noh, T.W.; et al. Study of spin-ordering and spin-reorientation transitions in hexagonal manganites through Raman spectroscopy. Sci. Rep. 2015, 5, 13366. [Google Scholar] [CrossRef] [PubMed]
- Hien, N.T.M.; Huyen, N.T.; Chen, X.B.; Park, Y.; Jung, Y.M.; Lee, D.; Noh, T.W.; Cheong, S.W.; Yang, I.S. Correlation between magnon and magnetic symmetries of hexagonal RMnO3 (R = Er, Ho, Lu). J. Mol. Struct. 2016, 1124, 103–109. [Google Scholar]
- Chen, X.B.; Guo, P.C.; Huyen, N.T.; Kim, S.; Yang, I.S.; Wang, X.; Cheong, S.W. Spin wave and spin flip in hexagonal LuMnO3 single crystal. Appl. Phys. Lett. 2017, 110, 122405. [Google Scholar] [CrossRef]
- Bartolo, B.D. Optical Interactions in Solids; Wiley: Hoboken, NJ, USA, 1968. [Google Scholar]
- Klemens, P.G. Anharmonic decay of optical phonons. Phys. Rev. 1966, 148, 845–848. [Google Scholar] [CrossRef]
- Chen, X.B.; Huso, J.; Morrison, J.L.; Bergman, L.; Purdy, A.P. Temperature response and anharmonicity of the optical phonons in GaN nanowires. J. Appl. Phys. 2005, 98, 26106. [Google Scholar] [CrossRef]
- Maradudin, A.A. Solid State Physics, Advances in Research and Applications; Seitz, E., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1966; Volume 18, p. 273. [Google Scholar]
- Weber, W.H.; Ford, G.W. Simple model for the linewidth of the two-magnon Raman feature observed in high-Tc superconductors. Phys. Rev. B 1989, 40, 6890–6895. [Google Scholar] [CrossRef] [PubMed]
- Pressl, M.; Mayer, M.; Knoll, P.; Lo, S.; Hohenester, U.; Holzinger-Schweiger, E. Magnetic Raman scattering in undoped and doped antiferromagnets. J. Raman Spectrosc. 1996, 27, 343–349. [Google Scholar] [CrossRef]
- Machtoub, L.H.; Suemoto, T.; Shimoyama, J.; Kishio, K. Relaxation study of elementary excitations in Bi2212 investigated by picosecond Raman spectroscopy. J. Raman Spectrosc. 2002, 33, 471–474. [Google Scholar] [CrossRef]
- Elliott, R.J.; Thorpe, M.F. The effects of magnon-magnon interaction on the two-magnon spectra of antiferromagnets. J. Phys. C Solid State Phys. 1969, 2, 1630–1643. [Google Scholar] [CrossRef]
- Parkinson, J.B. Optical properties of layer antiferromagnets with K2NiF4 structure. J. Phys. C Solid State Phys. 1969, 2, 2012–2021. [Google Scholar] [CrossRef]
- Singh, R.R.P.; Fleury, P.A.; Lyons, K.B.; Sulewski, P.E. Quantitative Determination of Quantum Fluctuations in the Spin-½ Planar Antiferromagnet. Phys. Rev. Lett. 1989, 62, 2736. [Google Scholar] [CrossRef]
- Sugai, S.; Sato, M.; Kobayashi, T.; Akimitsu, J.; Ito, T.; Takagi, H.; Uchida, S.; Hosoya, S.; Kajitani, T.; Fukuda, T. High-energy spin excitations in the insulating phases of high-superconducting cuprates. Phys. Rev. B 1990, 42, 1045. [Google Scholar] [CrossRef]
- Lyons, K.B.; Fleury, P.A. Spin fluctuations in superconducting cuprates. J. Appl. Phys. 1988, 64, 6075–6080. [Google Scholar] [CrossRef]
- Schmidt, A.B.; Pickel, M.; Donath, M.; Buczek, P.; Ernst, A.; Zhukov, V.P.; Echenique, P.M.; Sandratskii, L.M.; Chulkov, E.V.; Weinelt, M. Ultrafast magnon generation in an Fe film on Cu (100). Phys. Rev. Lett. 2010, 105, 197401. [Google Scholar] [CrossRef]
- Zakeri, K.; Zhang, Y.; Chuang, T.H.; Kirschner, J. Magnon lifetimes on the Fe (110) surface: The role of spin-orbit coupling. Phys. Rev. Lett. 2012, 108, 197205. [Google Scholar] [CrossRef]
- Yelon, W.B.; Berger, L. Magnon heat conduction and magnon scattering processes in Fe-Ni alloys. Phys. Rev. B 1972, 6, 1974–1985. [Google Scholar] [CrossRef]
- Hsu, Y.; Berger, L. Magnon heat conduction and magnon lifetimes in the metallic ferromagnet Fe68Co32 at low temperatures. Phys. Rev. B 1976, 114, 4059–4063. [Google Scholar] [CrossRef]
- Souchkov, A.B.; Simpson, J.R.; Quijada, M.; Ishibashi, H.; Hur, N.; Ahn, J.S.; Cheong, S.W.; Millis, A.J.; Drew, H.D. Exchange Interaction Effects on the Optical Properties of LuMnO3. Phys. Rev. Lett. 2003, 91, 027203. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.S.; Moon, S.J.; Seo, S.S.A.; Lee, D.; Lee, J.H.; Murugavel, P.; Noh, T.W.; Lee, Y.S. Optical spectroscopic investigation on the coupling of electronic and magnetic structure in multiferroic hexagonal RMnO3 (R = Gd, Tb, Dy, and Ho) thin films. Phys. Rev. B 2008, 78, 054440. [Google Scholar] [CrossRef]
- Fleury, P.A.; Loudon, R. Scattering of light by one-and two-magnon excitations. Phys. Rev. 1968, 166, 514–530. [Google Scholar] [CrossRef]
- Cardona, M. Light Scattering in Solid II; Cardona, M., Güntherodt, G., Eds.; Springer: New York, NY, USA, 1982. [Google Scholar]
- Blumberg, G.; Abbamonte, P.; Klein, M.V.; Lee, W.C.; Ginsberg, D.M.; Miller, L.L.; Zibold, A. Resonant two-magnon Raman scattering in cuprate antiferromagnetic insulators. Phys. Rev. B 1996, 53, R11930–R11933. [Google Scholar] [CrossRef] [PubMed]
- Chubukov, A.V.; Frenkel, D.M. Resonant two-magnon Raman scattering in antiferromagnetic insulators. Phys. Rev. Lett. 1995, 74, 3057. [Google Scholar] [CrossRef]
- Hanamura, E.; Dan, N.T.; Tanabe, Y. Excitons and two-magnon Raman scattering of the strongly correlated systems La2CuO4 and YBa2Cu3O6. Phys. Rev. B 2000, 62, 7033–7044. [Google Scholar] [CrossRef]
- Tohyama, T.; Onodera, H.; Tsutsui, K.; Maekawa, S. Resonant two-magnon Raman scattering and photoexcited states in two-dimensional Mott insulators. Phys. Rev. Lett. 2002, 89, 257405. [Google Scholar] [CrossRef]
- Shastry, B.S.; Shraiman, B.I. Theory of Raman scattering in Mott-Hubbard systems. Phys. Rev. Lett. 1990, 65, 1068. [Google Scholar] [CrossRef]
- Chen, X.B.; Choi, J.Y.; Kim, H.T. Raman spectroscopy studies of spin wave in V2O3 thin films. J. Phys. D Appl. Phys. 2016, 49, 465304. [Google Scholar] [CrossRef]
- Long, D.A. Intensities in Raman spectra I.A bond polarizability theory. Proc. R. Soc. Lond. Ser. A 1953, 217, 203–221. [Google Scholar]
- Swanson, L.R.; Maradudin, A.A. Pseudopotential calculation of the Raman tensor for homopolar semiconductors. Solid State Commun. 1970, 8, 859–865. [Google Scholar] [CrossRef]
- Tubino, R.; Piseri, L. Raman intensities in covalent crystals: A bond-polarizability approach. Phys. Rev. B 1975, 11, 5145–5152. [Google Scholar] [CrossRef]
- Maradudin, A.A.; Burstein, E. Relation between photoelasticity, electrostriction, and first-order Raman effect in crystals of the diamond structure. Phys. Rev. 1967, 164, 1081–1099. [Google Scholar] [CrossRef]
- Nakashima, S.; Katahama, H.; Nakakura, Y.; Mitsuishi, A.; Pal, B. Raman scattering intensity of the long-period polytypes of CdI2. Phys. Rev. B 1985, 31, 6531–6540. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, S.; Balkanski, M. Raman scattering intensities of layered crystals. Phys. Rev. B 1986, 34, 5801–5807. [Google Scholar] [CrossRef]
- Lewtas, H.J.; Boothroyd, A.T.; Rotter, M.; Prabhakaran, D.; Müller, H.; Le, M.D.; Roessli, B.; Gavilano, J.; Bourges, P. Magnetic excitations in multiferroic LuMnO3 studied by inelastic neutron scattering. Phys. Rev. B 2010, 82, 184420. [Google Scholar] [CrossRef]
- Muñoz, A.; Alonso, J.A.; Martínez-Lope, M.J.; Casáis, M.T.; Martínez, J.L.; Fernández-Díaz, M.T. Magnetic structure of hexagonal RMnO3 (R= Y, Sc): Thermal evolution from neutron powder diffraction data. Phys. Rev. B 2000, 62, 9498–9510. [Google Scholar] [CrossRef]
- Park, J.; Park, J.G.; Jeon, G.S.; Choi, H.Y.; Lee, C.; Jo, W.; Bewley, R.; McEwen, K.A.; Perring, T.G. Magnetic ordering and spin-liquid state of YMnO3. Phys. Rev. B 2003, 68, 104426. [Google Scholar] [CrossRef]
- Oseroff, A.; Pershan, P.S. Raman Scattering from Localized Magnetic Excitations in Ni2+-and Fe2+-Doped MnF2. Phys. Rev. Lett. 1968, 21, 1593. [Google Scholar] [CrossRef]
- Moch, P.; Parisot, G.; Dietz, R.E.; Guggenheim, H.J. Observation of Localized Magnons by Raman Scattering in Ni-Doped MnF2. Phys. Rev. Lett. 1968, 21, 1596–1599. [Google Scholar] [CrossRef]
- Oseroff, A.; Pershan, P.S.; Kestigian, M. Raman Scattering from Localized Magnons. Phys. Rev. 1969, 188, 1046–1047. [Google Scholar] [CrossRef]
- Nam, J.Y.; Kim, S.; Hien, N.T.M.; Chen, X.B.; Sim, H.; Park, J.G.; Lee, D.; Noh, T.W.; Yang, I.S. Nonmagnetic ion doping effect on spin excitations in hexagonal RMnGaO3 (R=Y, Ho), A20190315-0717. In Proceedings of the 11th International conference on Magnetic and Superconducting Materials, Seoul, Korea, 17–24 August 2019. [Google Scholar]
- Wolfram, T.; Callaway, F. Spin-wave impurity states in ferromagnets. Phys. Rev. 1963, 130, 2207–2217. [Google Scholar] [CrossRef]
- Takeno, S. Spin-Wave Impurity Levels in a Heisenberg Ferromagnet. Prog. Theor. Phys. 1963, 30, 731–741. [Google Scholar] [CrossRef]
- Frikkee, E. Calculations on magnon impurity modes of a pair defect in a face-centred cubic ferromagnet. J. Phys. C Solid State. Phys. 1969, 2, 345–355. [Google Scholar] [CrossRef]
- Parisot, G.; Allen, S.J.; Dietz, R.E.; Guggenheim, H.J.; Moyal, R.; Moch, P.; Dugautier, C. Impurity Magnons in MnF2:Co. J. Appl. Phys. 1970, 41, 890–891. [Google Scholar] [CrossRef]
- Galkina, E.G.; Ivanov, B.A. Magnon modes localized on defects in a two-dimensional array of magnetic microparticles with transverse anisotropy. JETP Lett. 2016, 104, 32–36. [Google Scholar] [CrossRef]
- Krupnitska, O.; Richter, J.; Derzhko, O. Localized-magnon chains and interchain interactions. Acta Phys. Pol. A 2017, 132, 1234–1237. [Google Scholar] [CrossRef]
- Evers, M.; Müller, C.A.; Nowak, U. Weak localization of magnons in chiral magnets. Phys. Rev. B 2018, 97, 184423. [Google Scholar] [CrossRef]
- Arakawa, N.; Ohe, J. Weak localization of magnons in a disordered two-dimensional antiferromagnet. Phys. Rev. B 2018, 97, 020407. [Google Scholar] [CrossRef]
- Lisiecki, F.; Rychły, J.; Kuświk, P.; Głowiński, H.; Kłos, J.W.; Groß, F.; Träger, N.; Bykova, I.; Weigand, M.; Zelent, M.; et al. Magnons in a Quasicrystal: Propagation, Extinction, and Localization of Spin Waves in Fibonacci Structures. Phys. Rev. Appl. 2019, 11, 054061. [Google Scholar] [CrossRef]
- Joannopoulous, J.D.; Villeneuve, P.R.; Fan, S. Photonic crystals: Putting a new twist on light. Nature 1997, 386, 143–149. [Google Scholar] [CrossRef]
- Goyal, A.K.; Dutta, H.S.; Pal, S. Recent advances and progress in photonic crystal-based gas sensors. J. Phys. D Appl. Phys. 2017, 50, 203001. [Google Scholar] [CrossRef]
- Sahani, P.; Vijaya, R. Polarizing properties of a 2D photonic crystal slab for simultaneous in-plane and out-of-plane light incidence. J. Phys. D Appl. Phys. 2018, 51, 355101. [Google Scholar] [CrossRef]
- Rashidi, A.; Hatef, A.; Namdar, A. On the enhancement of light absorption in vanadium dioxide/1D photonic crystal composite nanostructures. J. Phys. D Appl. Phys. 2018, 51, 375102. [Google Scholar] [CrossRef]
- Biggs, D.R.; Marcovati, A.; Cappelli, M.A. Millimeter wave control using a plasma filled photonic crystal resonator. J. Phys. D Appl. Phys. 2019, 52, 055202. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Deymier, P.A.; Chenni, B.; Djafari-Rouhani, B.; Dobrzynski, L.; Prevost, D. Experimental and theoretical evidence for the existence of absolute acoustic band gaps in two-dimensional solid phononic crystals. Phys. Rev. Lett. 2001, 86, 3012–3015. [Google Scholar] [CrossRef]
- Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic crystal plate with hollow pillars connected by thin bars. J. Phys. D Appl. Phys. 2017, 50, 035301. [Google Scholar] [CrossRef]
- Zhou, X.; Chen, J.; Li, Y.; Sun, Y.; Xing, Y. Thermal tuning on band gaps of 2D phononic crystals considering adhesive layers. J. Phys. D Appl. Phys. 2018, 51, 075105. [Google Scholar] [CrossRef]
- Muzar, E.; Aval, G.A.; Stotz, J.A.H. Wet-etched phononic crystal waveguiding on GaAs. J. Phys. D Appl. Phys. 2018, 51, 044001. [Google Scholar] [CrossRef]
- Tian, Y.; Tan, Z.; Han, X.; Li, W. Phononic crystal lens with an asymmetric scatterer. J. Phys. D Appl. Phys. 2019, 52, 025102. [Google Scholar] [CrossRef]
- Wang, Y.; Dou, S.; Shang, L.; Zhang, P.; Yan, X.; Zhang, K.; Zhao, J.; Li, Y. Effects of Microsphere Size on the Mechanical Properties of Photonic Crystals. Crystals 2018, 8, 453. [Google Scholar] [CrossRef]
- Sun, X.; He, C.; Liu, X.; Zou, Y.; Lu, M.; Hu, X.; Chen, Y. Photonic Topological States in a Two-Dimensional Gyrotropic Photonic Crystal. Crystals 2019, 9, 137. [Google Scholar] [CrossRef]
- Lanoy, M.; Bretagne, A.; Leroy, V.; Leroy, V.; Tourin, A. A Phononic Crystal-Based High Frequency Rheometer. Crystals 2018, 8, 195. [Google Scholar] [CrossRef]
- Oudich, M.; Djafari-Rouhani, B.; Bonello, B.; Pennec, Y.; Sarry, F. Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation. Crystals 2017, 7, 372. [Google Scholar] [CrossRef]
- Puurtinen, T.A.; Maasilta, I.J. Low-Temperature Coherent Thermal Conduction in Thin Phononic Crystal Membranes. Crystals 2016, 6, 72. [Google Scholar] [CrossRef]
- Gubbiotti, G.; Tacchi, S.; Madami, M.; Carlotti, G.; Adeyeye, A.O.; Kostylev, M. Brillouin light scattering studies of planar metallic magnonic crystals. J. Phys. D Appl. Phys. 2010, 43, 264003. [Google Scholar] [CrossRef]
- Kruglyak, V.V.; Keatley, P.S.; Neudert, A.; Hicken, R.J.; Childress, J.R.; Katine, J.A. Imaging collective magnonic modes in 2D arrays of magnetic nanoelements. Phys. Rev. Lett. 2010, 104, 027201. [Google Scholar] [CrossRef]
- Krawczyk, M.; Mamica, S.; Mruczkiewicz, M.; Klos, J.W.; Tacchi, S.; Madami, M.; Gubbiotti, G.; Duerr, G.; Grundler, D. Magnonic band structures in two-dimensional bi-component magnonic crystals with in-plane magnetization. J. Phys. D. Appl. Phys. 2013, 46, 495003. [Google Scholar] [CrossRef]
- Arikan, M.; Au, Y.; Vasile, G.; Ingvarsson, S.; Kruglyak, V.V. Broadband injection and scattering of spin waves in lossy width-modulated magnonic crystal waveguides. J. Phys. D Appl. Phys. 2013, 46, 135003. [Google Scholar] [CrossRef]
- Rychły, J.; Kłos, J.W. Spin wave surface states in 1D planar magnonic crystals. J. Phys. D Appl. Phys. 2017, 50, 164004. [Google Scholar] [CrossRef]
- Chumak, A.V.; Serga, A.A.; Hillebrands, B. Magnonic crystals for data processing. J. Phys. D Appl. Phys. 2017, 50, 244001. [Google Scholar] [CrossRef]
- Choudhury, S.; Barman, S.; Otani, Y.C.; Barman, A. Efficient Modulation of Spin Waves in Two-Dimensional Octagonal Magnonic Crystal. ACS Nano 2017, 11, 8814–8821. [Google Scholar] [CrossRef] [PubMed]
- Hussain, B.; Cottam, M.G. Spin waves in quasiperiodic magnonic crystal arrays of metallic nanostripes. J. Phys. D Appl. Phys. 2018, 51, 355003. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, H.-Y.; Yang, M.; Qiu, J.; Yang, I.-S.; Chen, X.-B. Anomalous Behaviors of Spin Waves Studied by Inelastic Light Scattering. Crystals 2019, 9, 357. https://doi.org/10.3390/cryst9070357
Hou H-Y, Yang M, Qiu J, Yang I-S, Chen X-B. Anomalous Behaviors of Spin Waves Studied by Inelastic Light Scattering. Crystals. 2019; 9(7):357. https://doi.org/10.3390/cryst9070357
Chicago/Turabian StyleHou, Hua-Yi, Ming Yang, Jin Qiu, In-Sang Yang, and Xiang-Bai Chen. 2019. "Anomalous Behaviors of Spin Waves Studied by Inelastic Light Scattering" Crystals 9, no. 7: 357. https://doi.org/10.3390/cryst9070357
APA StyleHou, H.-Y., Yang, M., Qiu, J., Yang, I.-S., & Chen, X.-B. (2019). Anomalous Behaviors of Spin Waves Studied by Inelastic Light Scattering. Crystals, 9(7), 357. https://doi.org/10.3390/cryst9070357





