Ice Crystal Coarsening in Ice Cream during Cooling: A Comparison of Theory and Experiment
Abstract
1. Introduction
2. Model Theory
2.1. Isothermal Coarsening
2.2. Coarsening during Cooling
3. Experimental Procedures and Data Analysis
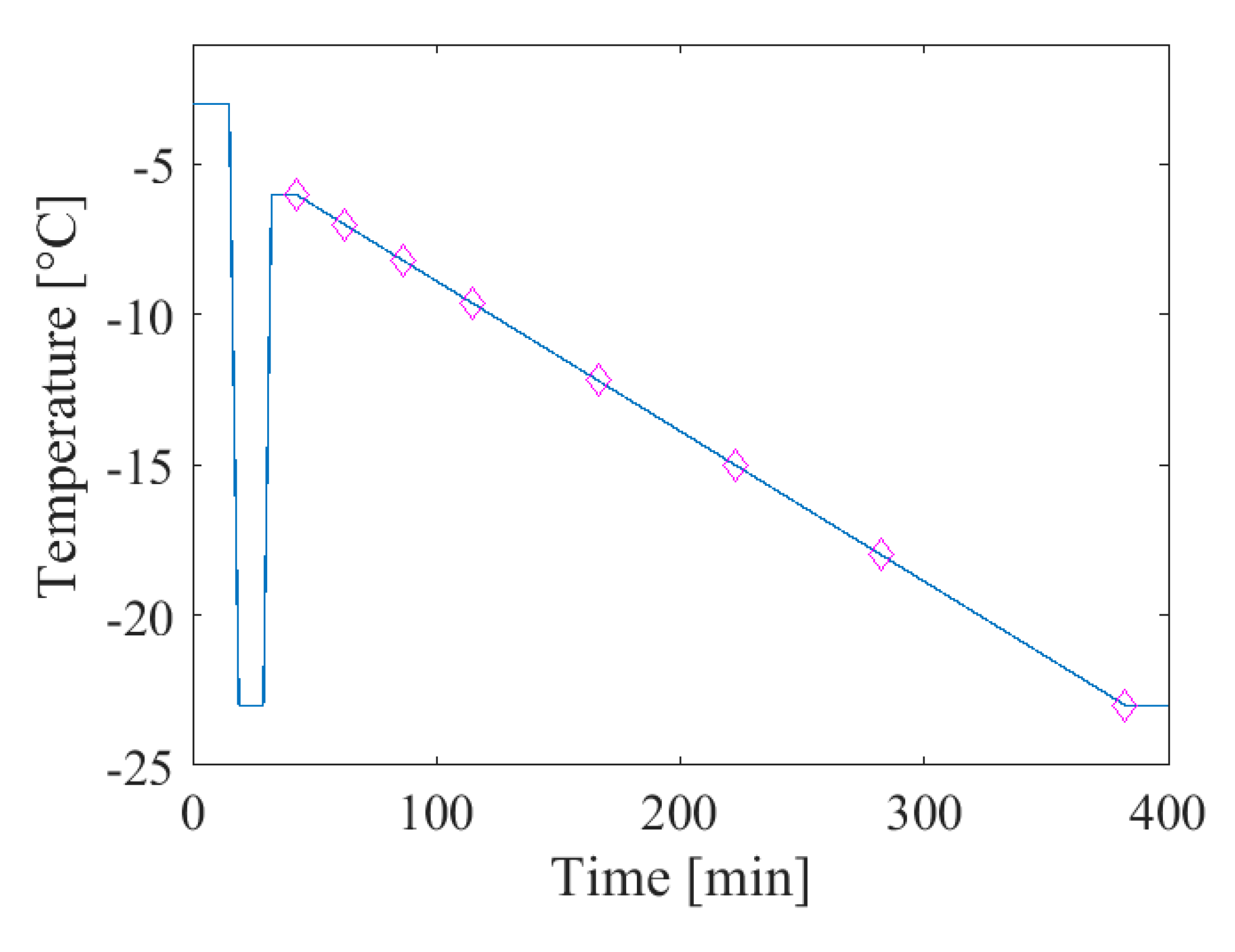
3.1. Sample Preparation and Thermal Cycling
3.2. Characterization by Synchrotron X–ray Computed Tomography (sCT)
3.3. Volume Data Reconstruction and Pre-Processing
3.4. 3D Based Quantification of Ice Crystal Dimensions
4. Results and Discussion
4.1. Model Calculations
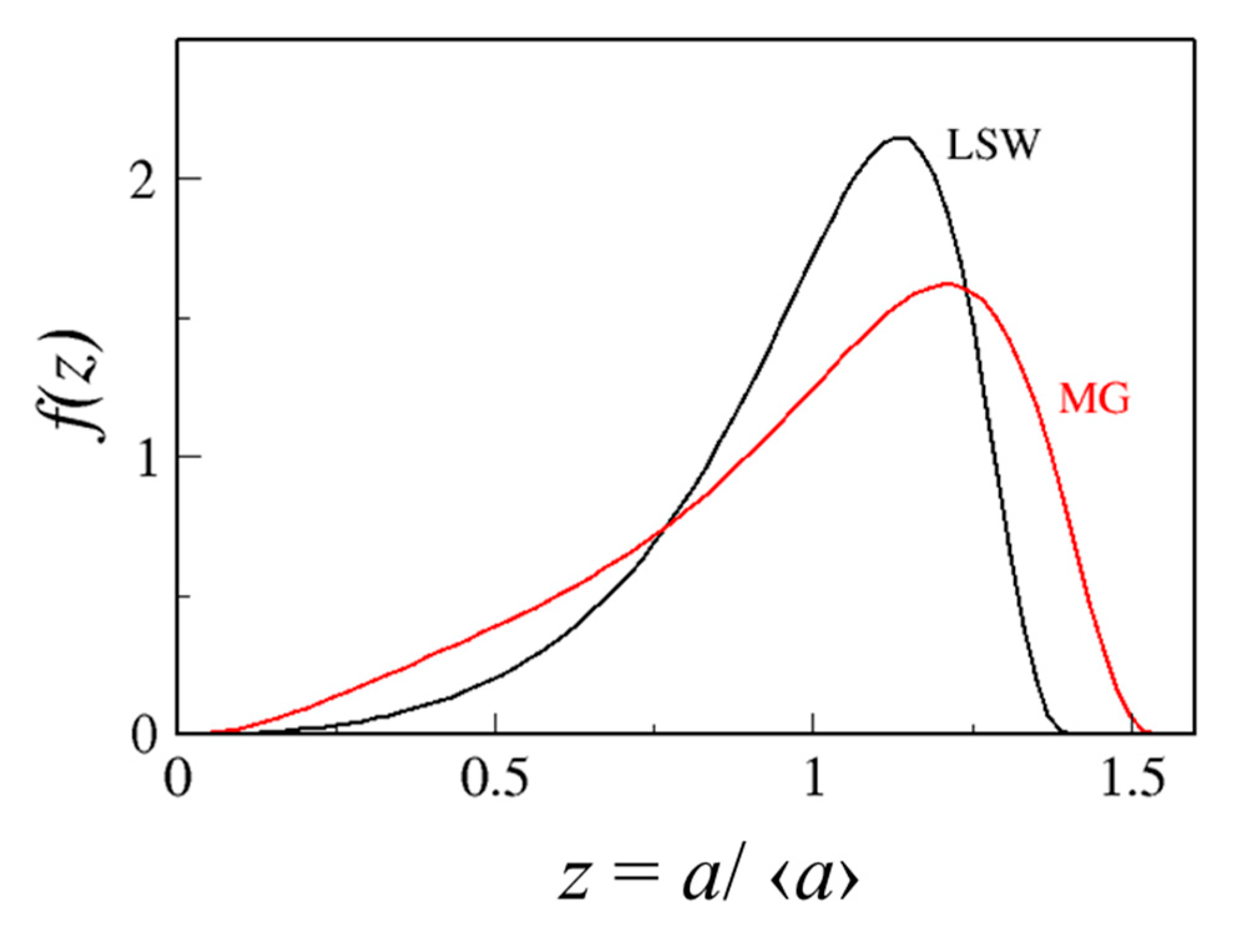
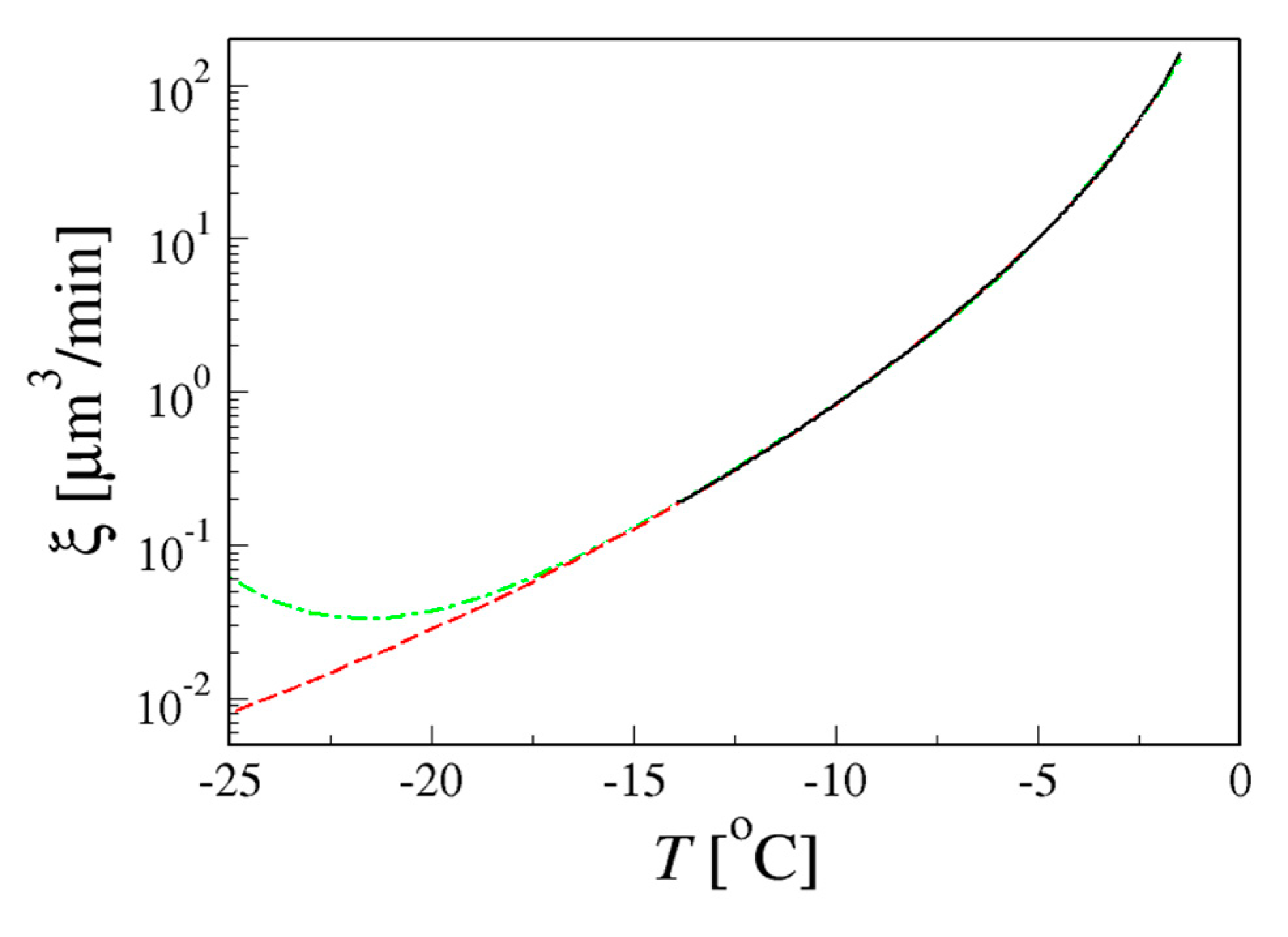
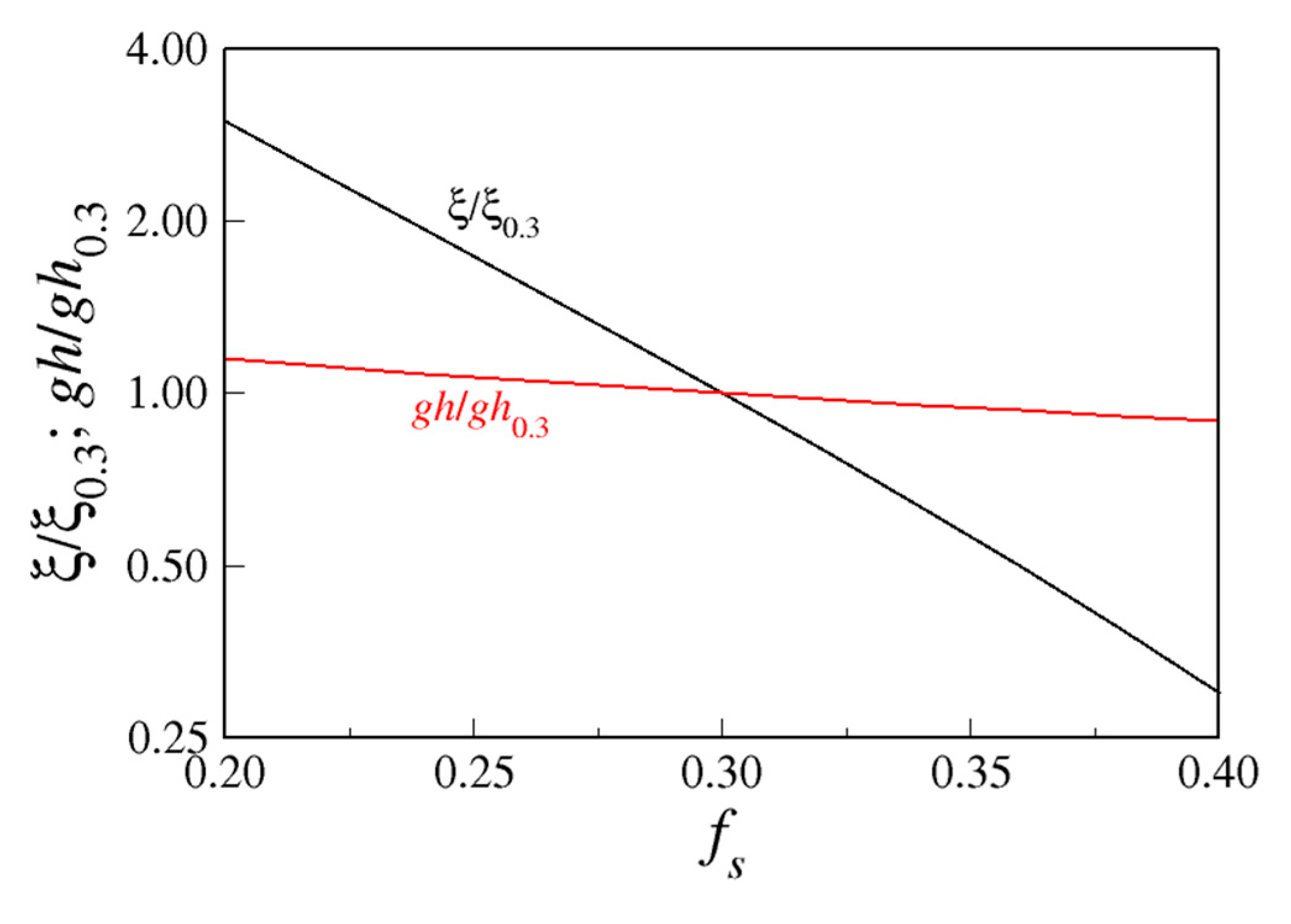
4.1.1. Relative Importance of Diffusivity and Ice Fraction
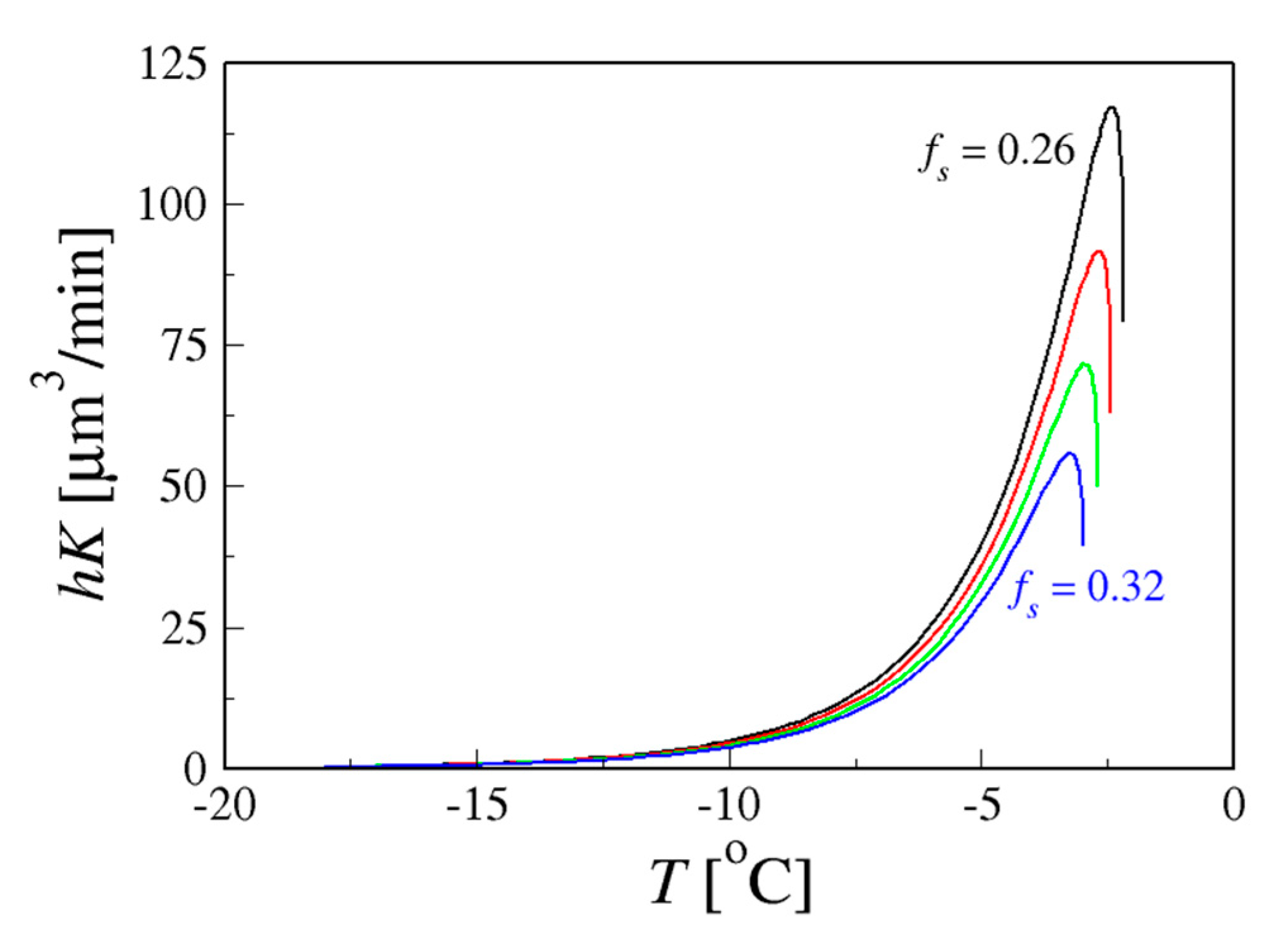
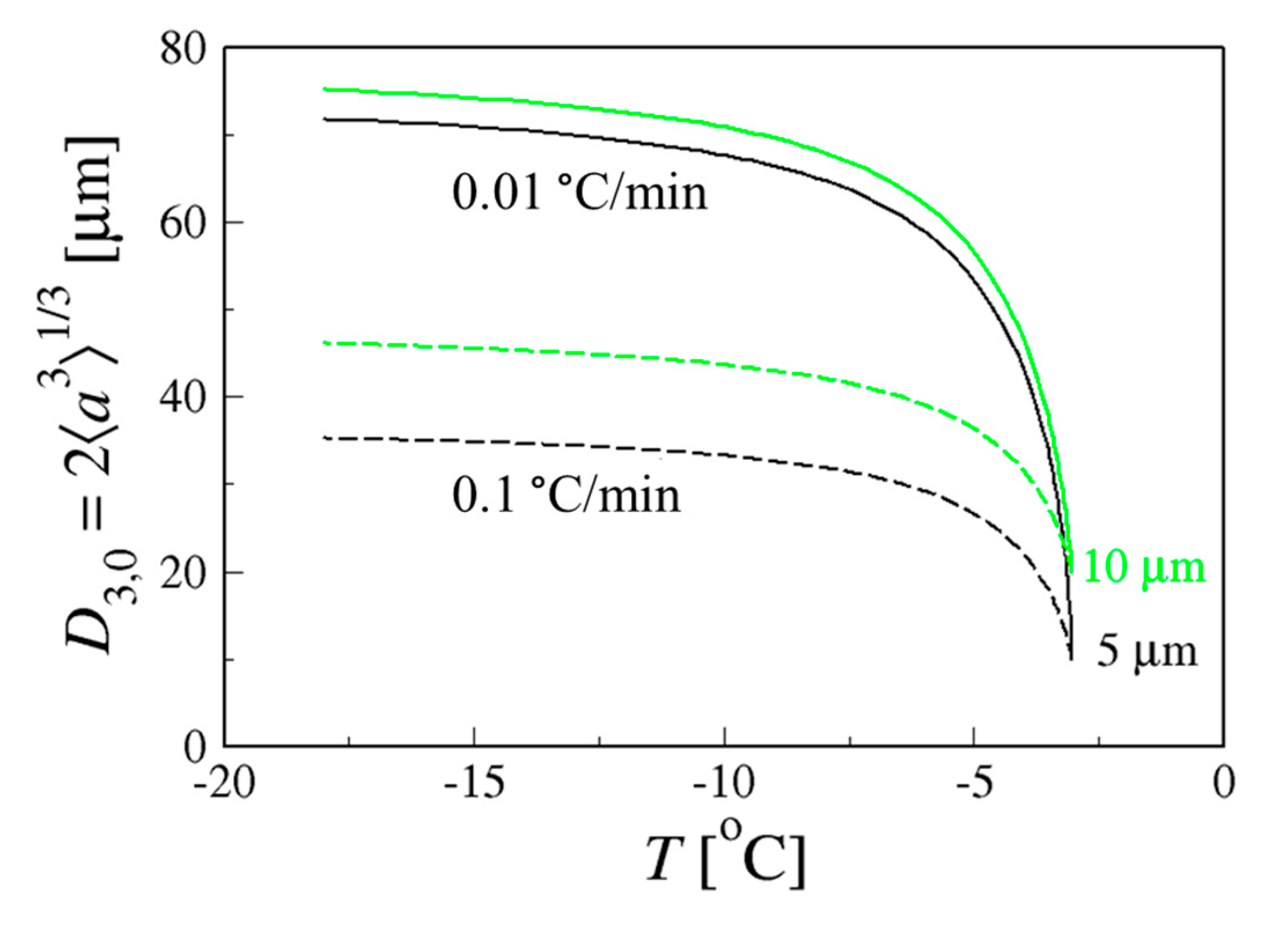
4.1.2. Coarsening at a Fixed Cooling Rate in Sucrose Solutions
4.1.3. Influence of Additives in Ice Cream Formulations
4.2. Experimental Observations and Comparison with Numerical Model
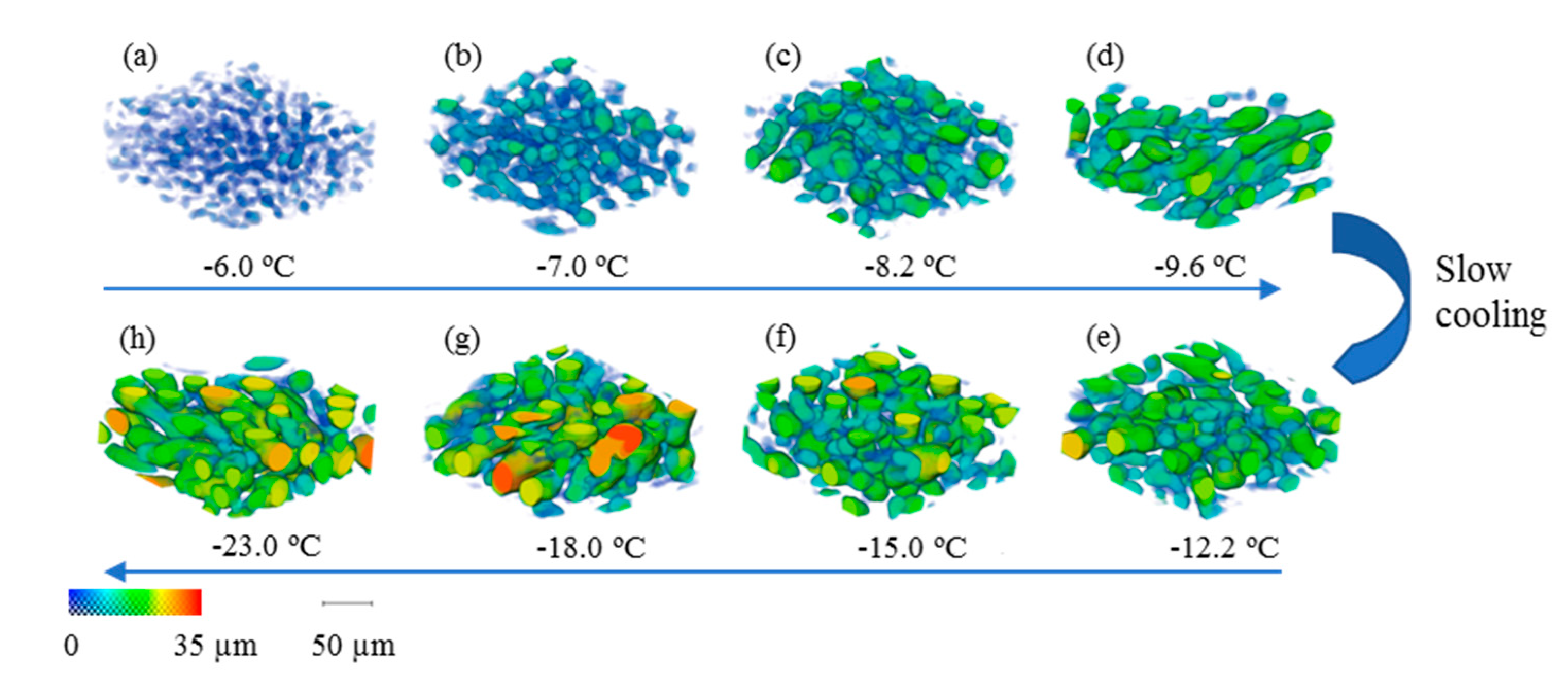
4.2.1. Morphological Evolution of Ice Crystals and Quantification of Dimensions
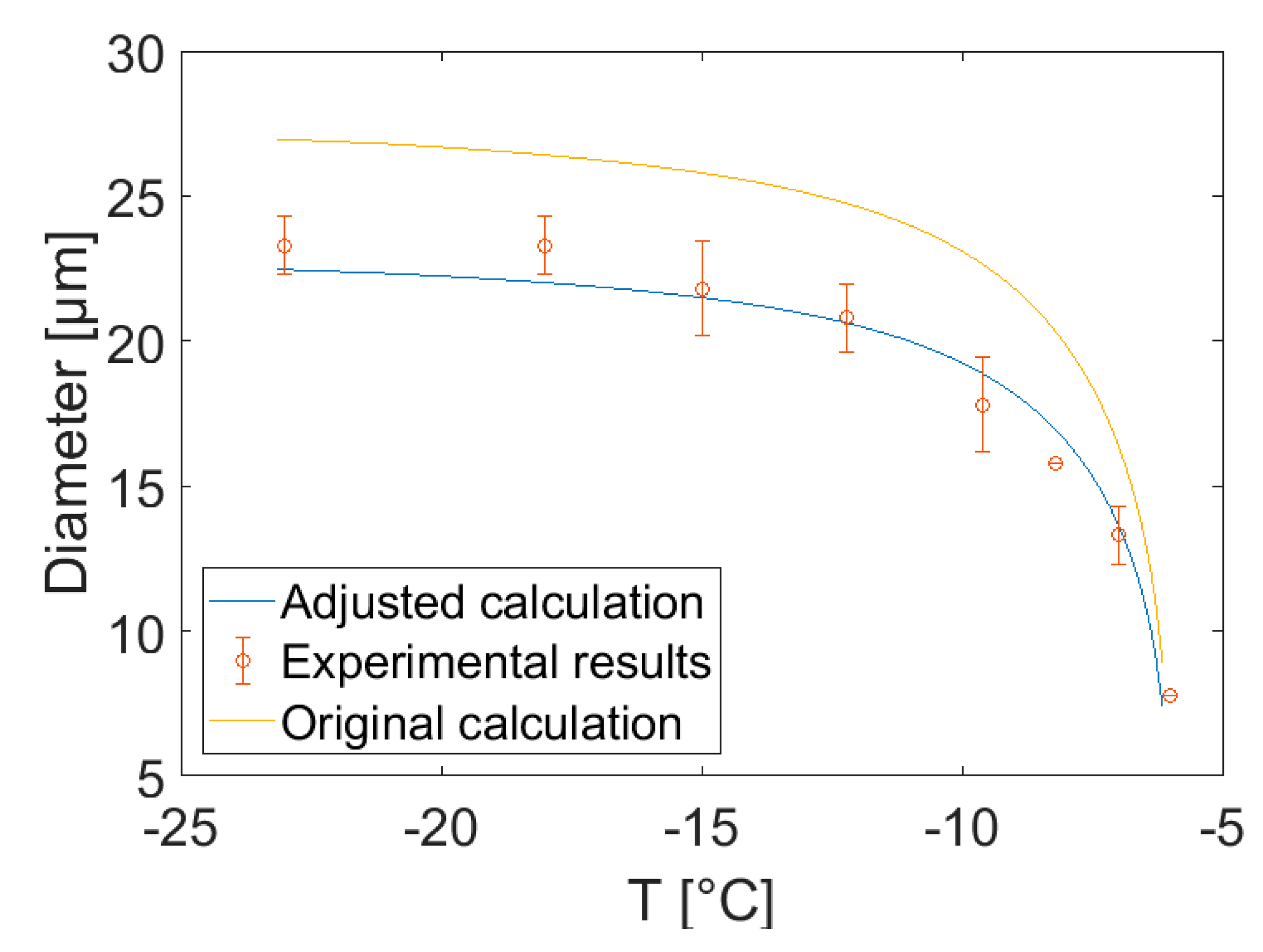
4.2.2. Comparison between Measured and Calculated Ice Crystal Dimensions
5. Conclusions
- (1)
- As expected, the 4D measurements (3D plus time) from synchrotron X-ray tomography show that coarsening of ice crystals occurs during cooling at 0.05 °C/min. The coarsening rate is rapid at high temperature (−6 to −15 °C) but slows down significantly as the temperature falls further. Qualitatively, the number density of crystals also decreases during the cooling.
- (2)
- The numerical model to calculate Ostwald ripening of ice crystals in a sucrose solution (with a finite volume fraction) cooled at a steady rate to −18 °C predicts that fast (0.1 °C/min) or slow cooling (0.01 °C/min) will lead to significantly different crystal sizes. The volumetric mean diameter, D3,0 differs by a factor of ~2 for the same sucrose mass fraction and starting crystal size.
- (3)
- The diameters of ice crystals in an ice cream formulation, measured by in situ sCT experiments, show good agreement with the model calculations if the diffusivity used in the calculations is reduced by a factor of 1.2 compared to that for a pure sucrose solution. Since the Ostwald ripening theory compares well with the experimental data for sucrose solutions [30,31] we conjecture that stabilisers and high molecular weight sugars in ice cream retard diffusion and hence slow down Ostwald ripening. More experiments are needed to confirm this conjecture.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
List of Symbols
| a | Particle radius |
| a* | Critical particle radius |
| Mean particle radius | |
| Mean particle radius at time t = 0 | |
| Mean value of the cube of the particle radius | |
| bi | Fitting constant in the equation for |
| B | Cooling rate |
| Cs | Concentration of solute in the matrix phase at the interface |
| Cs,eq | Thermodynamic equilibrium concentration of solute in the matrix phase |
| D | Fick diffusion coefficient |
| D3,0 | Mean cubed particle diameter = |
| d0 | Capillary length of the Gibbs Thomson equation |
| f | Ice phase mass fraction |
| fp | Polymer mass fraction |
| fs | Sucrose mass fraction |
| g(ϕ) | Non-dimensional geometric factor accounting for diffusion distance |
| h(ϕ) | Non-dimensional geometric factor relating radius and volume coarsening |
| K | Rate constant for isothermal coarsening |
| T | Temperature, °C |
| TH | Initial temperature, °C |
| TF | Final temperature, °C |
| t | Time |
| Δ | Supersaturation far away from the particle surface |
| ϕ | Particle or ice phase volume fraction |
| ξ(T) | Dimensional factor |
References
- Clarke, C. The Science of Ice Cream; Royal Society of Chemistry: London, UK, 2015. [Google Scholar]
- Goff, H.D.; Hartel, R.W. Ice Cream; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Goff, H.D. Colloidal aspects of ice cream—A review. Int. Dairy J. 1997, 7, 363–373. [Google Scholar] [CrossRef]
- Hartel, R.W. Mechanisms and kinetics of recrystallization in ice cream. In The Properties of Water in Foods ISOPOW 6; Springer: Boston, MA, USA, 1998; pp. 287–319. [Google Scholar]
- Hagiwara, T.; Hartel, R.W.; Matsukawa, S. Relationship between recrystallization rate of ice crystals in sugar solutions and water mobility in freeze-concentrated matrix. Food Biophys. 2006, 1, 74–82. [Google Scholar] [CrossRef]
- Cook, K.L.K.; Hartel, R.W. Mechanisms of ice crystallization in ice cream production. Compr. Rev. Food Sci. F. 2010, 9, 213–222. [Google Scholar] [CrossRef]
- Guo, E.; Zeng, G.; Kazantsev, D.; Rocketta, P.; Bentc, J.; Kirklandc, M.; Van Dalenc, G.; Eastwoodab, D.S.; StJohn, D.; Lee, P.D. Synchrotron X-ray tomographic quantification of microstructural evolution in ice cream–a multi-phase soft solid. Rsc Adv. 2017, 7, 15561–15573. [Google Scholar] [CrossRef]
- Ratke, L.; Voorhees, P.W. Growth and Coarsening: Ostwald Ripening in Material Processing; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Harper, E.K.; Shoemaker, C.F. Effect of locust bean gum and selected sweetening agents on ice recrystallization rates. J. Food Sci. 1983, 48, 1801–1803. [Google Scholar] [CrossRef]
- Donhowe, D.P.; Hartel, R.W. Recrystallization of ice in ice cream during controlled accelerated storage. Int. Dairy J. 1996, 6, 1191–1208. [Google Scholar] [CrossRef]
- Donhowe, D.P.; Hartel, R.W. Recrystallization of ice during bulk storage of ice cream. Int. Dairy J. 1996, 6, 1209–1221. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]
- Wagner, C. Theorie der alterung von niederschlägen durch umlösen (Ostwald-reifung). Zeitschrift für Elektrochemie, Berichte der Bunsengesellschaft für physikalische Chemie 1961, 65, 581–591. [Google Scholar]
- Marsh, S.P.; Glicksman, M.E. Kinetics of phase coarsening in dense systems. Acta Mater. 1996, 44, 3761–3771. [Google Scholar] [CrossRef]
- Baldan, A. Review progress in Ostwald ripening theories and their applications to nickel-base superalloys Part I: Ostwald ripening theories. J. Mater. Sci. 2002, 37, 2171–2202. [Google Scholar] [CrossRef]
- Ardell, A. The effect of volume fraction on particle coarsening: Theoretical considerations. Acta Metall. 1972, 20, 61–71. [Google Scholar] [CrossRef]
- Brailsford, A.; Wynblatt, P. The dependence of Ostwald ripening kinetics on particle volume fraction. Acta Metall. 1979, 27, 489–497. [Google Scholar] [CrossRef]
- Davies, C.; Nash, P.; Stevens, R.N. The effect of volume fraction of precipitate on Ostwald ripening. Acta Metall. 1980, 28, 179–189. [Google Scholar] [CrossRef]
- Marqusee, J.; Ross, J. Theory of Ostwald ripening: Competitive growth and its dependence on volume fraction. J. Chem. Phys. 1984, 80, 536–543. [Google Scholar] [CrossRef]
- Tsumuraya, K.; Miyata, Y. Coarsening models incorporating both diffusion geometry and volume fraction of particles. Acta Metall. 1983, 31, 437–452. [Google Scholar] [CrossRef]
- Wang, K.; Wang, G.Q. Phase coarsening in multicomponent systems. Phys. Rev. E 2017, 95, 022609. [Google Scholar] [CrossRef]
- Yan, H.; Wang, K.; Jones, J.E. Large-scale three-dimensional phase-field simulations for phase coarsening at ultrahigh volume fraction on high-performance architectures. Model. Simul. Mater. Sci. Eng. 2016, 24, 055016. [Google Scholar] [CrossRef]
- Van Westen, T.; Groot, R.D. Predicting the Kinetics of Ice Recrystallization in Aqueous Sugar Solutions. Cryst. Growth Des. 2018, 18, 2405–2416. [Google Scholar] [CrossRef]
- Van Westen, T.; Groot, R.D. Effect of Temperature Cycling on Ostwald Ripening. Cryst. Growth Des. 2018, 18, 4952–4962. [Google Scholar] [CrossRef]
- Pinzer, B.R.; Medebach, A.; Limbach, H.J.; Dubois, C.; Stampanoni, M.; Schneebeli, M. 3D-characterization of three-phase systems using X-ray tomography: Tracking the microstructural evolution in ice cream. Soft Matter 2012, 8, 4584–4594. [Google Scholar] [CrossRef]
- Guo, E.; Kazantsev, D.; Mo, J.; Bent, J.; Van Dalen, G.; Schuetz, P.; Rockett, P.; StJohn, D.; Lee, P.D. Revealing the microstructural stability of a three-phase soft solid (ice cream) by 4D synchrotron X-ray tomography. J. Food Eng. 2018, 237, 204–214. [Google Scholar] [CrossRef]
- Mo, J.; Guo, E.; McCartney, D.G.; Eastwood, D.S.; Bent, J.; Van Dalen, G.; Schuetz, P.; Rockett, P.; Lee, P.D. Time-Resolved Tomographic Quantification of the Microstructural Evolution of Ice Cream. Materials 2018, 11, 2031. [Google Scholar] [CrossRef]
- Wu, Z.Y.; Hill, R.G.; Yue, S.; Nightingale, D.; Lee, P.D.; Jones, J.R. Melt-derived bioactive glass scaffolds produced by a gel-cast foaming technique. Acta Biomater. 2011, 7, 1807–1816. [Google Scholar] [CrossRef]
- Yue, S. Non-Destructive quantification of tissue scaffolds and augmentation implants using X-ray microtomography. Ph.D. Theses, Imperial College London, London, UK, 2011. [Google Scholar]
- Peters, A.; Candau, S. Kinetics of swelling of spherical and cylindrical gels. Macromolecules 1988, 21, 2278–2282. [Google Scholar] [CrossRef]
- Li, Y.; Tanaka, T. Kinetics of swelling and shrinking of gels. J. Chem. Phys. 1990, 92, 1365–1371. [Google Scholar]
- Barrière, B.; Leibler, L. Kinetics of solvent absorption and permeation through a highly swellable elastomeric network. J. Polym. Sci. Pol. Phys. 2003, 41, 166–182. [Google Scholar] [CrossRef]
- Del Rio, A.R.; Ramírez-Gilly, M.; Tecante, A. Flow Properties of Lambda Carrageenan in Aqueous Systems. In Biological Activities and Application of Marine Polysaccharides; IntechOpen: London, UK, 2017. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mo, J.; Groot, R.D.; McCartney, G.; Guo, E.; Bent, J.; van Dalen, G.; Schuetz, P.; Rockett, P.; Lee, P.D. Ice Crystal Coarsening in Ice Cream during Cooling: A Comparison of Theory and Experiment. Crystals 2019, 9, 321. https://doi.org/10.3390/cryst9060321
Mo J, Groot RD, McCartney G, Guo E, Bent J, van Dalen G, Schuetz P, Rockett P, Lee PD. Ice Crystal Coarsening in Ice Cream during Cooling: A Comparison of Theory and Experiment. Crystals. 2019; 9(6):321. https://doi.org/10.3390/cryst9060321
Chicago/Turabian StyleMo, Jingyi, Robert D. Groot, Graham McCartney, Enyu Guo, Julian Bent, Gerard van Dalen, Peter Schuetz, Peter Rockett, and Peter D. Lee. 2019. "Ice Crystal Coarsening in Ice Cream during Cooling: A Comparison of Theory and Experiment" Crystals 9, no. 6: 321. https://doi.org/10.3390/cryst9060321
APA StyleMo, J., Groot, R. D., McCartney, G., Guo, E., Bent, J., van Dalen, G., Schuetz, P., Rockett, P., & Lee, P. D. (2019). Ice Crystal Coarsening in Ice Cream during Cooling: A Comparison of Theory and Experiment. Crystals, 9(6), 321. https://doi.org/10.3390/cryst9060321




