Topological Phase Transition in a One-Dimensional Elastic String System
Abstract
:1. Introduction
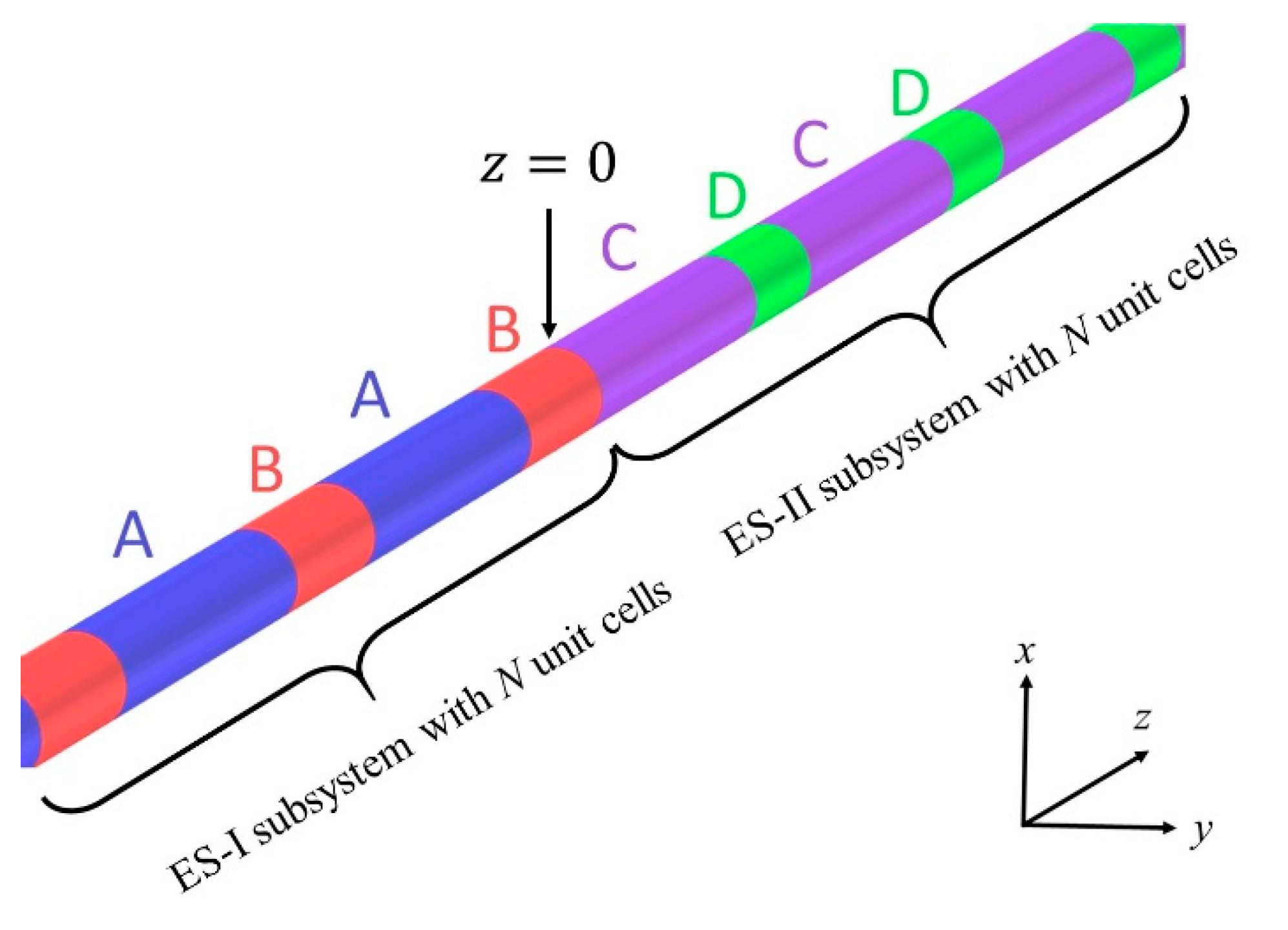
2. A One-Dimensional Periodic Elastic String
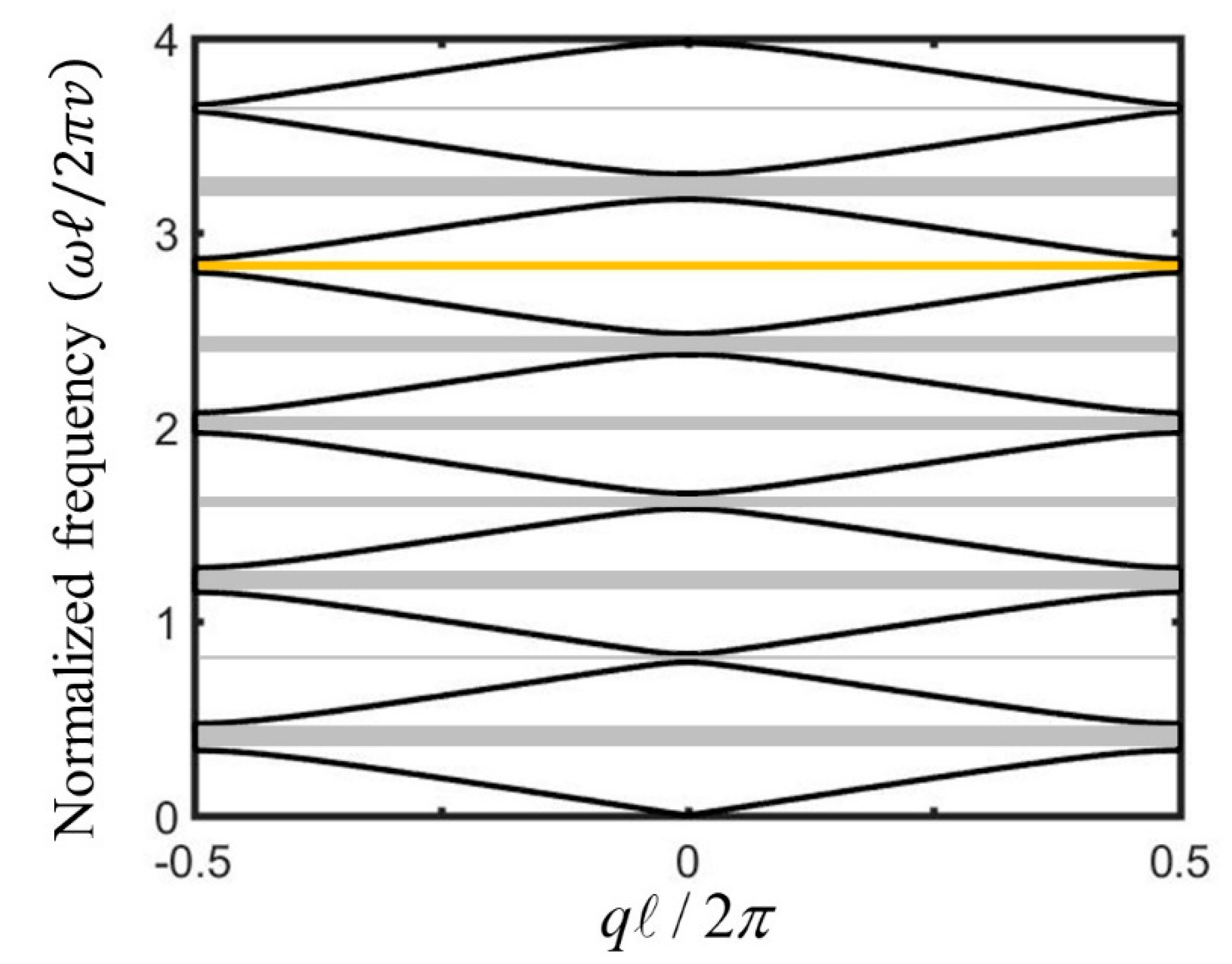
2.1. Dispersion Relation
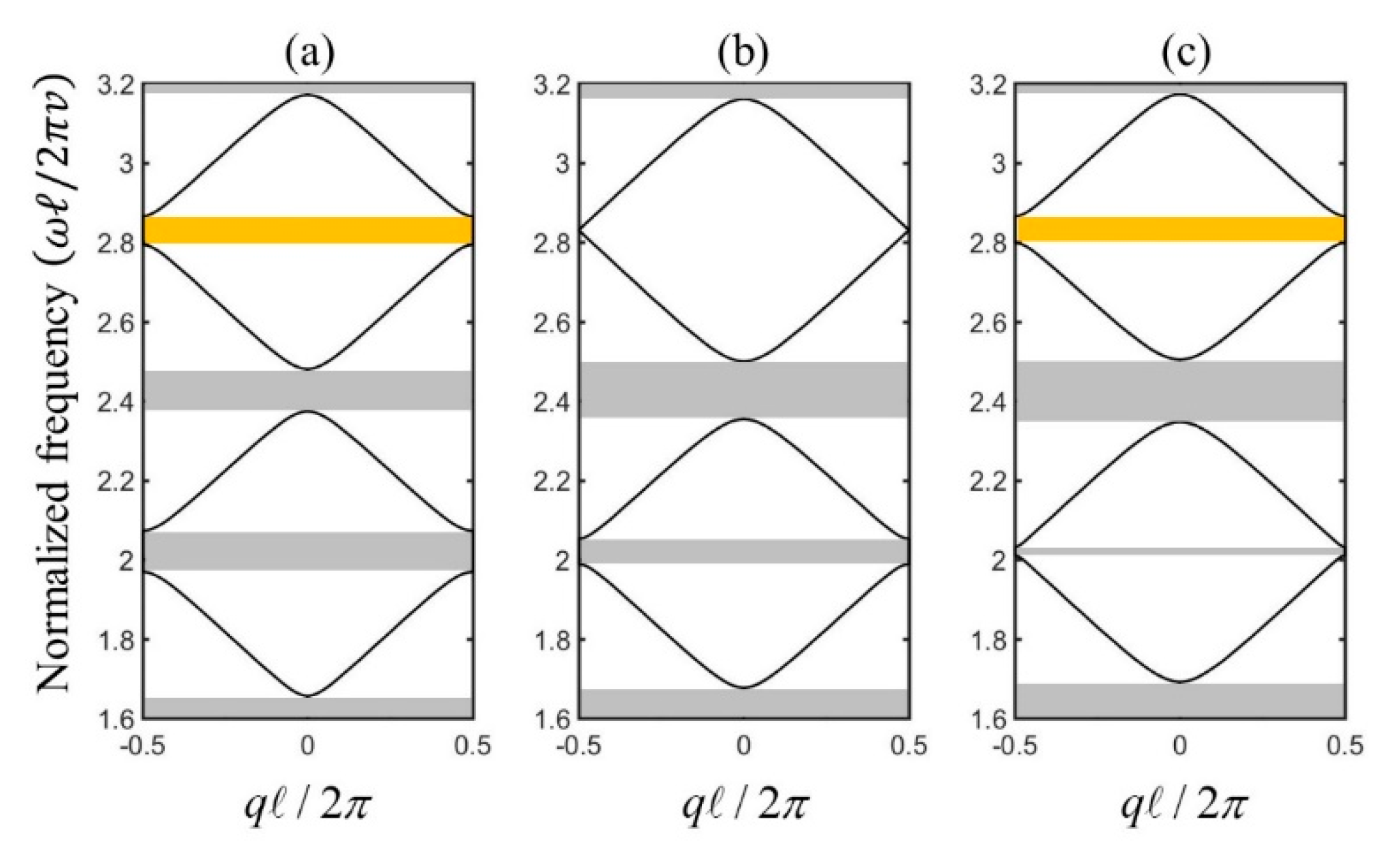
2.2. Band Crossing Condition
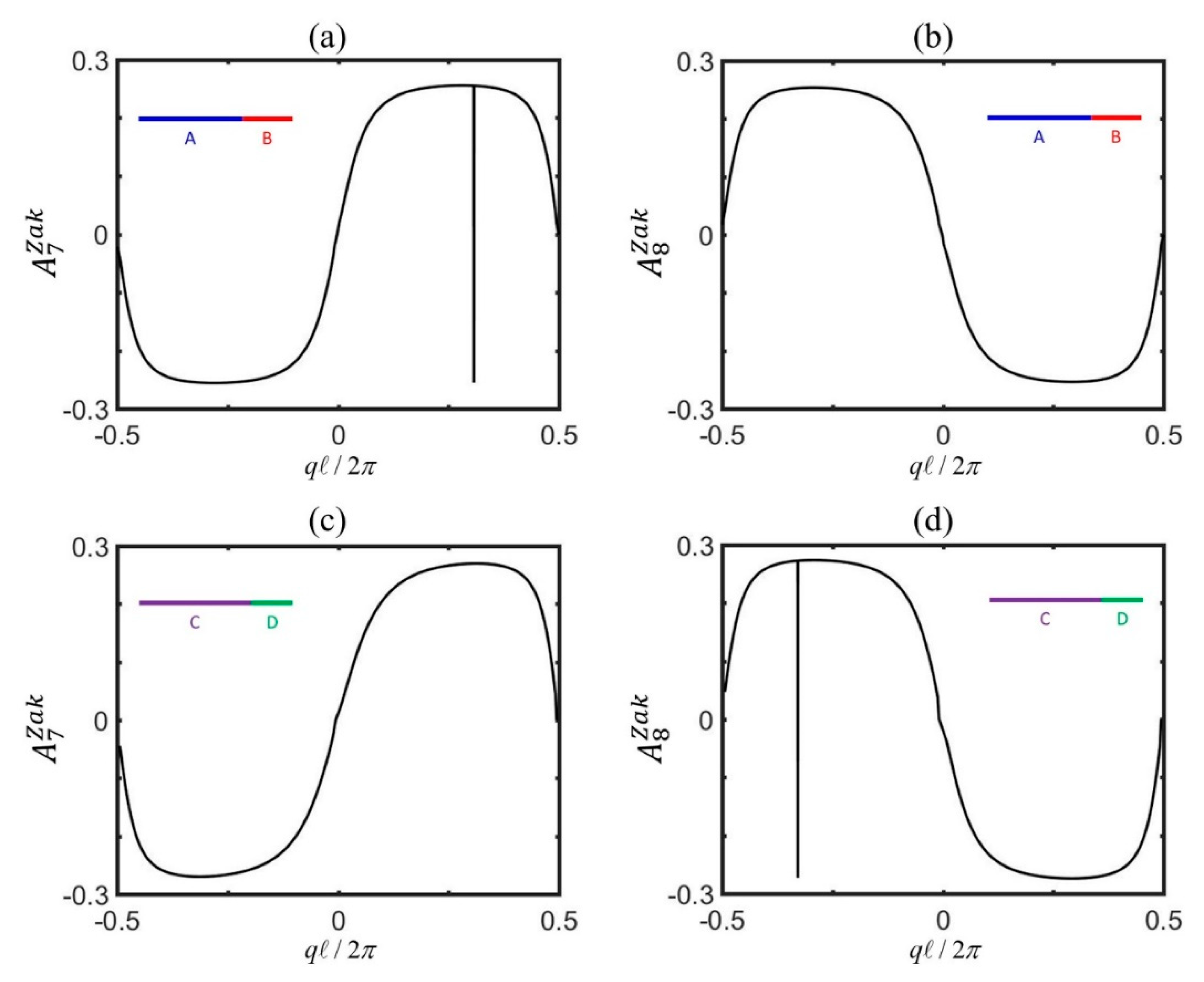
2.3. Zak Phase
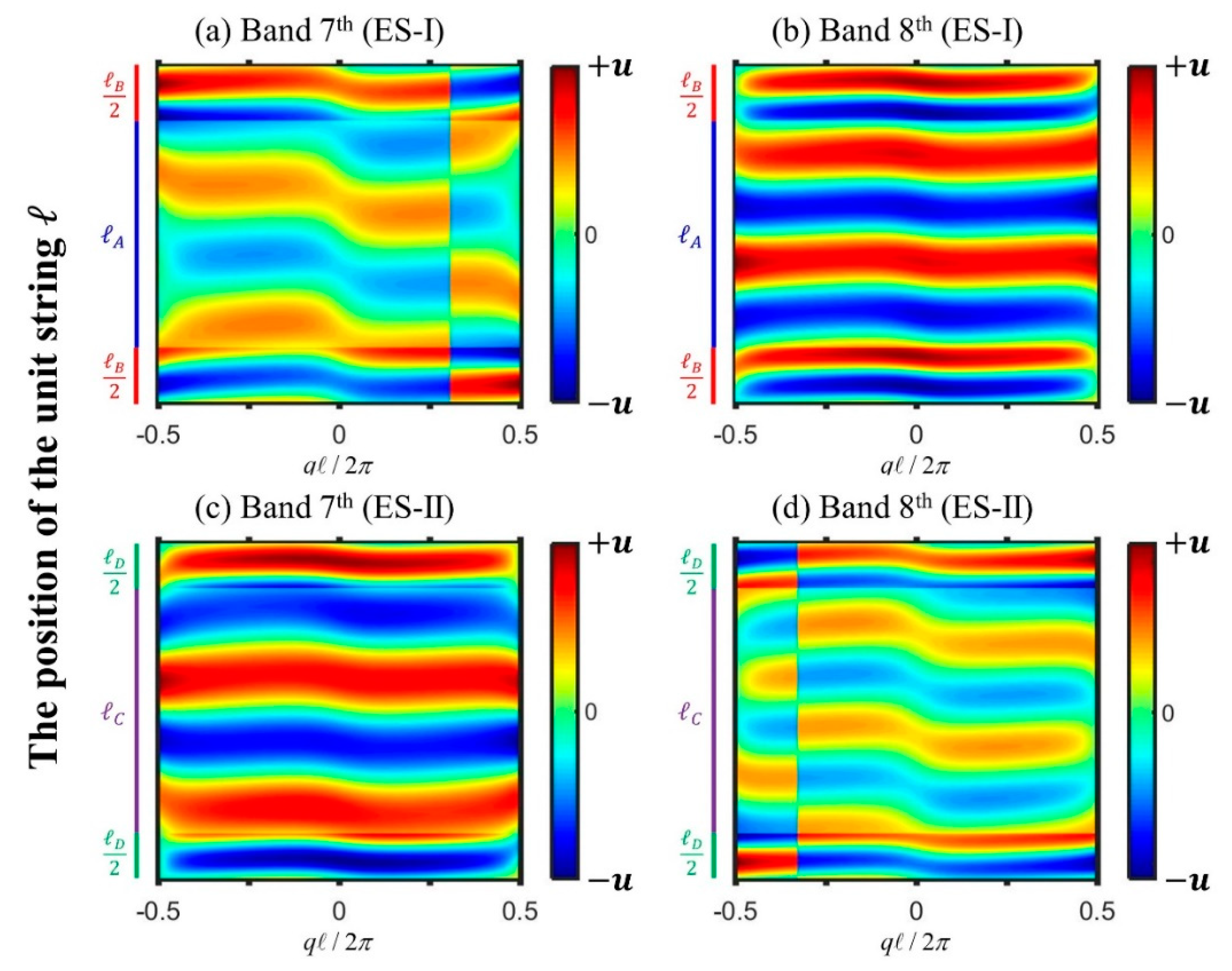
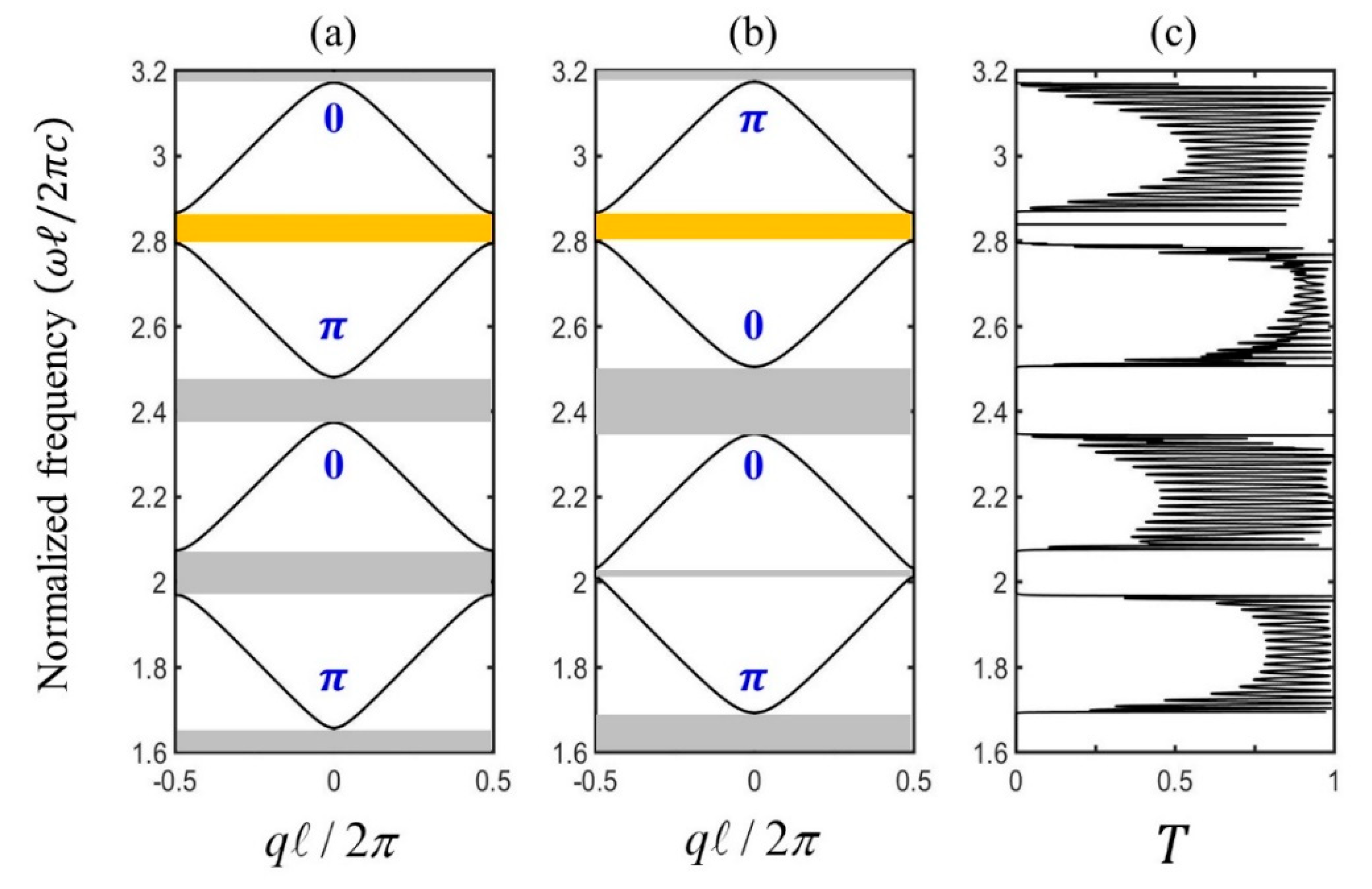
3. The Interface Mode
4. Possible Experimental Implementation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Band Crossing Condition
Appendix B. Zak Phase Calculation for Each Band
References
- Bernevig, B.A.; Hughes, T.L. Topological Insulators and Topological Superconductors; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Atala, M.; Aidelsburger, M.; Barreiro, J.T.; Abanin, D.; Kitagawa, T.; Demler, E.; Bloch, I. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 2013, 9, 795–800. [Google Scholar] [CrossRef]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef] [Green Version]
- Büttiker, M. Absence of backscattering in the quantum Hall effect in multiprobe conductors. Phys. Rev. B 1988, 38, 9375–9389. [Google Scholar] [CrossRef]
- Halperin, B.I. Quantized Hall conductance, current-carrying edge states, and the existence of extended states in a two-dimensional disordered potential. Phys. Rev. B 1982, 25, 2185–2190. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum spin Hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 2005, 95, 146802. [Google Scholar] [CrossRef]
- Un, I.W.; Yen, T.J. Interface States and Interface-Bulk Correspondence of One-dimensional Hyperbolic Metamaterials. Sci. Rep. 2017, 7, 43392. [Google Scholar] [CrossRef] [Green Version]
- Gao, W.; Lawrence, M.; Yang, B.; Liu, F.; Fang, F.; Beri, B.; Li, J.; Zhang, S. Topological photonic phase in chiral hyperbolic metamaterials. Phys. Rev. Lett. 2015, 114, 037402. [Google Scholar] [CrossRef]
- Ryu, S.; Hatsugai, Y. Topological origin of zero-energy edge states in particle-hole symmetric systems. Phys. Rev. Lett. 2002, 89, 077002. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.-C. Quantum Spin Hall Effect and Topological Phase Transition in HgTe Quantum Wells. Science 2006, 314, 1757. [Google Scholar] [CrossRef]
- Haldane, F.D. Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the “parity anomaly”. Phys. Rev. Lett. 1988, 61, 2015–2018. [Google Scholar] [CrossRef] [PubMed]
- Goldman, N.; Juzeliunas, G.; Ohberg, P.; Spielman, I.B. Light-induced gauge fields for ultracold atoms. Rep. Prog. Phys. 2014, 77, 126401. [Google Scholar] [CrossRef] [PubMed]
- Cooper, N.R. Rapidly rotating atomic gases. Adv. Phys. 2008, 57, 539–616. [Google Scholar] [CrossRef]
- Kohmoto, M. Topological Invariant and the Quantization of the Hall Conductance. Ann. Phys. 1985, 160, 343–354. [Google Scholar] [CrossRef]
- Thouless, D.J.; Kohmoto, M.; Nightingale, M.P.; den Nijs, M. Quantized Hall Conductance in a Two-Dimensional Periodic Potential. Phys. Rev. Lett. 1982, 49, 405–408. [Google Scholar] [CrossRef] [Green Version]
- Asbóth, J.K.; Oroszlány, L.; Pályi, A. A Short Course on Topological Insulators; Springer: Heidelberg, Germany, 2016. [Google Scholar]
- Su, W.P.; Schrieffer, J.R.; Heeger, A.J. Solitons in Polyacetylene. Phys. Rev. Lett. 1979, 42, 1698–1701. [Google Scholar] [CrossRef]
- Zak, J. Berry’s Phase for Energy Bands in Solids. Phys. Rev. Lett. 1989, 62, 2747. [Google Scholar] [CrossRef]
- Xiao, M.; Ma, G.; Yang, Z.; Sheng, P.; Zhang, Z.Q.; Chan, C.T. Geometric phase and band inversion in periodic acoustic systems. Nat. Phys. 2015, 11, 240–244. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, Z.Q.; Chan, C.T. Surface Impedance and Bulk Band Geometric Phases in One-Dimensional Systems. Phy. Rev. X 2014, 4, 021017. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Sun, Y.; Zhu, W.; Guo, Z.; Jiang, J.; Kariyado, T.; Chen, H.; Hu, X. Topological LC-circuits based on microstrips and observation of electromagnetic modes with orbital angular momentum. Nat. Commun. 2018, 9, 4598. [Google Scholar] [CrossRef]
- Albert, V.V.; Glazman, L.I.; Jiang, L. Topological properties of linear circuit lattices. Phys. Rev. Lett. 2015, 114, 173902. [Google Scholar] [CrossRef] [PubMed]
- Mei, F.; You, J.-B.; Nie, W.; Fazio, R.; Zhu, S.-L.; Kwek, L.C. Simulation and detection of photonic Chern insulators in a one-dimensional circuit-QED lattice. Phys. Rev. A 2015, 92, 041805. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic Floquet topological insulators. Nature 2013, 496, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Haldane, F.D.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, S.; Gao, W.; Zhang, Q.; Ma, S.; Zhang, L.; Liu, C.; Xiang, Y.J.; Cui, T.J.; Zhang, S. Topologically Protected Edge State in Two-Dimensional Su–Schrieffer–Heeger Circuit. Research 2019, 2019, 1–8. [Google Scholar]
- Cabot, A.; Galve, F.; Zambrini, R. Dynamical and quantum effects of collective dissipation in optomechanical systems. New J. Phys. 2017, 19, 113007. [Google Scholar] [CrossRef] [Green Version]
- Deymier, P.A.; Runge, K.; Vasseur, J.O. Geometric phase and topology of elastic oscillations and vibrations in model systems: Harmonic oscillator and superlattice. AIP Adv. 2016, 6, 121801. [Google Scholar] [CrossRef] [Green Version]
- Yin, J.; Ruzzene, M.; Wen, J.; Yu, D.; Cai, L.; Yue, L. Band transition and topological interface modes in 1D elastic phononic crystals. Sci. Rep. 2018, 8, 6806. [Google Scholar] [CrossRef] [PubMed]
- Yariv, A.; Yeh, P. Optical Waves in Crystals; Wiley: New York, NY, USA, 1948. [Google Scholar]
- Choi, K.H.; Ling, C.W.; Lee, K.F.; Tsang, Y.H.; Fung, K.H. Simultaneous multi-frequency topological edge modes between one-dimensional photonic crystals. Opt. Lett. 2016, 41, 1644–1647. [Google Scholar] [CrossRef]
- Prodan, E.; Dobiszewski, K.; Kanwal, A.; Palmieri, J.; Prodan, C. Dynamical Majorana edge modes in a broad class of topological mechanical systems. Nat. Commun. 2017, 8, 14587. [Google Scholar] [CrossRef] [PubMed]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, Y.-W.; Wang, Y.-T.; Luan, P.-G.; Yen, T.-J. Topological Phase Transition in a One-Dimensional Elastic String System. Crystals 2019, 9, 313. https://doi.org/10.3390/cryst9060313
Tsai Y-W, Wang Y-T, Luan P-G, Yen T-J. Topological Phase Transition in a One-Dimensional Elastic String System. Crystals. 2019; 9(6):313. https://doi.org/10.3390/cryst9060313
Chicago/Turabian StyleTsai, Ya-Wen, Yao-Ting Wang, Pi-Gang Luan, and Ta-Jen Yen. 2019. "Topological Phase Transition in a One-Dimensional Elastic String System" Crystals 9, no. 6: 313. https://doi.org/10.3390/cryst9060313
APA StyleTsai, Y.-W., Wang, Y.-T., Luan, P.-G., & Yen, T.-J. (2019). Topological Phase Transition in a One-Dimensional Elastic String System. Crystals, 9(6), 313. https://doi.org/10.3390/cryst9060313




