A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide
Abstract
1. Introduction
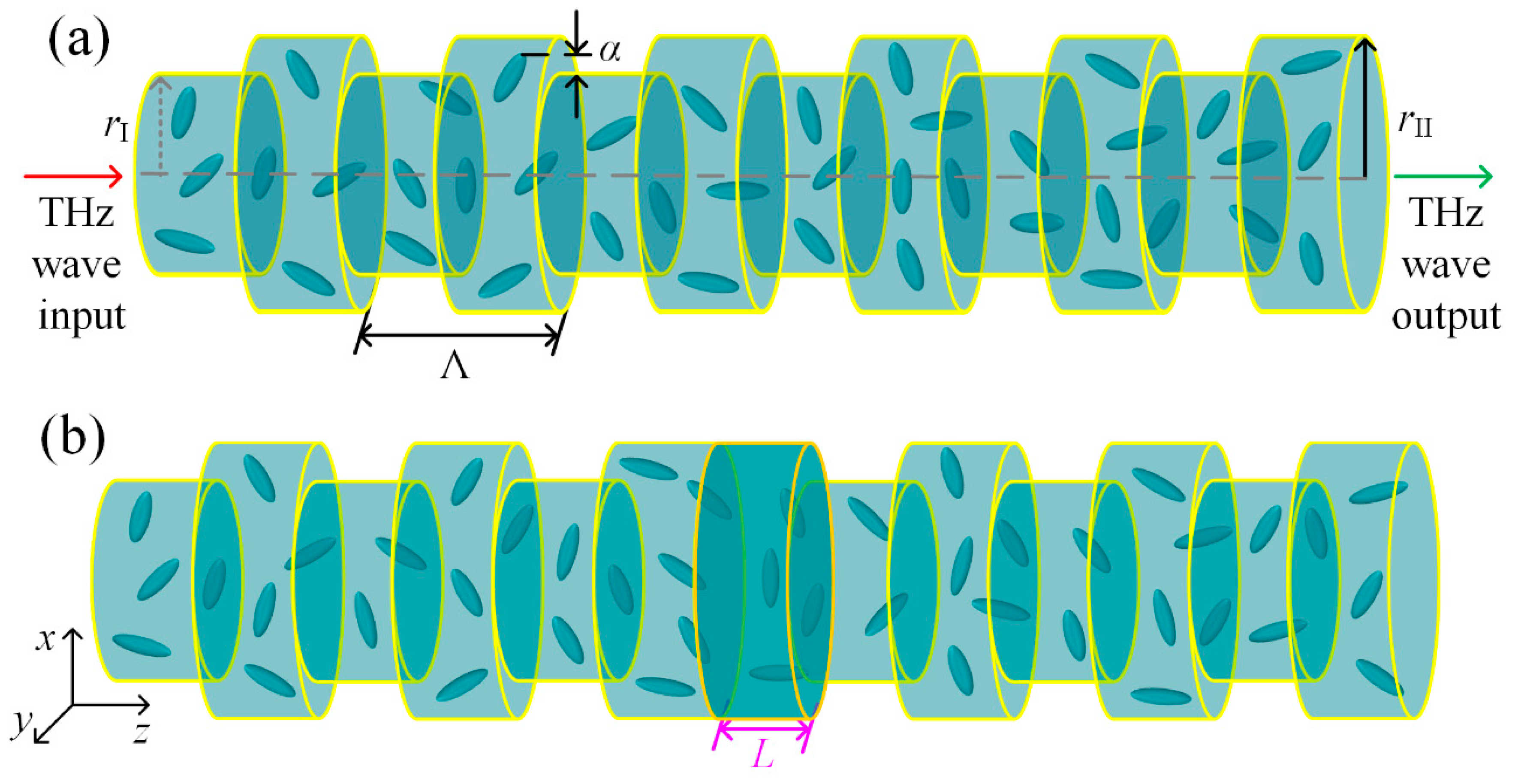
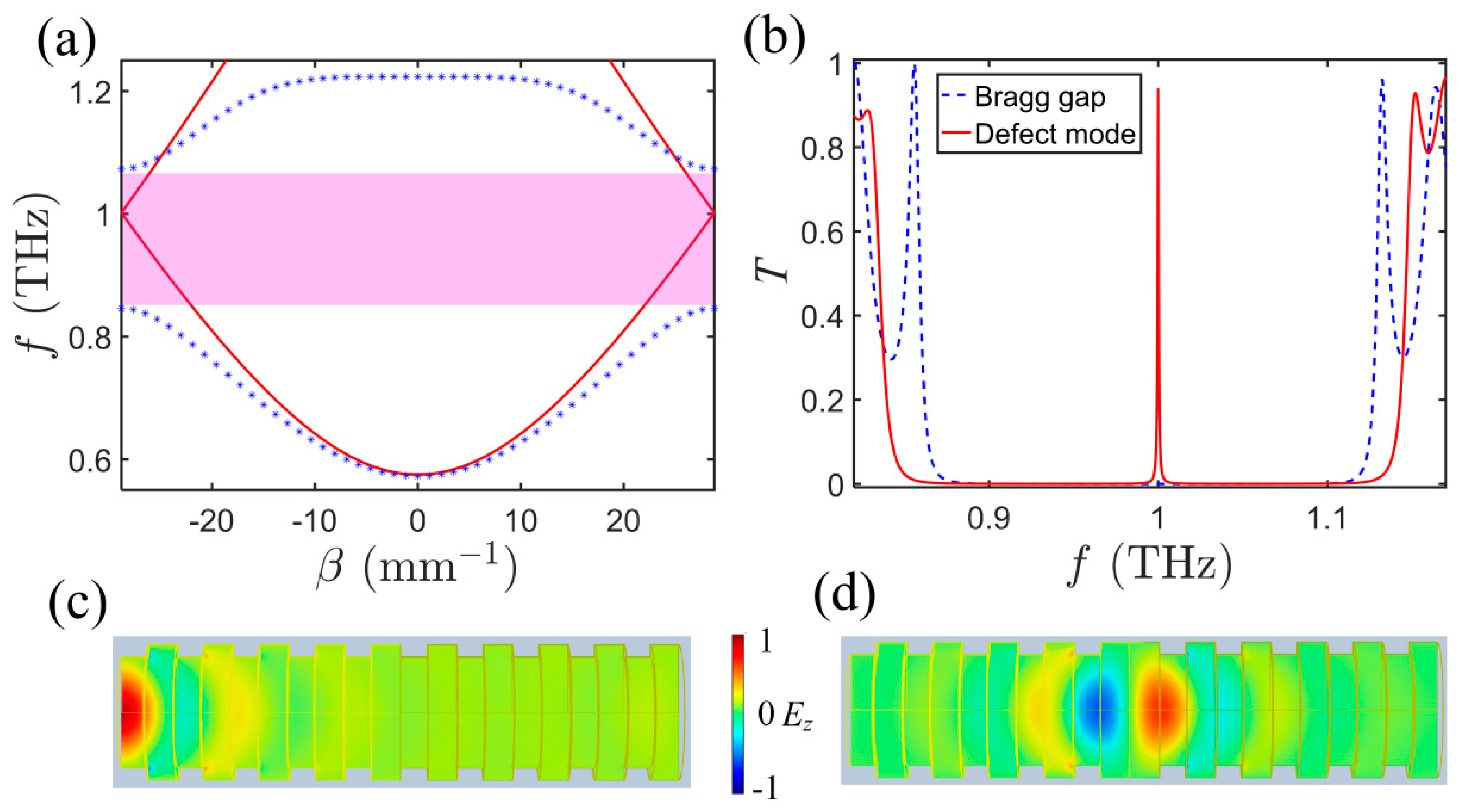
2. Bragg Defect Mode
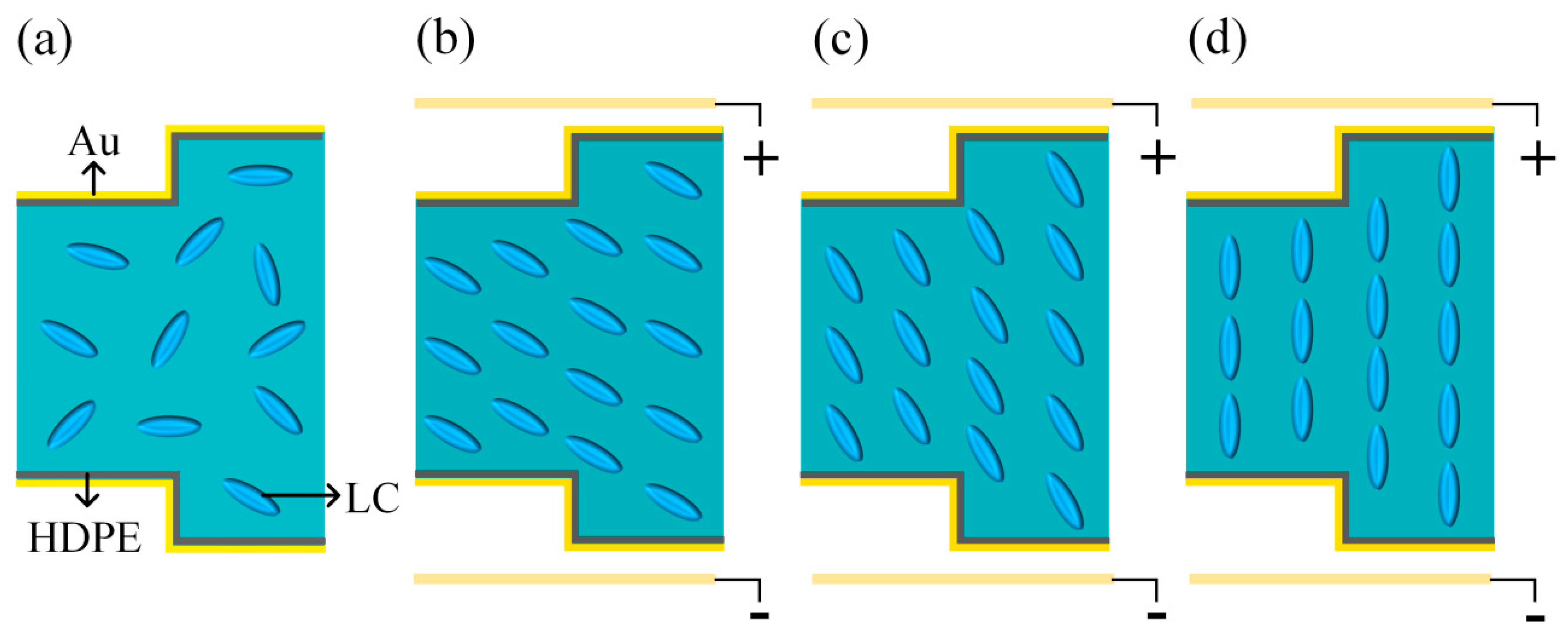
3. LC Materials
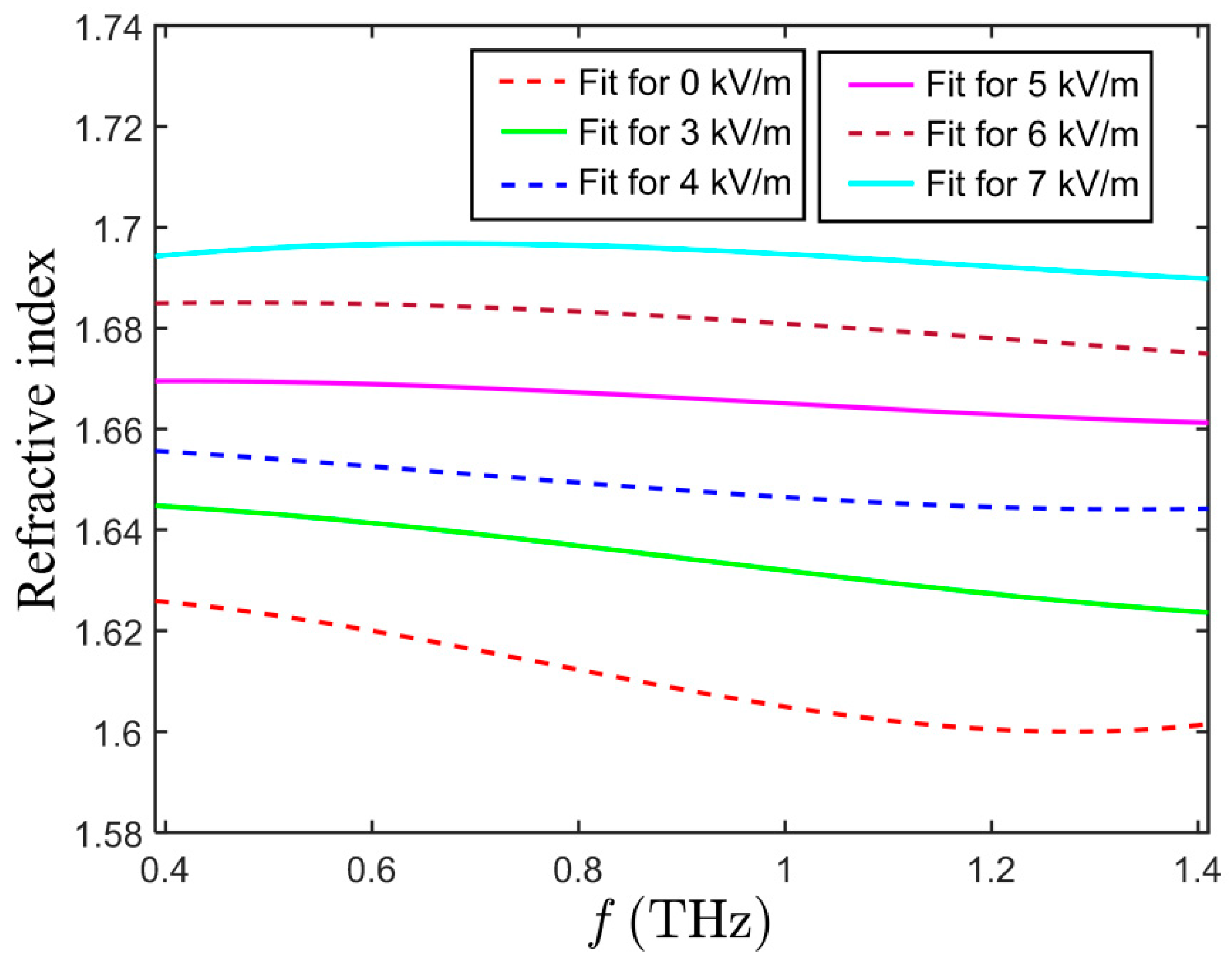
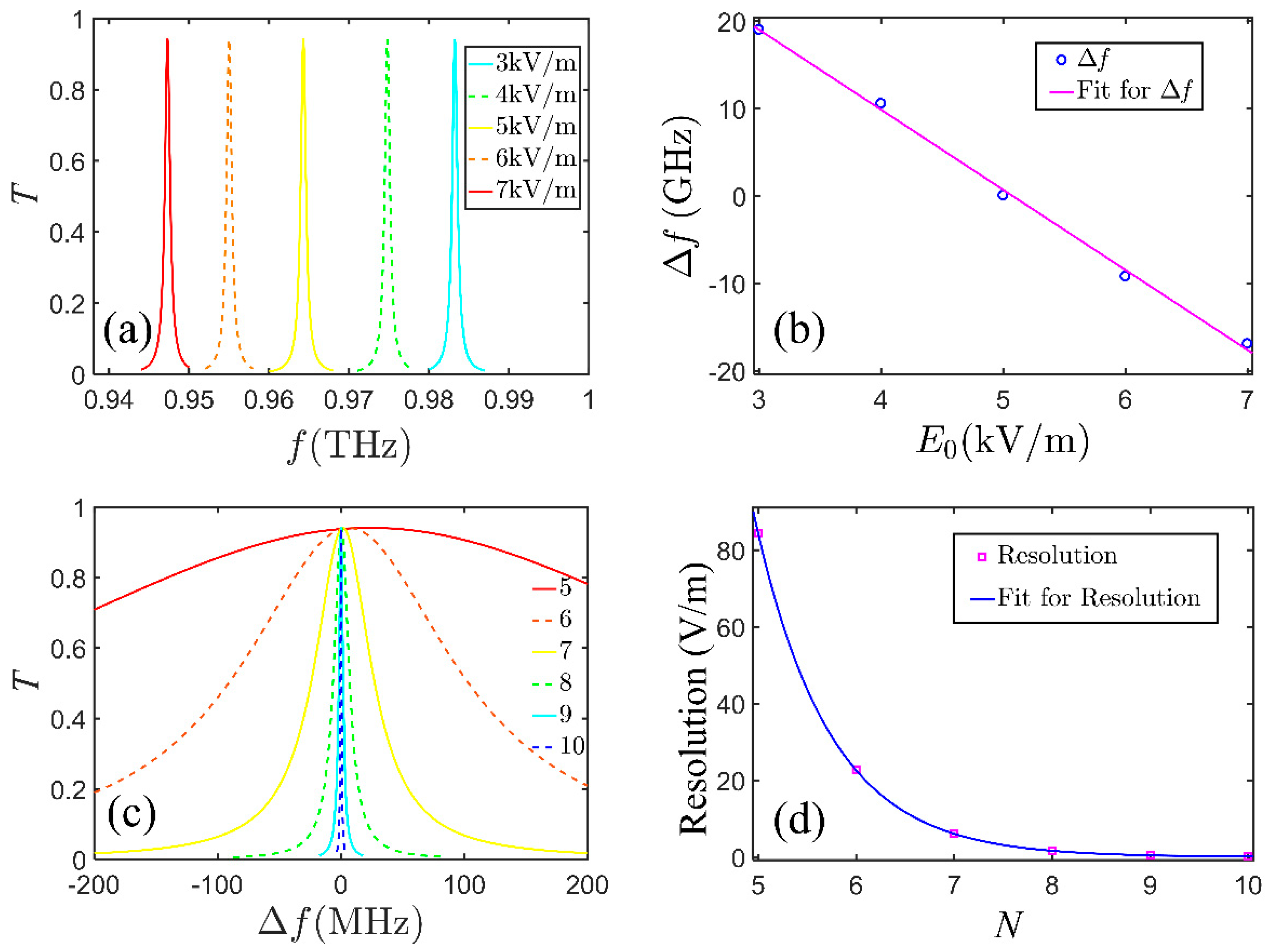
4. Sensitivity and Resolution
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Chattopadhyay, G. Technology, capabilities, and performance of low power terahertz sources. IEEE Trans. Terahertz Sci. Technol. 2011, 1, 33–53. [Google Scholar] [CrossRef]
- Hartmann, R.R.; Kono, J.; Portnoi, M.E. Terahertz science and technology of carbon nanomaterials. Nanotechnology 2014, 25, 322001. [Google Scholar] [CrossRef] [PubMed]
- Dhillon, S.S.; Vitiello, M.S.; Linfield, E.H.; Davies, A.G.; Hoffmann, M.C.; Booske, J.; Paoloni, C.; Gensch, M.; Weightman, P.; Williams, G.P.; et al. The 2017 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2017, 50, 043001. [Google Scholar] [CrossRef]
- Takano, K.; Morimoto, I.; Yokoyama, H.; Hangyo, M. Wire-grid polarizer in the terahertz region fabricated by nanoimprint technology. Opt. Lett. 2011, 36, 2665–2667. [Google Scholar] [CrossRef] [PubMed]
- Amenabar, I.; Lopez, F.; Mendikute, A. In introductory review to THz non-destructive testing of composite mater. J. Infrared Mill. Terahz. Waves 2013, 34, 152–169. [Google Scholar] [CrossRef]
- You, C.W.; Lu, C.; Wang, T.Y.; Qian, S.R.; Yang, Z.G.; Wang, K.J.; Liu, J.S.; Wang, S.L. Method for defect contour extraction in terahertz non-destructive testing conducted with a raster-scan THz imaging system. Appl. Opt. 2018, 57, 4884–4889. [Google Scholar] [CrossRef]
- Kawase, K.; Ogawa, Y.; Watanabe, Y. Non-destructive terahertz imaging of illicit drugsusing spectral fingerprints. Opt. Express 2003, 11, 2549–2554. [Google Scholar] [CrossRef]
- Kleine-ostmann, T.; Jastrow, C.; Baaske, K.; Heinen, B.; Schwerdtfeger, M.; Kärst, U.; Hintzsche, H.; Stopper, H.; Koch, M.; Schrader, T. Field Exposure and Dosimetry in the THz Frequency Range. IEEE Trans. Terahertz Sci. Technol. 2014, 4, 12–25. [Google Scholar] [CrossRef]
- Sunaguchi, N.; Sasaki, Y.; Maikusa, N.; Kawai, M.; Yuasa, T.; Otani, C. Depth-resolving THz imaging with tomosynthesis. Opt. Express 2009, 17, 9558–9570. [Google Scholar] [CrossRef]
- Li, J.; Takeda, M.; Wang, Z.; Shi, S.C.; Yang, J. Low-noise 0.5 THz all-NbN superconductor-insulator-superconductor mixer for submillimeter wave astronomy. Appl. Phys. Lett. 2008, 92, 222504. [Google Scholar] [CrossRef]
- Kawano, Y. Terahertz waves: A tool for condensed matter, the life sciences and astronomy. Contemp. Phys. 2013, 54, 143–165. [Google Scholar] [CrossRef]
- Parrott, E.P.J.; Sun, Y.; Pickwell-Macpherson, E. Terahertz spectroscopy: Its future role in medical diagnoses. J. Mol. Struct. 2011, 1006, 66–76. [Google Scholar] [CrossRef]
- Turchinovich, D.; Dijkhuis, J.I. Performance of combined ⟨1 0 0⟩–⟨1 1 0⟩ ZnTe crystals in an amplified THz time-domain spectrometer. Opt. Commun. 2007, 270, 96–99. [Google Scholar] [CrossRef]
- Qiao, W.; Stephan, D.; Hasselbeck, M.; Liang, Q.; Dekorsy, T. Low-temperature THz time domain waveguide spectrometer with butt-coupled emitter and detector crystal. Opt. Express 2012, 20, 19769–19777. [Google Scholar] [CrossRef] [PubMed]
- Zhou, S.F.; Reekie, L.; Chan, H.P.; Luk, K.M.; Chow, Y.T. Characterization of a fiber bragg grating for use in a THz spectrometer. IEEE Photonics Technol. Lett. 2013, 25, 734–736. [Google Scholar] [CrossRef]
- Hsieh, C.-F.; Pan, R.-P.; Tang, T.-T.; Chen, H.-L.; Pan, C.-L. Voltage-controlled liquid-crystal terahertz phase shifter and quarter-wave plate. Opt. Lett. 2006, 31, 1112–1114. [Google Scholar] [CrossRef] [PubMed]
- Han, Z.; Ohno, S.; Tokizane, Y.; Nawata, K.; Notake, T.; Takida, Y.; Minamide, H. Thin terahertz-wave phase shifter by flexible film metamaterial with high transmission. Opt. Express 2017, 25, 31186–31195. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, L.; Duan, D.; Fan, Y.X.; Tao, Z.Y. Wide band terahertz switch of undulated waveguide with VO2 film coated inner wall. J. Light. Technol. 2018, 36, 4401–4407. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, Y.X.; Liu, H.; Xu, L.L.; Xue, J.L.; Tao, Z.Y. Hypersensitive and Tunable Terahertz Wave Switch Based on Non-Bragg Structures Filled with Liquid Crystals. J. Light. Technol. 2017, 35, 3092–3098. [Google Scholar] [CrossRef]
- Islam, M.; Rao, S.J.M.; Kumar, G.; Pal, B.P.; Roy Chowdhury, D. Role of Resonance Modes on Terahertz Metamaterials based Thin Film Sensors. Sci. Rep. 2017, 7, 7355. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Hefferman, G.; Wei, T. A Sweep Velocity-Controlled VCSEL Pulse Laser to Interrogate Sub-THz-Range Fiber Sensors. IEEE Photonics Technol. Lett. 2017, 29, 1471–1474. [Google Scholar] [CrossRef]
- He, T.; Zhang, B.; Shen, J.; Zang, M.; Chen, T.; Hu, Y.; Hou, Y. High-efficiency THz modulator based on phthalocyanine-compound organic films. Appl. Phys. Lett. 2015, 106, 053303. [Google Scholar] [CrossRef]
- Nouman, M.T.; Kim, H.; Woo, J.M.; Hwang, J.H.; Kim, D.; Jang, J. Terahertz Modulator based on Metamaterials integrated with Varactors. Sci. Rep. 2016, 6, 26452. [Google Scholar] [CrossRef] [PubMed]
- Spirito, D.; Coquillat, D.; De Bonis, S.L.; Lombardo, A.; Bruna, M.; Ferrari, A.C.; Pellegrini, V.; Tredicucci, A.; Knap, W.; Vitiello, M.S. High performance bilayer-graphene Terahertz detectors. Appl. Phys. Lett. 2014, 104, 061111. [Google Scholar] [CrossRef]
- Koizumi, R.; Li, B.-X.; Lavrentovich, O. Effect of Crowding Agent Polyethylene Glycol on Lyotropic Chromonic Liquid Crystal Phases of Disodium Cromoglycate. Crystals 2019, 9, 160. [Google Scholar] [CrossRef]
- Črešnar, D.; Kyrou, C.; Lelidis, I.; Drozd-Rzoska, A.; Starzonek, S.; Rzoska, S.; Kutnjak, Z.; Kralj, S. Impact of Weak Nanoparticle Induced Disorder on Nematic Ordering. Crystals 2019, 9, 171. [Google Scholar] [CrossRef]
- Wang, Y.; Kanazawa, A.; Shiono, T.; Ikeda, T.; Matsuki, Y.; Takeuchi, Y. Homogeneous alignment of nematic liquid crystal induced by polyimide exposed to linearly polarized light. Appl. Phys. Lett. 1998, 72, 545–547. [Google Scholar] [CrossRef]
- Sinclair, E.J.; Carr, E.F. Flow Patterns in Bulk Samples of a Nematic Liquid Crystal Due To Electric Fields. Mol. Cryst. Liq. Cryst. 1976, 35, 143–153. [Google Scholar] [CrossRef]
- Mur, M.; Sofi, J.A.; Kvasić, I.; Mertelj, A.; Lisjak, D.; Niranjan, V.; Muševič, I.; Dhara, S. Magnetic-field tuning of whispering gallery mode lasing from ferromagnetic nematic liquid crystal microdroplets. Opt. Express 2017, 25, 1073–1083. [Google Scholar] [CrossRef]
- Madsen, L.A.; Dingemans, T.J.; Nakata, M.; Samulski, E.T. Thermotropic biaxial nematic liquid crystal. Phys. Rev. Lett. 2004, 92, 145505. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Wu, S.-T.; Brugioni, S.; Meucci, R.; Faetti, S. Infrared refractive indices of liquid crystals. J. Appl. Phys. 2005, 97, 073501. [Google Scholar] [CrossRef]
- Ma, M.; Li, S.; Jing, X.; Chen, H. Refractive indices of liquid crystal E7 depending on temperature and wavelengths. Opt. Eng. 2017, 56, 117109. [Google Scholar] [CrossRef]
- Wang, C.T.; Wang, C.Y.; Yu, J.H.; Kuo, I.T.; Tseng, C.W.; Jau, H.C.; Chen, Y.J.; Lin, T.H. Highly sensitive optical temperature sensor based on a SiN micro-ring resonator with liquid crystal cladding. Opt. Express 2016, 24, 1002–1007. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.K.; Yang, K.L. Liquid crystal based optical sensor for detection of vaporous butylamine in air. Sensors Actuators, B Chem. 2012, 173, 607–613. [Google Scholar] [CrossRef]
- Bi, X.; Hartono, D.; Yang, K.L. Real-time liquid crystal pH sensor for monitoring enzymatic activities of penicillinase. Adv. Funct. Mater. 2009, 19, 3760–3765. [Google Scholar] [CrossRef]
- Tichit, P.H.; Burokur, S.N.; Qiu, C.W.; De Lustrac, A. Experimental verification of isotropic radiation from a coherent dipole source via electric-field-driven LC resonator metamaterials. Phys. Rev. Lett. 2013, 111, 133901. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Zhang, Y.N.; Lv, R.Q.; Li, J. Electric Field Sensor Based on Photonic Crystal Cavity with Liquid Crystal Infiltration. J. Light. Technol. 2017, 35, 3440–3446. [Google Scholar] [CrossRef]
- Czapla, A.; Bock, W.J.; Woliński, T.R.; Mikulic, P.; Nowinowski-Kruszelnicki, E.; Dąbrowski, R. Improving the electric field sensing capabilities of the long-period fiber grating coated with a liquid crystal layer. Opt. Express 2016, 24, 5662–5673. [Google Scholar] [CrossRef]
- Yang, L.; Fan, F.; Chen, M.; Zhang, X.; Chang, S.J. Active terahertz metamaterials based on liquid-crystal induced transparency and absorption. Opt. Commun. 2017, 382, 42–48. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, 2nd ed.; Oxford University Press: New York, NY, USA, 1993; pp. 123–133. [Google Scholar]
- Yang, D.K.; Wu, S.T. Fundamentals of Liquid Crystal Devices, 2nd ed.; Wiley: Wiltshire, UK, 2015; pp. 153–165. [Google Scholar]
| a | b | c | d | σ (10−4) | |
|---|---|---|---|---|---|
| 0 | 0.05068 | −0.11660 | 0.04956 | 1.621 | 3.201 |
| 3 | 0.01520 | −0.04189 | 0.01373 | 1.645 | 5.324 |
| 4 | 0.01307 | −0.02724 | 0.00269 | 1.658 | 3.600 |
| 5 | 0.01110 | −0.03321 | 0.02184 | 1.665 | 5.317 |
| 6 | 0.00819 | −0.03082 | 0.02365 | 1.680 | 3.502 |
| 7 | 0.01717 | −0.06046 | 0.05830 | 1.680 | 6.392 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, L.-L.; Gong, Y.; Fan, Y.-X.; Tao, Z.-Y. A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide. Crystals 2019, 9, 302. https://doi.org/10.3390/cryst9060302
Xu L-L, Gong Y, Fan Y-X, Tao Z-Y. A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide. Crystals. 2019; 9(6):302. https://doi.org/10.3390/cryst9060302
Chicago/Turabian StyleXu, Lan-Lan, Yi Gong, Ya-Xian Fan, and Zhi-Yong Tao. 2019. "A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide" Crystals 9, no. 6: 302. https://doi.org/10.3390/cryst9060302
APA StyleXu, L.-L., Gong, Y., Fan, Y.-X., & Tao, Z.-Y. (2019). A High-Resolution Terahertz Electric Field Sensor Using a Corrugated Liquid Crystal Waveguide. Crystals, 9(6), 302. https://doi.org/10.3390/cryst9060302





