Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals
Abstract
1. Introduction
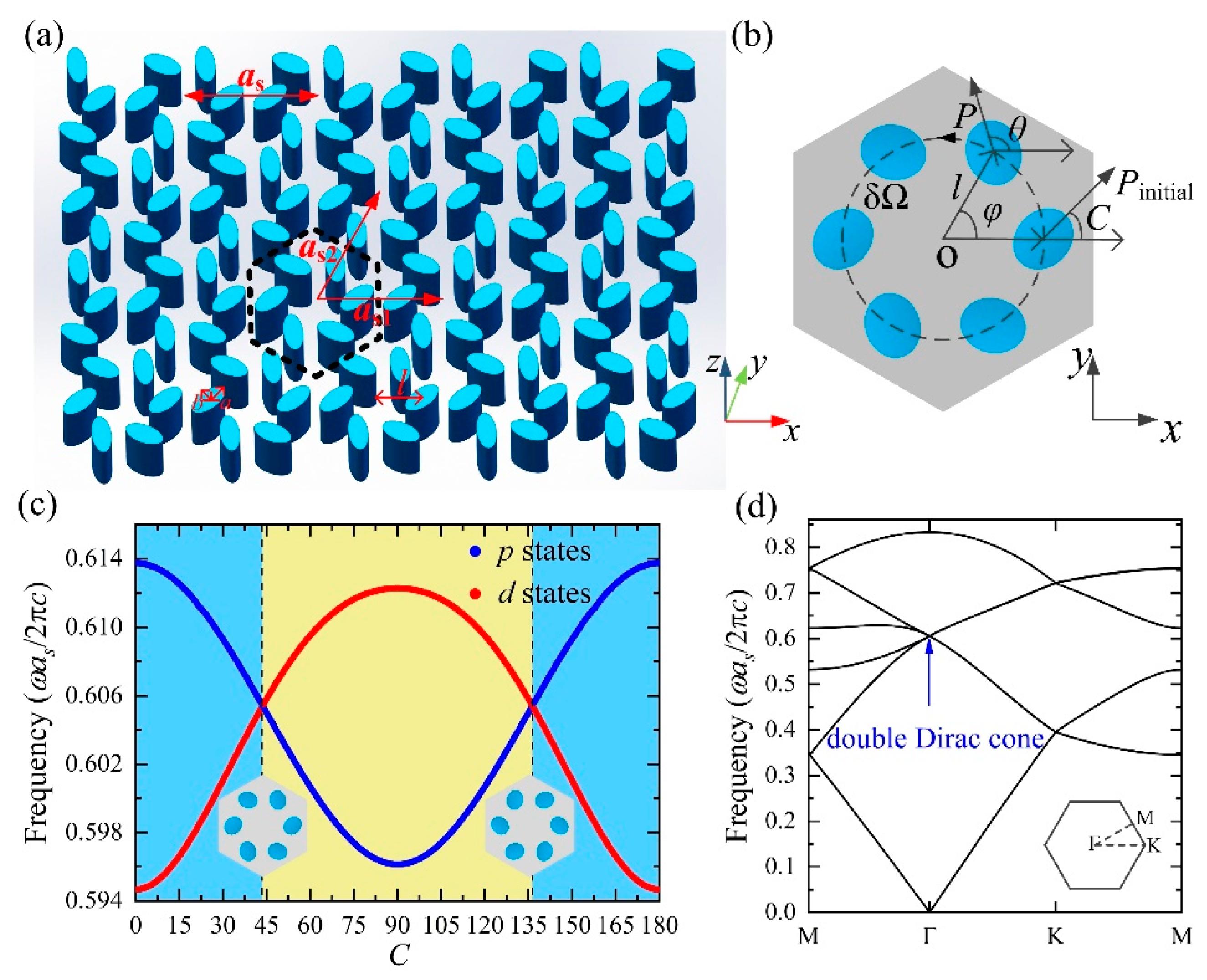
2. Simulation Methods and Models
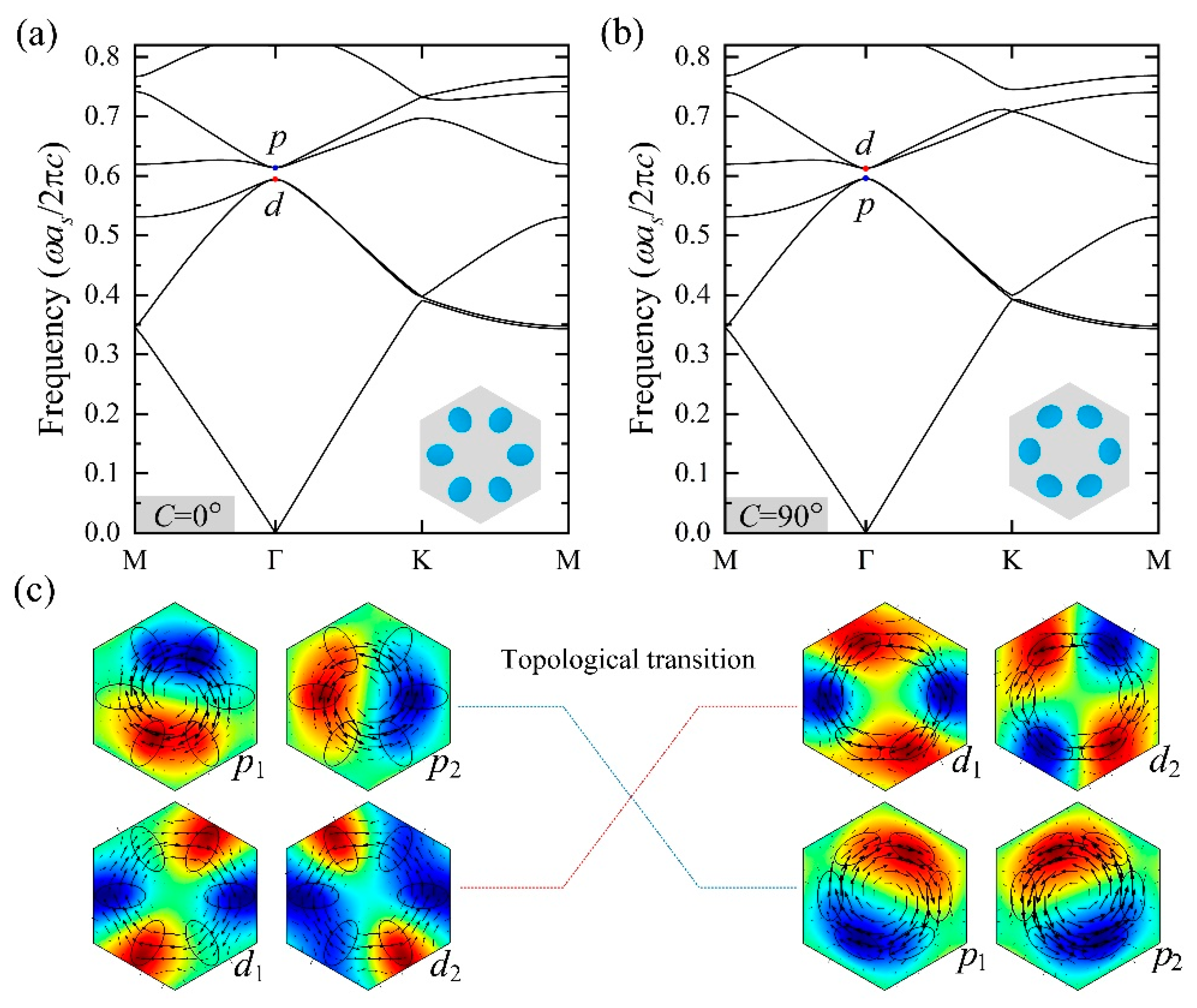
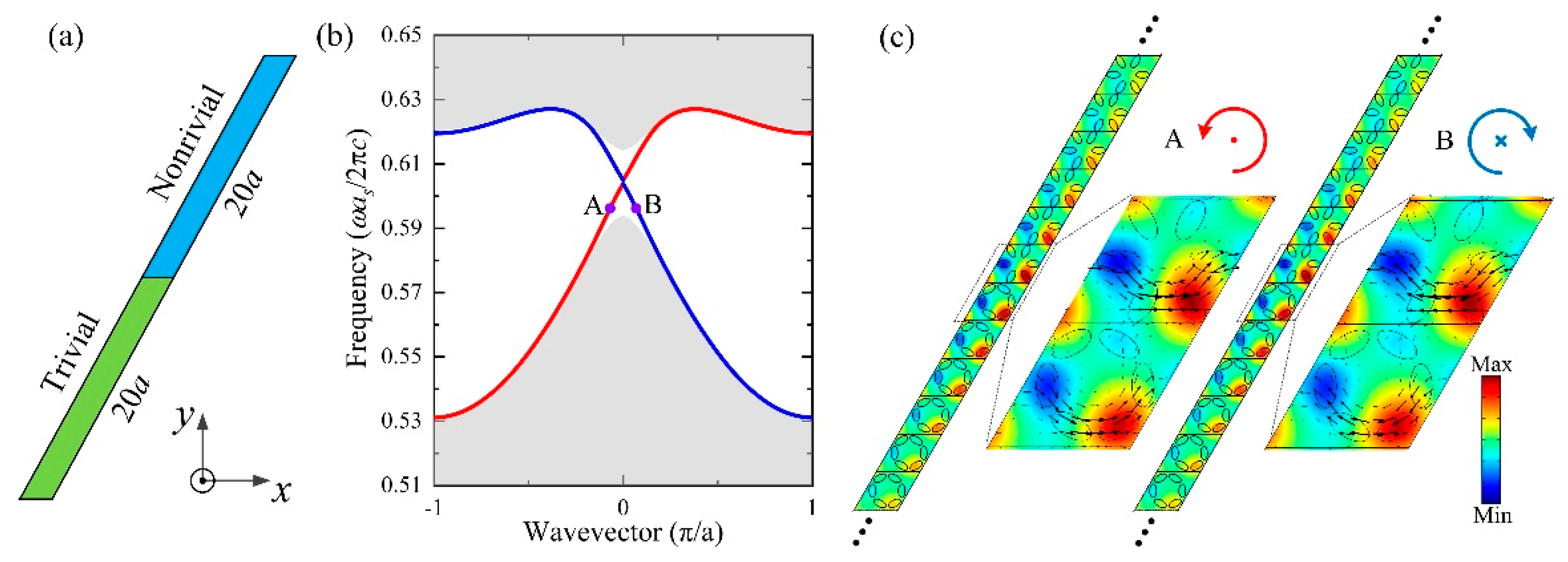
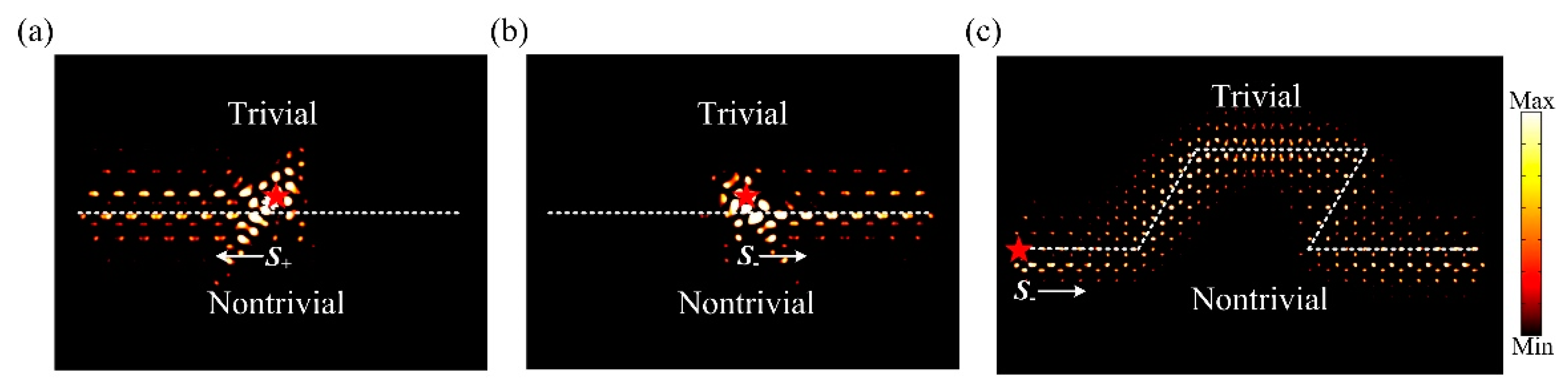
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, H.K.; Leaw, J.N.; Rodrigues, J.N.B.; Herbut, I.F.; Sengupta, P.; Assaad, F.F.; Adam, S. The role of electron-electron interactions in two-dimensional Dirac fermions. Science 2018, 361, 570–574. [Google Scholar] [CrossRef]
- Kane, C.L.; Mele, E.J. Quantum spin hall effect in graphene. Phys. Rev. Lett. 2005, 95, 226801. [Google Scholar] [CrossRef]
- Hasan, M.Z.; Kane, C.L. Colloquium: Topological insulators. Rev. Mod. Phys. 2010, 82, 3045. [Google Scholar] [CrossRef]
- Bernevig, B.A.; Hughes, T.L.; Zhang, S.C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 2006, 314, 1757–1761. [Google Scholar] [CrossRef]
- He, C.; Ni, X.; Ge, H.; Sun, X.C.; Chen, Y.B.; Lu, M.H.; Liu, X.P.; Chen, Y.F. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 2016, 12, 1124–1129. [Google Scholar] [CrossRef]
- Zhang, Z.; Wei, Q.; Cheng, Y.; Zhang, T.; Wu, D.; Liu, X. Topological creation of acoustic pseudospin multipoles in a flow-free symmetry-broken metamaterial lattice. Phys. Rev. Lett. 2017, 118, 084303. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Qiu, C.; Ye, L.; Fan, X.; Ke, M.; Zhang, F.; Liu, Z. Observation of topological valley transport of sound in sonic crystals. Nat. Phys. 2017, 13, 369–374. [Google Scholar] [CrossRef]
- Mousavi, S.H.; Khanikaev, A.B.; Wang, Z. Topologically protected elastic waves in phononic metamaterials. Nat. Commun. 2015, 6, 8682. [Google Scholar] [CrossRef]
- Huang, H.B.; Chen, J.J.; Huo, S.Y. Simultaneous topological Bragg and locally resonant edge modes of shear horizontal guided wave in one-dimensional structure. J. Phys. D: Appl. Phys. 2017, 50, 275102. [Google Scholar] [CrossRef]
- Chen, J.J.; Huang, H.B.; Huo, S.Y.; Tan, Z.H.; Xie, X.P.; Cheng, J.C.; Huang, G.L. Self-ordering induces multiple topological transitions for in-plane bulk waves in solid phononic crystals. Phys. Rev. B 2018, 98, 014302. [Google Scholar] [CrossRef]
- Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Theory. Science 2018, 359, 1230. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, 1231. [Google Scholar] [CrossRef]
- Lustig, E.; Weimann, S.; Plotnik, Y.; Lumer, Y.; Bandres, M.A.; Szameit, A.; Segev, M. Photonic topological insulator in synthetic dimensions. Nature 2019, 567, 356. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Z.; Xue, H.; Zhang, L.; He, M.; Yang, Z.; Singh, R.; Chong, Y.; Zhang, B.; Chen, H. Realization of a three-dimensional photonic topological insulator. Nature 2019, 565, 622. [Google Scholar] [CrossRef]
- Xie, B.Y.; Wang, H.F.; Wang, H.X.; Zhu, X.Y.; Jiang, J.H.; Lu, M.H.; Chen, Y.F. Second-order photonic topological insulator with corner states. Phys. Rev. B 2018, 98, 205147. [Google Scholar] [CrossRef]
- Haldane, F.D.M.; Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 2008, 100, 013904. [Google Scholar] [CrossRef]
- Raghu, S.; Haldane, F.D.M. Analogs of quantum-Hall-effect edge states in photonic crystals. Phys. Rev. A 2008, 78, 033834. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.D.; Joannopoulos, J.D.; Soljăcić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef]
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljăcić, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 2009, 461, 772–775. [Google Scholar] [CrossRef]
- Poo, Y.; Wu, R.-X.; Lin, Z.; Yang, Y.; Chan, C.T. Experimental realization of self-guiding unidirectional electromagnetic edge states. Phys. Rev. Lett. 2011, 106, 093903. [Google Scholar] [CrossRef]
- Hafezi, M.; Demler, E.A.; Lukin, M.D.; Taylor, J.M. Robust optical delay lines with topological protection. Nat. Phys. 2011, 7, 907–912. [Google Scholar] [CrossRef]
- Hafezi, M.; Mittal, S.; Fan, J.; Migdall, A.; Taylor, J.M. Imaging topological edge states in silicon photonics. Nat. Photon. 2013, 7, 1001–1005. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 2012, 6, 782–787. [Google Scholar] [CrossRef]
- Umucalılar, R.O.; Carusotto, I. Artificial gauge field for photons in coupled cavity arrays. Phys. Rev. A 2011, 84, 043804. [Google Scholar] [CrossRef]
- Fang, K.; Yu, Z.; Fan, S. Microscopic theory of photonic one-way edge mode. Phys. Rev. B 2011, 84, 075477. [Google Scholar] [CrossRef]
- Ma, T.; Khanikaev, A.B.; Mousavi, S.H.; Shvets, G. Guiding Electromagnetic Waves around Sharp Corners: Topologically Protected Photonic Transport in Metawaveguides. Phys. Rev. Lett. 2015, 114, 127401. [Google Scholar] [CrossRef]
- Chen, W.J.; Jiang, S.J.; Chen, X.D.; Zhu, B.; Zhou, L.; Dong, J.W.; Chan, C.T. Experimental realization of photonic topological insulator in a uniaxial metacrystal waveguide. Nat. Commun. 2014, 5, 5782. [Google Scholar] [CrossRef]
- Barik, S.; Miyake, H.; DeGottardi, W.; Waks, E.; Hafezi, M. Two-dimensionally confined topological edge states in photonic crystals. New J. Phys. 2016, 18, 113013. [Google Scholar] [CrossRef]
- Ma, T.X.; Wang, Y.S.; Zhang, C. Photonic and phononic surface and edge modes in three-dimensional phoxonic crystals. Phys. Rev. B 2018, 97, 134302. [Google Scholar] [CrossRef]
- Li, Y.; Mei, J. Double Dirac cones in two-dimensional dielectric photonic crystals. Opt. Express 2015, 23, 12089–12099. [Google Scholar] [CrossRef]
- Xu, L.; Wang, H.X.; Xu, Y.D.; Chen, H.Y.; Jiang, J.H. Accidental degeneracy in photonic bands and topological phase transitions in two-dimensional core-shell dielectric photonic crystals. Opt. Express 2016, 24, 18059–18071. [Google Scholar] [CrossRef]
- Fang, K.; Fan, S. Controlling the flow of light using the inhomogeneous effective gauge field that emerges from dynamic modulation. Phys. Rev. Lett. 2013, 111, 203901. [Google Scholar] [CrossRef]
- Reiskarimian, N.; Krishnaswamy, H. Magnetic-free non-reciprocity based on staggered commutation. Nat. Commun. 2016, 7, 11217. [Google Scholar] [CrossRef]
- Rechtsman, M.C.; Zeuner, J.M.; Plotnik, Y.; Lumer, Y.; Podolsky, D.; Dreisow, F.; Nolte, S.; Segev, M.; Szameit, A. Photonic floquet topological insulators. Nature 2013, 496, 196. [Google Scholar] [CrossRef]
- Cheng, X.; Jouvaud, C.; Ni, X.; Mousavi, S.H.; Genack, A.Z.; Khanikaev, A.B. Robust reconfigurable electromagnetic pathways within a photonic topological insulator. Nat. Mater. 2016, 15, 542. [Google Scholar] [CrossRef]
- Shalaev, M.I.; Desnavi, S.; Walasik, W.; Litchinitser, N.M. Reconfigurable topological photonic crystal. New J. Phys. 2018, 20, 023040. [Google Scholar] [CrossRef]
- Wu, L.-H.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Mermin, N.D. The topological theory of defects in ordered media. Rev. Mod. Phys. 1979, 51, 591. [Google Scholar] [CrossRef]
- Kleman, M.; Lavrentovich, O.D. Soft Matter Physics: An Introduction; Springer: New York, NY, USA, 2003. [Google Scholar]
- Podgornik, R. Principles of condensed matter physics. J. Stat. Phys. 1996, 83, 1263–1265. [Google Scholar] [CrossRef]
- Yves, S.; Fleury, R.; Berthelot, T.; Fink, M.; Lemoult, F.; Lerosey, G. Crystalline metamaterials for topological properties at subwavelength scales. Nat. Commun. 2017, 8, 16023. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Y.F.; Xu, T.; Wang, H.X.; Jiang, J.H.; Hu, X.; Hang, Z.H. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Huo, S.; Chen, J. Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals. Crystals 2019, 9, 221. https://doi.org/10.3390/cryst9040221
Huang H, Huo S, Chen J. Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals. Crystals. 2019; 9(4):221. https://doi.org/10.3390/cryst9040221
Chicago/Turabian StyleHuang, Hongbo, Shaoyong Huo, and Jiujiu Chen. 2019. "Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals" Crystals 9, no. 4: 221. https://doi.org/10.3390/cryst9040221
APA StyleHuang, H., Huo, S., & Chen, J. (2019). Reconfigurable Topological Phases in Two-Dimensional Dielectric Photonic Crystals. Crystals, 9(4), 221. https://doi.org/10.3390/cryst9040221




