Atomic Structure of Decagonal Al-Cu-Rh Quasicrystal–Revisited: New Correction for Phonons
Abstract
:1. Introduction
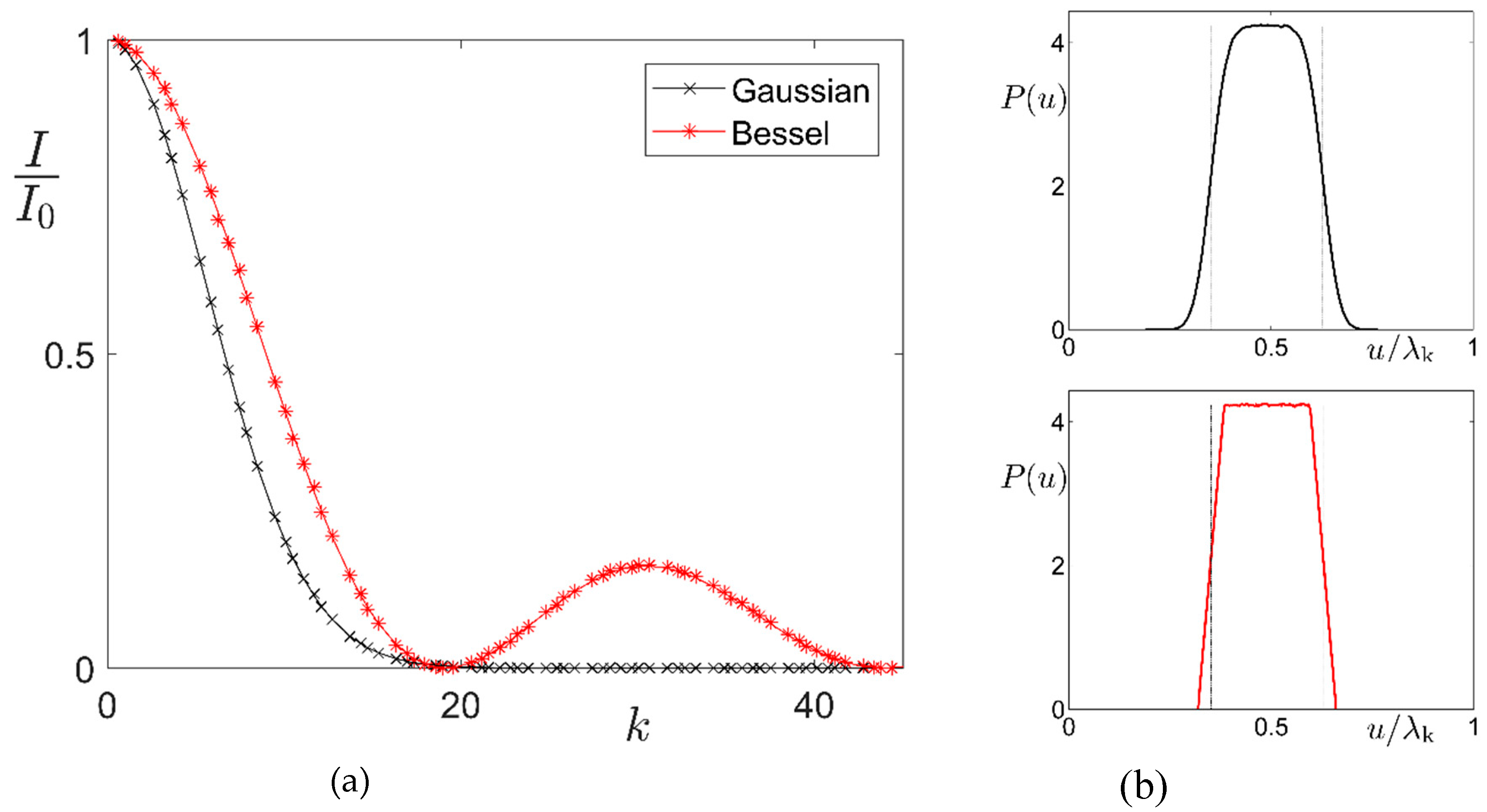
2. Phonons in Quasicrystals: A Statistical Approach
3. d-Al-Cu-Rh: Experimental Details and Starting Model
4. Structure Factor and Refinement Strategy
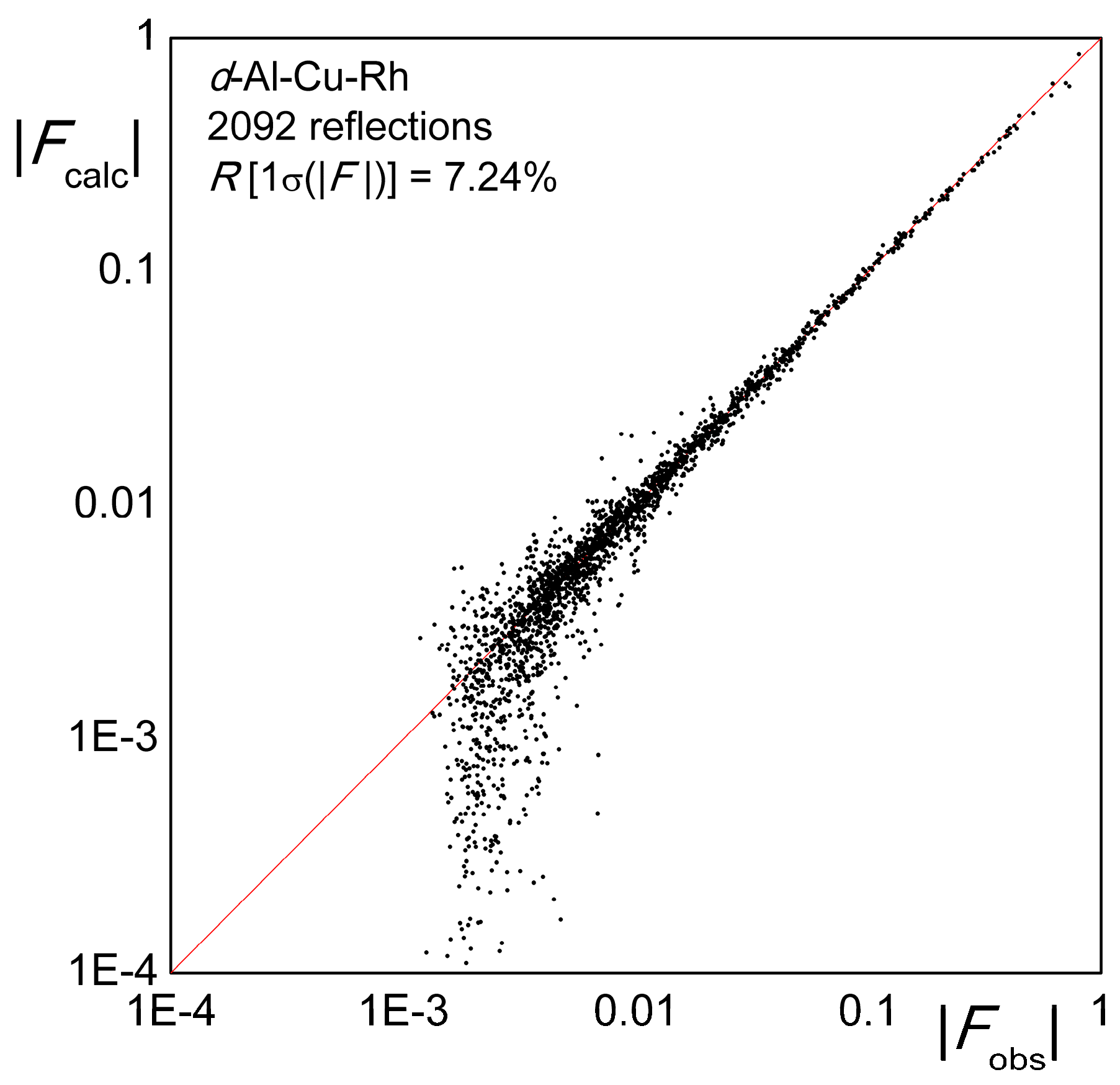
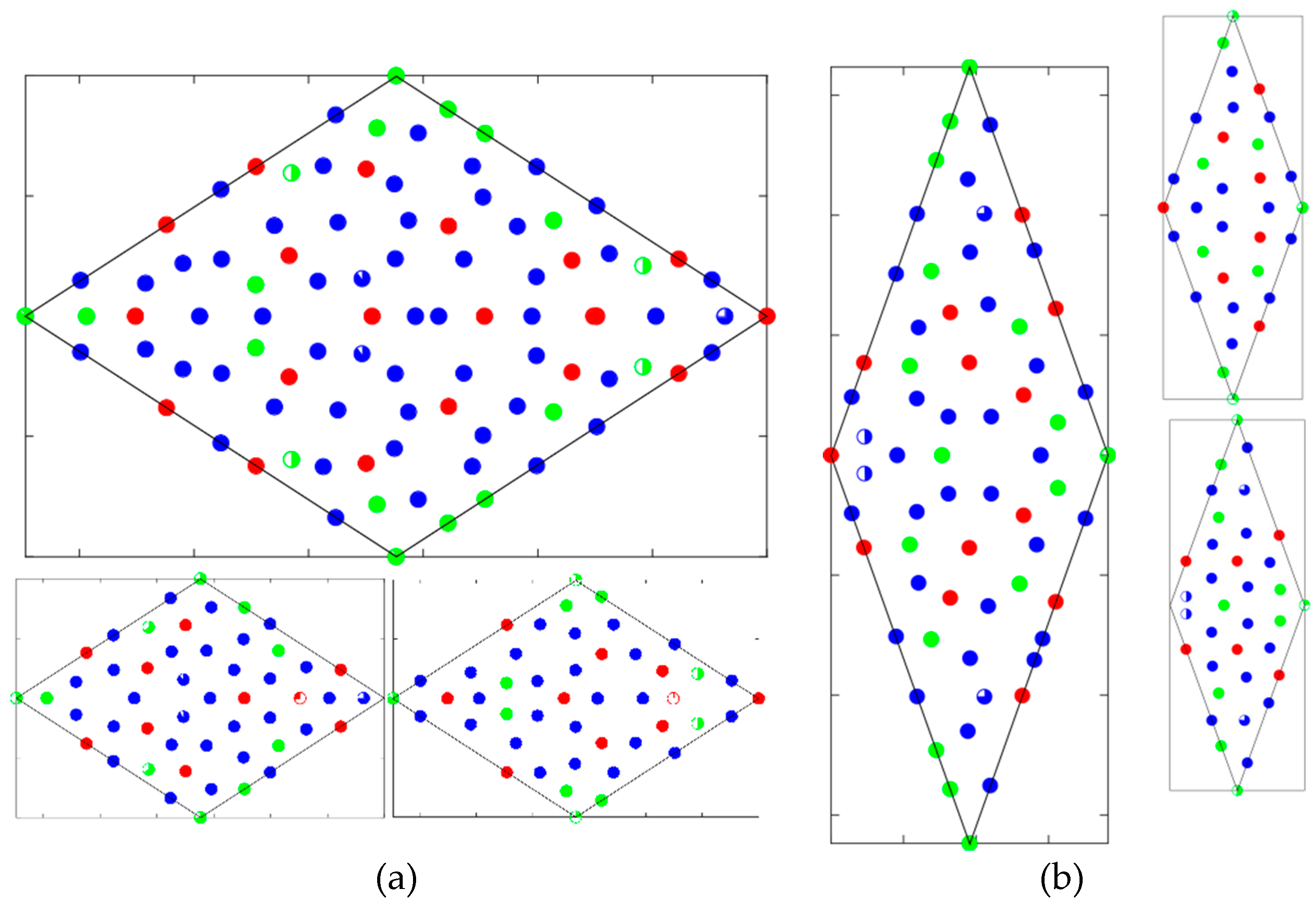
5. Refinement Results and Structure
6. Summary and Outlook
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Kuczera, P.; Wolny, J.; Steurer, W. Comparative structural study of decagonal quasicrystals in the systems Al–Cu–Me (Me = Co, Rh, Ir). Acta Cryst. B 2012, 68, 578–589. [Google Scholar] [CrossRef] [PubMed]
- Steurer, W.; Kuo, K.H. Five-dimensional structure analysis of decagonal Al65Cu20Co15. Acta Cryst. B 1990, 46, 703–712. [Google Scholar] [CrossRef]
- Wolny, J. The reference lattice concept and its application to the analysis of diffraction patterns. Philos. Mag. A 1998, 77, 395–412. [Google Scholar] [CrossRef]
- Wolny, J.; Kuczera, P.; Strzalka, R. Periodically distributed objects with quasicrystalline diffraction pattern. Appl. Phys. Lett. 2015, 106, 131905. [Google Scholar] [CrossRef]
- Strzalka, R.; Buganski, I.; Wolny, J. Statistical Approach to Diffraction of Periodic and Non-Periodic Crystals—Review. Crystals 2016, 6, 104. [Google Scholar] [CrossRef]
- Wolny, J.; Buganski, I.; Kuczera, P.; Strzalka, R. Pushing the limits of crystallography. J. Appl. Cryst. 2016, 49, 2106–2115. [Google Scholar] [CrossRef]
- Kuhs, W.F. Atomic displacement parameters. Int. Tables Crystallogr. D 2006, 1.9, 228–242. [Google Scholar]
- Wolny, J.; Buganski, I.; Strzalka, R. Phononic and Phasonic Debye-Waller Factors for 1D Quasicrystals. Acta Phys. Pol. A 2016, 130, 836–840. [Google Scholar] [CrossRef]
- Lubensky, T.C.; Ramaswamy, S.; Toner, J. Hydrodynamics of icosahedral quasicrystals. Phys. Rev. B 1985, 32, 7444–7452. [Google Scholar] [CrossRef]
- Levine, D.; Lubensky, T.C.; Ostlund, S.; Ramaswamy, S.; Steinhardt, P.J. Elasticity and dislocations in Pentagonal and Icosahedral Quasicrystals. Phys. Rev. Lett. 1985, 54, 1520–1523. [Google Scholar] [CrossRef]
- Li, X.F. Elastohydrodynamic problems in quasicrystal elasticity theory and wave propagation. Philos. Mag. 2013, 93, 1500–1519. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Matallic Phase with Long-Range Orientational Order and No Translational Symmetry. Phys. Rev. Lett. 1984, 53, 1951–1954. [Google Scholar] [CrossRef]
- Lu, J.P.; Odagaki, T.; Birman, J. Properties of one-dimensional quasilattices. Phys. Rev. B 1986, 33, 4809–4817. [Google Scholar] [CrossRef]
- Lu, J.P.; Birman, J. Acoustic-wave propagation in quasiperiodic, incommensurate, and random systems. Phys. Rev. B 1988, 38, 8067–8074. [Google Scholar] [CrossRef]
- Strandburg, K.J.; Tang, L.H.; Jaric, M.V. Phason elasticity in entropic quasicrystals. Phys. Rev. Lett. 1989, 63, 314–317. [Google Scholar] [CrossRef] [PubMed]
- Rochal, S.B. Second-order terms of the phonon-phason dynamic matrix of an icosahedral quasicrystal: Diffuse intensity and the profile shape around the Bragg peaks. Phys. Rev. B 2001, 64, 144204. [Google Scholar] [CrossRef]
- Mihalkovic, M.; Elhor, H.; Suck, J.-B. Low-energy phonon excitations in the decagonal quasicrystal Al70Co15Ni15 and in crystalline Al13Co4 phases. Mater. Sci. Eng. A 2000, 294, 654–657. [Google Scholar] [CrossRef]
- Trebin, H.-R.; Koschella, U.; Umezaki, M.; Odagaki, T. Investigation of phason statics and dynamics. Philos. Mag. 2006, 86, 1021–1028. [Google Scholar] [CrossRef]
- De Boissieu, M.; Boudard, M.; Hennion, B.; Bellissent, R.; Kycia, S.; Goldman, A.I.; Janot, C.; Audier, M. Diffuse Scattering and Phason Elasticity in the A1PdMn Icosahedral Phase. Phys. Rev. Lett. 1995, 75, 89–92. [Google Scholar] [CrossRef]
- Edagawa, K. Phonon–phason coupling in a Mg–Ga–Al–Zn icosahedral quasicrystal. Philos. Mag. Lett. 2006, 85, 455–462. [Google Scholar] [CrossRef]
- Boudard, M.; Boissieu, M.; Kycia, S.; Goldman, A.I.; Hennion, B.; Bellissent, R.; Quilichini, M.; Currat, R.; Janot, C. Optic modes in the AlPdMn icosahedral phase. J. Phys. Condens. Matter 1995, 7, 7299–7308. [Google Scholar] [CrossRef]
- De Boissieu, M.; Currat, R.; Francoual, S.; Kats, E. Sound-mode broadening in quasicrystals: A simple phenomenological model. Phys. Rev. B 2004, 69, 54205. [Google Scholar] [CrossRef]
- De Boissieu, M.; Francoual, S.; Mihalkovic, M.; Shibata, K.; Baron, A.Q.R.; Sidis, Y.; Ishimasa, T.; Wu, D.; Lograsso, T.; Regnault, L.P.; et al. Lattice dynamics of the Zn–Mg–Sc icosahedral quasicrystal and its Zn–Sc periodic 1/1 approximant. Nat. Mater. 2007, 6, 977–984. [Google Scholar] [CrossRef] [PubMed]
- Dugain, F.; de Boissieu, M.; Shibata, K.; Currat, R.; Sato, T.J.; Kortan, A.R.; Suck, J.-B.; Hradil, K.; Frey, F.; Tsai, A.P. Inelastic neutron scattering study of the dynamics of the AlNiCo decagonal phase. Eur. Phys. J. B 1999, 7, 513–516. [Google Scholar] [CrossRef]
- De Boissieu, M. Phonons, phasons and atomic dynamics in quasicrystals. Chem. Soc. Rev. 2012, 41, 6778–6786. [Google Scholar] [CrossRef]
- Krajci, M.; Hafner, J. Elementary excitations in quasicrystals. J. Non-Cryst. Solids 1993, 156, 887–890. [Google Scholar] [CrossRef]
- Janssen, T.; de Boissieu, M. Dynamics of quasicrystals. C. R. Phys. 2014, 15, 58–69. [Google Scholar] [CrossRef]
- Grushko, B.; Kowalski, W.; Przepiorzynski, B.; Pavlyuchkov, D. Constitution of the high-Al region of Al–Cu–Rh. J. Alloys Compd. 2008, 464, 227–233. [Google Scholar] [CrossRef]
- Kapush, D.; Grushko, B.; Velikanova, T.Y. Phase equilibria in the Al-rich region of Al–Cu–Ir. J. Alloys Compd. 2010, 493, 99–104. [Google Scholar] [CrossRef]
- Palatinus, L.; Chapuis, G. SUPERFLIP—A computer program for the solution of crystal structures by charge flipping in arbitrary dimensions. J. Appl. Cryst. 2007, 40, 786–790. [Google Scholar] [CrossRef]
- Oszlanyi, G.; Suto, A. The charge flipping algorithm. Acta Cryst. A 2008, 64, 123–134. [Google Scholar] [CrossRef] [PubMed]
- Wolny, J.; Kozakowski, B.; Repetowicz, P. Construction of average unit cell for Penrose tiling. J. All. Com. Compd. 2002, 342, 198–202. [Google Scholar] [CrossRef]
- Kozakowski, B.; Wolny, J. Structure factor for decorated Penrose tiling. Acta Cryst. A 2010, 66, 489–498. [Google Scholar] [CrossRef] [PubMed]
- Kuczera, P.; Wolny, J.; Fleischer, F.; Steurer, W. Structure refinement of decagonal Al-Ni-Co, superstructure type I. Philos. Mag. 2011, 90, 2500–2509. [Google Scholar] [CrossRef]
- Kuczera, P.; Wolny, J.; Steurer, W. High-temperature structural study of decagonal Al–Cu–Rh. Acta Cryst. B 2014, 70, 306–314. [Google Scholar] [CrossRef]
- Strzalka, R.; Wolny, J. Structure model for icosahedral quasicrystal based on Ammann tiling. Acta Phys. Pol. A 2014, 126, 585–588. [Google Scholar] [CrossRef]
- Strzalka, R.; Buganski, I.; Wolny, J. Structure factor for an icosahedral quasicrystal within a statistical approach. Acta Cryst. A 2015, 71, 279–290. [Google Scholar] [CrossRef]
- Strzalka, R.; Buganski, I.; Wolny, J. Simple decoration model of icosahedral quasicrystals in statistical approach. Acta Phys. Pol. A 2016, 130, 841–844. [Google Scholar] [CrossRef]
- Buganski, I.; Strzalka, R.; Wolny, J. The estimation of phason flips in 1D quasicrystal from the diffraction pattern. Phys. Stat. Solidi B 2016, 253, 450–457. [Google Scholar] [CrossRef]
- Wolny, J.; Buganski, I.; Strzalka, R. Model refinement of quasicrystals. Cryst. Rev. 2018, 43, 1–43. [Google Scholar] [CrossRef]
- Takakura, H.; Mizuno, R. Multiple Diffraction in an Icosahedral Al-Cu-Rh Quasicrystal: X-Ray Experiment and Simulation. Mater. Struct. 2015, 22, 281. [Google Scholar]
- Fan, C.Z.; Weber, T.; Deloudi, S.; Steurer, W. Multiple diffraction in an icosahedral Al-Cu-Fe quasicrystal. Philos. Mag. 2011, 91, 2528–2535. [Google Scholar]
- Chodyn, M.; Kuczera, P.; Wolny, J. Generalized Penrose tiling as a quasilattice for decagonal quasicrystal structure analysis. Acta Cryst. A 2015, 71, 161–168. [Google Scholar] [CrossRef] [PubMed]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Strzalka, R.; Buganski, I.; Kuczera, P.; Pytlik, L.; Wolny, J. Atomic Structure of Decagonal Al-Cu-Rh Quasicrystal–Revisited: New Correction for Phonons. Crystals 2019, 9, 78. https://doi.org/10.3390/cryst9020078
Strzalka R, Buganski I, Kuczera P, Pytlik L, Wolny J. Atomic Structure of Decagonal Al-Cu-Rh Quasicrystal–Revisited: New Correction for Phonons. Crystals. 2019; 9(2):78. https://doi.org/10.3390/cryst9020078
Chicago/Turabian StyleStrzalka, Radoslaw, Ireneusz Buganski, Pawel Kuczera, Lucjan Pytlik, and Janusz Wolny. 2019. "Atomic Structure of Decagonal Al-Cu-Rh Quasicrystal–Revisited: New Correction for Phonons" Crystals 9, no. 2: 78. https://doi.org/10.3390/cryst9020078
APA StyleStrzalka, R., Buganski, I., Kuczera, P., Pytlik, L., & Wolny, J. (2019). Atomic Structure of Decagonal Al-Cu-Rh Quasicrystal–Revisited: New Correction for Phonons. Crystals, 9(2), 78. https://doi.org/10.3390/cryst9020078




