Abstract
Crystal structure prediction is based on the assumption that the most thermodynamically stable structure will crystallize first. The existence of other structures such as polymorphs or from counterenantiomers requires an accurate calculation of the electronic energy. Using atom-centered Gaussian basis functions in periodic Density Functional Theory (DFT) calculations in Turbomole, the performance of two dispersion-corrected functionals, PBE-D3 and B97-D, is assessed for molecular organic crystals of the X23 benchmark set. B97-D shows a MAE (mean absolute error) of 4 kJ/mol, compared to 9 kJ/mol for PBE-D3. A strategy for the convergence of lattice energies towards the basis set limit is outlined. A simultaneous minimization of molecular structures and lattice parameters shows that both methods are able to reproduce experimental unit cell parameters to within 4–5%. Calculated lattice energies, however, deviate slightly more from the experiment, i.e., by 0.4 kJ/mol after unit cell optimization for PBE-D3 and 0.5 kJ/mol for B97-D. The accuracy of the calculated lattice energies compared to the experimental values demonstrates the ability of current DFT methods to assist in the quest for possible polymorphs and enantioselective crystallization processes.
1. Introduction
The determination and accurate calculation of the relative energies of even small molecular crystals is a challenge, both experimentally and theoretically. For the development of novel drug molecules or even active pharmaceutical ingredients (APIs), the isolation and separation of chiral molecules is of increasing scientific and industrial relevance because, since 1992, the US Food and Drug Administration (FDA) guidelines require new chiral drugs to be marked as single enantiomers for which a full control of the stereoselectivity must be guaranteed at every stage of the production process, or the absence of side effects for the other stereoisomer must be demonstrated [1,2,3]. However, it is not clear whether the crystallisation of pharmaceutical molecules is controlled by thermodynamics or kinetics [4]. The separation of enantiomers from their mixtures, as especially difficult process from the racemic (50:50) mixture, is most economically done by crystallization. Such a process design requires a good knowledge of the thermochemistry of the crystalline forms of the pure enantiomers and their mixtures [5]. Sometimes, the molecular association in solution does not correspond to that in the crystal [4]. Computational methods are of increasing practical use here, as their accuracy is converging to reproduce small energy differences between enantiopure and racemic crystals. For example, the lattice energy differences between different polymorphs are usually below 4 kJ/mol−1 (in 80% of the cases) [6], which is in the same range as the differences in lattice energy between enantiopure and racemic crystals [7,8].
The lattice energy, Elatt, is defined as the energy difference between a static, perfect, infinite crystal (ideal static solid, iss) and its related ideal static gas (isg) of non-interacting molecules in their lowest energy conformation at 0 K (Equation (1) where Z is the number of molecules in the unit cell).
The lattice energy is a measure of the energy released by the individual molecules which are associating and forming a crystal. It is thus a quantitative measure of the interactions in the solid state, and has a negative sign. The lattice energy can be obtained from experimental heats of sublimation or Born-Haber cycles; see [9] for a comparison of the two approaches. The challenges and approaches to calculating the interaction energies of molecular crystals have recently been reviewed in [10,11,12,13,14,15,16]. In particular, they originate from the weak intermolecular interactions due to hydrogen bonding and van-der-Waals forces. The consideration of dispersion interactions in Density Functional Theory (DFT) calculations of lattice energy is thus essential for obtaining reliable measurements of the lattice energies of molecular crystals. Among various dispersion models, the Grimme D1 and D2 models rely on strong parametrization and empiricism. The dispersion correction with minimal empirical fitting (D3) is clearly superior to D1 and D2, and has successfully been applied to molecular crystals [17,18].
The X23 benchmark set (Scheme 1) for the assessment of accuracy of calculated lattice energies was designed to contain small organic molecule crystals with as diverse properties and interaction energies as possible. In addition to the previous set, i.e., C21 [19], X23 also contains the systems of hexamine and succinic acid [20]. The molecular crystals belonging to the X23 set can be characterized by three categories of different types of intermolecular interaction properties, namely, purely van-der-Waals (vdW), hydrogen-bonding (H-bonds), and a mix of both types. The wide range of molecular crystal systems covered makes it possible to extrapolate the results to structures outside the benchmark set. The benchmark sets for lattice energies are derived from small organic molecular crystals for which the experimental heats of sublimation are available in the literature. These are adjusted to refer to 0 K by removing the thermal effects and zero-point vibrational energies to give the electronic (or lattice) energy only; the details can be found in the references. Thus, the calculated lattice energies for the X23 set can be directly compared to those ‘experimental’ values which were corrected for thermal effects.
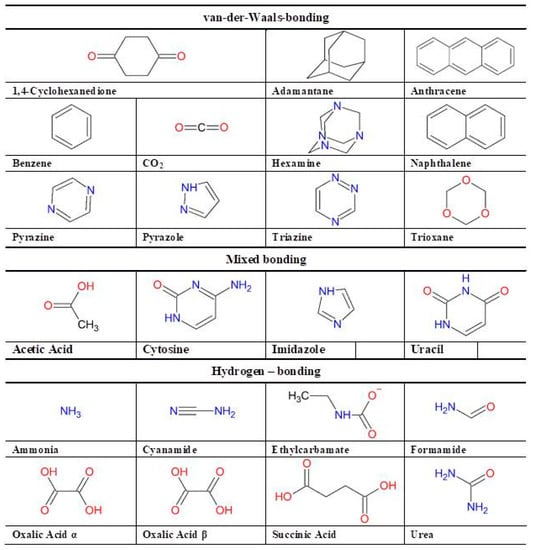
Scheme 1.
Molecules from benchmark set X23 of small organic molecular crystals sorted by dominating noncovalent interaction type (CSD codes are given in the Supplementary Information Table S1).
Most commonly, electronic energies of periodic systems are described using a plane-wave basis set. The use of atom-localized, Gaussian-type orbitals (GTOs) gives rise to an elegant and consistent treatment of molecules and a periodic system of any dimensionality on equal footing. A review of current theoretical approaches with which to calculate the lattice energies of organic crystals, and the results from benchmark studies, are given in [10]. For sparsely-packed systems, here, organic crystals, GTOs were shown to provide high accuracy with computational efficiency [21,22].
Previous results have shown that periodic DFT calculations with atom-centered basis functions in Turbomole are able to give reliable lattice energies for the molecules of the X23 benchmark set, and energy differences for enantiopure vs. racemic crystal forms using the PBE-D3 functional [23].
The development of the PBE [24,25] functional followed a less empirical and more systematic approach compared to other GGA functionals, i.e., the most important parameters were computed by first principles, and provided a consistent description across the whole periodic system. A description of the dispersion can be added by using the D3 corrections [26].
The B97-D functional [27] is a re-parametrization of the original Becke power-series ansatz [28]; it explicitly contains damped atom-pairwise dispersion corrections in the parametrization. Its performance was superior for small [27] and large systems [29], in particular, for noncovalently-bound systems, such as vdW complexes, and the B97-D results were close to the CCSD(T) results. Here, the short-range electron correlation is treated on the DFT level, whereas the medium- and long-range correlation is damped by an R−6 term. The accuracy of calculating noncovalent interaction energies prompted us to assess the B97-D functional in our calculation of the lattice energies of periodic molecular crystals which are held together by the same type of interactions (vdW, hydrogen bonding, and a mix of both). For an extensive discussion of the development of exchange-correlation functionals in DFT and an assessment of their performance, see [30].
Crystal structures may be determined under various experimental conditions (in particular, temperature and pressure). The sensitivity of the unit cell parameters to these external conditions can be captured by molecular dynamics techniques (see [31], to mention just one example). As an alternative, one can make use of quasiharmonic approximation and statistical mechanical contributions to static crystal models [32,33]. However, the capture of thermal expansion effects requires an evaluation of how the phonons change with crystal volume, which may be relevant also for the relative ranking of possible crystal structures [34,35].
In an initial stage of crystal structure prediction (CSP) of possible packings of molecules in a unit cell, the internal (e.g., electronic) energy at 0 K (CSP_0), rather than the finite-temperature effects, needs to be evaluated (CSP_thd) [36]. A simultaneous relaxation of molecular structural and unit cell parameters to a fictitious and ideal molecular organic crystal provides, on the one hand, an additional assessment of the accuracy of current DFT methods with which to describe crystal packing, and, on the other hand, a concept of the order of magnitude of energy differences between fixed experimental and relaxed theoretical unit cells.
A careful assessment of the performance of the B97-D exchange correlation functional for the X23 small molecular crystal benchmark set is presented; it was shown to be superior for chiral model compounds [23], but was not systematically evaluated. It outperforms the previous PBE-D3 results, in particular for weak vdW and mixed vdW/hydrogen bonding interactions, and gives a root mean square error of 5 kJ/mol in lattice energies. Following the development of an efficient numerical integration scheme for the calculation of the exchange-correlation (XC) energy [37] and analytic gradients [38], we present here, for the first time, an assessment of the relaxation of the unit cell parameters [39] in periodic Turbomole calculations and its effect on cell volumes and lattice energies of molecular organic crystals. Differences in unit cell volumes are below 1% for PBE-D3 and 4% B97-D, and do not significantly alter the calculated lattice energies (by less than 0.5 kJ/mol). This provides further confidence in the computational approach and its applicability in the prediction of polymorphous and solvate structures.
2. Materials and Methods
All calculations were performed with TURBOMOLE (Turbomole GmbH, version 7.3, Karlsruge, Germany) [40] 3 [41] using the PBE [24,25] and the B97-D [27] exchange correlation functions with a D3 dispersion term [26]. For all calculations, the “def2” basis sets by Ahlrichs and coworkers were used [42] in the resolution-of-identity approximation with suitable auxiliary basis sets [43,44].
The lattice energies for the organic molecules of the X23 benchmark set and related chiral compounds were found to have almost converged using the medium-sized, triple-zeta def2-TZVP basis set; the larger def2-TZVPP basis set did not significantly change the calculated lattice energies for representatives of either the vdW, mixed, and hydrogen-bonded molecular classes [23]. CP corrections also showed that a basis set error (BSSE) for the def2-TZVP basis set was, at most, 7% of the interaction energy of molecular compounds in the crystal. This reduced the calculated lattice energy and brought it even closer to experiment [23]. Further work on the implementation of the BSSE correction into periodic DFT with Gaussian basis functions is ongoing.
The fitting of the Coulomb density and continuous fast multipole methods (CFMM) [38,45] makes it possible to calculate the energies and structural optimizations using atom-centered Gaussian basis functions for molecular and periodic systems on the same grounds. For calculations on very large molecular systems, a low-memory modification of the RI approximation was implemented in the riper module [46]. Thus, the lattice energy can be directly calculated using the same atom-centered Ahlrichs’ Gaussian basis functions as the energy difference between the ideal solidstate and the ideal isolated, fully-relaxed molecule.
The periodic DFT implementation in Turbomole makes use of a Γ-point centered mesh of k points. In 3D periodic systems, each sampling point is defined by its components k1, k2, and k3 along the reciprocal lattice vectors b1, b2, and b3 as Equation (2):
k = k1b1 + k2b2 +k3b3
The unit cell is the smallest nonrepetitive representation of the crystal. It contains all symmetry inequivalent atoms. Calculations at the gamma-point (1 × 1 × 1 k-points) do not consider interactions with other atoms from neighboring unit cells. The 3 × 3 × 3 k-points specify the unit cell surrounded by the adjacent replicates of the cell, and interactions with atoms from neighboring unit cells are taken into account. It could be shown that a k-point sampling of 3 × 3 × 3 is necessary to achieve a convergence of lattice energies for molecular crystals [23].
For the first time, we present the accuracy of periodic Turbomole calculations with a simultaneous optimization of atomic positions and cell parameters or lattice vectors which relies on the availability of analytical gradients. Thus, the volume of the unit cell is minimized with respect to energy and gradients. The key component is a combination of density fitting (DF) approximation and the continuous fast multipole method (CFMM) that makes it possible to efficiently calculate the Coulomb energy gradient with asymptotic O(N) scaling [38,45,47].
Building on the work of Buchholz and Stein [23], who investigated the accuracy of the basis set def2-TZVP in combination with the PBE-D3 functional, the present work adds an investigation of the accuracy of the B97-D functional and the effect of the simultaneous relaxation of molecular structures and unit cell parameters on the unit cell volumes, vectors, angles, and calculated lattice energies.
3. Results
3.1. Calculated Lattice Energies for the X23 Benchmark Set
Molecular crystals were structurally optimized starting from the crystal structure X-ray coordinates from the CCDC database (The Cambridge Crystallographic Data Centre, Cambridge, UK). In a first stage, the experimental lattice constants are held fixed, and the unit cell provides a constraint to the displacement of the atomic coordinates.
Table 1 gives the calculated lattice energies, and the absolute and relative deviations from experiment. The ‘experimental’ lattice energies are obtained from a back-correction from experimental sublimation enthalpies ΔH0sub (298K) and vibrational contributions (Evib + 4RT, calculated using supercell phonon calculations with experimental Cp data, where available). [20] For benzene, naphthalene, and cytosine, revised recent values from [48] were used.

Table 1.
B97-D calculated lattice energies in kJ/mol for molecular crystals of the X23 benchmark set compared to experimental lattice energies. Absolute and relative deviations from the experiment are given.
The computed lattice energies show no systematic over- or under- estimation (see Figure 1) by B97-D. Still, for 14 out of the 23 systems, the calculated lattice energies are lower than the experiment. The overestimation of lattice energies is largest for hexamine (by −8.6 kJ/mol), and the underestimation largest for oxalic acid α (+6.8 kJ/mol). The results of the PBE-D3 calculated lattice energies in comparison to the recent set of experimental lattice energies are given in the Supplementary Material.
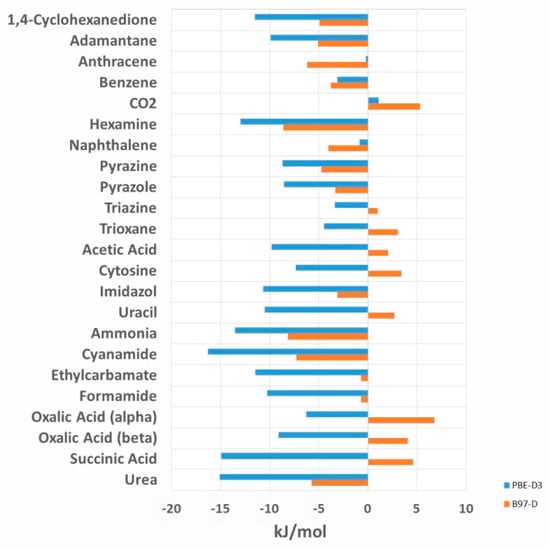
Figure 1.
Deviation in kJ/mol of calculated lattice energies with the PBE-D3 and B97-D functionals from experiment.
Figure 1 compared the deviation of B97-D and PBE-D3 calculated lattice energies from the experimental values.
One can group the benchmark molecule crystals by their dominant type of intermolecular interaction (see Scheme 1). Table 2 gives the root-mean-square deviation error (RMSE), the normalized root-mean-square error (NRMSE), the mean signed error (MSE), and the mean absolute error (MAE) for the three subgroups of intermolecular interactions and the entire data set.

Table 2.
Performance of the PBE-D3 and B97-D functionals in calculating lattice energies.
The B97-D functional gives lattice energies with a total mean absolute error of only 4.32 kJ/mol compared to 8.70 kJ/mol for PBE-D3. This superior performance may be ascribed to the parameterization which explicitly including damped atom-pairwise dispersion corrections. In particular, the B97-D functional yielded a balanced description of saturated vs. aromatic complexes and a simultaneous accurate description of hydrogen-bonded systems. It is this balanced description of weak intermolecular interactions that is also apparent for the X23 benchmark.
Other studies report a lower MAE of 4.8 kJ/mol and 2.8 kJ/mol for the C21 [19,49] and 4.6 kJ/mol and 1.4 kJ/mol for the X23 set with PBE-D3 [17,49] depending on the exact choice of the reference values. The authors employed the plane-wave DFT program VASP using PAW-potentials and a very large basis with a cutoff of 1000 eV and tight convergence criteria. Upon addition of the exact Hartree-Fock exchange in the hybrid PBE0-D3 functional, a MAE of 3.9 kJ/mol and 5.0 kJ/mol is stated in [17,20]. The embedding CE-B3LYP method from the quantum chemical charge distributions of unperturbed monomers gives a similar MAE of 5.1 kJ/mol. For an overview and compilation of other computational results for the X23 set, see Table 2 in [10] and Table 1 in [48]. It is clear that the PBE-D3 results here, with the moderately-sized GTO def2-TZVP basis set, do not approach the full basis set limit; eventually, the addition of more polarization and, in particular, diffuse functions, are expected to reduce the MAE and bring them closer to the results from (converged) VASP calculations (see below).
For B97-D, the MSE for the vdW group is largest and negative, indicating a slight overestimation of interaction energies (by −2.84 kJ/mol), but positive for mixed-type interactions (+1.27 kJ/mol). For h-bonded systems, the MSE is minimal (−0.88 kJ/mol; Table 2). The PBE-D3 functional shows a systematic overbinding with MSEs of 7.34, 9.58, and 12.12 kJ/mol for vdW, mixed, and h- bonded systems, respectively.
Since the absolute lattice energies of the molecules from the X23 set cover a range from −23.04 kJ/mol (for CO2) to −162.8 kJ/mol (for cytosine), a relative deviation from the experiment is a more appropriate measure. The B97-D functional shows a NRMSE of 7.94% from experiment compared to 13.23% for PBE.
With an NRMSE of 8.21% (9.76% for PBE-D3), the vdW-bonding group shows a moderate deviation from the experiment, followed by the mixed type bonding group (2.70% for B97-D and 10.16% for PBE-D3), and the largest deviation for the hydrogen bonding group (9.20% for B97-D but 17.91% for PBE-D3). Clearly, PBE-D3 systematically and significantly overestimates the stabilization by hydrogen bonding.
The total RMSE for B97-D is 4.82 kJ/mol and 9.84 kJ/mol for PBE-D3; both are in good agreement with the experiment, which itself has uncertainties of up to approximately 5 kJ/mol [23].
The lattice energies calculated with B97-D are generally closer to the experiment (see Table 2 and Figure 2). B97-D outperforms PBE-D3 and reduces the total RMSE by 5.02 kJ/mol compared to PBE-D3 and the MAE by 4.38 kJ/mol. The largest improvement is achieved for hydrogen bonded systems (a reduction from 17.91% to 9.20%). In contrast to B97-D, PBE-D3 leads to a systematic overestimation of the lattice energies for most of the calculated systems. Only for carbon dioxide, both B97-D and PBE-D3 slightly underestimate the (small) lattice energy of 28.4 kJ/mol (Figure 2).
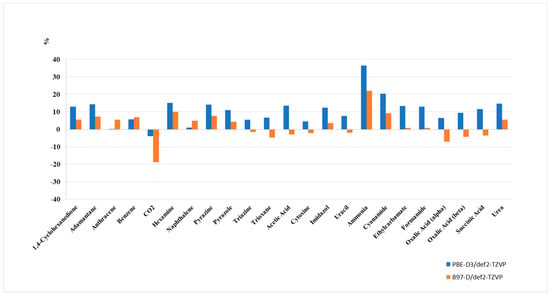
Figure 2.
Relative deviations of the PBE-D3 and B97-D calculated lattice energies from experiment.
As for the relative deviations from the experiment, overall, B97-D follows the PBE-D3 pattern (see Figure 2), which shows the consistency of both approaches. It significantly demonstrates superior performance for hydrogen bonded systems, whereas the description of interaction energies of weakly-interacting vdW-systems remains almost unchanged. While PBE-D3 systematically overestimates interaction energies, the situation is less systematic for B97-D.
When comparing the results with the recently suggested, new, back-corrected reference values Elatt ref,exp for the X23 benchmark set [49], we obtained a MSE of −7.91 kJ/mol for PBE-D3 and −0.75 for B97-D, which correspond to 11.8% and 7.7%, respectively. Thus, comparing our results with the new reference values only marginally affect the performance, and even slightly reduce the deviation from the experiment.
3.2. Convergence of Lattice Energies with Basis Set
The calculated lattice energy of organic molecular crystals is very sensitive to the choice of the basis set, since the intermolecular interactions are dominated by vdW and hydrogen bonding. These types of interactions require a large GTO basis set with polarization and diffuse functions.
In order to investigate the possible systematic error in our calculations, the convergence of the lattice energies with basis set size was systematically assessed for two representatives of each interaction type with large deviations from experiment (1,4-cyclohexanedion and hexamine for vdW; acetic acid and imidazole for H-bonding; cyanamide and succinic acid for mixed-type interactions; see Figure 3). The low temperature solid forms of gaseous substances such as carbon dioxide and ammonia were not considered because the absolute lattice energies are very small and prone to error from the experimental uncertainty.
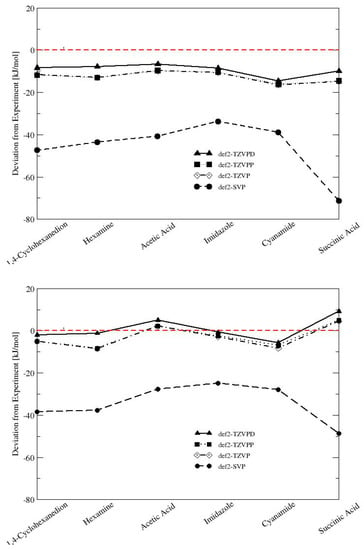
Figure 3.
Convergence of calculated lattice energies with basis set size. (Top): PBE-D3, (bottom): B97-D.
The small def2-SVP basis set is clearly not appropriate for the calculation of lattice energies. Deviations from experiment are as large as 70 kJ/mol for succinic acid using the PBE-D3 functional. The B97-D/def2-SVP results show a systematically smaller deviation from the experiment by 10–22 kJ/mol. The increase to afford a def2-TZVP or a def2-TZVPP basis set significantly reduces the error for PBE-D3 and B97-D, but the difference between the two basis sets is only marginal (<0.6 kJ/mol). The medium-sized def2-TZVP basis set is apparently a suitable compromise between computational timing and accuracy, and gives consistent results. Enlarging the basis set to def2-TZVPD reduces the deviation by another 3–6 kJ/mol for PBE-D3 and 3–7 kJ/mol for B97-D, and brings the calculated lattice energies in excellent agreement with the experiment.
Clearly, the addition of diffuse functions to fully describe hydrogen-bonded systems is critical [50], and full convergence for the X23 benchmark set will be addressed in more detail in a separate publication. It has to be stated that the incorporation of diffuse functions may lead to linear dependencies of basis functions, and increases the computational timing by a factor of 4–5.
The inclusion of a three-body Axilrod-Teller-Muto dispersion term was found not to reduce the deviation from experiment for the X23 benchmark set, and was not considered here [17]
Apparently the use of atom-cantered basis functions gives poorer overall statistics for the lattice energies of molecular crystals [51]. For the X23 set, Carter and Rohl obtained a MAE of 23 kJ/mol when applying local atomic orbitals using the SIESTA code versus 10 kJ/mol with plane-waves using Quantum ESPRESSO and the same functional. This can be partially overcome by applying the exchange-hole dipole moment (XDM) dispersion model. LeBlanc et al. obtained a MSE of −9.4 kJ/mol and a MAE of 10.0 kJ/mol when using PBE-XDM/TZP [52]. This can significantly be reduced only when applying counterpoise corrections to the crystal lattice energies [51,52].
3.3. Optimization of Unit Cell Parameters
Crystal structures are obtained under different experimental conditions (for example temperature, pressure etc.). The unit cell is defined by the |a|, |b|, and |c| lengths of the cell vectors, and the α, β, and γ unit cell angles. Simultaneous optimization of atomic positions and unit cell parameters make it possible to adapt the unit cell to the minimum energy molecular packing. This provides, on one hand, an additional assessment criterion by which to evaluate the accuracy of computational approaches to reproduce unit cell parameters. Second, the full structural relaxation of the unit cell to an ideal system at 0 K removes differences in unit cell parameters originating from different experimental conditions. This yields an ideal unit cell with lattice parameters in the absence of any finite temperature effect such as thermal expansion. This is highly relevant for the unbiased prediction of possible crystal structures starting from a molecular compound only (CSP_0), after which thermal corrections are employed in a second step (CSP_thd). The sensitivity of the lattice energy to the unit cell parameters cannot be estimated a priori, and is presented here for the first time for molecular crystals using periodic DFT calculations in Turbomole.
3.3.1. Changes of Unit Cell Volumes and Lattice Parameters
A comparison of the volume of the unit cell is a very sensitive means for comparing experiment and theory. A systematic error in lattice constants would scale cubically for the volume. In the absence of any thermal corrections, a decrease in lattice constants and unit cell volumes can be expected. Figure 4 shows the changes in unit cell volume for both the PBE-D3 and B97-D functionals.
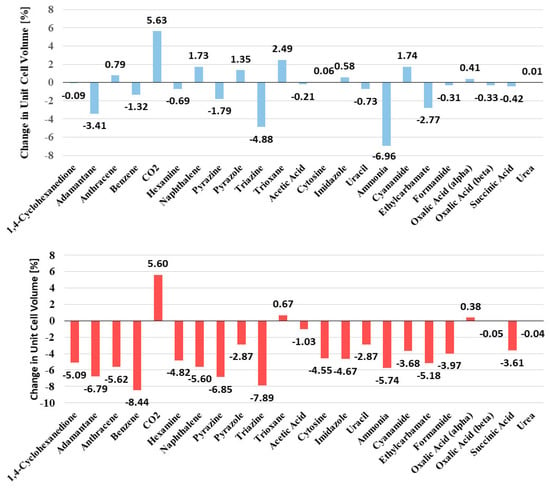
Figure 4.
Relative unit cells volume changes for organic crystals of the X23 benchmark set upon optimization of unit cell parameters with PBE-D3 (top) and B97-D (bottom).
For PBE-D3, only a very minor decrease in unit cell volume, i.e., by an average of −0.4%, can be observed. This is even smaller than the reported mean decrease by 1.1% for PBE-D3 in plane-wave calculations [17], and demonstrates that atom-centered Ahlrichs basis sets are well suited to optimizing the unit cell parameters of molecular crystals.
The changes are not systematic and cannot be assigned to a particular type of interaction. The largest decrease in unit cell volume can be seen for ammonia (from 911 a.u.3 to 848 a.u.3, i.e., by −6.96%), and the largest increase in unit cell volume occurs for CO2 (from 1220 a.u.3 to 1268 a.u.3, by +5.63%). These two crystal structures were obtained at very low temperatures, i.e., 160 K for ammonia [53] and 150 K for CO2 [54], and the gaseous systems are a challenge in terms of electronic and solid state structure determination. The overestimation of the CO2 unit cell volume was already noted by [17,19,20], and was shown not to originate from a particular type of dispersion correction method.
All other changes in volume are below 5% (Figure 4). The mean signed error of only −0.03 bohr for cell vectors and −0.03° in unit cell angles shows the suitability of the computational approach. Full results, including changes in lattice vectors and angles, are given in the Supplementary Information.
Changes in unit cell volumes are slightly more pronounced and more systematic for the B97-D functional. For 20 out of 23 crystals, a reduction in cell volumes can be detected, which was expected (see above). During optimization, the unit cell volumes decrease by an average of −3.79%, which is larger than for PBE-D3. There are, however, to our knowledge, no other results for B97-D in the literature to compare with. The unit cell vectors have a mean signed error of −0.15 bohr and +0.10° for angles (see Supplementary Information). The largest decrease in unit cell volume, i.e., by −8.44%, was seen for benzene. Overall, the changes in unit cell parameters are very small, with a mean average deviation of 1% for vectors and 0.24% for angles (PBE-D3), and 1.5% in lattice vectors and 0.4% in angles for B97-D.
Dolgonos et al. recently introduced new and revised reference values for the X23 benchmark set [49]. Experimental unit-cell volumes were back-corrected for thermal and zero-point energy effects, and now make it possible to directly compare the unit cell parameter optimizations from electronic structure calculations with their newly-introduced Vref el, which may serve as a reference for benchmarking volumes obtained via the minimization of electronic energies. On average, the Vref el values are 5% smaller than the experimentally-determined volumes. The plane-wave VASP PBE-D3 unit cell volumes had a MSE of 4.45% and a MAD of 0.93% from Vref el, which is very close to our GTO PBE-D3 values of 5.4% and 1.04%, respectively. The results of the comparison are given in detail in the Supplementary Information. Thus, both plane-wave and GTO basis functions are equally well-suited to obtaining accurate lattice parameters for the crystals of organic molecules.
3.3.2. Lattice Energies after Unit Cell Optimization
Table 3 and Figure 5 give the calculated lattice energies after the simultaneous minimization of molecular structures and unit cell parameters using PBE-D3 and B97-D. The changes in the deviations of the calculated lattice energies from the experimental values are given in kJ/mol and in percent. A negative value refers to an increase in the deviation between the calculated and experimental lattice energies. A positive value indicates better agreement with the experiment after the optimization of the unit cell.

Table 3.
Calculated lattice energies of the molecular crystals from the X23 benchmark set upon simultaneous optimization of the molecular structures and unit cell parameters.
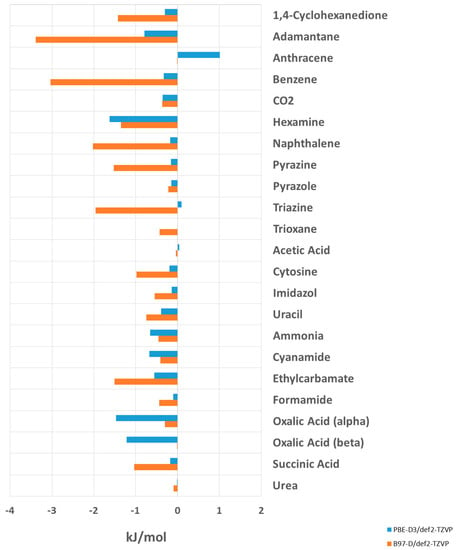
Figure 5.
Changes in deviation of the calculated lattice energies from the experiment upon minimization of the unit cell parameters. A negative number refers to an increase in the deviation; a positive number indicates better agreement with experiment.
The optimization of unit cell parameters does not lead to better agreement with the experimental lattice energies. For PBE-D3, the deviation of the calculated lattice energy from the experiment increases in 18 out of the 23 investigated systems. The increase in deviation from the experiment is, overall, not drastic, with the largest change being observed for hexamine, i.e., 1.62 kJ/mol (1.64%).
The deviations from the experimental lattice energies are more pronounced and systematic throughout for the B97-D functional. The unit cell optimization doesnot reduce or compensate for the error of the DFT calculations in any of the considered systems. Except for anthracene, for which the lattice energy does not change, all the calculated lattice energies deviate more from the experiment when the unit cell parameters are relaxed. The largest increase of deviation from the experiment is observed for adamantane, i.e., by −3.39 kJ/mol (4.55%), which is an intrinsically challenging system [20] due to the absence of any directed interaction.
In terms of the entire set, the PBE-D3 lattice energies after unit cell optimization (Table 4) show a mean absolute error of 9.10 kJ/mol, compared to 4.86 kJ/mol for B97-D. The RMSE is 10.26 kJ/mol (13.81%) for PBE-D3 and 5.47 kJ/mol (8.82%) for B97-D. In the case of the PBE-D3 calculations, the overall RMSE increases by 0.42%, with the largest increase occurring for hydrogen-bonded systems, (by 0.52%), and 0.45% for vdW, and 0.17% for hydrogen-bonded systems. For B97-D, the largest increase occurs in der vdW subgroup (by 1.25%), followed by the H-bonding group (0.08%), and a decrease in deviation by 0.26% was observed for the mixed group.

Table 4.
Performance of PBE-D3 and B97-D in calculating the lattice energies upon simultaneous optimization of the molecular structure and unit cell parameters.
The changes of lattice energies with full relaxation of the unit cell parameters are more pronounced for the B97-D calculations, but only lead to a minor change in the RMSE (increase from to 7.94 to 8.82%; MAE from 4.32 kJ/mol to 4.86 kJ/mol). Still, B97-D performs better than PBE-D3 (NRMSE 13.32% prior to unit cell optimization, 13.81% after; MAE increase from 8.70 kJ/mol to 9.10 kJ/mol).
The optimization of the unit cell parameters leads to an increase in the mean absolute error by 0.40 kJ/mol for PBE-D3 and 0.54 kJ/mol for B97-D.
Figure 6 shows the deviations from the experimental lattice energies for the PBE-D3 and B97-D functional uponsimultaneous minimization of molecular structural and unit cell parameters.
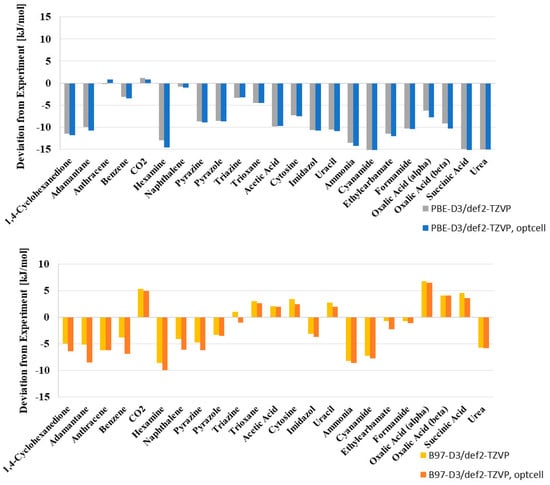
Figure 6.
Deviations from experimental lattice energies in kJ/mol from energy minimization and the simultaneous optimization of structural and unit cell parameters for PBE-D3 (top) and B97-D (bottom).
Generally speaking, the relaxation of lattice parameters has only a minor effect on the calculated lattice energies. The changes in lattice energies are below 2 kJ/mol (<2%) for PBE-D3, and only above 3 kJ/mol for adamantane and benzene (4–5%) with the B97-D functional. One has to be aware of the fact that the unit cell volume that minimizes the total energy at 0 K and 0 bar is not the one obtained at finite temperature and higher pressures.
In the development of a consistent workflow in CSP to go from a molecular structure to the existence of possible polymorphs, this knowledge of an energy range is an important threshold with which to assess the accuracy of (electronic) structure calculations [55].
4. Conclusions
The weak packing interactions in organic molecular crystals remain a challenge for current dispersion-corrected DFT calculations. Recent algorithmic developments now make it possible to use atom-centered Ahlrichs GTOs for the isolated molecule and the crystal, and a simultaneous minimization of molecular structures and unit cell parameters. This puts the treatment of molecular and crystal structures on equal footing.
The B97-D functional performs slightly more accurately than PBE-D3 for the lattice energies of molecular crystals with MAEs of 4.32 kJ/mol and 8.7 kJ/mol, respectively. Deviations from the experiment are more systematic for the PBE-D3 functional, as are changes in unit cell parameters and volumes. This does not remove PBE from the game, but indicates that a careful evaluation is required of the deficiencies and routes of improvement, such as the addition of diffuse functions, and corrections for the delocalization error.
For the first time, the accuracy of unit cell parameter optimization using Ahlrichs GTOs was demonstrated. When simultaneously minimizing molecular structure and lattice parameters, only minor changes, i.e., below a maximum of 7% for PBE-D3 and 8% for B97-D in unit cell volume, can be found. The minimization of the total energy of the system generates a fictitious, ideal solid state at 0 K. At the zeroth order crystal structure prediction step, possible molecular packings can be investigated by, e.g., electronic structure methods, for which errors of a few kJ/mol are to be expected. These, however, may make up to 20% of the lattice energy for weakly-interacting systems. For CSP_0, the actual choice of unit cell parameters is of less importance, since changes in the lattice parameters are only minor, and interaction energies are correctly described. Then, thermal expansion (another few kJ/mol error in lattice energies) plus finite temperature effects by harmonic approximations may be added (CPS_thd). Those may then eventually lead to a re-ranking of possible crystal structures which are close in energy.
More advanced treatment of dispersive interactions in periodic DFT such as many-body [56] or atomic charge-dependent corrections [57] might provide further small improvements in lattice energy calculations, as would the admixture of exact exchange [58]. Recent implementations of the XDM dispersion model, in combination with hybrid functionals in the plane-wave/pseudopotentials approach, significantly reduce the MAE of the X23 set to 3.5 kJ/mol for PBE0-XDM [59]. An even larger effect, however, is expected to arise from a concise treatment of electron correlation, for example, in periodic coupled-cluster calculations [60].
The analysis of the intermolecular stabilization of complex APIs or the quest for novel possible crystal structures, such as polymorphs, or the design of enantioselective crystallization processes require the calculation of accurate lattice energies; they make the largest contribution to the overall stabilization. The development of an efficient, low memory, periodic DFT implementation in Turbomole makes it possible to use atom-centered Ahlrichs GTOs and will certainly contribute to these issues.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4352/9/12/665/s1, Table S1: CSD reference codes of the molecules from the benchmark set X23, Table S2: Calculated lattice energies for the benchmark set X23 with PBE-D3/def2-TZVP are compared to experimental lattice energies, Table S3: Experimental unit cell parameters and volumes of the X23 benchmark set, Table S4: PBE-D3 calculated unit cell parameters for crystals from the X23 benchmark set, Table S5: B97-D calculated unit cell parameters for crystals from the X23 benchmark set. Table S6: Comparison of calculated unit cell volumes with back-corrected values Velref.
Author Contributions
Conceptualization, M.S.; validation, M.S. and M.H.; formal analysis, M.S. and M.H.; investigation, M.H.; writing—original draft preparation, M.S. and M.H.; writing—review and editing, M.S.; visualization, M.H.
Funding
This research was funded by the Max Planck Society for the Advancement of Science. The author would like to acknowledge the contribution of the COST Action CM1402 ‘Crystallize’. The APC was funded by Max-Planck-Gesellschaft.
Acknowledgments
We would like to thank Uwe Huniar (Cosmologic GmbH) and Marek Sierka (University of Jena) for scientific discussions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Food and Drug Administration. FDA’s policy statement for the development of new stereoisomeric drugs. Chirality 1992, 4, 338–340. [Google Scholar] [CrossRef] [PubMed]
- De Camp, W.H. Chiral drugs: The FDA perspective on manufacturing and control. J. Pharm. Biomed. Anal. 1993, 11, 1167–1172. [Google Scholar] [CrossRef]
- Brooks, W.H.; Guida, W.C.; Daniel, K.G. The significance of chirality in drug design and development. Curr. Top. Med. Chem. 2011, 11, 760–770. [Google Scholar] [CrossRef] [PubMed]
- Hylton, R.K.; Tizzard, G.J.; Threlfall, T.L.; Ellis, A.L.; Coles, S.J.; Seaton, C.C.; Schulze, E.; Lorenz, H.; Seidel-Morgenstern, A.; Stein, M.; et al. Are the crystal structures of enantiopure and racemic mandelic acids determined by kinetics or thermodynamics? J. Am. Chem. Soc. 2015, 137, 11095–11104. [Google Scholar] [CrossRef]
- Lorenz, H.; Seidel-Morgenstern, A. Processes to separate enantiomers. Angew. Chem. Int. Ed. 2014, 53, 1218–1250. [Google Scholar] [CrossRef]
- Cruz-Cabeza, A.J.; Reutzel-Edens, S.M.; Bernstein, J. Facts and fictions about polymorphism. Chem. Soc. Rev. 2015, 44, 8619–8635. [Google Scholar] [CrossRef]
- Gavezzotti, A.; Rizzato, S. Are racemic crystals favored over homochiral crystals by higher stability or by kinetics? Insights from comparative studies of crystalline stereoisomers. J. Org. Chem. 2014, 79, 4809–4816. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Static and lattice vibrational energy differences between polymorphs. CrystEngComm 2015, 17, 5154–5165. [Google Scholar] [CrossRef]
- Buchholz, H.K.; Hylton, R.K.; Brandenburg, J.G.; Seidel-Morgenstern, A.; Lorenz, H.; Stein, M.; Price, S.L. Thermochemistry of racemic and enantiopure organic crystals for predicting enantiomer separation. Cryst. Growth Des. 2017, 17, 4676–4686. [Google Scholar] [CrossRef]
- Beran, G.J.O. Modeling polymorphic molecular crystals with electronic structure theory. Chem. Rev. 2016, 116, 5567–5613. [Google Scholar] [CrossRef]
- Deringer, V.L.; George, J.; Dronskowski, R.; Englert, U. Plane-wave density functional theory meets molecular crystals: Thermal ellipsoids and intermolecular interactions. Acc. Chem. Res. 2017, 50, 1231–1239. [Google Scholar] [CrossRef] [PubMed]
- Stohr, M.; Van Voorhis, T.; Tkatchenko, A. Theory and practice of modeling van der waals interactions in electronic-structure calculations. Chem. Soc. Rev. 2019, 48, 4118–4154. [Google Scholar] [CrossRef] [PubMed]
- Hoja, J.; Reilly, A.M.; Tkatchenko, A. First-principles modeling of molecular crystals: Structures and stabilities, temperature and pressure. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2017, 7, e1294. [Google Scholar] [CrossRef]
- Kronik, L.; Tkatchenko, A. Understanding molecular crystals with dispersion-inclusive density functional theory: Pairwise corrections and beyond. Acc. Chem. Res. 2014, 47, 3208–3216. [Google Scholar] [CrossRef]
- Price, S.L. Computational prediction of organic crystal structures and polymorphism. Int. Rev. Phys. Chem. 2008, 27, 541–568. [Google Scholar] [CrossRef]
- Price, S.L. Predicting crystal structures of organic compounds. Chem. Soc. Rev. 2014, 43, 2098–2111. [Google Scholar] [CrossRef]
- Moellmann, J.; Grimme, S. Dft-D3 study of some molecular crystals. J. Phys. Chem. C 2014, 118, 7615–7621. [Google Scholar] [CrossRef]
- Brandenburg, J.G.; Grimme, S. Dispersion corrected Hartree-Fock and density functional theory for organic crystal structure prediction. Top. Curr. Chem. 2014, 345, 1–23. [Google Scholar]
- Otero-de-la-Roza, A.; Johnson, E.R. A benchmark for non-covalent interactions in solids. J. Chem. Phys. 2012, 137, 054103. [Google Scholar] [CrossRef]
- Reilly, A.M.; Tkatchenko, A. Understanding the role of vibrations, exact exchange, and many-body van der waals interactions in the cohesive properties of molecular crystals. J. Chem. Phys. 2013, 139, 024705. [Google Scholar] [CrossRef]
- Dovesi, R.; Orlando, R.; Erba, A.; Zicovich-Wilson, C.M.; Civalleri, B.; Casassa, S.; Maschio, L.; Ferrabone, M.; De La Pierre, M.; D’Arco, P.; et al. Crystal14: A program for the ab initio investigation of crystalline solids. Int. J. Quantum Chem. 2014, 114, 1287–1317. [Google Scholar] [CrossRef]
- Kudin, K.N.; Scuseria, G.E. Linear-scaling density-functional theory with gaussian orbitals and periodic boundary conditions: Efficient evaluation of energy and forces via the fast multipole method. Phys. Rev. B 2000, 61, 16440–16453. [Google Scholar] [CrossRef]
- Buchholz, H.K.; Stein, M. Accurate lattice energies of organic molecular crystals from periodic Turbomole calculations. J. Comput. Chem. 2018, 39, 1335–1343. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 2006, 27, 1787–1799. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. V. Systematic optimization of exchange-correlation functionals. J. Chem. Phys. 1997, 107, 8554–8560. [Google Scholar] [CrossRef]
- Antony, J.; Grimme, S. Density functional theory including dispersion corrections for intermolecular interactions in a large benchmark set of biologically relevant molecules. Phys. Chem. Chem. Phys. 2006, 8, 5287–5293. [Google Scholar] [CrossRef]
- Mardirossian, N.; Head-Gordon, M. Thirty years of density functional theory in computational chemistry: An overview and extensive assessment of 200 density functionals. Mol. Phys. 2017, 115, 2315–2372. [Google Scholar] [CrossRef]
- Raiteri, P.; Martoňák, R.; Parrinello, M. Exploring polymorphism: The case of benzene. Angew. Chem. Int. Ed. 2005, 44, 3769–3773. [Google Scholar] [CrossRef]
- Reilly, A.M.; Cooper, R.I.; Adjiman, C.S.; Bhattacharya, S.; Boese, A.D.; Brandenburg, J.G.; Bygrave, P.J.; Bylsma, R.; Campbell, J.E.; Car, R.; et al. Report on the sixth blind test of organic crystal structure prediction methods. Acta Crystallogr. Sect. B 2016, 72, 439–459. [Google Scholar] [CrossRef]
- Nyman, J.; Day, G.M. Modelling temperature-dependent properties of polymorphic organic molecular crystals. Phys. Chem. Chem. Phys. 2016, 18, 31132–31143. [Google Scholar] [CrossRef] [PubMed]
- Whittleton, S.R.; Otero-de-la-Roza, A.; Johnson, E.R. Exchange-hole dipole dispersion model for accurate energy ranking in molecular crystal structure prediction. J. Chem. Theory Comput. 2017, 13, 441–450. [Google Scholar] [CrossRef]
- Whittleton, S.R.; Otero-de-la-Roza, A.; Johnson, E.R. Exchange-hole dipole dispersion model for accurate energy ranking in molecular crystal structure prediction ii: Nonplanar molecules. J. Chem. Theory Comput. 2017, 13, 5332–5342. [Google Scholar] [CrossRef]
- Price, S.L. Is zeroth order crystal structure prediction (csp_0) coming to maturity? What should we aim for in an ideal crystal structure prediction code? Faraday Discuss. 2018, 211, 9–30. [Google Scholar] [CrossRef]
- Burow, A.M.; Sierka, M. Linear scaling hierarchical integration scheme for the exchange-correlation term in molecular and periodic systems. J. Chem. Theory Comput. 2011, 7, 3097–3104. [Google Scholar] [CrossRef]
- Łazarski, R.; Burow, A.M.; Grajciar, L.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole method: Analytical gradients. J. Comput. Chem. 2016, 37, 2518–2526. [Google Scholar] [CrossRef]
- Becker, M.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole method: Stress tensor. J. Comput. Chem. 2019, 40, 2563–2570. [Google Scholar] [CrossRef]
- Furche, F.; Ahlrichs, R.; Hattig, C.; Klopper, W.; Sierka, M.; Weigend, F. Turbomole. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 91–100. [Google Scholar] [CrossRef]
- Turbomole v7.3. 2018, a Development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, since 2007; Turbomole GmbH: Karlsruhe, Germany, 2017; Available online: http://www.turbomole.com (accessed on 9 December 2019).
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for h to rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. [Google Scholar] [CrossRef] [PubMed]
- Eichkorn, K.; Treutler, O.; Ohm, H.; Haser, M.; Ahlrichs, R. Erratum to: Auxiliary basis-sets to approximate coulomb potentials (240, pg 283, 1995). Chem. Phys. Lett. 1995, 242, 652–660. [Google Scholar] [CrossRef]
- Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Auxiliary basis sets for main row atoms and transition metals and their use to approximate coulomb potentials. Theor. Chem. Acc. 1997, 97, 119–124. [Google Scholar] [CrossRef]
- Łazarski, R.; Burow, A.M.; Sierka, M. Density functional theory for molecular and periodic systems using density fitting and continuous fast multipole methods. J. Chem. Theory Comput. 2015, 11, 3029–3041. [Google Scholar] [CrossRef]
- Grajciar, L. Low-memory iterative density fitting. J. Comput. Chem. 2015, 36, 1521–1535. [Google Scholar] [CrossRef]
- Burow, A.M.; Sierka, M.; Mohamed, F. Resolution of identity approximation for the coulomb term in molecular and periodic systems. J. Chem. Phys. 2009, 131, 214101. [Google Scholar] [CrossRef]
- Thomas, S.P.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. Accurate lattice energies for molecular crystals from experimental crystal structures. J. Chem. Theory Comput. 2018, 14, 1614–1623. [Google Scholar] [CrossRef]
- Dolgonos, G.A.; Hoja, J.; Boese, A.D. Revised values for the X23 benchmark set of molecular crystals. Phys. Chem. Chem. Phys. 2019, 21, 24333–24344. [Google Scholar] [CrossRef]
- Boese, A.D. Density functional theory and hydrogen bonds: Are we there yet? ChemPhysChem 2015, 16, 978–985. [Google Scholar] [CrossRef]
- Carter, D.J.; Rohl, A.L. Benchmarking calculated lattice parameters and energies of molecular crystals using van der waals density functionals. J. Chem. Theory Comput. 2014, 10, 3423–3437. [Google Scholar] [CrossRef]
- LeBlanc, L.M.; Weatherby, J.A.; Otero-de-la-Roza, A.; Johnson, E.R. Non-covalent interactions in molecular crystals: Exploring the accuracy of the exchange-hole dipole moment model with local orbitals. J. Chem. Theory Comput. 2018, 14, 5715–5724. [Google Scholar] [CrossRef] [PubMed]
- Boese, R.; Niederprüm, N.; Bläser, D.; Maulitz, A.; Antipin, M.Y.; Mallinson, P.R. Single-crystal structure and electron density distribution of ammonia at 160 k on the basis of x-ray diffraction data. J. Phys. Chem. B 1997, 101, 5794–5799. [Google Scholar] [CrossRef]
- Simon, A.; Peters, K. Single-crystal refinement of the structure of carbon dioxide. Acta Crystallogr. Sect. B 1980, 36, 2750–2751. [Google Scholar] [CrossRef]
- Heit, Y.N.; Beran, G.J.O. How important is thermal expansion for predicting molecular crystal structures and thermochemistry at finite temperatures? Acta Crystallogr. Sect. B 2016, 72, 514–529. [Google Scholar] [CrossRef]
- Bučko, T.; Lebègue, S.; Gould, T.; Ángyán, J.G. Many-body dispersion corrections for periodic systems: An efficient reciprocal space implementation. J. Phys. Condens. Matter 2016, 28, 045201. [Google Scholar] [CrossRef]
- Caldeweyher, E.; Bannwarth, C.; Grimme, S. Extension of the D3 dispersion coefficient model. J. Chem. Phys. 2017, 147, 034112. [Google Scholar] [CrossRef]
- Irmler, A.; Burow, A.M.; Pauly, F. Robust periodic fock exchange with atom-centered Gaussian basis sets. J. Chem. Theory Comput. 2018, 14, 4567–4580. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; LeBlanc, L.M.; Johnson, E.R. Dispersion XDM with hybrid functionals: Delocalization error and halogen bonding in molecular crystals. J. Chem. Theory Comput. 2019, 15, 4933–4944. [Google Scholar] [CrossRef]
- Zhang, I.Y.; Grüneis, A. Coupled cluster theory in materials science. Front. Mater. 2019, 6, 123. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).