Multi-Step Concanavalin A Phase Separation and Early-Stage Nucleation Monitored Via Dynamic and Depolarized Light Scattering
Abstract
1. Introduction
2. Materials and Methods
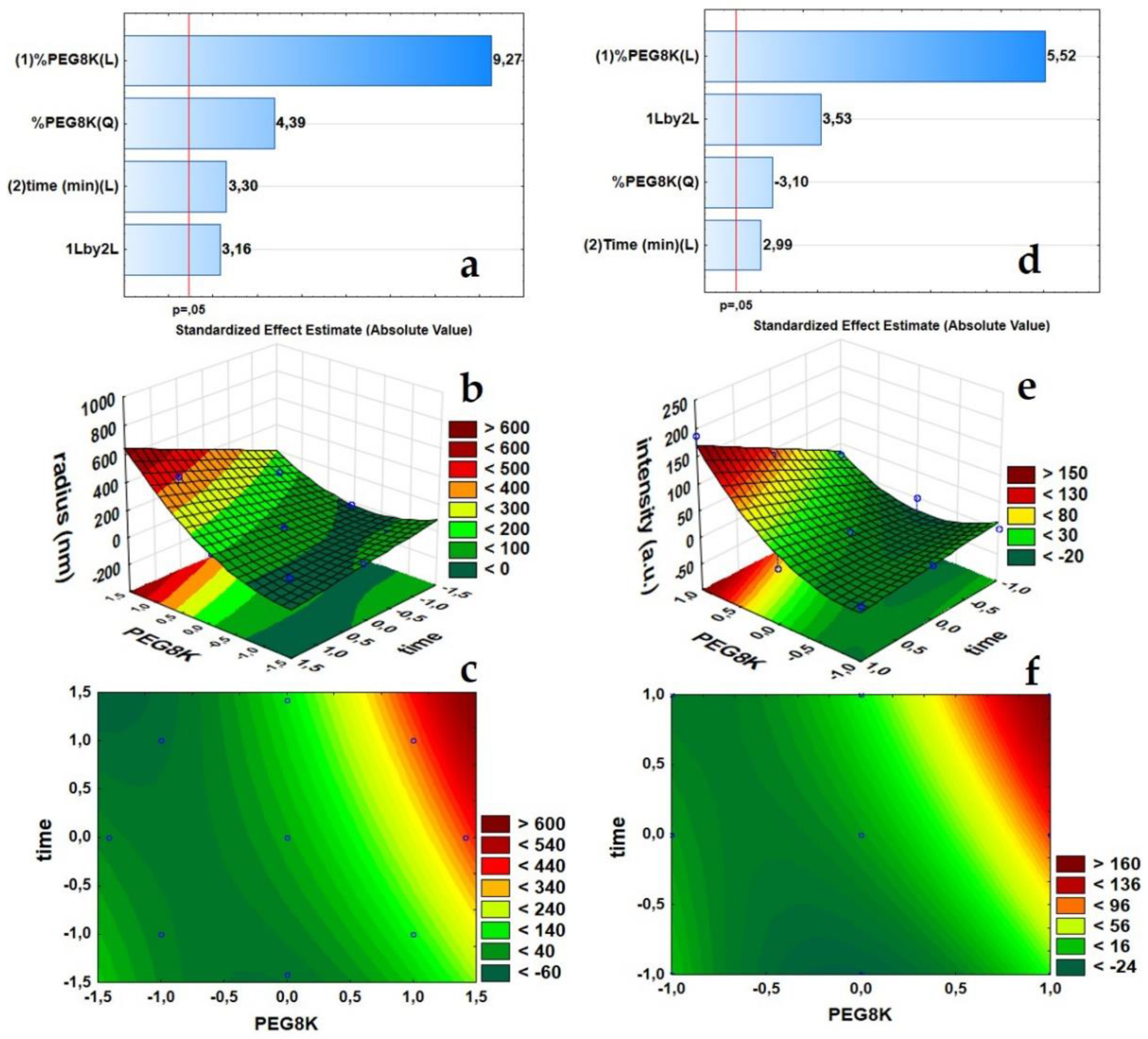
2.1. Response Surface Methodology (RSM) Using Central Composite and Full Factorial Designs
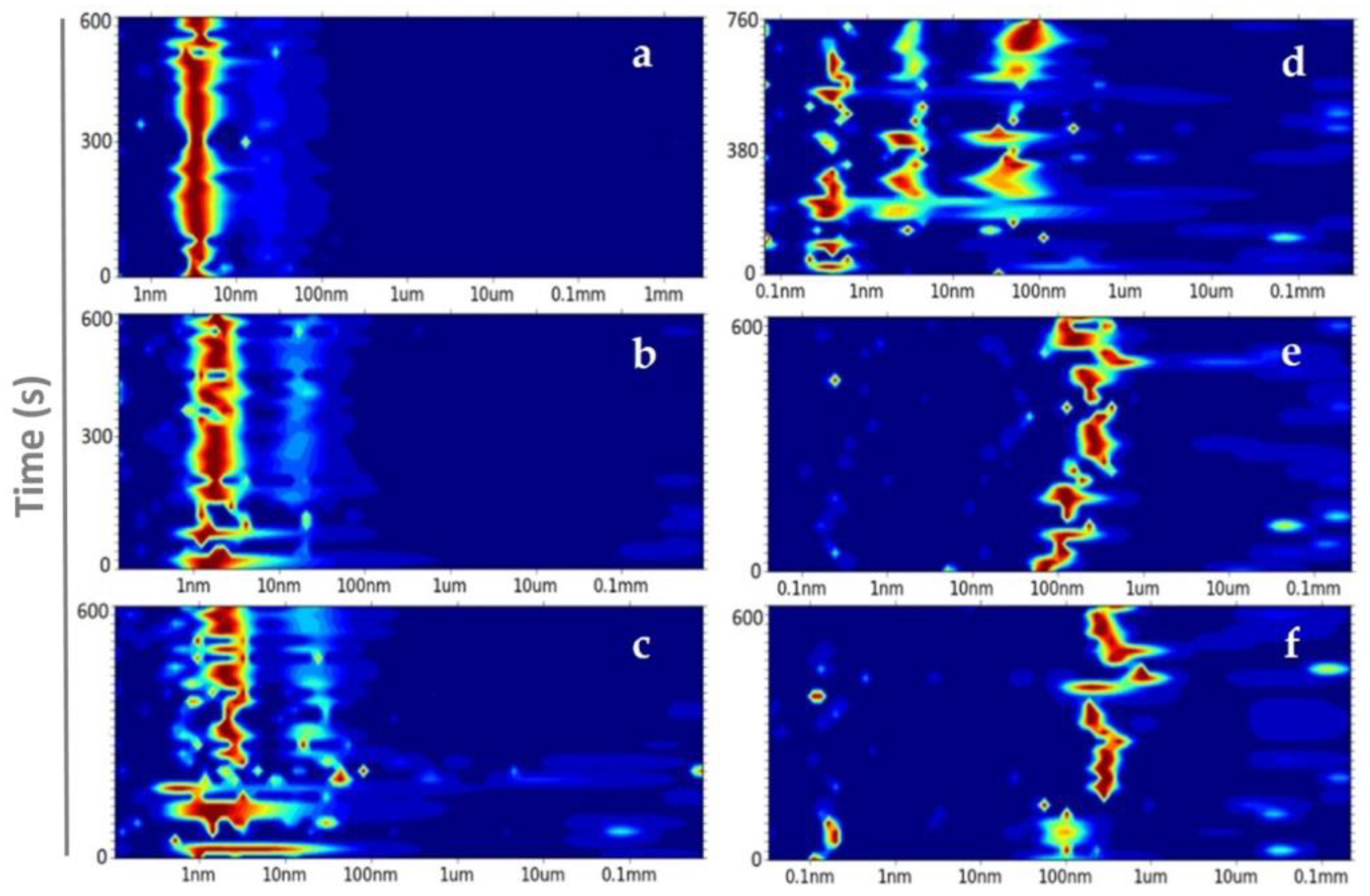
2.2. Dynamic Light Scattering (DLS) and Depolarized Dynamic Light Scattering (DDLS)
2.3. Circular Dichroism
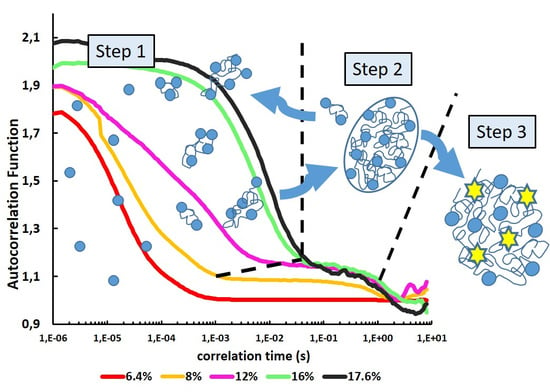
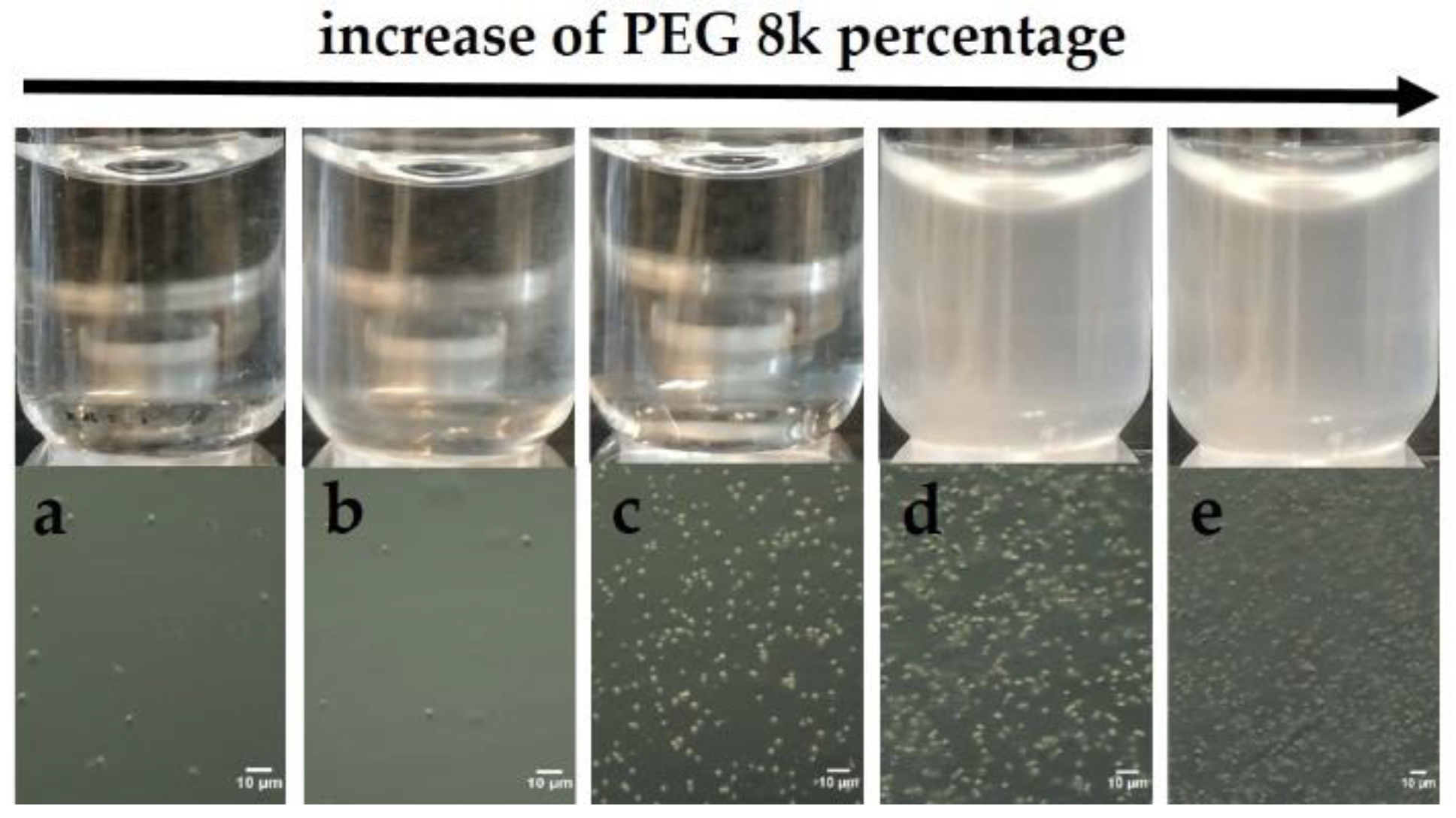
3. Results
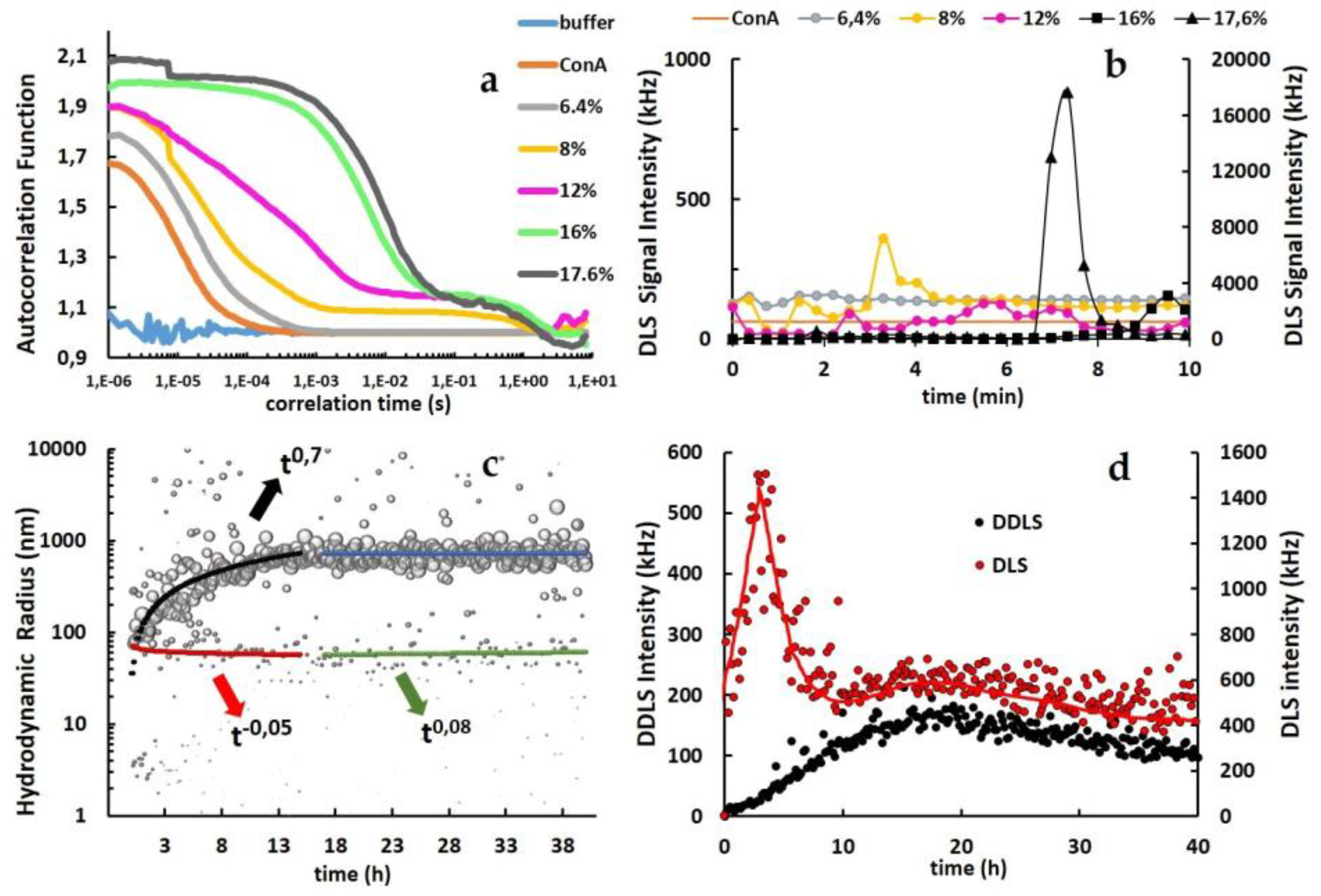
3.1. Optimization of ConA Cluster Formation
3.2. From Soluble Protein Toward Enriched Clusters and a Crystalline Phase
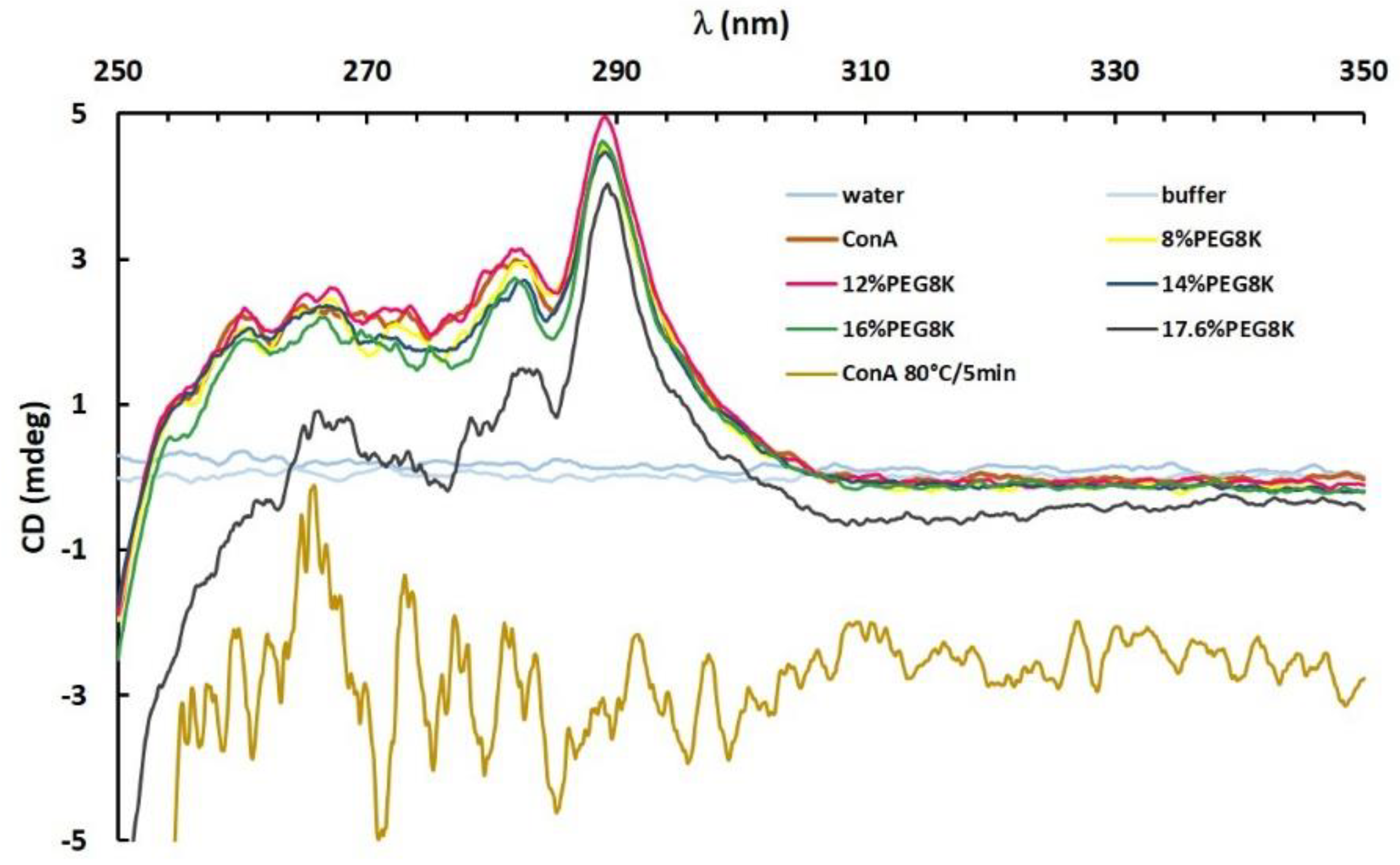
3.3. Tertiary Structure Conformation by Near-UV Circular Dichroism (CD) Spectroscopy
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Factor | R2 = 0.95454 R2adj = 0.92423 MSresidual = 1719.379 | ||||
|---|---|---|---|---|---|
| SS | df | MS | F | p | |
| (1)%PEG8k(Linear) | 147,606.9 | 1 | 147,606.9 | 85.84899 | 0.000089 |
| %PEG8K (Quadratic) | 33,066.3 | 1 | 33,066.3 | 19.23155 | 0.004641 |
| (2)Time (min)(Linear) | 18,768.7 | 1 | 18,768.7 | 10.91595 | 0.016328 |
| (1)Linear by (2)Linear | 17,157.1 | 1 | 17,157.1 | 9.97864 | 0.019592 |
| Error | 10,316.3 | 6 | 1719.4 | ||
| Total SS | 226,915.3 | 10 | |||
| Factor | R2 = 0.93889 R2adj = 0.8777 MSresidual = 509.1356 | ||||
|---|---|---|---|---|---|
| SS | df | MS | F | p | |
| (1)%PEG8k(Linear) | 15,486.89 | 1 | 15,486.89 | 30.41800 | 0.005275 |
| %PEG8K (Quadratic) | 4890.93 | 1 | 4890.93 | 9.60635 | 0.036242 |
| (2)Time (min)(Linear) | 4571.11 | 1 | 4571.11 | 8.97818 | 0.040086 |
| (1)Linear by (2)Linear | 6338.55 | 1 | 6338.55 | 12.44963 | 0.024265 |
| Error | 2036.54 | 4 | 509.14 | ||
| Total SS | 33,324.03 | 8 | |||
References
- Boeynaems, S.; Alberti, S.; Fawzi, N.L.; Mittag, T.; Polymenidou, M.; Rousseau, F.; Schymkowitz, J.; Shorter, J.; Wolozin, B.; Van Den Bosch, L.; et al. Protein Phase Separation: A New Phase in Cell Biology. Trends Cell Biol. 2018, 28, 420–435. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Gladfelter, A.; Mittag, T. Considerations and Challenges in Studying Liquid-Liquid Phase Separation and Biomolecular Condensates. Cell 2019, 176, 419–434. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, K.K.; Vibhute, M.A.; Spruijt, E. Biomolecular Chemistry in Liquid Phase Separated Compartments. Front. Mol. Biosci. 2019, 6, 21. [Google Scholar] [CrossRef] [PubMed]
- Bahn, S.Y.; Jo, B.H.; Choi, Y.S.; Cha, H.J. Control of nacre biomineralization by Pif80 in pearl oyster. Sci. Adv. 2017, 3, e1700765. [Google Scholar] [CrossRef] [PubMed]
- Alberti, S.; Dormann, D. Liquid–Liquid Phase Separation in Disease. Annu. Rev. Genet. 2019, 53. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Brangwynne, C.P. Liquid phase condensation in cell physiology and disease. Science 2017, 357, eaaf4382. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. Viscoelastic phase separation in soft matter and foods. Faraday Discuss. 2012, 158, 371–406. [Google Scholar] [CrossRef]
- Luebbert, C.; Wessner, M.; Sadowski, G. Mutual Impact of Phase Separation/Crystallization and Water Sorption in Amorphous Solid Dispersions. Mol. Pharm. 2018, 15, 669–678. [Google Scholar] [CrossRef]
- Gibson, B.A.; Doolittle, L.K.; Jensen, L.E.; Gamarra, N.; Redding, S.; Rosen, M.K. Organization and Regulation of Chromatin by Liquid-Liquid Phase Separation. BioRxiv 2019. [Google Scholar] [CrossRef]
- Schubert, R.; Meyer, A.; Baitan, D.; Dierks, K.; Perbandt, M.; Betzel, C. Real-Time Observation of Protein Dense Liquid Cluster Evolution during Nucleation in Protein Crystallization. Cryst. Growth Des. 2017, 17, 954–958. [Google Scholar] [CrossRef]
- Dumetz, A.C.; Chockla, A.M.; Kaler, E.W.; Lenhoff, A.M. Protein phase behavior in aqueous solutions: Crystallization, liquid-liquid phase separation, gels, and aggregates. Biophys. J. 2008, 94, 570–583. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F. Nonclassical nucleation pathways in protein crystallization. J. Phys. Condens. Matter 2017, 29, 443002. [Google Scholar] [CrossRef] [PubMed]
- Le Ferrand, H.; Duchamp, M.; Gabryelczyk, B.; Cai, H.; Miserez, A. Time-Resolved Observations of Liquid–Liquid Phase Separation at the Nanoscale Using in Situ Liquid Transmission Electron Microscopy. J. Am. Chem. Soc. 2019, 141, 7202–7210. [Google Scholar] [CrossRef] [PubMed]
- Berry, J.; Brangwynne, C.P.; Haataja, M. Physical principles of intracellular organization via active and passive phase transitions. Rep. Prog. Phys. 2018, 81, 46601. [Google Scholar] [CrossRef]
- Bray, A.J. Theory of phase-ordering kinetics. Adv. Phys. 2002, 51, 481–587. [Google Scholar] [CrossRef]
- Furukawa, H. A dynamic scaling assumption for phase separation. Adv. Phys. 1985, 34, 703–750. [Google Scholar] [CrossRef]
- Madras, G.; McCoy, B.J. Ostwald ripening with size-dependent rates: Similarity and power-law solutions. J. Chem. Phys. 2002, 117, 8042–8049. [Google Scholar] [CrossRef]
- Da Vela, S.; Braun, M.K.; Dörr, A.; Greco, A.; Möller, J.; Fu, Z.; Zhang, F.; Schreiber, F. Kinetics of liquid-liquid phase separation in protein solutions exhibiting LCST phase behavior studied by time-resolved USAXS and VSANS. Soft Matter 2016, 12, 9334–9341. [Google Scholar] [CrossRef]
- Vorontsova, M.A.; Chan, H.Y.; Lubchenko, V.; Vekilov, P.G. Lack of Dependence of the Sizes of the Mesoscopic Protein Clusters on Electrostatics. Biophys. J. 2015, 109, 1959–1968. [Google Scholar] [CrossRef]
- Zhang, F.; Roosen-Runge, F.; Sauter, A.; Roth, R.; Skoda, M.W.A.; Jacobs, R.M.J.; Sztucki, M.; Schreiber, F. The role of cluster formation and metastable liquid-liquid phase separation in protein crystallization. Faraday Discuss. 2012, 159, 313–325. [Google Scholar] [CrossRef]
- Vivarès, D.; Kaler, E.W.; Lenhoff, A.M. Quantitative imaging by confocal scanning fluorescence microscopy of protein crystallization via liquid-liquid phase separation. Acta Crystallogr. Sect. D Biol. Crystallogr. 2005, 61, 819–825. [Google Scholar] [CrossRef] [PubMed]
- Grouazel, S.; Perez, J.; Astier, J.P.; Bonneté, F.; Veesler, S. BPTI liquid-liquid phase separation monitored by light and small angle X-ray scattering. Acta Crystallogr. Sect. D Biol. Crystallogr. 2002, 58, 1560–1563. [Google Scholar] [CrossRef] [PubMed]
- Xu, R. Light scattering: A review of particle characterization applications. Particuology 2015, 18, 11–21. [Google Scholar] [CrossRef]
- Owen, R.L.; Garman, E. A new method for predetermining the diffraction quality of protein crystals: Using SOAP as a selection tool. Acta Crystallogr. Sect. D 2005, 61, 130–140. [Google Scholar] [CrossRef] [PubMed]
- Chayen, N.; Dieckmann, M.; Dierks, K.; Fromme, P. Size and Shape Determination of Proteins in Solution by a Noninvasive Depolarized Dynamic Light Scattering Instrument. Ann. N. Y. Acad. Sci. 2004, 1027, 20–27. [Google Scholar] [CrossRef] [PubMed]
- Fang, L.; Brown, W.; Konak, C. Dynamic light scattering study of the sol-gel transition. Macromolecules 1991, 24, 6839–6842. [Google Scholar] [CrossRef]
- Takata, S.; Norisuye, T.; Tanaka, N.; Shibayama, M. Heat-Induced Gelation of β-Lactoglobulin. 1. Time-Resolved Dynamic Light Scattering. Macromolecules 2000, 33, 5470–5475. [Google Scholar] [CrossRef]
- Norisuye, T.; Shibayama, M.; Nomura, S. Time-resolved light scattering study on the gelation process of poly(N-isopropyl acrylamide. Polymer 1998, 39, 2769–2775. [Google Scholar] [CrossRef]
- Matsunaga, T.; Shibayama, M. Gel point determination of gelatin hydrogels by dynamic light scattering and rheological measurements. Phys. Rev. E 2007, 76, 30401. [Google Scholar] [CrossRef]
- Shibayama, M.; Okamoto, M. Dynamic light scattering study on gelatin aqueous solutions and gels. J. Chem. Phys. 2001, 115, 4285–4291. [Google Scholar] [CrossRef]
- Edelman, G.M.; Cunningham, B.A.; Reeke, G.N., Jr.; Becker, J.W.; Waxdal, M.J.; Wang, J.L. The covalent and three-dimensional structure of concanavalin A. Proc. Natl. Acad. Sci. USA 1972, 69, 2580–2584. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.R.; Kim, D.S.; Lee, D.-H.; Kang, H.G.; Park, J.H.; Lee, S.J. Cadmium-substituted concanavalin A and its trimeric complexation. J. Microbiol. Biotechnol. 2018, 28, 2106–2112. [Google Scholar] [CrossRef] [PubMed]
- Baş, D.; Boyacı, İ.H. Modeling and optimization I: Usability of response surface methodology. J. Food Eng. 2007, 78, 836–845. [Google Scholar] [CrossRef]
- Konda, R.; Rajurkar, K.P.; Bishu, R.R.; Guha, A.; Person, M. Design of experiments to study and optimize process performance. Int. J. Qual. Reliab. Manag. 1999, 16, 56–71. [Google Scholar] [CrossRef]
- Ganesamoorthi, B.; Kalaivanan, S.; Dinesh, R.; Naveen kumar, T.; Anand, K. Optimization Technique using Response Surface Method for USMW process. Procedia Soc. Behav. Sci. 2015, 189, 169–174. [Google Scholar] [CrossRef]
- De Benedetto, G.; Di Masi, S.; Pennetta, A.; Malitesta, C. Response Surface Methodology for the Optimisation of Electrochemical Biosensors for Heavy Metals Detection. Biosensors 2019, 9, 26. [Google Scholar] [CrossRef]
- Owolabi, R.U.; Usman, M.A.; Kehinde, A.J. Modelling and optimization of process variables for the solution polymerization of styrene using response surface methodology. J. King Saud Univ. Eng. Sci. 2018, 30, 22–30. [Google Scholar] [CrossRef]
- Saeidi, M.; Ghaemi, A.; Tahvildari, K.; Derakhshi, P. Exploiting response surface methodology (RSM) as a novel approach for the optimization of carbon dioxide adsorption by dry sodium hydroxide. J. Chin. Chem. Soc. 2018, 65, 1465–1475. [Google Scholar] [CrossRef]
- Rekha, H.B.; Srinidhi, M.S.; Murthy, U.N. Textile Wastewater Treatment by Electrochemical Oxidation—Response Surface Methodology. In Waste Water Recycling and Management; Ghosh, S.K., Ed.; Springer: Singapore, 2019; pp. 251–263. [Google Scholar]
- Lanka, S.; Naveena, J.; Latha, J.N.L. Response Surface Methodology as a Statistical Tool for Fermentation Media Optimization in Lipase Production by Palm Oil Mill Effluent (POME) Isolate Emericella nidulans NFCCI 3643. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 2535–2545. [Google Scholar]
- Ben Mefteh, F.; Frikha, F.; Daoud, A.; Bouket, A.C.; Luptakova, L.; Alenezi, F.; Al-Anzi, B.; Oszako, T.; Gharsallah, N.; Belbahri, L. Response Surface Methodology Optimization of an Acidic Protease Produced by Penicillium bilaiae Isolate TDPEF30, a Newly Recovered Endophytic Fungus from Healthy Roots of Date Palm Trees (Phoenix dactylifera L.). Microorganisms 2019, 7, 74. [Google Scholar] [CrossRef]
- Belloni, L. Colloidal interactions. J. Phys. Condens. Matter 2000, 12, R549–R587. [Google Scholar] [CrossRef]
- Schubert, R.; Meyer, A.; Dierks, K.; Kapis, S.; Reimer, R.; Einspahr, H.; Perbandt, M.; Betzel, C. Reliably distinguishing protein nanocrystals from amorphous precipitate by means of depolarized dynamic light scattering. J. Appl. Crystallogr. 2015, 48, 1476–1484. [Google Scholar] [CrossRef]
- Provencher, S.W. CONTIN: A general purpose constrained regularization program for inverting noisy linear algebraic and integral equations. Comput. Phys. Commun. 1982, 27, 229–242. [Google Scholar] [CrossRef]
- Wang, J.L.; Cunningham, B.A.; Edelman, G.M. Unusual fragments in the subunit structure of concanavalin A. Proc. Natl. Acad. Sci. USA 1971, 68, 1130–1134. [Google Scholar] [CrossRef] [PubMed]
- Pan, W.; Kolomeisky, A.B.; Vekilov, P.G. Nucleation of ordered solid phases of proteins via a disordered high-density state: Phenomenological approach. J. Chem. Phys. 2005, 122, 174905. [Google Scholar] [CrossRef]
- Ranjbar, B.; Gill, P. Circular Dichroism Techniques: Biomolecular and Nanostructural Analyses—A Review. Chem. Biol. Drug Des. 2009, 74, 101–120. [Google Scholar] [CrossRef]
- Harden, J.L.; Guo, H.; Bertrand, M.; Shendruk, T.N.; Ramakrishnan, S.; Leheny, R.L. Enhanced gel formation in binary mixtures of nanocolloids with short-range attraction. J. Chem. Phys. 2018, 148, 44902. [Google Scholar] [CrossRef]
- Kulkarni, A.M.; Dixit, N.M.; Zukoski, C.F. Ergodic and non-ergodic phase transitions in globular protein suspensions. Faraday Discuss. 2003, 123, 37–50. [Google Scholar] [CrossRef]
- Shibayama, M.; Norisuye, T. Gel Formation Analyses by Dynamic Light Scattering. Bull. Chem. Soc. Jpn. 2002, 75, 641–659. [Google Scholar] [CrossRef]
- Liluashvili, A.; Ónody, J.; Voigtmann, T. Mode-coupling theory for active Brownian particles. Phys. Rev. E 2017, 96, 62608. [Google Scholar] [CrossRef]
- Cardinaux, F.; Gibaud, T.; Stradner, A.; Schurtenberger, P. Interplay between Spinodal Decomposition and Glass Formation in Proteins Exhibiting Short-Range Attractions. Phys. Rev. Lett. 2007, 99, 118301. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsova, I.M.; Turoverov, K.K.; Uversky, V.N. What macromolecular crowding can do to a protein. Int. J. Mol. Sci. 2014, 15, 23090–23140. [Google Scholar] [CrossRef] [PubMed]
| Central Composite Design (Hydrodynamic Radius Response) | Full Factorial Design (DDLS Signal Intensity Response) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Assay No. | Independent Variable | Coded Independent Variable | Assay No. | Independent Variable | Coded Independent Variable | ||||
| %PEG8k | Time (min) | PEG8k | Time | %PEG8k | Time (min) | PEG8k | Time | ||
| 1 | 8 | 2 | −1 | −1 | 1 | 8 | 2 | −1 | −1 |
| 2 | 8 | 10 | −1 | 1 | 2 | 8 | 5 | −1 | 0 |
| 3 | 16 | 2 | 1 | −1 | 3 | 8 | 10 | −1 | 1 |
| 4 | 16 | 10 | 1 | 1 | 4 | 12 | 2 | 0 | −1 |
| 5 | 6.4 | 5 | −1.4 | 0 | 5 | 12 | 5 | 0 | 0 |
| 6 | 17.6 | 5 | +1.4 | 0 | 6 | 12 | 10 | 0 | 1 |
| 7 | 12 | 1 | 0 | −1.4 | 7 | 16 | 2 | 1 | −1 |
| 8 | 12 | 12 | 0 | +1.4 | 8 | 16 | 5 | 1 | 0 |
| 9 | 12 | 5 | 0 | 0 | 9 | 16 | 10 | 1 | 1 |
| 10 | 12 | 5 | 0 | 0 | -- | -- | -- | -- | -- |
| 11 | 12 | 5 | 0 | 0 | -- | -- | -- | -- | -- |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brognaro, H.; Falke, S.; Nzanzu Mudogo, C.; Betzel, C. Multi-Step Concanavalin A Phase Separation and Early-Stage Nucleation Monitored Via Dynamic and Depolarized Light Scattering. Crystals 2019, 9, 620. https://doi.org/10.3390/cryst9120620
Brognaro H, Falke S, Nzanzu Mudogo C, Betzel C. Multi-Step Concanavalin A Phase Separation and Early-Stage Nucleation Monitored Via Dynamic and Depolarized Light Scattering. Crystals. 2019; 9(12):620. https://doi.org/10.3390/cryst9120620
Chicago/Turabian StyleBrognaro, Hévila, Sven Falke, Celestin Nzanzu Mudogo, and Christian Betzel. 2019. "Multi-Step Concanavalin A Phase Separation and Early-Stage Nucleation Monitored Via Dynamic and Depolarized Light Scattering" Crystals 9, no. 12: 620. https://doi.org/10.3390/cryst9120620
APA StyleBrognaro, H., Falke, S., Nzanzu Mudogo, C., & Betzel, C. (2019). Multi-Step Concanavalin A Phase Separation and Early-Stage Nucleation Monitored Via Dynamic and Depolarized Light Scattering. Crystals, 9(12), 620. https://doi.org/10.3390/cryst9120620