Avalanches in Compressed Sandstone: Crackling Noise under Confinement
Abstract
1. Introduction
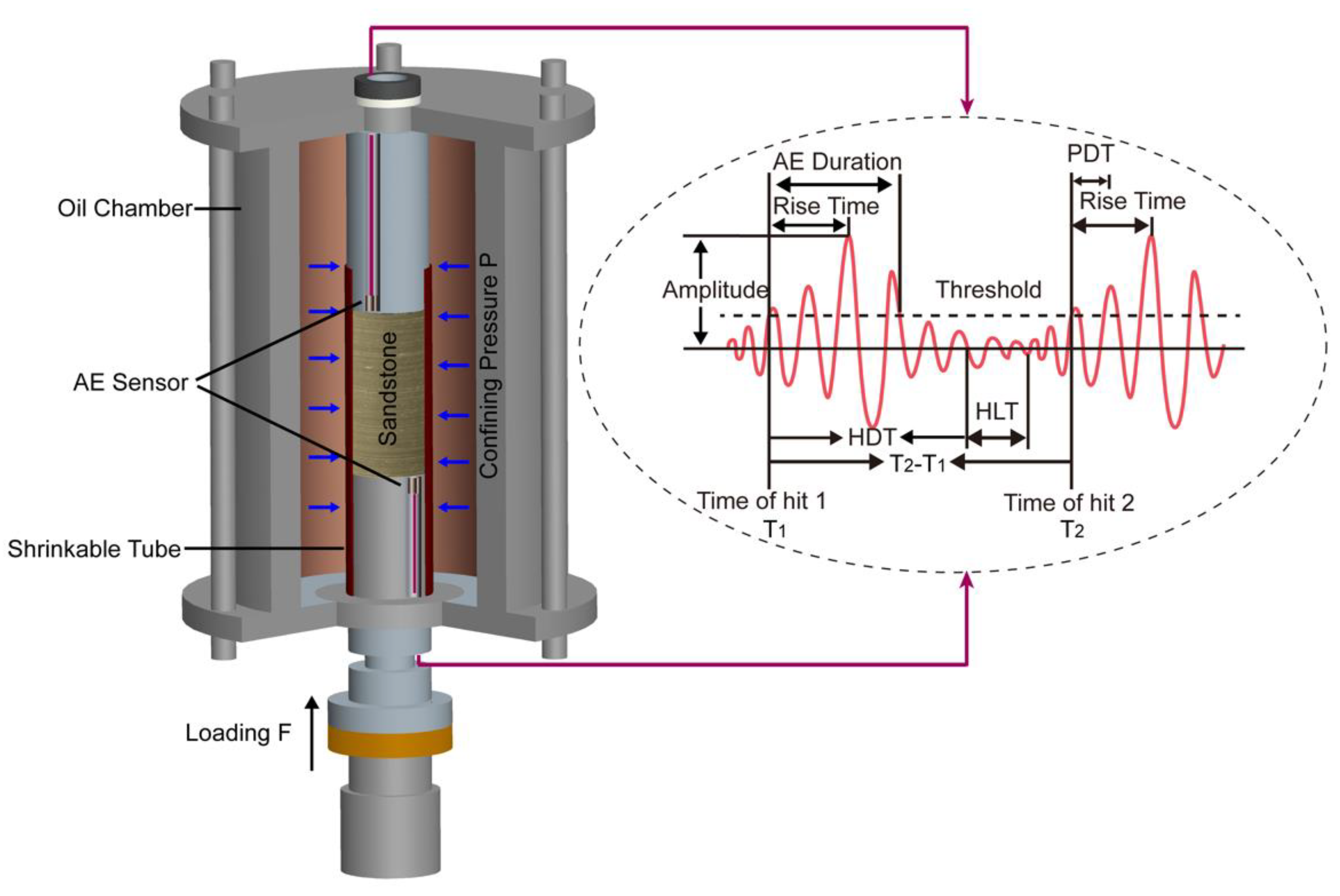
2. Experimental
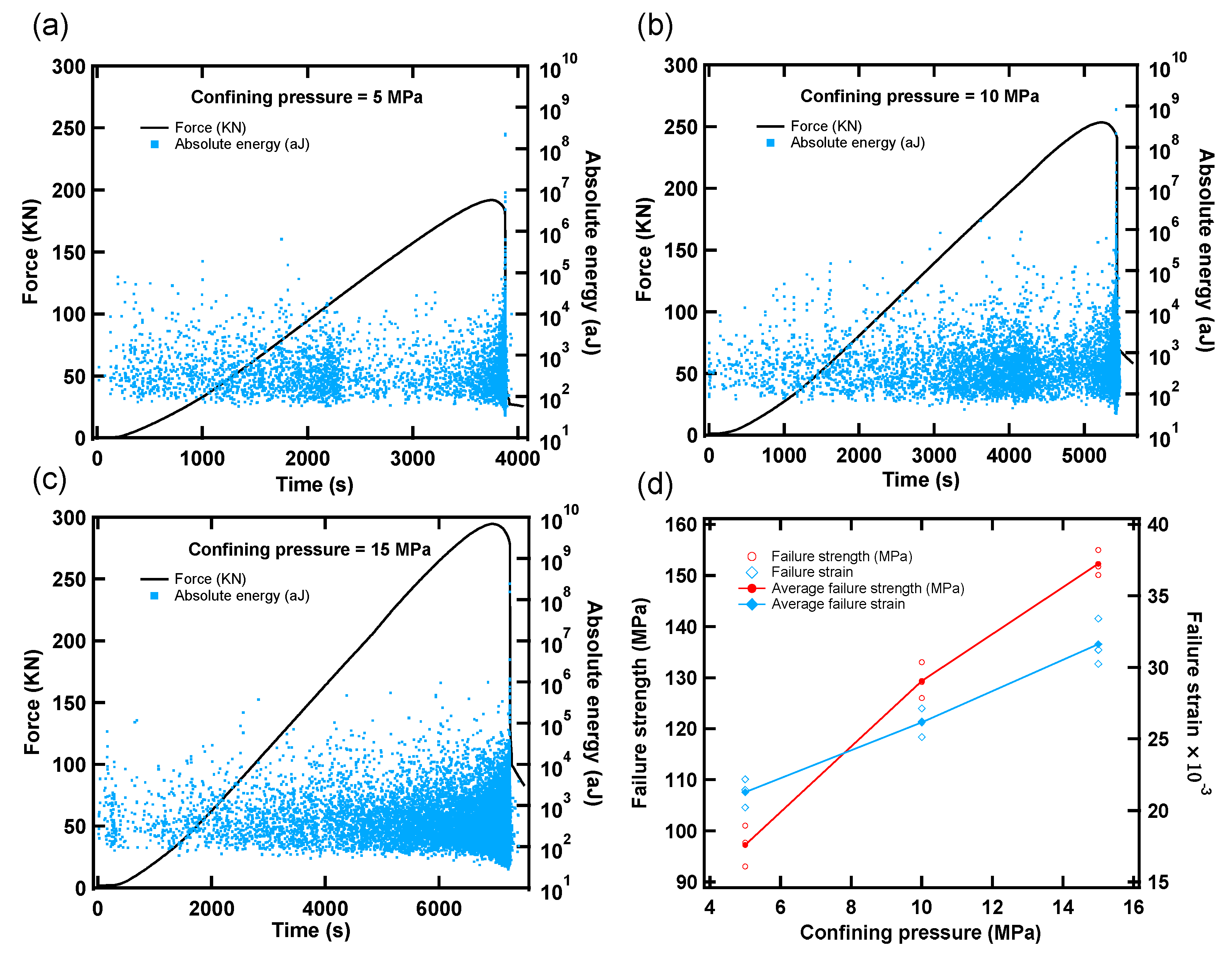
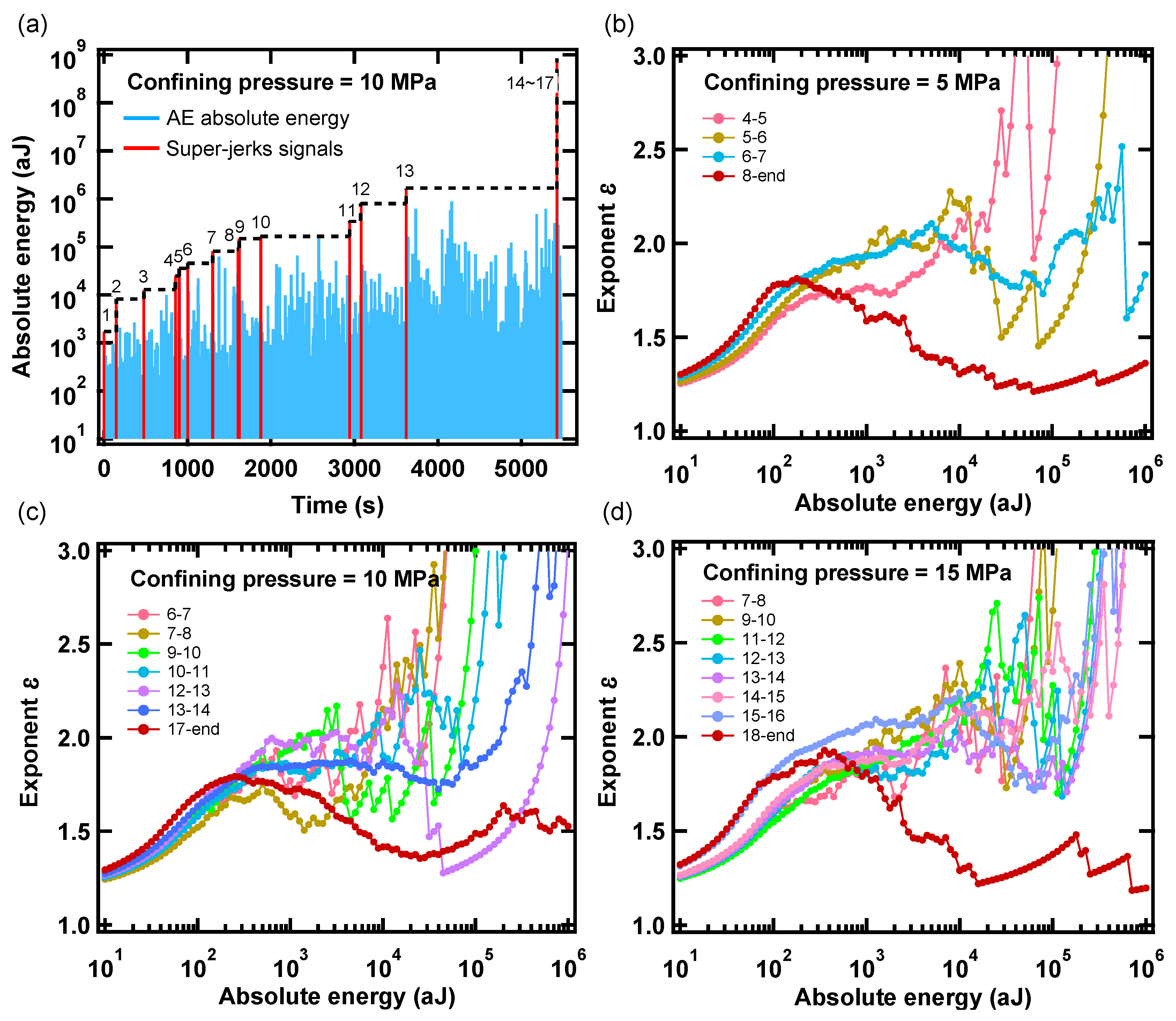
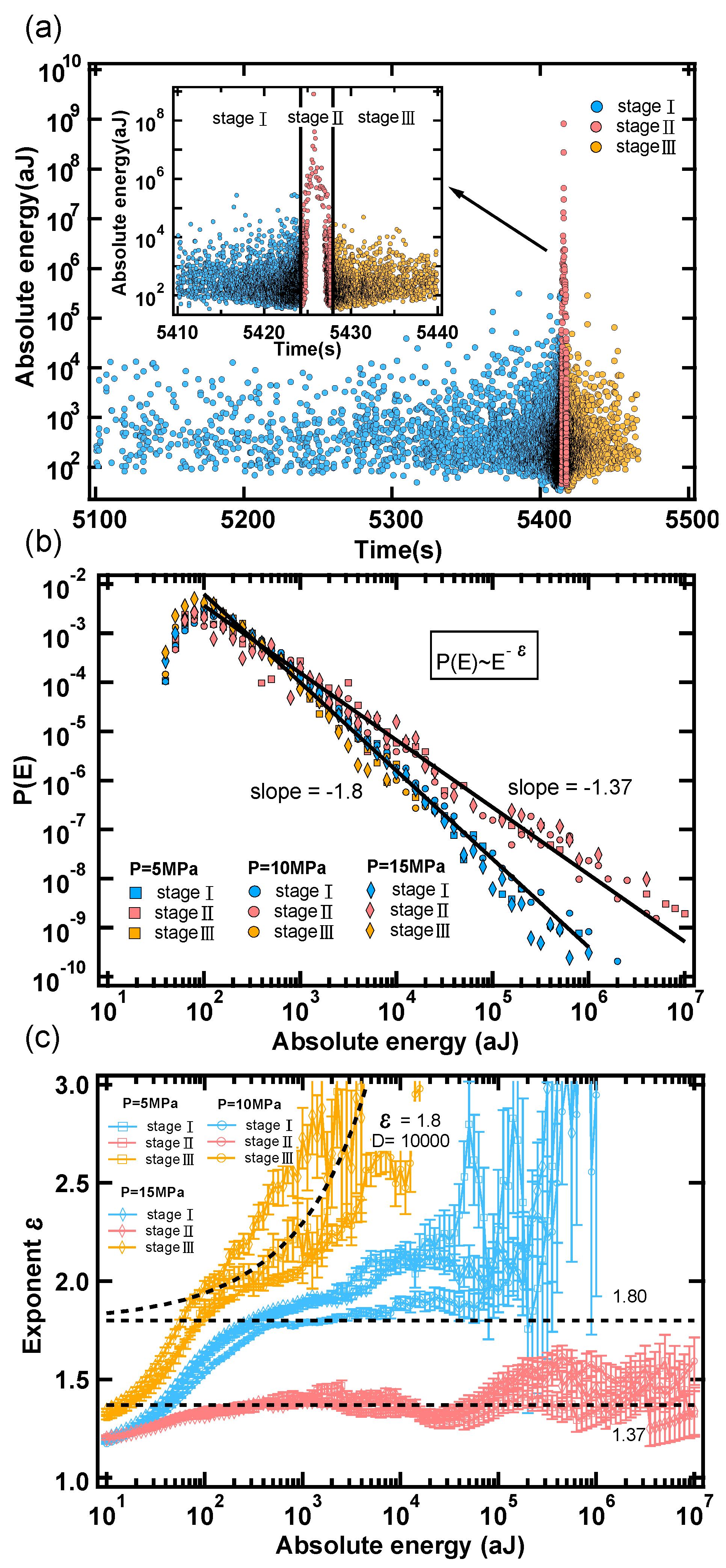
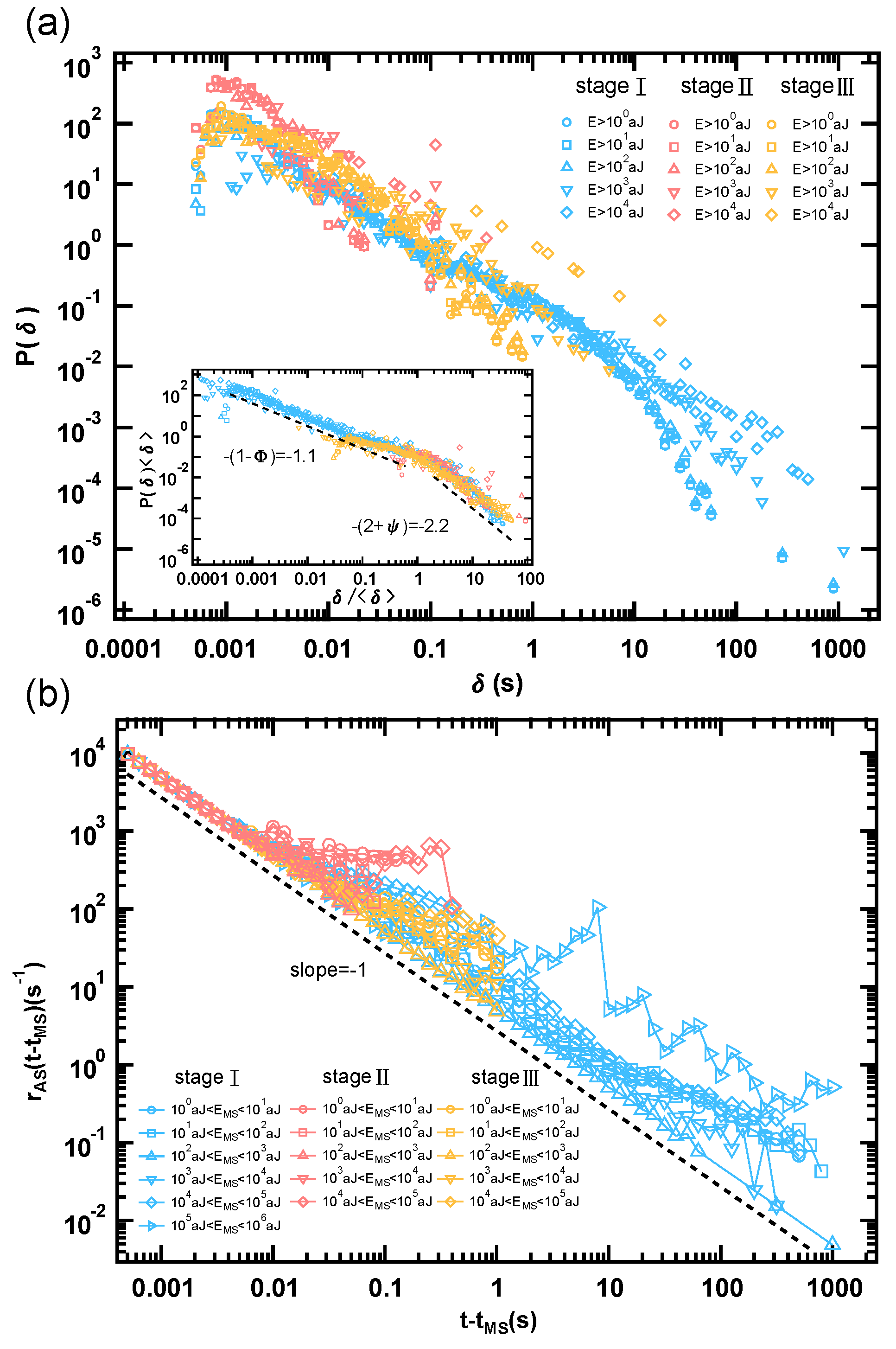
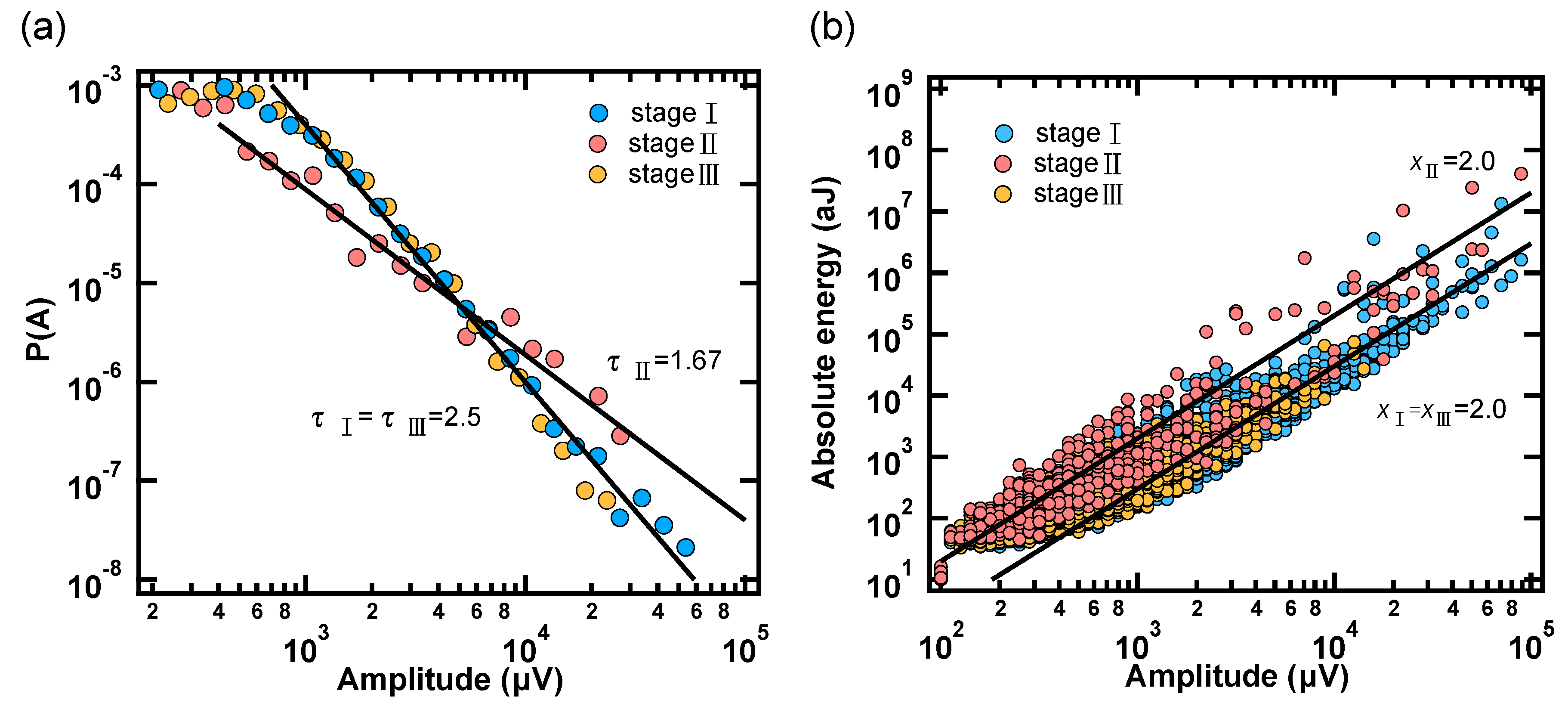
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cote, P.J.; Meisel, L.V. Self-organized criticality and the barkhausen effect. Phys. Rev. Lett. 1991, 67, 1334–1337. [Google Scholar] [CrossRef] [PubMed]
- Jaeger, H.M.; Nagel, S.R.; Behringer, R.P. Granular solids, liquids, and gases. Rev. Mod. Phys. 1996, 68, 1259–1273. [Google Scholar] [CrossRef]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. A simple analytic theory for the statistics of avalanches in sheared granular materials. Nat. Phys. 2011, 7, 554–557. [Google Scholar] [CrossRef]
- Zaiser, M. Scale invariance in plastic flow of crystalline solids. Adv. Phys. 2006, 55, 185–245. [Google Scholar] [CrossRef]
- Dahmen, K.A.; Ben-Zion, Y.; Uhl, J.T. Micromechanical Model for Deformation in Solids with Universal Predictions for Stress-Strain Curves and Slip Avalanches. Phys. Rev. Lett. 2009, 102, 175501. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Xue, D.; Ding, X.; Dahmen, K.A.; Scott, J.F. Ferroelectric switching and scale invariant avalanches in BaTiO3. Phys. Rev. Mater. 2019, 3, 014415. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Lampronti, G.I.; Soto-Parra, D.E.; Baro, J.; Planes, A.; Vives, E. Noise of collapsing minerals: Predictability of the compressional failure in goethite mines. Am. Miner. 2013, 98, 609–615. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Enrique Soto-Parra, D.; Planes, A.; Vives, E.; Reinecker, M.; Schranz, W. Failure mechanism in porous materials under compression: Crackling noise in mesoporous SiO2. Philos. Mag. Lett. 2011, 91, 554–560. [Google Scholar] [CrossRef]
- Friedman, N.; Ito, S.; Brinkman, B.A.W.; Shimono, M.; DeVille, R.E.L.; Dahmen, K.A.; Beggs, J.M.; Butler, T.C. Universal Critical Dynamics in High Resolution Neuronal Avalanche Data. Phys. Rev. Lett. 2012, 108, 208102. [Google Scholar] [CrossRef]
- Vajente, G. Crackling noise in advanced gravitational wave detectors: A model of the steel cantilevers used in the test mass suspensions. Phys. Rev. D 2017, 96, 022003. [Google Scholar] [CrossRef]
- Sheikh, M.A.; Weaver, R.L.; Dahmen, K.A. Avalanche Statistics Identify Intrinsic Stellar Processes near Criticality in KIC 8462852. Phys. Rev. Lett. 2016, 117, 261101. [Google Scholar] [CrossRef] [PubMed]
- Salje, E.K.H.; Saxena, A.; Planes, A. Avalanches in Functional Materials and Geophysics; Part of the Understanding Complex Systems Book Series (UCS); Springer: Berlin, Germany, 2017. [Google Scholar]
- Bismayer, U. Early warning signs for mining accidents: Detecting crackling noise. Am. Miner. 2017, 102, 3–4. [Google Scholar] [CrossRef]
- Nataf, G.F.; Castillo-Villa, P.O.; Baro, J.; Illa, X.; Vives, E.; Planes, A.; Salje, E.K.H. Avalanches in compressed porous SiO2-based materials. Phys. Rev. E 2014, 90, 022405. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ding, X.; Fang, D.; Sun, J.; Salje, E.K.H. Acoustic Emission from Porous Collapse and Moving Dislocations in Granular Mg-Ho Alloys under Compression and Tension. Sci. Rep. 2019, 9, 1330. [Google Scholar] [CrossRef]
- Baro, J.; Shyu, P.; Pang, S.; Jasiuk, I.M.; Vives, E.; Salje, E.K.H.; Planes, A. Avalanche criticality during compression of porcine cortical bone of different ages. Phys. Rev. E 2016, 93, 053001. [Google Scholar] [CrossRef]
- Makinen, T.; Miksic, A.; Ovaska, M.; Alava, M.J. Avalanches in Wood Compression. Phys. Rev. Lett. 2015, 115, 055501. [Google Scholar] [CrossRef]
- Davidsen, J.; Stanchits, S.; Dresen, G. Scaling and universality in rock fracture. Phys. Rev. Lett. 2007, 98, 125502. [Google Scholar] [CrossRef]
- Deschanel, S.; Vanel, L.; Godin, N.; Maire, E.; Vigier, G.; Ciliberto, S. Mechanical response and fracture dynamics of polymeric foams. J. Phys. D Appl. Phys. 2009, 42, 214001. [Google Scholar] [CrossRef]
- Guarino, A.; Ciliberto, S.; Garcimartin, A.; Zei, M.; Scorretti, R. Failure time and critical behaviour of fracture precursors in heterogeneous materials. Eur. Phys. J. B 2002, 26, 141–151. [Google Scholar] [CrossRef]
- Guarino, A.; Garcimartin, A.; Ciliberto, S. An experimental test of the critical behaviour of fracture precursors. Eur. Phys. J. B 1998, 6, 13–24. [Google Scholar] [CrossRef]
- Hirata, T. Omoris power law aftershock sequences of micro-fracturing in rock fracture experiment. J. Geophys. Res. Solid Earth 1987, 92, 6215–6221. [Google Scholar] [CrossRef]
- Miksic, A.; Koivisto, J.; Alava, M. Statistical properties of low cycle fatigue in paper. J. Stat. Mech. Theory Exp. 2011. [Google Scholar] [CrossRef]
- Rosti, J.; Koivisto, J.; Alava, M.J. Statistics of acoustic emission in paper fracture: Precursors and criticality. J. Stat. Mech. Theory Exp. 2010. [Google Scholar] [CrossRef]
- Rosti, J.; Koivisto, J.; Traversa, P.; Illa, X.; Grasso, J.-R.; Alava, M.J. Line creep in paper peeling. Int. J. Fract. 2008, 151, 281–297. [Google Scholar] [CrossRef]
- Scholz, C.H. Micro-fracturing and inelastic deformation of rock in compression. J. Geophys. Res. 1968, 73, 1417–1432. [Google Scholar] [CrossRef]
- Stojanova, M.; Santucci, S.; Vanel, L.; Ramos, O. High Frequency Monitoring Reveals Aftershocks in Subcritical Crack Growth. Phys. Rev. Lett. 2014, 112, 115502. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Dul’kin, E.; Roth, M. Acoustic emission during the ferroelectric transition Pm3m to P4mm in BaTiO3 and the ferroelastic transition R3m-C2/c in Pb3(PO4)2. Appl. Phys. Lett. 2015, 106, 152903. [Google Scholar] [CrossRef]
- Baro, J.; Corral, A.; Illa, X.; Planes, A.; Salje, E.K.H.; Schranz, W.; Soto-Parra, D.E.; Vives, E. Statistical Similarity between the Compression of a Porous Material and Earthquakes. Phys. Rev. Lett. 2013, 110, 088702. [Google Scholar] [CrossRef]
- Jiang, X.; Jiang, D.; Chen, J.; Salje, E.K.H. Collapsing minerals: Crackling noise of sandstone and coal, and the predictability of mining accidents. Am. Miner. 2016, 101, 2751–2758. [Google Scholar] [CrossRef]
- Kun, F.; Varga, I.; Lennartz-Sassinek, S.; Main, I.G. Approach to failure in porous granular materials under compression. Phys. Rev. E 2013, 88, 062207. [Google Scholar] [CrossRef]
- Kun, F.; Varga, I.; Lennartz-Sassinek, S.; Main, I.G. Rupture Cascades in a Discrete Element Model of a Porous Sedimentary Rock. Phys. Rev. Lett. 2014, 112, 065501. [Google Scholar] [CrossRef] [PubMed]
- Scholz, C.H. Frequency-magnetude relation of micro-fracturing in rock and its relation to earthquakes. Bull. Seismol. Soc. Am. 1968, 58, 399–415. [Google Scholar]
- Fairhurst, C.E.; Hudson, J.A. Draft ISRM suggested method for the complete stress–strain curve for intact rock in uniaxial compression. Int. J. Rock Mech. Min. Sci. 1999, 36, 281–289. [Google Scholar]
- Salje, E.K.H.; Dahmen, K.A. Crackling Noise in Disordered Materials. Annu. Rev. Condens. Matter Phys. 2014, 5, 233–254. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, H.; Main, I.G.; Salje, E.K.H. Predicting mining collapse: Superjerks and the appearance of. record-breaking events in coal as collapse precursors. Phys. Rev. E 2017, 96, 023004. [Google Scholar] [CrossRef]
- Clauset, A.; Shalizi, C.R.; Newman, M.E.J. Power-Law Distributions in Empirical Data. SIAM Rev. 2009, 51, 661–703. [Google Scholar] [CrossRef]
- Salje, E.K.H.; Planes, A.; Vives, E. Analysis of crackling noise using the maximum-likelihood method: Power-law mixing and exponential damping. Phys. Rev. E 2017, 96, 042122. [Google Scholar] [CrossRef]
- Corral, A. Local distributions and rate fluctuations in a unified scaling law for earthquakes. Phys. Rev. E 2003, 68, 035102. [Google Scholar] [CrossRef]
- Bak, P.; Christensen, K.; Danon, L.; Scanlon, T. Unified scaling law for earthquakes. Phys. Rev. Lett. 2002, 88, 178501. [Google Scholar] [CrossRef]
- Sethna, J.P.; Dahmen, K.A.; Myers, C.R. Crackling noise. Nature 2001, 410, 242–250. [Google Scholar] [CrossRef]
- Fisher, D.S.; Dahmen, K.; Ramanathan, S.; Ben-Zion, Y. Statistics of earthquakes in simple models of heterogeneous faults. Phys. Rev. Lett. 1997, 78, 4885–4888. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Ranjith, P.G.; Gui, Y.-L. Experimental Study of Mechanical Behavior and X-Ray Micro CT Observations of Sandstone under Conventional Triaxial Compression. Geotech. Test. J. 2015, 38, 179–197. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Costa, L.S.; Alves, L.G.A.; Santoro, P.A.; Picoli, S.; Lenzi, E.K.; Mendes, R.S. Analogies Between the Cracking Noise of Ethanol-Dampened Charcoal and Earthquakes. Phys. Rev. Lett. 2015, 115, 025503. [Google Scholar] [CrossRef] [PubMed]
- Papanikolaou, S.; Dimiduk, D.M.; Choi, W.; Sethna, J.P.; Uchic, M.D.; Woodward, C.F.; Zapperi, S. Quasi-periodic events in crystal plasticity and the self-organized avalanche oscillator. Nature 2012, 490, 517–522. [Google Scholar] [CrossRef]
- Jagla, E.A. Realistic spatial and temporal earthquake distributions in a modified Olami-Feder-Christensen model. Phys. Rev. E 2010, 81, 046117. [Google Scholar] [CrossRef]
- Song, H.; Dimiduk, D.; Papanikolaou, S. Universality Class of Nanocrystal Plasticity: Localization and Self-Organization in Discrete Dislocation Dynamics. Phys. Rev. Lett. 2019, 122, 178001. [Google Scholar] [CrossRef]
- Papanikolaou, S.; Bohn, F.; Sommer, R.L.; Durin, G.; Zapperi, S.; Sethna, J.P. Universality beyond power laws and the average avalanche shape. Nat. Phys. 2011, 7, 316. [Google Scholar] [CrossRef]
| Confining Pressure | Parameter | MF Value/Force Integrated | Experimental | ||
|---|---|---|---|---|---|
| Stage I | Stage II | Stage Ⅲ | |||
| 5 MPa | <ε> | 1.33/1.67 | 1.90 ± 0.07 | 1.38 ± 0.06 | 1.90 ± 0.12 |
| <τ> | 1.67/2.33 | 2.47 ± 0.07 | 1.65 ± 0.09 | 2.47 ± 0.10 | |
| <x> | 2.0/2.0 | 1.88 ± 0.05 | 1.91 ± 0.05 | 1.88 ± 0.03 | |
| 10 MPa | <ε> | 1.33/1.67 | 1.80 ± 0.10 | 1.37 ± 0.05 | 1.80 ± 0.15 |
| <τ> | 1.67/2.33 | 2.50 ± 0.08 | 1.67 ± 0.12 | 2.50 ± 0.08 | |
| <x> | 2.0/2.0 | 2.00 ± 0.02 | 2.00 ± 0.05 | 2.00 ± 0.02 | |
| 15 MPa | <ε> | 1.33/1.67 | 1.89 ± 0.12 | 1.37 ± 0.05 | 1.89 ± 0.13 |
| <τ> | 1.67/2.33 | 2.46 ± 0.08 | 1.67 ± 0.10 | 2.46 ± 0.10 | |
| <x> | 2.0/2.0 | 1.94 ± 0.06 | 1.95 ± 0.05 | 1.94 ± 0.03 | |
| Confining Pressure | Correlation | Theoretical Value MF/Force Integrated | Experimental | ||
|---|---|---|---|---|---|
| Stage I | Stage II | Stage Ⅲ | |||
| 5 MPa | <τ> −1 | 0.66/1.33 | 1.47 ± 0.07 | 0.65 ± 0.09 | 1.47 ± 0.10 |
| <x>(<ε> − 1) | 1.69 ± 0.12 | 0.73 ± 0.11 | 1.69 ± 0.15 | ||
| 10 MPa | <τ> −1 | 1.50 ± 0.08 | 0.67 ± 0.12 | 1.50 ± 0.08 | |
| <x>(<ε> − 1) | 1.60 ± 0.12 | 0.74 ± 0.10 | 1.60 ± 0.17 | ||
| 15 MPa | <τ> −1 | 1.46 ± 0.08 | 0.67 ± 0.10 | 1.46 ± 0.10 | |
| <x>(<ε> − 1) | 1.73 ± 0.18 | 0.72 ± 0.10 | 1.73 ± 0.16 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Liu, H.; Xie, K.; Salje, E.K.H.; Jiang, X. Avalanches in Compressed Sandstone: Crackling Noise under Confinement. Crystals 2019, 9, 582. https://doi.org/10.3390/cryst9110582
Zhao Y, Liu H, Xie K, Salje EKH, Jiang X. Avalanches in Compressed Sandstone: Crackling Noise under Confinement. Crystals. 2019; 9(11):582. https://doi.org/10.3390/cryst9110582
Chicago/Turabian StyleZhao, Yunfeng, Hanlong Liu, Kainan Xie, Ekhard K.H. Salje, and Xiang Jiang. 2019. "Avalanches in Compressed Sandstone: Crackling Noise under Confinement" Crystals 9, no. 11: 582. https://doi.org/10.3390/cryst9110582
APA StyleZhao, Y., Liu, H., Xie, K., Salje, E. K. H., & Jiang, X. (2019). Avalanches in Compressed Sandstone: Crackling Noise under Confinement. Crystals, 9(11), 582. https://doi.org/10.3390/cryst9110582




