Magneto-Optical Isolator Based on Ultra-Wideband Photonic Crystals Waveguide for 5G Communication System
Abstract
1. Introduction
2. Materials and Methods
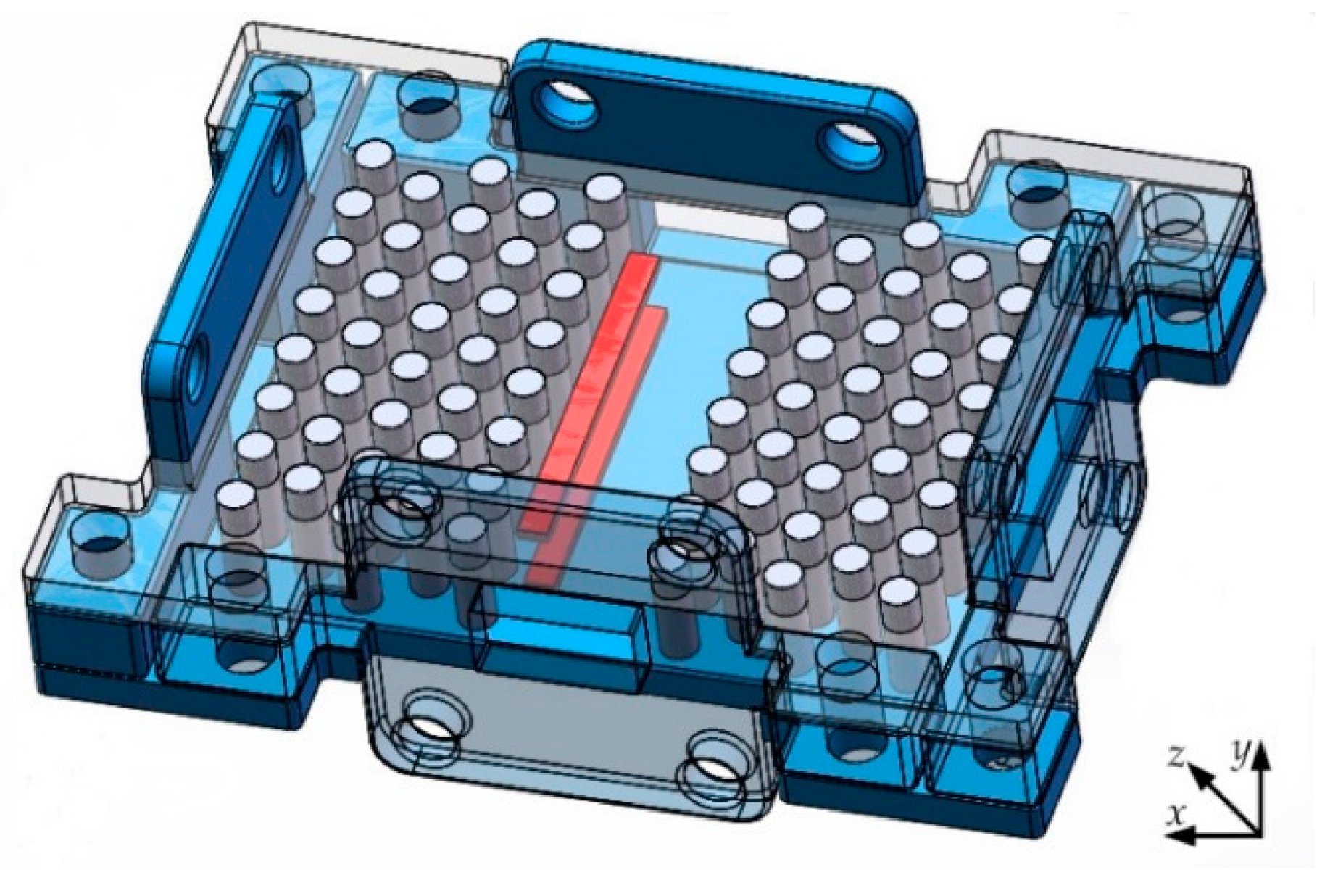
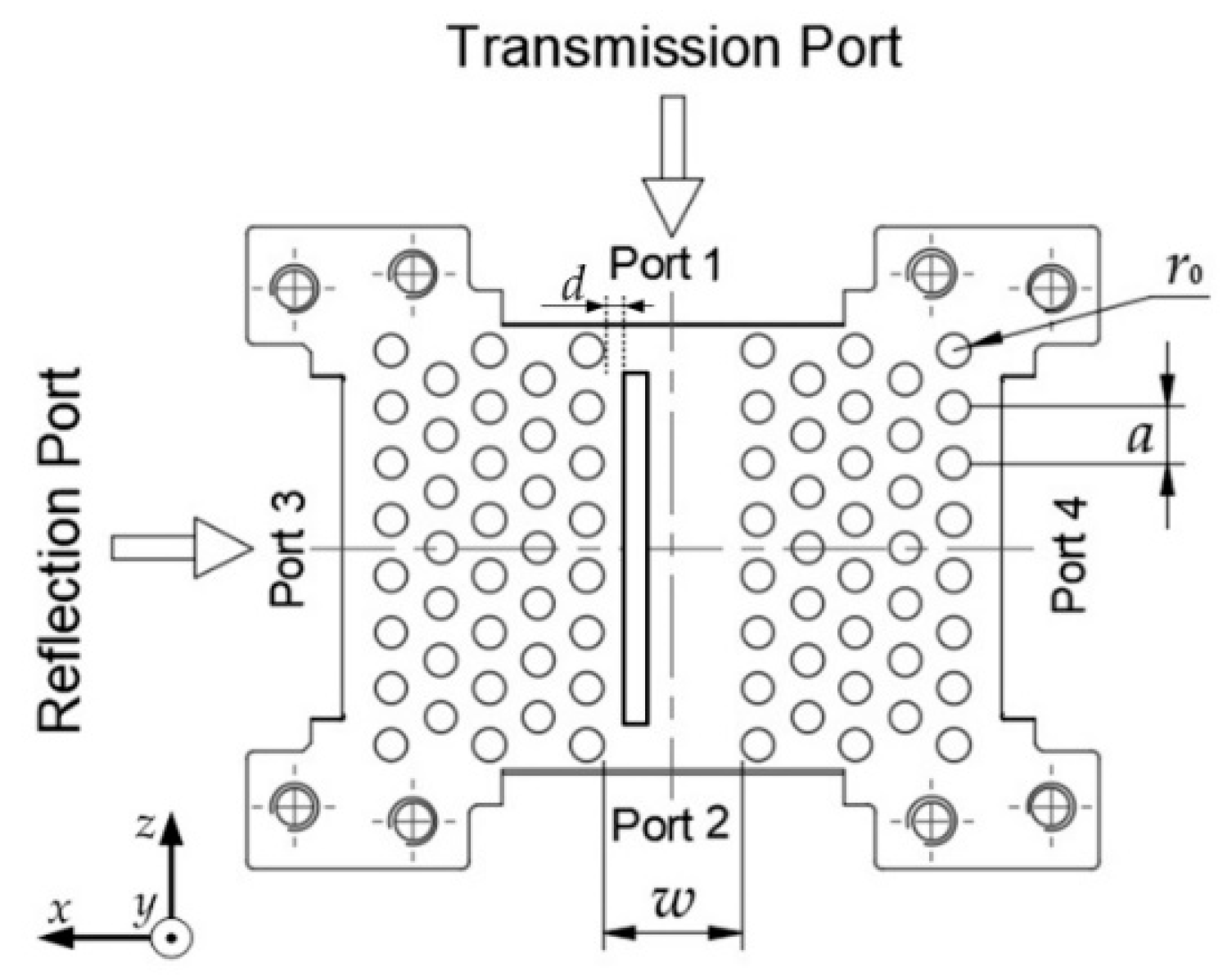
2.1. Design of MO Isolator
2.2. Ultra-Wideband PCW with PBG
3. MO Isolator
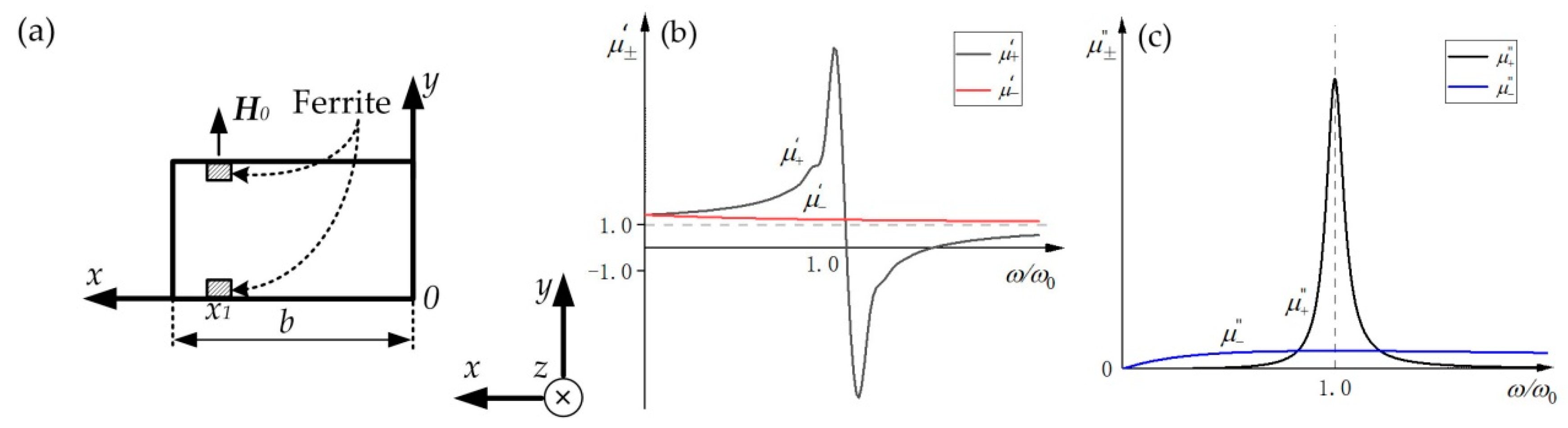
3.1. Theoretical Model of MO Isolator
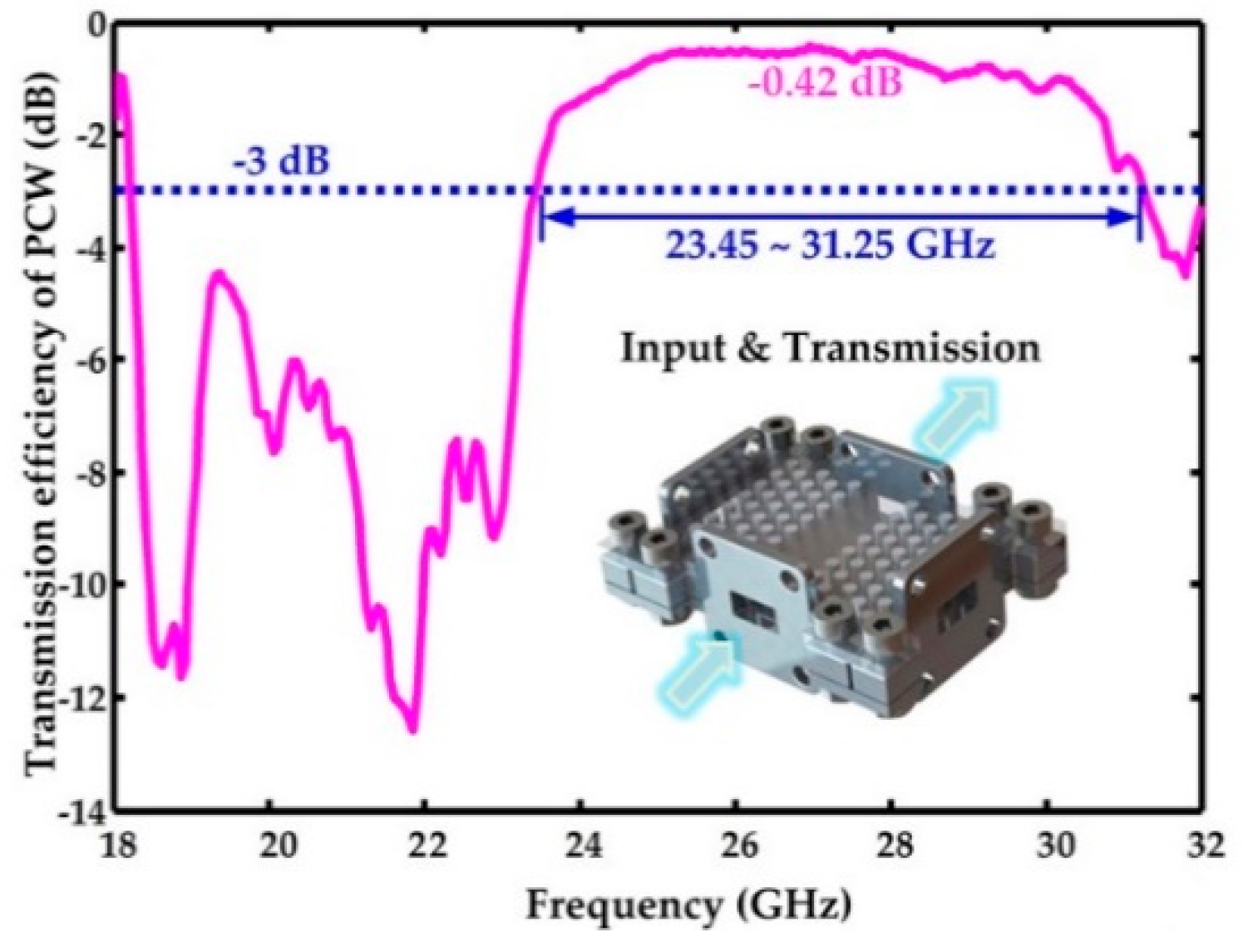
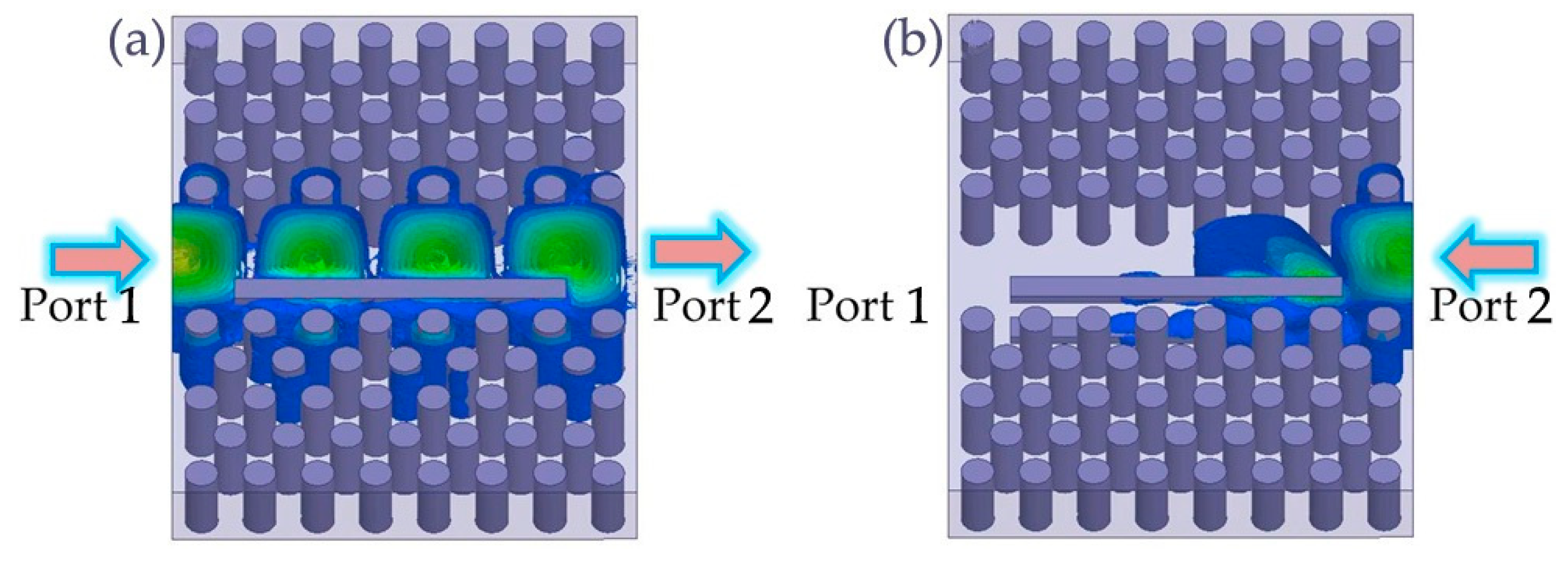
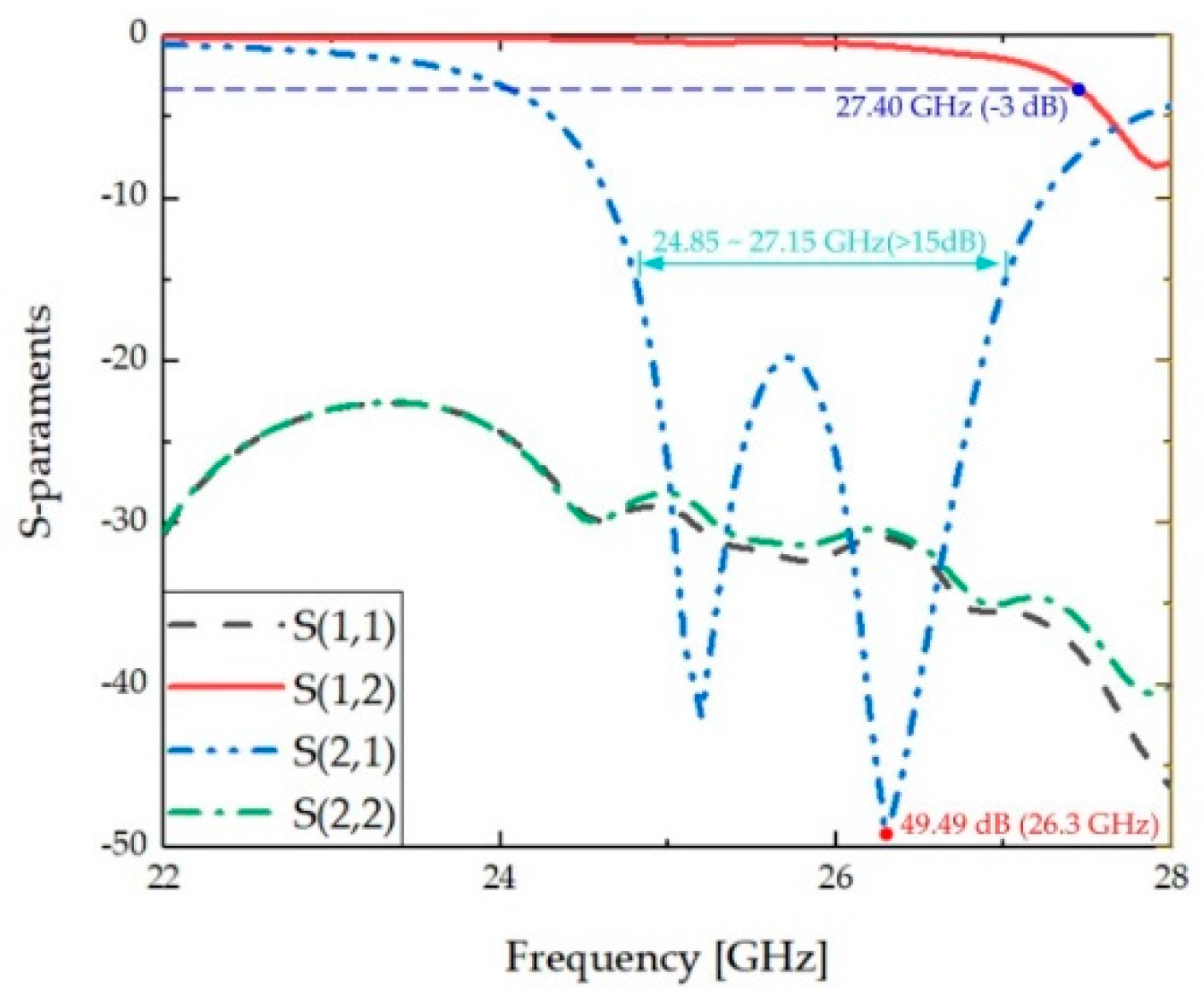
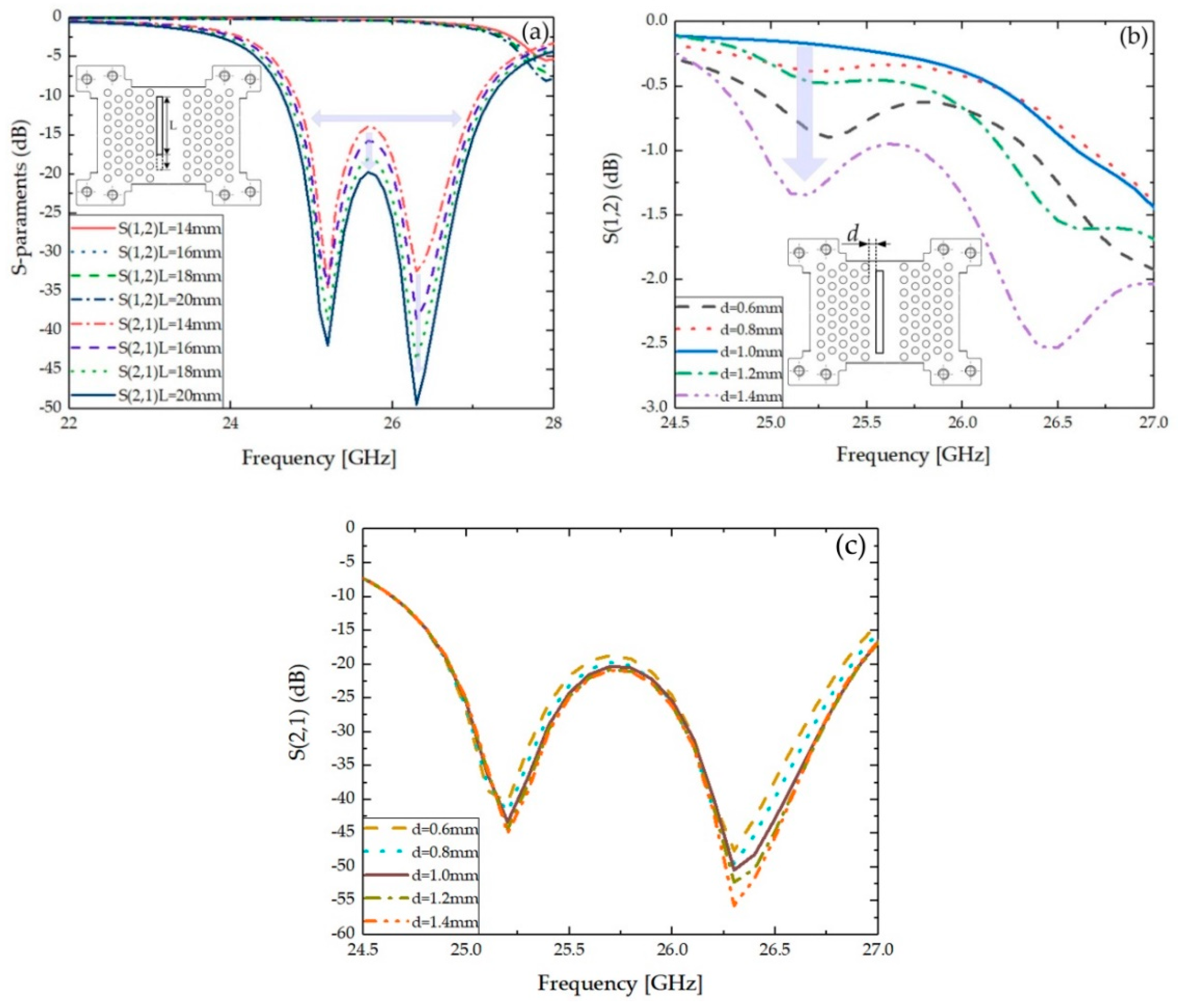
3.2. Numerical Results
3.3. Disscusion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yablonovitch, E. Inhitited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef]
- John, S. Strong localization of photons in certain disordered dielectric super-lattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef]
- Bruyant, A.; Lérondel, G.; Reece, P.J.; Gal, M. Allsilicon omnidirectional mirrors based on one-dimensional photonic crystals. Appl. Phys. Lett. 2003, 82, 3227–3229. [Google Scholar] [CrossRef]
- Happ, T.D.; Markard, A.; Kamp, M. InP-Based short cavity lasers with 2D photonic crystal mirror. Electron. Lett. 2001, 37, 428–429. [Google Scholar] [CrossRef]
- Stockermans, R.J.; Rochon, P.L. Modeling of Photonic Bandgaps in Resonant Waveguide Grating Systems Using a Simple Theory for 1-D Photonic Crystals. J. Lightwave Technol. 2007, 25, 952–956. [Google Scholar] [CrossRef]
- Qiu, M.; Jaskorzynska, B. Design of a channel drop filter in a two-dimensional triangular photonic crystal. Appl. Phys. Lett. 2003, 83, 1074–1076. [Google Scholar] [CrossRef]
- Akahane, Y.; Asano, T.; Song, B.S. High-Q photonic nanocavity in a two-dimensional photonic crystal. Natural 2003, 425, 944–947. [Google Scholar] [CrossRef]
- Akahane, Y.; Mochizuki, M.; Asano, T.; Tanaka, Y.; Noda, S. Design of a channel drop filter by using a donor-type cavity with high-quality factor in a two-dimensional photonic crystal slab. Appl. Phys. Lett. 2003, 82, 1341–1343. [Google Scholar] [CrossRef]
- Chutinan, A.; Okano, M.; Noda, S. Waveguides and waveguide bends in two-dimensional photonic crystal slabs. Appl. Phys. Lett. 2002, 80, 1698–1700. [Google Scholar] [CrossRef]
- Duan, S.Q.; Chen, Y.P.; Li, G.Z.; Zhu, C.Y.; Chen, X.F. Broadband polarization beam splitter based on a negative refractive lithium niobate photonic crystal slab. Chin. Opt. Lett. 2016, 14, 042301–042304. [Google Scholar] [CrossRef]
- Wang, Z.; Fan, S.H. Optical circulators in two dimensional magneto-optical photonic crystals. Opt. Lett. 2005, 15, 1989–1991. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Ouyang, Z.B.; Li, J.Z. Low-Loss Y-junction two-dimensional magneto-photonic crystals circulator using a ferrite cylinder. Opt. Commun. 2016, 369, 1–6. [Google Scholar] [CrossRef]
- Jalali, A.A.; Friberg, A.T. Faraday rotation in a two dimensional photonic crystal with a magneto-optic defect. Opt. Lett. 2005, 30, 1213–1215. [Google Scholar] [CrossRef]
- Yin, Z.; Ji, D.J.; Lei, L.; Hao, H.; Xiu, H.D.; Liang, Z.X. A 40-Gbit/s 1-to-2 photonic data distributor empploying a single semiconductor optical amplifier. Chin. Phys. Lett. 2011, 28, 064212. [Google Scholar]
- Chen, K.X.; Chiang, K.S.; Chan, H.P. Broadband multiport dynamic optical power distributor based on thermooptic polymer waveguide vertical couplers. IEEE Photonics Technol. Lett. 2008, 20, 273–275. [Google Scholar] [CrossRef]
- Zhu, Z.H.; Ye, W.M.; Ji, J.R.; Yuan, X.D.; Zen, C. High-Contrast light-by-light switching and AND gate based on nonlinear photonic crystals. Opt. Express 2006, 14, 1783–1788. [Google Scholar] [CrossRef]
- Liu, Q.; Ouyang, Z.; Wu, C.J. All-Optical half adder based on cross structures in two-dimensional photonic crystals. Opt. Express 2008, 16, 18992–19000. [Google Scholar] [CrossRef]
- Kato, H.; Matsushita, T.; Takayama, A.; Egawa, M.; Nishimura, K.; Inoue, M. Properties of one-dimensional magnetophotonic crystals for use in optical isolator devices. IEEE Trans. Magn. 2002, 28, 3246–3248. [Google Scholar] [CrossRef]
- Hiroyuki, T.; Sajeev, J. Compact optical one-way waveguide isolators for photonic-band-gap microchips. Phys. Rev. A 2008, 78, 023804. [Google Scholar]
- Haddadan, F.; Soroosh, M. Low-Power all-optical 8-to-3 encoder using photonic crystal-based waveguides. Photonics Net. Commun. 2019, 37, 83–89. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Xu, B.G.; Dong, Z.; Zeng, X.K.; Pei, J.H.; Xu, S.X.; Xue, Q. Four ports double Y-shaped ultra-wideband magneto-photonic crystals circulator for 5G communication system. IEEE Access 2019, 7, 120463–120474. [Google Scholar] [CrossRef]
- Gardiol, F.E.; Vorst, A.S.V. Computer Analysis of E-Plane resonance isolators. IEEE Trans. Microw. Theory Technol. 1971, 19, 315–322. [Google Scholar] [CrossRef]
- Von Aulock, W.H.V.; Fay, C.E. Linear Ferrite Devices for Microwave Applications; Academic Press: New York, NY, USA, 1968. [Google Scholar]
- Lax, B.; Button, K.J. Microwave Ferrites and Ferrimagnetics; McGraw-Hill: New York, NY, USA, 1962. [Google Scholar]
- Weiss, M.T. Improved Rectangular Waveguide Resonance Isolators. IRE Trans. Microw. Theory Technol. 1956, 4, 240–243. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, D.G.; Xu, S.X.; Xu, B.G.; Dong, Z. H-Plane cross-shaped waveguide circulator in magneto-photonic crystals with five ferrite posts. Chin. Opt. Lett. 2017, 15, 111601. [Google Scholar] [CrossRef]
- Rodenas, A.; Gu, M.; Corrielli, G.; Paie, P.; John, S.; Kar, A.K.; Osellame, R. Three-Dimensional femtosecond laser nanolithography of crystals. Nat. Photonics 2019, 13, 105. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Xu, B.; Zhang, D.; Xu, S.; Dong, Z.; Zeng, X.; Lu, X.; Pei, J. Magneto-Optical Isolator Based on Ultra-Wideband Photonic Crystals Waveguide for 5G Communication System. Crystals 2019, 9, 570. https://doi.org/10.3390/cryst9110570
Wang Y, Xu B, Zhang D, Xu S, Dong Z, Zeng X, Lu X, Pei J. Magneto-Optical Isolator Based on Ultra-Wideband Photonic Crystals Waveguide for 5G Communication System. Crystals. 2019; 9(11):570. https://doi.org/10.3390/cryst9110570
Chicago/Turabian StyleWang, Yong, Biaogang Xu, Dengguo Zhang, Shixiang Xu, Zheng Dong, Xuanke Zeng, Xiaowei Lu, and Jihong Pei. 2019. "Magneto-Optical Isolator Based on Ultra-Wideband Photonic Crystals Waveguide for 5G Communication System" Crystals 9, no. 11: 570. https://doi.org/10.3390/cryst9110570
APA StyleWang, Y., Xu, B., Zhang, D., Xu, S., Dong, Z., Zeng, X., Lu, X., & Pei, J. (2019). Magneto-Optical Isolator Based on Ultra-Wideband Photonic Crystals Waveguide for 5G Communication System. Crystals, 9(11), 570. https://doi.org/10.3390/cryst9110570




