Miniaturized Metalens Based Optical Tweezers on Liquid Crystal Droplets for Lab-on-a-Chip Optical Motors
Abstract
1. Introduction
2. Materials and Methods
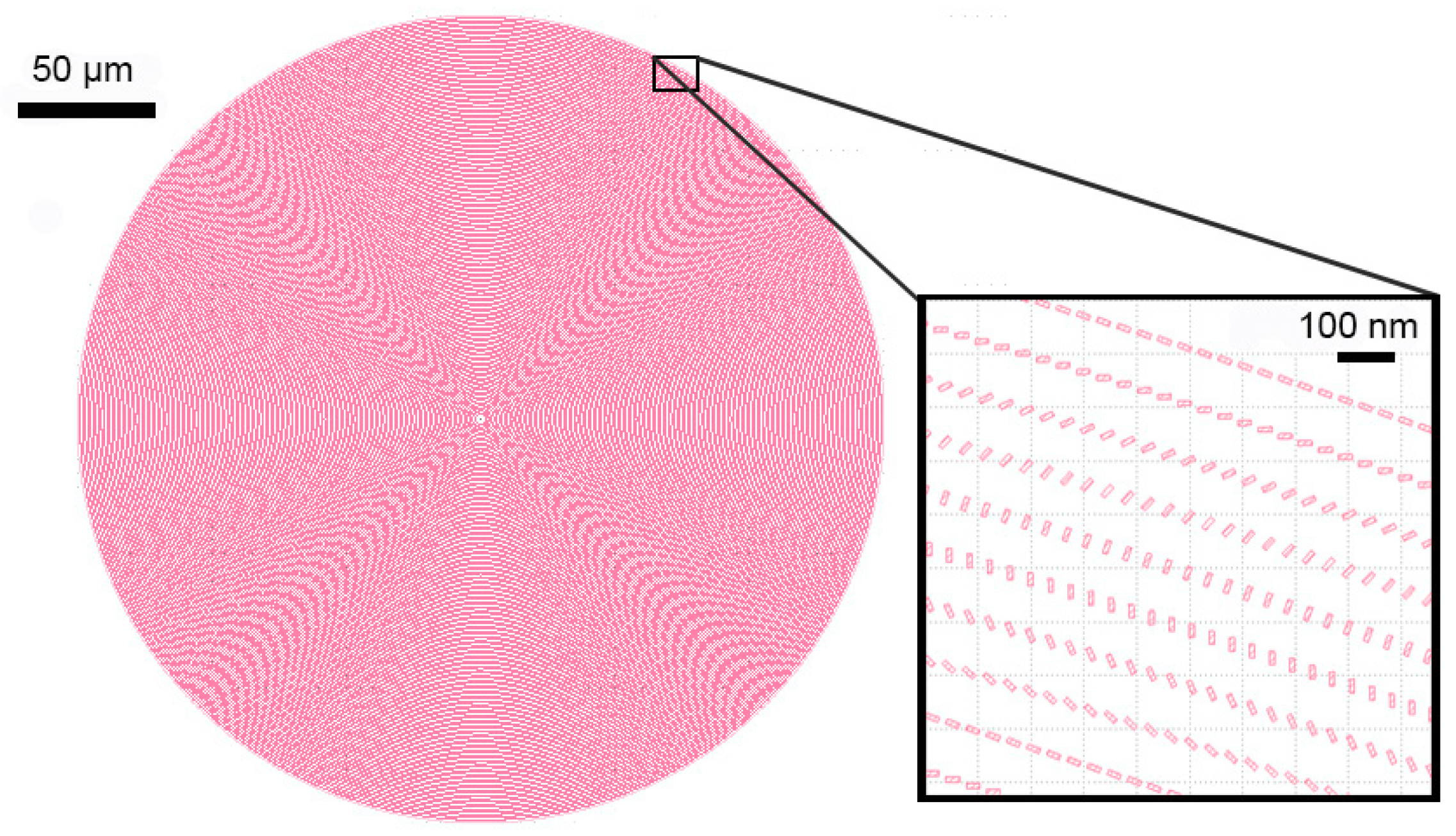
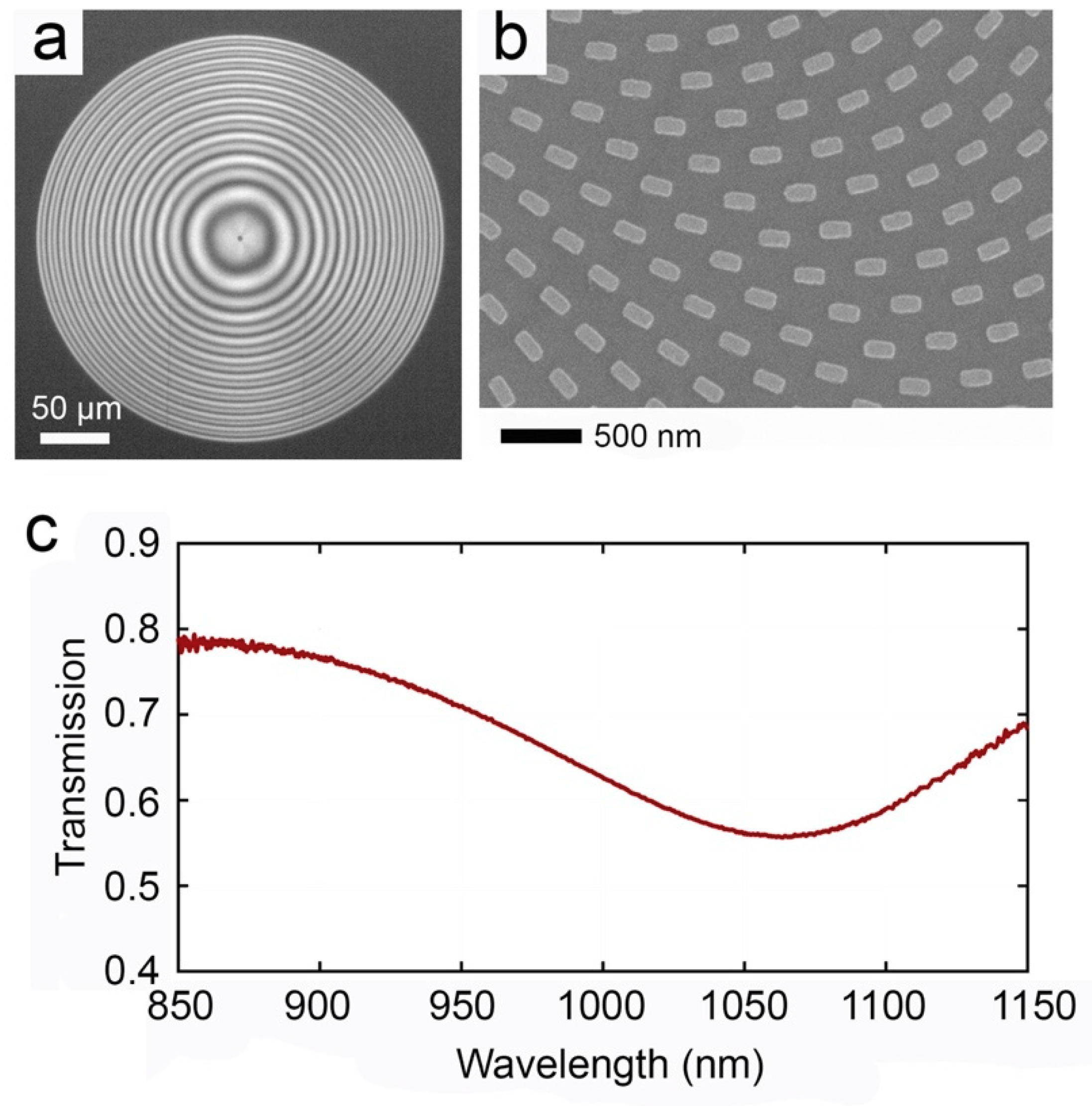
2.1. Design and Fabrication of the Metalens
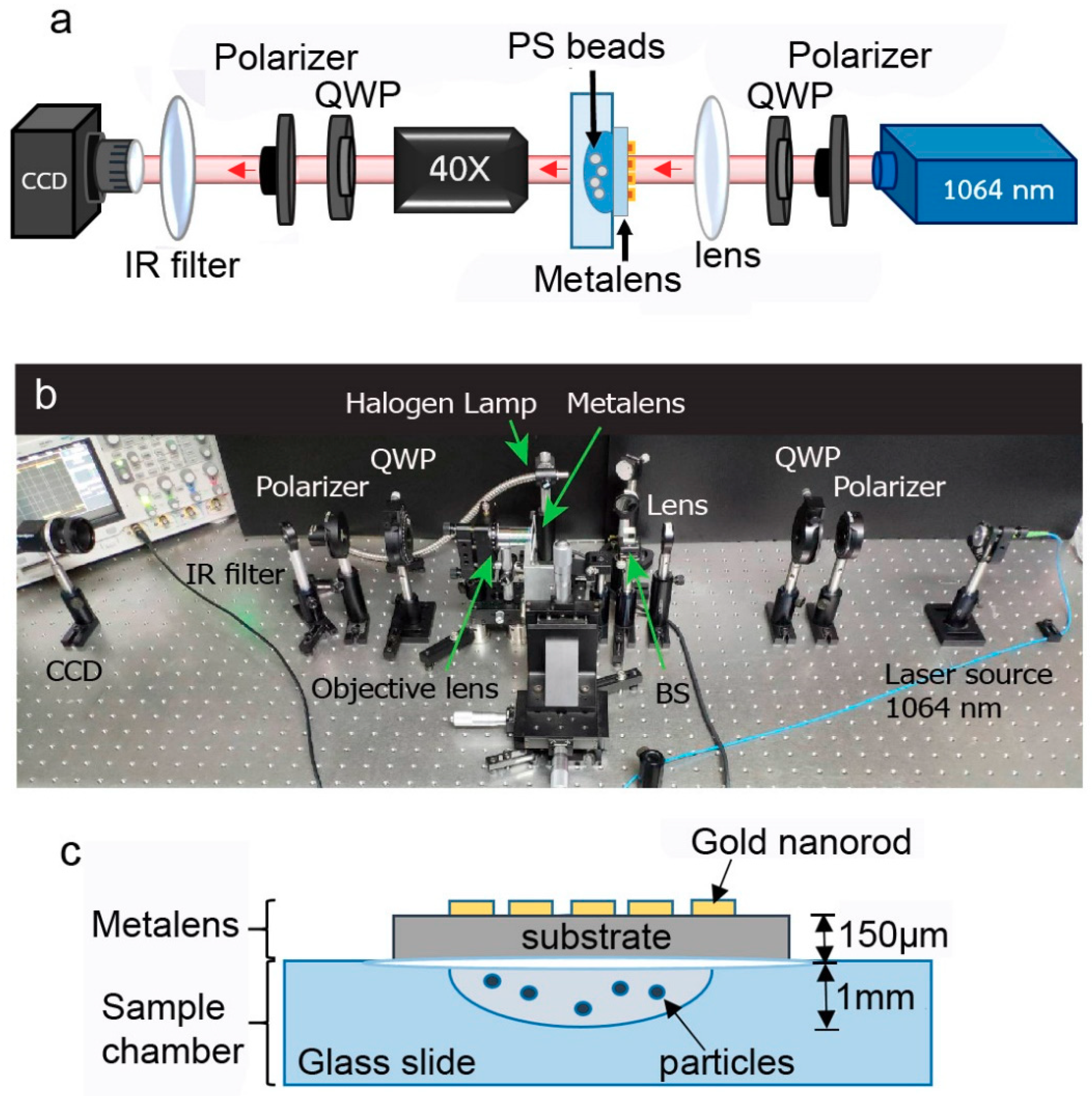
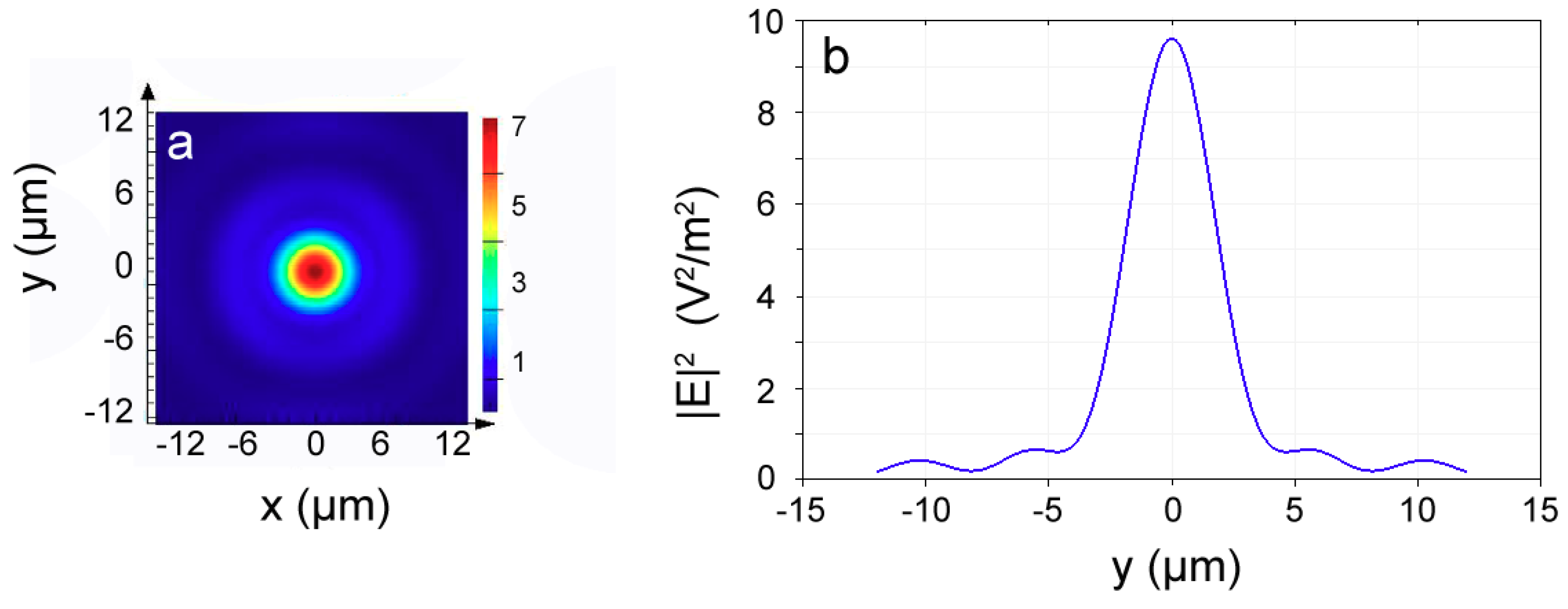
2.2. Optical Trapping of Particles with the Metalens
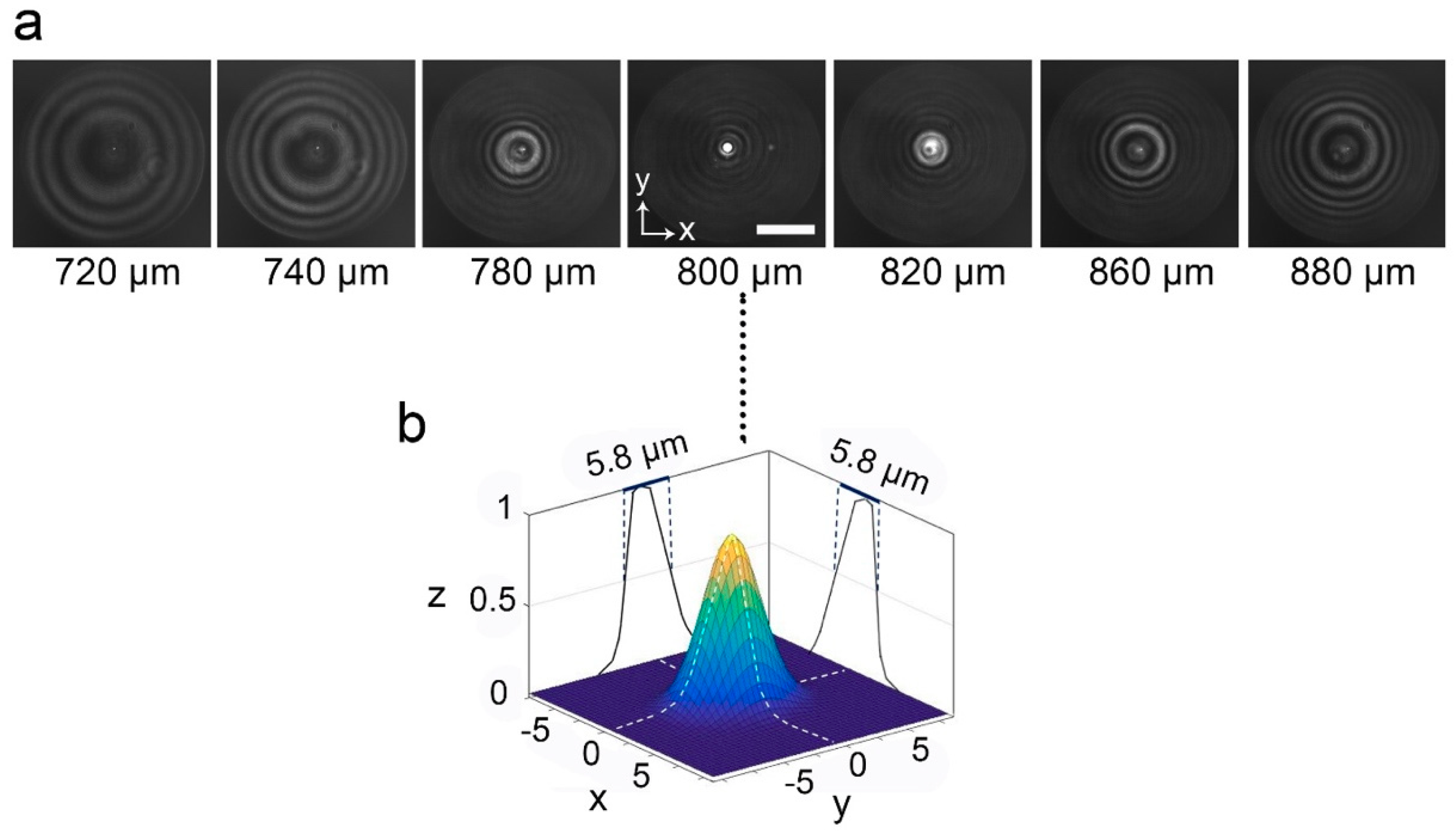
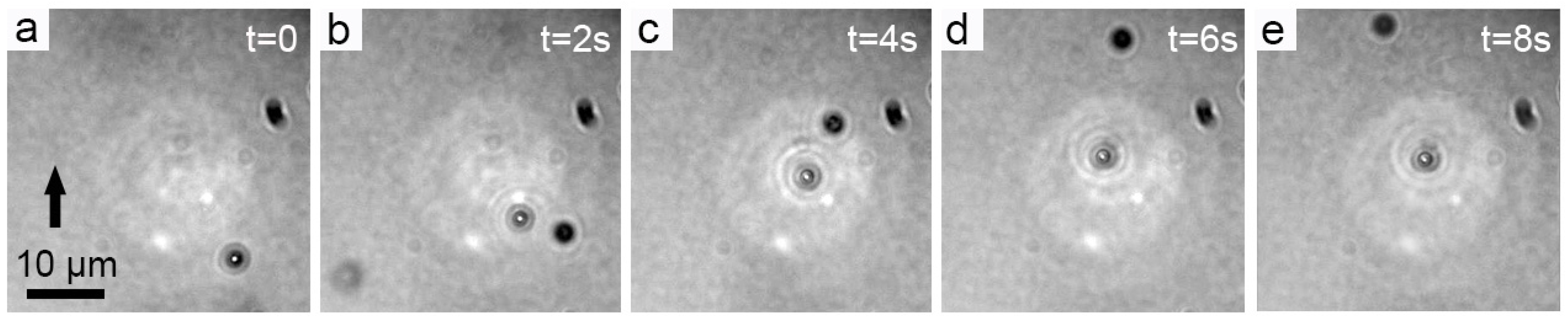
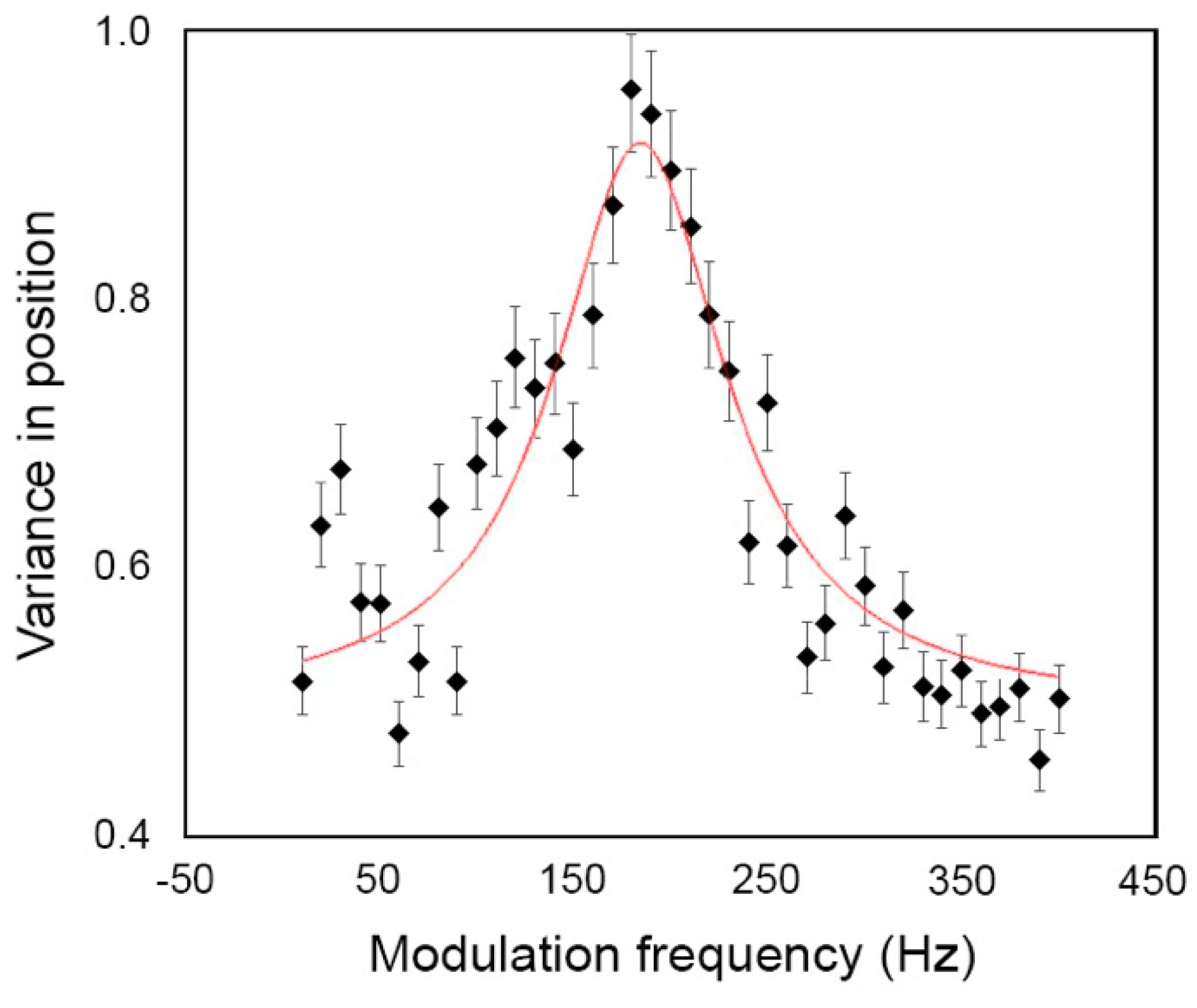
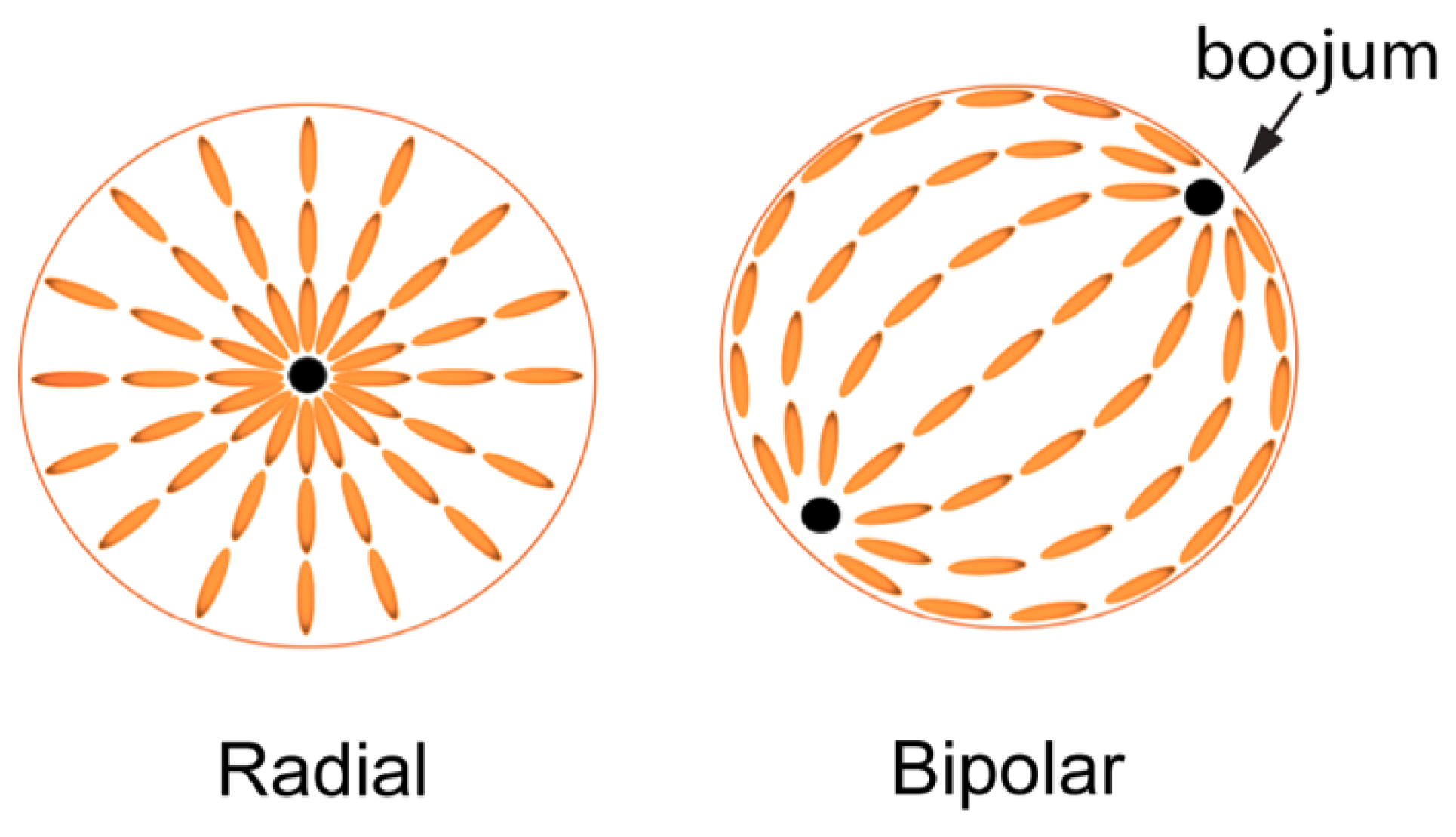
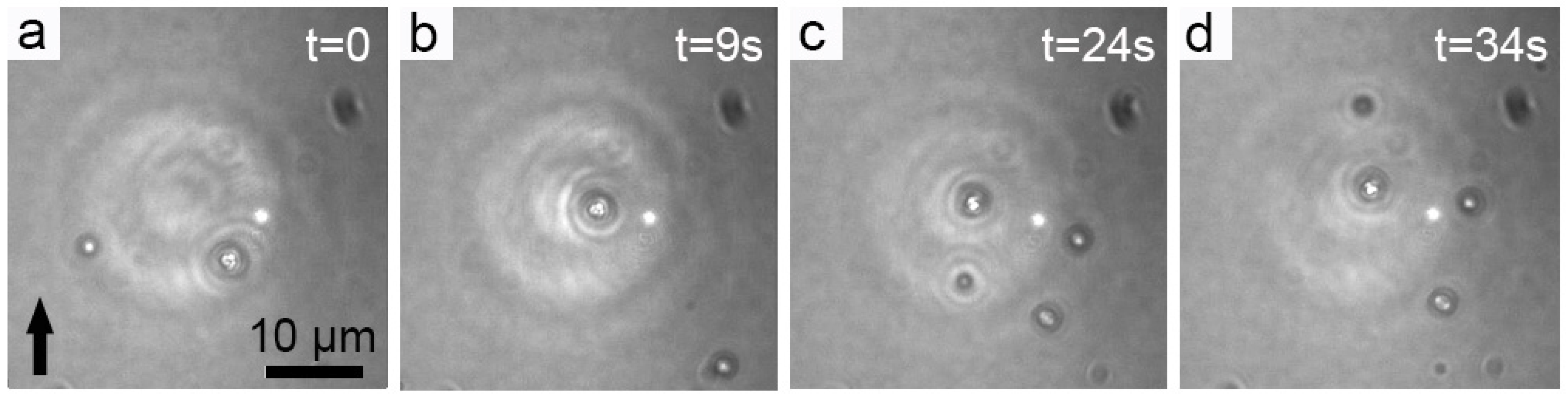
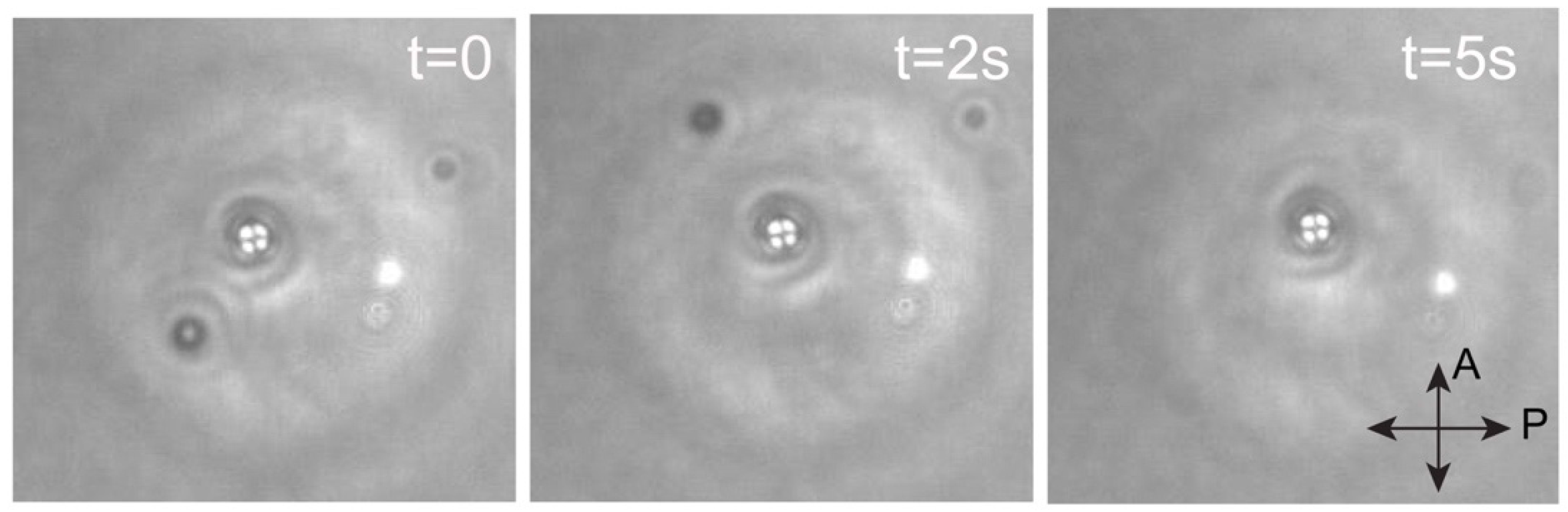
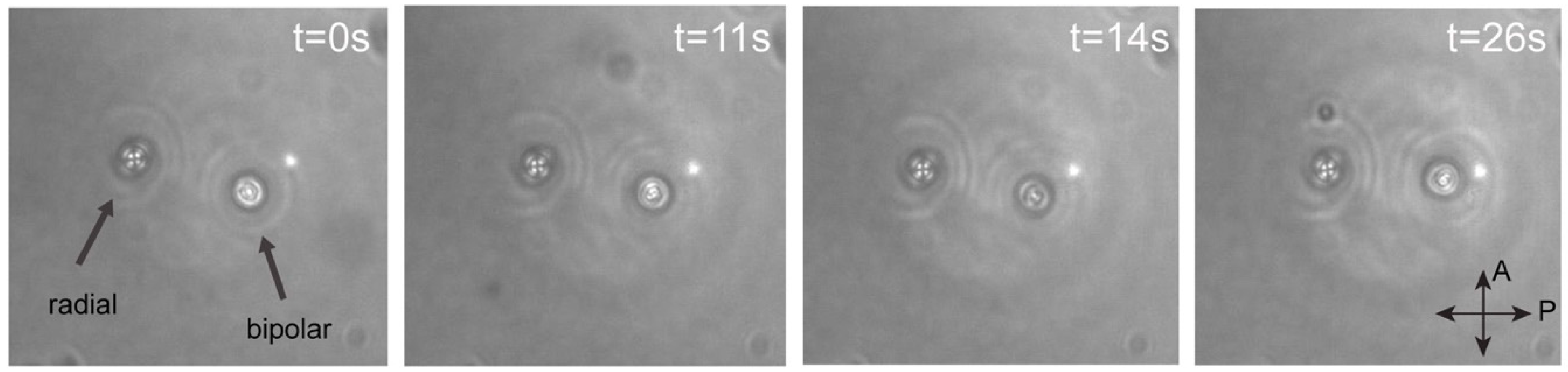
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Edwards, B.; Alù, A.; Silveirinha, M.G.; Engheta, N. Experimental verification of plasmonic cloaking at microwave frequencies with metamaterials. Phys. Rev. Lett. 2009, 103, 153901. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.A.; Smith, D.R.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77. [Google Scholar] [CrossRef] [PubMed]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376. [Google Scholar] [CrossRef] [PubMed]
- Dolling, G.; Wegener, M.; Soukoulis, C.M.; Linden, S. Negative-index metamaterial at 780 nm wavelength. Opt. Lett. 2007, 32, 53–55. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Qiu, C.-W.; Zentgraf, T.; Zhang, S. Reversible Three-dimensional focusing of visible light with ultrathin plasmonic flat lens. Adv. Opt. Mater. 2013, 1, 517–521. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Muhlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Qiu, C.-W.; Zhang, S.; Zentgraf, T. Dual-polarity plasmonic metalens for visible light. Nat. Commun. 2012, 3, 1198. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Mueller, J.P.B.; Wang, Q.; Yuan, G.; Antoniou, N.; Yuan, X.-C.; Capasso, F. Polarization-controlled tunable directional coupling of surface plasmon polaritons. Science 2013, 340, 331–334. [Google Scholar]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light propagation with phase discontinuities: Generalized laws of reflection and refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Genevet, P.; Capasso, F.; Aieta, F.; Khorasaninejad, M.; Devlin, R. Recent advances in planar optics: From plasmonic to dielectric metasurfaces. Optica 2017, 4, 139–152. [Google Scholar] [CrossRef]
- Yu, N.; Aieta, F.; Genevet, P.; Kats, M.A.; Gaburro, Z.; Capasso, F. A broadband, background-free quarter-wave plate based on plasmonic metasurfaces. Nano Lett. 2012, 12, 6328–6333. [Google Scholar] [CrossRef]
- D’Aguanno, G.; Mattiucci, N.; Bloemer, M.; Desyatnikov, A. Optical vortices during a superresolution process in a metamaterial. Phys. Rev. A 2008, 77, 043825. [Google Scholar] [CrossRef]
- Yin, X.; Ye, Z.; Rho, J.; Wang, Y.; Zhang, X. Photonic spin hall effect at metasurfaces. Science 2013, 339, 1405–1407. [Google Scholar] [CrossRef] [PubMed]
- Shitrit, N.; Yulevich, I.; Maguid, E.; Ozeri, D.; Veksler, D.; Kleiner, V.; Hasman, E. Spin-optical metamaterial route to spin-controlled photonics. Science 2013, 340, 724–726. [Google Scholar] [CrossRef] [PubMed]
- Pors, A.; Nielsen, M.G.; Bernardin, T.; Weeber, J.-C.; Bozhevolnyi, S.I. Efficient unidirectional polarization-controlled excitation of surface plasmon polaritons. Light Sci. Appl. 2014, 3, e197. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Helicity dependent directional surface plasmon polariton excitation using a metasurface with interfacial phase discontinuity. Light Sci. Appl. 2013, 2, e70. [Google Scholar] [CrossRef]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190–1194. [Google Scholar] [CrossRef] [PubMed]
- She, A.; Zhang, S.; Shian, S.; Clarke, D.R.; Capasso, F. Large area metalenses: Design, characterization, and mass manufacturing. Opt. Express 2018, 26, 1573–1585. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A.; Dziedzic, J.M.; Yamane, T. Optical trapping and manipulation of single cells using infrared laser beams. Nature 1987, 330, 769–771. [Google Scholar] [CrossRef] [PubMed]
- Friese, M.E.J.; Nieminen, T.A.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optical alignment and spinning of laser-trapped microscopic particles. Nature 1998, 394, 348–350. [Google Scholar] [CrossRef]
- Tkachenko, G.; Stellinga, D.; Ruskuc, A.; Chen, M.; Dholakia, K.; Krauss, T.F. Optical trapping with planar silicon metalenses. Opt. Lett. 2018, 43, 3224. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Dispersionless phase discontinuities for controlling light propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Zhang, F.; Li, Q.; Wu, J.; Wu, L. A high-efficiency dual-wavelength achromatic metalens based on Pancharatnam-Berry phase manipulation. Opt. Express 2018, 26, 34919–34927. [Google Scholar] [CrossRef] [PubMed]
- Walter, F.; Li, G.; Meier, C.; Zhang, S.; Zentgraf, T. Ultrathin nonlinear metasurface for optical image encoding. Nano Lett. 2017, 17, 3171–3175. [Google Scholar] [CrossRef] [PubMed]
- Harada, Y.; Asakura, T. Radiation forces on a dielectric sphere in the Rayleigh scattering regime. Opt. Commun. 1996, 124, 529–541. [Google Scholar]
- Joykutty, J.; Mathur, V.; Venkataraman, V.; Natarajan, V. Direct measurement of the oscillation frequency in an optical-tweezers trap by parametric excitation. Phys. Rev. Lett. 2005, 95, 193902. [Google Scholar] [CrossRef] [PubMed]
- Grier, D.G. A revolution in optical manipulation. Nature 2003, 424, 810–816. [Google Scholar] [CrossRef]
- Murazawa, N.; Juodkazis, S.; Misawa, H. Characterization of bipolar and radial nematic liquid crystal droplets using laser-tweezers. J. Phys. D Appl. Phys. 2005, 38, 2923–2927. [Google Scholar] [CrossRef]
- Phanphak, S.; Pattanaporkratana, A.; Limtrakul, J.; Chattham, N. Precession mechanism of nematic liquid crystal droplets under low power optical tweezers. Ferroelectrics 2014, 468, 114–122. [Google Scholar] [CrossRef]
- Allersma, M.W.; Gittes, F.; deCastro, M.J.; Stewart, R.J.; Schmidt, C.F. Two-dimensional tracking of ncd motility by back focal plane interferometry. Biophys. J. 1998, 74, 1074–1085. [Google Scholar] [CrossRef]
- Byrnes, S.J.; Lenef, A.; Aieta, F.; Capasso, F. Designing large, high-efficiency, high-numerical-aperture, transmissive meta-lenses for visible light. Opt. Express 2016, 24, 5110–5124. [Google Scholar] [CrossRef]
- Lagerwall, J.P.F.; Scalia, G. A new era for liquid crystal research: Applications of liquid crystals in soft matter nano-, bio- and microtechnology. Curr. Appl. Phys. 2012, 12, 1387–1412. [Google Scholar] [CrossRef]
- Lavrentovich, O.D. Topological defects in dispersed words and worlds around liquid crystals, or liquid crystal drops. Liq. Cryst. 1998, 24, 117–126. [Google Scholar] [CrossRef]
- Doane, J.W.; Golemme, A.; West, J.L.; Whitehead, J.B.; Wu, B.G. Polymer dispersed liquid crystals for display application. Mol. Cryst. Liq. Cryst. 1988, 165, 511–532. [Google Scholar] [CrossRef]
- Che, K.-J.; Yang, Y.-J.; Lin, Y.-L.; Shan, Y.-W.; Ge, Y.-H.; Li, S.-S.; Chen, L.-J.; Yang, C.J. Microfluidic generation of cholesteric liquid crystal droplets with an integrative cavity for dual-gain and controllable lasing. Lab Chip 2019, 19, 3116–3122. [Google Scholar] [CrossRef] [PubMed]
- Brasselet, E.; Murazawa, N.; Misawa, H.; Juodkazis, S. Optical vortices from liquid crystal droplets. Phys. Rev. Lett. 2009, 103, 103903. [Google Scholar] [CrossRef] [PubMed]
- Juodkazis, S.; Matsuo, S.; Murazawa, N.; Hasegawa, I.; Misawa, H. High-efficiency optical transfer of torque to a nematic liquid crystal droplet. Appl. Phys. Lett. 2003, 82, 4657–4659. [Google Scholar] [CrossRef]
- Wood, T.A.; Gleeson, H.F.; Dickinson, M.R.; Wright, A.J. Mechanisms of optical angular momentum transfer to nematic liquid crystalline droplets. Appl. Phys. Lett. 2004, 84, 4292–4294. [Google Scholar] [CrossRef]
- Cairns, D.R.; Sibulkin, M.; Crawford, G.P. Switching dynamics of suspended mesogenic polymer microspheres. Appl. Phys. Lett. 2001, 78, 2643–2645. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Suwannasopon, S.; Meyer, F.; Schlickriede, C.; Chaisakul, P.; T-Thienprasert, J.; Limtrakul, J.; Zentgraf, T.; Chattham, N. Miniaturized Metalens Based Optical Tweezers on Liquid Crystal Droplets for Lab-on-a-Chip Optical Motors. Crystals 2019, 9, 515. https://doi.org/10.3390/cryst9100515
Suwannasopon S, Meyer F, Schlickriede C, Chaisakul P, T-Thienprasert J, Limtrakul J, Zentgraf T, Chattham N. Miniaturized Metalens Based Optical Tweezers on Liquid Crystal Droplets for Lab-on-a-Chip Optical Motors. Crystals. 2019; 9(10):515. https://doi.org/10.3390/cryst9100515
Chicago/Turabian StyleSuwannasopon, Satayu, Fabian Meyer, Christian Schlickriede, Papichaya Chaisakul, Jiraroj T-Thienprasert, Jumras Limtrakul, Thomas Zentgraf, and Nattaporn Chattham. 2019. "Miniaturized Metalens Based Optical Tweezers on Liquid Crystal Droplets for Lab-on-a-Chip Optical Motors" Crystals 9, no. 10: 515. https://doi.org/10.3390/cryst9100515
APA StyleSuwannasopon, S., Meyer, F., Schlickriede, C., Chaisakul, P., T-Thienprasert, J., Limtrakul, J., Zentgraf, T., & Chattham, N. (2019). Miniaturized Metalens Based Optical Tweezers on Liquid Crystal Droplets for Lab-on-a-Chip Optical Motors. Crystals, 9(10), 515. https://doi.org/10.3390/cryst9100515





