The Predictive Power of Different Projector-Augmented Wave Potentials for Nuclear Quadrupole Resonance
Abstract
1. Background
2. Methods
2.1. Computational Methods
2.2. Relationship between EFG and NQR Frequencies
2.2.1. Spin-1
2.2.2. Spin-3/2
2.2.3. Spin-5/2
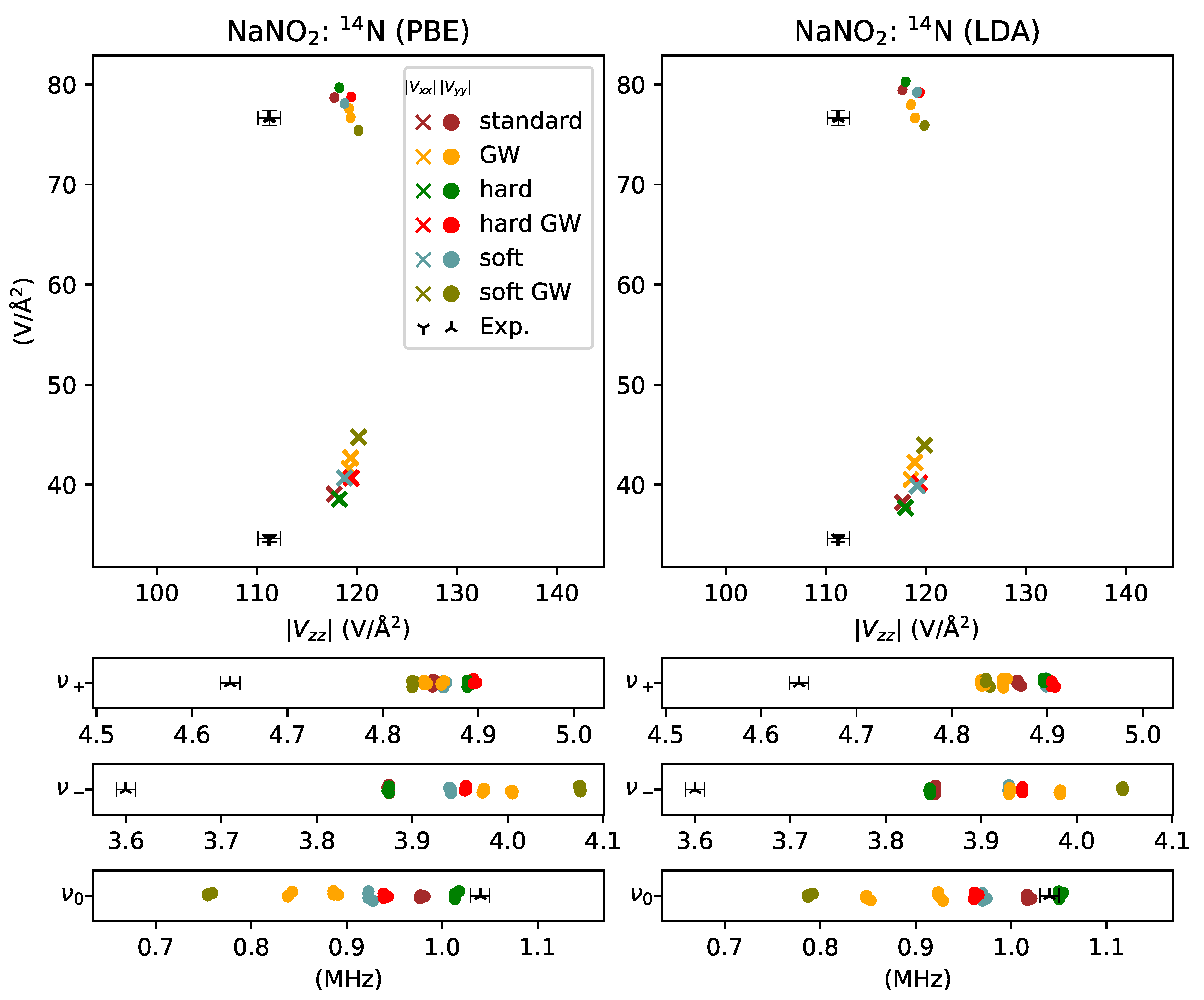
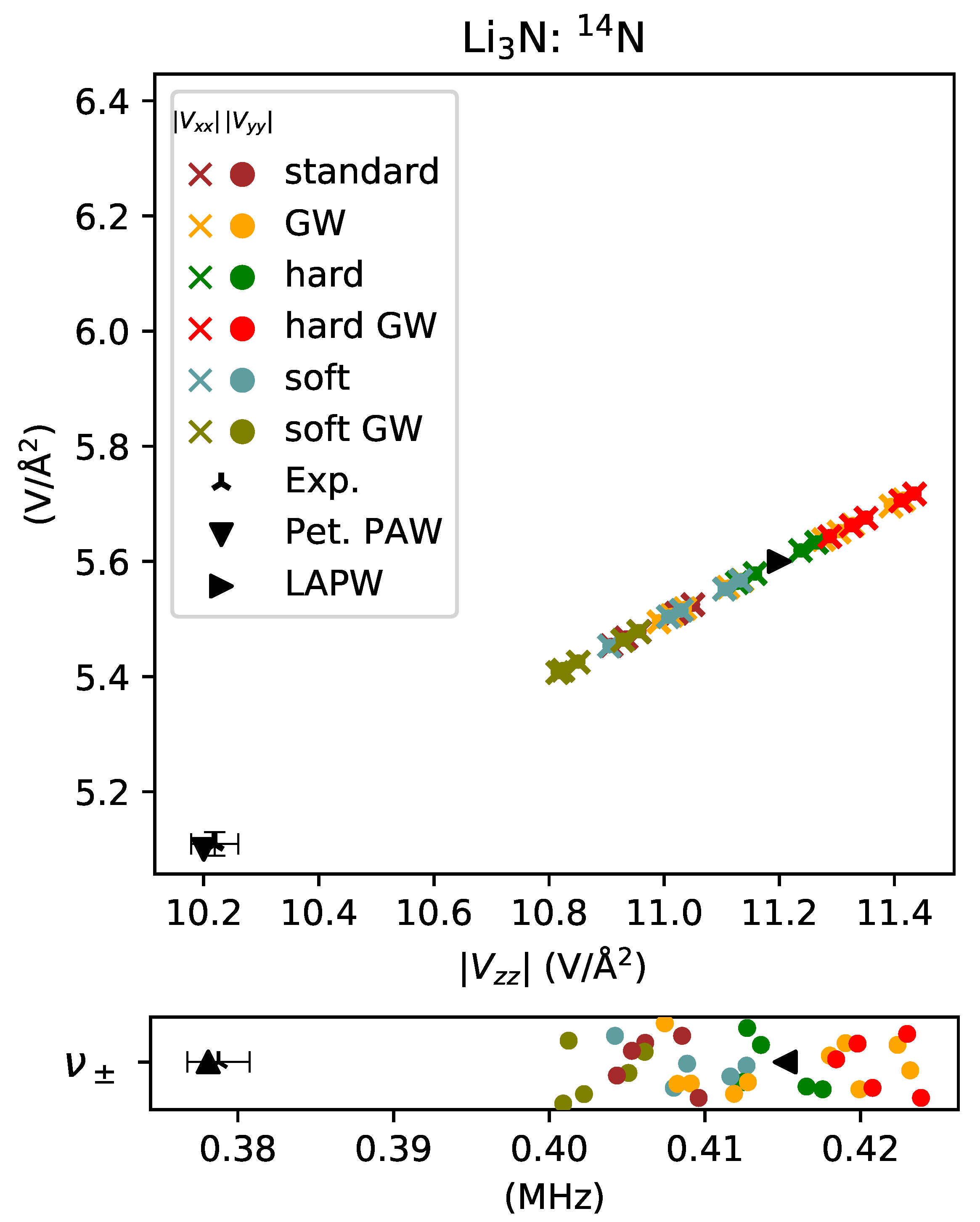
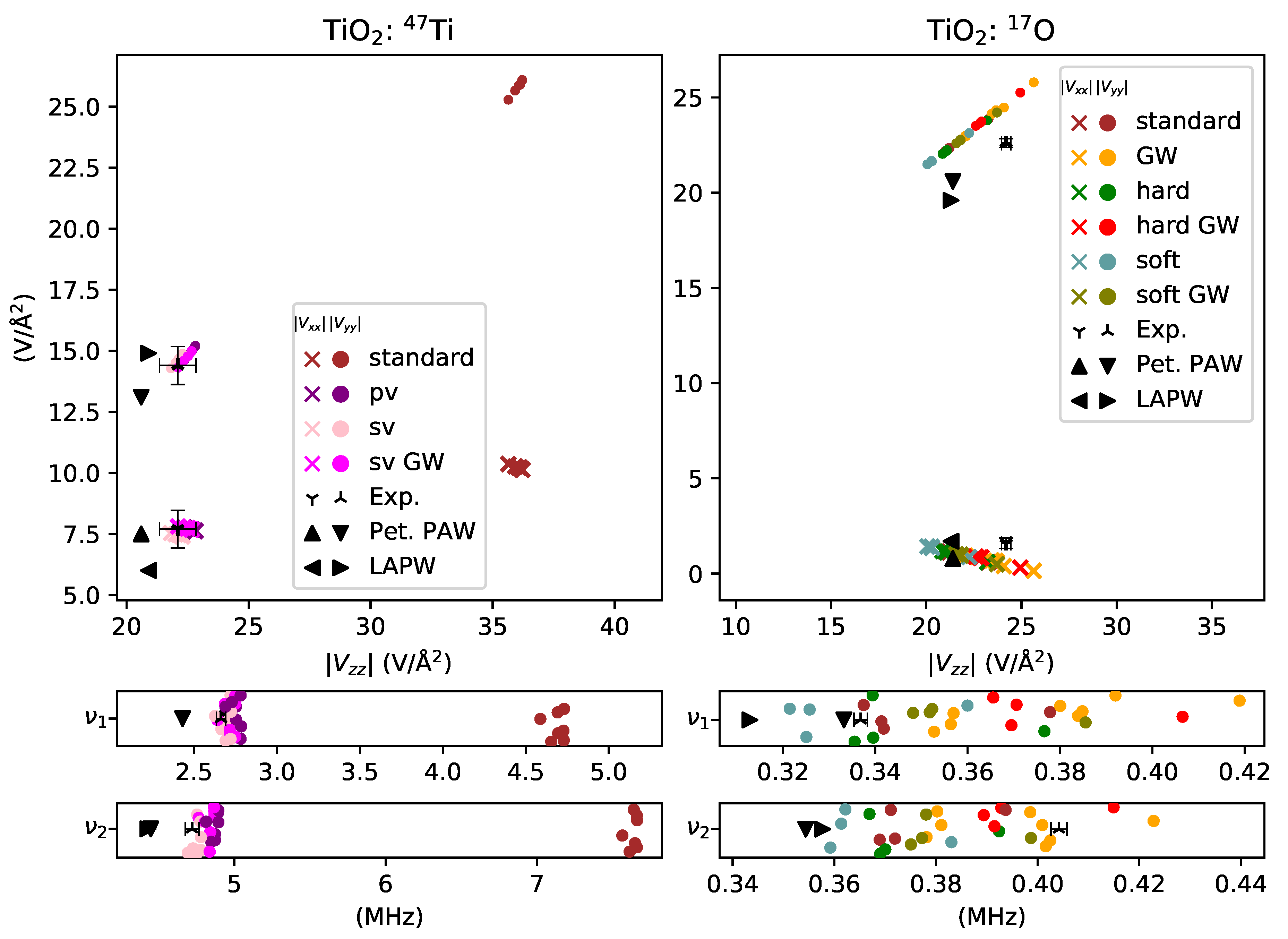
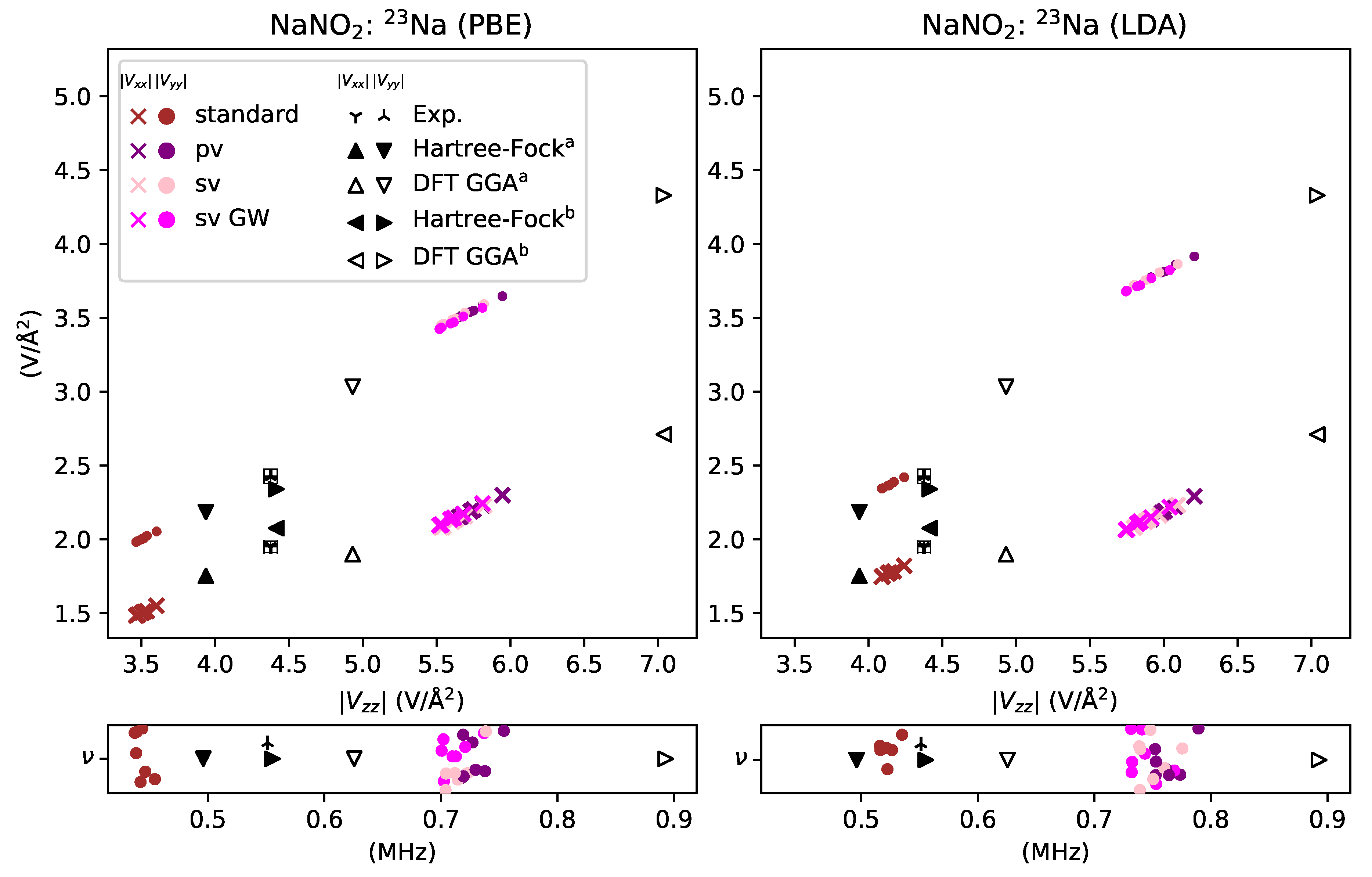
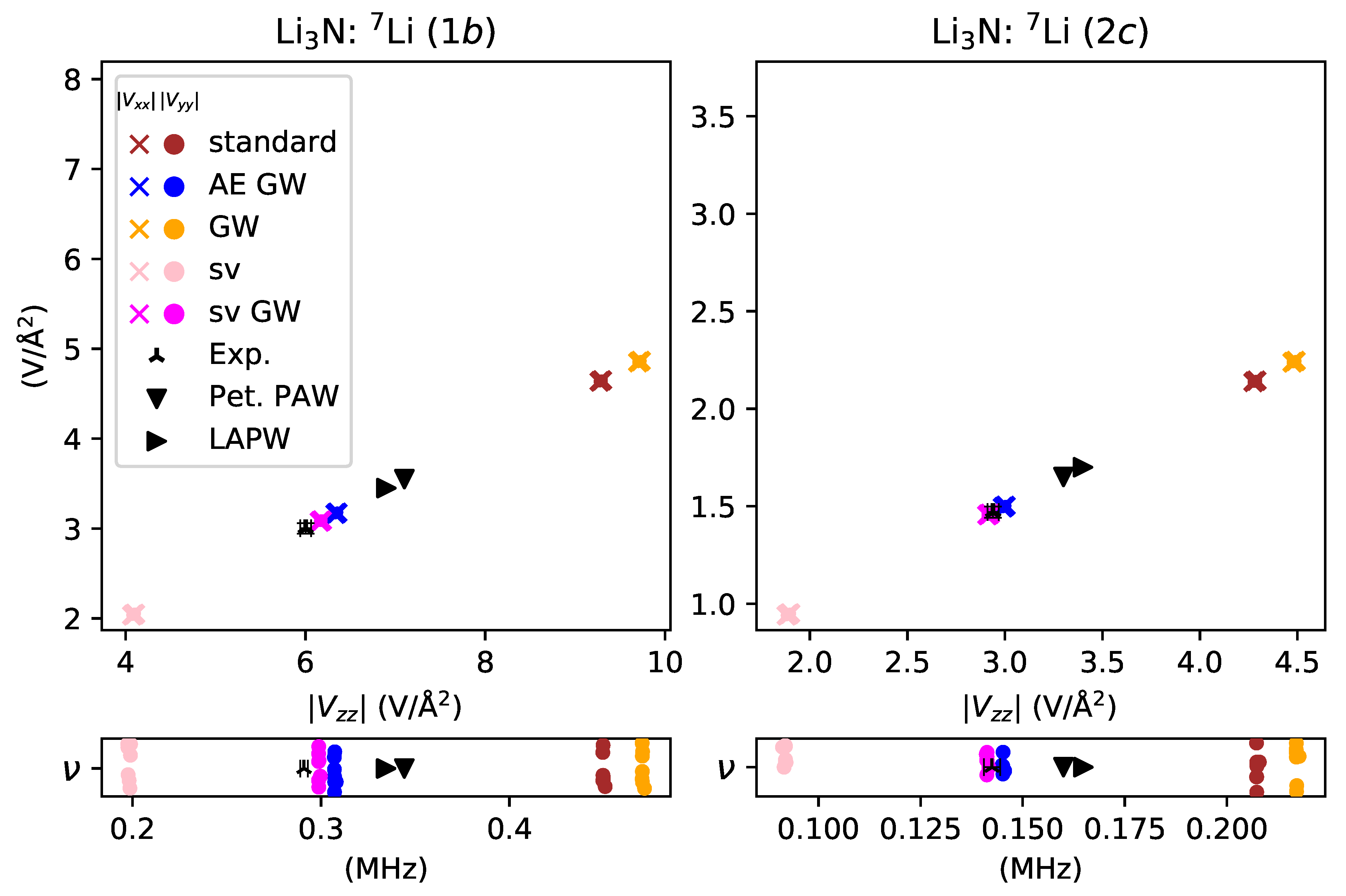
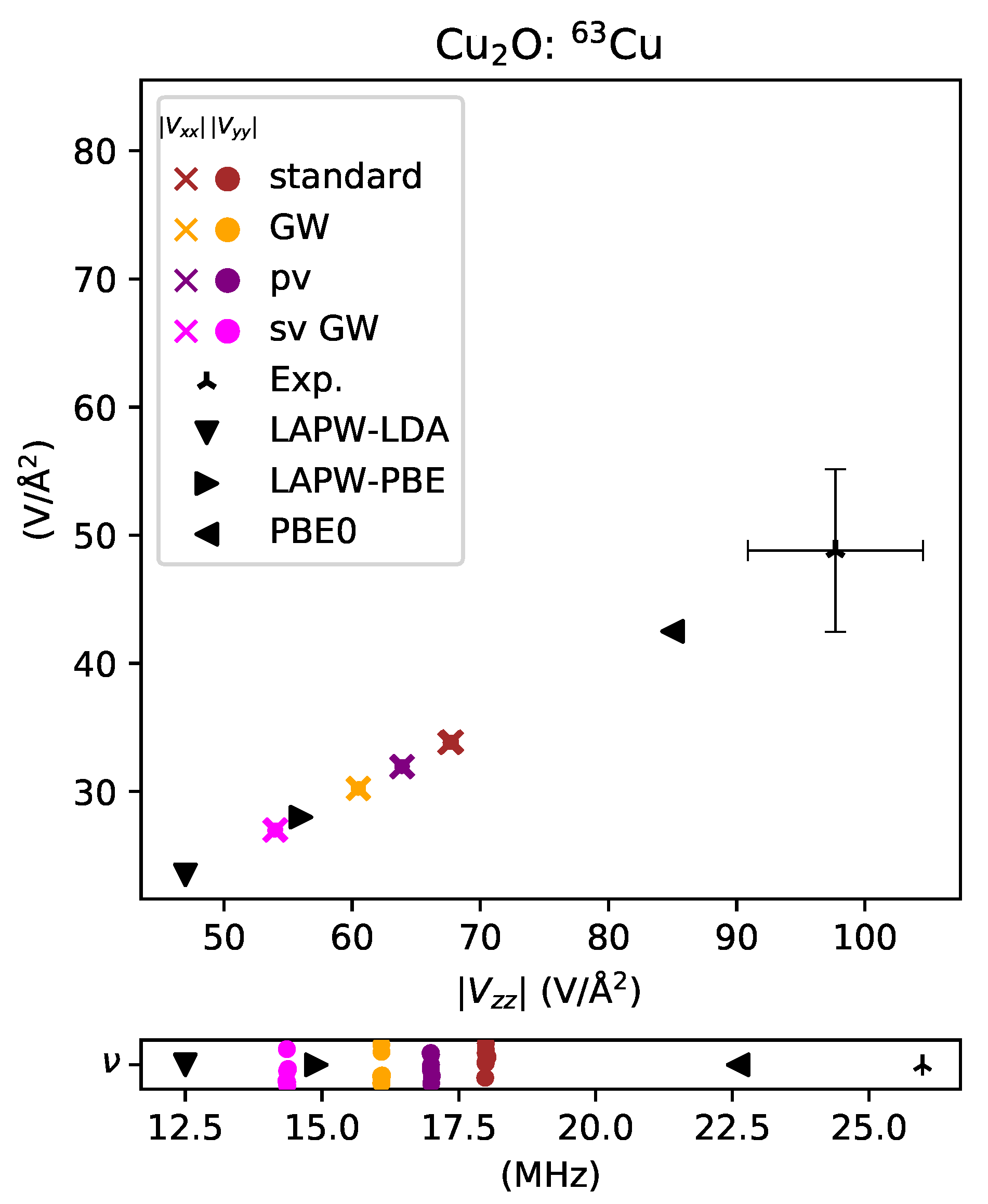
3. Results and Discussion
3.1. Reactive Nonmetals
3.2. Simple Metals
3.3. Transition Metal Elements
4. Conclusions
- overestimated by % for sodium in NaNO2,
- well-predicted, , for titanium in TiO2,
- underestimated by for lithium in Li3N with no other modifications of the potential,
- underestimated by for sodium in NaNO2,
- overestimated by for titanium in TiO2,
- overestimated by for lithium in Li3N.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Suits, B.H. Nuclear quadrupole resonance spectroscopy. In Handbook of Applied Solid State Spectroscopy; Vij, D.R., Ed.; Springer: Boston, MA, USA, 2006; pp. 65–96. [Google Scholar] [CrossRef]
- Poleshchuk, O.; Latosińska, J.; Latosińska, M. Nuclear Quadrupole Resonance, Applications. In Encyclopedia of Spectroscopy and Spectrometry; Academic Press: Cambridge, MA, USA, 2016. [Google Scholar] [CrossRef]
- Seliger, J.; Žagar, V.; Apih, T.; Gregorovič, A.; Latosińska, M.; Olejniczak, G.A.; Latosińska, J.N. Polymorphism and disorder in natural active ingredients. Low and high-temperature phases of anhydrous caffeine: Spectroscopic (1H–14N NMR–NQR/14N NQR) and solid-state computational modelling (DFT/QTAIM/RDS) study. Eur. J. Pharm. Sci. 2016, 85, 18–30. [Google Scholar] [CrossRef]
- Trontelj, Z.; Lužnik, J.; Pirnat, J.; Jazbinšek, V.; Lavrič, Z.; Srčič, S. Polymorphism in Sulfanilamide: 14N Nuclear Quadrupole Resonance Study. J. Pharm. Sci. 2019, 108, 2865–2870. [Google Scholar] [CrossRef] [PubMed]
- Latosińska, J. Nuclear Quadrupole Resonance spectroscopy in studies of biologically active molecular systems—A review. J. Pharm. Biomed. Anal. 2005, 38, 577–587. [Google Scholar] [CrossRef]
- Barras, J.; Althoefer, K.; Rowe, M.D.; Poplett, I.J.; Smith, J.A.S. The Emerging Field of Medicines Authentication by Nuclear Quadrupole Resonance Spectroscopy. Appl. Magn. Reson. 2012, 43, 511–529. [Google Scholar] [CrossRef]
- Grechishkin, V.S.; Sinyavskii, N.Y. New technologies: Nuclear quadrupole resonance as an explosive and narcotic detection technique. Physics-Uspekhi 1997, 40, 393–406. [Google Scholar] [CrossRef]
- Yesinowski, J.P.; Buess, M.L.; Garroway, A.N.; Ziegeweid, M.; Pines, A. Detection of 14N and 35Cl in Cocaine Base and Hydrochloride Using NQR, NMR, and SQUID Techniques. Anal. Chem. 1995, 67, 2256–2263. [Google Scholar] [CrossRef]
- Garroway, A.N.; Buess, M.L.; Miller, J.B.; Suits, B.H.; Hibbs, A.D.; Barrall, G.A.; Matthews, R.; Burnett, L.J. Remote sensing by nuclear quadrupole resonance. IEEE Trans. Geosci. Remote. Sens. 2001, 39, 1108–1118. [Google Scholar] [CrossRef]
- Klanjsek, M.; Zorko, A.; Zitko, R.; Mravlje, J.; Jaglicic, Z.; Biswas, P.K.; Prelovsek, P.; Mihailovic, D.; Arcon, D. A high-temperature quantum spin liquid with polaron spins. Nat. Phys. 2017, 13, 1130 EP. [Google Scholar] [CrossRef]
- Yasuoka, H.; Kubo, T.; Kishimoto, Y.; Kasinathan, D.; Schmidt, M.; Yan, B.; Zhang, Y.; Tou, H.; Felser, C.; Mackenzie, A.P.; et al. Emergent Weyl Fermion Excitations in TaP Explored by 181Ta Quadrupole Resonance. Phys. Rev. Lett. 2017, 118, 236403. [Google Scholar] [CrossRef]
- Ding, Q.P.; Rana, K.; Nishine, K.; Kawamura, Y.; Hayashi, J.; Sekine, C.; Furukawa, Y. Ferromagnetic spin fluctuations in the filled skutterudite SrFe4As12 revealed by 75As NMR-NQR measurements. Phys. Rev. B 2018, 98, 155149. [Google Scholar] [CrossRef]
- Sunami, K.; Iwase, F.; Miyagawa, K.; Horiuchi, S.; Kobayashi, K.; Kumai, R.; Kanoda, K. Variation in the nature of the neutral-ionic transition in DMTTF-QCl4 under pressure probed by NQR and NMR. Phys. Rev. B 2019, 99, 125133. [Google Scholar] [CrossRef]
- Luo, J.; Yang, J.; Zhou, R.; Mu, Q.G.; Liu, T.; Ren, Z.A.; Yi, C.J.; Shi, Y.G.; Zheng, G.Q. Tuning the Distance to a Possible Ferromagnetic Quantum Critical Point in A2Cr3As3. Phys. Rev. Lett. 2019, 123, 047001. [Google Scholar] [CrossRef] [PubMed]
- Blaha, P.; Schwarz, K.; Herzig, P. First-Principles Calculation of the Electric Field Gradient of Li3N. Phys. Rev. Lett. 1985, 54, 1192–1195. [Google Scholar] [CrossRef] [PubMed]
- Petrilli, H.M.; Blöchl, P.E.; Blaha, P.; Schwarz, K. Electric field-gradient calculations using the projector-augmented wave method. Phys. Rev. B 1998, 57, 14690–14697. [Google Scholar] [CrossRef]
- Schwarz, K.; Ambrosch-Draxl, C.; Blaha, P. Charge distribution and electric field gradients in YBa2Cu3O7−x. Phys. Rev. B 1990, 42, 2051–2061. [Google Scholar] [CrossRef] [PubMed]
- Latosińska, J.N. NQR parameters: Electric field gradient tensor and asymmetry parameter studied in terms of density functional theory. Int. J. Quantum Chem. 2003, 91, 284–296. [Google Scholar] [CrossRef]
- Schwerdtfeger, P.; Pernpointner, M.; Nazarewicz, W. Calculation of Nuclear Quadrupole Coupling Constants. In Calculation of NMR and EPR Parameters; John Wiley and Sons: Hoboken, NJ, USA, 2004; Chapter 17; pp. 279–291. [Google Scholar] [CrossRef]
- Errico, L.A.; Rentería, M.; Petrilli, H.M. Augmented wave ab initio EFG calculations: Some methodological warnings. Phys. B Condens. Matter 2007, 389, 37–44. [Google Scholar] [CrossRef]
- Zwanziger, J.W. Computing Electric Field Gradient Tensors. In eMagRes; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous- semiconductor transition in germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef] [PubMed]
- Laskowski, R.; Blaha, P.; Schwarz, K. Charge distribution and chemical bonding in Cu2O. Phys. Rev. B 2003, 67, 075102. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P. Implementation of screened hybrid functionals based on the Yukawa potential within the LAPW basis set. Phys. Rev. B 2011, 83, 235118. [Google Scholar] [CrossRef]
- Koller, D.; Tran, F.; Blaha, P. Merits and limits of the modified Becke-Johnson exchange potential. Phys. Rev. B 2011, 83, 195134. [Google Scholar] [CrossRef]
- Tran, F.; Blaha, P.; Betzinger, M.; Blügel, S. Comparison between exact and semilocal exchange potentials: An all-electron study for solids. Phys. Rev. B 2015, 91, 165121. [Google Scholar] [CrossRef]
- Moore, E.A.; Johnson, C.; Mortimer, M.; Wigglesworth, C. A comparison of ab initio cluster and periodic calculations of the electric field gradient at sodium in NaNO2. Phys. Chem. Chem. Phys. 2000, 2, 1325–1331. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048–5079. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector-augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector-augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Hedin, L. New Method for Calculating the One-Particle Green’s Function with Application to the Electron-Gas Problem. Phys. Rev. 1965, 139, A796–A823. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef] [PubMed]
- Gohda, T.; Ichikawa, M.; Gustafsson, T.; Olovsson, I. The Refinement of the Structure of Ferroelectric Sodium Nitrite. J. Korean Phys. Soc. 1996, 29, 551. [Google Scholar]
- Slichter, C. Principles of Magnetic Resonance; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Sauer, K.L.; Suits, B.H.; Garroway, A.N.; Miller, J.B. Secondary echoes in three-frequency nuclear quadrupole resonance of spin-1 nuclei. J. Chem. Phys. 2003, 118, 5071–5081. [Google Scholar] [CrossRef]
- Differt, K.; Messer, R. NMR spectra of Li and N in single crystals of Li3N: Discussion of ionic nature. J. Phys. C Solid State Phys. 1980, 13, 717–724. [Google Scholar] [CrossRef]
- Pyykkö, P. Year-2017 nuclear quadrupole moments. Mol. Phys. 2018, 116, 1328–1338. [Google Scholar] [CrossRef]
- Graham, R.G.; Riedi, P.C.; Wanklyn, B.M. Pressure dependence of the electric field gradient at the 63Cu nucleus of Cu2O and CuO; implications for the analysis of NQR measurements on high Tc superconductors. J. Phys. Condens. Matter 1991, 3, 135–139. [Google Scholar] [CrossRef]
- Weiss, A. Das Resonanzspektrum des Kernspins von Na23 in Einkristallen von Natriumnitrit, NaNO2. Z. Naturf. A 2014, 15, 536–542. [Google Scholar] [CrossRef][Green Version]
- Pyykkö, P. Year-2008 nuclear quadrupole moments. Mol. Phys. 2008, 106, 1965–1974. [Google Scholar] [CrossRef]
- Gabuthuler, C.; Hundt, E.E.; Brun, E. Magnetic resonance and related phenomena. In Proceedings of the XVIIth Congress AMPERE; Hovi, V., Ed.; North-Holland: Amsterdam, The Netherlands, 1973; p. 499. [Google Scholar]
- Petersen, G.; Bray, P.J. 14N nuclear quadrupole resonance and relaxation measurements of sodium nitrite. J. Chem. Phys. 1976, 64, 522–530. [Google Scholar] [CrossRef]
- The PAW and US-PP Database. Available online: https://www.vasp.at/vasp-workshop/slides/pseudoppdatabase.pdf (accessed on 31 July 2019).
- Paier, J.; Marsman, M.; Hummer, K.; Kresse, G.; Gerber, I.C.; Ángyán, J.G. Screened hybrid density functionals applied to solids. J. Chem. Phys. 2006, 124, 154709. [Google Scholar] [CrossRef] [PubMed]
- Kushida, T.; Benedek, G.B.; Bloembergen, N. Dependence of the Pure Quadrupole Resonance Frequency on Pressure and Temperature. Phys. Rev. 1956, 104, 1364–1377. [Google Scholar] [CrossRef]
| Chemical Formula | Spacegroup | a | b | c | x | |||
|---|---|---|---|---|---|---|---|---|
| Cu2O [16] | Pn-3m | 4.252 | 4.252 | 4.252 | 90 | 90 | 90 | |
| TiO2 [16] | P4/mnm | 4.594 | 4.594 | 2.959 | 90 | 90 | 90 | 0.305 |
| Li3N [16] | P6/mmm | 3.641 | 3.641 | 3.872 | 90 | 90 | 120 | |
| NaNO2 [37] | Im2m | 3.5653 | 5.5728 | 5.3846 | 90 | 90 | 90 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ansari, J.N.; Sauer, K.L.; Glasbrenner, J.K. The Predictive Power of Different Projector-Augmented Wave Potentials for Nuclear Quadrupole Resonance. Crystals 2019, 9, 507. https://doi.org/10.3390/cryst9100507
Ansari JN, Sauer KL, Glasbrenner JK. The Predictive Power of Different Projector-Augmented Wave Potentials for Nuclear Quadrupole Resonance. Crystals. 2019; 9(10):507. https://doi.org/10.3390/cryst9100507
Chicago/Turabian StyleAnsari, Jaafar N., Karen L. Sauer, and James K. Glasbrenner. 2019. "The Predictive Power of Different Projector-Augmented Wave Potentials for Nuclear Quadrupole Resonance" Crystals 9, no. 10: 507. https://doi.org/10.3390/cryst9100507
APA StyleAnsari, J. N., Sauer, K. L., & Glasbrenner, J. K. (2019). The Predictive Power of Different Projector-Augmented Wave Potentials for Nuclear Quadrupole Resonance. Crystals, 9(10), 507. https://doi.org/10.3390/cryst9100507




