1. Introduction
The role of hydrogen bonds in the arrangement of molecules in crystal structures is very well known, and there are numerous early and recent studies describing this kind of interaction [
1,
2,
3]. However also other interactions are crucial in crystal engineering, and the number of studies related to these interactions has significantly increased recently [
4,
5,
6]. The names these interactions are related for the most part to whole groups of periodic systems (for example, tetrel bonds or halogen bonds) or to single elements (hydrogen bonds, lithium bonds, carbon bonds, and others). Such names are usually related to the element or to the group of elements that plays the role of the Lewis acid center [
7,
8]. It has been proven that the mechanisms steering these interactions, for majority of them, can be explained in terms of the σ-hole and π-hole concept; thus, these interactions are usually classified as σ-hole bonds and π-hole bonds [
5,
6,
7].
Recently, the name “triel bond” was introduced for interactions involving the 13th group of elements acting as Lewis acid centers with electron rich sites [
9,
10]. It has also been pointed out that the Lewis acid site of the triel center, usually the region with the positive electrostatic potential, is not classified as the σ-hole; it is rather the π-hole. Thus, the triel bond is a type of π-hole bond. However, triel bonds with a σ-hole triel area acting as the Lewis acid site have also been considered, and it seems that such interactions may occur.
Different triel trifluorides were considered as the Lewis acid units interacting through the π-holes of triel centers (boron, aluminium, gallium, indium, and thallium) with Lewis base units; individual properties were detected for each triel element [
9]. It has been discussed that trivalent triel centers, which are characterized by hypovalency, often strongly interact with one ligand, leading to tetravalent configurations when the octet rule is obeyed. However, if the trivalent triel center interacts with two ligands, it may lead to hypervalency and the corresponding trigonal bipyramid configuration [
9]; the corresponding structures in crystals have been discussed [
10]. Triel bonds have been compared with other interactions, and it has been found that they are much stronger than their counterparts such as hydrogen bonds, dihydrogen bonds, and halogen bonds [
10]. It was found that triel centers can interact with π-electron systems like acetylene, ethylene, and benzene [
11,
12]; the corresponding crystal structures were analyzed, confirming the existence of triel...π electron interactions [
11,
13].
The interactions of triel centers with σ-electrons, especially with molecular hydrogen, were a subject of early experimental [
14] and theoretical [
15] studies. Three types of triel bond have been specified: interactions with the single-atom Lewis base center, with π-electrons, and with σ-electrons. Similarly the three types of the hydrogen bond occur are labeled A–H...B, A–H...π, and A–H...σ [
16]. The A–H here designates the proton donating bond, B is the Lewis base center, and π and σ refer to the abovementioned electrons.
It has been found that interactions in aluminum complexes are stronger than in their boron analogues [
9]. However, a subsequent strength increase was not observed for complexes with heavier triel elements, such as gallium, thallium, and indium; rather, a slight strength decrease was detected for these in comparison with the aluminum species, especially for indium complexes [
9]. In the case of σ-hole bonds, a clear tendency towards increasing strength of interaction for heavier centers in the same group of elements has been demonstrated in numerous studies [
5,
6].
The goal of this study was partly connected with other analogies between the hydrogen bond and the triel bond. The calculations herein were performed on anionic complexes of 1,8-bis(dichloroboryl)naphthalene and 1,2-bis(dichloroboryl)benzene, which are analogous to protonated sponges [
17,
18]. Protonated 1,8-bis(dimethylamino)naphthalene, with its intramolecular (N...H...N)
+ hydrogen bond, is an example of the latter system [
17]. There are numerous such systems with the proton located between two nitrogen centers; however, other arrangements have also been analyzed, like, for example, protonated sponges with phosphorus Lewis base centers [
19,
20].
The species analyzed here may be classified as the reverse of the protonated sponges, since an anion, hydride or halide, is located between triel atoms that play the role of Lewis acid centers. The BHB
− or BFB
− arrangements are examples of these interactions. These arrangements have been analyzed in previous studies; for example, the synthesis of complexes of 1,8-naphtalenediylbis(dimethylborane) with hydride, fluoride, and hydroxide was performed and accompanied by IR and NMR measurements and X-ray diffraction measurements of the corresponding crystal structures [
21,
22]. There have been other studies, such as, for example, those on the first bis boron chloride chelate, i.e., 1,8-naphtalenediylbis(dichloroborane) chloride [
23], on 1,8-bis(boryl)naphthalene fluorides [
24], and on 1,2-diborylbenzene halides [
25]. The analysis described herein was related to the characterization of such BHB
−, BFB
−, and BClB
− arrangements.
2. Computational Methods
The MP2 method [
26] and the Dunning style aug-cc-pVTZ basis set [
27] (Gaussian16 set of codes [
28]) were applied to perform calculations for chlorides, fluorides, and hydrides of 1,2-bis(dichloroboryl)benzene and 1,8-bis(dichloroboryl)naphthalene (
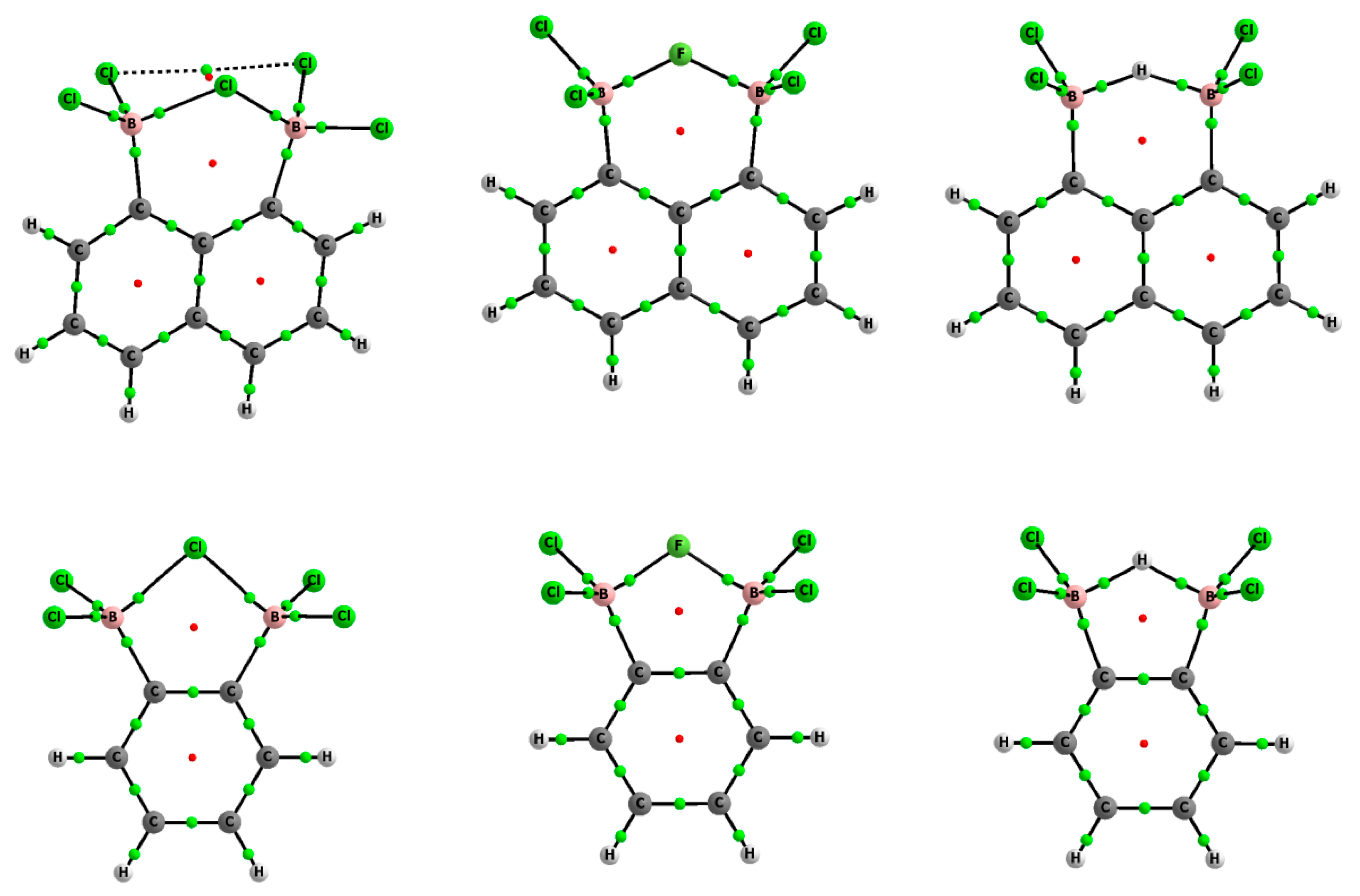
Figure 1 shows molecular graphs of these complexes). Frequency calculations were carried out at the same level as optimizations to confirm that the structures optimized corresponded to the energetic minima.
The interaction energy, E
int, is defined here as the difference between the energy of the complex and the energies of the monomers, with geometries taken from the complex, while for the binding energy, E
bin, the energies of monomers correspond to their optimized geometries [
29]. The E
bin energy differs from E
int by the inclusion of the deformation energy, E
def, (E
bin = E
int + E
def) [
30]. The counterpoise correction approach was applied to calculate the basis set superposition error (BSSE) [
31]. The quantum theory of atoms in molecules (QTAIM) [
32] was applied to analyze bond paths (BPs) and the characteristics of the corresponding bond critical points (BCPs). The AIMAll program [
33] was used to perform QTAIM calculations.
Energy decomposition analysis (EDA) [
34,
35] was carried out using the gradient-corrected functional BP86 [
36,
37] in conjunction with the Grimme dispersion corrections (BP86-D3) [
38], using uncontracted Slater-type orbitals (STOs) [
39] as basis functions for all elements with triple-ζ quality (ADF-basis set TZ2P). The EDA calculations were performed for the complexes analyzed here with the geometries resulting from the optimizations carried out at the same level; the same DFT level frequency calculations were performed to check that the systems corresponded to the energetic minima. The program package ADF2013.01 [
35] was used for the EDA calculations and corresponding optimizations. The interaction energy was partitioned according to the following equation.
where ΔE
elstat corresponds to the electrostatic interaction between the unperturbed charge distributions of the prepared atoms, ΔE
Pauli is the Pauli repulsion, ΔE
orb is the orbital interaction that accounts for charge transfer, and ΔE
disp is the additional dispersion term.
The NBO method [
40,
41] was used to calculate the atomic charges and energies of orbital–orbital interactions. The ADF NBO Version 6.0 [
35,
42] was applied, and the NBO calculations were performed here at the same level as were the decomposition of energies of interaction.
3. Results and Discussion
3.1. Interactions in Complexes of 1,2-Bis(Dichloroboryl)Benzene and 1,8-Bis(Dichloroboryl)Naphthalene with Hydride and Halide Anions
Chlorine substituents at the boron centers were considered for the species calculated here (
Figure 1), since such arrangements often occur in crystal structures.
Table 1 presents the energetic and geometrical parameters of the complexes analyzed here. The calculated interaction and binding energies, E
int and E
bin, respectively, were related to the partitioning of the complex considered into the 1,2-bis(dichloroboryl)benzene or 1,8-bis(dichloroboryl)naphthalene unit and the halide or hydride anion, which is located between boron centers. Thus, two sub-samples can be indicated: complexes of 1,8-bis(dichloroboryl)naphthalene and complexes of 1,2-bis(dichloroboryl)benzene.
Very strong interactions occurred between hydride or halide anions and the remaining part of a complex. For each of the sub-samples, the strength of interaction related to the anion center between boron atoms increased in the order Cl
− < F
− < H
−, since this order is in agreement with the increase of the −E
int and −E
bin values. The difference between E
bin and E
int, the deformation energy, E
def [
7,
30] exceeded 50 kcal/mol for almost all complexes considered (
Table 1); the 1,8-bis(dichloroboryl)naphthalene hydride was the only exception, since E
def amounted here to ~48 kcal/mol. This means that the insertion of an anion between two boron centers leads to great changes of the geometries of neutral 1,2-bis(dichloroboryl)benzene and 1,8-bis(dichloroboryl)naphthalene moieties.
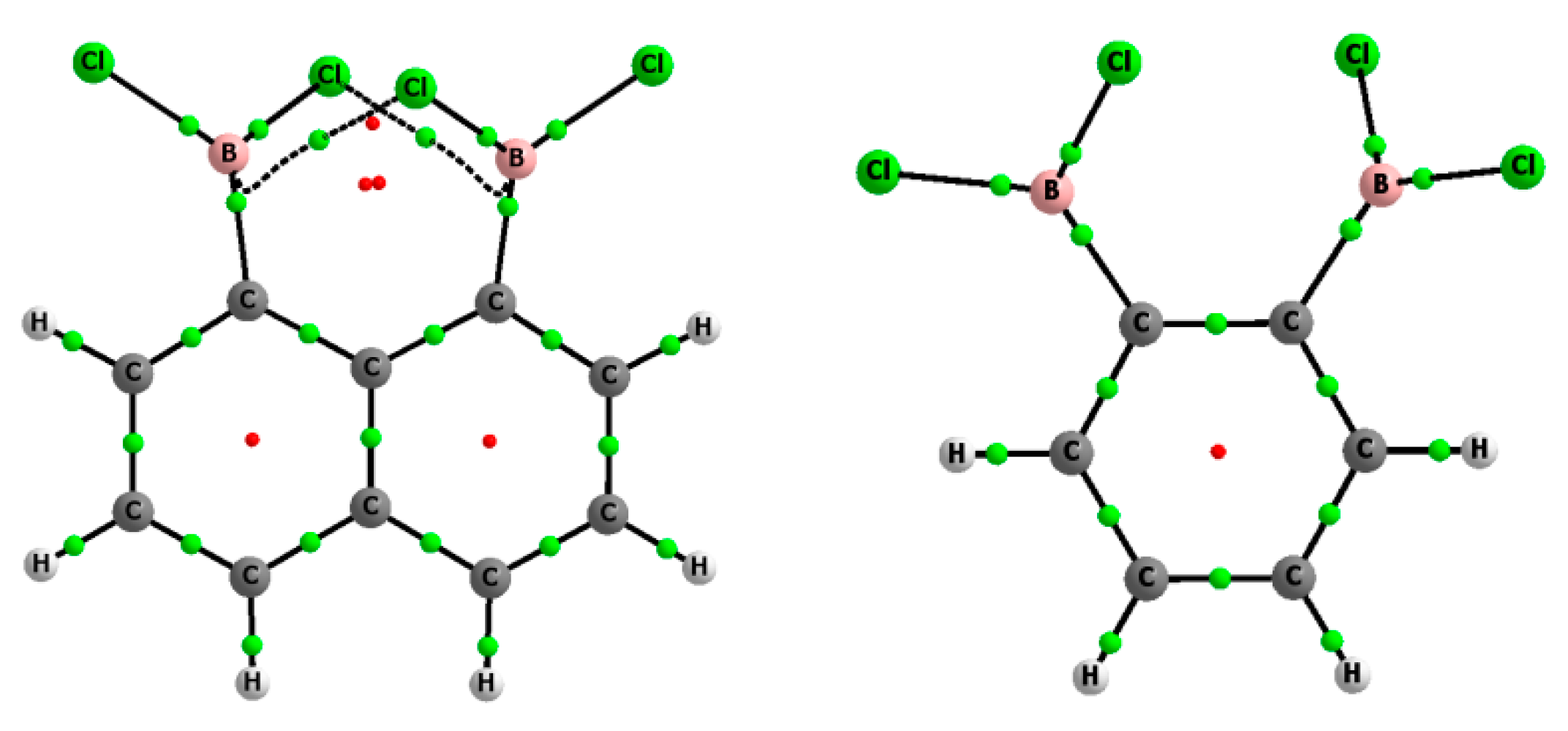
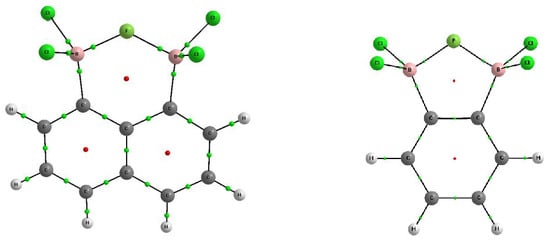
Figure 1 shows the molecular graphs of the complexes analyzed, while
Figure 2 presents the molecular graphs of these neutral moieties. The latter figure shows that the neutral moieties were characterized by the BCl
2 groups being “twisted” against each other, probably mainly due to the repulsion between chlorine substituents. The insertion of anions between BCl
2 groups leads to large geometrical changes, since in complexes, these groups are perpendicular or nearly so to the plane of the benzene or naphthalene fragment (
Figure 1). These anions stabilize arrangements closely related to tetrahedral structures. For a typical tetrahedron, like in the structure of methane, the H–C–H angles are equal to 109.5°. In the complexes analyzed here (
Figure 1), the Cl–B–Cl angles for the BCl
2 groups fell within the range of 110.5–112.9° (
Table 1). In the case of the neutral species (
Figure 2) the Cl–B–Cl angles of 116.3° and 117.5° were closer to a trigonal structure (where this angle is equal to 120°).
The B…X/H distances in the B–(H/X)–B arrangements were practically equal in these calculated model complexes (X marks a halogen center). Slight difference of 0.005 Å between these distances occurred for 1,8-bis(dichloroboryl)naphthalene fluoride; a greater difference of 0.016 Å was observed for 1,8-bis(dichloroboryl)naphthalene chloride. The B–(H/X)–B angle increased in each group of complexes in the following order of anions inserted between the boron centers: Cl− < F− < H−; thus, it can be seen that these links were closer to linearity for stronger interactions and for smaller anions.
3.2. QTAIM Analysis
The strong interactions expressed by great −E
int and −E
bin values may indicate the covalent character of the B…X/H contacts. The latter supposition was partly supported by the quantum theory of atoms in molecules (QTAIM) analysis [
32], particularly by the characteristics of the corresponding bond-critical points (BCPs;
Table 2). The Laplacian of the electron density at the bond-critical point, ∇
2ρ
BCP, was positive for all BCPs of the B…X/H bond paths. However, the total electron energy density at BCP, H
BCP, was always negative, with values situated between −0.05 and −0.10 au. This meant that all these contacts were treated at least as partially covalent in nature in terms of the QTAIM approach [
43,
44]. The electron density at the BCPs for these contacts amounted to ~0.09 – 0.11 au, which is typical for covalent bonds, where the ρ
BCP is of the order of 0.1 au [
32]. The values of ρ
BCP followed those of −E
int and −E
bin; they increased with the increase of the absolute values of these energies in the sub-groups related to naphthalene and benzene skeleton species.
Table 2 also presents the ellipticities of the links between the central anion (hydride or halide) and the boron center; they were lower for stronger interactions. The latter relationship has been previously observed for hydrogen-bonded systems [
45]; for a typical single covalent bond, the ellipticity is equal to zero [
32]. Another QTAIM parameter, presented in
Table 2, is the delocalization index (DI), which expresses the covalent character of interaction [
46,
47]. According to the DI parameter, the B…H/X interactions in chlorides possessed the most covalent character, while such interactions in fluorides were the least covalent in nature.
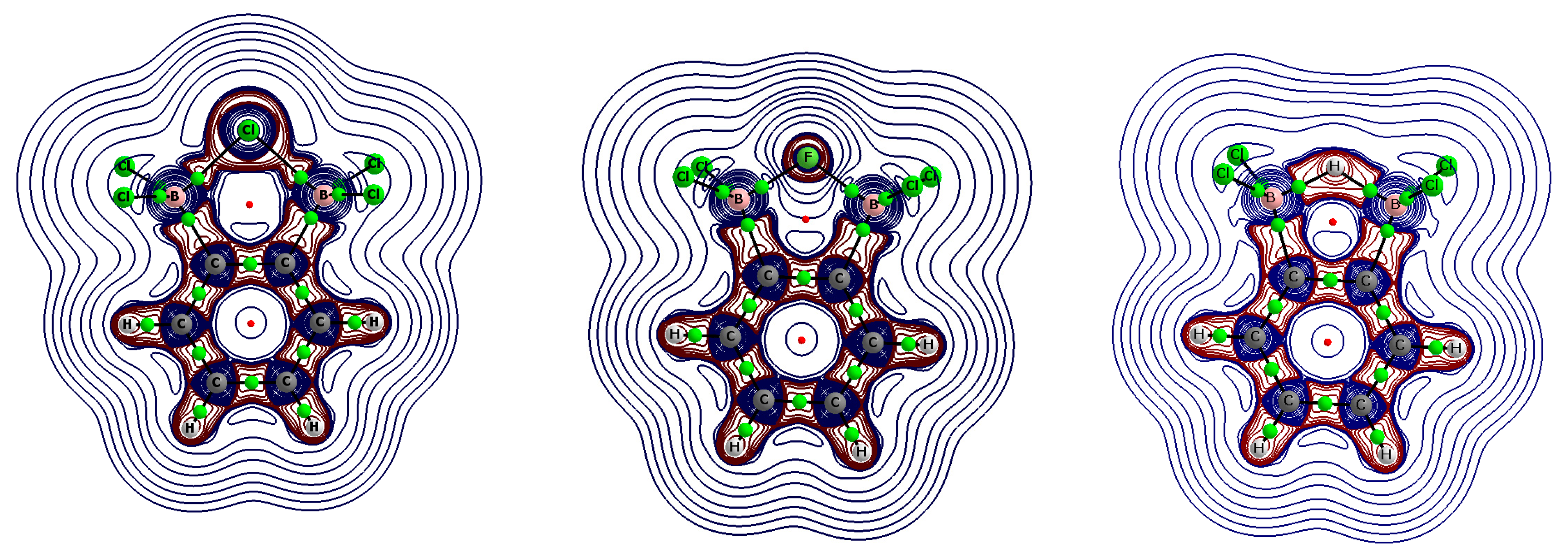
Figure 3 presents the contour maps of the Laplacians of electron density (the Laplacian isolines) for the 1,2-bis(dichloroboryl)benzene complexes to highlight the [B–(H/X)–B]
− region (similar contour maps for this region were observed for the 1,8-bis(dichloroboryl)naphthalene complexes). In the case of a fluoride complex, the spherical electron charge of the anion was only slightly deformed due to its interactions with the boron centers. In the case of chloride and hydride complexes, this deformation was much more visible, since negative Laplacian values were also observed for large regions between the central chloride or hydride anion and the boron atoms. The H/X…B BCPs were, however, located slightly outside these regions of negative Laplacian.
The NBO and QTAIM charges are presented in
Table 3. The NBO atomic charge was calculated from the occupancies of the orbitals related to the atom considered, while for the QTAIM atomic charge, the electron density within the atomic basin was taken into account; in both cases, the charge of the nucleus was also included. It appeared that the NBO atomic charges better corresponded to various chemical reactions and processes related to electron charge shifts between orbitals than the QTAIM charges, where such shifts were accompanied by changes of basins’ volumes.
For the complexes calculated here, in both the NBO and QTAIM approaches, an anion inserted between boron centers lost its electron charge, since there was an electron charge shift from this anion to the remaining parts of the complex. The smallest shift, but still significant, was observed for the fluoride anion, which lost its negative charge to a lesser extent than the hydride and chloride anions. For the latter anions, larger electron density shifts were observed, even for the 1,8-bis(dichloroboryl)naphthalene chloride in which the NBO charge of the chlorine center was close to zero (
Table 3). This was in line with the Laplacian maps presented in
Figure 3. One might then expect that the electrostatic attraction as a part of the interaction between anion and remaining part of the complex is more important for the fluoride complexes than for the hydride and chloride analogues. For the latter, non-fluorine complexes, the interaction energy terms related to the electron charge shifts should be more important.
Figure 1 shows an additional bond path between chlorine atoms in the complex of chloride of 1,8-bis(dichloroboryl)naphthalene while
Figure 2 indicates two bond paths connecting chlorine center with the BCP of the B-C bond in the neutral 1,8-bis(dichloroboryl)naphthalene species. The electron density at corresponding BCP, ρ
BCP, is lower than 0.005 au in all these cases that shows these are negligible interactions. It is rather non-stabilizing Cl…Cl interaction in the first case occurring in the complex. The existence of such energetically non-stabilizing interactions was discussed first time by Mixon and Cioslowski [
48] and that was further a subject of numerous debates and disputes [
49].
It is worth to comment here NBO results concerning the energies of orbital-orbital interactions. For both chlorides of 1,8-bis(dichloroboryl)naphthalene and 1,2-bis(dichloroboryl)benzene the divalent character of chlorine center located between boron atoms is detected in the NBO approach. The polarization of these B-Cl bonds is equal to 76–77% that is the percentage of electron density at the chlorine center. These results indicate the tetravalency of boron centers. The similar situation occurs for the hydrogen center between boron atoms in the complex of hydride of 1,8-bis(dichloroboryl)naphthalene, this center forms covalent bonds with boron atoms according to the NBO approach. For two B-H bonds the percentage of electron density at the hydrogen center amounts 66%. For the hydride of 1,2-bis(dichloroboryl)benzene the 3c-2e (three center – two electrons) B-H-B bond is observed with the percentage of electron density at the hydrogen of 52%.
Only for the 1,8-bis(dichloroboryl)naphthalene and 1,2-bis(dichloroboryl)benzene fluorides the nF → σBCl* overlaps are observed (four for each complex since each boron center forms two B-Cl bonds) with the summed energies of ~7 kcal/mol and 4 kcal/mol, respectively. This is in line with previous results presented here that the fluorine anion does not form covalent bonds with boron centers. The B…F interactions are mostly electrostatic in nature that is also confirmed in the results of next section.
3.3. Decomposition of the Energy of Interaction
To check the suppositions of the last section based on the analysis of QTAIM parameters and the NBO atomic charges, the decomposition of the energy of interaction [
34,
35] was performed for complexes discussed here (
Table 3). This concerns the interaction of the H
− hydride or X
− halide anion with the remaining part of the complex. The results of the energy partitioning concerning the DFT optimizations were calculated with the use of the ADF TZP basis set (see the section on computational details) [
35]. It is worth mentioning that the level of calculations that was chosen for optimizations, and subsequently for the decomposition of energies of interaction, was in good agreement with the level applied earlier in this study, MP2/aug-cc-pVTZ, to analyze these model systems.
Figures S1 and S2 show excellent linear correlations between the MP2 and DFT results of calculations for the B…H/X bond lengths and for the B–(H/X)–B angles, respectively. These bonds and angles, calculated with the use of both methods, are collected in
Table S1 (Supplementary Information, SI).
Table 3 shows that in a case of the fluorine complexes, the electrostatic interaction energy was the most important attractive term. It overwhelmed the orbital energy by 30–31%. The latter interaction energy term expresses electron charge shifts resulting from complexation. In the case of species analyzed here, this complexation concerned an insertion of H
− or X
− anion between boron centers. The dispersion interaction energy term was negligible if compared with other attractive terms. For all complexes analyzed here, not only for fluorine ones, its absolute value is situated between 1.9 kcal/mol and 2.5 kcal/mol. The electrostatic and orbital terms were comparable for chlorine complexes, i.e., for the 1,2-bis(dichloroboryl)benzene and 1,8-bis(dichloroboryl)naphthalene chlorides, while for hydrides, the orbital energy overwhelmed the electrostatic term by 7.3% and 12.2%, respectively.
Table 3 also presents (in parentheses) the percentage contributions to the attractive interaction (in relation to the sum of all attractive interaction terms, i.e., ΔE
elstat + ΔE
orb + ΔE
disp). This clearly showed that the fluorine species were characterized by the most important electrostatic interactions, and that the dispersion energy was rather negligible, in comparison with other attractive terms, for all complexes analyzed here. However, all attractive terms can be treated as a response of the system when considering the Pauli repulsion [
7].
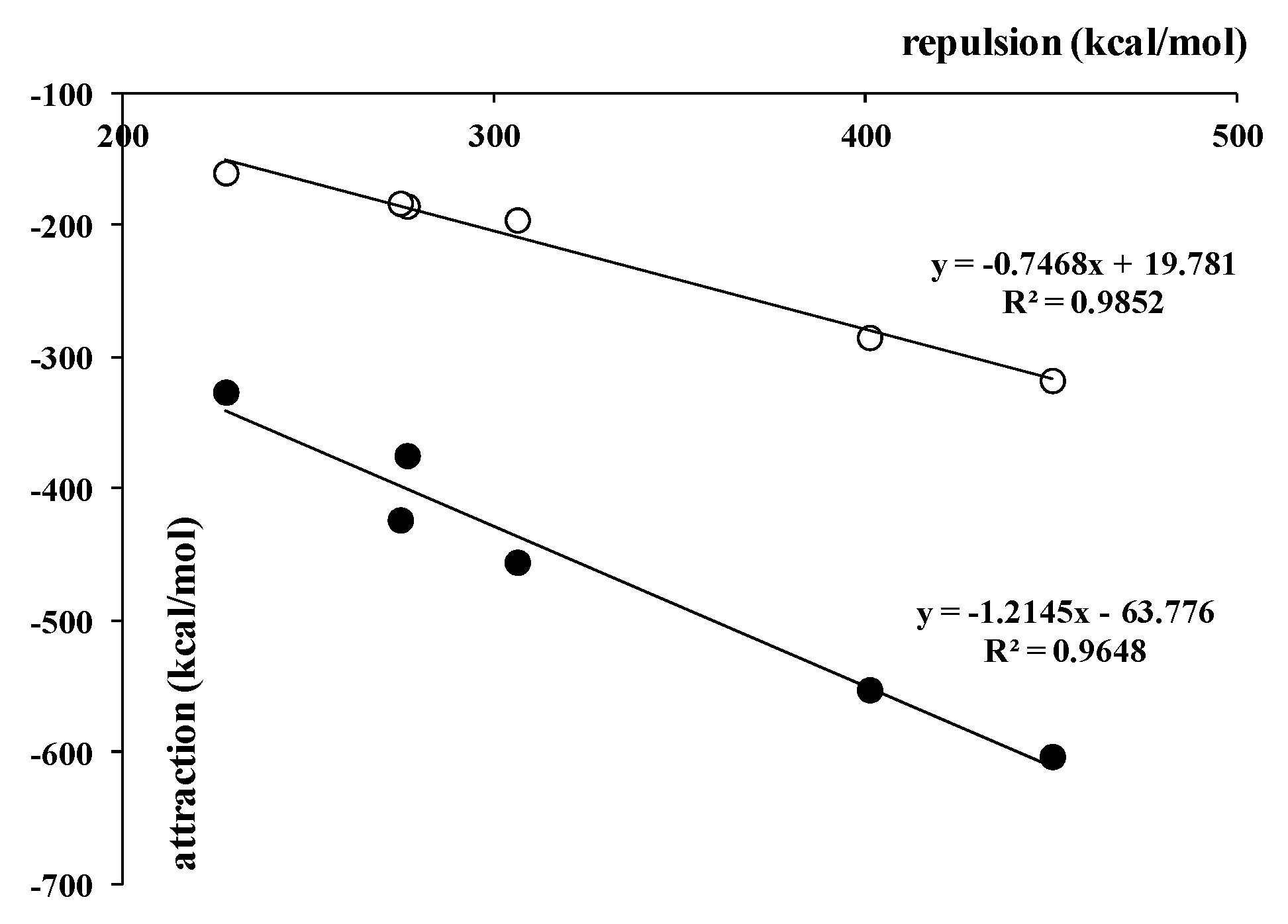
Figure 4 shows a good linear correlation between the repulsion interaction energy term and the sum of all the attractive terms. However, if someone considered only the term related to electron charge shifts, i.e., the orbital energy; thus, this correlation was even slightly better (
Figure 4). It is worth mentioning that for complexes linked by other types of interactions than those analyzed in this study, similar excellent linear correlations were observed. It seems that it is a general feature of attractive interactions: that they may be treated as responses for Pauli repulsion [
7].
3.4. The Crystal Structures of Hydrides and Halides of Diboryl Sponges and Their Analogues
Two classes of compounds were prototypes for the Cambridge Structural Database (CSD) [
50,
51] searches that were performed here: hydrides and halides of 1,2-bis(dichloroboryl)benzene and of 1,8-bis(dichloroboryl)naphthalene. The goal was to find species containing BHB
− arrangements and their halide analogues, BXB
−. These links may be classified as special types of the triel bond.
To extend a sample which would be rather small if restricted to the abovementioned species, not only boron centers were taken into account in these searches, but also their counterparts with other triel atoms, and the central atom within the abovementioned arrangement was expanded to include all halogen atoms, and hydrogen and its deuterium isotopes. Two boron centers were characterized by chlorine substituents in the model systems analyzed in the previous sections; for searches performed relating to these, the triel centers attached to the benzene or naphthalene ring could be connected with any other atoms, not only chlorines. Moreover, H atoms of the benzene and naphtalene skeletons could be replaced by more or less complex substituents.
The results of the searches are presented in
Table S2 (2019 CSD April release). The following conditions for searches were taken into account: exclude structures with unresolved errors, exclude powder structures, R ≤ 10%, no restrictions for e.s.d.s of bond lengths. The aim of these searches was not to present precise geometrical parameters, but rather to show possible structures where this unique type of triel bond can exist. It is worth mentioning that the name “triel bond” here relates to the centers that act as the Lewis acid; thus, these interactions could be formally designated as C–T...H and C–T...X interactions (where T is the triel center). Since for each system there are two links between C–T bonds and the same hydride or halide anion, these interactions could be classified as bifurcated, charge-assisted triel bonds. However, if these interactions were related to the central hydride and halide anions, they could be named hydride and halide bonds, respectively. In spite of the described extensions to the search, there were not many structures found in the CSD. There were only 19 systems characterized by the intramolecular link described above: 9 containing with benzene skeletons and 10 with naphthalene skeletons.
It can be seen (
Table S2) that in the case of structures with naphthalene skeletons, three of the abovementioned links, BHB
−, BFB
−, and BClB
−, were found.
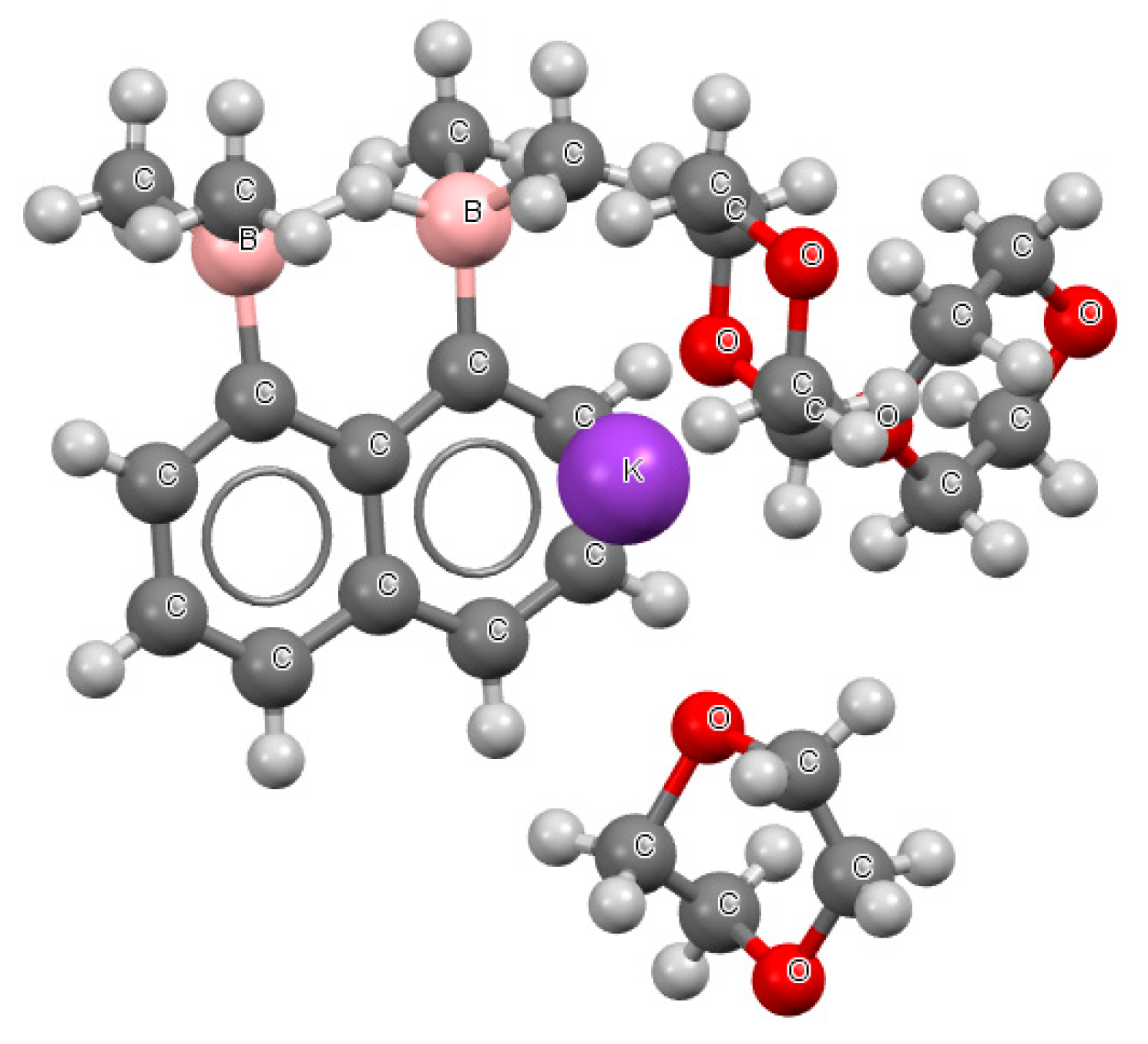
Figure 5 presents a fragment of the crystal structure where the BHB
− system occurred (refcode CUTFUS).
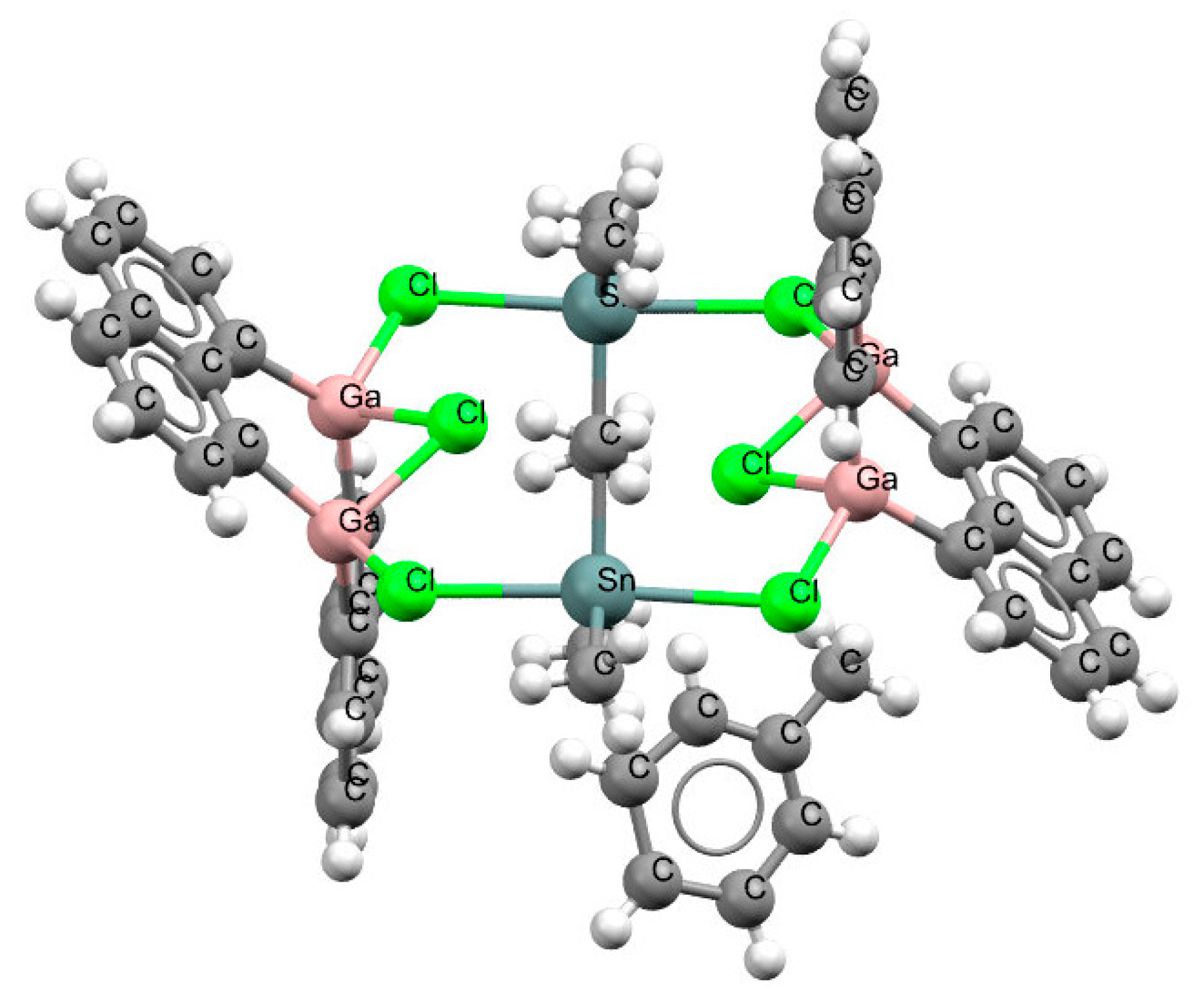
Only one structure was found to contain a naphthalene skeleton and a triel center that was not the boron one. This was the GaClGa
− link observed in the crystal structure of tetrakis (μ
2-1,8-naphthalenediyl)-hexakis(μ
2-chloro)-hexamethyl-tetra-gallium(iii)-di-tin toluene solvate (refcode YIRHIQ).
Figure 6 shows that the chlorine atoms attached to gallium centers were linked with Sn atoms, and a more complex ring was formed that contained Ga, Cl, and Sn centers; this was a twelve-member ring, i.e., containing twelve bonds. The chlorine atoms of the two GaClGa
− arrangements of this ring were located rather far from the Ga…Ga lines, the Ga–Cl–Ga angles were equal to ~77°, and the Ga…Cl distances amounted to 2.37–2.40 Å. However, the high e.s.d. values for bond lengths, which were equal to 0.011–0.030 Å (
Table S3), did not allow precise final conclusions to be drawn concerning these links.
In a case of structures with benzene skeletons, two links containing boron centers, BFB
− and BClB
−, and one structure with an AlClAl
− link, were found. A BHB
− arrangement with a benzene skeleton did not occur.
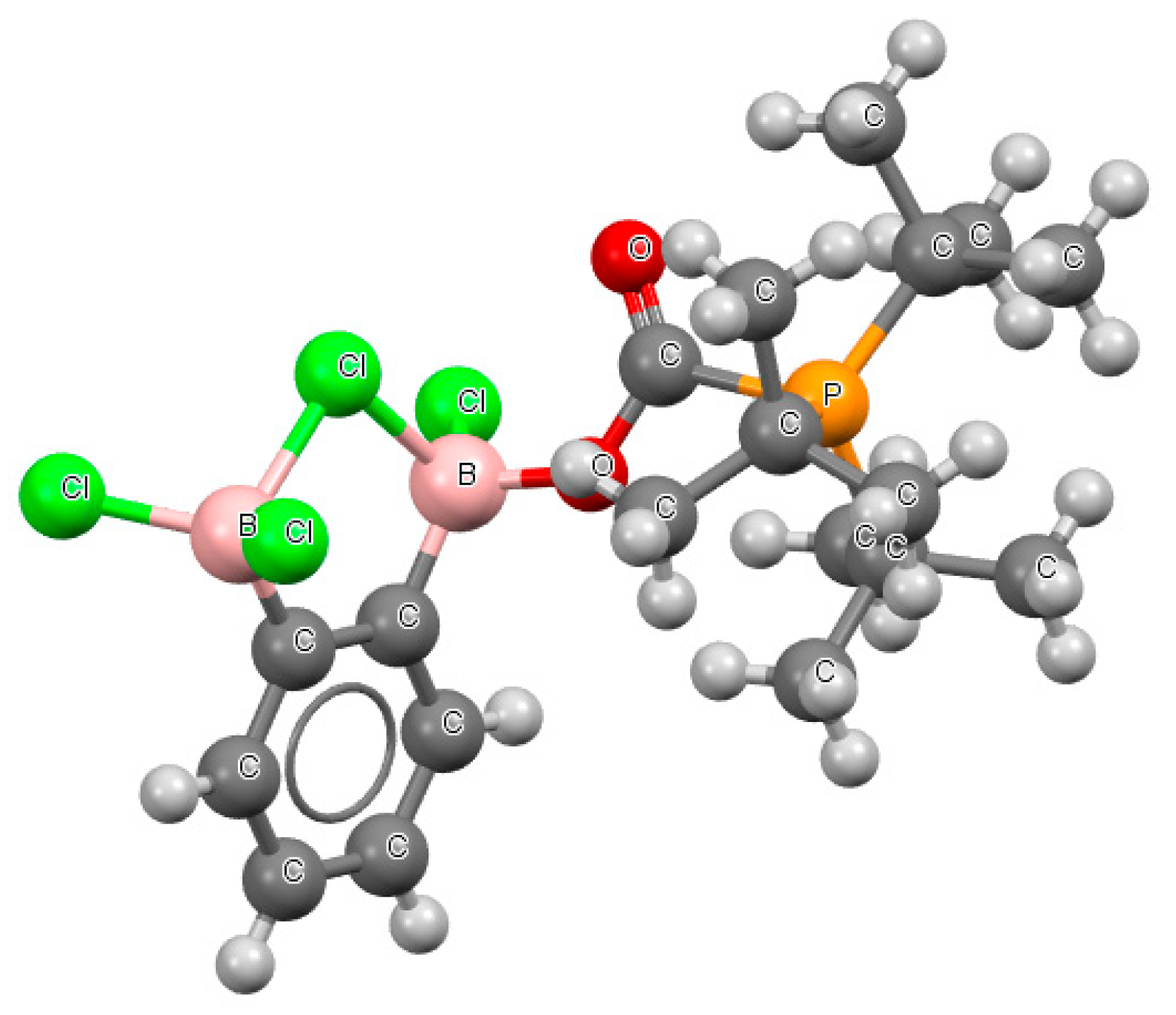
Figure 7 presents a fragment of the crystal structure with the BClB
− arrangement (refcode GAYRUV).
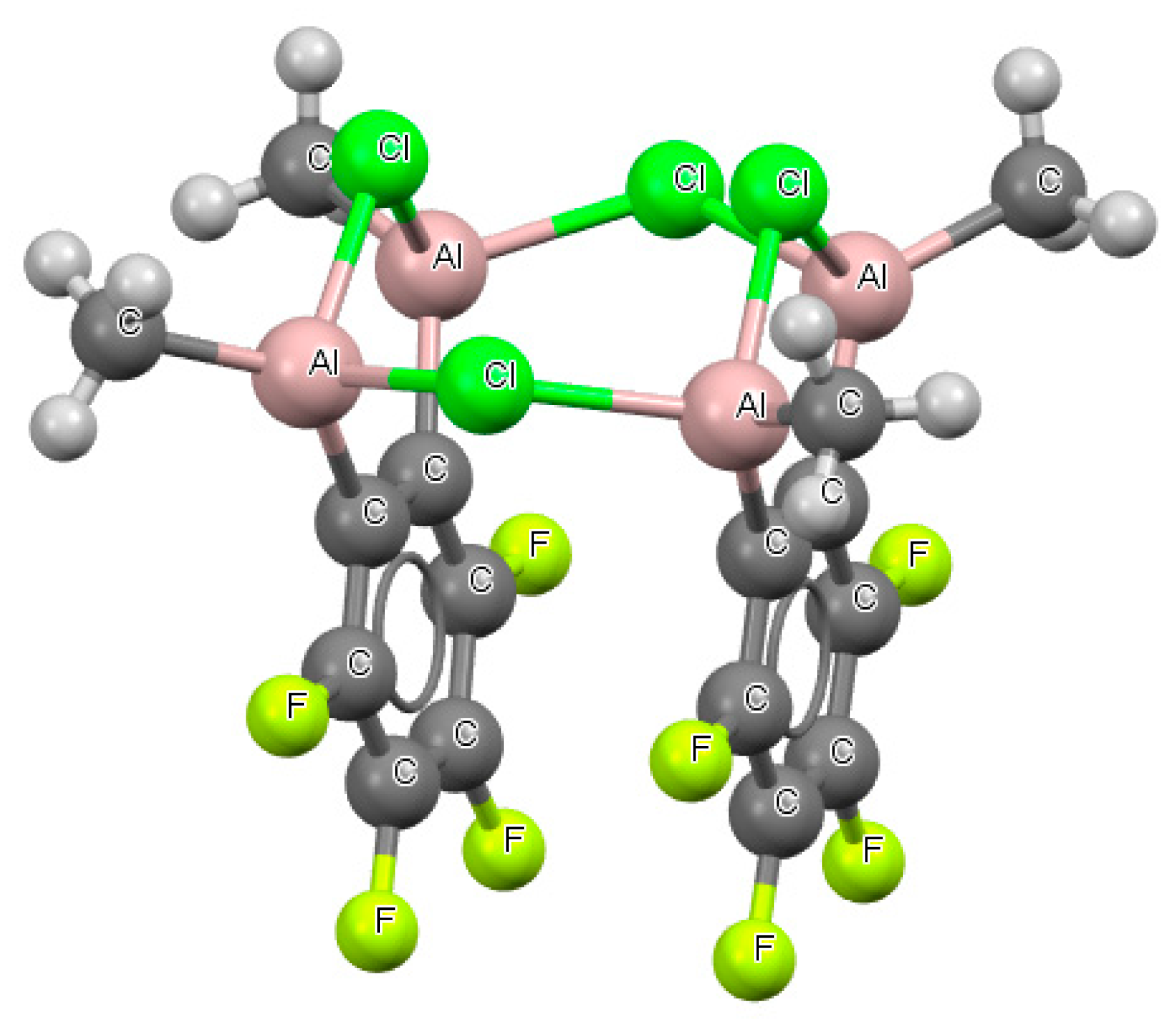
Figure 8 shows the fragment of the crystal structure (refcode GOTNEI) where two AlClAl
− systems occurred, which were connected by chlorine atoms in such a way that an eight-member ring was formed. For the AlClAl
− systems, an angle of 98–99° was observed. For two of these systems, the Cl…Al distances occurring in the crystal structure were almost equal to one another for each of these links (
Table S2).
Disorder was detected for a few of the structures shown in
Table S2. However, it did not influence the geometrical parameters presented in this table, since it concerned neither atoms participating in the THT
− and TXT
− links nor atoms neighboring these links; the FIGRAO structure was the only exception, where the disorder affects the BClB
− arrangement.
Most of the crystal structures discussed in
Table S2 were not characterized by precise geometry;
Table S3 presents the e.s.d.s for the C–C bond lengths of structures collected. However, it seems that the approximate conclusion may be drawn that for links containing benzene skeletons, the central halide or hydride anion is almost equidistant from both triel centers, while for links in structures containing naphtalene skeletons, differences between these distances occur more often.
The searches performed here show that for both samples of structures (i.e., for benzene-skeleton and for naphthalene-skeleton structures), only fluorine and chlorine atoms participate in the TXT
− links discussed in this paper, and that there were not such links containing other halogen atoms—at least, such arrangements were not found in the CSD searches performed here. Structures with a deuterium isotope situated between triel centers were also not found.
Figures S3–S6 show a few other fragments of crystal structures containing links to hydride and halide anions, which were discussed here and are included in
Table S1.