On Plowing Frictional Behavior during Scratch Testing: A Comparison between Experimental and Theoretical/Numerical Results
Abstract
1. Introduction
- (1)
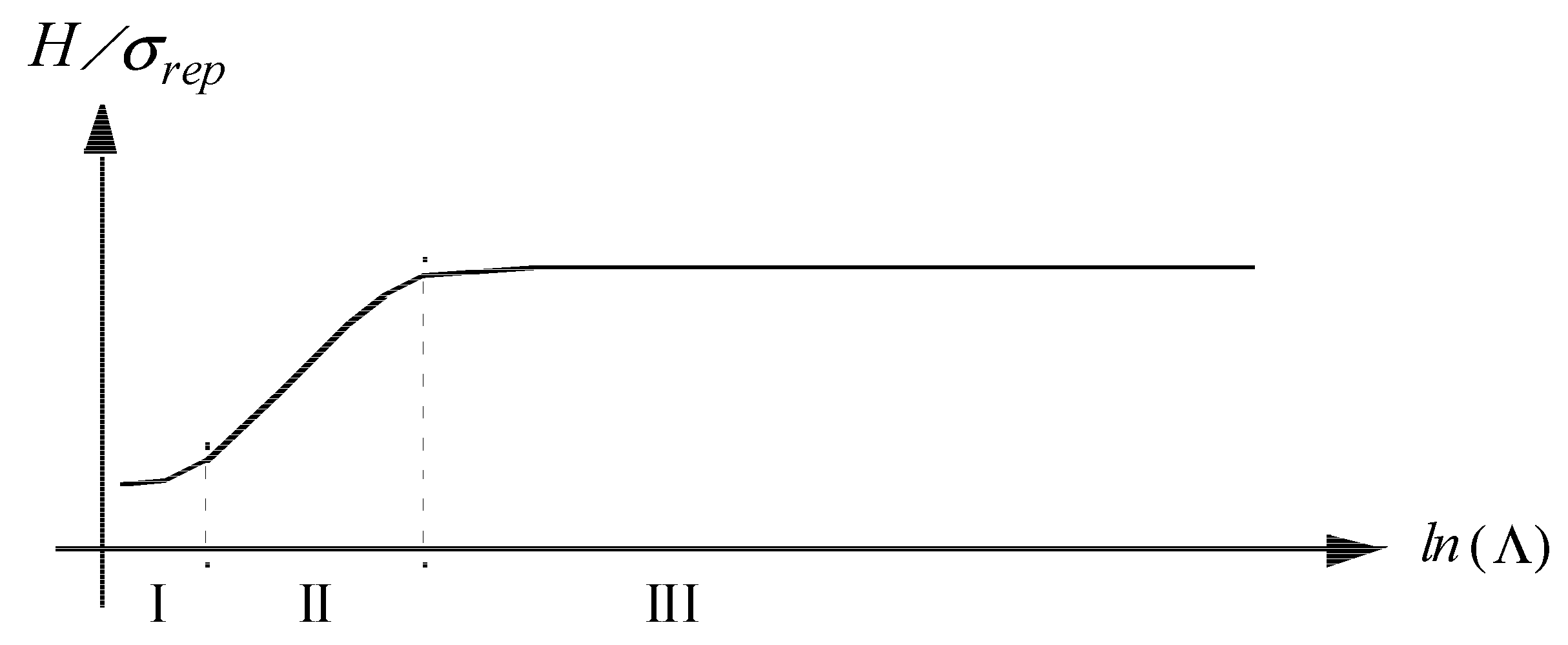
- Level I: Dominating elastic deformations, i.e., low indentation load, where elastic contact analysis is sufficient.
- (2)
- Level II: Elastic and plastic deformations are of equal magnitude.
- (3)
- Level III: Plastic deformations are dominant in the contact region.
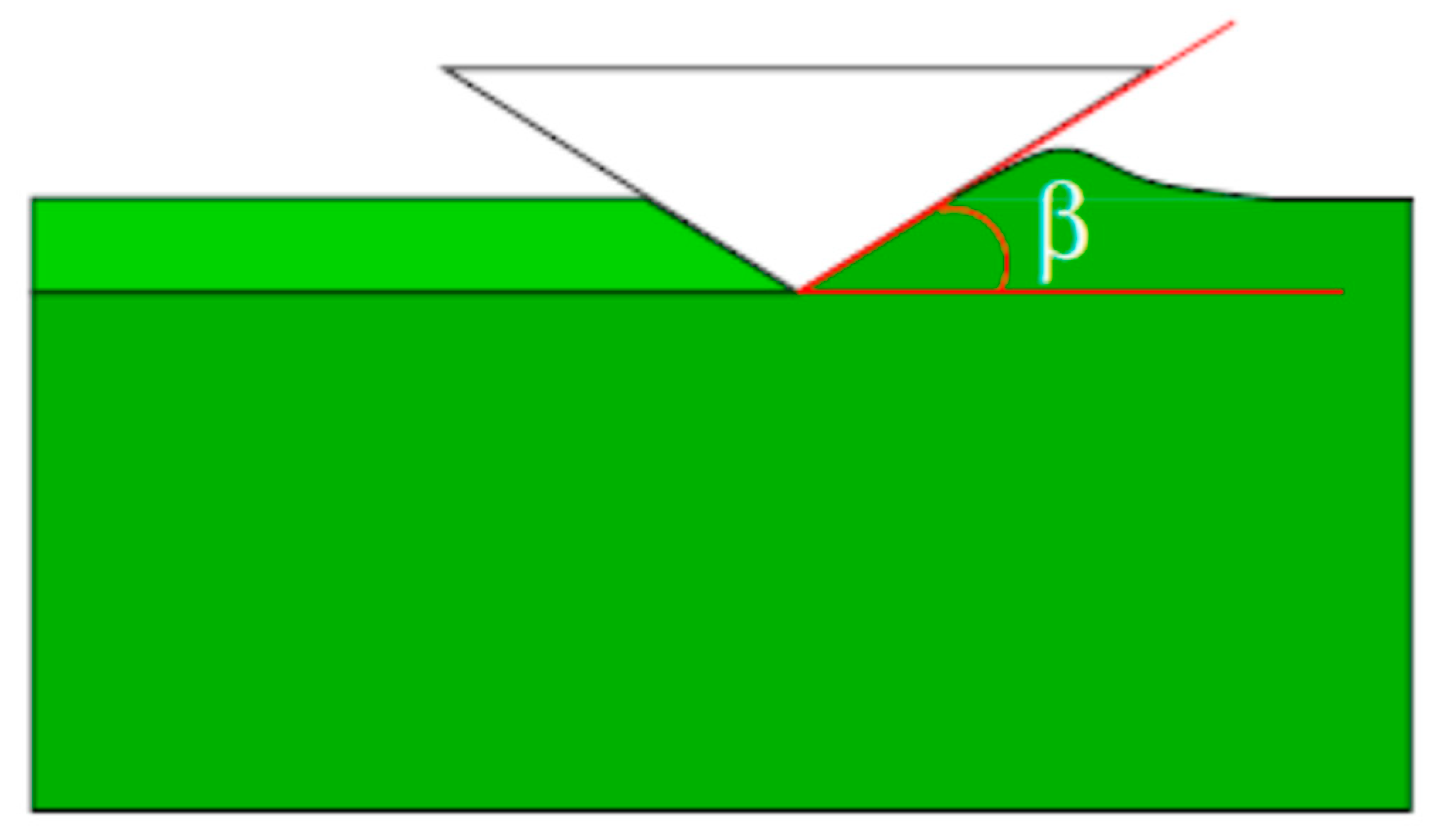
2. Theoretical Background
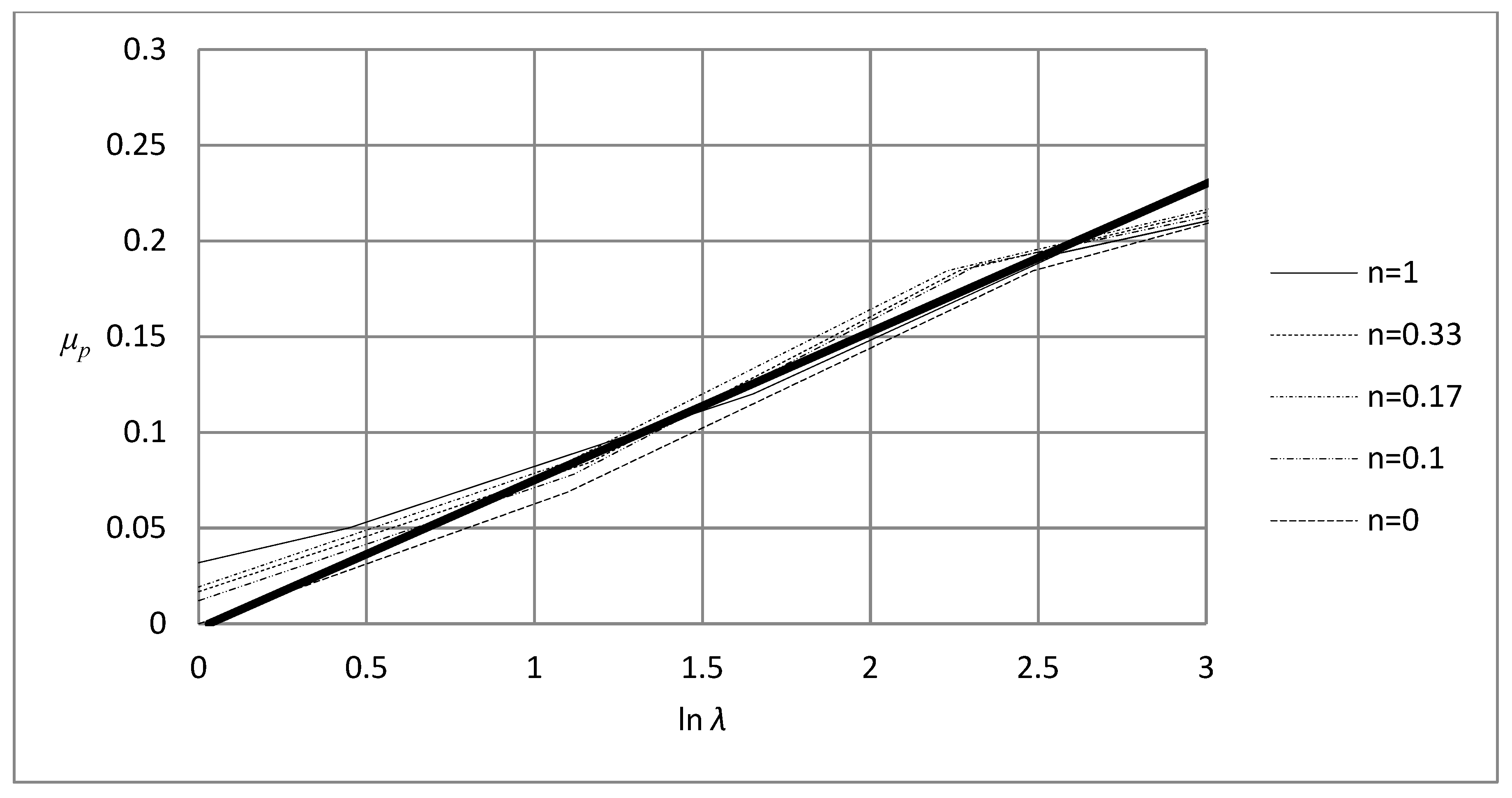
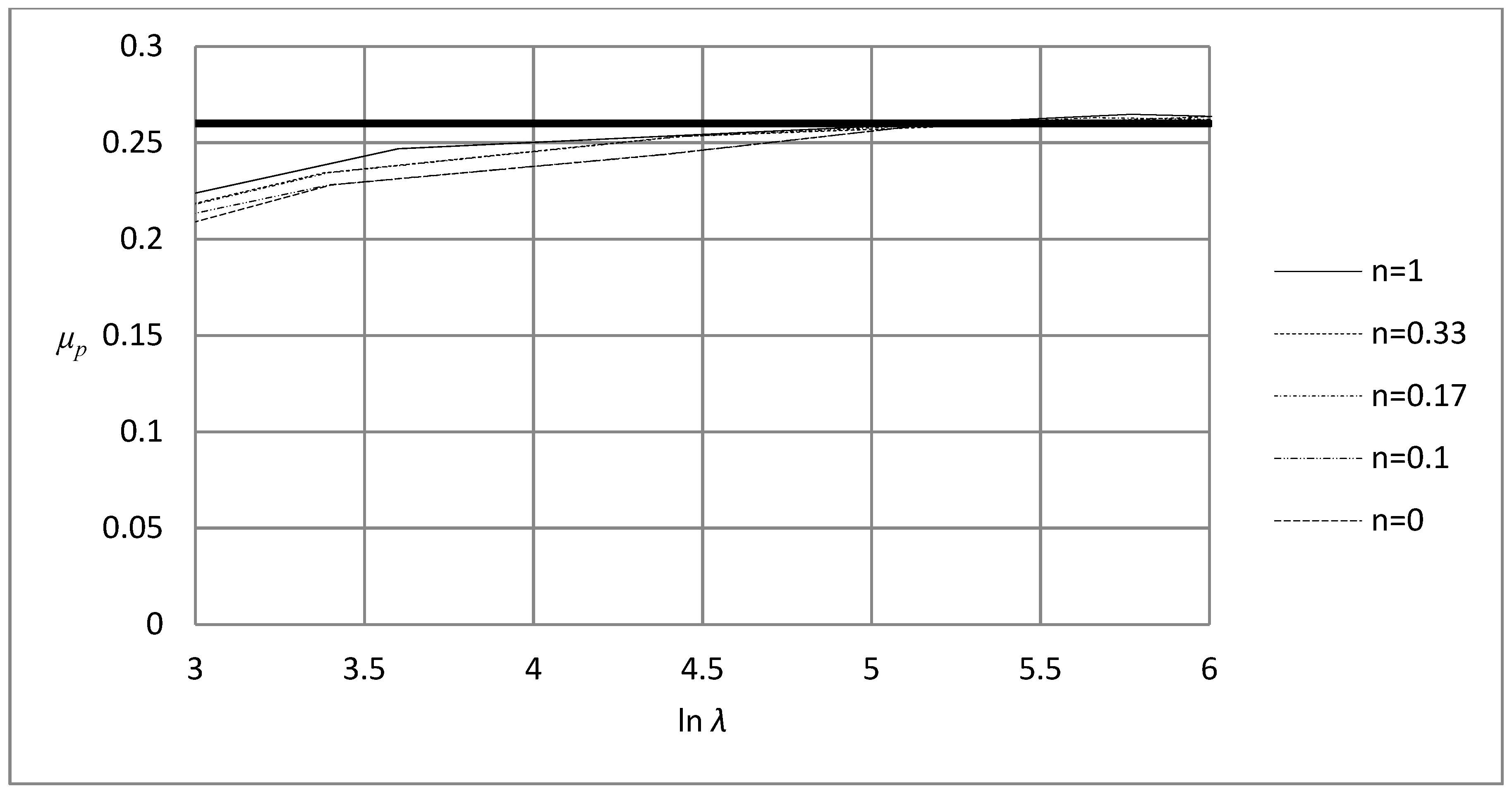
μp(Λ) = 0.26 (Level III, Λ ≥ 50 approximately),
σrep = σ(εp = 0.39) (Level III, Λ ≥ 25 approximately).
3. Experiments and Materials
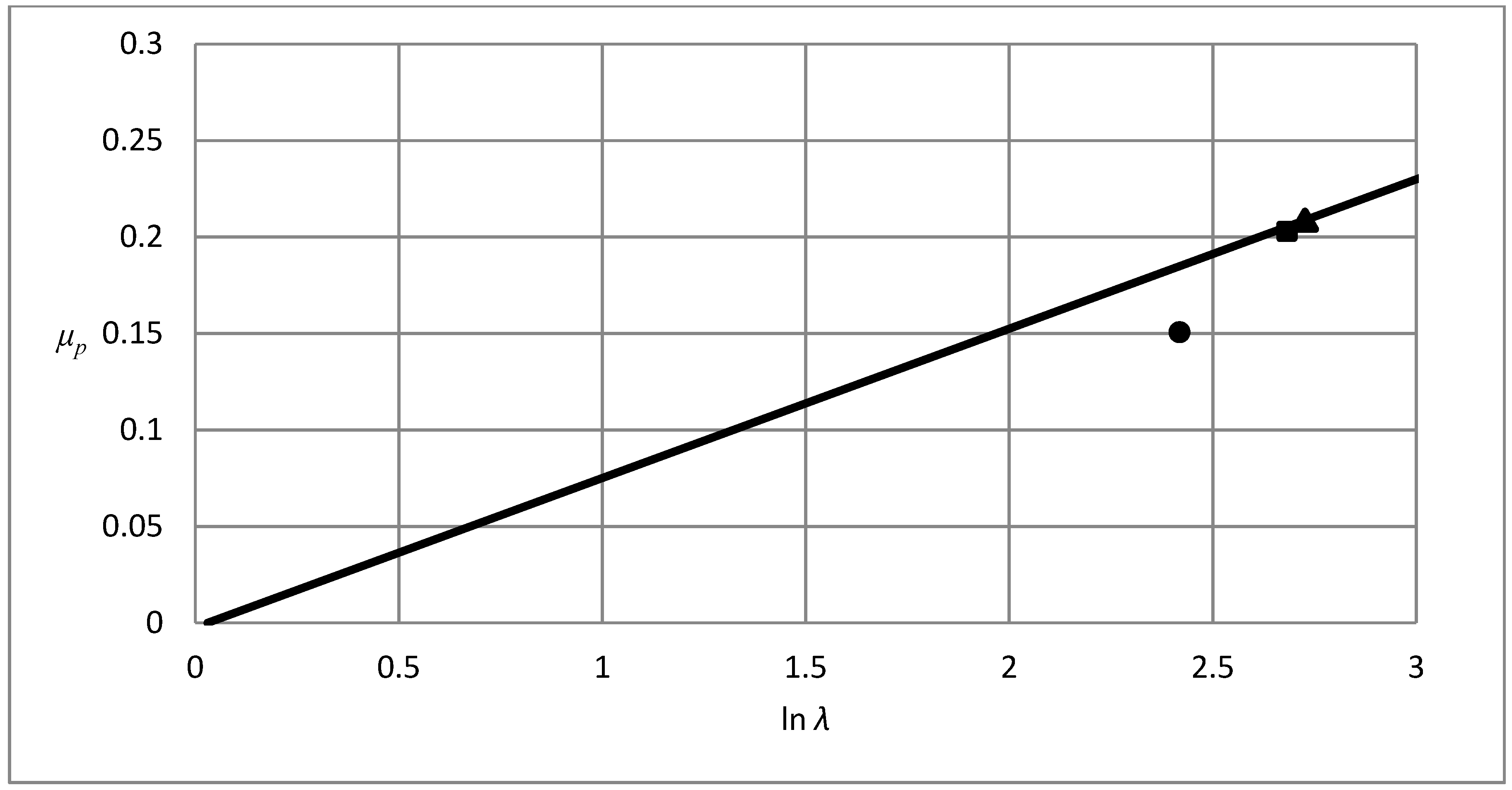
4. Results and Discussion
- Material characterization (together with similar relations for global scratch properties).
- Determination of the interfacial friction coefficient.
- Determination of the cracking behavior at scratching based on FEM calculations where the frictional behavior is properly accounted for.
5. Conclusions
Funding
Conflicts of Interest
References
- Tabor, D. Hardness of Metals; Cambridge University Press: Cambridge, UK, 1951. [Google Scholar]
- Johnson, K.L. The correlation of indentation experiments. J. Mech. Phys. Solids 1970, 18, 115–126. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Atkins, A.G.; Tabor, D. Plastic indentation in metals with cones. J. Mech. Phys. Solids 1965, 13, 149–164. [Google Scholar] [CrossRef]
- Giannakopoulos, A.E.; Larsson, P.L.; Vestergaard, R. Analysis of Vickers indentation. Int. J. Solids Struct. 1994, 31, 2679–2708. [Google Scholar] [CrossRef]
- Larsson, P.L.; Giannakopoulos, A.E.; Söderlund, E.; Rowcliffe, D.J.; Vestergaard, R. Analysis of Berkovich indentation. Int. J. Solids Struct. 1996, 33, 221–248. [Google Scholar] [CrossRef]
- Mesarovic, S.D.; Fleck, N.A. Spherical indentation of elastic-plastic solids. Int. J. Solids Struct. 2000, 37, 7071–7091. [Google Scholar] [CrossRef]
- Bhattachharya, A.K.; Nix, W.D. Finite element simulation of indentation experiments. Int. J. Solids Struct. 1988, 24, 881–891. [Google Scholar] [CrossRef]
- Bhattachharya, A.K.; Nix, W.D. Analysis of elastic and plastic deformation associated with indentation testing of thin films on substrates. Int. J. Solids Struct. 1988, 24, 1287–1298. [Google Scholar] [CrossRef]
- Laursen, T.A.; Simo, J.C. A study of the mechanics of microindentation using finite elements. J. Mater. Res. 1992, 7, 618–626. [Google Scholar] [CrossRef]
- Mesarovic, S.D.; Fleck, N.A. Frictionless indentation of dissimilar elastic–plastic spheres. Proc. R. Soc. Lond. A 1999, 455, 2707–2728. [Google Scholar] [CrossRef]
- Larsson, P.L. Investigation of sharp contact at rigid plastic conditions. Int. J. Mech. Sci. 2001, 43, 895–920. [Google Scholar] [CrossRef]
- Bucaille, J.L.; Felder, E.; Hochstetter, G. Mechanical analysis of the scratch test on elastic and perfectly plastic materials with three-dimensional finite element modeling. Wear 2001, 249, 422–432. [Google Scholar] [CrossRef]
- Bucaille, J.L.; Felder, E.; Hochstetter, G. Experimental and three-dimensional finite element study of scratch test of polymers at large deformations. J. Tribol. 2004, 126, 372–379. [Google Scholar] [CrossRef]
- Felder, E.; Bucaille, JL. Mechanical analysis of the scratching of metals and polymers with conical indenters at moderate and large strains. Tribol. Int. 2006, 39, 70–87. [Google Scholar] [CrossRef]
- Bellemare, S.; Dao, M.; Suresh, S. The frictional sliding response of elasto-plastic materials in contact with a conical indenter. Int. J. Solids Struct. 2007, 44, 1970–1989. [Google Scholar] [CrossRef]
- Wredenberg, F.; Larsson, P.L. On the numerics and correlation of scratch testing. J. Mech. Mater. Struct. 2007, 2, 573–594. [Google Scholar] [CrossRef]
- Ben Tkaya, M.; Zidi, M.; Mezlini, S.; Zahouani, H.; Kapsa, P. Influence of the attack angle on the scratch testing of an aluminium alloy by cones: Experimental and numerical studies. Mater. Des. 2008, 29, 98–104. [Google Scholar] [CrossRef]
- Wredenberg, F.; Larsson, P.L. Scratch testing of metals and polymers—Experiments and numerics. Wear 2009, 266, 76–83. [Google Scholar] [CrossRef]
- Aleksy, N.; Kermouche, G.; Vautrin, A.; Bergheau, J.M. Numerical study of scratch velocity effect on recovery of viscoelastic-viscoplastic solids. Int. J. Mech. Sci. 2010, 52, 455–463. [Google Scholar] [CrossRef]
- Bellemare, S.; Dao, M.; Suresh, S. A new method for evaluating the plastic properties of materials through instrumented frictional sliding tests. Acta Mater. 2010, 58, 6385–6392. [Google Scholar] [CrossRef]
- Larsson, P.L. On the correlation of scratch testing using separated elastoplastic and rigid plastic descriptions of the representative stress. Mater. Des. 2013, 43, 153–160. [Google Scholar] [CrossRef]
- Larsson, P.L. On representative stress correlation of global scratch quantities at scratch testing of elastoplastic materials. Mater. Des. 2013, 49, 536–544. [Google Scholar] [CrossRef]
- Bowden, F.P.; Tabor, D. The Friction and Lubrication of Solids; Clarendon Press: Oxford, UK, 1950. [Google Scholar]
- Goddard, J.; Wilman, H. A theory of friction and wear during the abrasion of metals. Wear 1962, 5, 114–135. [Google Scholar] [CrossRef]
- Subhash, G.; Zhang, W. Investigation of the overall friction coefficient in single-pass scratch test. Wear 2002, 252, 123–134. [Google Scholar] [CrossRef]
- Bull, S.J. Failure modes in scratch adhesion testing. Surf. Coat. Technol. 1991, 50, 25–32. [Google Scholar] [CrossRef]
- Frey, N.; Mettraux, P.; Zambelli, G.; Landolt, D. Modified scratch test for study of the adhesion of ductile coatings. Surf. Coat. Technol. 1993, 63, 167–172. [Google Scholar] [CrossRef]
- Thouless, M.D. An analysis of spalling in the microscratch test. Eng. Fract. Mech. 1998, 61, 75–81. [Google Scholar] [CrossRef]
- Malzbender, J.; De With, G. Scratch testing of hybrid coatings of float glass. Surf. Coat. Technol. 2001, 135, 202–207. [Google Scholar] [CrossRef]
- Yueguang, W.; Manhong, Z.; Shan, T. Characterization of the fracture work for ductile film undergoing the micro-scratch. Acta Mech. Sin. 2002, 18, 494–505. [Google Scholar] [CrossRef]
- Holmberg, K.; Laukkanen, A.; Ronkainen, H.; Wallin, K.; Varjus, S. A model for stresses, crack generation and fracture toughness calculation in scratched tin-coated steel surfaces. Wear 2003, 254, 278–291. [Google Scholar] [CrossRef]
- Larsson, P.L.; Wredenberg, F. On indentation and scratching of thin films on hard substrates. J. Phys. D Appl. Phys. 2008, 41, 074022. [Google Scholar] [CrossRef]
- Kermouche, G.; Aleksy, N.; Loubet, J.L.; Bergheau, J.M. Finite element modeling of the scratch response of a coated time-dependent solid. Wear 2009, 267, 1945–1953. [Google Scholar] [CrossRef]
- Wredenberg, F.; Larsson, P.L. Delamination of thin coatings at scratching—Experiments and numerics. J. Mech. Mater. Struct. 2009, 4, 1041–1062. [Google Scholar] [CrossRef]
- Culha, O.; Zor, M.; Gungor, M.A.; Arman, Y.; Toparli, M. Evaluating the bond strength of opaque material on porcelain fused to metal restorations (PFM) alloys by scratch test method. Mater. Des. 2009, 30, 3225–3228. [Google Scholar] [CrossRef]
- Roy, S.; Darque-Ceretti, E.; Felder, E.; Raynal, F.; Bispo, I. Experimental analysis and finite element modelling of nano-scratch test applied on 40–120 nm SiCN thin films deposited on Cu/Si substrate. Thin Solid Films 2010, 518, 3859–3865. [Google Scholar] [CrossRef]
- Zheng, X.H.; Tu, J.P.; Song, R.G. Microstructure and tribological performance of CN(x)–TiN(x) composite films prepared by pulsed laser. Mater. Des. 2010, 31, 1716–1719. [Google Scholar] [CrossRef]
- Larsson, P.L. On delamination buckling and growth in circular and annular orthotropic plates. Int. J. Solids Struct. 1991, 27, 15–28. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Suo, Z. Mixed mode cracking in layered materials. Adv. Appl. Mech. 1992, 29, 63–191. [Google Scholar]

| Material | E | σY | σ(εp = 0.25) | σ(εp = 0.39) | Λ(εp = 0.25) | Λ(εp = 0.39) |
|---|---|---|---|---|---|---|
| Vinyl Ester | 3.5 | 108 | 108 | 108 | 15 | 15 |
| PMMA | 2.9 | 110 | 110 | 110 | 12 | 12 |
| Epoxy | 3.1 | 97 | 97 | 97 | 14 | 14 |
| Al7050 | 70 | 560 | 724 | 816 | 42.5 | 38 |
| Stainless steel | 200 | 560 | 625 | 805 | 146 | 113 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larsson, P.-L. On Plowing Frictional Behavior during Scratch Testing: A Comparison between Experimental and Theoretical/Numerical Results. Crystals 2019, 9, 33. https://doi.org/10.3390/cryst9010033
Larsson P-L. On Plowing Frictional Behavior during Scratch Testing: A Comparison between Experimental and Theoretical/Numerical Results. Crystals. 2019; 9(1):33. https://doi.org/10.3390/cryst9010033
Chicago/Turabian StyleLarsson, Per-Lennart. 2019. "On Plowing Frictional Behavior during Scratch Testing: A Comparison between Experimental and Theoretical/Numerical Results" Crystals 9, no. 1: 33. https://doi.org/10.3390/cryst9010033
APA StyleLarsson, P.-L. (2019). On Plowing Frictional Behavior during Scratch Testing: A Comparison between Experimental and Theoretical/Numerical Results. Crystals, 9(1), 33. https://doi.org/10.3390/cryst9010033





