Structural Chemistry of Halide including Thallides A8Tl11X1−n (A = K, Rb, Cs; X = Cl, Br; n = 0.1–0.9)
Abstract
:1. Introduction
2. Materials and Methods
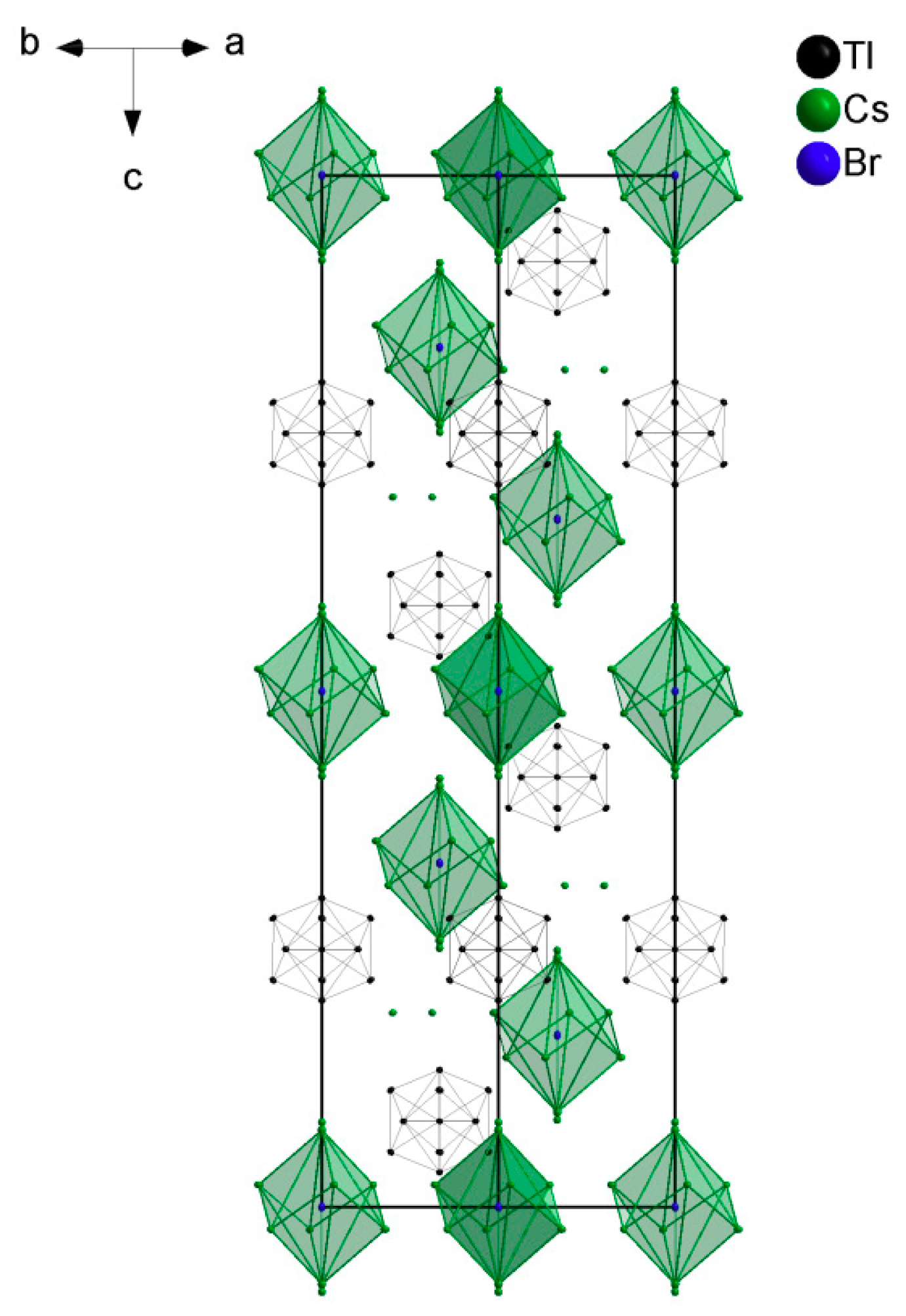
3. Results
4. Discussions
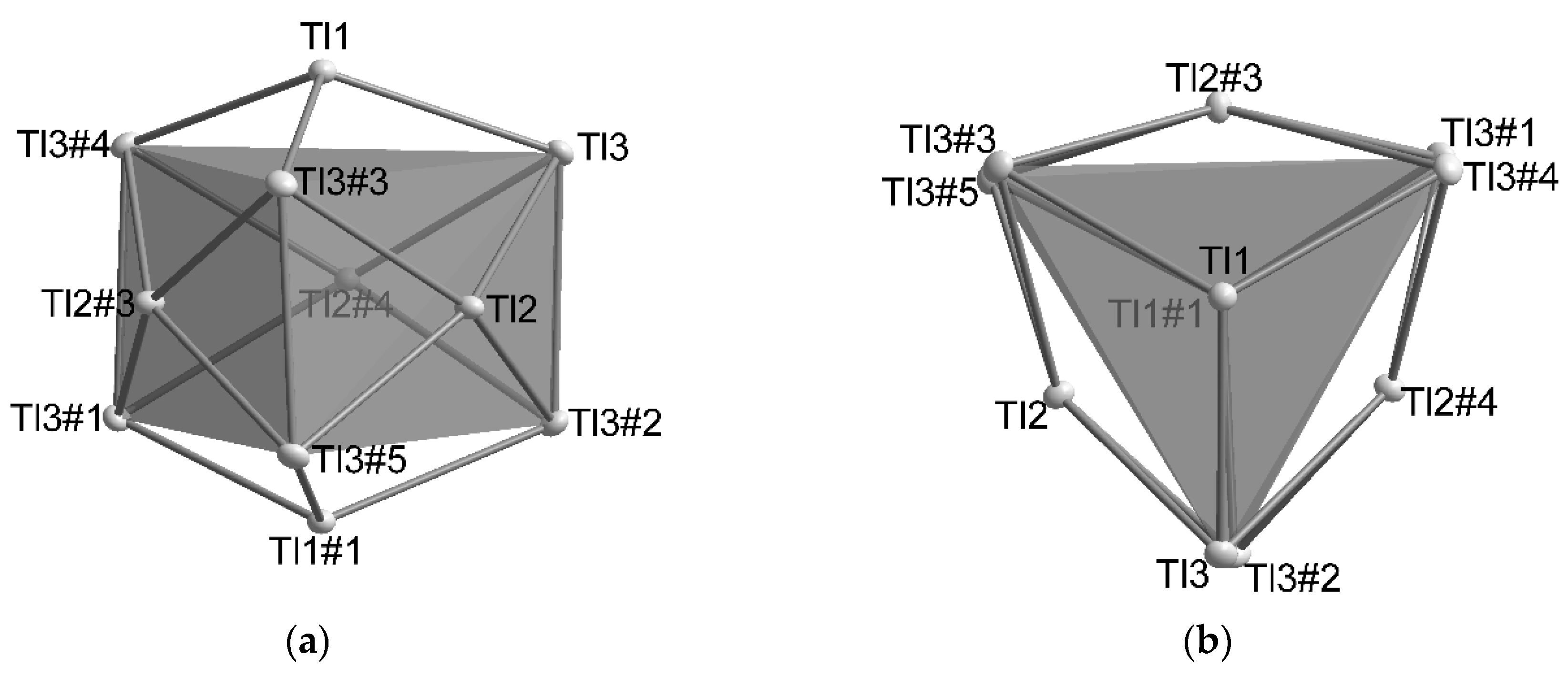
4.1. How Does the Geometry of the Thallide Cluster Change on Halide Incorporation?
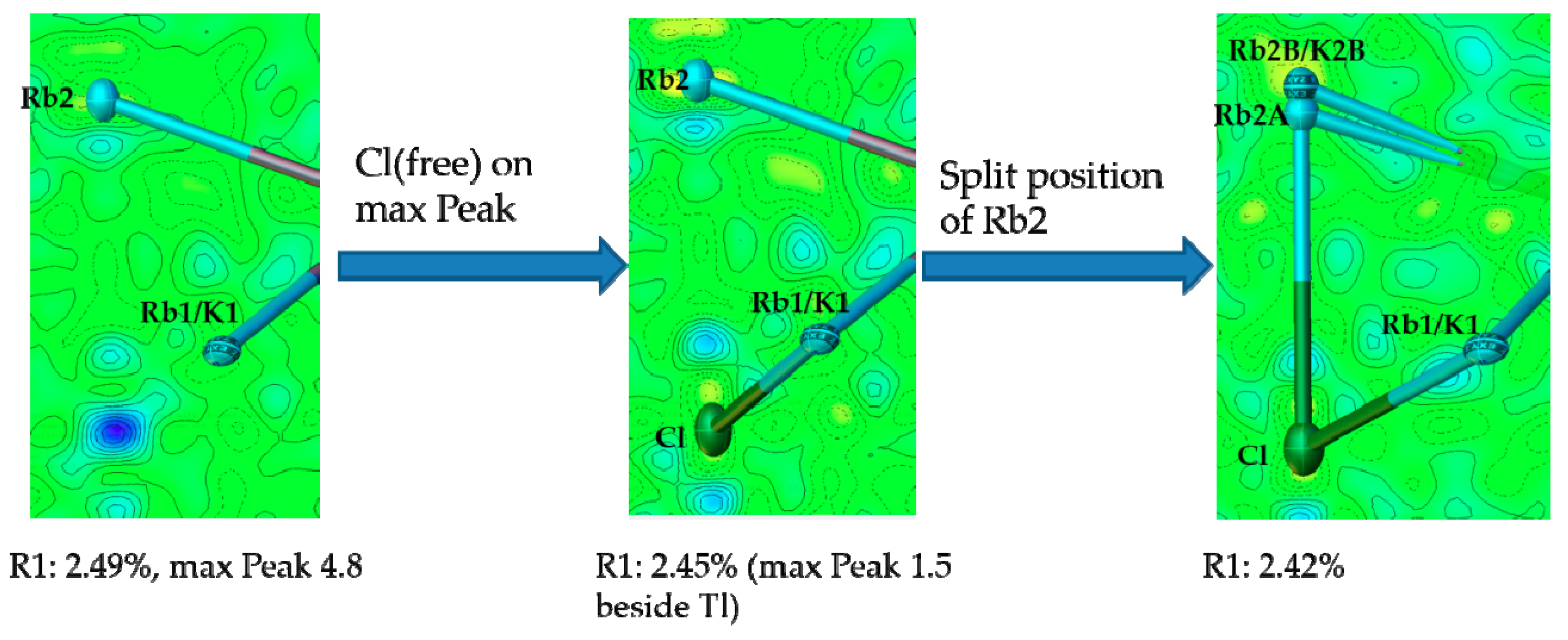
4.2. Is There a Rb8Tl11Cl?
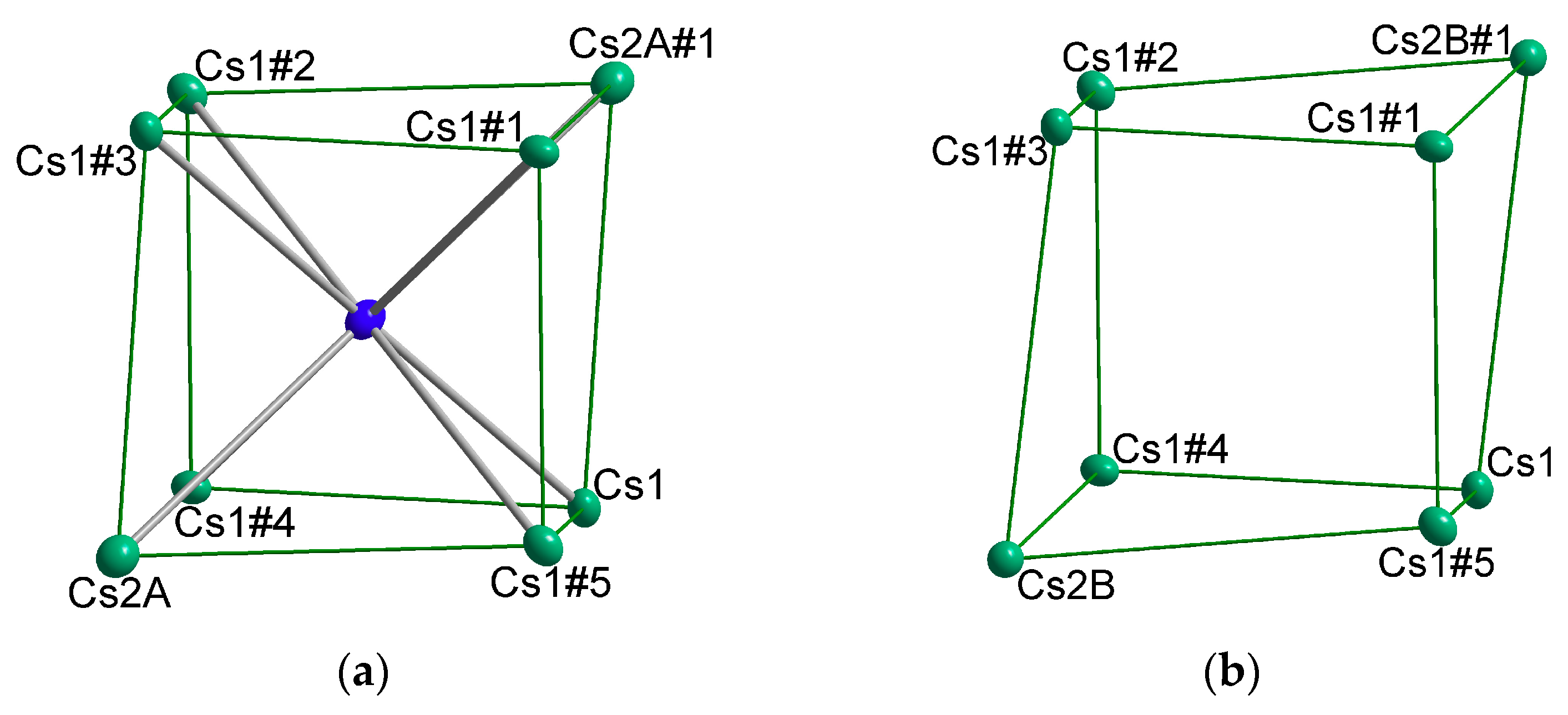
4.3. How Do Mixed Cation Sites Affect the Amount of Halide Incorporation?
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Gärtner, S.; Korber, N. Polyanions of group 14 and group 15 elements in alkali and alkaline earth metal solid state compounds and solvate structures. In Zintl Ions Principles and Recent Developments, Fässler, T.F., Ed.; Springer: Berlin, Germany, 2011; pp. 25–56. [Google Scholar]
- Gärtner, S.; Korber, N. Chapter 1.09-Zintl anions. In Comprehensive Inorganic Chemistry II, 2nd ed.; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 251–267. [Google Scholar]
- Corbett, J.D. Polyanionic clusters and networks of the early p-element metals in the solid state: Beyond the zintl boundary. Angew. Chem. Int. Ed. 2000, 39, 670–690. [Google Scholar] [CrossRef]
- Scharfe, S.; Kraus, F.; Stegmaier, S.; Schier, A.; Fässler, T.F. Zintl ions, cage compounds, and intermetalloid clusters of group 14 and group 15 elements. Angew. Chem. Int. Ed. 2011, 50, 3630–3670. [Google Scholar] [CrossRef] [PubMed]
- Zintl, E.; Goubeau, J.; Dullenkopf, W. Salzartige Verbindungen und intermetallische Phasen des Natriums in flüssigem Ammoniak. Z. Phys. Chem. 1931, 154, 1–46. [Google Scholar] [CrossRef]
- Zintl, E.; Dullenkopf, W. Über den Gitterbau von NaTl und seine Beziehung zu den Strukturen des β-Messings. Z. Phys. Chem. 1932, B16, 195–205. [Google Scholar] [CrossRef]
- Eisenmann, B.; Cordier, G. Structural patterns of homo-and heteronuclear anions in zintl phases and related intermetallic compounds and concepts for their interpretation. In Chemistry, Structure and Bonding of Zintl Phases and Ions; Kauzlarich, S.M., Ed.; VCH Verlagsgesellschaft mbH: Weinheim, Germany, 1996; pp. 61–137. [Google Scholar]
- Guloy, A.M. Polar intermetallics and zintl phases along the zintl border. In Inorganic Cemistry in Focus III; Wiley-VCH Verlag GmbH & Co.: Weinheim, Germany, 2006. [Google Scholar]
- Hansen, D.A.; Smith, J.F. Structure and bonding model for Na2Tl. Acta Cryst. 1967, 22, 836–845. [Google Scholar] [CrossRef]
- Marsh, R.E.; Shoemaker, D.P. The crystal structure of NaPb. Acta Cryst. 1953, 197–205. [Google Scholar] [CrossRef]
- Busmann, E. Die kristallstrukturen von KSi, RbSi, KGe, RbGe und CsGe. Z. Anorg. Allg. Chem. 1961, 313, 90–106. [Google Scholar] [CrossRef]
- Lorenz, C.; Gärtner, S.; Korber, N. Ammoniates of zintl phases: Similarities and differences of binary phases A4E4 and their corresponding solvates. Crystals 2018, 8, 276. [Google Scholar] [CrossRef]
- Blase, W.; Cordier, G.; Muller, V.; Haussermann, U.; Nesper, R.; Somer, M. Preparation and crystal-structures of Rb8In11,K8Tl11, and Rb8Tl11 band-structure calculations on K8In11. Z. Naturforsch. B 1993, 48, 754–760. [Google Scholar] [CrossRef]
- Dong, Z.-C.; Corbett, J.D. A8Tl11 (A = K, Rb, or Cs) Phases with Hypoelectronic Tl117− cluster anions: Syntheses, structure, bonding and properties. J. Cluster Sci. 1995, 6, 187–201. [Google Scholar] [CrossRef]
- Dong, Z.C.; Corbett, J.D. A15Tl27 (A = Rb,Cs): A structural type containing both isolated clusters and condensed layers based on the tl-11 fragment. Syntheses, structure, properties, and band structure. Inorg. Chem. 1996, 35, 1444–1450. [Google Scholar] [CrossRef] [PubMed]
- Sevov, S.C.; Corbett, J.D. A remarkable hypoelectronic indium cluster in K8In11. Inorg. Chem. 1991, 30, 4875–4877. [Google Scholar] [CrossRef]
- Wang, F.; Wedig, U.; Prasad, D.; Jansen, M. Deciphering the chemical bonding in anionic thallium clusters. J. Am. Chem. Soc. 2012, 134, 19884–19894. [Google Scholar] [CrossRef] [PubMed]
- Henning, R.W.; Corbett, J.D. Cs8Ga11, a new isolated cluster in a binary gallium compound. A family of valence analogues A8Tr11X: A = Cs, Rb; Tr = Ga, In, Tl; X = Cl, Br, I. Inorg. Chem. 1997, 36, 6045–6049. [Google Scholar] [CrossRef] [PubMed]
- Falk, M.; El Addad, A.; Röhr, C. Crystal and electronic structure of alkali triele halogenides of the K8In11-type structure. In Proceedings of the 25th Annual Conference of the German Crystallographic Society, Karlsruhe, Germany, 27–30 March 2017. [Google Scholar]
- Hackspill, L. Sur quelques properiétés des métaux alcalins. Helv. Chim. Acta 1928, 11, 1003–1026. [Google Scholar] [CrossRef]
- Agilent. Crysalis pro. v.39.37b ed.; Agilent Technologies Ltd.: Yarnton, UK, 2014. [Google Scholar]
- Computer Program: STOE WinXPOW; STOE & Cie 2000 Darmstadt: Darmstadt, Germany, 2011.
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. Olex2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 2009, 42, 339–341. [Google Scholar] [CrossRef]


| Compound | Cs8Tl11Cl0.80 | Cs8Tl11Br0.92 | Cs5.13Rb2.87Tl11Cl0.49 | Cs5.67K2.33Tl11Cl0.60 | K3.98Rb4.02Tl11Cl0.1 |
|---|---|---|---|---|---|
| CSD number * | 434541 | 434540 | 434539 | 434538 | 1856564 |
| Mr [g·mol−1] | 3339.71 | 3385.20 | 3192.52 | 3114.02 | 2751.04 |
| Crystal system | Trigonal | Trigonal | Trigonal | Trigonal | Trigonal |
| Space group | R-3c | R−3c | R-3c | R-3c | R-3c |
| a [Å] | 10.4691 (4) | 10.5608 (3) | 10.3791 (5) | 10.3291 (9) | 10.0948 (4) |
| b [Å] | 10.4691 (4) | 10.5608 (3) | 10.3791 (5) | 10.3291 (9) | 10.0948 (4) |
| c [Å] | 53.297 (3) | 53.401(2) | 52.437 (3) | 51.909 (5) | 51.0274 (18) |
| α [°] | 90 | 90 | 90 | 90 | 90 |
| β [°] | 90 | 90 | 90 | 90 | 90 |
| γ [°] | 120 | 120 | 120 | 120 | 120 |
| V [Å3] | 5058.8 (5) | 5157.9 (4) | 4892.0 (5) | 4796.3 (9) | 4503.3 (4) |
| Z | 6 | 6 | 6 | 6 | 6 |
| F(000) | 8068.0 | 8180.0 | 7726.0 | 7544.0 | 6703.0 |
| ρcalc [g·cm−3] | 6.578 | 6.539 | 6.502 | 6.469 | 6.087 |
| μ [mm−1] | 60.902 | 60.745 | 64.052 | 61.908 | 65.822 |
| 2θ-range for data collection [°] | 7.59 to 58.982 | 7.558 to 69.266 | 7.694 to 54.202 | 7.758 to 54.198 | 7.91 to 69.18 |
| Reflections collected/independent | 79177/1473 | 12097/2374 | 3174/1194 | 3394/1176 | 5040/1934 |
| Data/restraints/parameters | 1473/0/36 | 2374/0/36 | 1194/0/34 | 1176/0/34 | 1934/1/37 |
| Goodness-of-fit on F2 | 1.244 | 1.136 | 1.089 | 1.148 | 1.033 |
| Final R indices [I > 2σ(I)] | R1 = 0.0280 wR2 = 0.0619 | R1 = 0.0242 wR2 = 0.0528 | R1 = 0.0392 wR2 = 0.0928 | R1 = 0.0456 wR2 = 0.0996 | R1 = 0.0242 wR2 = 0.0461 |
| R indices (all data) | R1 = 0.0309 wR2 = 0.0629 | R1 = 0.0280 wR2 = 0.0541 | R1 = 0.0466 wR2 = 0.0970 | R1 = 0.0566 wR2 = 0.1034 | R1 = 0.0292 wR2 = 0.0478 |
| Rint | 0.0497 | 0.0385 | 0.0446 | 0.0449 | 0.0280 |
| Largest diff. peak/hole [e·Å−3] | 2.96/−1.38 | 1.83/−3.38 | 4.82/−2.29 | 3.62/−2.21 | 1.48/−1.67 |
| Atom 1 | Atom 2 | K8Tl11 | Rb8Tl11 |
|---|---|---|---|
| Tl2 | Tl3 | 3.0476 (4) | 3.060 |
| Tl2 | Tl33 | 3.1396 (4) | 3.157 |
| Tl1 | Tl31 | 3.1304 (4) | 3.147 |
| Tl3 | Tl33 | 3.2054 (7) | 3.219 |
| Tilt [°] | 4.69 (2) | 4.90 | |
| cdd/cdav [%] | 2.97 | 3.12 | |
| Atom 1 | Atom 2 | Cs8Tl11Cl0.8 | Cs8Tl11Br0.9 | Cs5Rb3Tl11Cl0.5 | Cs5.7K2.3Tl11Cl0.6 | K4Rb4Tl11Cl0.1 |
|---|---|---|---|---|---|---|
| Tl2 | Tl3 | 3.0656 (4) | 3.0743 (2) | 3.0605 (6) | 3.0554 (7) | 3.0564 (2) |
| Tl2 | Tl33 | 3.0632 (4) | 3.0766 (2) | 3.0896 (6) | 3.0656 (4) | 3.1298 (3) |
| Tl1 | Tl31 | 3.0894 (4) | 3.1006 (2) | 3.1049 (7) | 3.0884 (8) | 3.1274 (3) |
| Tl3 | Tl33 | 3.2019 (11) | 3.2102 (4) | 3.2025 (11) | 3.1873 (11) | 3.2104 (4) |
| Tilt [°] | 0.12 (2) | 0.069 (7) | 0.94 (2) | 0.34 (5) | 2.352 (7) | |
| cdd/cdav [%] | 0.08 | 0.07 | 0.95 | 0.32 | 2.38 | |
| Position 1–Position 2 | Cs8Tl11Br0.9 | Cs8Tl11Cl0.8 | Position 1–Position 2 | K4Rb4Tl11Cl0.1 |
|---|---|---|---|---|
| Cs2A-X1 | 3.990 (2) | 3.991 (9) | Rb2A-X1 | 3.80 (2) |
| Cs2B-void | 4.388 | 4.354 | K2B/Rb2B-void | 4.096 (3) |
| Cs1-X1/void | 3.6705 (4) | 3.5876 (7) | K1/Rb1-X1/void | 3.5994 (9) |
| s.o.f. (X1/Cs2A) | 0.924 (6) | 0.76 (2) | s.o.f. (X1/Rb2A) | 0.103 (13) |
| Position 1–Position 2 | Cs5Rb3Tl11Cl0.5 | Cs5.7K2.3Tl11Cl0.6 |
|---|---|---|
| A2-X1/void | 4.099 (2) | 4.002 |
| A1-X1/void | 3.6160 (13) | 3.5492 (2) |
| s.o.f. (A1 = Cs) | 0.521 (12) | 0.612 (9) |
| s.o.f. (X1) | 0.50 (4) | 0.60 (4) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gärtner, S.; Tiefenthaler, S.; Korber, N.; Stempfhuber, S.; Hischa, B. Structural Chemistry of Halide including Thallides A8Tl11X1−n (A = K, Rb, Cs; X = Cl, Br; n = 0.1–0.9). Crystals 2018, 8, 319. https://doi.org/10.3390/cryst8080319
Gärtner S, Tiefenthaler S, Korber N, Stempfhuber S, Hischa B. Structural Chemistry of Halide including Thallides A8Tl11X1−n (A = K, Rb, Cs; X = Cl, Br; n = 0.1–0.9). Crystals. 2018; 8(8):319. https://doi.org/10.3390/cryst8080319
Chicago/Turabian StyleGärtner, Stefanie, Susanne Tiefenthaler, Nikolaus Korber, Sabine Stempfhuber, and Birgit Hischa. 2018. "Structural Chemistry of Halide including Thallides A8Tl11X1−n (A = K, Rb, Cs; X = Cl, Br; n = 0.1–0.9)" Crystals 8, no. 8: 319. https://doi.org/10.3390/cryst8080319
APA StyleGärtner, S., Tiefenthaler, S., Korber, N., Stempfhuber, S., & Hischa, B. (2018). Structural Chemistry of Halide including Thallides A8Tl11X1−n (A = K, Rb, Cs; X = Cl, Br; n = 0.1–0.9). Crystals, 8(8), 319. https://doi.org/10.3390/cryst8080319





