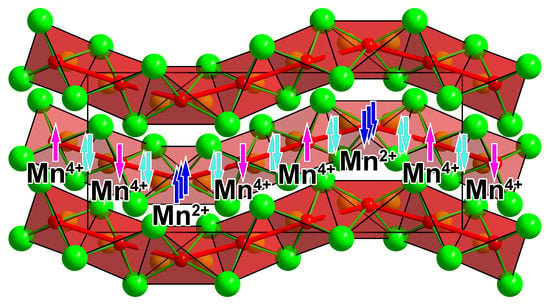
Ba4[Mn3N6], a Quasi-One-Dimensional Mixed-Valent Nitridomanganate (II, IV)
Abstract
1. Introduction
2. Materials and Methods
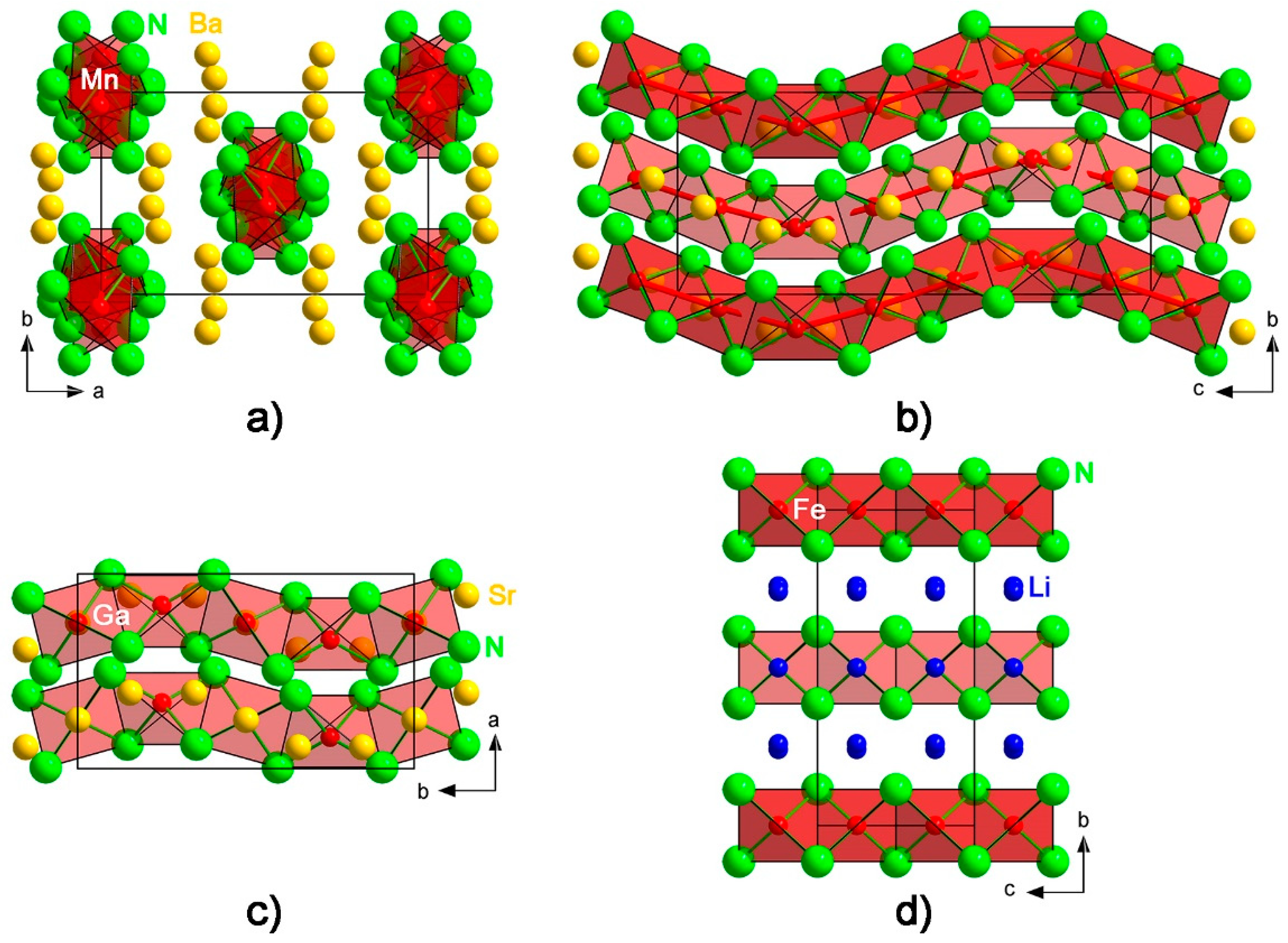
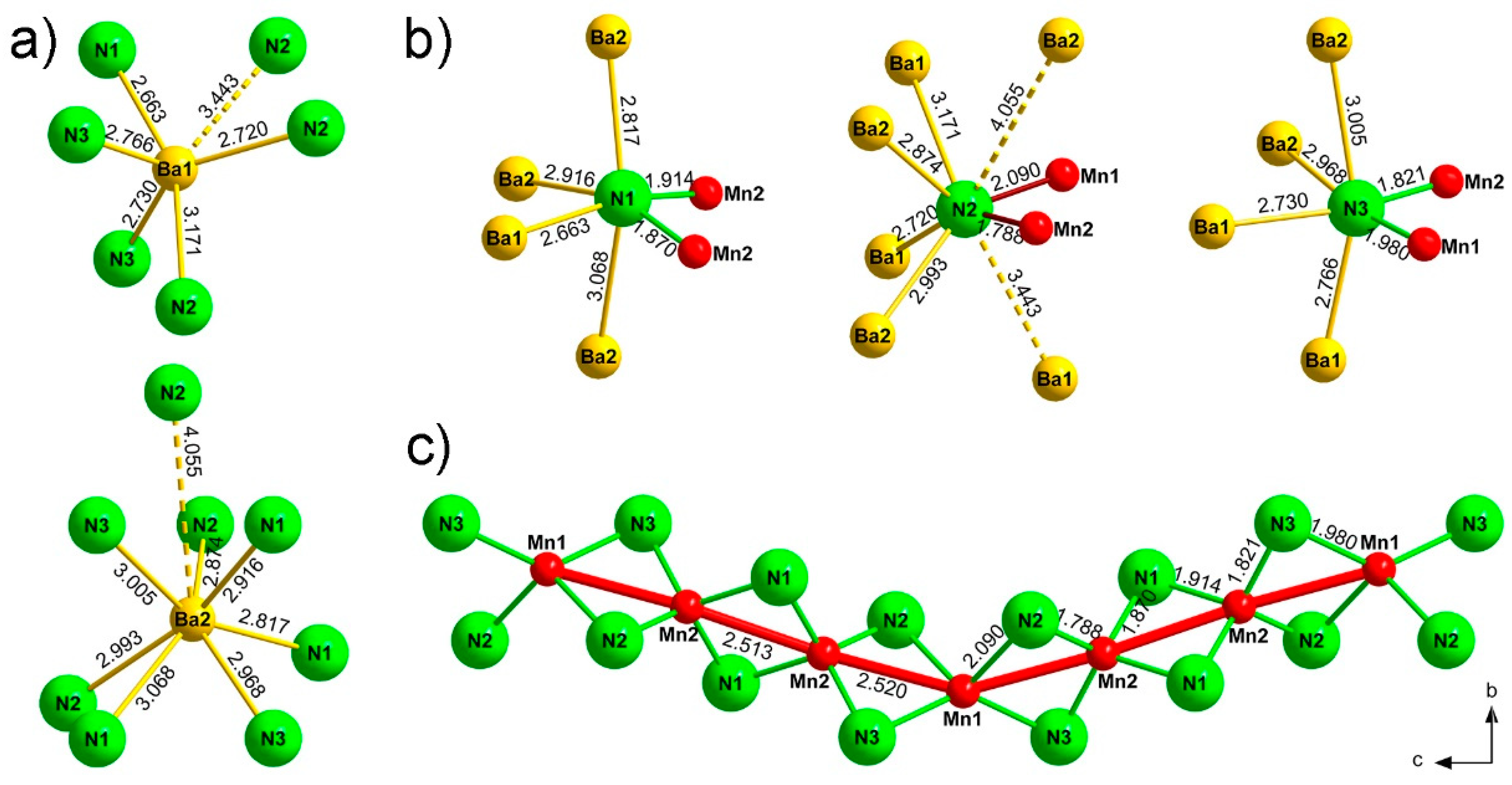
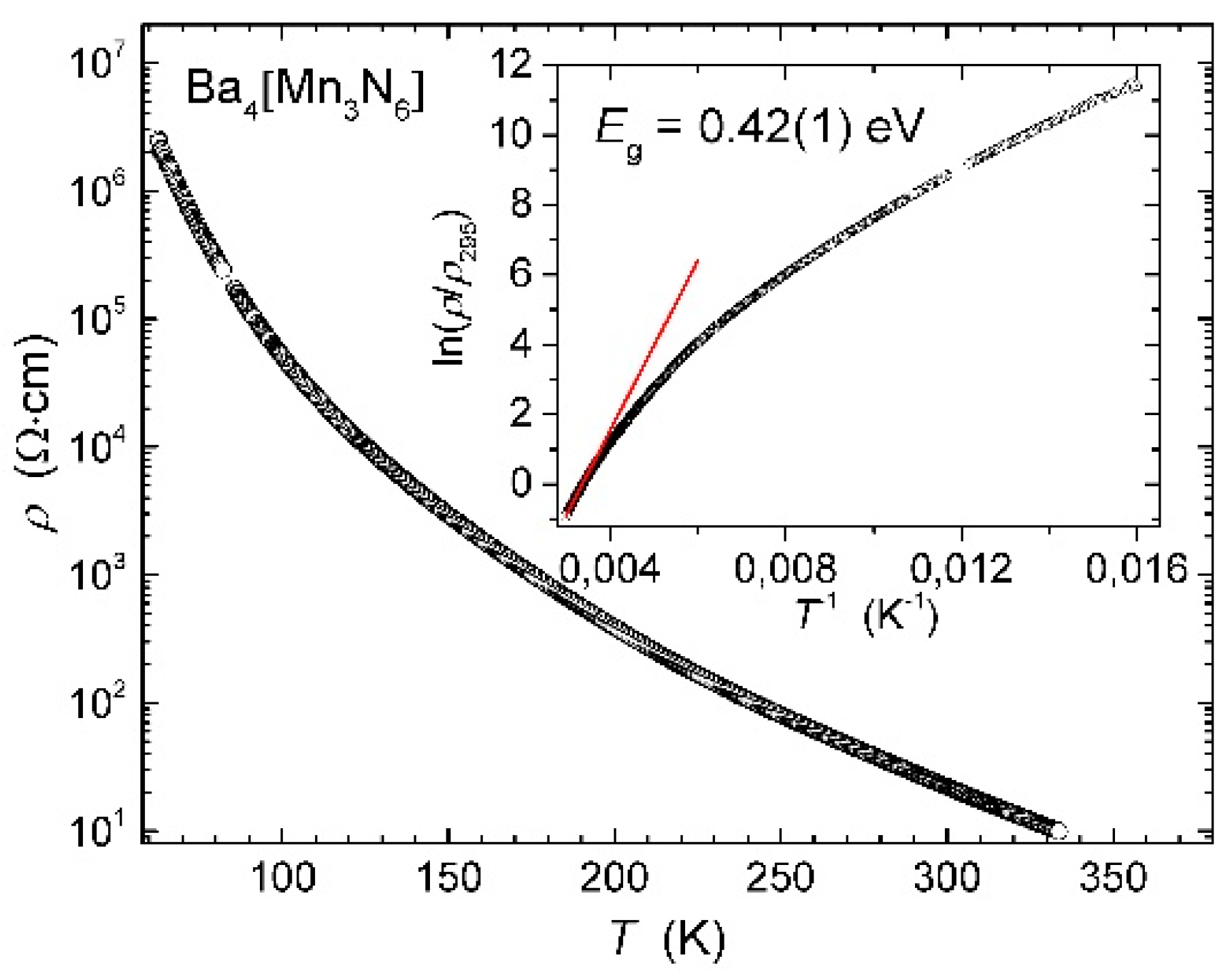
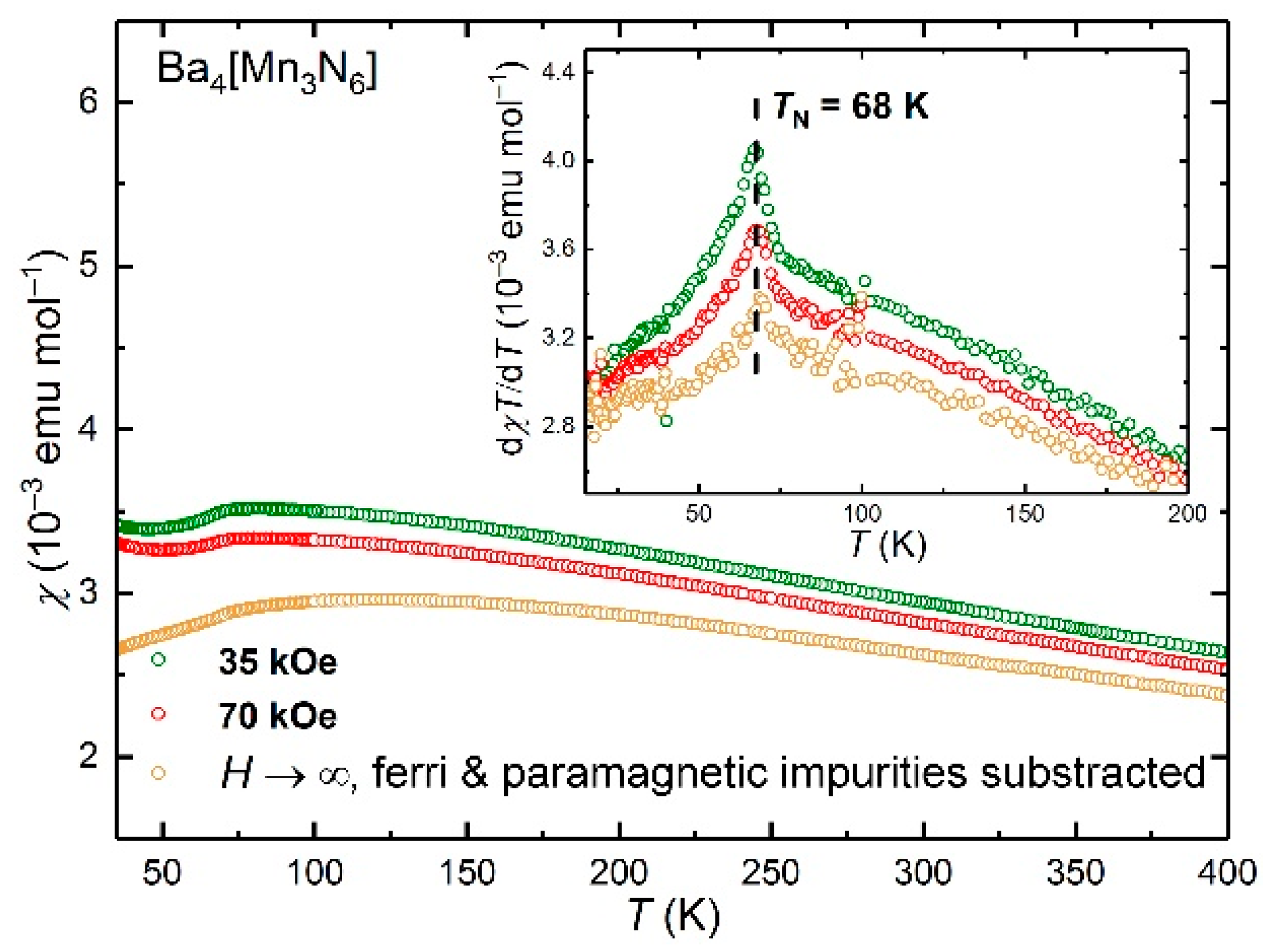
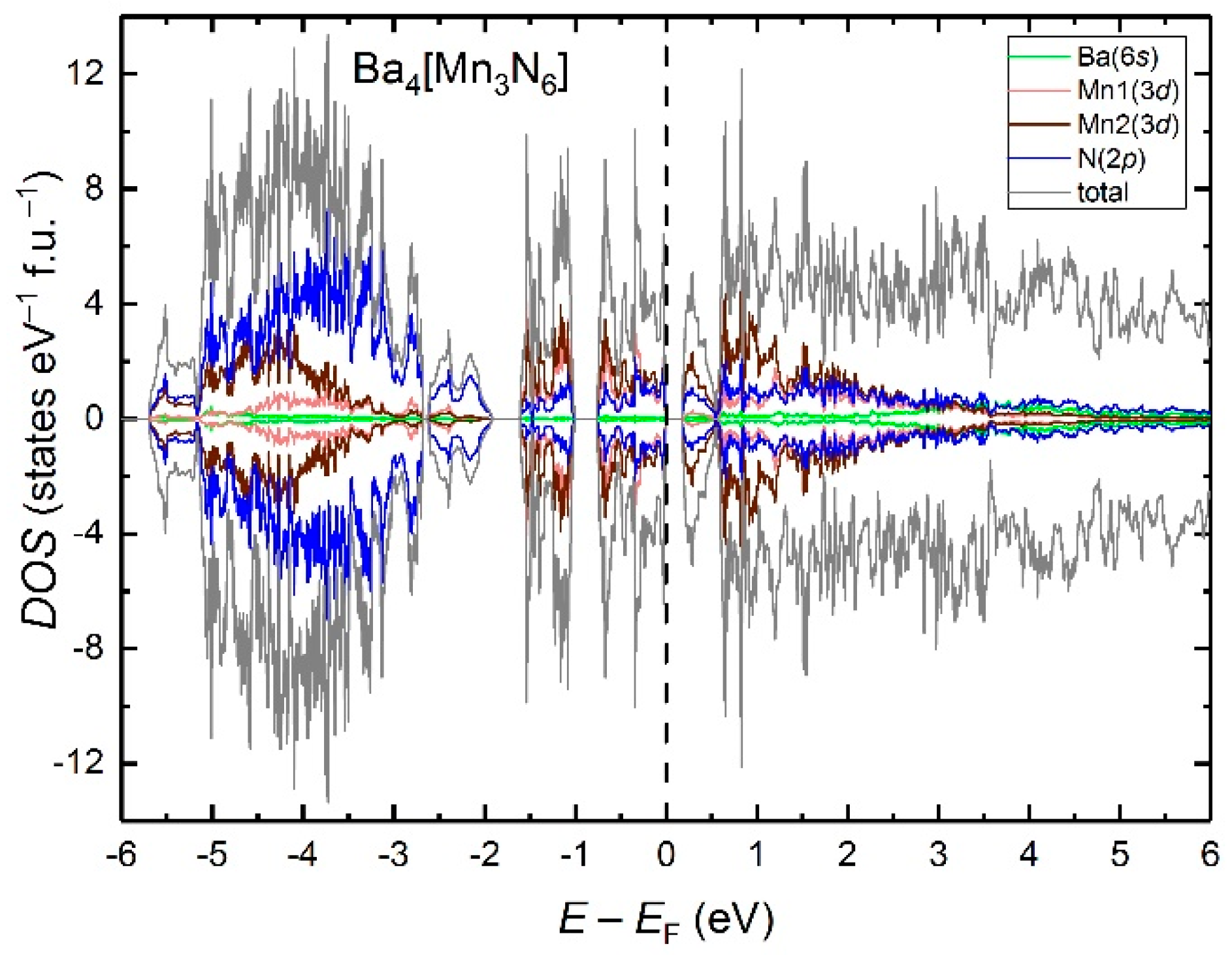
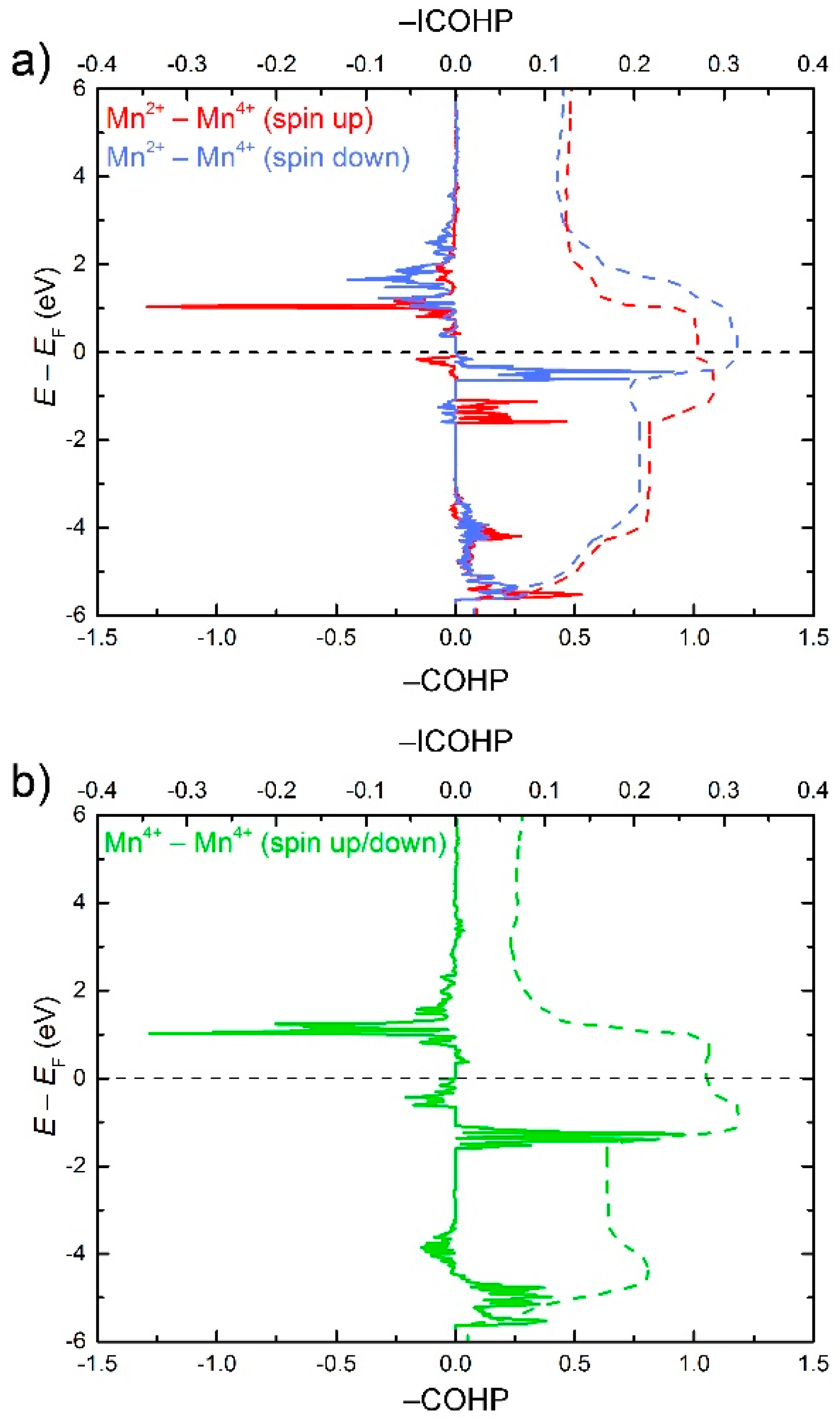
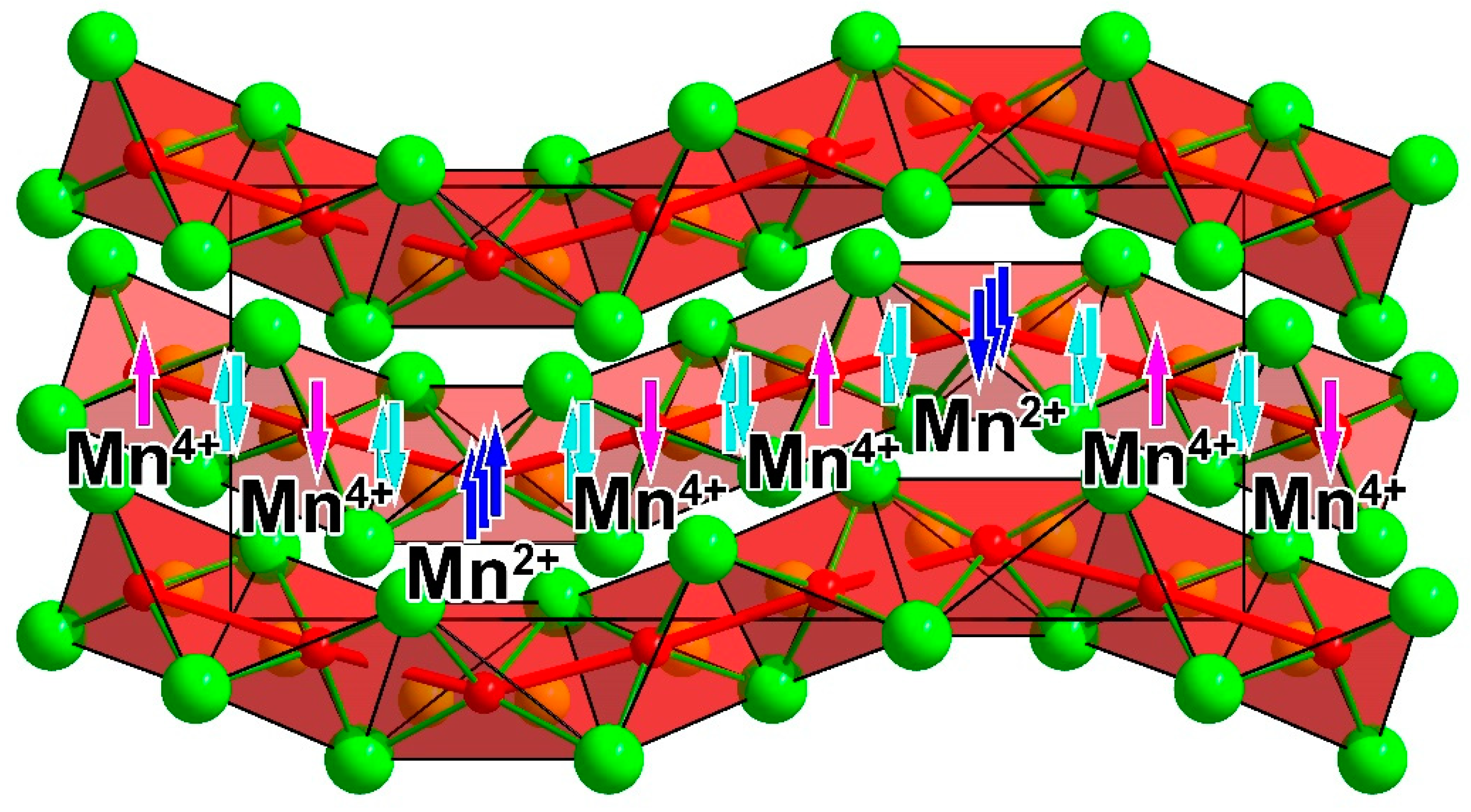
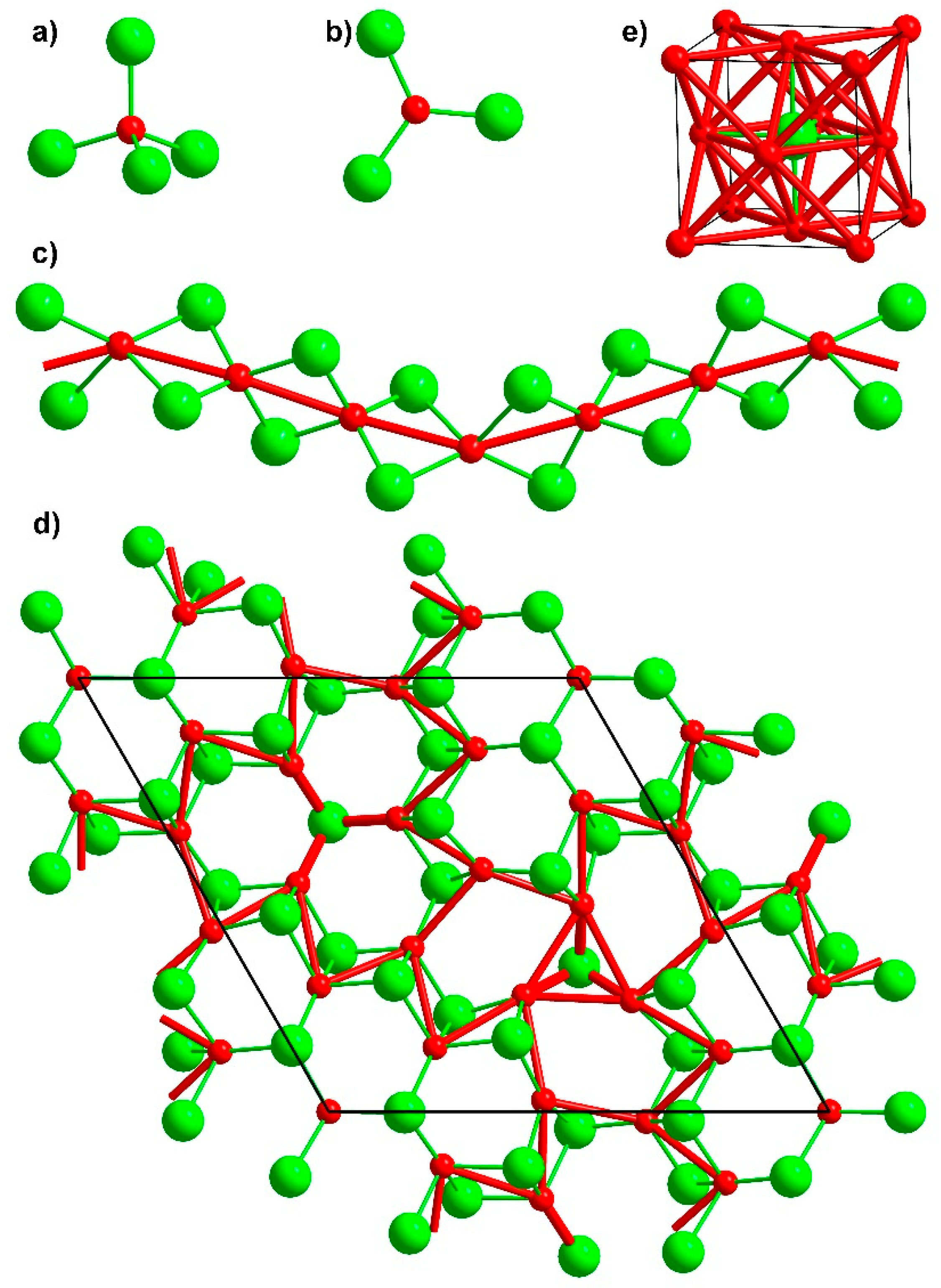
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Zhang, W.X.; Ishikawa, R.; Breedlove, B.; Yamashita, M. Single-chain magnets: Beyond the Glauber model. RSC Adv. 2013, 3, 3772–3798. [Google Scholar] [CrossRef]
- Ma, X.S.; Dakic, B.; Naylor, W.; Zeilinger, A.; Walther, P. Quantum simulation of the wavefunction to probe frustrated Heisenberg spin systems. Nat. Phys. 2011, 7, 399–405. [Google Scholar] [CrossRef]
- Bauer, B.; Cincio, L.; Keller, B.P.; Dolfi, M.; Vidal, G.; Trebst, S.; Ludwig, A.W.W. Chiral spin liquid and emergent anyons in a Kagome lattice Mott insulator. Nat. Commun. 2014, 5, 5137. [Google Scholar] [CrossRef] [PubMed]
- Modic, K.A.; Smidt, T.E.; Kimchi, I.; Breznay, N.P.; Biffin, A.; Choi, S.; Johnson, R.D.; Coldea, R.; Watkins-Curry, P.; McCandless, G.T.; et al. Realization of a three-dimensional spin-anisotropic harmonic honeycomb iridate. Nat. Commun. 2014, 5, 4203. [Google Scholar] [CrossRef] [PubMed]
- Pereiro, M.; Yudin, D.; Chico, J.; Etz, C.; Eriksson, O.; Bergman, A. Topological excitations in a Kagome magnet. Nat. Commun. 2014, 5, 4815. [Google Scholar] [CrossRef] [PubMed]
- Van Well, N.; Foyevtsova, K.; Gottlieb-Schönmeyer, S.; Ritter, F.; Manna, R.S.; Wolf, B.; Meven, M.; Pfleiderer, C.; Lang, M.; Assmus, W.; et al. Low-temperature structural investigations of the frustrated quantum antiferromagnets Cs2Cu(Cl4-xBrx). Phys. Rev. B 2015, 91, 035124. [Google Scholar] [CrossRef]
- Bisogni, V.; Kourtis, S.; Monney, C.; Zhou, K.J.; Kraus, R.; Sekar, C.; Strocov, V.; Büchner, B.; van den Brink, J.; Braicovich, L.; et al. Femtosecond Dynamics of Momentum-Dependent Magnetic Excitations from Resonant Inelastic X-Ray Scattering in CaCu2O3. Phys. Rev. Lett. 2014, 112, 147401. [Google Scholar] [CrossRef] [PubMed]
- Pak, C.; Kamali, S.; Pham, J.; Lee, K.; Greenfield, J.T.; Kovnir, K. Chemical Excision of Tetrahedral FeSe2 Chains from the Superconductor FeSe: Synthesis, Crystal Structure, and Magnetism of Fe3Se4(en)2. J. Am. Chem. Soc. 2013, 135, 19111–19114. [Google Scholar] [CrossRef] [PubMed]
- Kniep, R.; Höhn, P. 2.06—Low-Valency Nitridometalates. In Comprehensive Inorganic Chemistry II, 2nd ed.; Reedijk, J., Poeppelmeier, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; pp. 137–160. [Google Scholar]
- Bailey, M.S.; Obrovac, M.N.; Baillet, E.; Reynolds, T.K.; Zax, D.B.; DiSalvo, F.J. Ca6(Cr2N6)H, the first quaternary nitride–Hydride. Inorg. Chem. 2003, 42, 5572–5578. [Google Scholar] [CrossRef] [PubMed]
- Höhn, P.; Ballé, J.T.; Fix, M.; Prots, Y.; Jesche, A. Single Crystal Growth and Anisotropic Magnetic Properties of Li2Sr[Li1-xFexN]2. Inorganics 2016, 4, 4040042. [Google Scholar] [CrossRef]
- STOE & Cie GmbH. WinXPow; STOE & Cie GmbH: Darmstadt, Germany, 2003. [Google Scholar]
- Altomare, A.; Camalli, M.; Cuocci, C.; Giacovazzo, C.; Moliterni, A.; Rizzi, R. EXPO2009: Structure solution by powder data in direct and reciprocal space. J. Appl. Crystallogr. 2009, 42, 1197–1202. [Google Scholar] [CrossRef]
- Petřiček, V.; Dušek, M.; Palatinus, L. Crystallographic Computing System JANA2006: General features. Z. Kristallogr. 2014, 229, 345–352. [Google Scholar] [CrossRef]
- Honda, K. Die thermomagnetischen Eigenschaften der Elemente. Ann. Phys. 1910, 337, 1027–1063. [Google Scholar] [CrossRef]
- Koepernik, K.; Eschrig, H. Full-potential nonorthogonal local-orbital minimum-basis band-structure scheme. Phys. Rev. B 1999, 59, 1743–1757. [Google Scholar] [CrossRef]
- Jepsen, O.; Burkhardt, A.; Andersen, O.K. The Stuttgart Tight-Binding LMTO-ASA Program; Version 4.7; Max-Planck-Institut für Festkörperforschung: Stuttgart, Germany, 1998. [Google Scholar]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
- Von Barth, U.; Hedin, L. Local exchange-correlation potential for spin polarized case: 1. J. Phys. C Solid State 1972, 5, 1629–1642. [Google Scholar] [CrossRef]
- Andersen, O.K. Linear Methods in Band Theory. Phys. Rev. B 1975, 12, 3060–3083. [Google Scholar] [CrossRef]
- Dronskowski, R.; Blöchl, P.E. Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations. J. Phys. Chem. 1993, 97, 8617–8624. [Google Scholar] [CrossRef]
- Kohout, M. DGRID 4.6; Springer: Radebeul, Germany, 2011. [Google Scholar]
- Bader, R.F.W. Atoms in Molecules—A Quantum Theory, 2003 ed.; Clarendon Press: Oxford, UK, 1994; Volume 22, pp. 1–456. [Google Scholar]
- Ludwig, M.; Niewa, R.; Kniep, R. Dimers [Al2N6]12− and chains 1∞[AlN4/23−] in the crystal structures of Ca6[Al2N6] and Ba3[Al2N4]. Z. Naturforsch. B 1999, 54, 461–465. [Google Scholar] [CrossRef]
- Blase, W.; Cordier, G.; Ludwig, M.; Kniep, R. Sr3[Al2N4]: Ein Nitridoaluminat mit gewellten Tetraederketten 1∞[AlN4/23−]. Z. Naturforsch. B 1994, 49, 501–505. [Google Scholar] [CrossRef]
- Clarke, S.J.; DiSalvo, F.J. Synthesis and structure of one-, two-, and three-dimensional alkaline earth metal gallium nitrides: Sr3Ga2N4, Ca3Ga2Ne4, and Sr3Ga3N5. Inorg. Chem. 1997, 36, 1143–1148. [Google Scholar] [CrossRef] [PubMed]
- Yamane, H.; DiSalvo, F.J. Ba3Ga2N4. Acta Crystallogr. C 1996, 52, 760–761. [Google Scholar] [CrossRef]
- Park, D.G.; Gál, Z.A.; DiSalvo, F.J. Sr3GeMgN4: New quaternary nitride containing Mg. J. Alloy. Compd. 2003, 360, 85–89. [Google Scholar] [CrossRef]
- Park, D.G.; DiSalvo, F.J. A Structural Comparison between a New Quaternary Nitride, Ba3GeMgN4, and Its Isostructural Sr analogue. Bull. Korean Chem. Soc. 2011, 32, 353–355. [Google Scholar] [CrossRef]
- Gudat, A.; Kniep, R.; Rabenau, A.; Bronger, W.; Ruschewitz, U. Li3FeN2, a ternary nitride with 1∞[FeN3−4/2] chains: Crystal structure and magnetic properties. J. Less Common Met. 1990, 161, 31–36. [Google Scholar] [CrossRef]
- Bérar, J.F.; Lelann, P. E.s.d.s and estimated probable-error obtained in Rietveld refinements with local correlations. J. Appl. Crystallogr. 1991, 24, 1–5. [Google Scholar] [CrossRef]
- Tennstedt, A.; Röhr, C.; Kniep, R. Sr3[MnN3] and Ba3[MnN3], the First Nitridomanganates(III): Trigonal-Planar Anions [MnIIIN3]6−. Z. Naturforsch. B 1993, 48, 794–796. [Google Scholar] [CrossRef]
- Yamada, T.; Fujii, Y. The Crystal Structure of α-Mn Reexamined on Single Crystal Specimens. J. Phys. Soc. Jpn. 1970, 28, 1503–1507. [Google Scholar] [CrossRef]
- Shoemaker, C.B.; Shoemaker, D.P.; Hopkins, T.E.; Yindepit, S. Refinement of the structure of b-manganese and of a related phase in the Mn-Ni-Si system. Acta Crystallogr. B 1978, 34, 3573–3576. [Google Scholar] [CrossRef]
- Aoki, M.; Yamane, H.; Shimada, M.; Kajiwara, T. Single crystal growth of Mn2N using an In-Na flux. Mater. Res. Bull. 2004, 39, 827–832. [Google Scholar] [CrossRef]
- Juza, R.; Deneke, K.; Puff, H. Ferrimagnetismus der Mischkristalle von Mn4N mit Chrom, Eisen und Nickel—41. Mitteilung über Metallnitride und -amide. Z. Elektrochem. 1959, 63, 551–557. [Google Scholar]
- Brese, N.E.; O’Keeffe, M. Bond-valence parameters for solids. Acta Crystallogr. B 1991, 47, 192–197. [Google Scholar] [CrossRef]
- Wintenberger, M.; Guyader, J.; Maunaye, M. Étude cristallographique et magnétique de MnGeN2 par diffraction neutronique. Solid State Commun. 1972, 11, 1485–1488. [Google Scholar] [CrossRef]
- Grins, J.; Käll, P.O.; Svensson, G. Synthesis and structural characterisation of MnWN2 prepared by ammonolysis of MnWO4. J. Mater. Chem. 1995, 5, 571–575. [Google Scholar] [CrossRef]
- Niewa, R.; Wagner, F.R.; Schnelle, W.; Hochrein, O.; Kniep, R. Li24[MnN3]3N2 and Li5[(Li1-xMnx)N]3, Two Intermediates in the Decomposition Path of Li7[MnN4] to Li2[(Li1-xMnx)N]: An Experimental and Theoretical Study. Inorg. Chem. 2001, 40, 5215–5222. [Google Scholar] [CrossRef] [PubMed]
- Coey, J.M.D.; Viret, M.; von Molnar, S. Mixed-valence manganites. Adv. Phys. 1999, 48, 167–293. [Google Scholar] [CrossRef]
- Nuss, J.; Dasari, P.L.V.K.; Jansen, M. K5Mn3O6 and Rb8Mn5O10, New Charge Ordered Quasi One-Dimensional Oxomanganates (II, III). Z. Anorg. Allg. Chem. 2015, 641, 316–321. [Google Scholar] [CrossRef]
- Michel, C.; Baranovskii, S.D.; Klar, P.J.; Thomas, P.; Goldlucke, B. Strong non-Arrhenius temperature dependence of the resistivity in the regime of traditional band transport. Appl. Phys. Lett. 2006, 89, 112116. [Google Scholar] [CrossRef]
- Ming, X.; Wang, X.L.; Du, F.; Han, B.; Wang, C.Z.; Chen, G. Unusual intermediate spin Fe3+ ion in antiferromagnetic Li3FeN2. J. Appl. Phys. 2012, 111, 063704. [Google Scholar] [CrossRef]
- Bronger, W.; Baranov, A.; Wagner, F.R.; Kniep, R. Atom Volumina and Charge Distributions in Nitridometalates. Z. Anorg. Allg. Chem. 2007, 633, 2553–2557. [Google Scholar] [CrossRef]
- Jiang, H.C.; Kruger, F.; Moore, J.E.; Sheng, D.N.; Zaanen, J.; Weng, Z.Y. Phase diagram of the frustrated spatially-anisotropic S = 1 antiferromagnet on a square lattice. Phys. Rev. B 2009, 79, 174409. [Google Scholar] [CrossRef]
- Ovchinnikov, A.; Bobnar, M.; Prots, Y.; Borrmann, H.; Sichelschmidt, J.; Grin, Y.; Höhn, P. Ca12[Mn19N23] and Ca133[Mn216N260]: Structural complexity by 2D intergrowth. Angew. Chem. 2018. [Google Scholar] [CrossRef]
- Niewa, R.; Zherebtsov, D.A.; Schnelle, W.; Wagner, F.R. Metal-metal bonding in ScTaN2. A new compound in the system ScN-TaN. Inorg. Chem. 2004, 43, 6188–6194. [Google Scholar] [CrossRef] [PubMed]
- Bolvin, H.; Wagner, F.R. Case of a Strong Antiferromagnetic Exchange Coupling Induced by Spin Polarization of a Mn-Mn Partial Single Bond. Inorg. Chem. 2012, 51, 7112–7118. [Google Scholar] [CrossRef] [PubMed]
- Höhn, P.; Niewa, R. Nitrides of Non-Main Group Elements. In Handbook of Solid State Chemistry, Part 1. Materials and Structure of Solids; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2017; pp. 251–359. [Google Scholar]
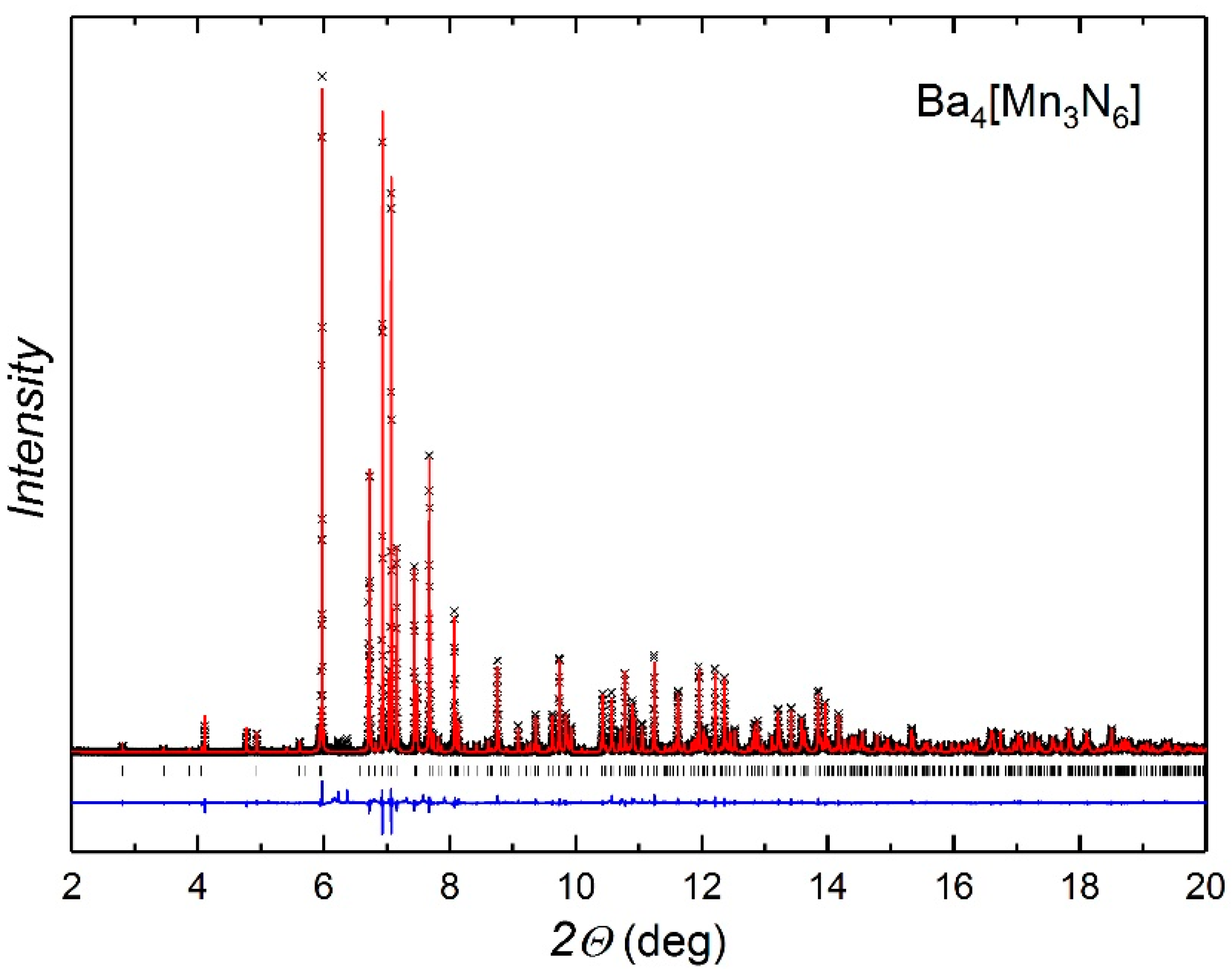
| Composition | Ba4Mn3N6 |
|---|---|
| Molecular weight/g mol−1 | 798.16 |
| Space group | Pbcn (#60) |
| Lattice parameters 1 | |
| a/Å | 9.9930(1) |
| b/Å | 6.17126(8) |
| c/Å | 14.4692(2) |
| V/Å3 | 892.31(2) |
| Z | 4 |
| ρcalcd/g cm−3 | 5.94 |
| T/K | 298 |
| Device | beamline ID22, ESRF |
| Radiation, λ/Å | 0.35434 |
| 2Θ max/o | 38 |
| 2Θ step/o | 0.002 |
| RI/Rp | 0.044/0.058 |
| Residual electron density peaks/e Å−3 | +1.10, −0.94 |
| Atom | Site | x | y | z | Uiso*/Ueq |
|---|---|---|---|---|---|
| Ba1 | 8d | 0.82617(7) | 0.68848(10) | 0.19158(4) | 0.00687(19) |
| Ba2 | 8d | 0.65129(6) | 0.93009(10) | 0.94504(4) | 0.0077(2) |
| Mn1 | 4c | 0 | 0.1719(4) | 1/4 | 0.0066(6)* |
| Mn2 | 8d | 0.00844(13) | 0.0660(3) | 0.08193(10) | 0.0055(4)* |
| N1 | 8d | 0.9009(7) | 0.8512(11) | 0.0291(5) | 0.0067(11)* 2 |
| N2 | 8d | 0.1212(7) | 0.9716(10) | 0.1690(5) | 0.0067* 2 |
| N3 | 8d | 0.9288(7) | 0.3008(12) | 0.1347(5) | 0.0067* 2 |
| Atom | U11 | U22 | U33 | U12 | U13 | U23 |
|---|---|---|---|---|---|---|
| Ba1 | 0.0088(3) | 0.0061(3) | 0.0058(3) | 0.0003(4) | 0.0016(3) | −0.0008(3) |
| Ba2 | 0.0066(3) | 0.0079(3) | 0.0085(4) | 0.0004(3) | −0.0015(4) | −0.0011(4) |
| Structure | AFM1 | AFM2 |
|---|---|---|
| energy E with respect to AFM1 (meV f.u.−1) | 0 | 0.7 |
| electronic bandgap Eg (eV) | 0.17 | 0.18 |
| magnetic moment on Mn2+ (μB) | 2.96 | 2.96 |
| magnetic moment on Mn4+ (μB) | 1.10 | 1.09 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ovchinnikov, A.; Bobnar, M.; Prots, Y.; Schnelle, W.; Höhn, P.; Grin, Y. Ba4[Mn3N6], a Quasi-One-Dimensional Mixed-Valent Nitridomanganate (II, IV). Crystals 2018, 8, 235. https://doi.org/10.3390/cryst8060235
Ovchinnikov A, Bobnar M, Prots Y, Schnelle W, Höhn P, Grin Y. Ba4[Mn3N6], a Quasi-One-Dimensional Mixed-Valent Nitridomanganate (II, IV). Crystals. 2018; 8(6):235. https://doi.org/10.3390/cryst8060235
Chicago/Turabian StyleOvchinnikov, Alexander, Matej Bobnar, Yurii Prots, Walter Schnelle, Peter Höhn, and Yuri Grin. 2018. "Ba4[Mn3N6], a Quasi-One-Dimensional Mixed-Valent Nitridomanganate (II, IV)" Crystals 8, no. 6: 235. https://doi.org/10.3390/cryst8060235
APA StyleOvchinnikov, A., Bobnar, M., Prots, Y., Schnelle, W., Höhn, P., & Grin, Y. (2018). Ba4[Mn3N6], a Quasi-One-Dimensional Mixed-Valent Nitridomanganate (II, IV). Crystals, 8(6), 235. https://doi.org/10.3390/cryst8060235