Coupling between Spin and Charge Order Driven by Magnetic Field in Triangular Ising System LuFe2O4+δ
Abstract
:1. Introduction
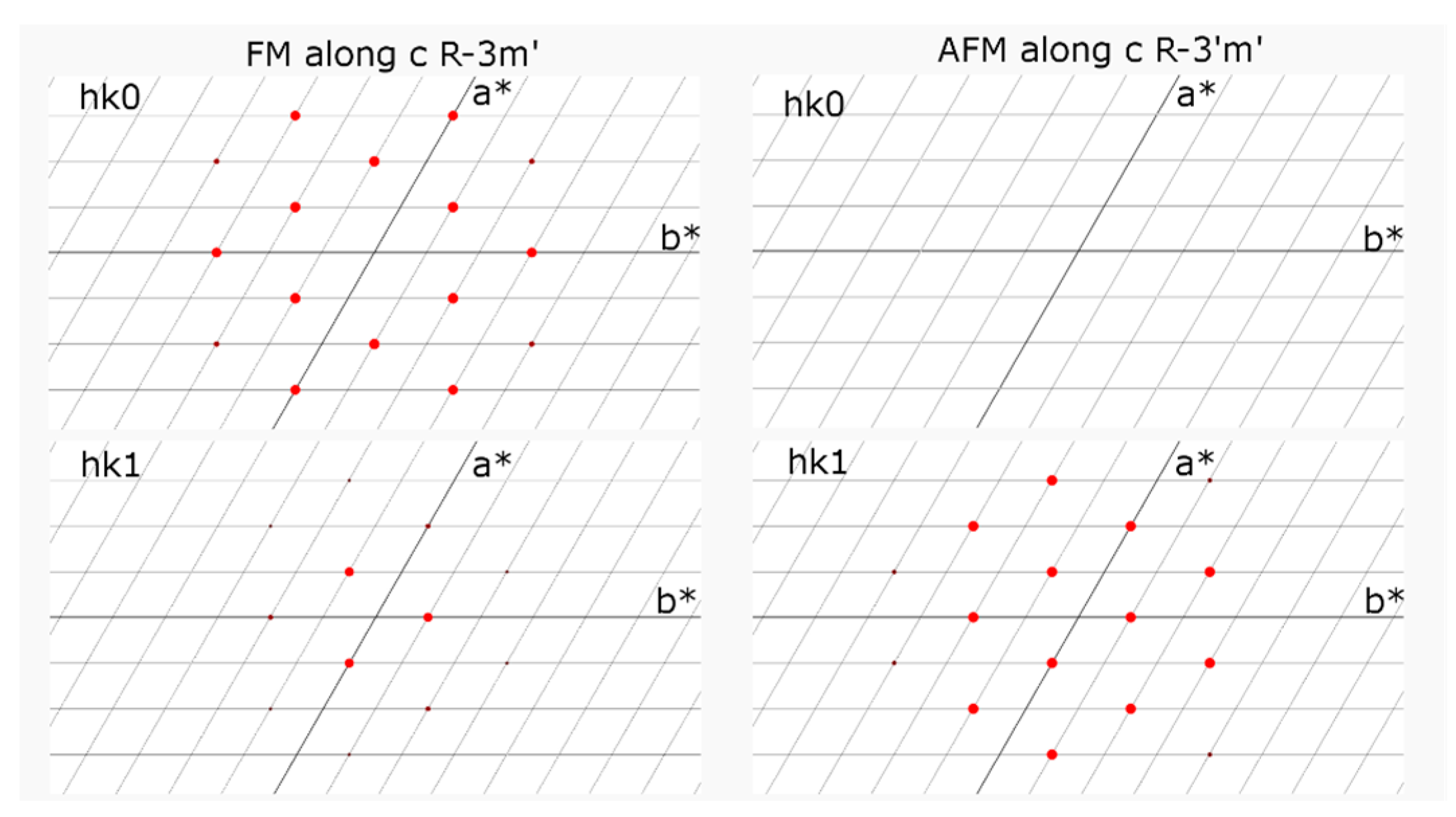
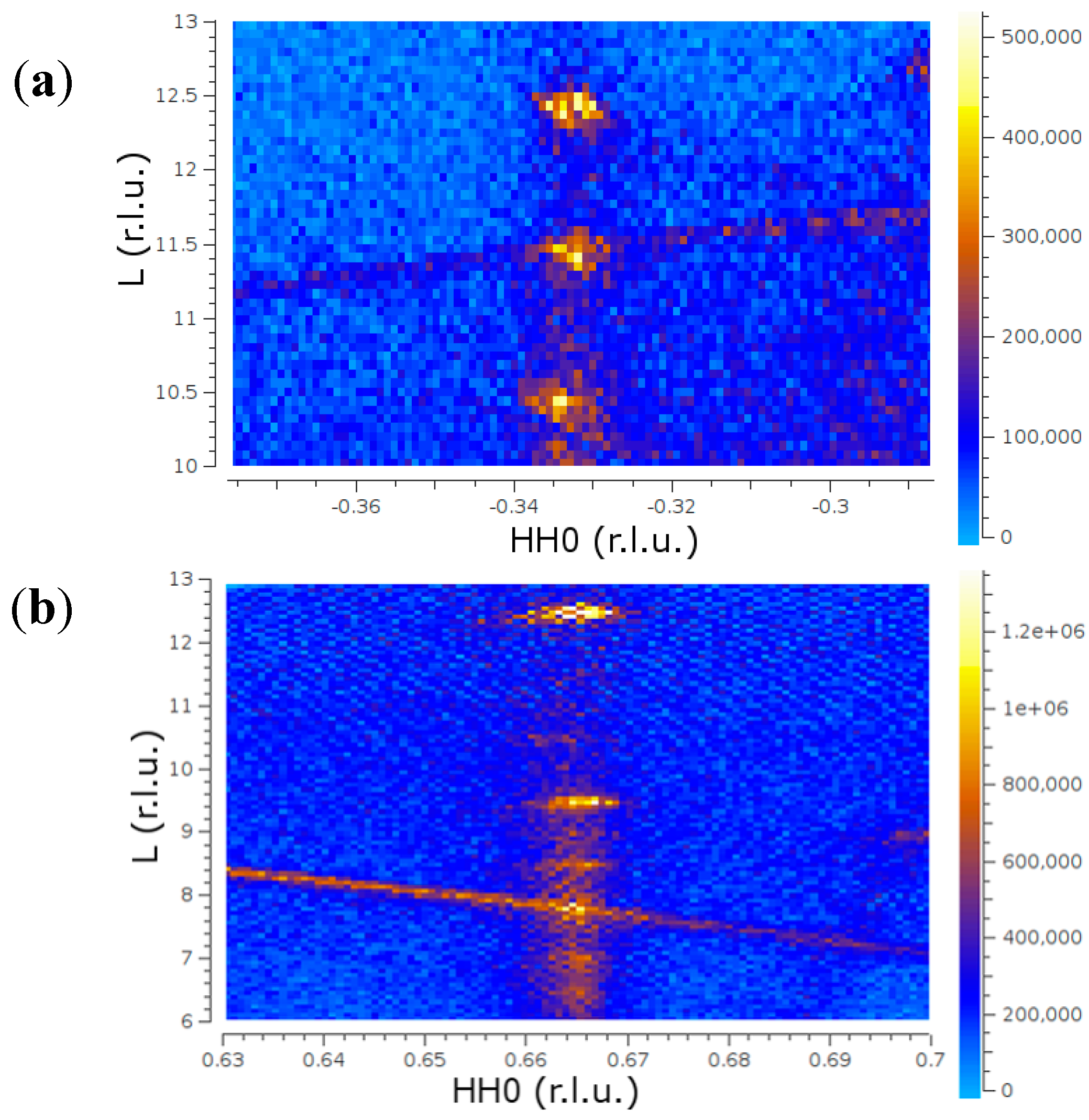
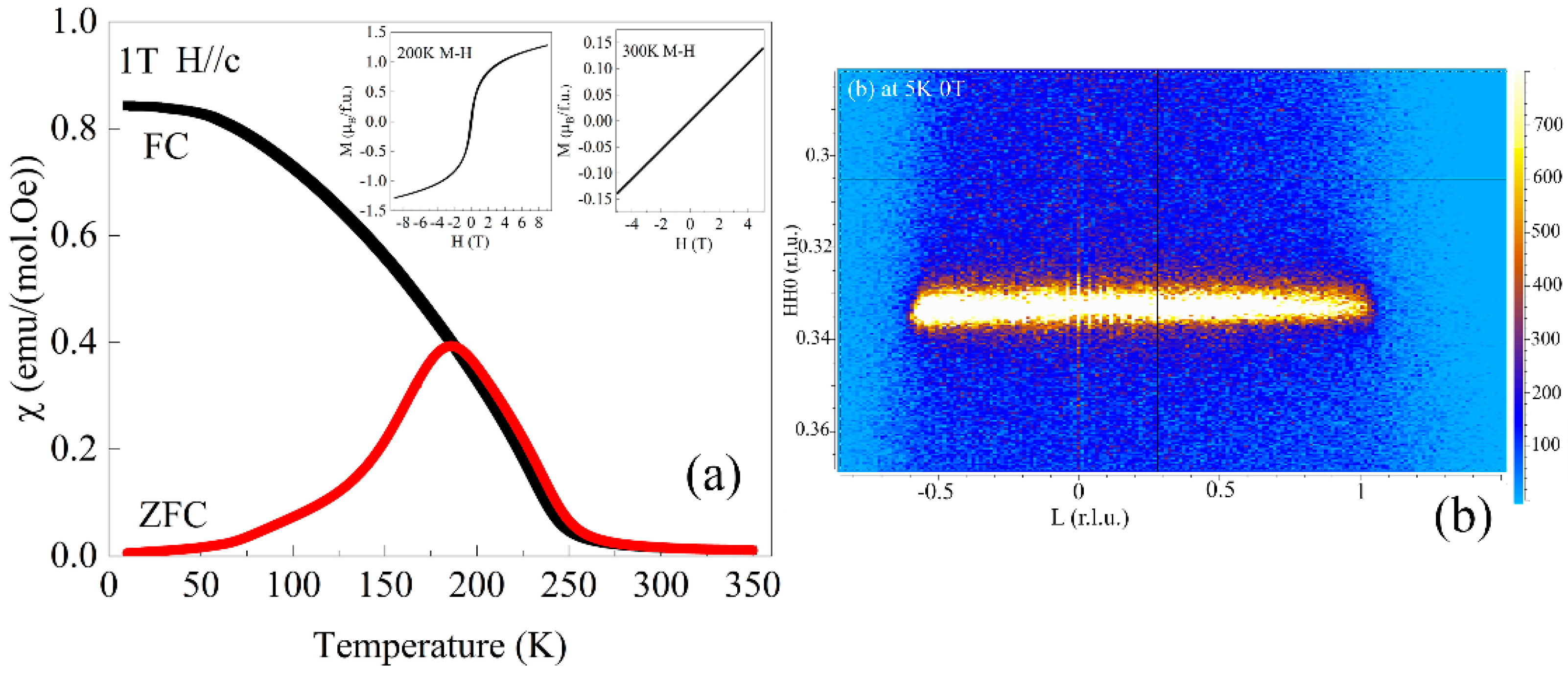
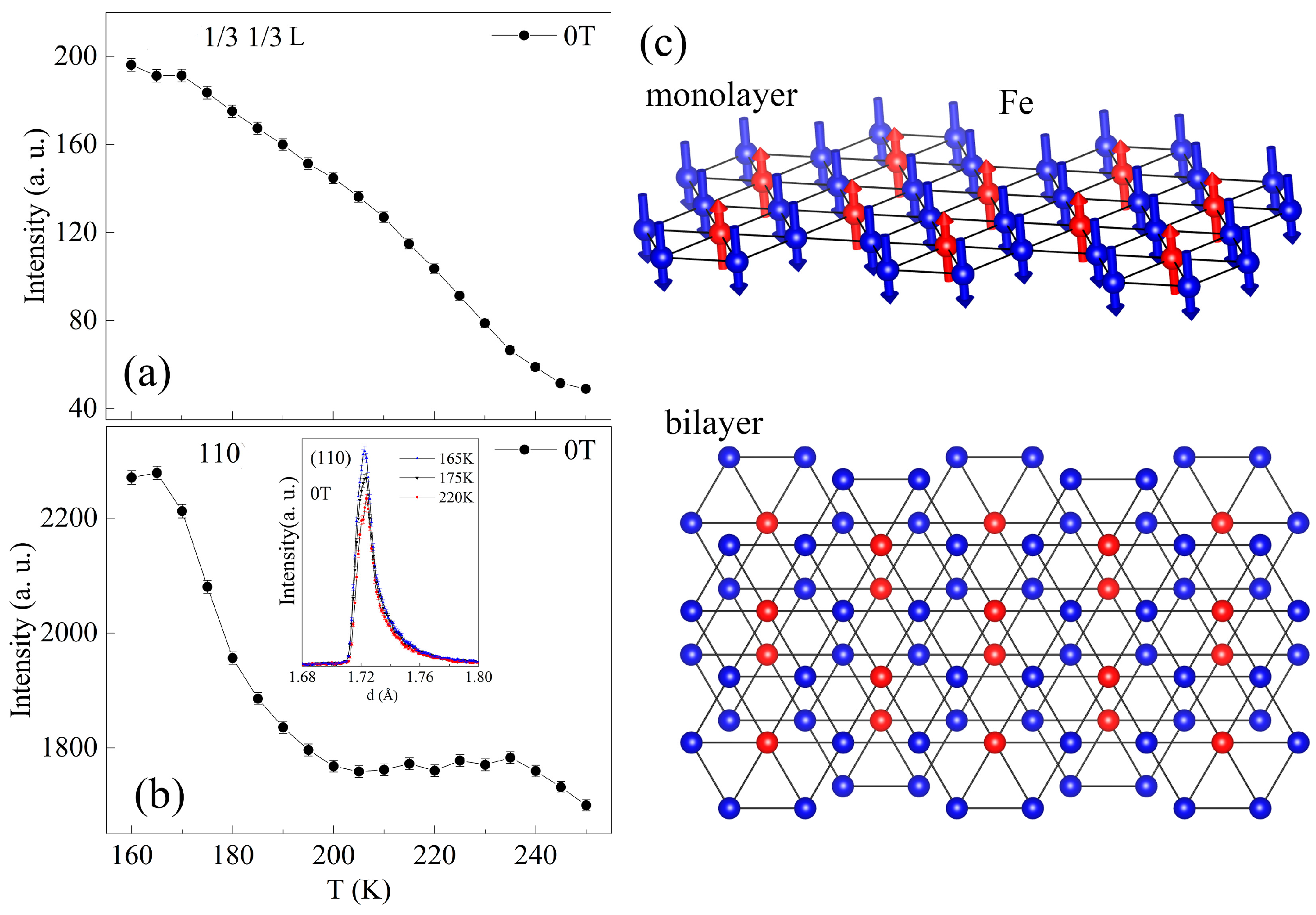
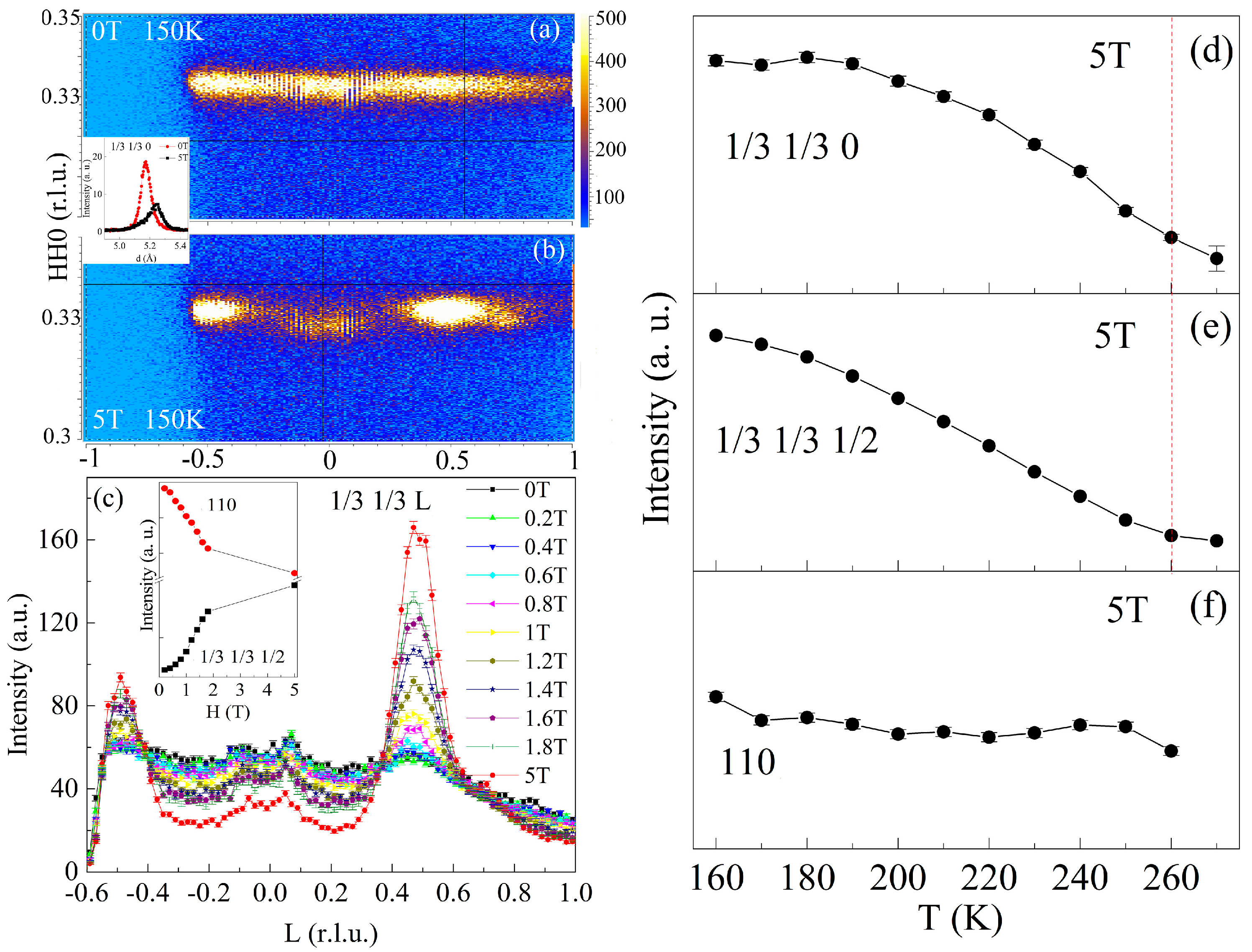
2. Results
3. Discussion
4. Experiments and Methods
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Iida, J.; Tanaka, M.; Nakagawa, Y.; Funahashi, S.; Kimizuka, N.; Takekawa, S. Magnetization and spin correlation of two-dimensional triangular antiferromagnet LuFe2O4. J. Phys. Soc. Jpn. 1993, 62, 1723–1735. [Google Scholar] [CrossRef]
- Yamada, Y.; Kitsuda, K.; Nohdo, S.; Ikeda, N. Charge and spin ordering process in the mixed-valence system LuFe2O4: Charge ordering. Phys. Rev. B 2000, 62, 12167–12174. [Google Scholar] [CrossRef]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakurai, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from iron valence ordering in the charge-frustrated system LuFe2O4. Nature 2005, 436, 1136–1138. [Google Scholar] [CrossRef] [PubMed]
- Nagano, A.; Naka, M.; Nasu, J.; Ishihara, S. Electric polarization, magnetoelectric effect, and orbital state of a layered iron oxide with frustrated geometry. Phys. Rev. Lett. 2007, 99, 217202. [Google Scholar] [CrossRef] [PubMed]
- Xiang, H.J.; Whangbo, M.H. Charge order and the origin of giant magnetocapacitance in LuFe2O4. Phys. Rev. Lett. 2007, 98, 246403. [Google Scholar] [CrossRef] [PubMed]
- Angst, M.; Hermann, R.P.; Christianson, A.D.; Lumsden, M.D.; Lee, C.; Whangbo, M.H.; Kim, J.W.; Ryan, P.J.; Nagler, S.E.; Tian, W.; et al. Charge order in LuFe2O4: Antiferroelectric ground state and coupling to magnetism. Phys. Rev. Lett. 2008, 101, 227601. [Google Scholar] [CrossRef] [PubMed]
- De Groot, J.; Mueller, T.; Rosenberg, R.A.; Keavney, D.J.; Islam, Z.; Kim, J.W.; Angst, M. Charge order in LuFe2O4: An unlikely route to ferroelectricity. Phys. Rev. Lett. 2012, 108, 187601. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, N.; Nagata, T.; Kano, J.; Mori, S. Present status of the experimental aspect of RFe2O4 study. J. Phys. Condens. Matter 2015, 27, 053201. [Google Scholar] [CrossRef] [PubMed]
- Xu, X.S.; De Groot, J.; Sun, Q.C.; Sales, B.C.; Mandrus, D.; Angst, M.; Litvinchuk, A.P.; Musfeldt, J.L. Lattice dynamical probe of charge order and antipolar bilayer stacking in LuFe2O4. Phys. Rev. B 2010, 82, 014304. [Google Scholar] [CrossRef]
- Ko, K.T.; Noh, H.J.; Kim, J.Y.; Park, B.G.; Park, J.H.; Tanaka, A.; Kim, S.B.; Zhang, C.L.; Cheong, S.W. Electronic origin of giant magnetic anisotropy in multiferroic LuFe2O4. Phys. Rev. Lett. 2009, 103, 207202. [Google Scholar] [CrossRef] [PubMed]
- Wen, J.S.; Xu, G.Y.; Gu, G.D.; Shapiro, S.M. Magnetic-field control of charge structures in the magnetically disordered phase of multiferroic LuFe2O4. Phys. Rev. B 2009, 80, 020403. [Google Scholar] [CrossRef]
- Mulders, A.M.; Bartkowiak, M.; Hester, J.R.; Pomjakushina, E.; Conder, K. Ferroelectric charge order stabilized by antiferromagnetism in multiferroic LuFe2O4. Phys. Rev. B 2011, 84, 140403(R). [Google Scholar] [CrossRef]
- Harris, A.B.; Yildirim, T. Charge and spin ordering in the mixed-valence compound LuFe2O4. Phys. Rev. B 2010, 81, 134417. [Google Scholar] [CrossRef]
- Christianson, A.D.; Lumsden, M.D.; Angst, M.; Yamani, Z.; Tian, W.; Jin, R.; Payzant, E.A.; Nagler, S.E.; Sales, B.C.; Mandrus, D. Three-dimensional magnetic correlations in multiferroic LuFe2O4. Phys. Rev. Lett. 2008, 100, 107601. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Kim, J.; Kim, Y.; Gu, G.D. Spin-glass behaviour in in LuFe2O4+δ. Phys. Rev. B 2009, 80, 024419. [Google Scholar] [CrossRef]
- Bourgeois, J.; Andre, G.; Petit, S.; Robert, J.; Poienar, M.; Rouquette, J.; Elkaim, E.; Hervieu, M.; Maignan, A.; Martin, C.; et al. Evidence of magnetic phase separation in LuFe2O4. Phys. Rev. B 2012, 86, 024413. [Google Scholar] [CrossRef]
- Hervieu, M.; Guesdon, A.; Bourgeois, J.; Elkaim, E.; Poienar, M.; Damay, F.; Rouquette, J.; Maignan, A.; Martin, C. Oxygen storage capacity and structural flexibility of LuFe2O4+x (0 ≤ x ≤ 0.5). Nat. Mater. 2013, 13, 74–80. [Google Scholar] [CrossRef] [PubMed]
- Bourgeois, J.; Hervieu, M.; Poienar, M.; Abakumov, A.M.; Elkaim, E.; Sougrati, M.T.; Porcher, F.; Damay, F.; Rouquette, J.; Van Tendeloo, G.; et al. Evidence of oxygen-dependent modulation in LuFe2O4. Phys. Rev. B 2012, 85, 064102. [Google Scholar] [CrossRef]
- Xu, X.S.; Angst, M.; Brinzari, T.V.; Hermann, R.P.; Musfeldt, J.L.; Christianson, A.D.; Mandrus, D.; Sales, B.C.; McGill, S.; Kim, J.W.; et al. Charge order, dynamics, and magnetostructural transition in multiferroic LuFe2O4. Phys. Rev. Lett. 2008, 101, 227602. [Google Scholar] [CrossRef] [PubMed]
- De Groot, J.; Marty, K.; Lumsden, M.D.; Christianson, A.D.; Nagler, S.E.; Adiga, S.; Borghols, W.J.H.; Schmalzl, K.; Yamani, Z.; Bland, S.R.; et al. Competing Ferri- and Antiferromagnetic phases in geometrically frustrated LuFe2O4. Phys. Rev. Lett. 2012, 108, 037206. [Google Scholar] [CrossRef] [PubMed]
- Kuepper, K.; Raekers, M.; Taubitz, C.; Prinz, M.; Derks, C.; Neumann, M.; Postnikov, A.V.; De Groot, F.M.F.; Piamonteze, C.; Prabhakaran, D.; et al. Charge order, enhanced orbital moment, and absence of magnetic frustration in layered multiferroic LuFe2O4. Phys. Rev. Lett. 2009, 80, 220409(R). [Google Scholar]
- Gaw, S.M.; Lewtas, H.J.; McMorrow, D.F.; Kulda, J.; Ewings, R.A.; Perring, T.G.; McKinnon, R.A.; Balakrishnan, G.; Prabhakaran, D.; Boothroyd, A.T. Magnetic excitation spectrum of LuFe2O4 measured with inelastic neutron scattering. Phys. Rev. B 2015, 91, 035103. [Google Scholar] [CrossRef]
- Xiang, H.J.; Kan, E.J.; Wei, S.H.; Whangbo, M.H.; Yang, J.L. Origin of the Ising ferrimagnetism and spin-charge coupling in LuFe2O4. Phys. Rev. B 2009, 80, 132408. [Google Scholar] [CrossRef]
- Chapon, L.; Manuel, P.; Radaelli, P.G.; Benson, C.; Perrott, L.; Ansell, S.; Rhodes, N.J.; Raspino, D.; Duxbury, D.; Spill, E.; et al. Wish: The new powder and single crystal magnetic diffractometer on the second target station. Neutron News 2011, 22, 22–25. [Google Scholar] [CrossRef]
- Campbell, B.J.; Stokes, H.T.; Tanner, D.E.; Hatch, D.M. ISODISPLACE: A web-based tool for exploring structural distortions. J. Appl. Cryst. 2006, 39, 607–614. [Google Scholar] [CrossRef]
- Perez-Mato, J.M.; Gallego, S.V.; Tasci, E.S.; Elcoro, L.; de la Flor, G.; Aroyo, M.I. Symmetry-based computational tools for magnetic crystallography. Annu. Rev. Mater. Res. 2015, 45, 217–248. [Google Scholar] [CrossRef]
- Petricek, V.; Dusek, M.; Palatinus, L. Crystallographic computing system JANA2006: General features. Z. Kristallogr. Cryst. Mater. 2014, 229, 345–352. [Google Scholar] [CrossRef]

| Irrep | {3+|0,0,0} | {2xx|0,0,0} | {−1|0,0,0} | |
|---|---|---|---|---|
| Γ2+ | 1 | −1 | 1 | |
| Y1 | ||||
| Y2 | ||||
| Irrep | {1|1,0,0} | {1|0,0,1} | ||
| Γ2+ | 1 | 1 | ||
| Y1 | ||||
| Y2 | ||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Orlandi, F.; Khalyavin, D.D.; Boothroyd, A.T.; Prabhakaran, D.; Balakrishnan, G.; Manuel, P. Coupling between Spin and Charge Order Driven by Magnetic Field in Triangular Ising System LuFe2O4+δ. Crystals 2018, 8, 88. https://doi.org/10.3390/cryst8020088
Ding L, Orlandi F, Khalyavin DD, Boothroyd AT, Prabhakaran D, Balakrishnan G, Manuel P. Coupling between Spin and Charge Order Driven by Magnetic Field in Triangular Ising System LuFe2O4+δ. Crystals. 2018; 8(2):88. https://doi.org/10.3390/cryst8020088
Chicago/Turabian StyleDing, Lei, Fabio Orlandi, Dmitry D. Khalyavin, Andrew T. Boothroyd, Dharmalingam Prabhakaran, Geetha Balakrishnan, and Pascal Manuel. 2018. "Coupling between Spin and Charge Order Driven by Magnetic Field in Triangular Ising System LuFe2O4+δ" Crystals 8, no. 2: 88. https://doi.org/10.3390/cryst8020088
APA StyleDing, L., Orlandi, F., Khalyavin, D. D., Boothroyd, A. T., Prabhakaran, D., Balakrishnan, G., & Manuel, P. (2018). Coupling between Spin and Charge Order Driven by Magnetic Field in Triangular Ising System LuFe2O4+δ. Crystals, 8(2), 88. https://doi.org/10.3390/cryst8020088





