Analysis of Bending Waves in Phononic Crystal Beams with Defects
Abstract
:1. Introduction
2. Method of Reverberation-Ray Matrix
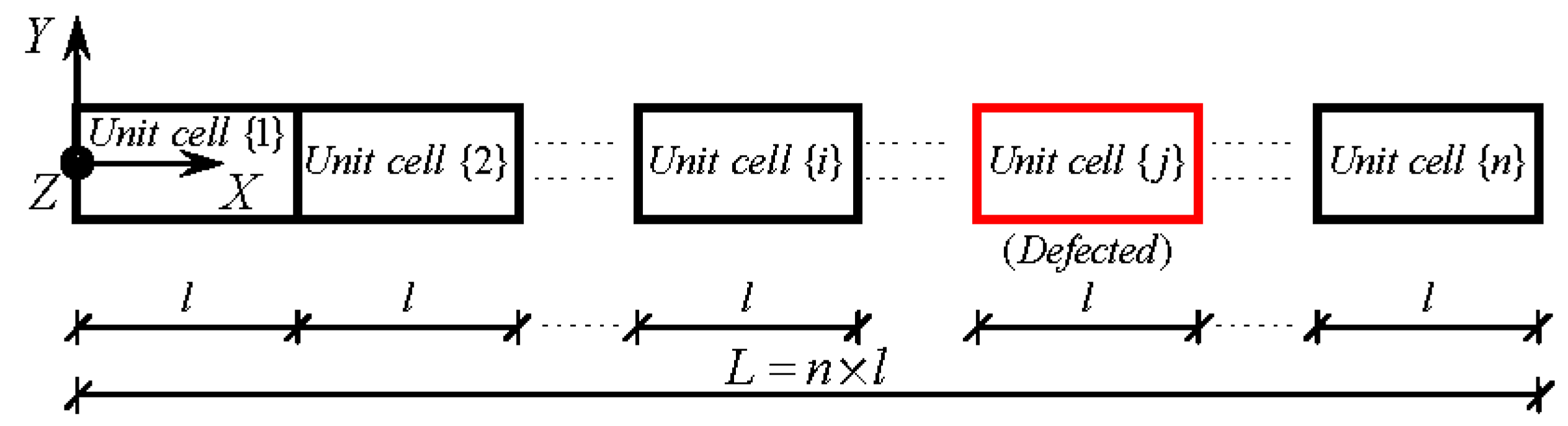
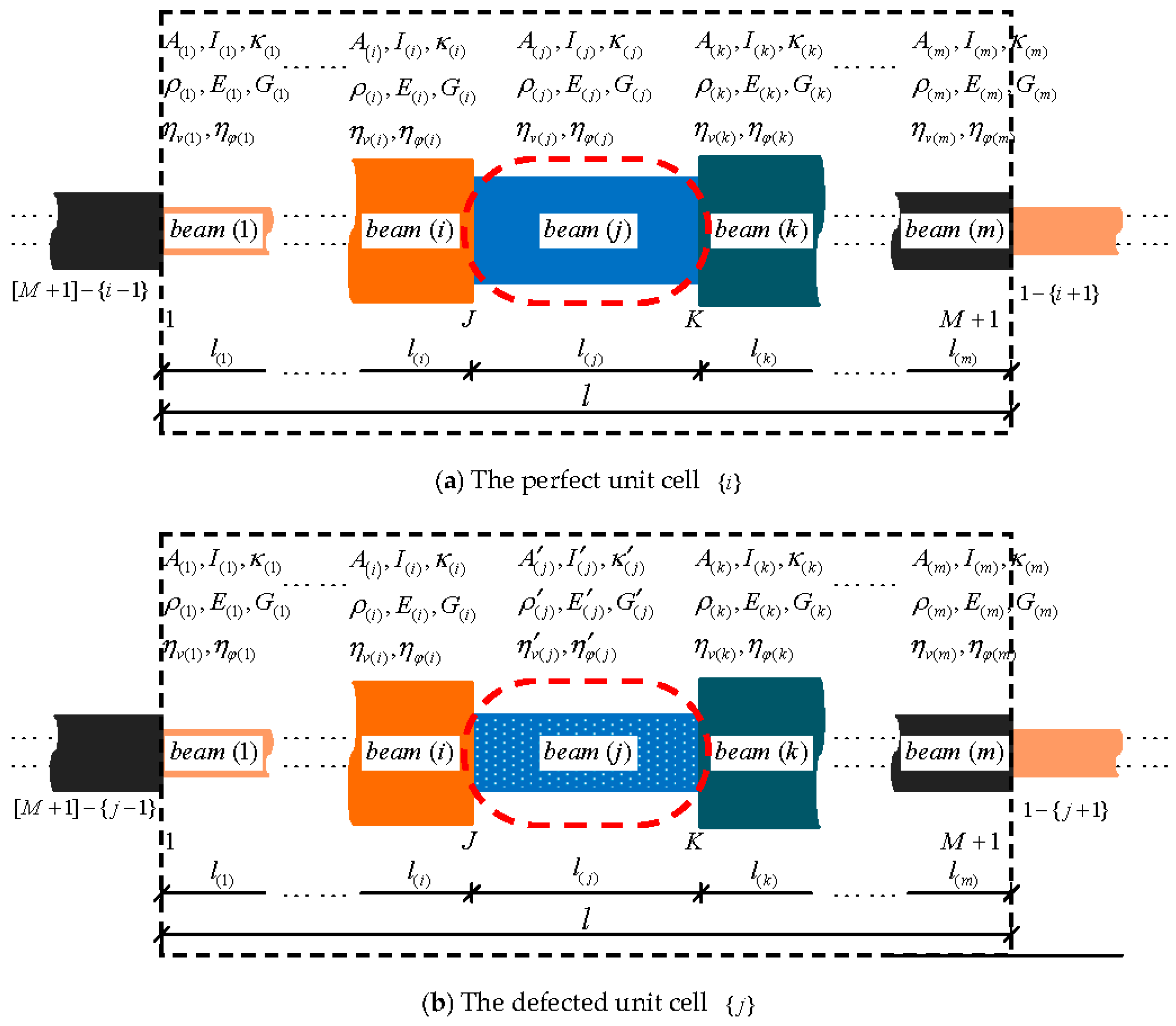
2.1. Analysis Model
2.2. Analysis of Members and Phase Relations
2.2.1. Governing Equations and Their Wave Solutions
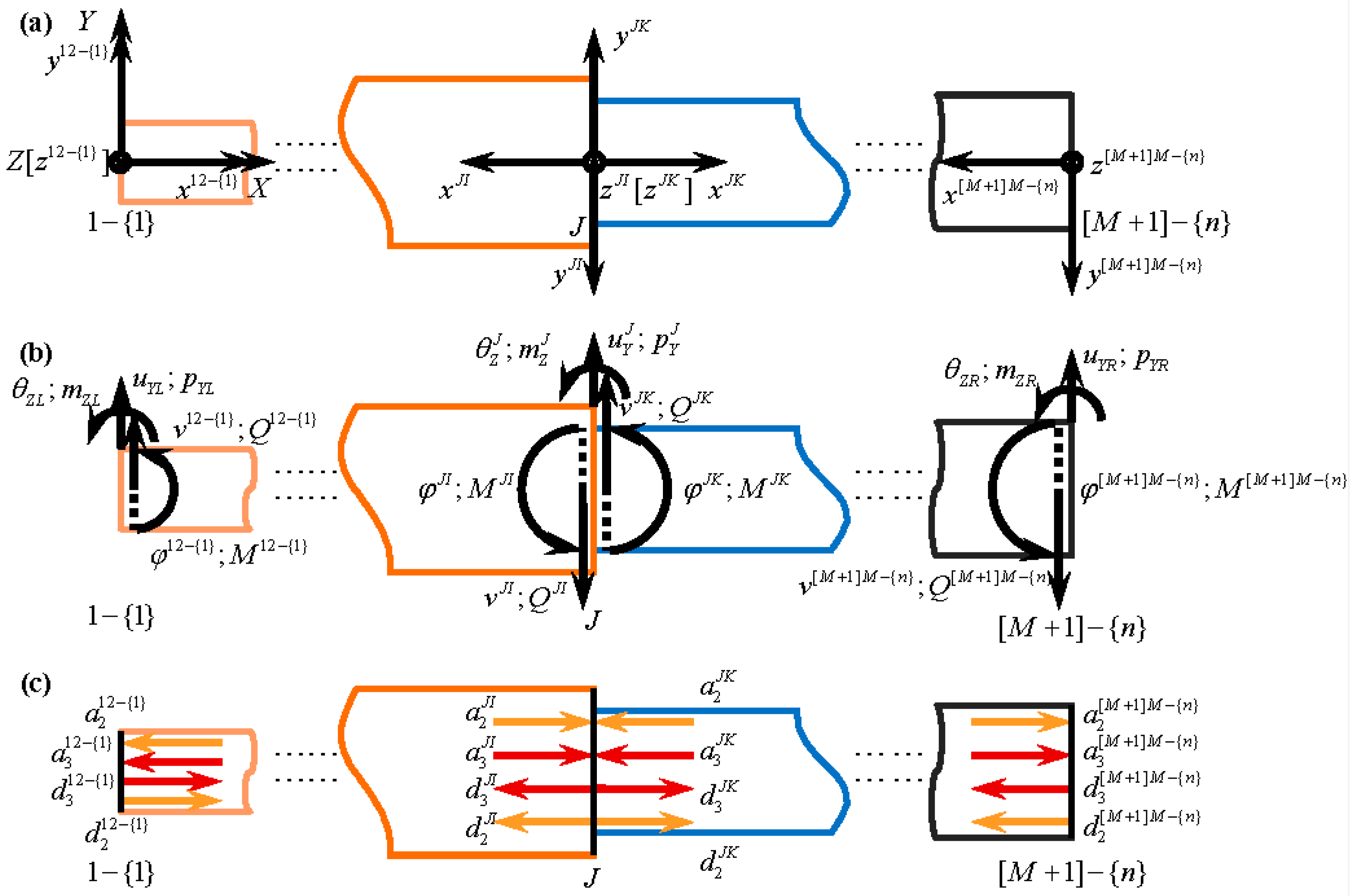
2.2.2. Relations between Wave Solutions in Dual Coordinates
2.2.3. Phase Relations of a Member
2.2.4. Global Phase Relations of the System
2.3. Analysis of Joints and the Scattering Relations
2.3.1. Continuous Equations and Scattering Relations at an Interior Joint
2.3.2. Coupling Equations and Scattering Relations of the Pair of Exterior Joints
2.3.3. Global Scattering Relations of the System
2.4. Analysis of Bending Wave Dispersion and Transmission from the System Equation
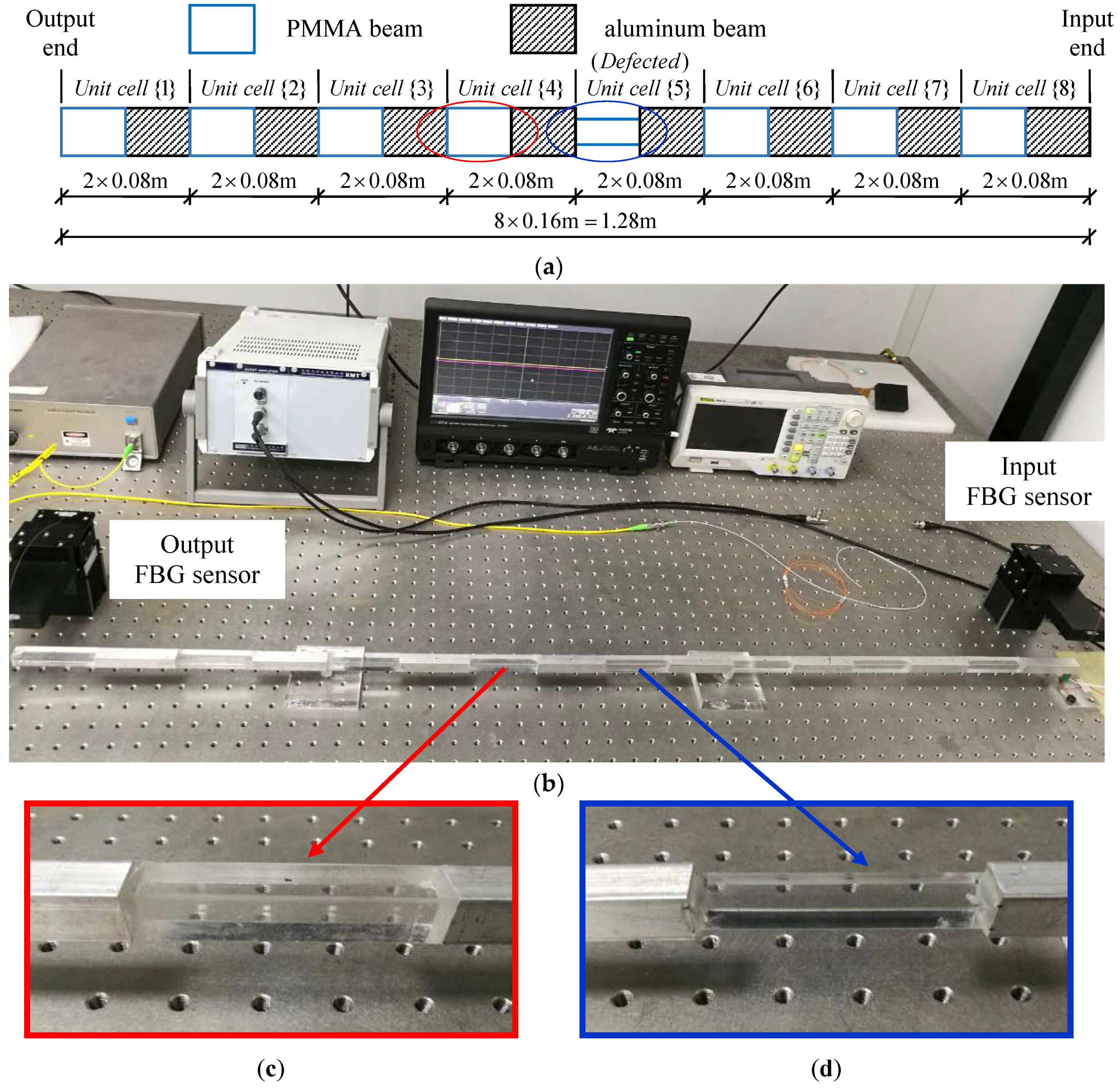
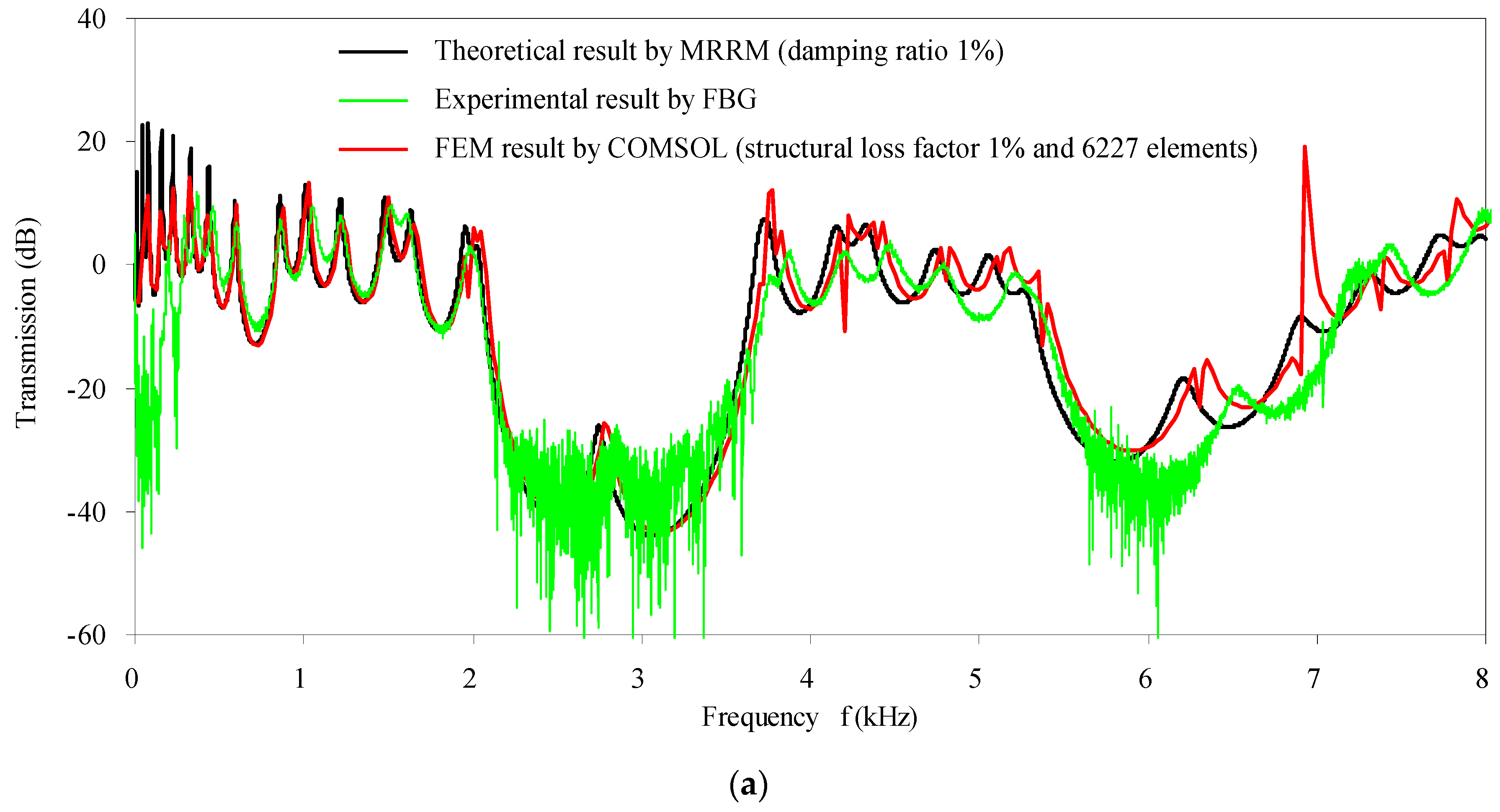
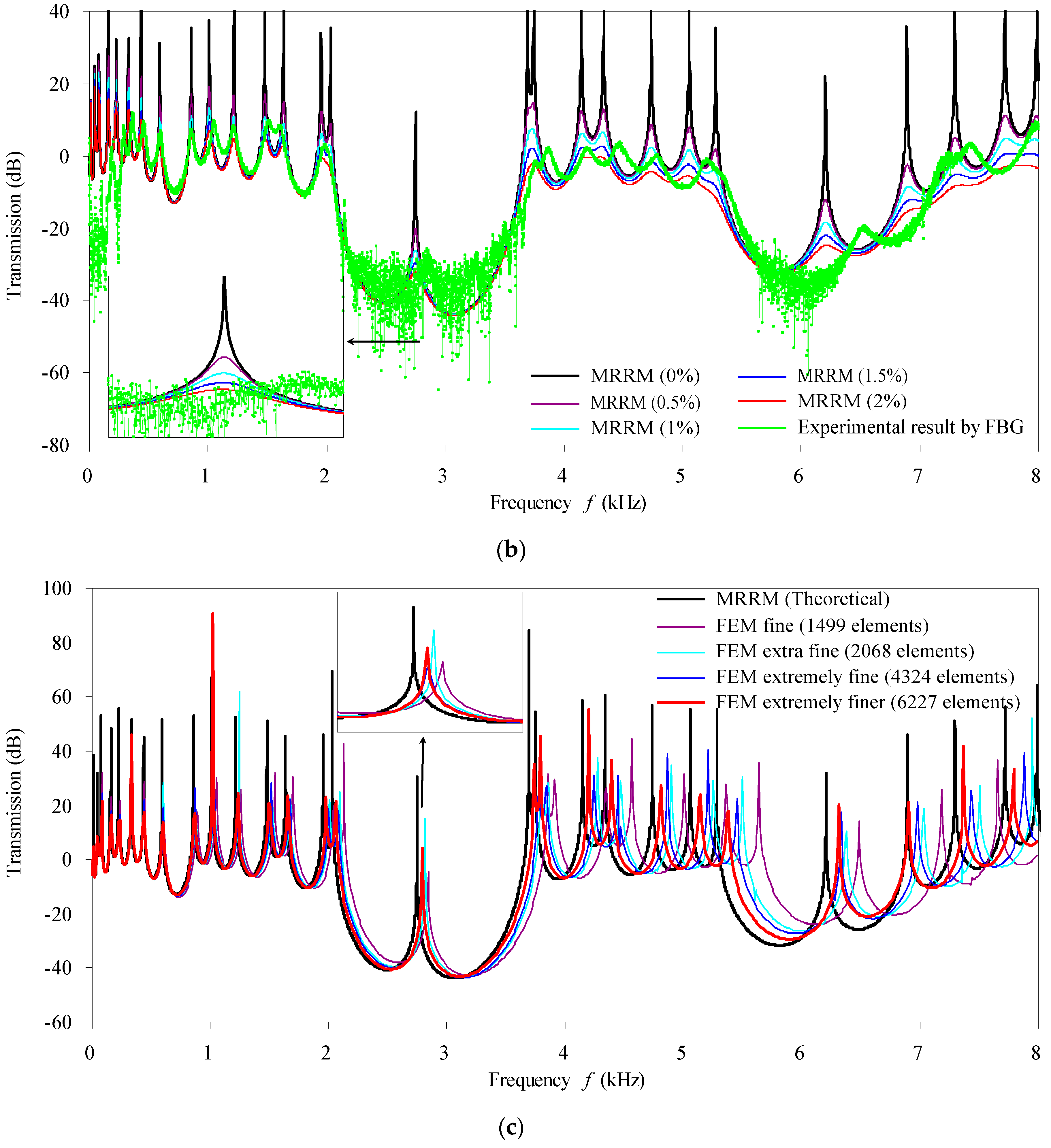
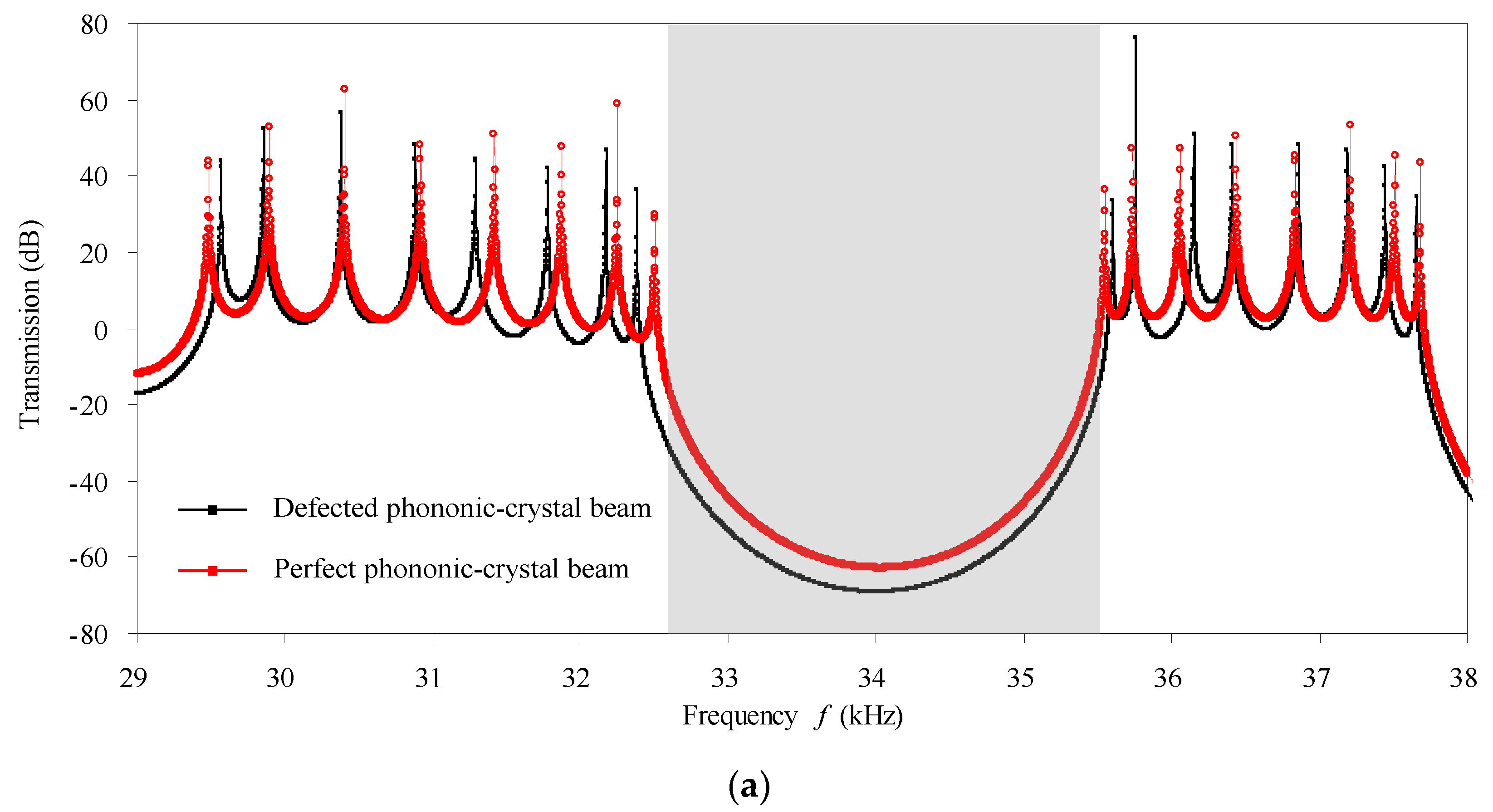
3. Validation of Theoretical Method by Experimental Measurement and Numerical Simulation
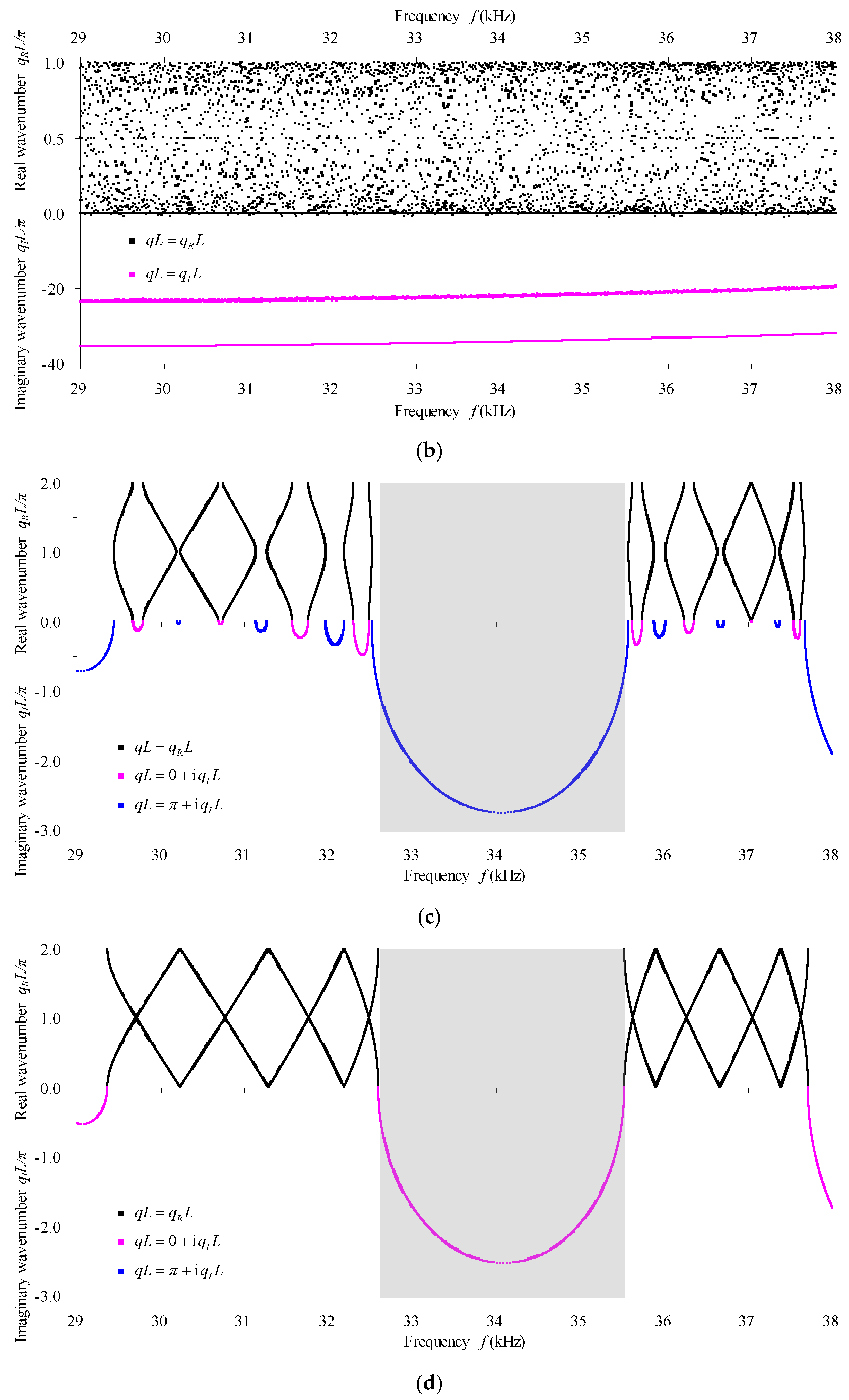
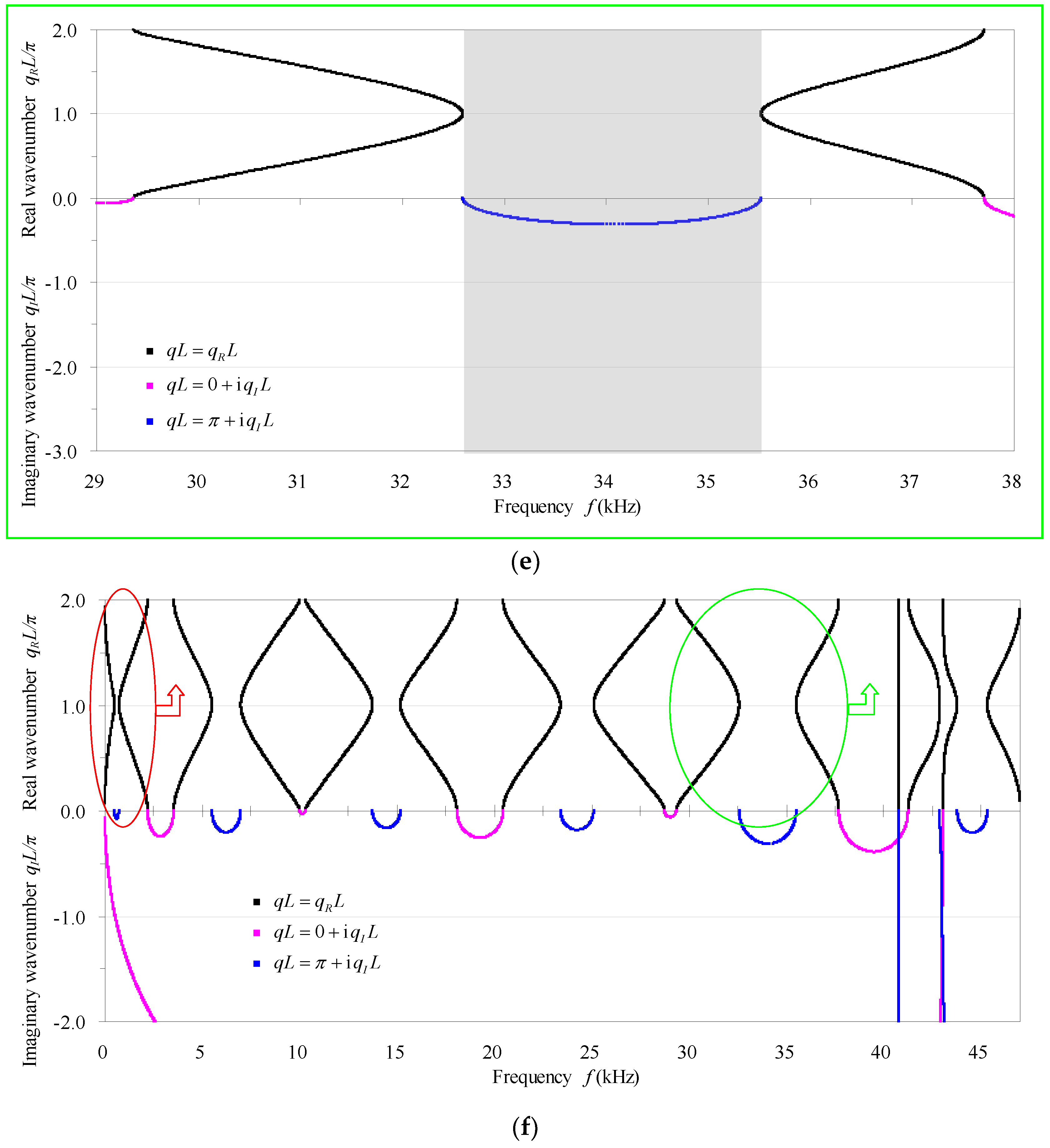
4. Results and Discussion
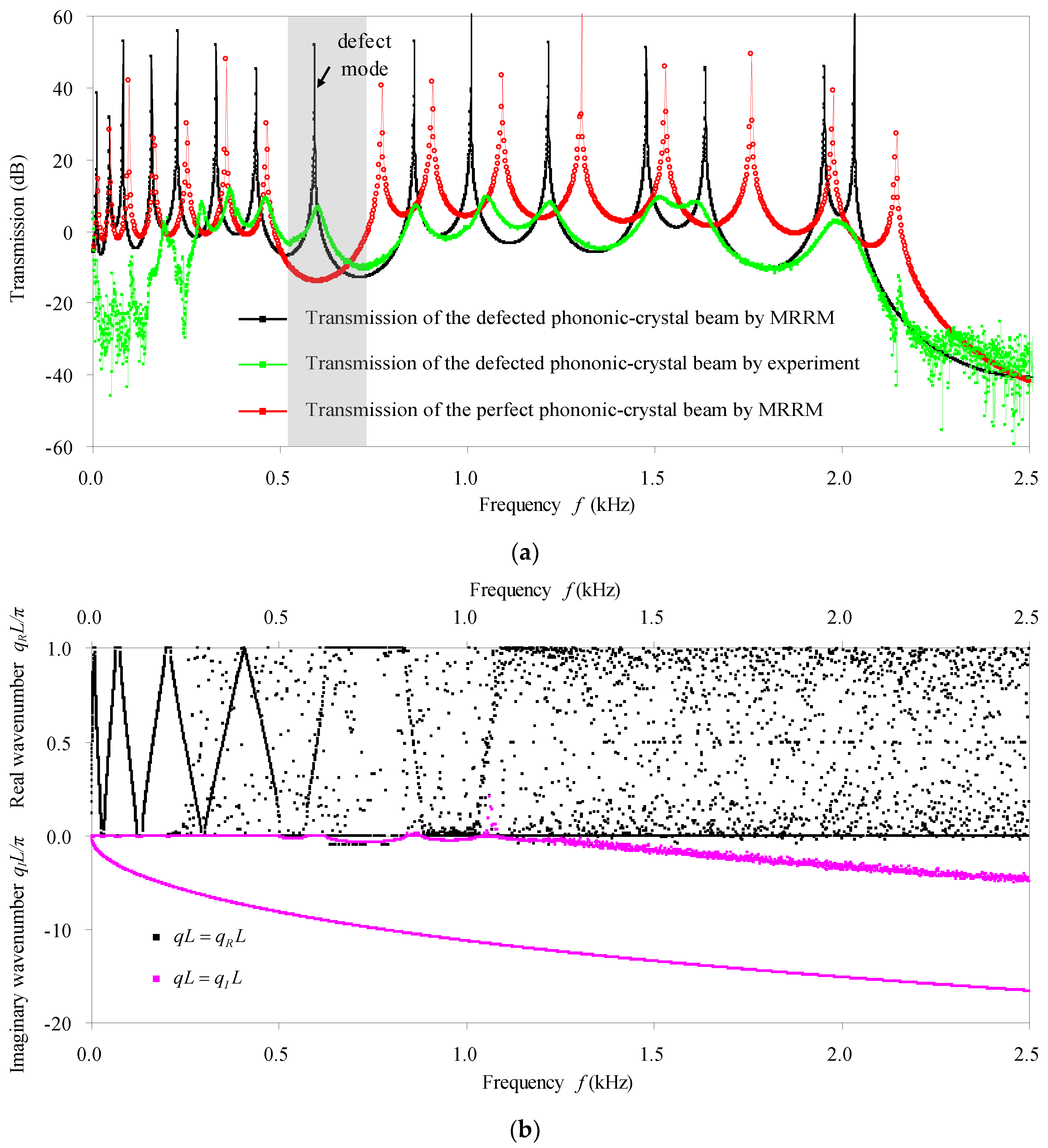
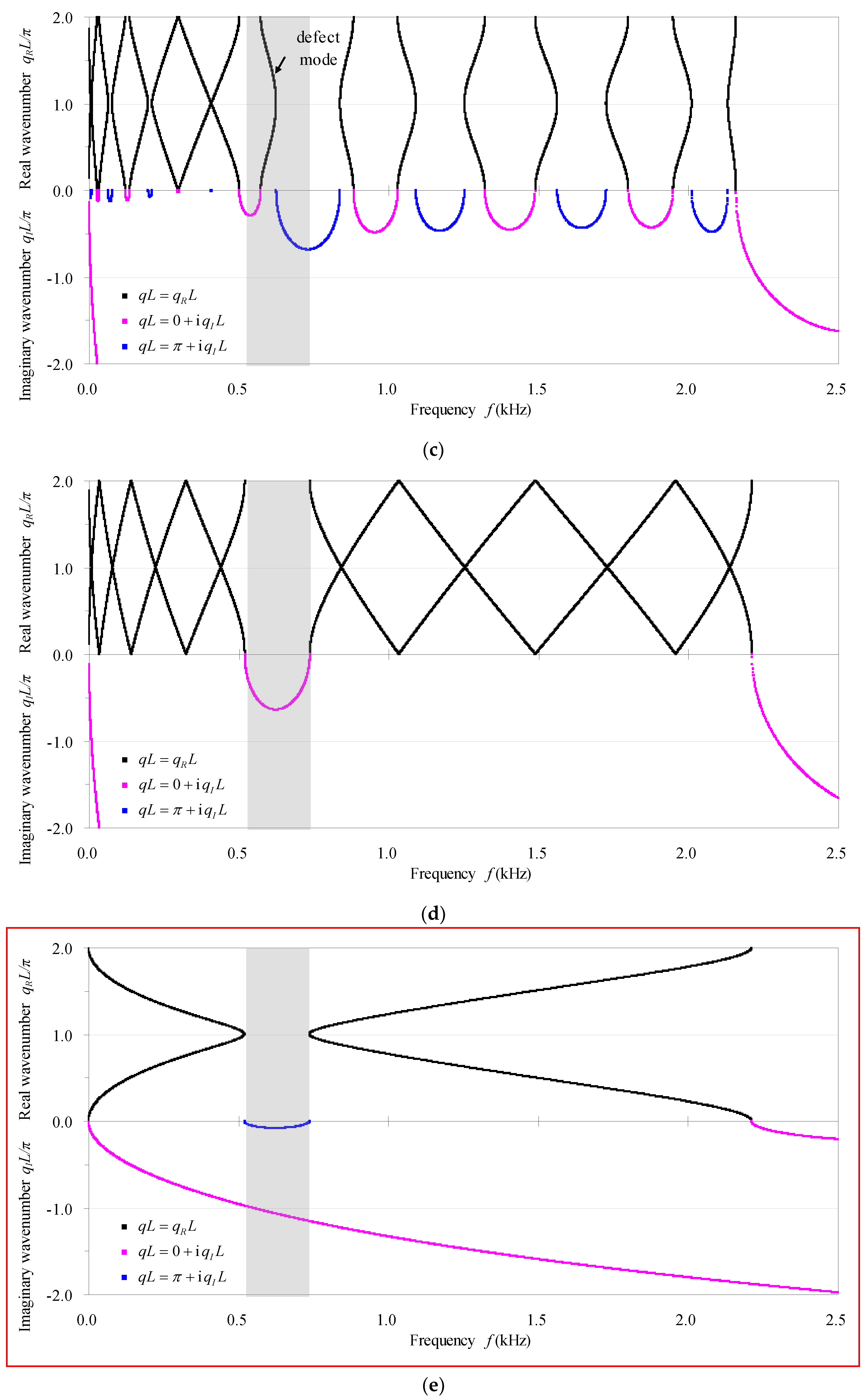
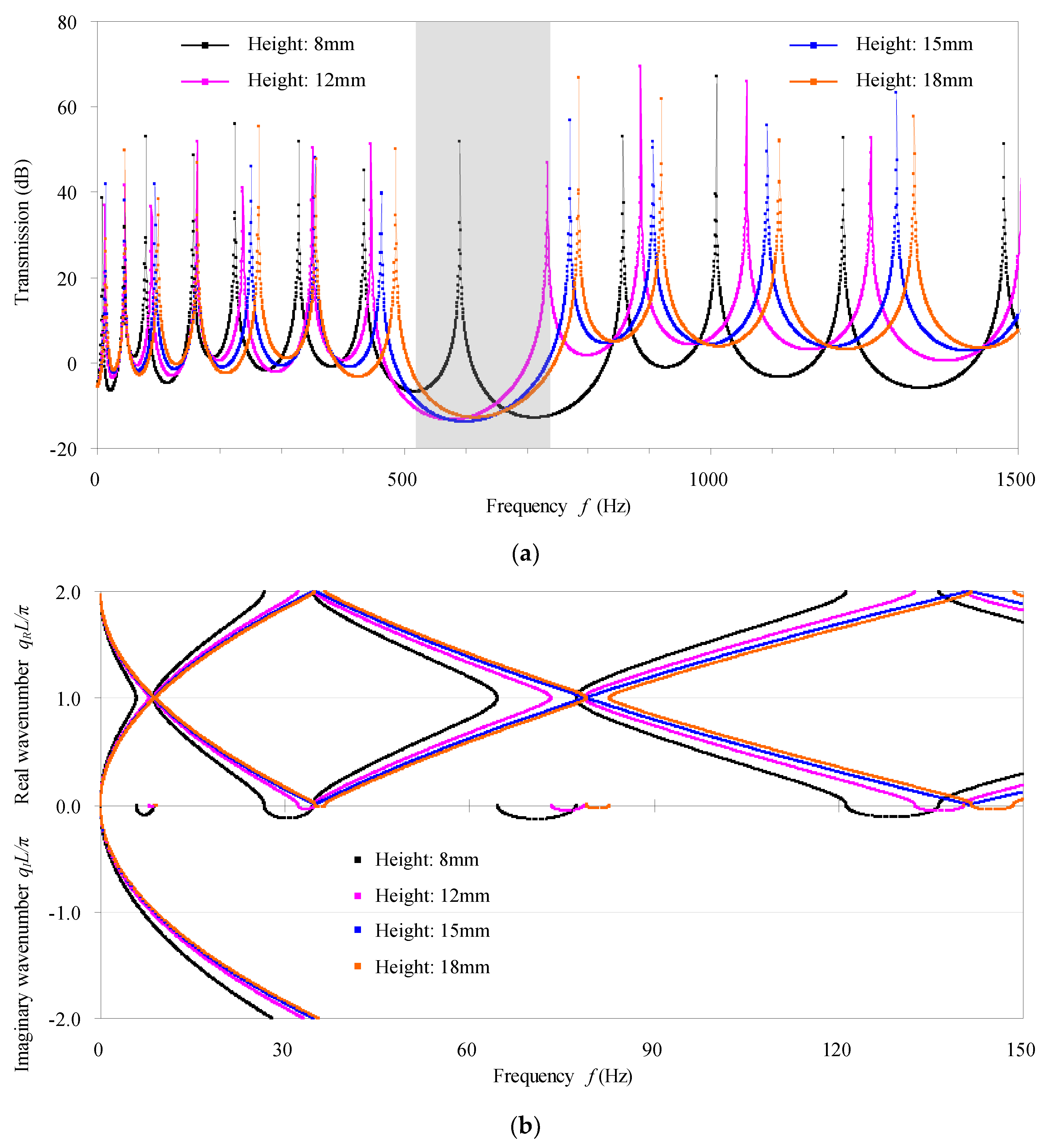
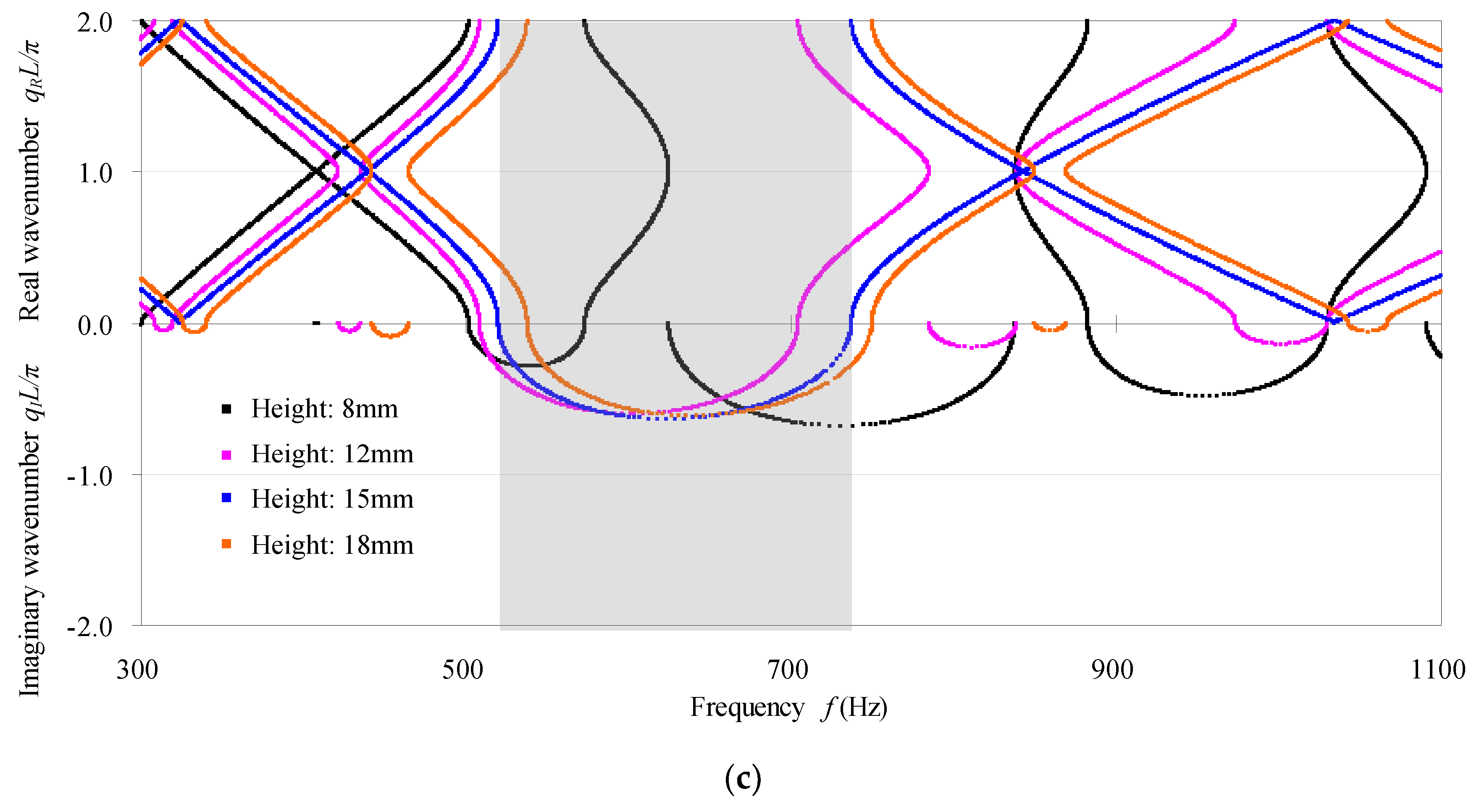
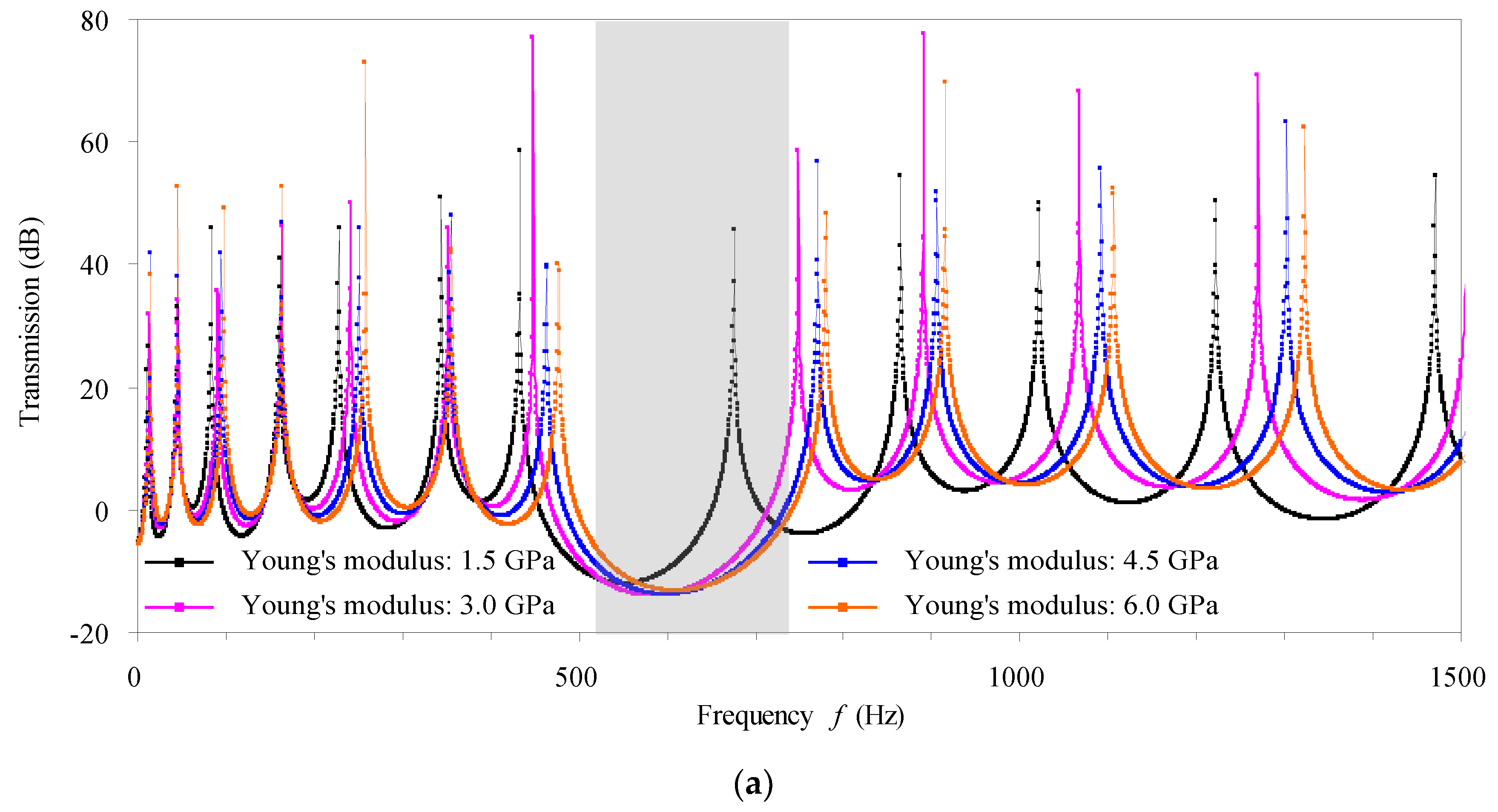
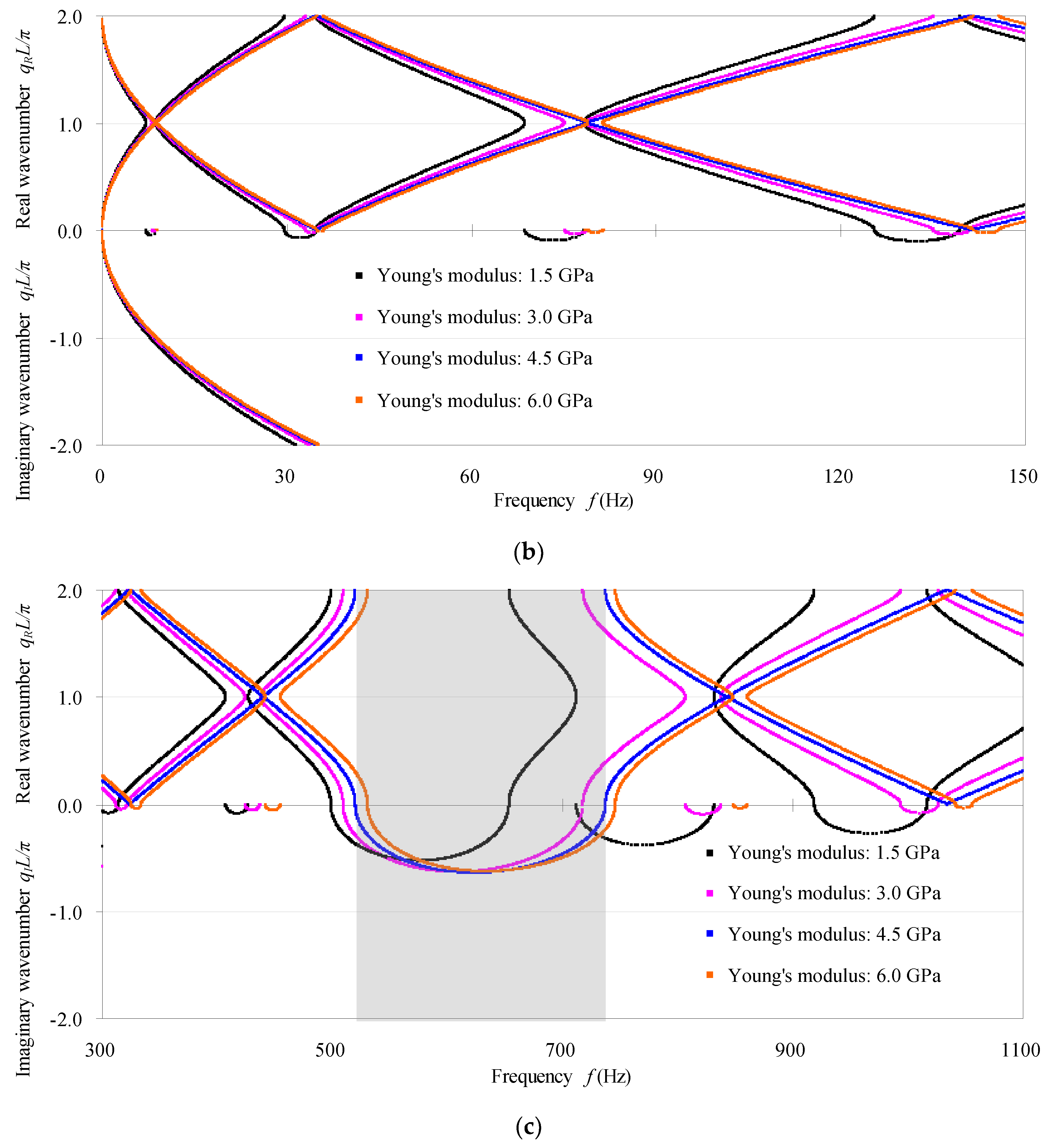
4.1. Effect of Defect Size and Defect Form
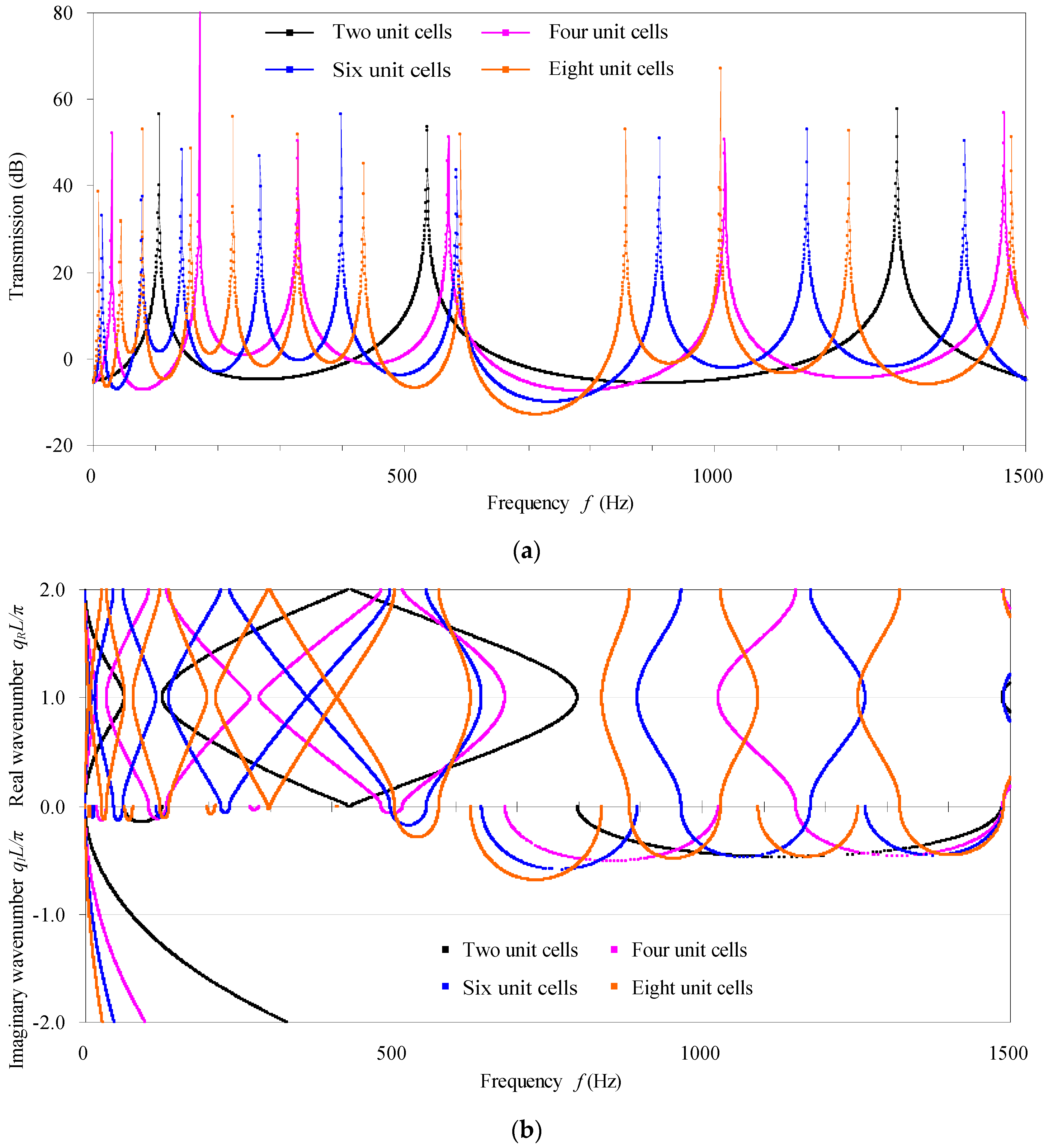
4.2. The Effect of Unit-Cell Number
5. Conclusions
- (1)
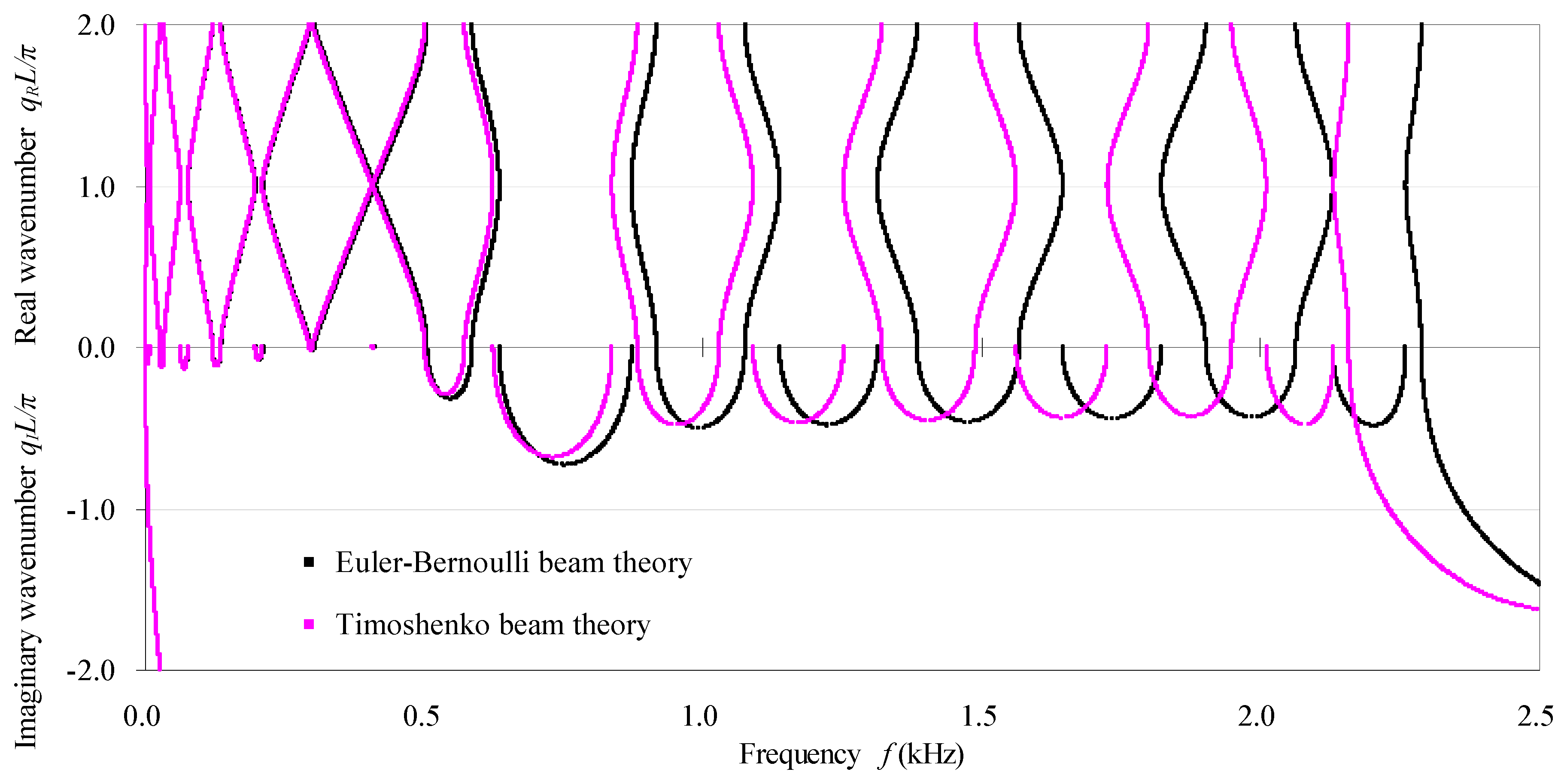
- From the comparisons of computational results and element requirements of the MRRM and those of the FEM, it is found that the main advantage of MRRM versus FEM should be that the MRRM needs less computational effort. From the comparison of the results by the MRRM and by the TMM (transfer matrix method) both at low and high frequency ranges, it has been proven that the proposed MRRM indeed eliminates the numerical instability problem in the TMM. Based on the Timoshenko or the Euler–Bernoulli beam theory, the proposed MRRM can be applied to calculate the dynamics of phononic crystal beams from zero up to high frequency as long as the respective beam theory is still valid to model the constituent beams.
- (2)
- According to the fact that defects actually increase (decrease) the natural/characteristic frequencies, the transmission/phase-constant spectra shift to the higher (lower) frequency side with respect to those of the perfect counterpart. A localized mode forms as a resonant frequency that is very close to the high (low) bounding frequency of the passband shifts into the adjacent higher (lower) stopband. The defect modes become harder and harder to be discerned from the transmission spectra as the damping in the defected phononic crystal beam increases, because the resonant amplitudes decrease more obviously while the resonant frequencies are nearly unchanged with the increasing of damping. In addition, the effect of the point defect seen from the band structures for infinite structures can be reflected by the transmission spectra for practical finite structures. The transmission spectra and the band structures at higher frequency ranges are generally more sensitive to the point defect.
- (3)
- The defect in the cross-sectional dimensions has identical effect on the transmission spectra and the band structures as the defect in the material moduli does. The defects introduced by predominantly reducing the flexural/shear stiffness of the structural beam, like reducing the cross-sectional dimension or the material moduli, move the transmission spectra and the phase constant spectra in each passband towards the lower frequency direction, and vice versa. The bigger the defect degree is, generally the wider the bandgaps are.
- (4)
- Increasing the unit-cell number by times will folding times the transmission spectra and the phase constant spectra in each passband, and will magnify the attenuation constants times in the stopbands. The larger is the unit-cell number, the more and narrower are the frequency bands in a specified frequency range.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Deymier, P.A. (Ed.) Acoustic Metamaterials and Phononic Crystals; Springer: Berlin, Germany, 2013. [Google Scholar]
- Khelif, A.; Adibi, A. (Eds.) Phononic Crystals: Fundamentals and Applications; Springer: New York, NY, USA, 2016. [Google Scholar]
- Laude, V. Phononic Crystals: Artificial Crystals for Sonic, Acoustic, and Elastic Waves; De Gruyter Publishers: Berlin, Germany, 2015. [Google Scholar]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. ASME Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Li, F.M.; Wang, Y.Z. Elastic wave propagation and localization in band gap materials: A review. Sci. China-Phys. Mech. Astron. 2012, 55, 1734–1746. [Google Scholar] [CrossRef]
- Brillouin, L. Wave Propagation in Periodic Structures: Electric Filters and Crystal Lattices, 2nd ed.; Dover Publications: New York, NY, USA, 1953. [Google Scholar]
- Chan, H.C.; Cai, C.W.; Cheung, Y.K. Exact Analysis of Structures with Periodicity Using U-Transformation; World Scientific: Singapore, 1998. [Google Scholar]
- Cai, C.W.; Liu, J.K.; Chan, H.C. Exact Analysis of Bi-Periodic Structures; World Scientific: Singapore, 2002. [Google Scholar]
- Banakh, L.Y.; Kempner, M.L. Vibrations of Mechanical Systems with Regular Structure; Springer: Berlin, Germany, 2010. [Google Scholar]
- Elachi, C. Waves in active and passive periodic structures: A review. Proc. IEEE 1976, 64, 1666–1698. [Google Scholar] [CrossRef]
- Gulyaev, Y.V.; Plesskii, V.P. Propagation of acoustic surface waves in periodic structures. Sov. Phys. Uspekhi 1989, 32, 51–74. [Google Scholar] [CrossRef]
- Sen Gupta, G. Vibration of periodic structures. Shock Vib. Dig. 1980, 12, 17–31. [Google Scholar] [CrossRef]
- Lin, Y.K. Random vibration of periodic and almost periodic structures. In Mechanics Today; Nemat-Nasser, S., Ed.; Pergamon Press Inc.: Oxford, UK, 1976; Volume 3, pp. 93–124. [Google Scholar]
- Lin, Y.K. Dynamics of disordered periodic structures. ASME Appl. Mech. Rev. 1996, 49, 57–64. [Google Scholar] [CrossRef]
- Mead, D.J. Wave propagation in continuous periodic structures: Research contributions from Southampton, 1964–1995. J. Sound Vib. 1996, 190, 495–524. [Google Scholar] [CrossRef]
- Li, D.; Benaroya, H. Dynamics of periodic and near-periodic structures. ASME Appl. Mech. Rev. 1992, 45, 447–459. [Google Scholar] [CrossRef]
- Mester, S.S.; Benaroya, H. Periodic and near-periodic structures. Shock Vib. 1995, 2, 69–95. [Google Scholar] [CrossRef]
- Brunskog, J.; Hammer, P. Prediction models of impact sound insulation on timber floor structures; a literature survey. Build. Acoust. 2000, 7, 89–112. [Google Scholar] [CrossRef]
- Pierre, C.; Castanier, M.P.; Chen, W.J. Wave localization in multi-coupled periodic structures: Application to truss beams. ASME Appl. Mech. Rev. 1996, 49, 65–86. [Google Scholar] [CrossRef]
- Manohar, C.S.; Ibrahim, R.A. Progress in structural dynamics with stochastic parameter variations: 1987–1998. ASME Appl. Mech. Rev. 1999, 52, 177–197. [Google Scholar] [CrossRef]
- Bendiksen, O.O. Localization phenomena in structural dynamics. Chaos Solitons Fractals 2000, 11, l62l–1660. [Google Scholar] [CrossRef]
- Chandrashaker, A.; Adhikari, S.; Friswell, M.I. Quantification of vibration localization in periodic structures. ASME J. Vib. Acoust. 2016, 138, 021002. [Google Scholar] [CrossRef]
- Yang, J.N.; Lin, Y.K. Frequency response functions of a disordered periodic beam. J. Sound Vib. 1975, 38, 317–340. [Google Scholar] [CrossRef]
- Ariaratnam, S.T.; Xie, W.-C. On the localization phenomenon in randomly disordered engineering structures. In Nonlinear Stochastic Mechanics; Bellomo, N., Casciati, F., Eds.; Springer: Berlin, Germany, 1992; pp. 13–24. [Google Scholar]
- Ariaratnam, S.T.; Xie, W.-C. Wave localization in randomly disordered nearly periodic long continuous beams. J. Sound Vib. 1995, 181, 7–22. [Google Scholar] [CrossRef]
- Kissel, G.J. Randomly disordered periodic structures. In Proceedings of the Third International Conference on Recent Advances in Structural Dynamics (Volume I), Southampton, UK, 18–22 July 1988; Petyt, M., Wolfe, H.F., Mei, C., Eds.; University of Southampton: Southampton, UK, 1988; pp. 45–54. [Google Scholar]
- Langley, R.S. The statistics of wave transmission through disordered periodic waveguides. J. Sound Vib. 1996, 189, 421–441. [Google Scholar] [CrossRef]
- Bouzit, D.; Pierre, C. An experimental investigation of vibration localization in disordered multi-span beams. J. Sound Vib. 1995, 187, 649–669. [Google Scholar] [CrossRef]
- Xu, M.B.; Huang, L. Control of multi-span beam vibration by a random wave reflector. J. Sound Vib. 2002, 250, 591–608. [Google Scholar] [CrossRef]
- Lin, Y.K.; Yang, J.N. Free vibration of a disordered periodic beam. ASME J. Appl. Mech. 1974, 41, 383–391. [Google Scholar] [CrossRef]
- Mead, D.J.; Bansal, A.S. Mono-coupled periodic systems with a single disorder: Response to convected loading. J. Sound Vib. 1978, 61, 497–515. [Google Scholar] [CrossRef]
- Bansal, A.S.; Aggarwal, V. Periodic systems with one of the constraints displaced: Response to convected loadings. In Structural Vibrations and Acoustics, Proceedings of the 18th International Congress on Acoustics (ICA2004), Kyoto, Japan, 4–9 April 2004; International Commission for Acoustics: Kyoto, Japan, 2004; pp. IV2919–IV2922. [Google Scholar]
- Bansal, A.S. Free wave motion in periodic systems with multiple disorders. J. Sound Vib. 1978, 60, 389–400. [Google Scholar] [CrossRef]
- Bansal, A.S. Flexural wave motion in beam-type disordered periodic systems: Coincidence phenomenon and sound radiation. J. Sound Vib. 1979, 62, 39–49. [Google Scholar] [CrossRef]
- Bansal, A.S. Flexural waves and deflection mode shapes of periodic and disordered beams. J. Acoust. Soc. Am. 1982, 72, 476–481. [Google Scholar] [CrossRef]
- Bansal, A.S. Free-wave propagation through combinations of periodic and disordered systems. J. Acoust. Soc. Am. 1980, 67, 377–389. [Google Scholar] [CrossRef]
- Bansal, A.S. Collective and localized modes of mono-coupled multi-span beams with large deterministic disorders. J. Acoust. Soc. Am. 1997, 102, 3806–3809. [Google Scholar] [CrossRef]
- Langley, R.S. Mode localization up to high frequencies in coupled one-dimensional subsystems. J. Sound Vib. 1995, 185, 79–91. [Google Scholar] [CrossRef]
- Zhou, S.L.; Li, F.M.; Zhang, C.Z. Vibration characteristics analysis of disordered two-span beams with numerical and experimental methods. J. Vib. Control 2017, 1–17. [Google Scholar] [CrossRef]
- Langley, R.S.; Bardell, N.S.; Loasby, P.M. The optimal design of near-periodic structures to minimize vibration transmission and stress levels. J. Sound Vib. 1997, 207, 627–646. [Google Scholar] [CrossRef]
- Al-Jawi, A.A.N.; Pierre, C.; Ulsoy, A.G. Vibration localization in dual-span, axially moving beams, part I: Formulation and results. J. Sound Vib. 1995, 179, 243–266. [Google Scholar] [CrossRef]
- Al-Jawi, A.A.N.; Pierre, C.; Ulsoy, A.G. Vibration localization in dual-span, axially moving beams, part II: Perturbation analysis. J. Sound Vib. 1995, 179, 267–287. [Google Scholar] [CrossRef]
- Bouzit, D.; Pierre, C. Vibration confinement phenomena in disordered, mono-coupled, multi-span beams. ASME J. Vib. Acoust. 1992, 114, 521–530. [Google Scholar] [CrossRef]
- Bouzit, D.; Pierre, C. Localization of vibration in disordered multi-span beams with damping. J. Sound Vib. 1995, 187, 625–648. [Google Scholar] [CrossRef]
- Langley, R.S. Wave transmission through one-dimensional near periodic structures: Optimum and random disorder. J. Sound Vib. 1995, 188, 717–743. [Google Scholar] [CrossRef]
- Lin, Y.K.; Cai, G.Q. Disordered periodic structures. In Computational Stochastic Mechanics; Spanos, P.D., Brebbia, C.A., Eds.; Computational Mechanics Publications: Southampton, UK, 1991; pp. 777–788. [Google Scholar]
- Cai, G.Q.; Lin, Y.K. Localization of wave propagation in disordered periodic structures. AIAA J. 1991, 29, 450–456. [Google Scholar] [CrossRef]
- Cai, G.Q.; Lin, Y.K. Statistical distribution of frequency response in disordered periodic structures. AIAA J. 1992, 30, 1400–1407. [Google Scholar] [CrossRef]
- Pierre, C.; Tang, D.M.; Dowell, E.H. Localized vibrations of disordered multispan beams: Theory and experiment. AIAA J. 1987, 25, 1249–1257. [Google Scholar] [CrossRef]
- Pierre, C. Mode localization and eigenvalue loci veering phenomena in disordered structures. J. Sound Vib. 1988, 126, 485–502. [Google Scholar] [CrossRef]
- Kim, D.-O.; Lee, I.-W. A study on mode localization phenomena: Influences of the stiffness and the mass of the coupler on mode localization. J. Sound Vib. 1998, 216, 53–73. [Google Scholar] [CrossRef]
- Kim, D.-O.; Lee, I.-W. Mode localization in non-periodic structures. In Proceedings of the Asia-Pacific Vibration Conference ’97, Kyongju, Korea, 9–13 November 1997; pp. 1170–1175. [Google Scholar]
- Mead, D.J.; Bansal, A.S. Mono-coupled periodic systems with a single disorder: Free wave propagation. J. Sound Vib. 1978, 61, 481–496. [Google Scholar] [CrossRef]
- Bansal, A.S. Free waves in periodically disordered systems: Natural and bounding frequencies of unsymmetric systems and normal mode localization. J. Sound Vib. 1997, 207, 365–382. [Google Scholar] [CrossRef]
- Lust, S.D.; Friedmann, P.P.; Bendiksen, O.O. Mode localization in multispan beams. AIAA J. 1993, 31, 348–355. [Google Scholar] [CrossRef]
- Lust, S.D.; Friedmann, P.P.; Bendiksen, O.O. Free and forced response of multi-span beams and multi-bay trusses with localized modes. J. Sound Vib. 1995, 180, 313–332. [Google Scholar] [CrossRef]
- Castanier, M.P.; Pierre, C. Lyapunov exponents and localization phenomena in multi-coupled nearly periodic systems. J. Sound Vib. 1995, 183, 493–515. [Google Scholar] [CrossRef]
- Bouzit, D.; Pierre, C. Wave localization and conversion phenomena in multi-coupled multi-span beams. Chaos Solitons Fractals 2000, 11, 1575–1596. [Google Scholar] [CrossRef]
- Li, F.M.; Wang, Y.S.; Hu, C.; Huang, W.H. Localization of elastic waves in randomly disordered multi-coupled multi-span beams. Waves Random Media 2004, 14, 217–227. [Google Scholar] [CrossRef]
- Li, F.-M.; Wang, Y.-S. Wave localization in randomly disordered multi-coupled multi-span beams on elastic foundations. Waves Random Complex Media 2006, 16, 261–279. [Google Scholar] [CrossRef]
- Qiu, C.X.; Lin, Y.K. Localization of mono- and multichannel waves in disordered periodic systems. ASCE J. Eng. Mech. 1997, 123, 830–836. [Google Scholar] [CrossRef]
- Tan, C.A.; Riedel, C.H. Wave analysis of mode localization and delocalization in elastically constrained strings and beams. ASME J. Vib. Acoust. 1999, 121, 169–173. [Google Scholar] [CrossRef]
- Yan, Z.-Z.; Zhang, C.Z.; Wang, Y.-S. Attenuation and localization of bending waves in a periodic/disordered fourfold composite beam. J. Sound Vib. 2009, 327, 109–120. [Google Scholar] [CrossRef]
- Wang, Y.-Z.; Li, F.-M.; Kishimoto, K. Flexural wave localization in randomly disordered periodic beams with axial load. Key Eng. Mater. 2011, 462–463, 837–842. [Google Scholar] [CrossRef]
- Chuang, K.-C.; Zhang, Z.-Q.; Wang, H.-X. Experimental study on slow flexural waves around the defect modes in a phononic crystal beam using fiber Bragg gratings. Phys. Lett. A 2016, 380, 3963–3969. [Google Scholar] [CrossRef]
- Doyle, J.F. Wave Propagation in Structures, 2nd ed.; Springer: New York, NY, USA, 1997; pp. 75–78, 131–137. [Google Scholar]
- Pestel, E.C.; Leckie, F.A. Matrix Methods in Elasto Mechanics; McGraw-Hill: New York, NY, USA, 1963. [Google Scholar]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier: Oxford, UK, 2013; pp. 226–234, 493–543. [Google Scholar]
- Pao, Y.-H.; Chen, W.-Q. Elastodynamic theory of framed structures and reverberation-ray matrix analysis. Acta Mech. 2009, 204, 61–79. [Google Scholar] [CrossRef]
- Guo, Y.Q.; Fang, D.N. Formation of bending-wave band structures in bicoupled beam-type phononic crystals. ASME J. Appl. Mech. 2014, 81, 011009. [Google Scholar] [CrossRef]
- Martienssen, W.; Warlimont, H. (Eds.) Springer Handbook of Condensed Matter and Materials Data; Springer: Berlin, Germany, 2005; pp. 172, 192–194, 498. [Google Scholar]
- Tabatabaian, M. COMSOL® 5 for Engineers; Mercury Learning and Information: Dulles, VA, USA, 2016; Chapters 2 and 3. [Google Scholar]
- De Silva, C.W. (Ed.) Vibration Damping, Control, and Design; CRC Press: New York, NY, USA, 2007; Chapters 1 and 2. [Google Scholar]
- Harrison, W.A. Solid State Theory; Dover Publications: New York, NY, USA, 1980; pp. 278–283. [Google Scholar]
- Mead, D.J. Wave propagation and natural modes in periodic systems: II. Multi-coupled systems, with and without damping. J. Sound Vib. 1975, 40, 19–39. [Google Scholar] [CrossRef]

| Type of Exterior Joint | Vector of Known Quantities | Vector of Unknown Quantities | ||
|---|---|---|---|---|
| free end | ||||
| clamped end | ||||
| simple support | ||||
| guided support |
| Type of Exterior Joint | Vector of Known Quantities | Vector of Unknown Quantities | ||
|---|---|---|---|---|
| free end | ||||
| clamped end | ||||
| simple support | ||||
| guided support |
| Geometrical Parameters | Beam Type | Cross-Sectional Area () | Second Moment of Inertia () | Shear Coefficient | Length () |
| perfect PMMA beam | 0.015 0.015 | 5/6 | 0.08 | ||
| defected PMMA beam | 0.0150.008 | 5/6 | 0.08 | ||
| aluminum beam | 0.0150.015 | 5/6 | 0.08 | ||
| Material Parameters | Material | Young’s Modulus () | Poisson’s Ratio | Shear Modulus () | Density () |
| PMMA | 4.50 | 0.33 | 1.69 | 1142 | |
| aluminum | 74.60 | 0.33 | 28.00 | 2735 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Li, L.; Chuang, K.-C. Analysis of Bending Waves in Phononic Crystal Beams with Defects. Crystals 2018, 8, 21. https://doi.org/10.3390/cryst8010021
Guo Y, Li L, Chuang K-C. Analysis of Bending Waves in Phononic Crystal Beams with Defects. Crystals. 2018; 8(1):21. https://doi.org/10.3390/cryst8010021
Chicago/Turabian StyleGuo, Yongqiang, Longfei Li, and Kuo-Chih Chuang. 2018. "Analysis of Bending Waves in Phononic Crystal Beams with Defects" Crystals 8, no. 1: 21. https://doi.org/10.3390/cryst8010021
APA StyleGuo, Y., Li, L., & Chuang, K.-C. (2018). Analysis of Bending Waves in Phononic Crystal Beams with Defects. Crystals, 8(1), 21. https://doi.org/10.3390/cryst8010021






