Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane
Abstract
1. Introduction
(i) the axis of the HX molecule coincides with the supposed axis of a non-bonding electron pair of B, as conventionally envisaged or, if B has no nonbonding electron pairs but has π-bonding electron pairs, (ii) the axis of the HX molecule intersects the internuclear axis of the atoms forming the π-bond and is perpendicular to the plane of symmetry of the π-bond. Rule (i) is definitive when B has both non-bonding and π-bonding pairs.
2. Computational Details
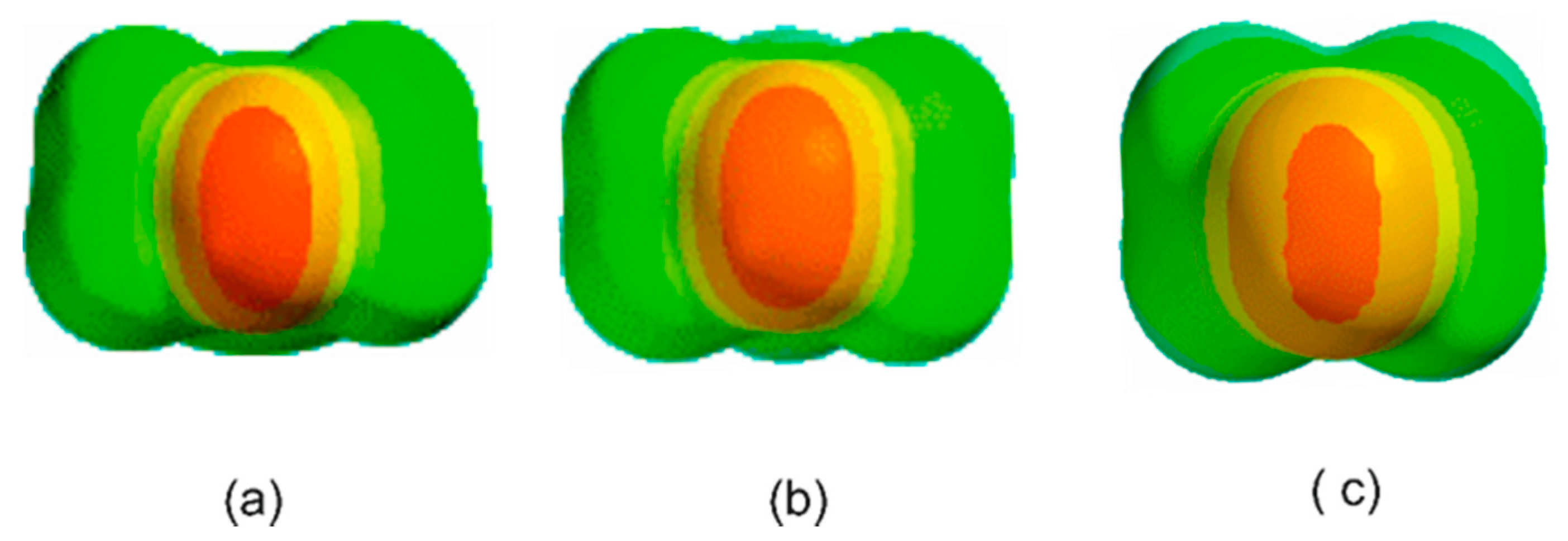
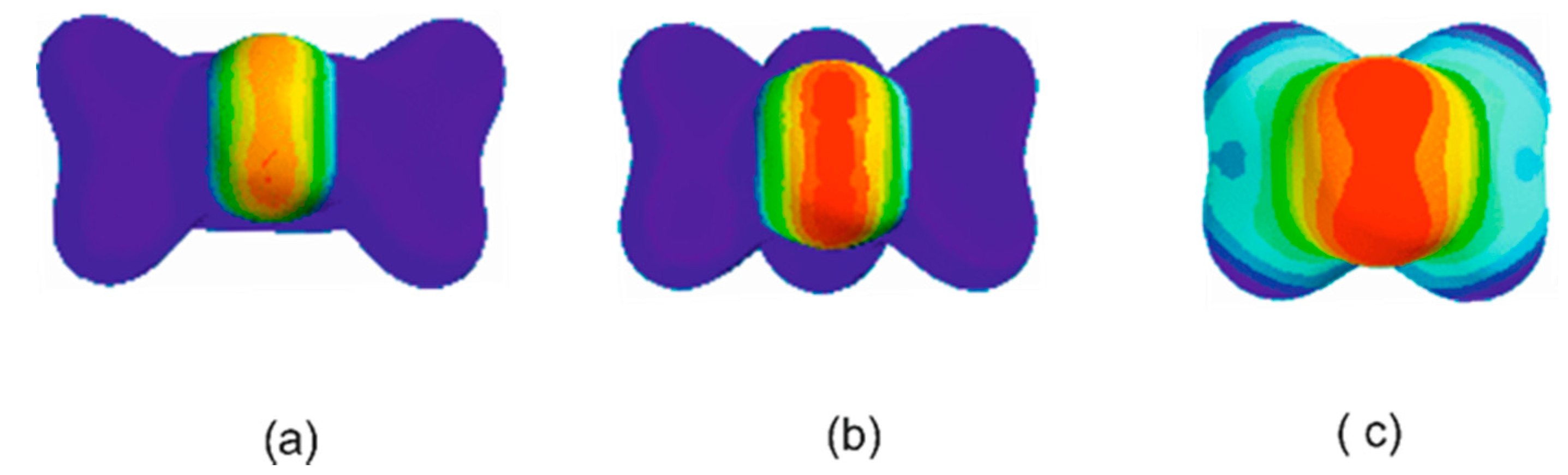
3. Results and Discussion
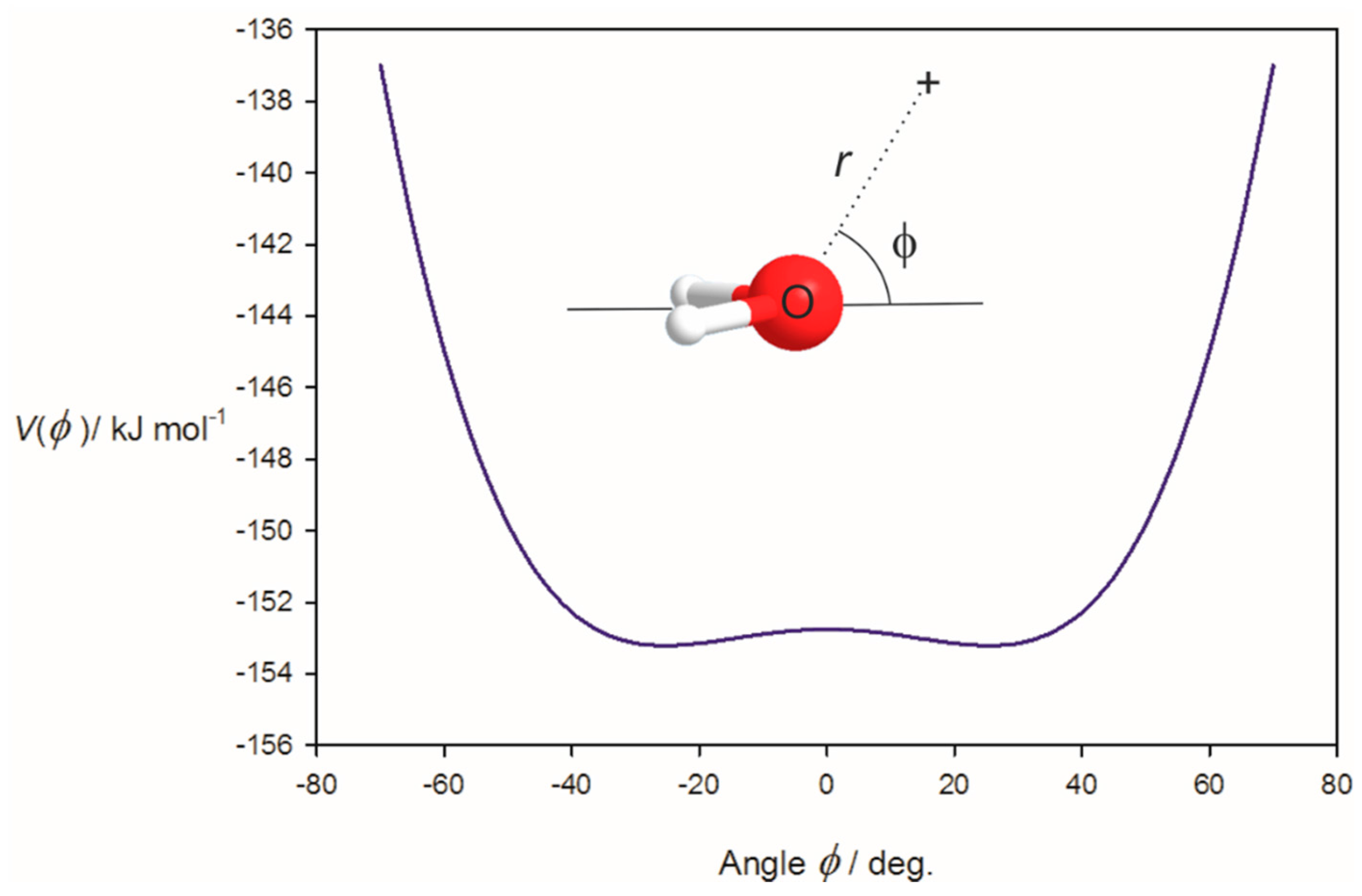
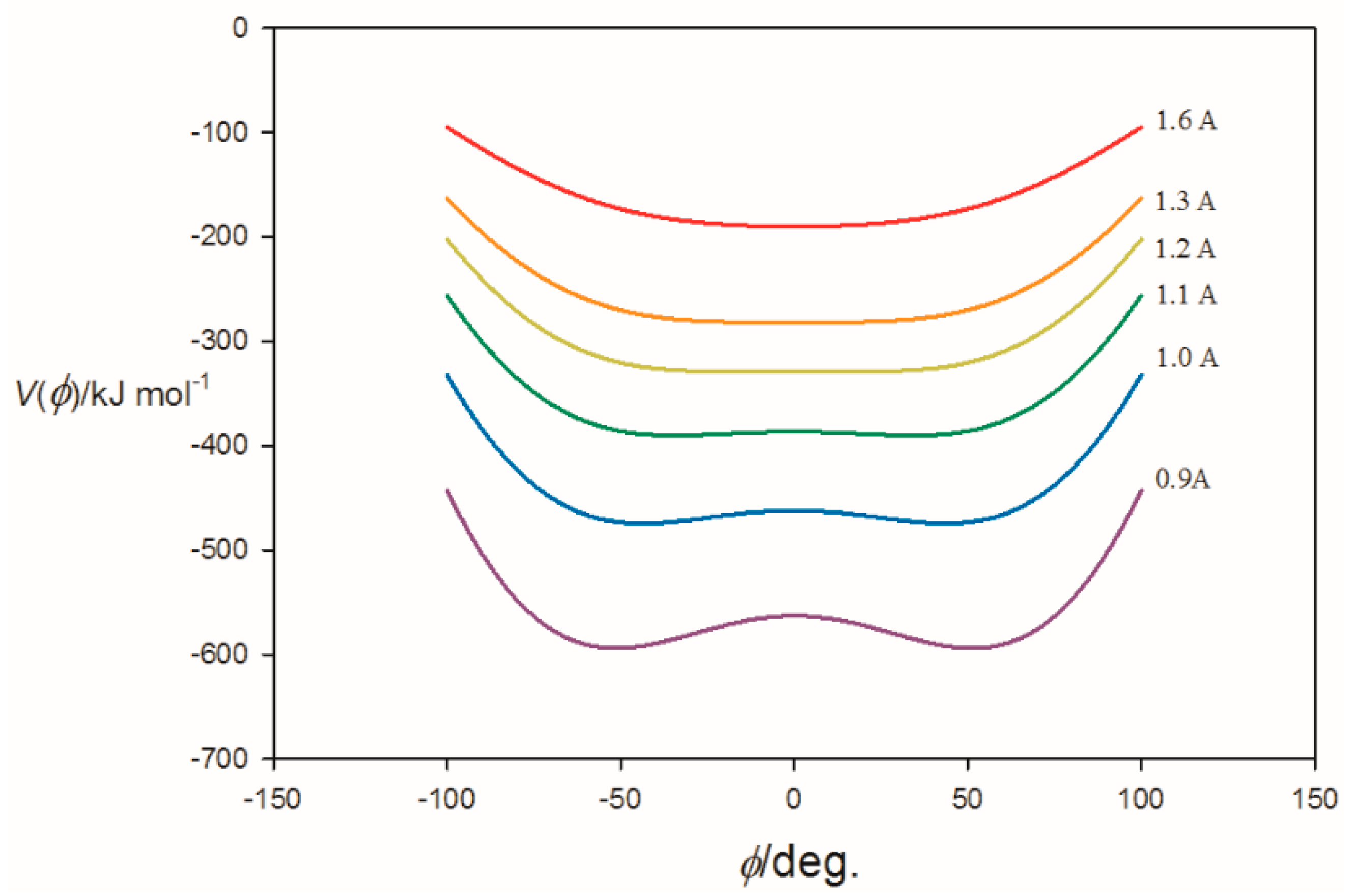
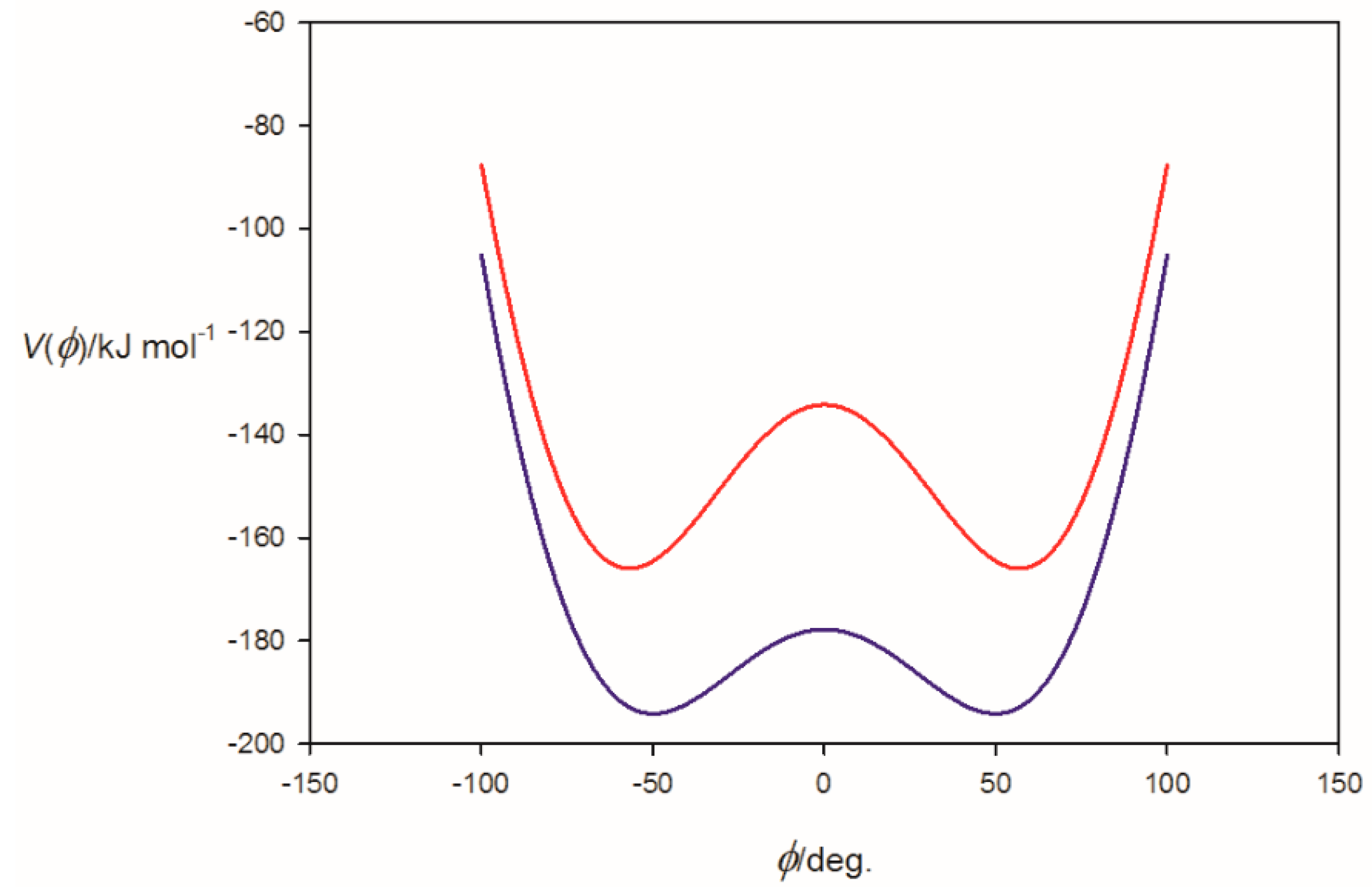
3.1. Electrostatic Potential V(φ) as a Function of the Angle φ
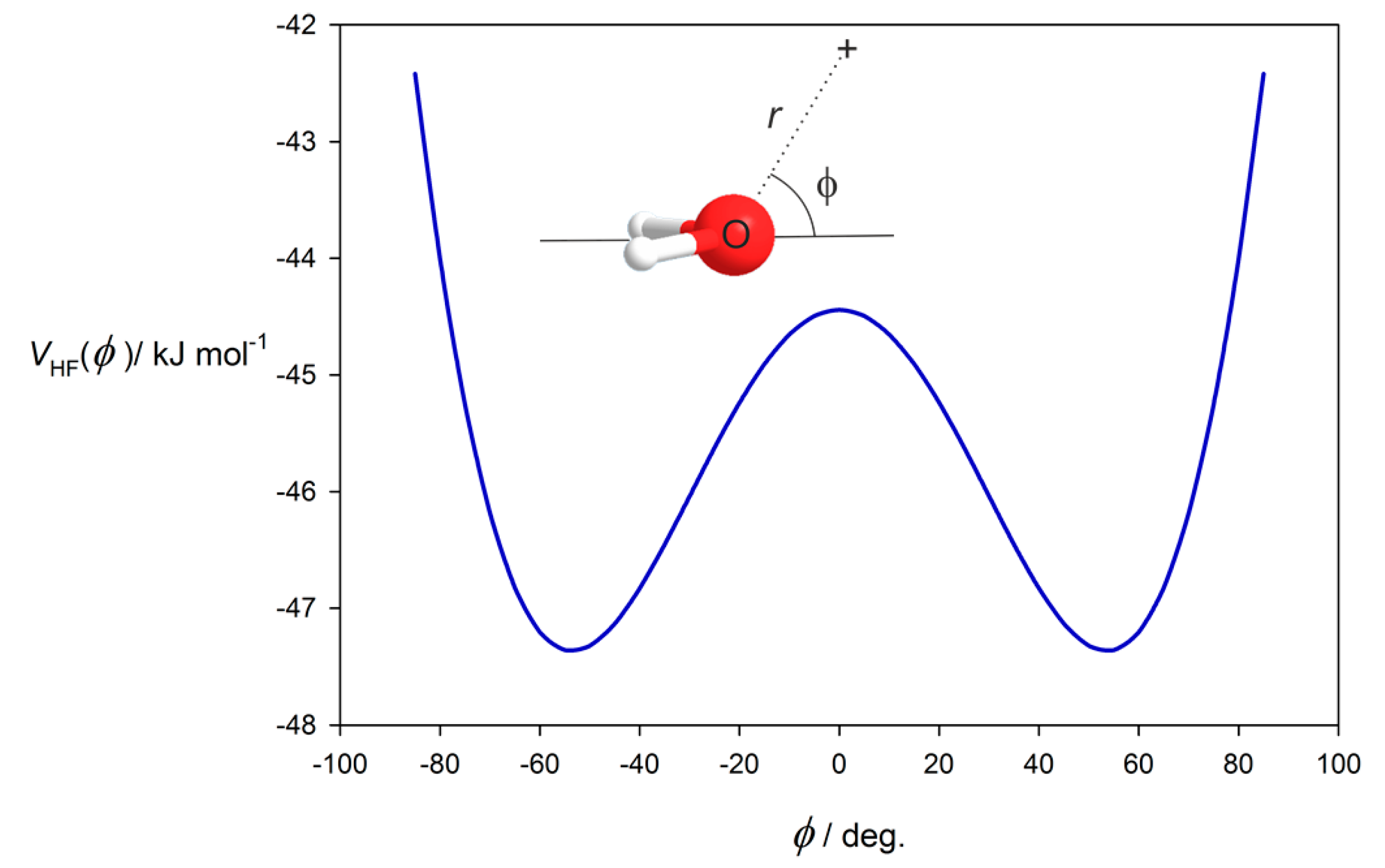
3.2. Potential Energy of an Extended Electric Dipole Model of HF as a Function of Angle φ
4. Conclusions
Supplementary Materials
Author Contributions
Conflicts of Interest
References
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Defining the hydrogen bond: An account (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 1619–1636. [Google Scholar] [CrossRef]
- Desiraju, G.R.; Shing Ho, P.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.A.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef] [PubMed]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P.A. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Clark, T.; Riley, K.E.; Politzer, P.A. σ-Holes, π-holes and electrostatically-driven interactions. J. Mol. Model. 2012, 18, 541–548. [Google Scholar] [CrossRef] [PubMed]
- Legon, A.C.; Millen, D.J. Determination of properties of hydrogen-bonded dimers by rotational spectroscopy and a classification of dimer geometries. Faraday Discuss. Chem. Soc. 1982, 73, 71–87. [Google Scholar] [CrossRef]
- Legon, A.C.; Millen, D.J. Angular geometries and other properties of hydrogen-bonded dimers: A simple electrostatic interpretation based on the success of the electron-pair model. Chem. Soc. Rev. 1987, 16, 467–498. [Google Scholar] [CrossRef]
- Buckingham, A.D.; Fowler, P.W. A model for the geometries of van der Waals complexes. Can. J. Chem. 1985, 63, 2018–2025. [Google Scholar] [CrossRef]
- Kisiel, Z.; Legon, A.C.; Millen, D.J. Spectroscopic investigations of hydrogen bonding interactions in the gas phase. VII. The equilibrium conformation and out-of-plane bending potential energy function of the hydrogen-bonded heterodimer H2O⋯HF determined from its microwave rotational spectrum. Proc. R. Soc. Lond. A 1982, 381, 419–442. [Google Scholar] [CrossRef]
- Guelachvili, G. Absolute wavenumber measurements of 1-0, 2-0, HF and 2-0 H35Cl and H37Cl absorption bands. Opt. Commun. 1976, 19, 150–154. [Google Scholar] [CrossRef]
- Georgiou, A.S.; Legon, A.C.; Millen, D.J. Spectroscopic investigations of hydrogen-bonding interactions in the gas phase. V. The identification and determination of the geometry and electric dipole moment of the hydrogen-bonded heterodimer formed between oxirane and hydrogen fluoride, (CH2)2O⋯HF, by infrared and microwave spectroscopy. Proc. R. Soc. Lond. A 1980, 373, 511–526. [Google Scholar]
- Georgiou, A.S.; Legon, A.C.; Millen, D.J. Spectroscopic investigations of hydrogen bonding interactions in the gas phase. VI. A microwave spectroscopic determination of geometry for the heterodimer (CH2)3O⋯HF formed between oxetane and hydrogen fluoride: Hydrogen bonding as a probe for lone pairs. J. Mol. Struct. 1980, 69, 69–78. [Google Scholar] [CrossRef]
- Collins, R.A.; Millen, D.J.; Legon, A.C. Conformations of hydrogen-bonded dimers formed by cyclic ethers with hydrogen fluoride: Rotational spectrum of 2,5-dihydrofuran⋯HF. J. Mol. Struct. 1987, 162, 31–40. [Google Scholar] [CrossRef]
- López, J.C.; Alonso, J.L.; Wlodarczak, G.; Demaison, J. The Millimeter-Wave Spectrum and ab Initio Calculations of 2,5-Dihydrofuran. J. Mol. Spectrosc. 1993, 160, 158–171. [Google Scholar] [CrossRef]
- Creswell, R.A. Molecular structure of oxetane. Mol. Phys. 1975, 30, 217–222. [Google Scholar] [CrossRef]
- Hirose, C. The microwave spectra and r0, rs, and rm structures of ethylene oxide. Bull. Chem. Soc. Jpn. 1974, 47, 1311–1318. [Google Scholar] [CrossRef]
- López, J.C.; Blanco, S.; Lessari, A.; Sanz, M.E.; Lorenzo, F.J.; Alonso, J.L. HF inversion in the 2,5-dihydrofuran⋯HF complex. J. Chem. Phys. 2001, 114, 9421–9429. [Google Scholar] [CrossRef]
- Sanz, M.E.; Sanz, V.M.; López, J.C.; Alonso, J.L. Oxetane-hydrogen fluoride complex: A rotational study. Chem. Phys. Lett. 2001, 342, 32–38. [Google Scholar] [CrossRef]
- Legon, A.C.; Wallwork, A.L.; Millen, D.J. Observation of c-type transitions and H,F nuclear spin-nuclear spin coupling in the rotational spectrum of (CH2)2O⋯HF. Chem. Phys. Lett. 1991, 178, 279–284. [Google Scholar] [CrossRef]
- Clark, T.; Politzer, P.; Murray, J.S. Correct electrostatic treatment of noncovalent interactions: The importance of polarization. WIREs Comput. Mol. Sci. 2015, 5, 169–177. [Google Scholar] [CrossRef]
- Wang, C.; Guan, L.; Danovich, D.; Shaik, S.; Mo, Y. The Origins of the Directionality of Noncovalent Intermolecular Interactions. J. Comput. Chem. 2016, 37, 34–45. [Google Scholar] [CrossRef] [PubMed]
- Mustoe, C.L.; Gunabalasingam, M.; Yu, D.; Patrick, B.O.; Kennepohl, P. Probing covalency in halogen bonds through donor K-edge X-ray absorption spectroscopy: Polyhalides as coordination complexes. Faraday Discuss. 2017. [Google Scholar] [CrossRef] [PubMed]
- Scheiner, S. The Interplay between Charge Transfer, Rehybridization, and Atomic Charges in the Internal Geometry of Subunits in Noncovalent Interactions. Int. J. Quantum Chem. 2015, 115, 28–33. [Google Scholar] [CrossRef]
- Kolár, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
- Stone, A.J. Distributed multipole analysis, or how to describe a molecular charge distribution. Chem. Phys. Lett. 1981, 83, 233–239. [Google Scholar] [CrossRef]
- Hättig, C.; Tew, D.P.; Köhn, A. Communications: Accurate and efficient approximations to explicitly correlated coupled-cluster singles and doubles, CCSD-F12. J. Chem. Phys. 2010, 132, 231102. [Google Scholar] [CrossRef] [PubMed]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schutz, M.; Celani, P.; Gyorffy, W.; Kats, D.; Korona, T.; Lindh, R.; et al. Molpro, a Package of ab Initio Programs, Version 2015.1; University of Stuttgart: Stuttgart, Germany, 2015. [Google Scholar]
- Werner, H.-J.; Knowles, P.J.; Knizia, G.; Manby, F.R.; Schütz, M. Molpro: A general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 242–253. [Google Scholar] [CrossRef]
- Peterson, K.A.; Adler, T.B.; Werner, H.-J. Systematically convergent basis sets for explicitly correlated wavefunctions: The atoms H, He, B-Ne, and Al-Ar. J. Chem. Phys. 2008, 128, 084102. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. A fully direct RI-HF algorithm: Implementation, optimized auxiliary basis sets, demonstration of accuracy and efficiency. Phys. Chem. Chem. Phys. 2002, 4, 4285–4291. [Google Scholar] [CrossRef]
- Kritikou, S.; Hill, J.G. Auxiliary Basis Sets for Density Fitting in Explicitly Correlated Calculations: The Atoms H-Ar. J. Chem. Theory Comput. 2015, 11, 5269–5276. [Google Scholar] [CrossRef] [PubMed]
- Valeev, E.F. Improving on the resolution of the identity in linear R12 ab initio theories. Chem. Phys. Lett. 2004, 395, 190–195. [Google Scholar] [CrossRef]
- Yousaf, K.E.; Peterson, K.A. Optimized auxiliary basis sets for explicitly correlated methods. J. Chem. Phys. 2008, 129, 184108. [Google Scholar] [CrossRef] [PubMed]
- Dunning, T.H., Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. [Google Scholar] [CrossRef]
- Korona, T.; Moszynski, R.; Jeziorski, B. Electrostatic interactions between molecules from relaxed one-electron density matrices of the coupled cluster singles and doubles model. Mol. Phys. 2002, 100, 1723–1734. [Google Scholar] [CrossRef]
- Krishnan, R.; Binkley, J.S.; Seeger, R.; Pople, J.A. Self-consistent molecular orbital methods. XX. A basis set for correlated wave functions. J. Chem. Phys. 1980, 72, 650–654. [Google Scholar] [CrossRef]
- Deppmeier, B.J.; Driessen, A.J.; Hehre, T.S.; Hehre, W.J.; Johnson, J.A.; Klunzinger, P.E.; Leonard, J.M.; Pham, I.N.; Pietro, W.J.; Yu, J.; et al. SPARTAN’14 Mechanics Program: (Win/64b), Release 1.1.8, Wavefunction Inc.; Spartan Inc.: Bakersfield, CA, USA, 2014. [Google Scholar]
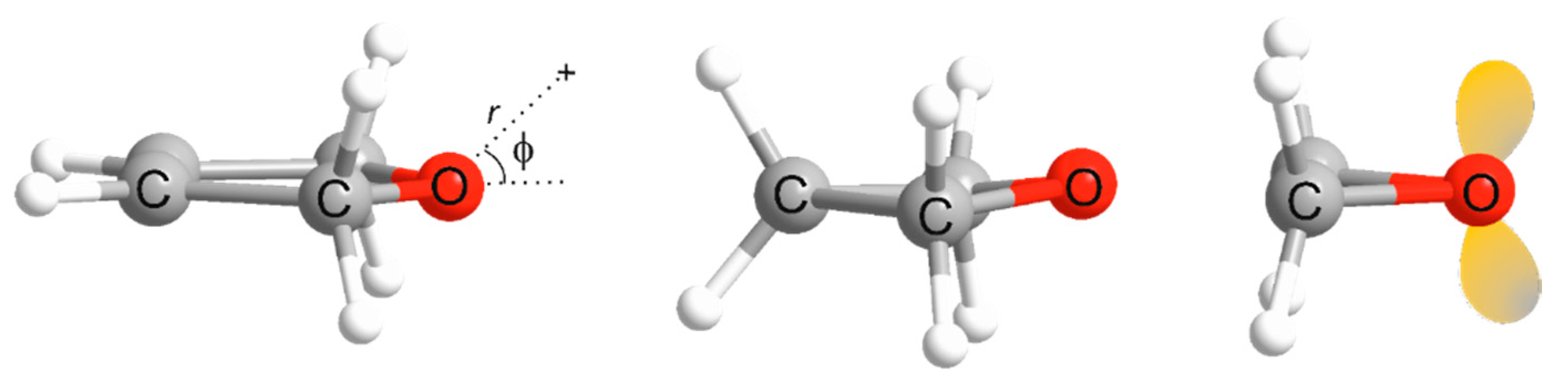
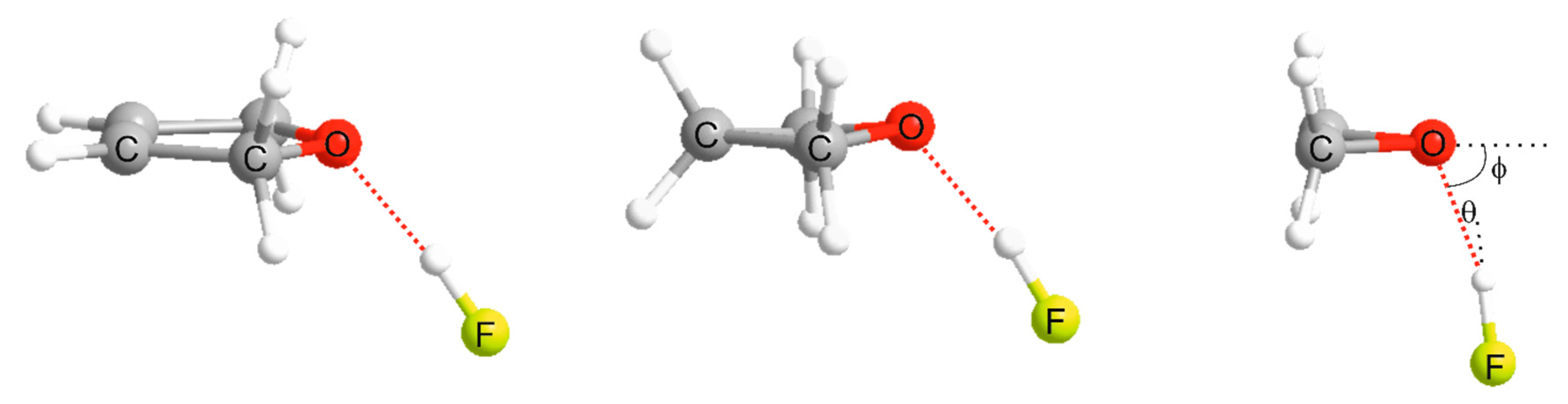
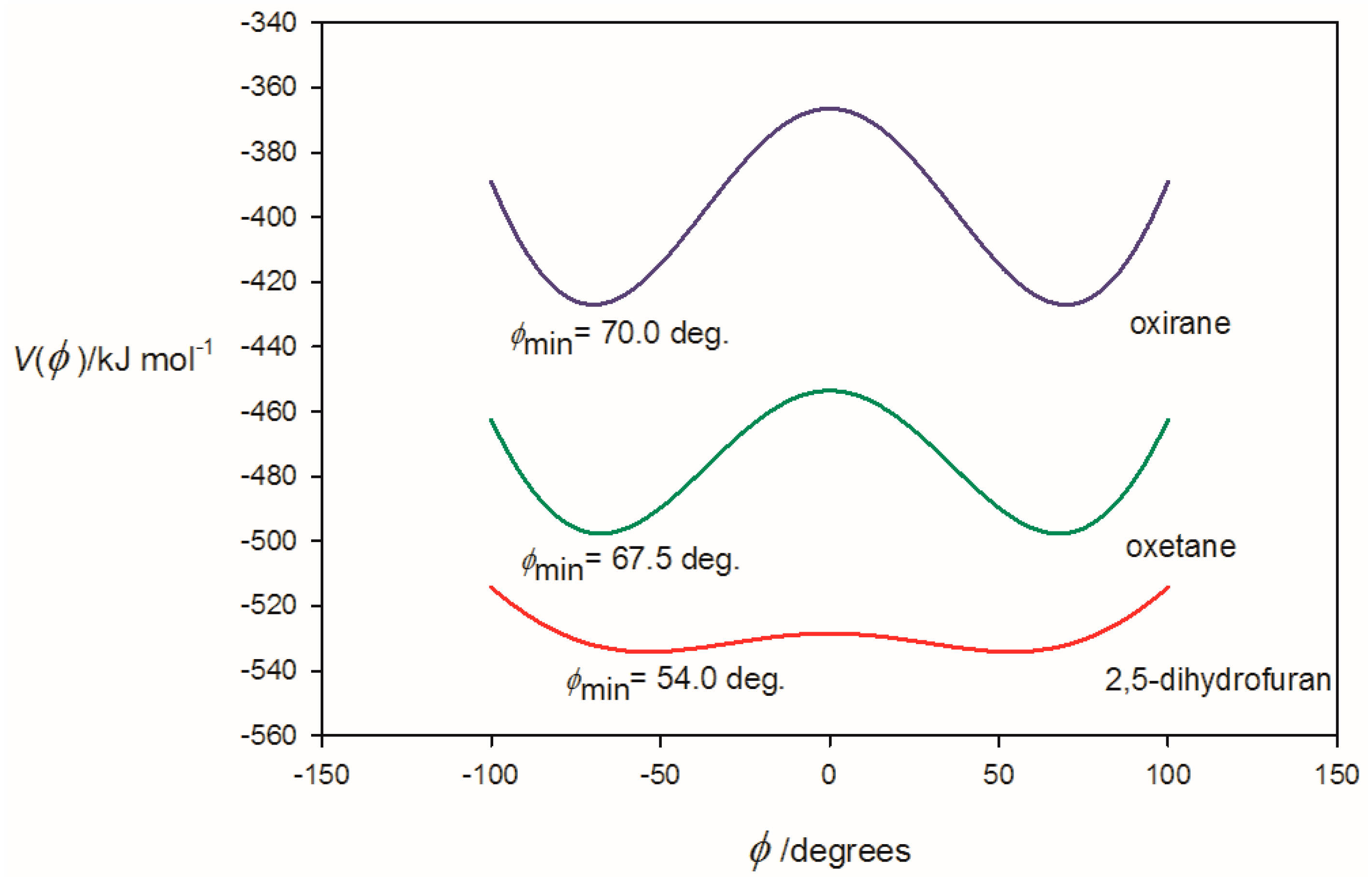
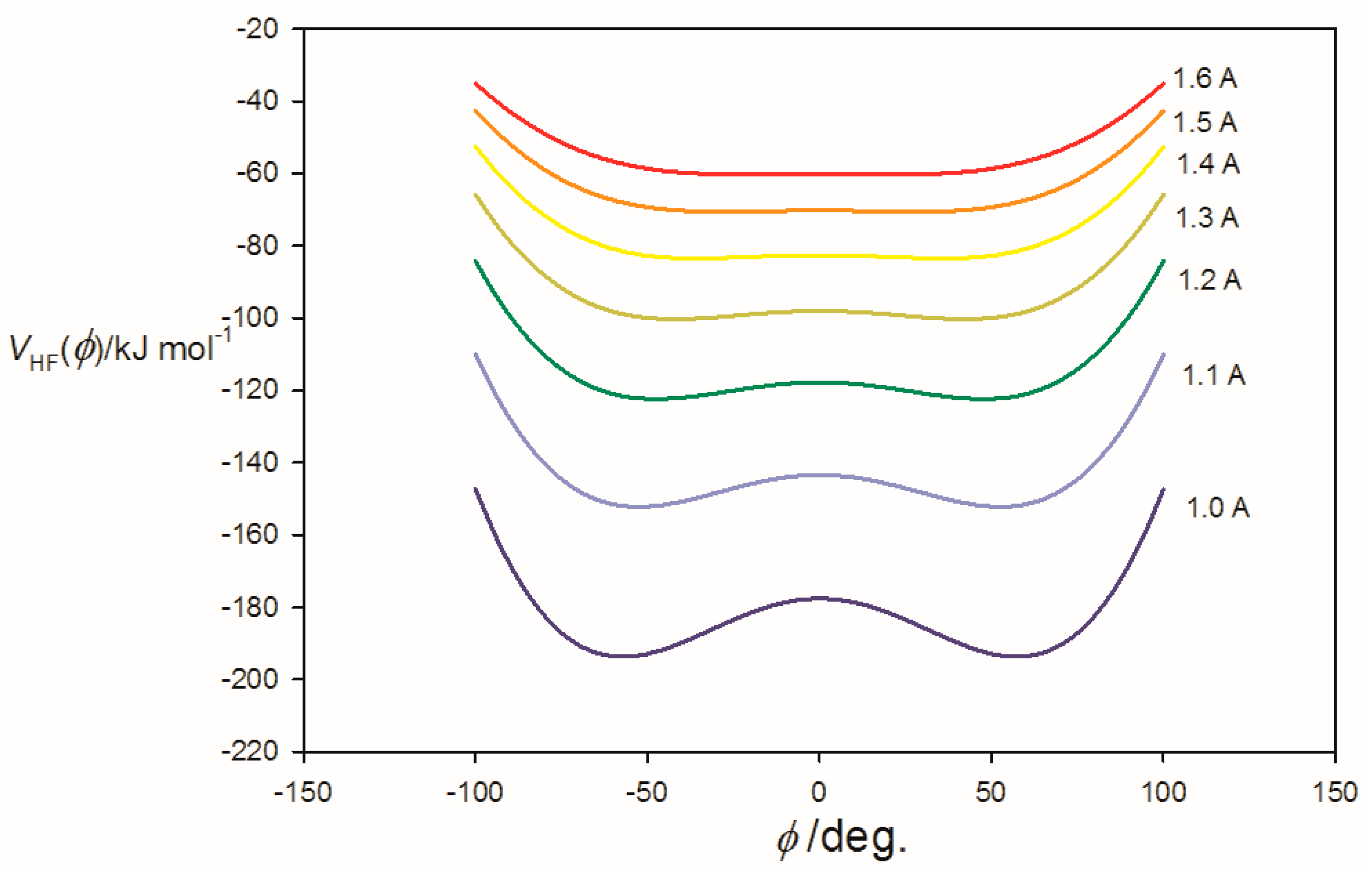
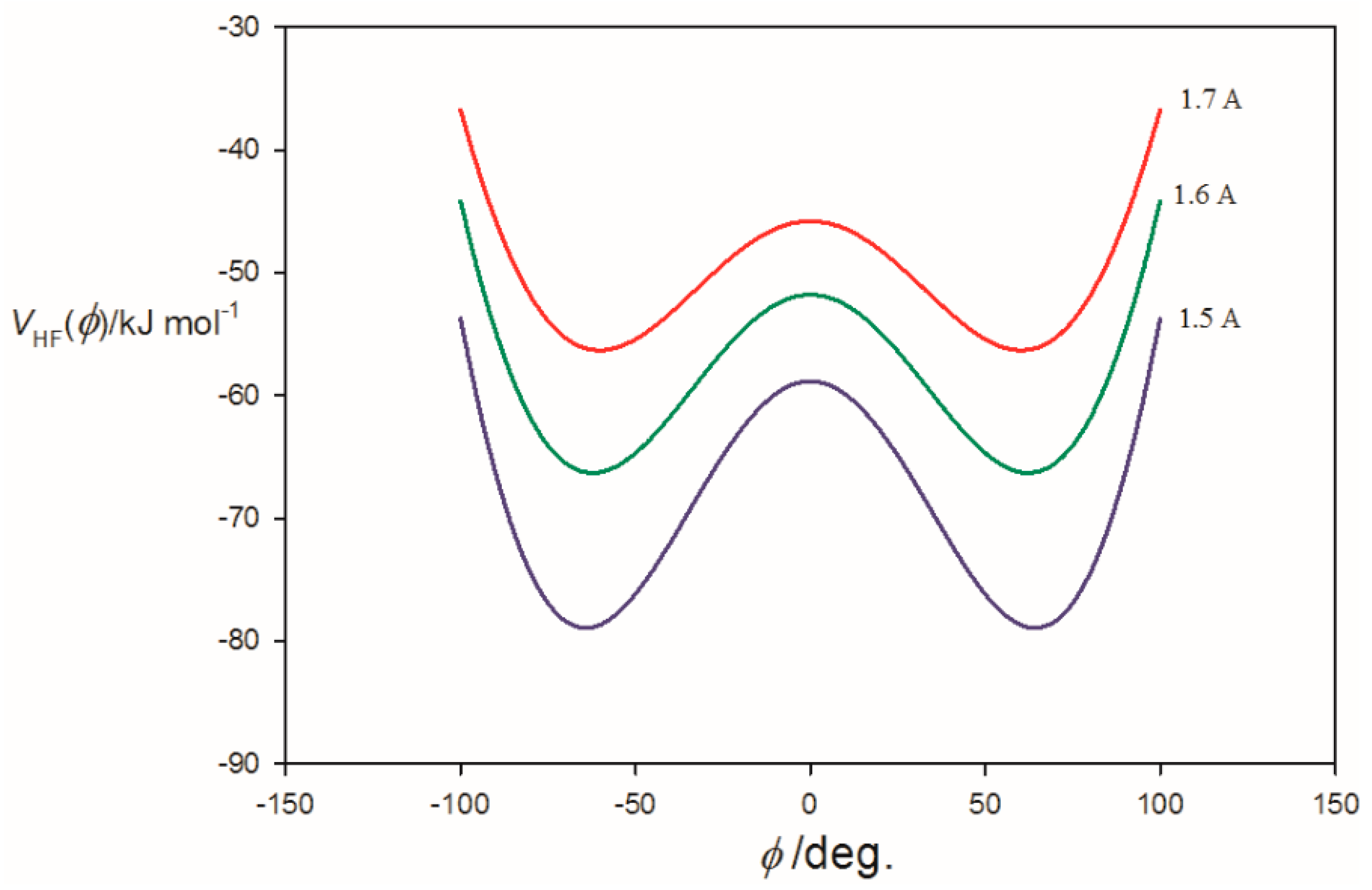
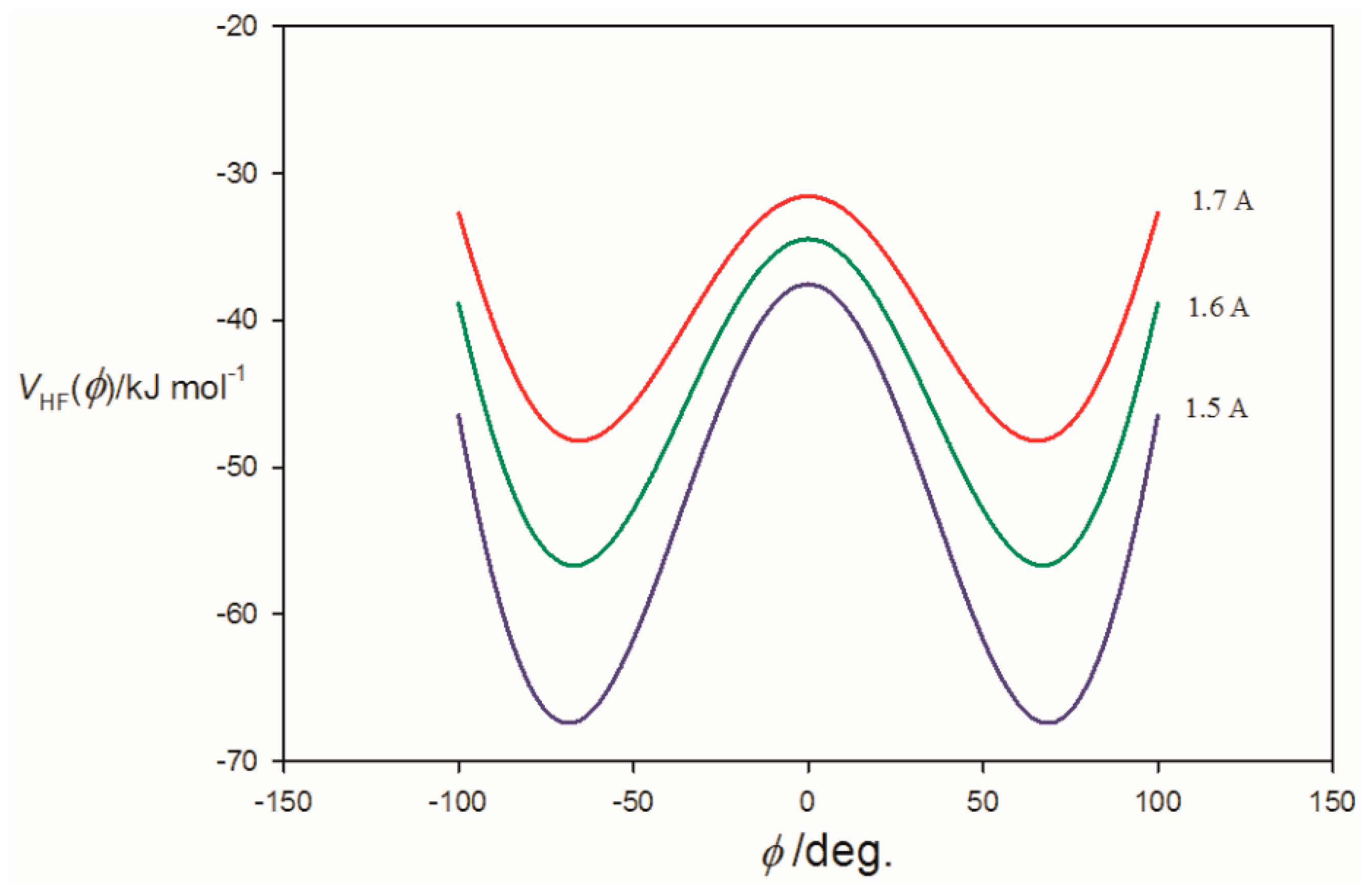
| Property | 2,5-Dihydrofuran⋯HF | Oxetane⋯HF | Oxirane⋯HF |
|---|---|---|---|
| re(O⋯H)/Å | 1.631 a | 1.622 a | 1.663 a |
| r0(O⋯H)/Å | 1.674 b | 1.660 c | 1.701 d |
| φe/° | 48.24 a | 57.36 a | 73.08 a |
| θe/° e | 6.05 | 9.26 | 13.20 |
| φ0/° | 46.3 b | 57.9 c | 72.0 d |
| φmin(at re) f/° | ~14 | 62.0 | 66.0 |
| φmin(at r0) g/° | ~0 | 61.0 | 65.5 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hill, J.G.; Legon, A.C. Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane. Crystals 2017, 7, 261. https://doi.org/10.3390/cryst7090261
Hill JG, Legon AC. Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane. Crystals. 2017; 7(9):261. https://doi.org/10.3390/cryst7090261
Chicago/Turabian StyleHill, J. Grant, and Anthony C. Legon. 2017. "Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane" Crystals 7, no. 9: 261. https://doi.org/10.3390/cryst7090261
APA StyleHill, J. G., & Legon, A. C. (2017). Electrostatic Potential and a Simple Extended Electric Dipole Model of Hydrogen Fluoride as Probes of Non-Bonding Electron Pairs in the Cyclic Ethers 2,5-Dihydrofuran, Oxetane and Oxirane. Crystals, 7(9), 261. https://doi.org/10.3390/cryst7090261






