Ultrafast Electron and Molecular Dynamics in Photoinduced and Electric-Field-Induced Neutral–Ionic Transitions
Abstract
:1. Introduction
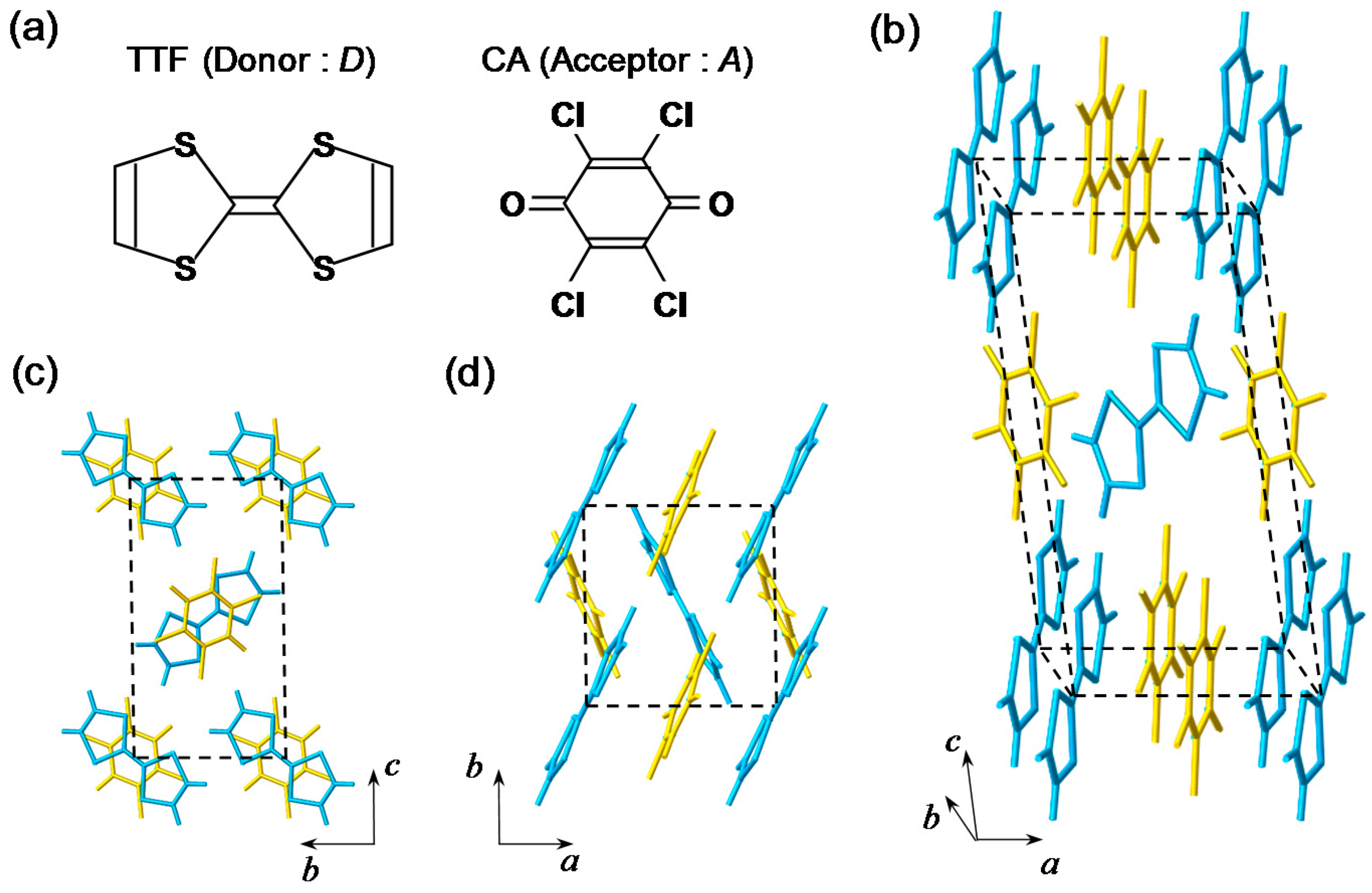
2. Fundamental Properties of TTF-CA
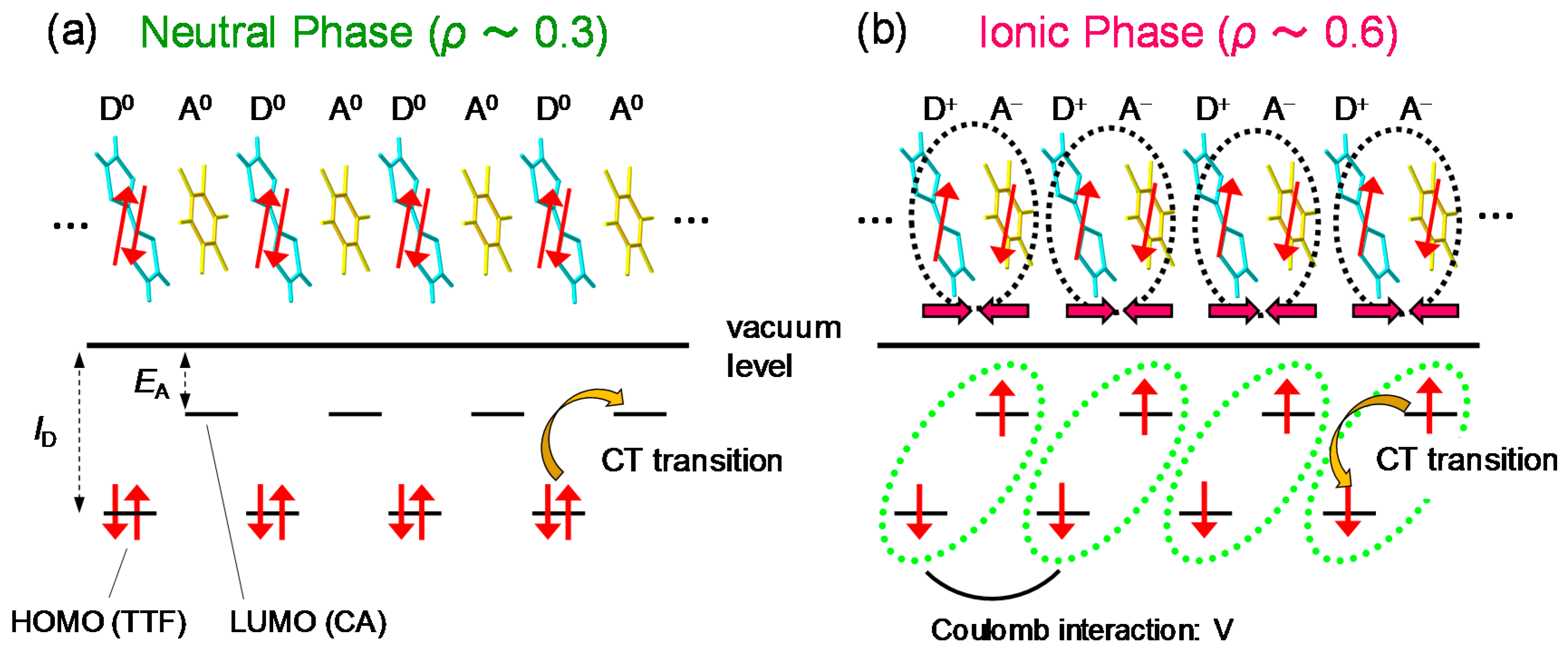
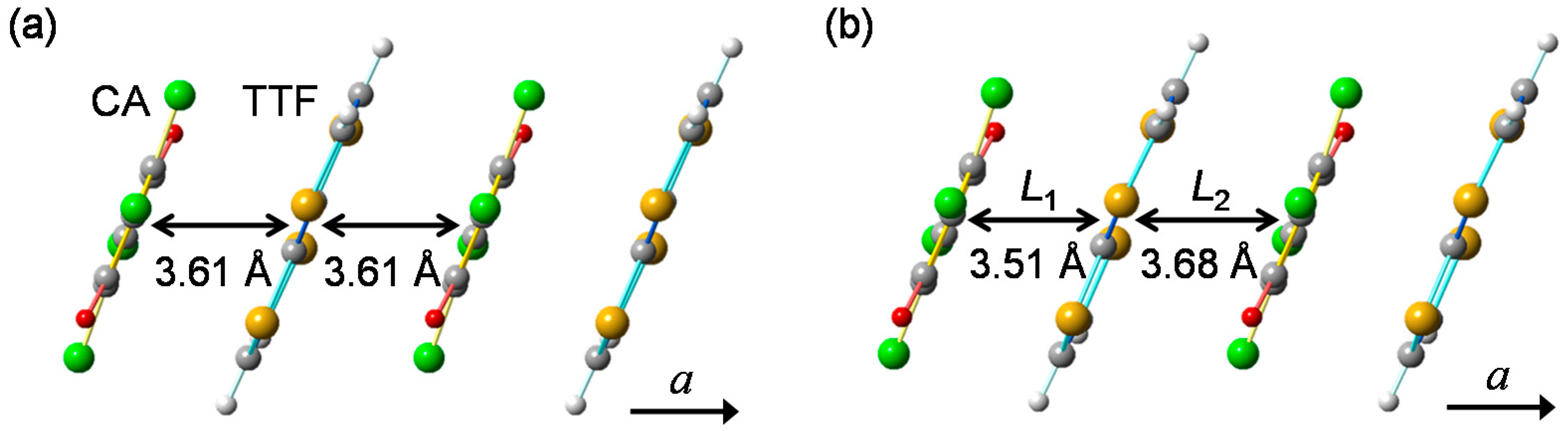
2.1. Neutral-to-Ionic Phase Transition
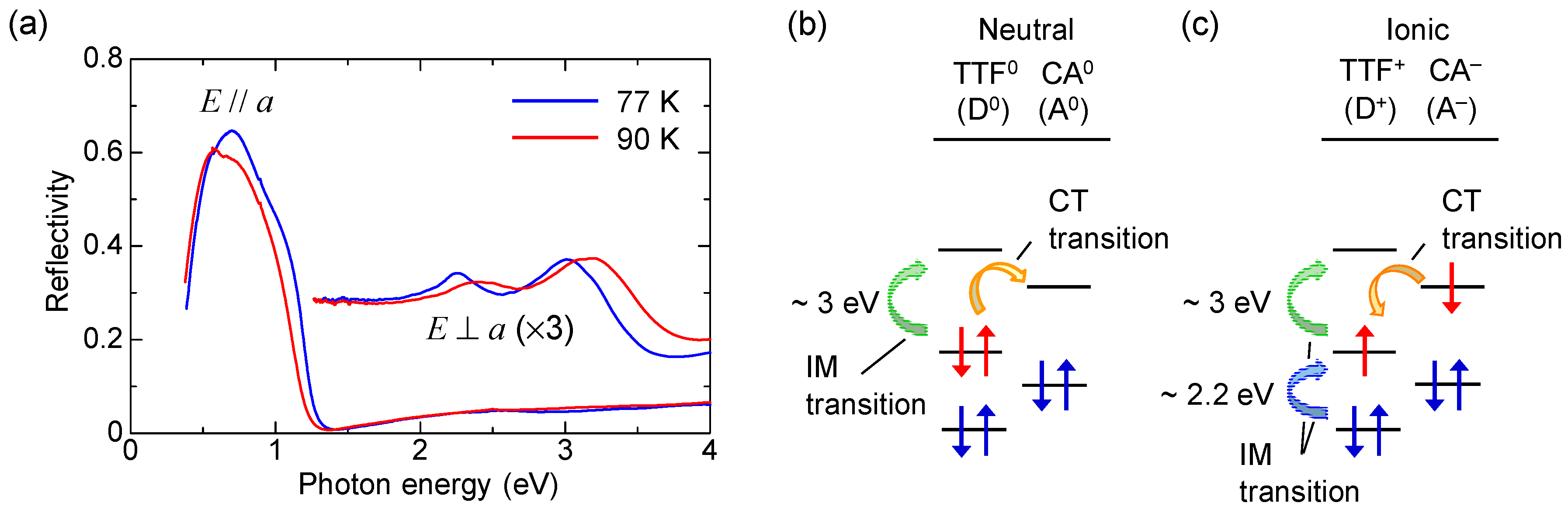
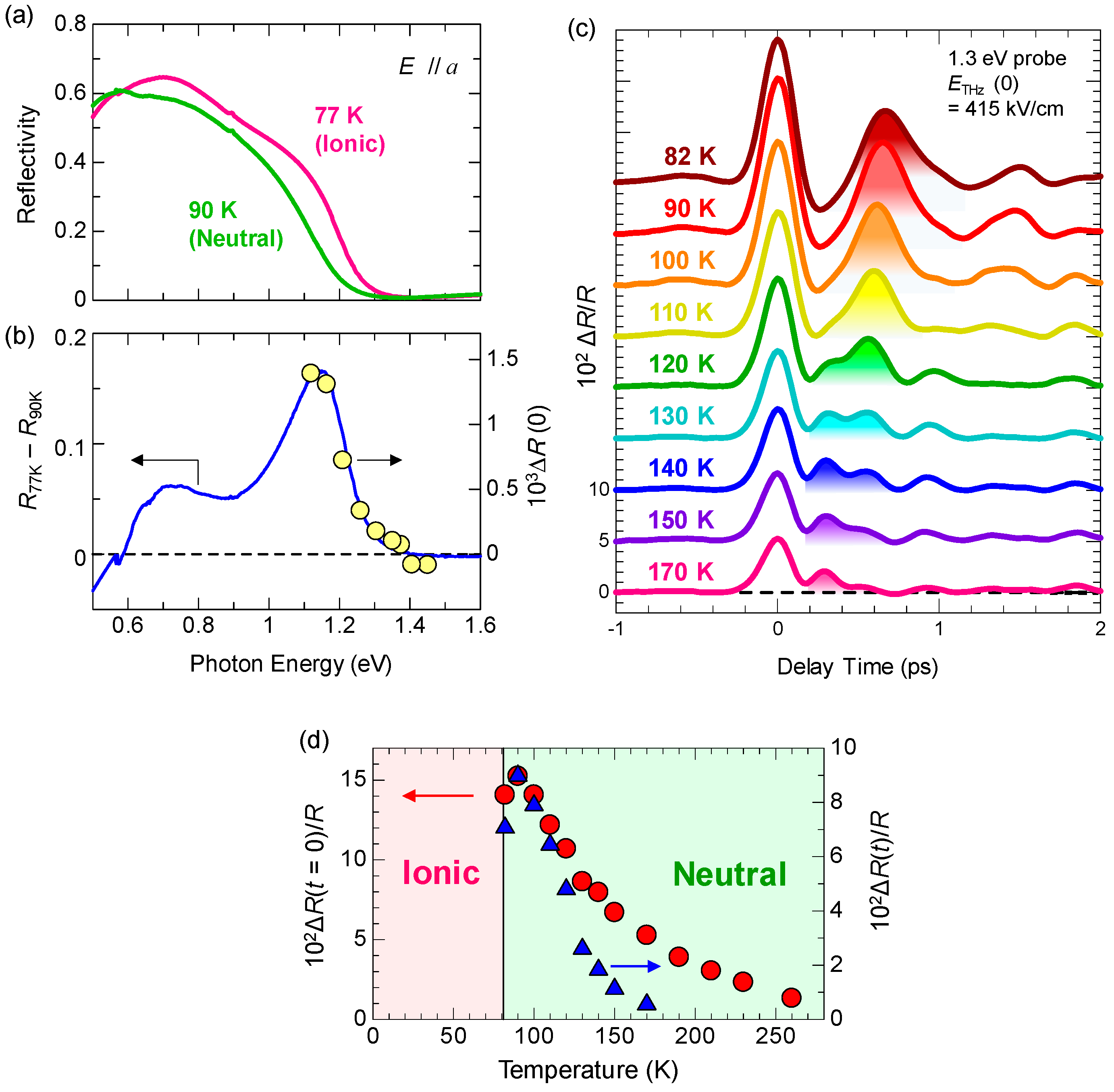
2.2. Optical Reflectivity Spectra
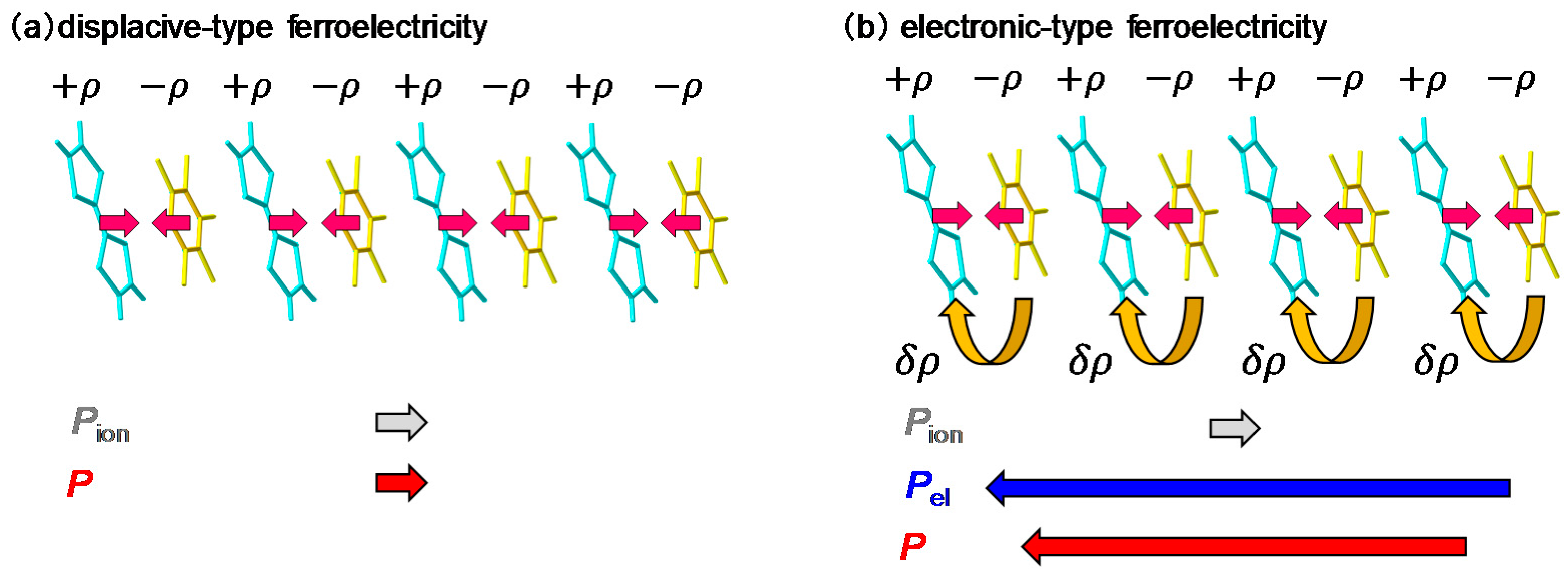
2.3. Electronic Ferroelectricity
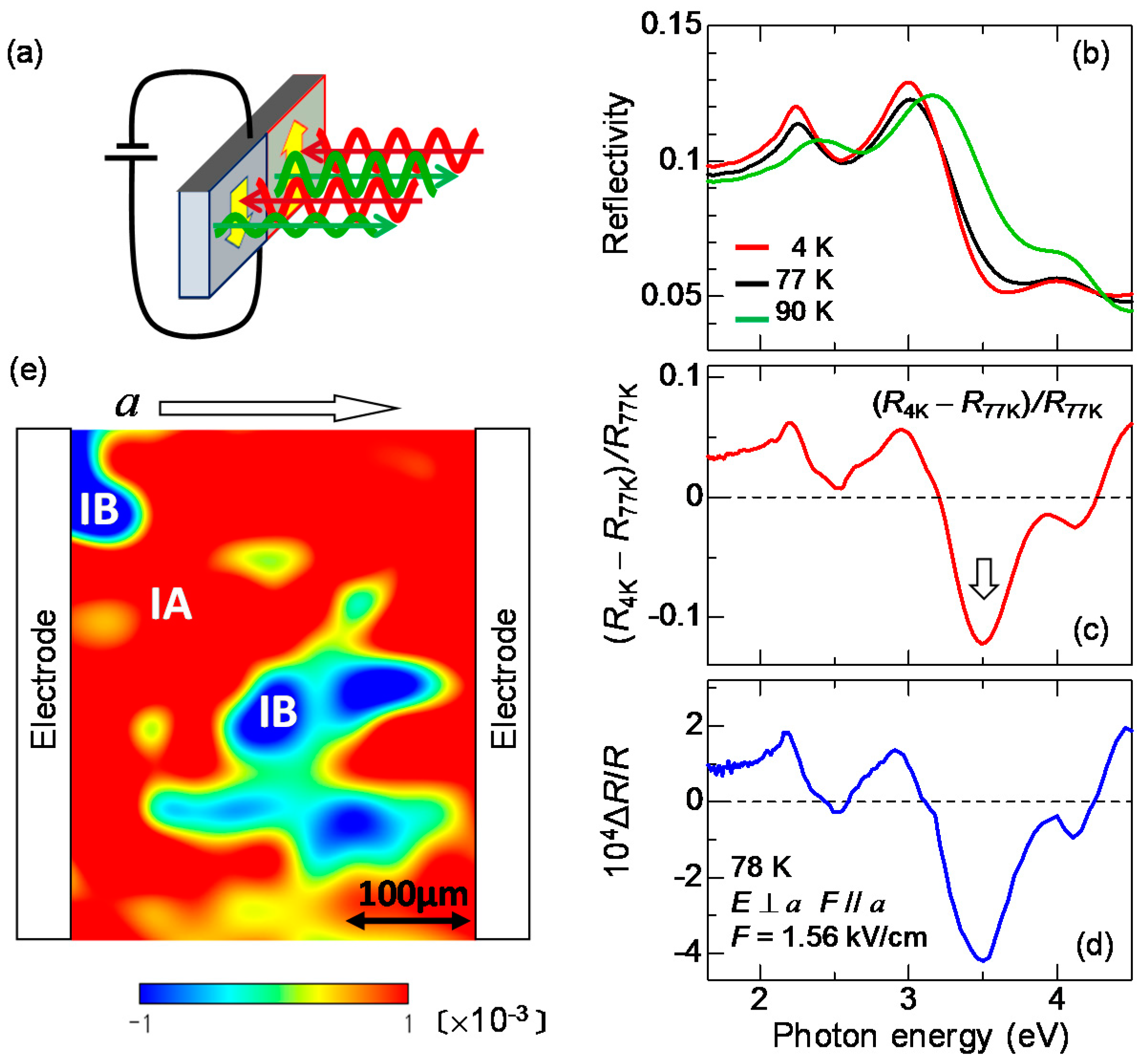
2.4. Imaging of Ferroelectric Domains
3. Time-Resolved Laser Spectroscopy
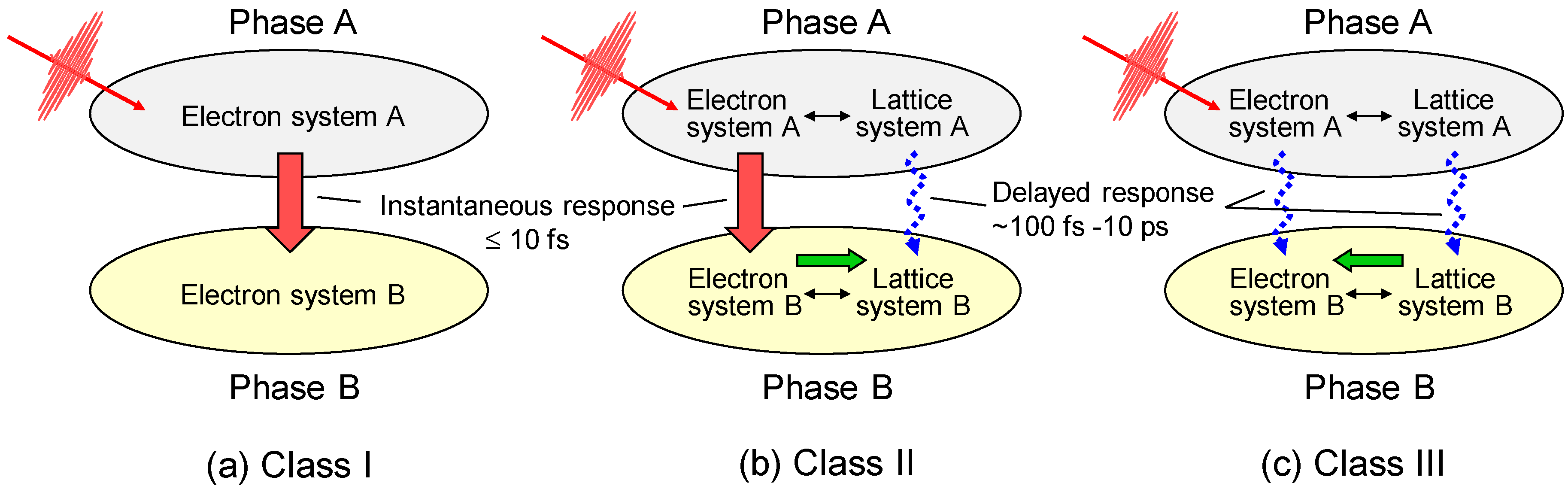
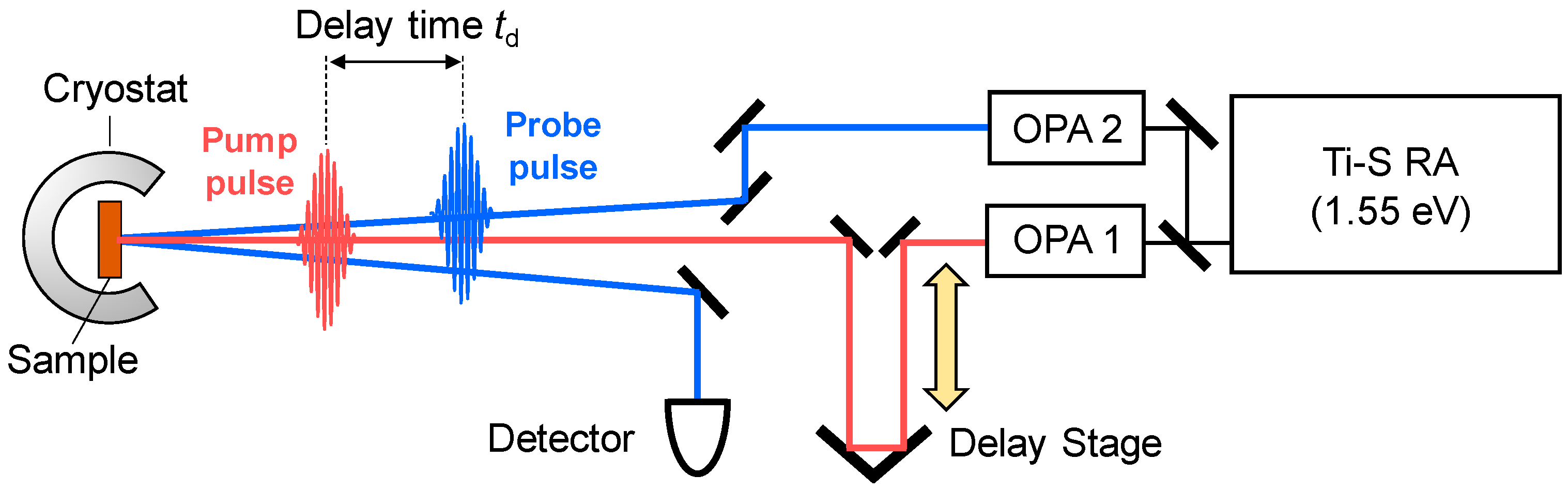
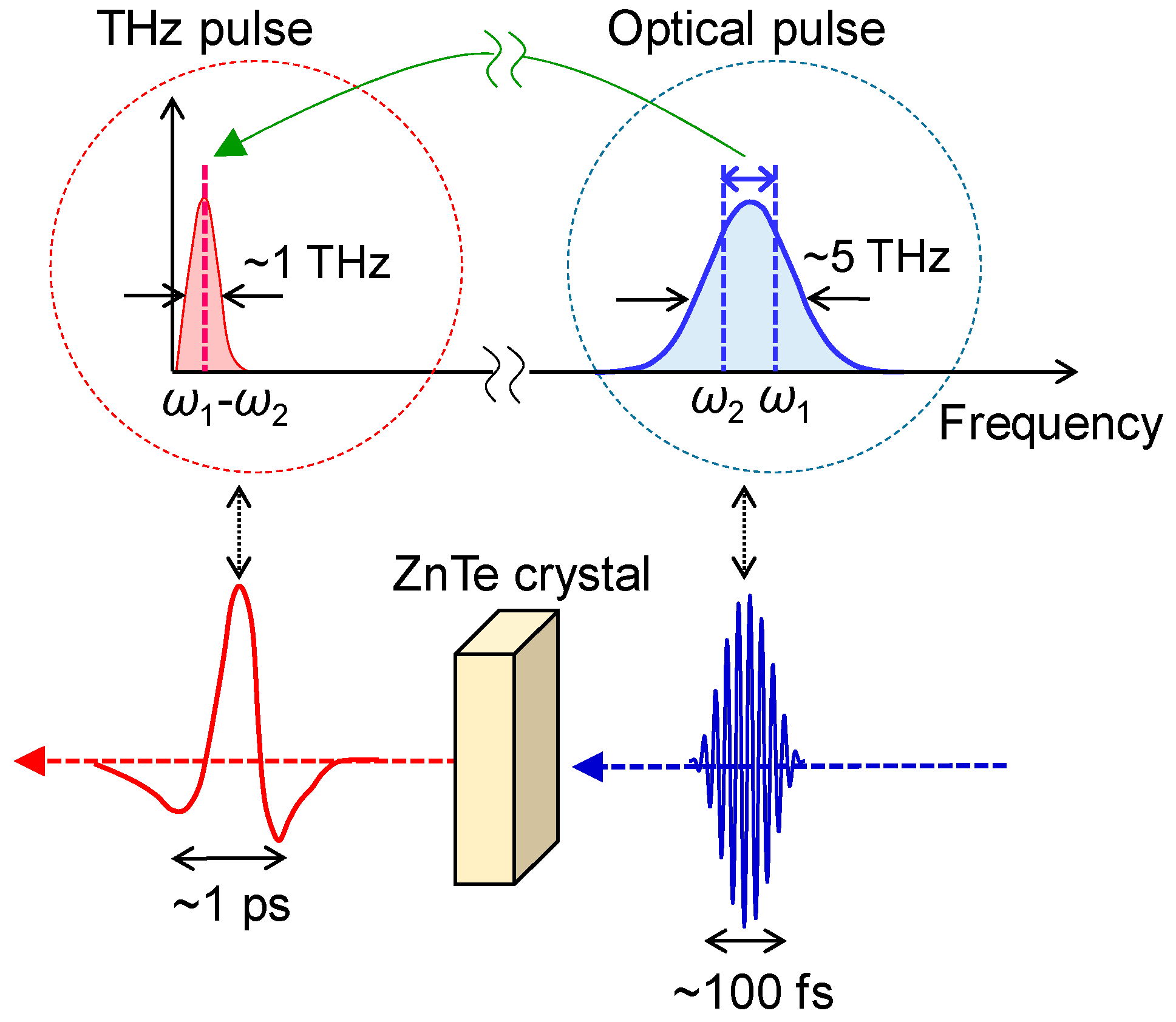
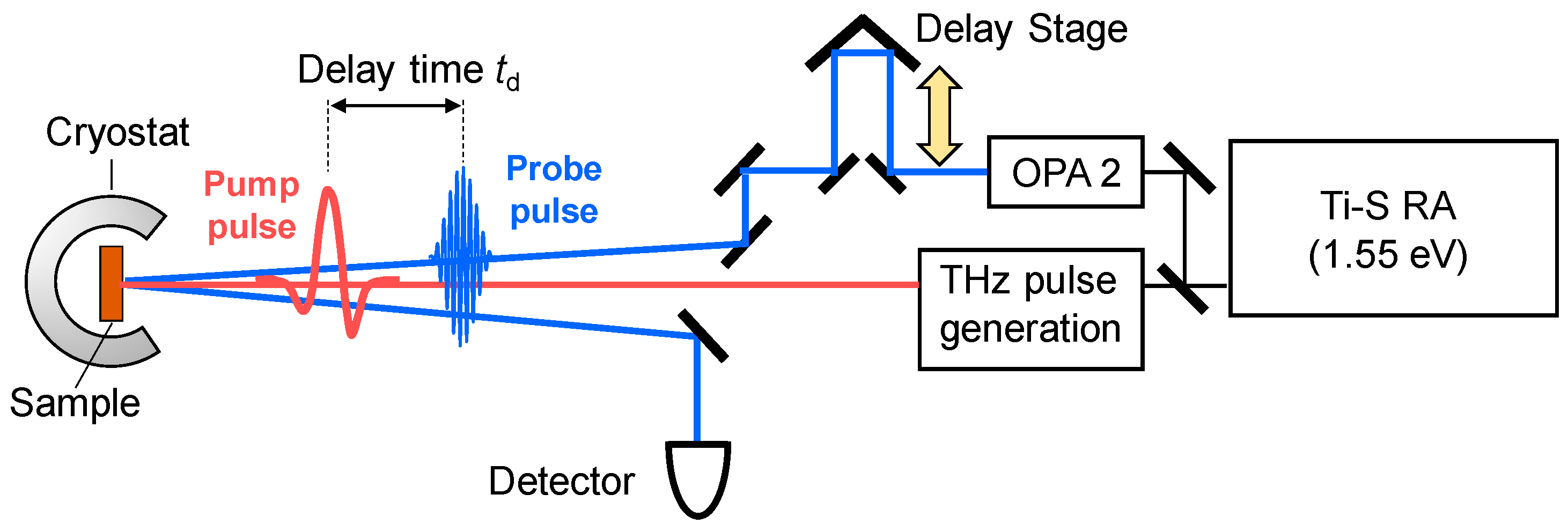
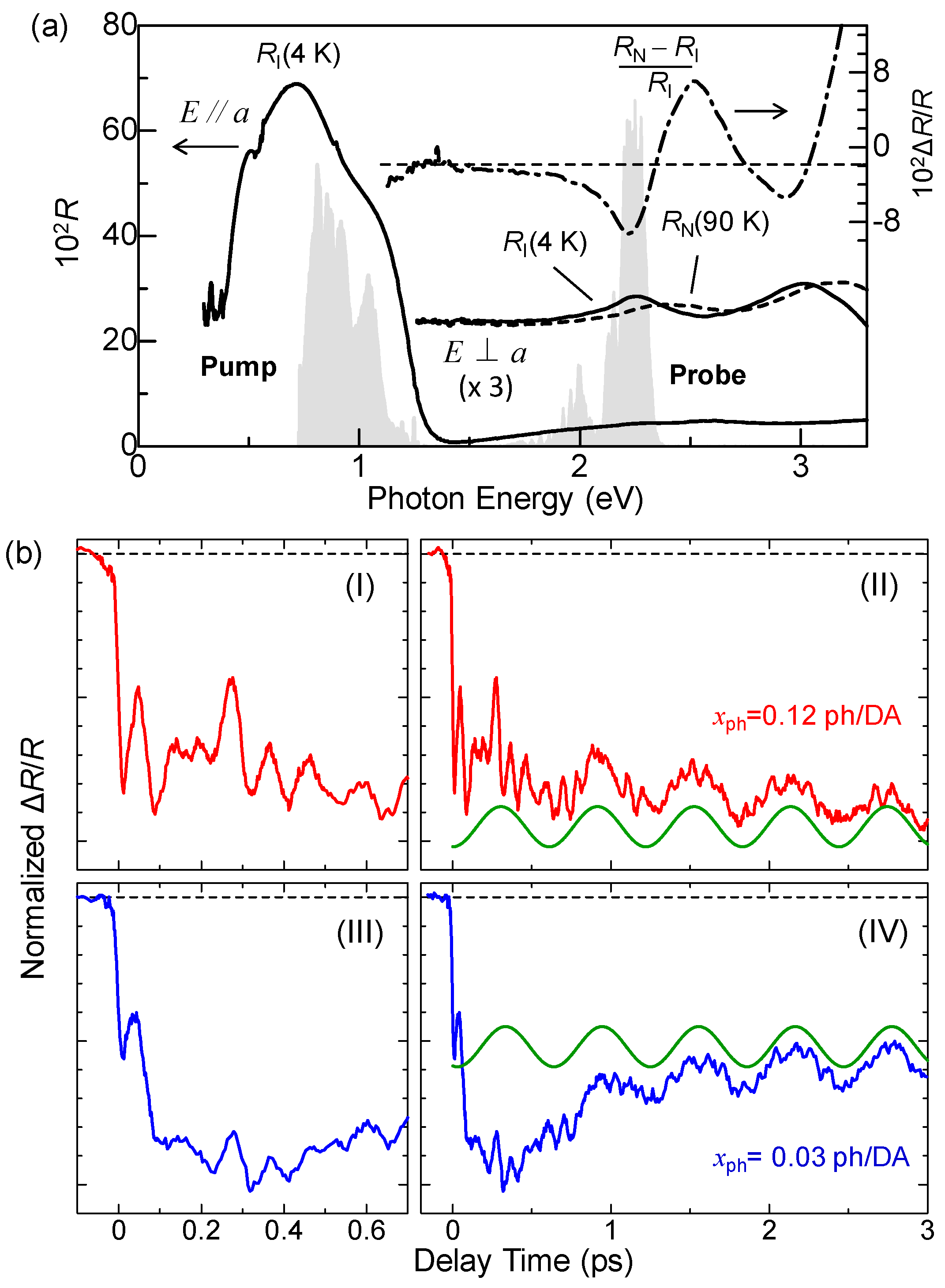
3.1. Femtosecond-Pump–Probe Spectroscopy and Necessary Time Resolution
3.2. Terahertz-Pump Optical-Probe Spectroscopy
4. Photoinduced Neutral to Ionic Phase Transition in TTF-CA
4.1. Photoinduced Neutral-to-Ionic Transition
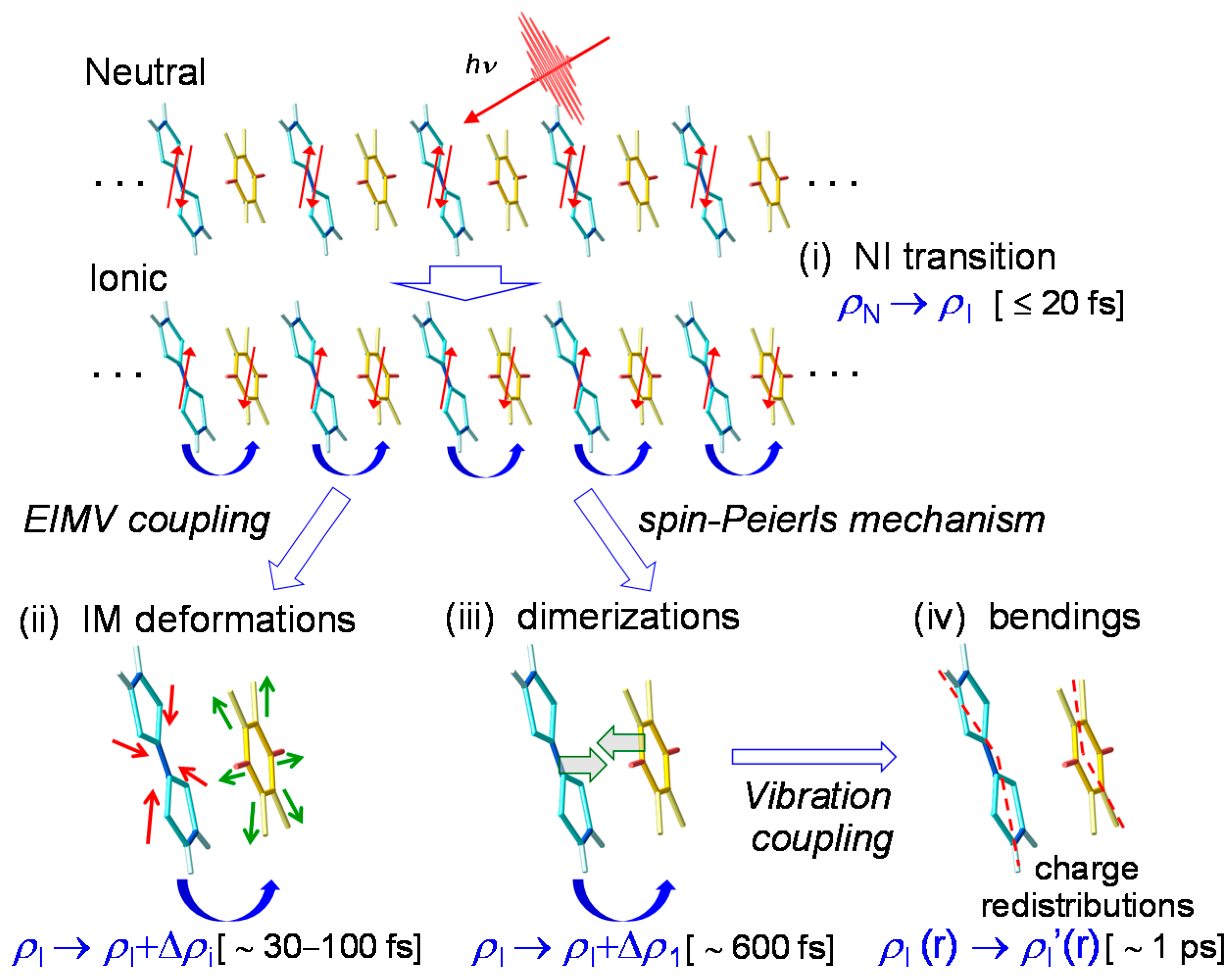
4.2. Ultrafast Dynamics of Ionic Domain Formation
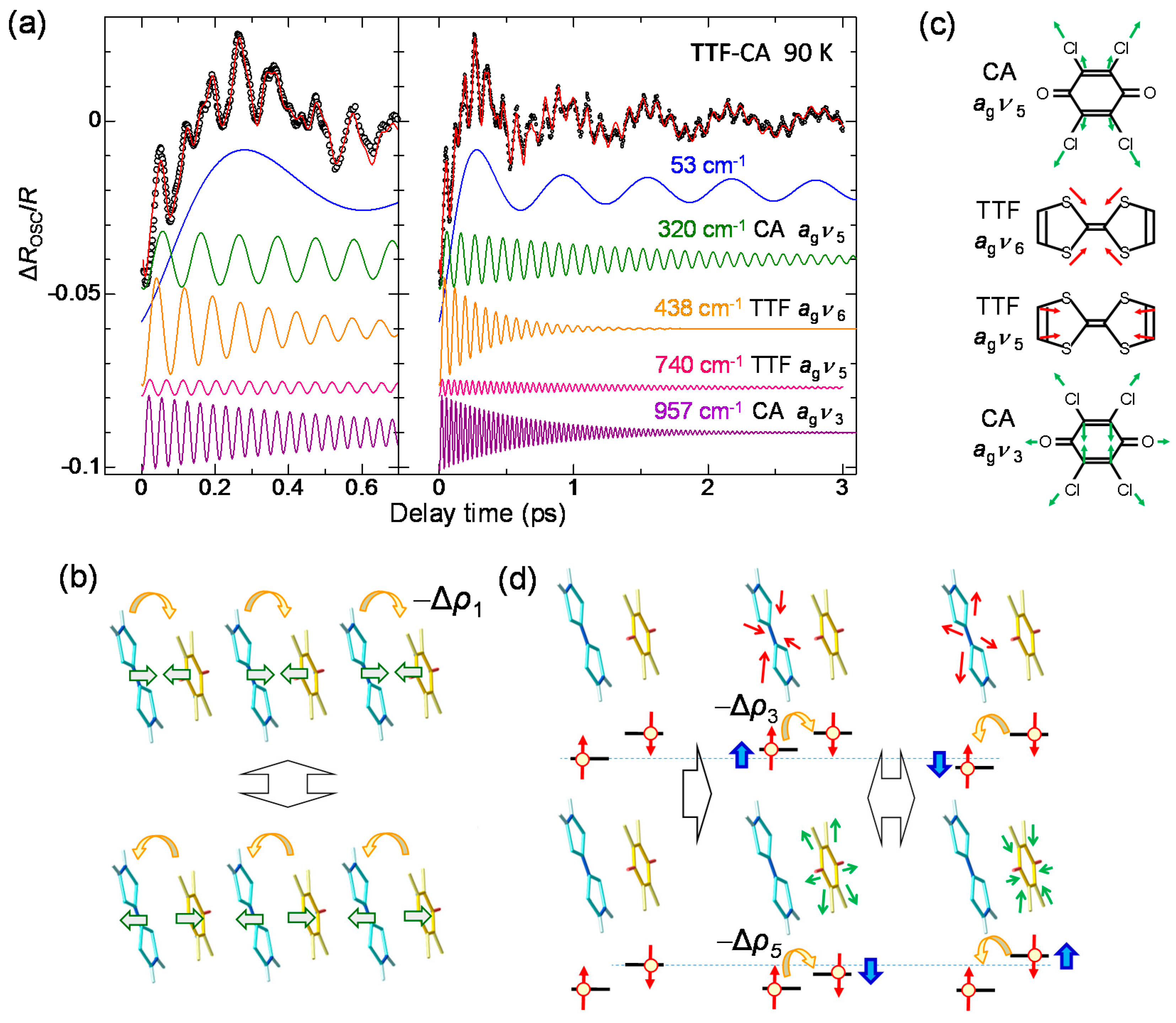
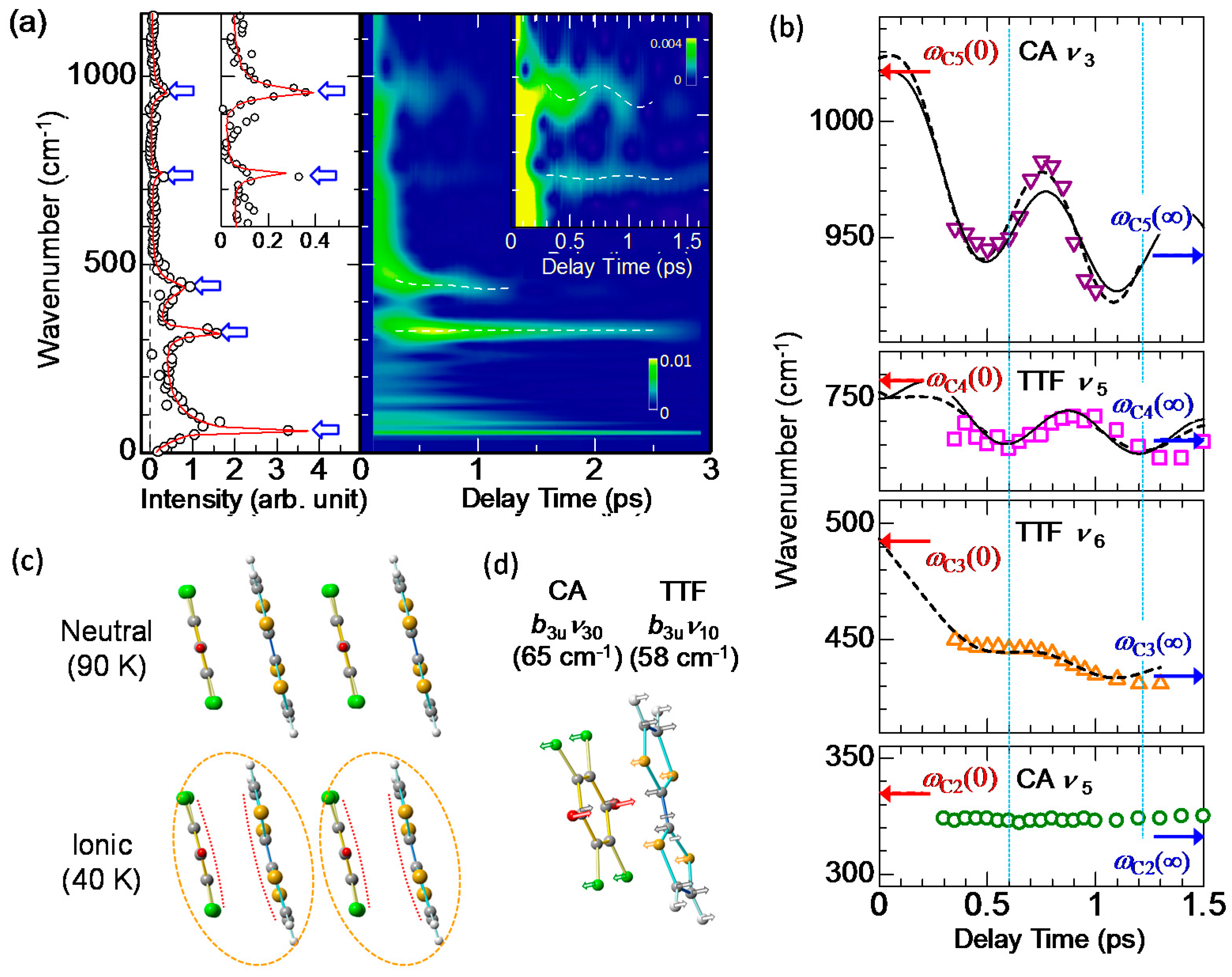
4.3. Stabilization of an Ionic Domain by Molecular Displacements and Deformations
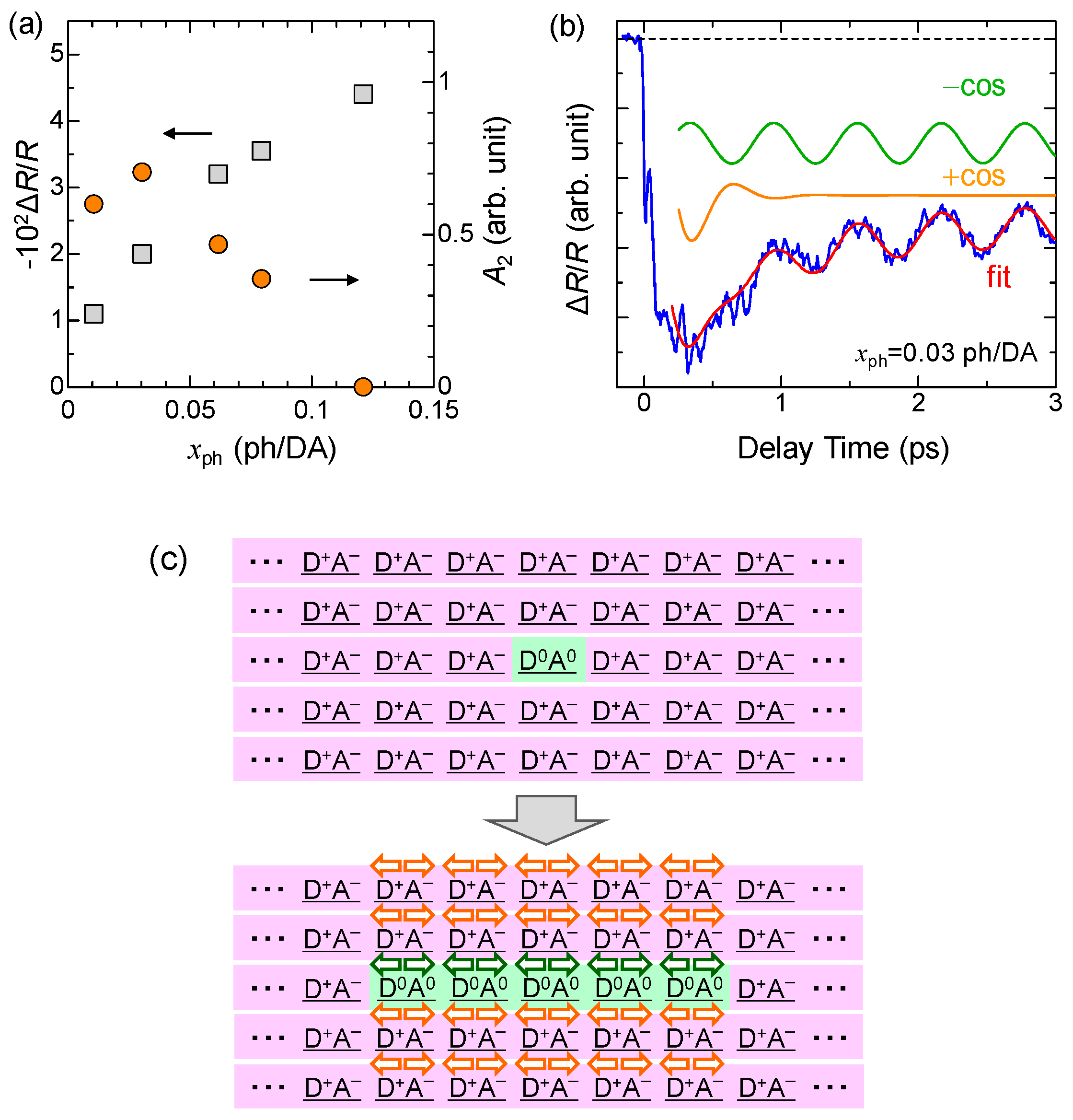
4.4. Charge and Molecular Dynamics Deduced from Oscillation Analyses
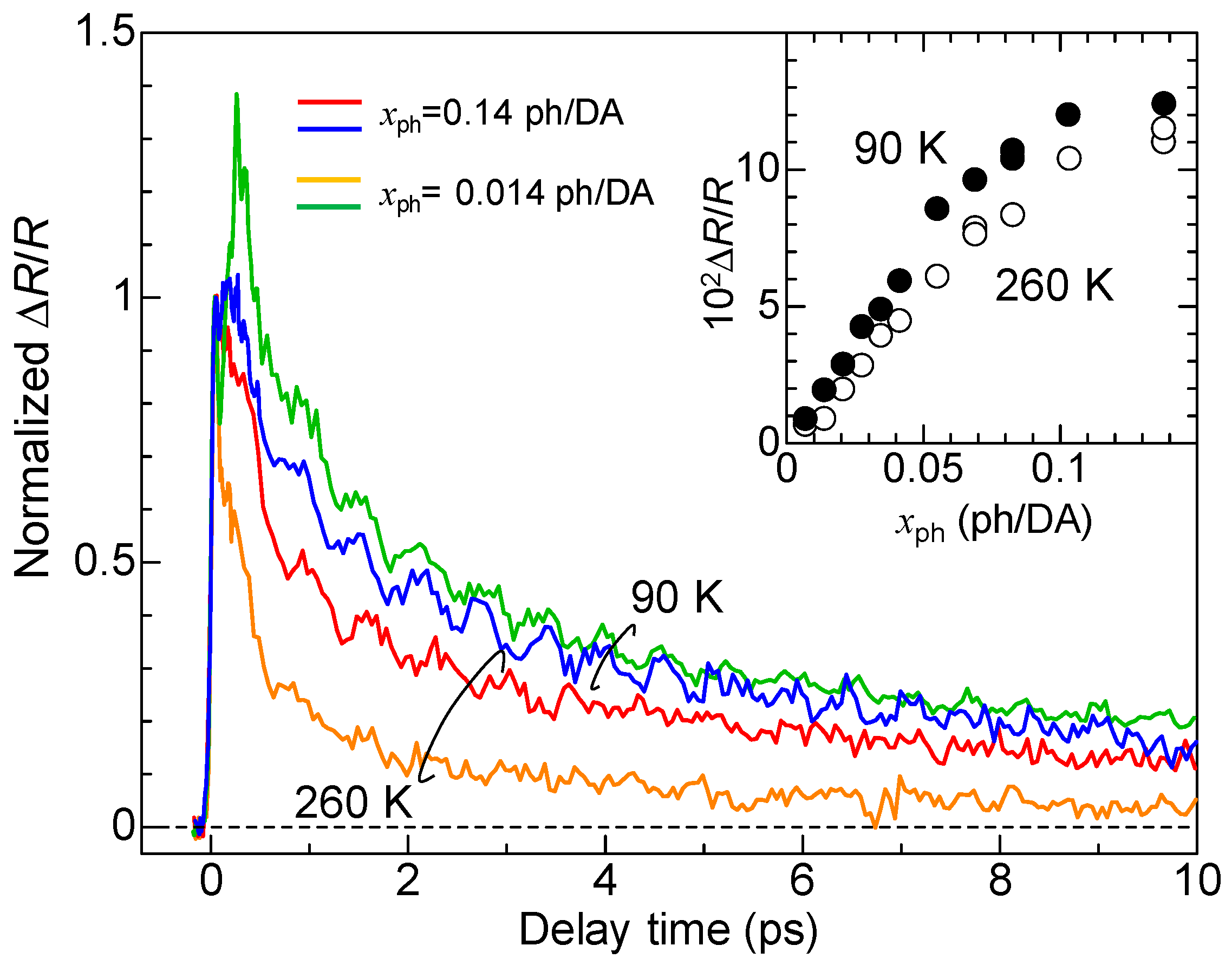
4.5. Macroscopic Feature of Photoinduced Neutral-to-Ionic Transition
5. Photoinduced Ionic-to-Neutral Phase Transition in TTF-CA
5.1. Photoinduced Ionic-to-Neutral Transition
5.2. Ultrafast Dynamics of Neutral Domain Formation and Multiplication
5.3. Collective Molecular Dynamics
6. Control of Ferroelectric Polarization by Terahertz Electric Field in the Ionic Phase of TTF-CA
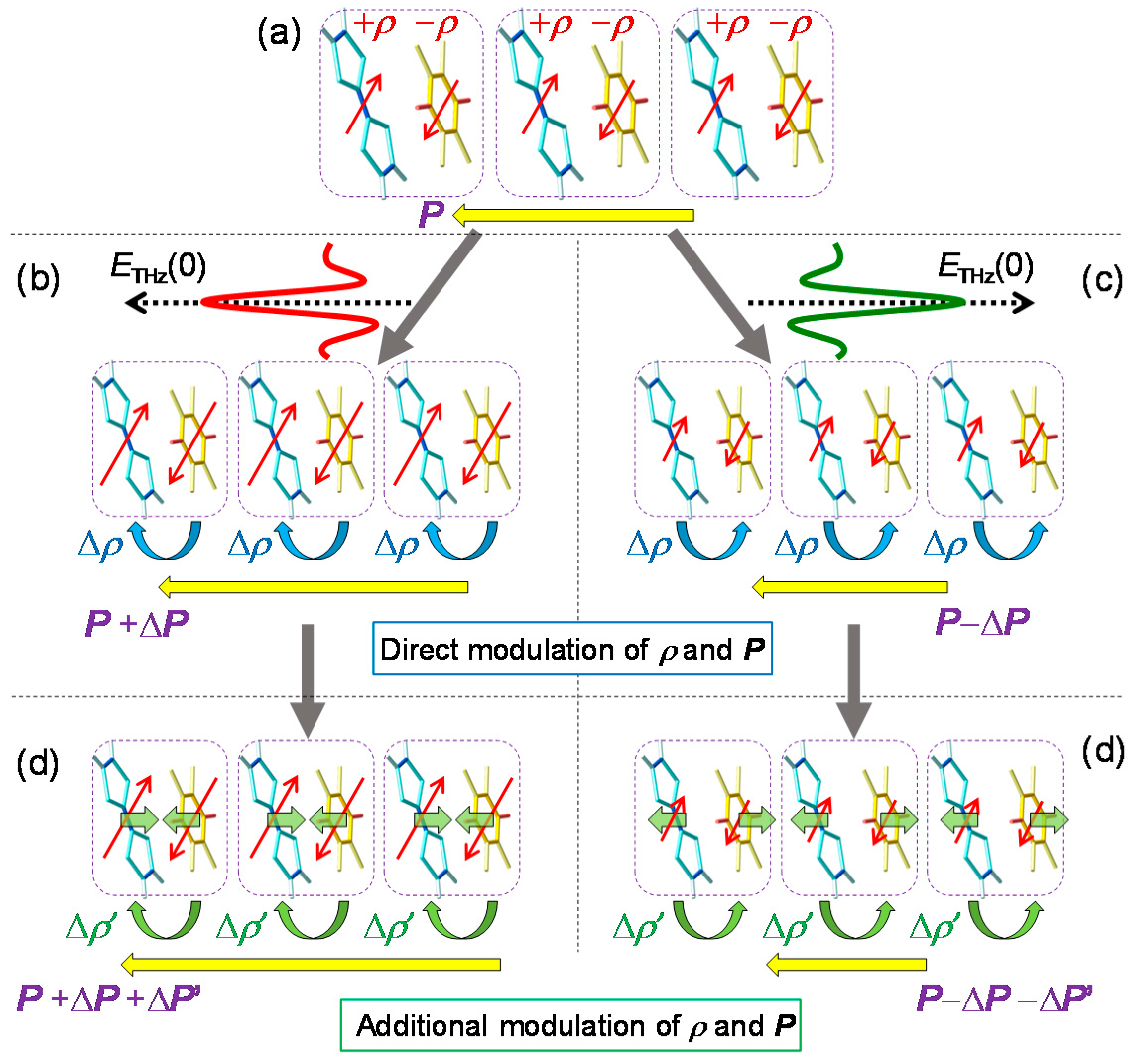
6.1. Rapid Modulation of Ferroelectric Polarization
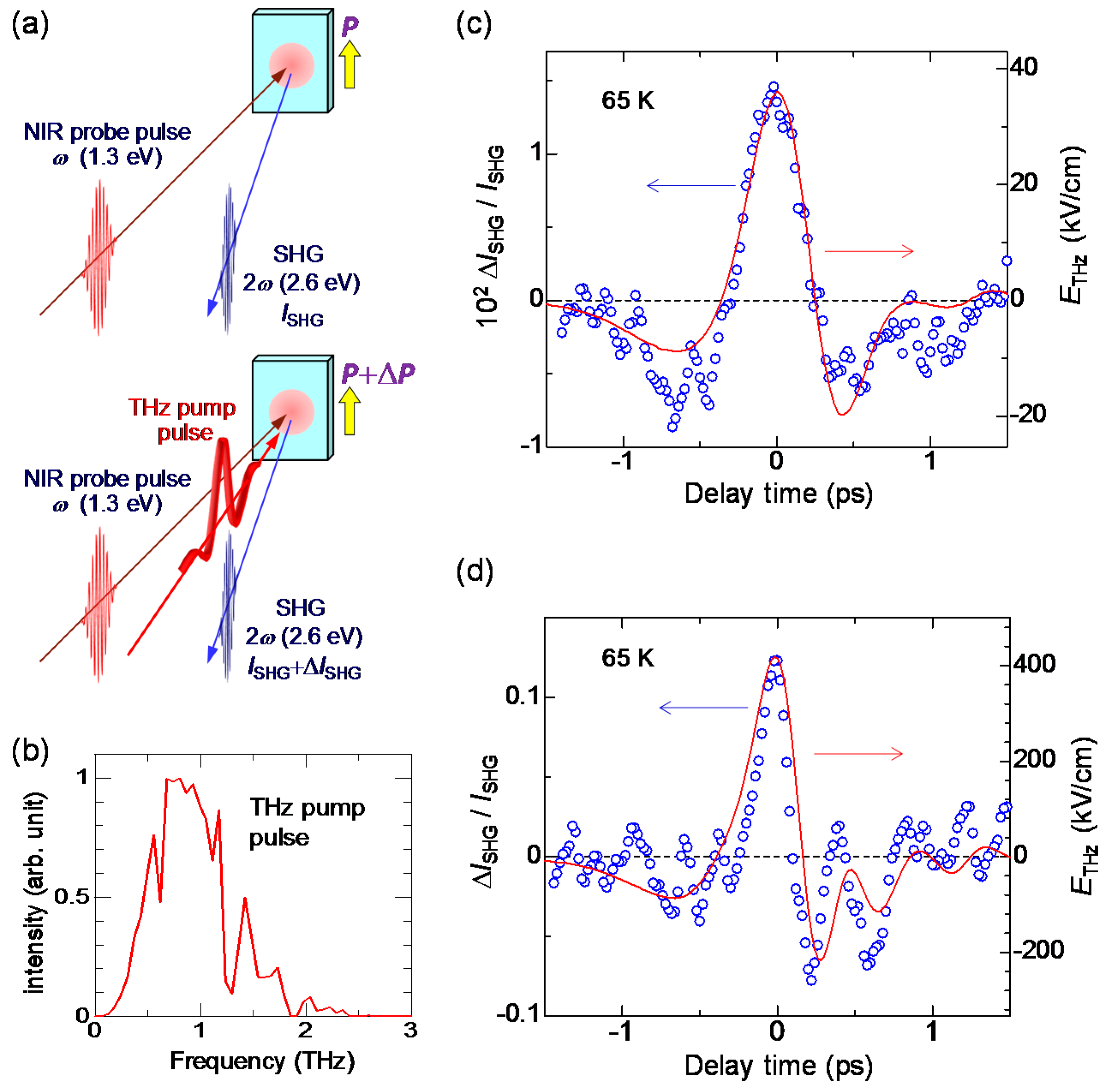
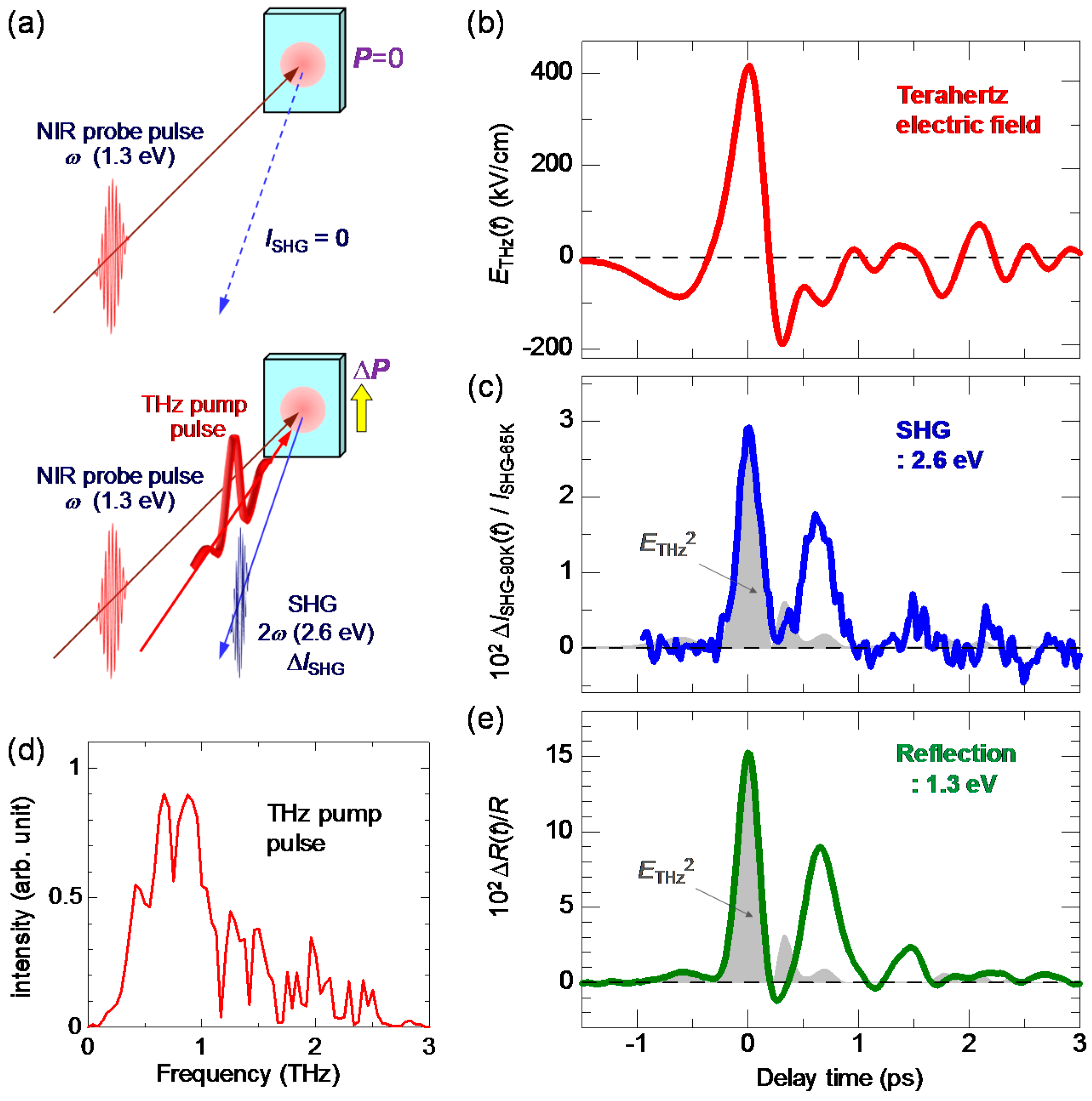
6.2. Terahertz-Pulse-Pump Second-Harmonic-Generation-Probe Measurements in the Ionic Phase
6.3. Terahertz-Pulse-Pump Optical-Reflectivity-Probe Measurements in the Ionic Phase
6.4. Magnitudes of Polarization Modulation
6.5. Coherent Oscillation Generated by Electric-Field-Induced Polarization Modulation
7. Generation of Ferroelectric Polarization by Terahertz Electric-Field Pulse in the Neutral Phase of TTF-CA
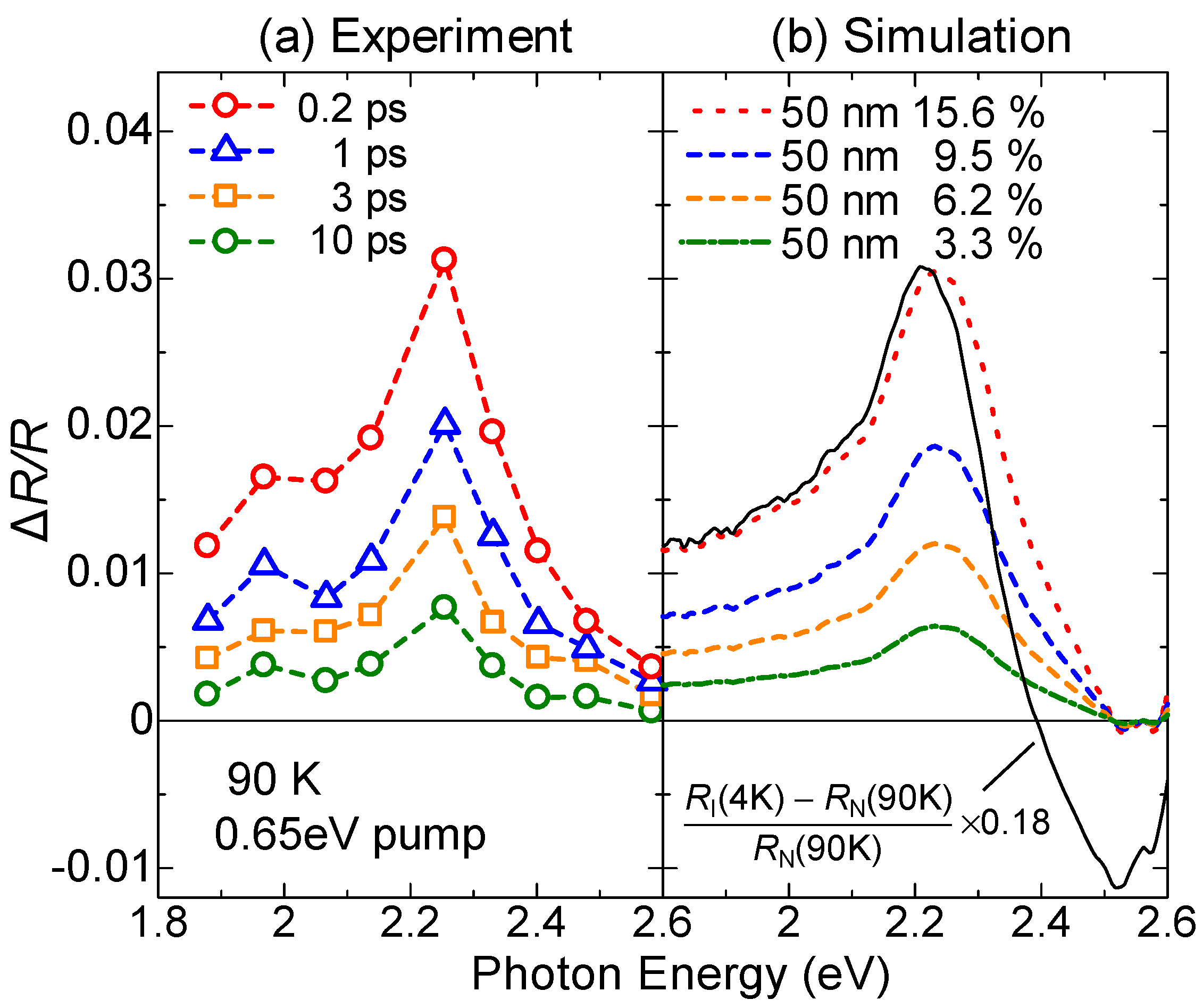
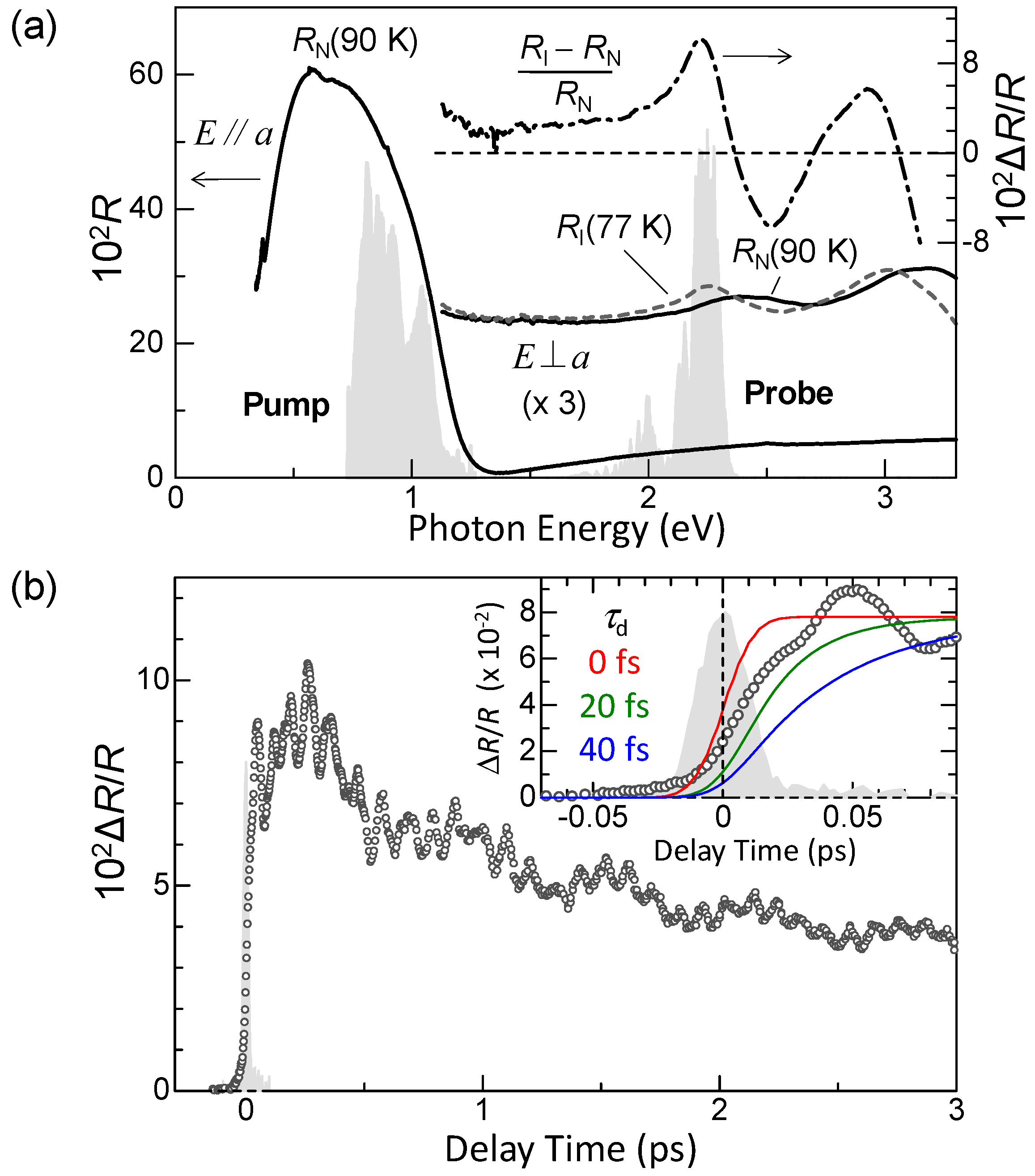
7.1. Rapid Generation of Large Polarization
7.2. Terahertz-Pulse-Pump Second-Harmonic-Generation-Probe Measurements in the Neutral Phase
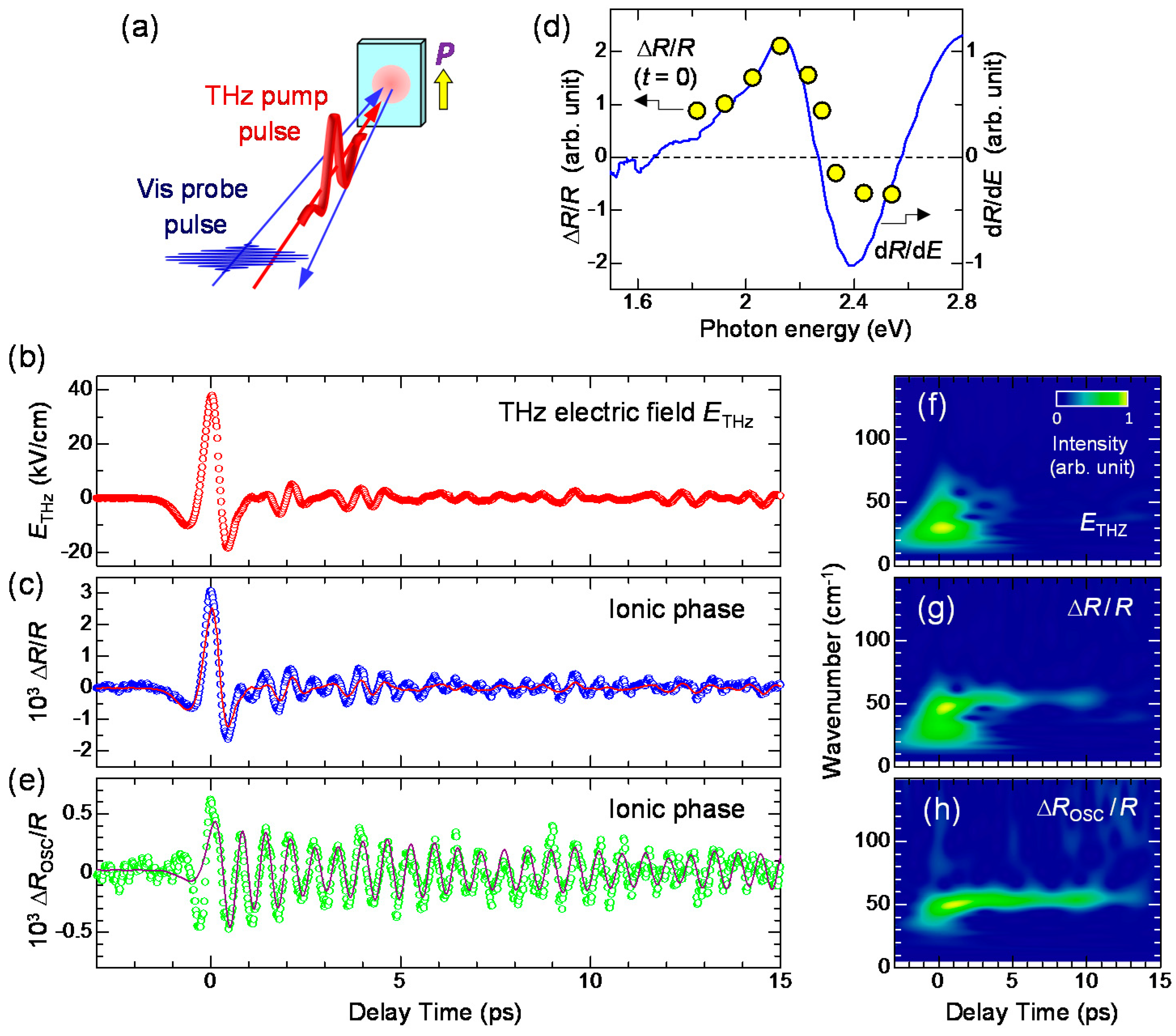
7.3. Terahertz-Pulse-Pump Optical-Reflectivity-Probe Measurements in the Neutral Phase
7.4. Dynamical Aspects of Electric-Field-Induced Polarization Generation
- (1)
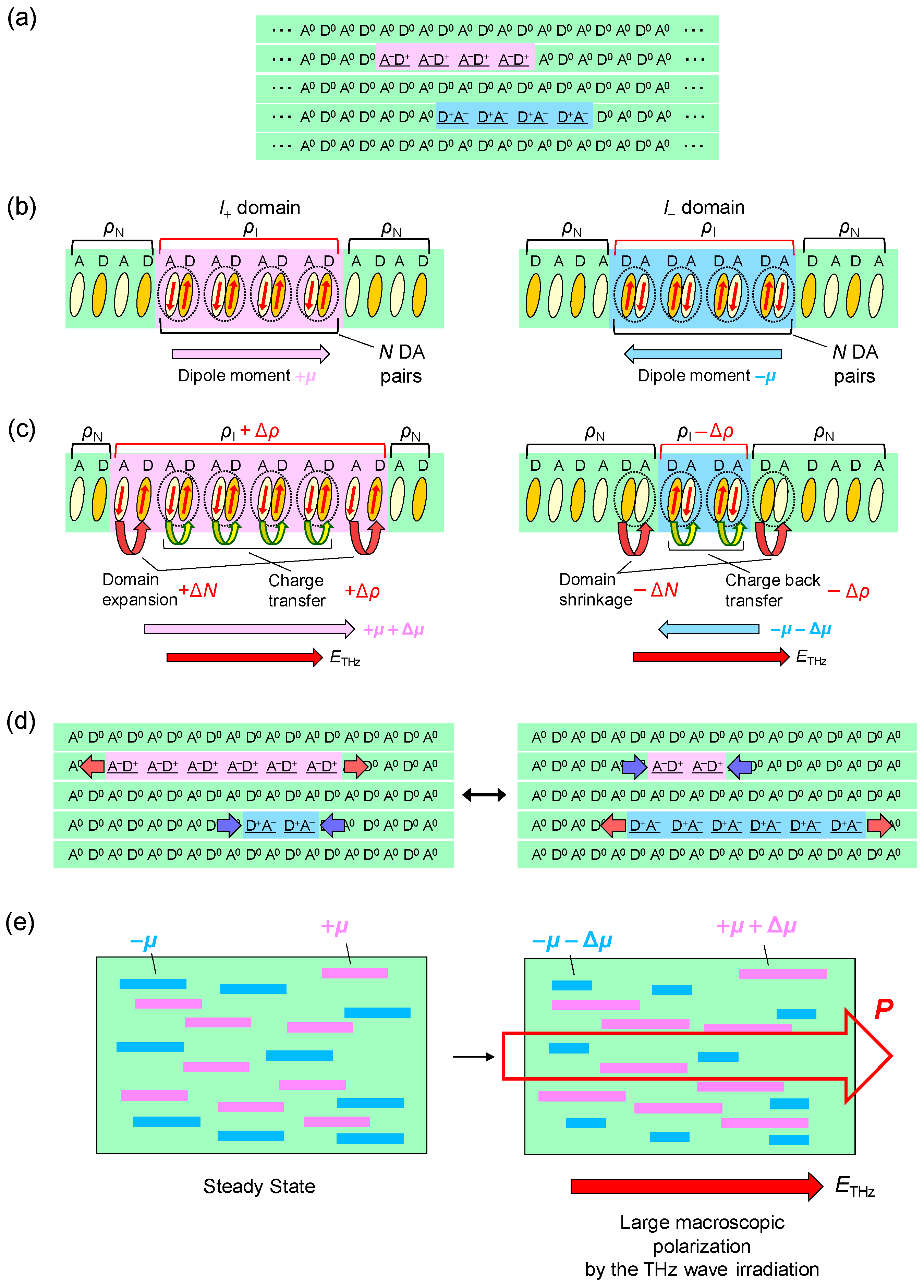
- The large polarization generation by the terahertz electric field around the time origin originates from the expansions and shrinkages of microscopic I domains via the charge transfer processes shown by the red arrows in Figure 26c, as well as the intermolecular fractional charge transfers within the original I domains shown by the yellow arrows in the same figure. These charge transfer processes are electronic and the responses in and around the time origin are very fast.
- (2)
- We estimated the change in the degree of charge transfer within the DA molecules in an I domain and the change in the size of a microscopic I domain by the terahertz electric field to be and , respectively, at and 90 K. That is, the terahertz electric-field pulse increases by ~27% and the I-domain size by ~43%. This causes the formation of the large macroscopic polarization reaching 17% of the ferroelectric polarization in the ferroelectric I phase.
- (3)
- The expanded or shrunken I domains are stabilized by molecular displacements and also probably by molecular deformations. In their recovery processes after the electric field disappears, the coherent breathing oscillations of NIDW pairs occur and their frequency is in the terahertz region. The frequency of the oscillation changes from 32 cm−1 at 170 K to 19 cm−1 at 82 K. Such a softening can be explained by the fact that the energy difference between the N and I states decreases as the temperature approaches Tc.
8. Summary
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nasu, K. Photoinduced Phase Transitions; World Scientific: Singapore, 2004. [Google Scholar]
- Iwai, S.; Okamoto, H. Ultrafast Phase Control in One-Dimensional Correlated Electron Systems. J. Phys. Soc. Jpn. 2006, 75, 011007:1–011007:21. [Google Scholar] [CrossRef]
- Okamoto, H. Molecular Electronic and Related Materials-Control and Probe with Light; Naito, T., Ed.; Transworld Research Network: Trivandrum, India, 2010; pp. 59–97. [Google Scholar]
- Iwai, S.; Ono, M.; Maeda, A.; Matsuzaki, H.; Kishida, H.; Okamoto, H.; Tokura, Y. Ultrafast Optical Switching to a Metallic State by Photoinduced Mott Transition in a Halogen-Bridged Nickel-Chain Compound. Phys. Rev. Lett. 2003, 91, 057401:1–057401:4. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, H.; Matsuzaki, H.; Wakabayashi, T.; Takahashi, Y.; Hasegawa, T. Photoinduced Metallic State Mediated by Spin-Charge Separation in a One-Dimensional Organic Mott Insulator. Phys. Rev. Lett. 2007, 98, 037401:1–037401:4. [Google Scholar] [CrossRef] [PubMed]
- Uemura, H.; Matsuzaki, H.; Takahashi, Y.; Hasegawa, T.; Okamoto, H. Ultrafast Charge Dynamics in One-Dimensional Organic Mott Insulators. J. Phys. Soc. Jpn. 2008, 77, 113714:1–113714:4. [Google Scholar] [CrossRef]
- Okamoto, H.; Miyagoe, T.; Kobayashi, K.; Uemura, H.; Nishioka, H.; Matsuzaki, H.; Sawa, A.; Tokura, Y. Ultrafast Charge Dynamics in Photoexcited Nd2CuO4 and La2CuO4 Cuprate Compounds Investigated by Femtosecond Absorption Spectroscopy. Phys. Rev. B 2010, 82, 060513(R):1–060513(R):4. [Google Scholar] [CrossRef]
- Okamoto, H.; Miyagoe, T.; Kobayashi, K.; Uemura, H.; Nishioka, H.; Matsuzaki, H.; Sawa, A.; Tokura, Y. Photoinduced Transition from Mott Insulator to Metal in the Undoped Cuprates Nd2CuO4 and La2CuO4. Phys. Rev. B 2011, 83, 125102:1–125102:10. [Google Scholar] [CrossRef]
- Torrance, J.B.; Vazquez, J.E.; Mayerle, J.J.; Lee, V.Y. Discovery of a Neutral-to-Ionic Phase Transition in Organic Materials. Phys. Rev. Lett. 1981, 46, 253–257. [Google Scholar] [CrossRef]
- Torrance, J.B.; Girlando, A.; Mayerle, J.J.; Crowley, J.I.; Lee, V.Y.; Batail, P.; LaPlaca, S.J. Anomalous Nature of Neutral-to-Ionic Phase Transition in Tetrathiafulvalene-Chloranil. Phys. Rev. Lett. 1981, 47, 1747–1750. [Google Scholar] [CrossRef]
- Koshihara, S.; Tokura, Y.; Mitani, T.; Saito, G.; Koda, T. Photoinduced Valence Instability in the Organic Molecular Compound Tetrathiafulvalene-p-Chloranil (TTF-CA). Phys. Rev. B 1990, 42, 6853–6856. [Google Scholar] [CrossRef]
- Toyozawa, Y. Condensation of Relaxed Excions in Static and Dynamic Phase Transitions. Solid State Commun. 1992, 84, 255–257. [Google Scholar] [CrossRef]
- Suzuki, T.; Sakamaki, T.; Tanimura, K.; Koshihara, S.; Tokura, Y. Ionic-to-Neutral Phase Transformation Induced by Photoexcitation of the Charge-Transfer Band in Tetrathiafulvalene-p-Chloranil Crystals. Phys. Rev. B 1999, 60, 6191–6193. [Google Scholar] [CrossRef]
- Koshihara, S.; Takahashi, Y.; Sakai, H.; Tokura, Y.; Luty, T. Photoinduced Cooperative Charge Transfer in Low-Dimensional Organic Crystals. J. Phys. Chem. B 1999, 103, 2592–2600. [Google Scholar] [CrossRef]
- Huai, P.; Zheng, H.; Nasu, K. Theory for Photoinduced Ionic-Neutral Structural Phase Transition in Quasi One-Dimensional Organic Molecular Crystal TTF-CA. J. Phys. Soc. Jpn. 2000, 69, 1788–1800. [Google Scholar] [CrossRef]
- Luty, T.; Cailleau, H.; Koshihara, S.; Collet, E.; Takesada, M.; Lemée-Cailleau, M.H.; Cointe, M.B.L.; Nagaosa, N.; Tokura, Y.; Zienkiewicz, E.; et al. Static and Dynamic Order of Cooperative Multi-Electron Transfer. Europhys. Lett. 2002, 59, 619–625. [Google Scholar] [CrossRef]
- Iwai, S.; Tanaka, S.; Fujinuma, K.; Kishida, H.; Okamoto, H.; Tokura, Y. Ultrafast Optical Switching from an Ionic to a Neutral State in Tetrathiafulvalene-p-Chloranil (TTF-CA) Observed in Femtosecond Reflection Spectroscopy. Phys. Rev. Lett. 2002, 88, 057402:1–057402:4. [Google Scholar] [CrossRef] [PubMed]
- Collet, E.; Lemée-Cailleau, M.H.; Cointe, M.B.L.; Cailleau, H.; Wulff, M.; Luty, T.; Koshihara, S.; Meyer, M.; Toupet, L.; Rabiller, P.; et al. Laser-Induced Ferroelectric Structural Order in an Organic Charge-Transfer Crystal. Science 2003, 300, 612–615. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, H.; Ishige, Y.; Tanaka, S.; Kishida, H.; Iwai, S.; Tokura, Y. Photoinduced Phase Transition in Tetrathiafulvalene-p-Chloranil Observed in Femtosecond Reflection Spectroscopy. Phys. Rev. B 2004, 70, 165202:1–165202:18. [Google Scholar] [CrossRef]
- Guérin, L.; Collet, E.; Lemée-Cailleau, M.H.; Cointe, M.B.L.; Cailleau, H.; Plech, A.; Wulff, M.; Koshihara, S.Y.; Luty, T. Probing Photoinduced Phase Transition in a Charge-Transfer Molecular Crystal by 100 Picosecond X-Ray Diffraction. Chem. Phys. 2004, 299, 163–170. [Google Scholar] [CrossRef]
- Tanimura, K. Femtosecond Time-Resolved Reflection Spectrescopy of Photoinduced Ionic-Neutral Phase Transition in TTF-CA Crystals. Phys. Rev. B 2004, 70, 144112:1–144112:11. [Google Scholar] [CrossRef]
- Yonemitsu, K. Phase Transition in a One-Dimensional Extended Peierls-Hubbard Model with a Pulse of Oscillating Electric Field: II. Linear Behavior in Neutral-to-Ionic Transition. J. Phys. Soc. Jpn. 2004, 73, 2879–2886. [Google Scholar] [CrossRef]
- Yonemitsu, K.; Nasu, K. Theory of Photoinduced Phase Transitions. J. Phys. Soc. Jpn. 2006, 75, 011008:1–011008:8. [Google Scholar] [CrossRef]
- Iwai, S.; Ishige, Y.; Tanaka, S.; Okimoto, Y.; Tokura, Y.; Okamoto, H. Coherent Control of Charge and Lattice Dynamics in a Photoinduced Neutral-to-Ionic Transition of a Charge-Transfer Compound. Phys. Rev. Lett. 2006, 96, 057403:1–057403:4. [Google Scholar] [CrossRef] [PubMed]
- Yonemitsu, K. Interchain Coupling Effects on Photoinduced Phase Transitions between Neutral and Ionic Phases in an Extended Hubbard Model with Alternating Potentials and an Electron–lattice Coupling. Phys. Rev. B 2006, 73, 155120:1–155120:7. [Google Scholar] [CrossRef]
- Iwano, K. Direct Photoexcitation of Appreciable Size of Domains without Lattice Motion in Neutral–Ionic Transition Systems. Phys. Rev. Lett. 2006, 97, 226404:1–226404:4. [Google Scholar] [CrossRef] [PubMed]
- Iwano, K. Detection of Domain Dynamics by High Energy Photons: Proposals in One-Dimensional Photoinduced Phase Transition Systems. Phys. Rev. Lett. 2009, 102, 106405:1–106405:4. [Google Scholar] [CrossRef] [PubMed]
- Nasu, K. sp3 Domain in Graphite by Visible Light and Photoinduced Phase Transitions. Eur. Phys. J. B 2010, 75, 415–430. [Google Scholar] [CrossRef]
- Guerin, L.; Hebert, J.; Cointe, M.B.L.; Adachi, S.; Koshihara, S.; Cailleau, H.; Collet, E. Capturing One-Dimensional Precursors of a Photoinduced Transformation in a Material. Phys. Rev. Lett. 2010, 105, 246101:1–246101:4. [Google Scholar] [CrossRef] [PubMed]
- Uemura, H.; Okamoto, H. Direct Detection of the Ultrafast Response of Charges and Molecules in the Photoinduced Neutral-to-Ionic Transition of the Organic Tetrathiafulvalene-p-Chloranil Solid. Phys. Rev. Lett. 2010, 105, 258302:1–258302:4. [Google Scholar] [CrossRef] [PubMed]
- Yonemitsu, K. Effects of Lattice and Molecular Phonons on Photoinduced Neutral-to-Ionic Transition Dynamics in Tetrathiafulvalene-p-Chloranil. J. Phys. Soc. Jpn. 2011, 80, 084707:1–084707:7. [Google Scholar] [CrossRef]
- Matsubara, Y.; Okimoto, Y.; Yoshida, T.; Ishikawa, T.; Koshihara, S.; Onda, K. Photoinduced Neutral-to-Ionic Phase Transition in Tetrathiafulvalene-p-Chloranil Studied by Time-Resolved Vibrational Spectroscopy. J. Phys. Soc. Jpn. 2011, 80, 124711:1–124711:5. [Google Scholar] [CrossRef]
- Miyamoto, T.; Uemura, H.; Okamoto, H. Role of Coulomb Interactions and Spin-Peierls Dimerizations in Neutral-to-Ionic Phase Transition Investigated by Femtosecond Reflection Spectroscopy. J. Phys. Soc. Jpn. 2012, 81, 073703:1–073703:4. [Google Scholar] [CrossRef]
- Hoshino, M.; Nozawa, S.; Sato, T.; Tomita, A.; Adachi, S.; Koshihara, S. Time-Resolved X-Ray Crystal Structure Analysis for Elucidating the Hidden “over-Neutralized” Phase of TTF-CA. RSC Adv. 2013, 3, 16313–16317. [Google Scholar] [CrossRef]
- Miyamoto, T.; Kimura, K.; Hamamoto, T.; Uemura, H.; Yada, H.; Matsuzaki, H.; Horiuchi, S.; Okamoto, H. Measurement of a Photoinduced Transition from a Nonordered Phase to a Transient Ordered Phase in the Organic Quantum-Paraelectric Compound Dimethyltetrathiafulvalene-Dibromodichloro-p-Benzoquinone Using Femtosecond Laser Irradiation. Phys. Rev. Lett. 2013, 111, 187801:1–187801:5. [Google Scholar] [CrossRef] [PubMed]
- Brazovskii, S.; Kirova, N. Excitonic Mechanism of Local Phase Transformations by Optical Pumping. J. Supercond. Nov. Magn. 2014, 27, 1009–1013. [Google Scholar] [CrossRef]
- Yi, T.; Kirova, N.; Brazovskii, S. Dynamical patterns of phase transformations from self-trapping of quantum excitons. Phys. B 2015, 460, 73–78. [Google Scholar] [CrossRef]
- Cavatorta, L.; Painelli, A.; Soos, Z.G. Coherent Excitations at the Neutral–ionic Transition: Femtosecond Dynamics on Diabatic Potential Energy Surfaces. Phys. Rev. B 2015, 91, 174301:1–174301:10. [Google Scholar] [CrossRef]
- Kirova, N.; Brazovskii, S. Electronic ferroelectricity in carbon based materials. Synth. Met. 2016, 216, 11–22. [Google Scholar] [CrossRef]
- Brazovskii, S.; Kirova, N. Dynamical phase transitions and pattern formation induced by a pulse pumping of excitons to a system near a thermodynamic instability. Phy. Rev. B 2016, 94, 054302:1–054302:7. [Google Scholar] [CrossRef]
- Miyamoto, T.; Yada, H.; Yamakawa, H.; Okamoto, H. Ultrafast Modulation of Polarization Amplitude by Terahertz Fields in Electronic-Type Organic Ferroelectrics. Nat. Commun. 2013, 4, 2586:1–2586:9. [Google Scholar] [CrossRef] [PubMed]
- Morimoto, T.; Miyamoto, T.; Yamakawa, H.; Terashige, T.; Ono, T.; Kida, N.; Okamoto, H. Terahertz-Field-Induced Large Macroscopic Polarization and Domain-Wall Dynamics in an Organic Molecular Dielectric. Phys. Rev. Lett. 2017, 118, 107602:1–107602:6. [Google Scholar] [CrossRef] [PubMed]
- McConnell, H.M.; Hoffman, B.M.; Metzger, R.M. Charge Transfer in Molecular Crystals. Proc. Natl. Acad. Sci. USA 1965, 53, 46–50. [Google Scholar] [CrossRef] [PubMed]
- Girlando, A.; Marzola, F.; Pecile, C.; Torrance, J.B. Vibrational Spectroscopy of Mixed Stack Organic Semiconductors: Neutral and Ionic Phases of Tetrathiafulvalene-chloranil (TTF-CA) Charge Transfer Complex. J. Chem. Phys. 1983, 79, 1075–1085. [Google Scholar] [CrossRef]
- Tokura, Y.; Kaneko, Y.; Okamoto, H.; Tanuma, S.; Koda, T.; Mitani, T.; Saito, G. Spectroscopic Study of the Neutral-to-Ionic Phase Transition in TTF-Chloranil. Mol. Cryst. Liq. Cryst. 1985, 125, 71–80. [Google Scholar] [CrossRef]
- Takaoka, K.; Kaneko, Y.; Okamoto, H.; Tokura, Y.; Koda, T.; Mitani, T.; Saito, G. Infrared Molecular-Vibration Spectra of Tetrathiafulvalene-Chloranil Crystal at Low Temperature and High Pressure. Phys. Rev. B 1987, 36, 3884–3887. [Google Scholar] [CrossRef]
- Horiuchi, S.; Okimoto, Y.; Kumai, R.; Tokura, Y. Anomalous Valence Fluctuation near a Ferroelectric Transition in an Organic Charge-Transfer Complex. J. Phys. Soc. Jpn. 2000, 69, 1302–1305. [Google Scholar] [CrossRef]
- Kanai, Y.; Tani, M.; Kagoshima, S.; Tokura, Y.; Koda, T. X-Ray Evidence for the Molecular Dimerization in TTF-Chloranil. Synth. Met. 1984, 10, 157–160. [Google Scholar] [CrossRef]
- Cointe, M.L.; Lemée-Cailleau, M.H.; Cailleau, H.; Toudic, B.; Toupet, L.; Heger, G.; Moussa, F.; Schweiss, P.; Kraft, K.H.; Karl, N. Symmetry Breaking and Structural Changes at the Neutral-to-Ionic Transition in Tetrathiafulvalene-p-Chloranil. Phys. Rev. B 1995, 51, 3374–3386. [Google Scholar] [CrossRef]
- Lemée-Cailleau, M.H.; Cointe, M.B.L.; Cailleau, H.; Luty, T.; Moussa, F.; Roos, J.; Brinkmann, D.; Toudic, B.; Ayache, C.; Karl, N. Thermodynamics of the Neutral-to-Ionic Transition as Condensation and Crystallization of Charge-Transfer Excitations. Phys. Rev. Lett. 1997, 79, 1690–1693. [Google Scholar] [CrossRef]
- Tokura, Y.; Koda, T.; Mitani, T.; Saito, G. Neutral-to-Ionic Transition in Tetrathiafulvalene-p-Chloranil as Investigated by Optical Reflection Spectra. Solid State Commun. 1982, 43, 757–760. [Google Scholar] [CrossRef]
- Tokura, Y.; Koda, T.; Saito, G.; Mitani, T. Effect of Substitutional Impurities on the Neutral-to-Ionic Phase Transition in TTF-p-Chloranil Crystal. J. Phys. Soc. Jpn. 1984, 53, 4445–4455. [Google Scholar] [CrossRef]
- Kobayashi, K.; Horiuchi, S.; Kumai, R.; Kagawa, F.; Murakami, Y.; Tokura, Y. Electronic Ferroelectricity in a Molecular Crystal with Large Polarization Directing Antiparallel to Ionic Displacement. Phys. Rev. Lett. 2012, 108, 237601:1–237601:5. [Google Scholar] [CrossRef] [PubMed]
- Giovannetti, G.; Kumar, S.; Stroppa, A.; Van Den Brink, J.; Picozzi, S. Multiferroicity in TTF-CA Organic Molecular Crystals Predicted through Ab Initio Calculations. Phys. Rev. Lett. 2009, 103, 266401:1–266401:4. [Google Scholar] [CrossRef] [PubMed]
- Ishibashi, S.; Terakura, K. First-Principles Study of Spontaneous Polarization in Tetrathiafulvalene-p-Chloranil (TTF-CA). Phys. B 2010, 405, S338–S340. [Google Scholar] [CrossRef]
- Portengen, T.; Östreich, T.; Sham, L.J. Theory of Electronic Ferroelectricity. Phys. Rev. B 1996, 54, 17452–17463. [Google Scholar] [CrossRef]
- Yamamoto, K.; Iwai, S.; Boyko, S.; Kashiwazaki, A.; Hiramatsu, F.; Okabe, C.; Nishi, N.; Yakushi, K. Strong Optical Nonlinearity and its Ultrafast Response Associated with Electron Ferroelectricity in an Organic Conductor. J. Phys. Soc. Jpn. 2008, 77, 074709:1–074709:6. [Google Scholar] [CrossRef]
- Yamakawa, H.; Miyamoto, T.; Morimoto, T.; Yada, H.; Kinoshita, Y.; Sotome, M.; Kida, N.; Yamamoto, K.; Iwano, K.; Matsumoto, Y.; et al. Novel Electronic Ferroelectricity in an Organic Charge-Order Insulator Investigated with Terahertz-Pump Optical-Probe Spectroscopy. Sci. Rep. 2016, 6, 20571:1–20571:10. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, N.; Ohsumi, H.; Ohwada, K.; Ishii, K.; Inami, T.; Kakurai, K.; Murakami, Y.; Yoshii, K.; Mori, S.; Horibe, Y.; et al. Ferroelectricity from Iron Valence Ordering in the Charge-Frustrated System LuFe2O4. Nature 2005, 436, 1136–1138. [Google Scholar] [CrossRef] [PubMed]
- Uesu, Y.; Kurimura, S.; Yamamoto, Y. Optical Second Harmonic Images of 90° Domain Structure in BaTiO3 and Periodically Inverted Antiparallel Domains in LiTaO3. Appl. Phys. Lett. 1995, 66, 2165–2167. [Google Scholar] [CrossRef]
- Kishida, H.; Takamatsu, H.; Fujinuma, K.; Okamoto, H. Ferroelectric Nature and Real-Space Observations of Domain Motions in the Organic Charge-Transfer Compound Tetrathiafulvalene-p-Chloranil. Phys. Rev. B 2009, 80, 205201:1–205201:7. [Google Scholar] [CrossRef]
- Kampfrath, T.; Sell, A.; Klatt, G.; Pashkin, A.; Mährlein, S.; Dekorsy, T.; Wolf, M.; Fiebig, M.; Leitenstorfer, A.; Huber, R. Coherent Terahertz Control of Antiferromagnetic Spin Waves. Nat. Photonics 2011, 5, 31–34. [Google Scholar] [CrossRef]
- Liu, M.; Hwang, H.Y.; Tao, H.; Strikwerda, A.C.; Fan, K.; Keiser, G.R.; Sternbach, A.J.; West, K.G.; Kittiwatanakul, S.; Lu, J.; et al. Terahertz-Field-Induced Insulator-to-Metal Transition in Vanadium Dioxide Metamaterial. Nature 2012, 487, 345–348. [Google Scholar] [CrossRef] [PubMed]
- Kampfrath, T.; Tanaka, K.; Nelson, K.A. Resonant and Nonresonant Control over Matter and Light by Intense Terahertz Transients. Nat. Photonics 2013, 7, 680–690. [Google Scholar] [CrossRef]
- Yada, H.; Miyamoto, T.; Okamoto, H. Terahertz-Field-Driven Sub-Picosecond Optical Switching Enabled by Large Third-Order Optical Nonlinearity in a One-Dimensional Mott Insulator. Appl. Phys. Lett. 2013, 102, 091104:1–091104:4. [Google Scholar] [CrossRef]
- Kubacka, T.; Johnson, J.A.; Hoffmann, M.C.; Vicario, C.; de Jong, S.; Beaud, P.; Grübel, S.; Huang, S.W.; Huber, L.; Patthey, L.; et al. Large-Amplitude Spin Dynamics Driven by a THz Pulse in Resonance with an Electromagnon. Science 2014, 343, 1333–1337. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, R.; Tsuji, N.; Fujita, H.; Sugioka, A.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Aoki, H.; Shimano, R. Light-Induced Collective Pseudospin Precession Resonating with Higgs Mode in a Superconductor. Science 2014, 345, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
- Hebling, J.; Almasi, G.; Kozma, I.Z.; Kuhl, J. Velocity Matching by Pulse Front Tilting for Large Area THz-Pulse Generation. Opt. Express 2002, 10, 1161–1166. [Google Scholar] [CrossRef] [PubMed]
- Hirori, H.; Doi, A.; Blanchard, F.; Tanaka, K. Single-Cycle Terahertz Pulses with Amplitudes Exceeding 1 MV/cm Generated by Optical Rectification in LiNbO3. Appl. Phys. Lett. 2011, 98, 091106:1–091106:3. [Google Scholar] [CrossRef]
- Ma, H.M.; Liu, Y.X.; Fei, Y.; Li, F.M. The Influence of Electron-Hole Density Profile on the Picosecond Time-Resolved Reflectivity Measurement in Silicon. J. Appl. Phys. 1989, 65, 5031–5034. [Google Scholar] [CrossRef]
- Nagaosa, N.; Takimoto, J. Theory of Neutal-Ionic Transition in Organic Crystals. II. Effect of the Intersite Coulomb Interaction. J. Phys. Soc. Jpn. 1986, 55, 2745–2753. [Google Scholar] [CrossRef]
- Jacobsen, C.S.; Torrance, J.B. Behavior of Charge-Transfer Absorption upon Passing through the Neutral–Ionic Phase Transition. J. Chem. Phys. 1983, 78, 112–115. [Google Scholar] [CrossRef]
- Cavalleri, A.; Dekorsy, T.; Chong, H.H.W.; Kieffer, J.C.; Schoenlein, R.W. Evidence for a Structurally-Driven Insulator-to-Metal Transition in VO2: A View from the Ultrafast Timescale. Phys. Rev. B 2004, 70, 161102(R):1–161102(R):4. [Google Scholar] [CrossRef]
- Chollet, M.; Guerin, L.; Uchida, N.; Fukaya, S.; Shimoda, H.; Ishikawa, T.; Matsubara, K.; Hasegawa, T.; Ota, A.; Yamochi, H.; et al. Gigantic Photoresponse in 1/4-Filled-Band Organic Salt (EDO-TTF)2PF6. Science 2005, 307, 86–89. [Google Scholar] [CrossRef] [PubMed]
- Matsuzaki, H.; Yamashita, M.; Okamoto, H. Ultrafast Photoconversion from Charge Density Wave State to Mott-Hubbard State in One-Dimensional Extended Peierls-Hubbard System of Br-Bridged Pd Compound. J. Phys. Soc. Jpn. 2006, 75, 123701–123704. [Google Scholar] [CrossRef]
- Okamoto, H.; Ikegami, K.; Wakabayashi, T.; Ishige, Y.; Togo, J.; Kishida, H.; Matsuzaki, H. Ultrafast Photoinduced Melting of a Spin-Peierls Phase in an Organic Charge-Transfer Compound, K-Tetracyanoquinodimethane. Phys. Rev. Lett. 2006, 96, 037405:1–037405:4. [Google Scholar] [CrossRef] [PubMed]
- Perfetti, L.; Loukakos, P.A.; Lisowski, M.; Bovensiepen, U.; Berger, H.; Biermann, S.; Cornaglia, P.S.; Georges, A.; Wolf, M. Time Evolution of the Electronic Structure of 1T-TaS2 through the Insulator-Metal Transition. Phys. Rev. Lett. 2006, 97, 067402:1–067402:4. [Google Scholar] [CrossRef] [PubMed]
- Iwai, S.; Yamamoto, K.; Kashiwazaki, A.; Hiramatsu, F.; Nakaya, H.; Kawakami, Y.; Yakushi, K.; Okamoto, H.; Mori, H.; Nishio, Y. Photoinduced Melting of a Stripe-Type Charge-Order and Metallic Domain Formation in a Layered BEDT-TTF-Based Organic Salt. Phys. Rev. Lett. 2007, 98, 097402:1–097402:4. [Google Scholar] [CrossRef] [PubMed]
- Ikegami, K.; Ono, K.; Togo, J.; Wakabayashi, T.; Ishige, Y.; Matsuzaki, H.; Kishida, H.; Okamoto, H. Ultrafast Photoinduced Melting of Spin-Peierls Phase in the Organic Charge-Transfer Compounds Alkali-Tetracyanoquinodimethane. Phys. Rev. B 2007, 76, 085106:1–085106:12. [Google Scholar] [CrossRef]
- Polli, D.; Rini, M.; Wall, S.; Schoenlein, R.W.; Tomioka, Y.; Tokura, Y.; Cerullo, G.; Cavalleri, A. Coherent Orbital Waves in the Photo-Induced Insulator-Metal Dynamics of a Magnetoresistive Manganite. Nat. Mater. 2007, 6, 643–647. [Google Scholar] [CrossRef] [PubMed]
- Kubler, C.; Ehrke, H.; Huber, R.; Lopez, R.; Halabica, A.; Haglund, R.F.; Leitenstorfer, A. Coherent Structural Dynamics and Electronic Correlations during an Ultrafast Insulator-to-Metal Phase Transition in VO2. Phys. Rev. Lett. 2007, 99, 116401:1–116401:4. [Google Scholar] [CrossRef] [PubMed]
- Tomeljak, A.; Schäfer, H.; Städter, D.; Beyer, M.; Biljakovic, K.; Demsar, J. Dynamics of Photoinduced Charge-Density-Wave to Metal Phase Transition in K0.3MoO3. Phys. Rev. Lett. 2009, 102, 066404:1–066404:4. [Google Scholar] [CrossRef] [PubMed]
- Kimura, K.; Matsuzaki, H.; Takaishi, S.; Yamashita, M.; Okamoto, H. Ultrafast Photoinduced Transitions in Charge Density Wave, Mott Insulator, and Metallic Phases of an Iodine-Bridged Platinum Compound. Phys. Rev. B 2009, 79, 075116:1–075116:5. [Google Scholar] [CrossRef]
- Matsuzaki, H.; Uemura, H.; Matsubara, M.; Kimura, T.; Tokura, Y.; Okamoto, H. Detecting Charge and Lattice Dynamics in Photoinduced Charge-Order Melting in Perovskite-Type Manganites Using a 30-Femtosecond Time Resolution. Phys. Rev. B 2009, 79, 235131:1–235131:7. [Google Scholar] [CrossRef]
- Yusupov, R.; Mertelj, T.; Kabanov, V.V.; Brazovskii, S.; Kusar, P.; Chu, J.-H.; Fisher, I.R.; Mihailovic, D. Coherent Dynamics of Macroscopic Electronic Order through a Symmetry-Breaking Transition. Nat. Phys. 2010, 6, 681–684. [Google Scholar] [CrossRef]
- Matsuzaki, H.; Iwata, M.; Miyamoto, T.; Terashige, T.; Iwano, K.; Takaishi, S.; Takamura, M.; Kumagai, S.; Yamashita, M.; Takahashi, R.; et al. Excitation-Photon-Energy Selectivity of Photoconversions in Halogen-Bridged Pd-Chain Compounds: Mott Insulator to Metal or Charge-Density-Wave State. Phys. Rev. Lett. 2014, 113, 096403:1–096403:6. [Google Scholar] [CrossRef] [PubMed]
- Uemura, H.; Iwasawa, K.; Yamakawa, H.; Miyamoto, T.; Yada, H.; Okamoto, H. Photoinduced Complete Melting of Spin-Peierls Phase in Na-Tetracyanoquinodimethane Revealed by Frequency Doubling of Coherent Molecular Oscillations. Phys. Rev. B 2015, 91, 125111:1–125111:6. [Google Scholar] [CrossRef]
- Katan, C.; Blöchl, P.E.; Margl, P.; Koenig, C. First-Principles Molecular-Dynamics Simulations for Neutral p-Chloranil and its Radical Anion. Phys. Rev. B 1996, 53, 12112–12120. [Google Scholar] [CrossRef]
- Katan, C. First-Principles Study of the Structures and Vibrational Frequencies for Tetrathiafulvalene TTF and TTF-d4 in Different Oxidation States. J. Phys. Chem. A 1999, 103, 1407–1413. [Google Scholar] [CrossRef]
- Moreac, A.; Girard, A.; Delugeard, Y.; Marqueton, Y. The Neutral-to-Ionic Phase Transition of TTF-CA: A Raman and Infrared Study versus Temperature at Atmospheric Pressure. J. Phys. Condens. Matter 1996, 8, 3553–3567. [Google Scholar] [CrossRef]
- Moreac, A.; Girard, A.; Delugeard, Y. The Neutral-to-Ionic Phase Transition of TTF-CA: A Raman Study of the Influence of Temperature and Hydrostatic Pressure. J. Phys. Condens. Matter 1996, 8, 3569–3580. [Google Scholar] [CrossRef]
- Rice, M.J.; Lipari, N.O. Electron-Molecular-Vibration Coupling in Tetrathiafulvalene-tetracyanoquinodimethane (TTF-TCNQ). Phys. Rev. Lett. 1977, 38, 437–439. [Google Scholar] [CrossRef]
- Painelli, A.; Girlando, A. Electron-Molecular Vibration (E-MV) Coupling in Charge-Transfer Compounds and its Consequences on the Optical Spectra: A Theoretical Framework. J. Chem. Phys. 1986, 84, 5655–5671. [Google Scholar] [CrossRef]
- Gomi, H.; Yamagishi, N.; Mase, T.; Inagaki, T.J.; Takahashi, A. Instantaneous Charge and Dielectric Response to Terahertz Pulse Excitation in TTF-CA. Phys. Rev. B 2017, 95, 094116:1–094116:9. [Google Scholar] [CrossRef]
- Masino, M.; Girlando, A.; Brillante, A.; Della Valle, R.G.; Venuti, E.; Drichko, N.; Dressel, M. Lattice Dynamics of TTF-CA across the Neutral–Ionic Transition. Chem. Phys. 2006, 325, 71–77. [Google Scholar] [CrossRef]
- Tokura, Y.; Okamoto, H.; Koda, T.; Mitani, T.; Saito, G. Nonlinear Electric Transport and Switching Phenomenon in the Mixed-Stack Charge-Transfer Crystal Tetrathiafulvalene-p-Chloranil. Phys. Rev. B 1988, 38, 2215–2218. [Google Scholar] [CrossRef]
- Tokura, Y.; Koshihara, S.; Iwasa, Y.; Okamoto, H.; Komatsu, T.; Koda, T.; Iwasawa, N.; Saito, G. Domain-Wall Dynamics in Organic Charge-Transfer Compounds with One-Dimensional Ferroelectricity. Phys. Rev. Lett. 1989, 63, 2405–2408. [Google Scholar] [CrossRef] [PubMed]
- Okamoto, H.; Mitani, T.; Tokura, Y.; Koshihara, S.; Komatsu, T.; Iwasa, Y.; Koda, T.; Saito, G. Anomalous Dielectric Response in Tetrathiafulvalene-p-Chloranil as Observed in Temperature- and Pressure-Induced Neutral-to-Ionic Phase Transition. Phys. Rev. B 1991, 43, 8224–8232. [Google Scholar] [CrossRef]
- Collet, E.; Lemée-Cailleau, M.H.; Cointe, M.B.L.; Cailleau, H.; Ravy, S.; Luty, T.; Bérar, J.F.; Czarnecki, P.; Karl, N. Direct Evidence of Lattice-Relaxed Charge Transfer Exciton Strings. Europhys. Lett. 2002, 57, 67–73. [Google Scholar] [CrossRef]
- Matsuzaki, H.; Takamatsu, H.; Kishida, H.; Okamoto, H. Valence Fluctuation and Domain-Wall Dynamics in Pressure-Induced Neutral-to-Ionic Phase Transition of Organic Charge-Transfer Crystal. J. Phys. Soc. Jpn. 2005, 74, 2925–2928. [Google Scholar] [CrossRef]
- Cointe, M.B.L.; Lemée-Cailleau, M.H.; Cailleau, H.; Ravy, S.; Bérar, J.F.; Rouzière, S.; Elkaïm, E.; Collet, E. One-Dimensional Fluctuating Nanodomains in the Charge-Transfer Molecular System TTF-CA and Their First-Order Crystallization. Phys. Rev. Lett. 2006, 96, 205503:1–205503:4. [Google Scholar]
- Okimoto, Y.; Horiuchi, S.; Saitoh, E.; Kumai, R.; Tokura, Y. Far-Infrared Optical Response of Neutral–ionic Phase Transition in an Organic Charge-Transfer Complex. Phys. Rev. Lett. 2001, 87, 187401:1–187401:4. [Google Scholar] [CrossRef]
- Masino, M.; Girlando, A.; Soos, Z.G. Evidence for a Soft Mode in the Temperature Induced Neutral–Ionic Transition of TTF-CA. Chem. Phys. Lett. 2003, 369, 428–433. [Google Scholar] [CrossRef]
- Girlando, A.; Painelli, A.; Bewick, S.A.; Soos, Z.G. Charge Fluctuations and Electron-Phonon Coupling in Organic Charge-Transfer Salts with Neutral–Ionic and Peierls Transitions. Synth. Met. 2004, 141, 129–138. [Google Scholar] [CrossRef]
- D’Avino, G.; Girlando, A.; Painelli, A.; Lemée-Cailleau, M.H.; Soos, Z.G. Anomalous Dispersion of Optical Phonons at the Neutral–Ionic Transition: Evidence from Diffuse X-Ray Scattering. Phys. Rev. Lett. 2007, 99, 156407:1–156407:4. [Google Scholar] [CrossRef] [PubMed]
- Girlando, A.; Masino, M.; Painelli, A.; Drichko, N.; Dressel, M.; Brillante, A.; Della Valle, R.G.; Venuti, E. Direct Evidence of Overdamped Peierls-Coupled Modes in the Temperature-Induced Phase Transition in Tetrathiafulvalene-Chloranil. Phys. Rev. B 2008, 78, 045103:1–045103:12. [Google Scholar] [CrossRef]
- Tomić, S.; Dressel, M. Ferroelectricity in Molecular Solids: A Review of Electrodynamic Properties. Rep. Prog. Phys. 2015, 78, 096501:1–096501:26. [Google Scholar] [CrossRef] [PubMed]


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Morimoto, T.; Miyamoto, T.; Okamoto, H. Ultrafast Electron and Molecular Dynamics in Photoinduced and Electric-Field-Induced Neutral–Ionic Transitions. Crystals 2017, 7, 132. https://doi.org/10.3390/cryst7050132
Morimoto T, Miyamoto T, Okamoto H. Ultrafast Electron and Molecular Dynamics in Photoinduced and Electric-Field-Induced Neutral–Ionic Transitions. Crystals. 2017; 7(5):132. https://doi.org/10.3390/cryst7050132
Chicago/Turabian StyleMorimoto, Takeshi, Tatsuya Miyamoto, and Hiroshi Okamoto. 2017. "Ultrafast Electron and Molecular Dynamics in Photoinduced and Electric-Field-Induced Neutral–Ionic Transitions" Crystals 7, no. 5: 132. https://doi.org/10.3390/cryst7050132
APA StyleMorimoto, T., Miyamoto, T., & Okamoto, H. (2017). Ultrafast Electron and Molecular Dynamics in Photoinduced and Electric-Field-Induced Neutral–Ionic Transitions. Crystals, 7(5), 132. https://doi.org/10.3390/cryst7050132




