Abstract
The chiral optical Tamm state (COTS) is a special localized state at the interface of a handedness-preserving mirror and a structurally chiral medium such as a cholesteric liquid crystal or a chiral sculptured thin film. The spectral behavior of COTS, observed as reflection resonances, is described by the temporal coupled-mode theory. Mode coupling is different for two circular light polarizations because COTS has a helical structure replicating that of the cholesteric. The mode coupling for co-handed circularly polarized light exponentially attenuates with the cholesteric layer thickness since the COTS frequency falls into the stop band. Cross-handed circularly polarized light freely goes through the cholesteric layer and can excite COTS when reflected from the handedness-preserving mirror. The coupling in this case is proportional to anisotropy of the cholesteric and theoretically only anisotropy in magnetic permittivity can ultimately cancel this coupling. These two couplings being equal result in a polarization crossover (the Kopp–Genack effect) for which a linear polarization is optimal to excite COTS. The corresponding cholesteric thickness and scattering matrix for COTS are generally described by simple expressions.
PACS:
42.70.Df; 61.30.Gd; 42.79.Ci; 42.60.Da; 42.87.Bg
1. Introduction
Matter tends to order thus forming crystals. Orientational alignment is the preferred order in liquid crystals. Due to its cyclic nature, an echo of a translational order can be additionally generated in chiral superlattices of cholesteric liquid crystal. As a result, polarized light with the same handedness as that of the helically structured cholesteric liquid crystal diffracts (Figure 1), whereas the cross-handed circularly polarized wave travels virtually unaffected. This phenomenon is referred to as the selective reflection [1] or, alternatively, the Bragg circular diffraction for electromagnetic and acoustic waves [2].
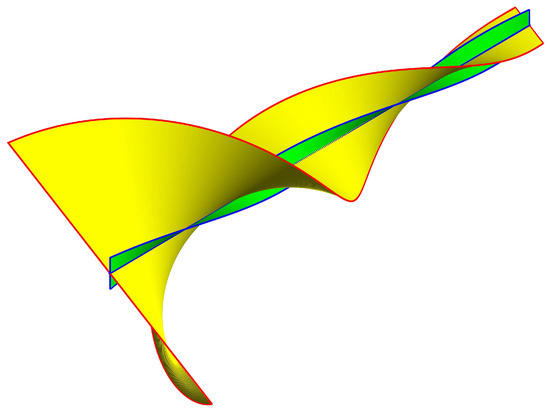
Figure 1.
Circular Bragg diffraction forming COTS. The cholesteric director is shown in blue and green, and the electric field is in red and yellow. The angle between them does not change with depth.
The results obtained are readily generalized for any material with a helix-like response, including widely tunable heliconical structures [3]. The selective reflection obstructs observation of localized states when the order at the interface or at the structural defect is disturbed. This is paid off by a simpler description of the states, which is an advantage offered by smooth helix symmetry [1,4] as opposed to discrete translational symmetry of crystals. The structural defect is conventionally represented as a cavity confined by mirrors, where the role of mirrors is played by the Bragg grating. This counterpart of a Fabry–Perot resonator possesses a number of defect modes. These defect modes are localized optical states normally corresponding to the whole numbers of halfwaves accommodated in the cavity. There are a number of distinctive polarization features [5,6,7,8,9,10,11] associated with the chiral defect applications [2,12,13,14,15], among which the twist defect, lacking an intermediate layer and having zero thickness, is most prominent [16,17]. Strict theoretical [4,18,19,20] and experimental [16,21,22] studies of the phenomenon gave rise to a discussion on polarization and relaxation time of the localized state [23,24]. Theoretically, infinite relaxation time is only possible if there is anisotropy in magnetic permittivity [4,25]. Otherwise, it appears impossible to simultaneously match electric and magnetic field strengths at the interface. Note that infinitely increasing the cholesteric thickness does not provide infinite improvement of the quality factor. The quality factor saturates with increasing cholesteric thickness and circular polarization of the transmitted light changes from co-handed to cross-handed. This polarization crossover [17] is termed the Kopp–Genack effect [26]. Unlike the Fabry–Perot resonator, the twist defect generates a single localized state. The spatial field distribution curve in this case has no flat top; it consists of two waves exponentially descending in opposite directions. This resembles a surface wave, with the only difference that, for the twist defect, there is no limitation on the angle of incidence of the excitation wave, and surface waves at the cholesteric-isotropic dielectric interface are only observed at the angles ensuring the total internal reflection [27].
There exists a surface wave beyond the restriction of total internal reflection. It is known as an optical Tamm state (OTS) [28,29,30,31,32,33,34], which is similar to the Tamm state of electrons at the superlattice interface. The dispersion of OTS lies outside the light cone given by [35]. Such a state can be excited even perpendicular to the surface without energy transfer along the surface, which is advantageous for various applications. A question naturally arises is whether there is an OTS at the cholesteric-metal interface when the light is normally incident. When dealing with this problem, one should bear in mind two things: first, semitransparence of the cholesteric due to the circular Bragg diffraction and, second, polarization change caused by alternating circular polarizations in that reflection from cholesteric does not change the handedness of circular polarization, whereas reflection from metal does [36]. This alternation acts like traffic lights: a co-handed circular polarized wave is not allowed to go through the cholesteric until after it has been twice reflected from the metal [37]. The polarization match at the interface between chiral and achiral mirrors can be achieved by adding an extra anisotropic layer. This layer produces a set of localized states with nontrivial polarization properties [38,39]. Various combinations involving two mirrors have been extensively studied and proposed for practical applications [36,40], including less-than-one-pitch chiral layer [41,42,43,44,45,46]. The closer to the mirror, the higher the energy density of the states may become, but still the states are not localized at surface but within the bulk of the extra layer. It is possible to do so without an extra layer provided a special mirror is used. This mirror is known as a handedness-preserving mirror (HPM) [24]. Today, there are several experimentally measured HPMs based on metasurfaces [47,48,49]. HPM retains not only the handedness but also the ellipticity magnitude upon reflection, therefore, such a mirror is also referred to as a polarization-preserving anisotropic mirror [50]. Furthermore, HPM can be defined as a reflector with the effect of a half-wave phase plate [49]. A localized state at the HPM/cholesteric interface is described in the low-anisotropy approximation of cholesteric liquid crystal and is called a chiral optical Tamm state (COTS) [44].
In this paper, we seek to answer the question of whether this state is possible in principle with an ideal HPM and a semi-infinite non-absorbing cholesteric layer having finite anisotropy. A detailed description is given by the simplest case when the electric and magnetic anisotropies are identical. Two types of deviations are considered: the lack of magnetic anisotropy and the finite thickness of the cholesteric layer. The ideal state here becomes a resonance with a finite quality factor and relaxation time.
A Method to Describe Spectral Peaks
The spectra of interest and the field distribution are conveniently described by the Berreman formalism [51]. For normal incidence on cholesteric, there is an uncomplicated exact solution [52,53,54,55]. By matching the tangential field strengths at the cholesteric interface, one can write down general closed-form equations [4,18,19,20]. For the sake of simplicity and clarity, we additionally use an approximate analytical method—the temporal coupled-mode theory (TCMT); that is, the theory of coupled modes in the time domain [56,57,58]. TCMT provides an instrument to describe the field in coupled resonators where coupling occurs between the resonator and the waveguide. Here, the spatial structure of the localized mode is not involved. It is the complex amplitude of this mode and its time derivative that matter for this theory. TCMT is a popular approach for dealing with stationary processes where the time derivative is zero. The first word, ‘temporal’, in the term [59] can be treated as historically coined. Essentially, the same method is employed to describe open resonators [60,61] and it goes back to the Lippmann and Schwinger’s solution of the scattering problem in quantum mechanics [62]. This method is not to be confused with the theory of coupled waves [63,64,65], or the spatial theory of coupled modes widely used in the optics of cholesterics [27,66,67,68,69]. While both approaches rely on the concept of coupled modes [70], the latter theory deals with coupled amplitudes of propagating waves, leaving the amplitude of the resonator mode outside the scope of consideration.
2. Model
A sketch of the cholesteric interface is shown in Figure 1. The cholesteric helical axis is normal to the mirror surface. In other words, the cholesteric director, i.e., the unit vector of the preferred orientation of molecules, is constant in the interface-parallel cross-sections, and it uniformly rotates with increasing distance from the interface. Near the interface, a chiral optical Tamm state (COTS) is possible, described in [44] in the limit of low cholesteric anisotropy. This state can be represented as a superposition of two circularly polarized counter-propagating co-handed waves with their strengths rotating in time in opposite directions. The resultant polarization is linear at each point of space, and the plane of polarization uniformly rotates together with the cholesteric director as the distance from the interface increases. The amplitude exponentially drops without standing-wave nodes and antinodes.
Figure 2 compares HPM with a conventional mirror. In a conventional metallic mirror, the electric field, when reflected, reverses its phase whereas the magnetic field does not. A reverse situation is possible, in which case the mirror is called a magnetic mirror. HPM combines the electric and magnetic types of reflection [48]. Let y be such an axis in the HPM plane that an electric field linearly polarized along that axis changes its phase after reflection. The orthogonal axis x corresponds to magnetic reflection. It is important that the magnetic field is orthogonal to the electric one, and hence to the x-axis, and is directed along y. In other words, the electric and magnetic field components directed along y are subject to a phase jump and yield a node, i.e., zero intensity. It is only x-components of the field that remain non-zero.

Figure 2.
HPM and a conventional mirror. The x-polarized light reflection is different. For HPM, the reflected electric strength preserves its phase and the phase of the magnetic strength alters instead.
Maxwell Equations in the Basis Associated with the Cholesteric Director
Here, we limit ourselves to the case of normal light incidence. For , the Maxwell equation for a wave propagating along the helical axis z can be written as
The wave is described by a vector of complex amplitudes for the electric field components in the orthogonal directions x and y. Projection of the dielectric permittivity tensor on the plane at the depth of z in the cholesteric is given by
Here, the optical axis coinciding with the cholesteric director is given by the twist angle , which is measured from the x-axis toward the y-axis; p is the helical pitch. The positive pitch refers to a right-handed helix, and the negative pitch refers to a left-handed one. Taking magnetic permittivity into account makes an explicit form of the magnetic strength expression more preferable and increases the field vector dimensionality from 2 to 4:
Consequently, the order of the differential equation goes down from second to first. Let us assume that the principal axes of the magnetic and electric permittivity tensors coincide. On this assumption, we can use the orthonormal basis uniformly rotating together with the cholesteric director so that the u-axis always goes along the director:
By the Berreman method [51], Maxwell’s equations in a stationary case have the following form:
A differential transfer matrix for rotating basis is formulated in [4,18] and it can be reduced to
where is the dimensionless wavelength and is the dimensionless coordinate. There are different units for electric and magnetic strengths in the SI system; therefore, they have to be normalized via the vacuum impedance .
3. Solution without the Low-Anisotropy Approximation
Four normal waves (eigenmodes) correspond to Equation (3). They are determined by the eigenvalues of the matrix. These eigenvalues have the sense of refractive indices n and the respective eigenvectors of the matrix have the sense of polarizations . Based on the z-axis reversal symmetry , these four normal waves can be classified as two pairs of counter-directed waves. In each pair, the wave with a larger refractive index has a lower phase velocity. We refer to this wave as a slow wave. The other wave is called a fast wave:
Substituting the solution for into Equation (3) yields:
where is the unit matrix, the index + in has been omitted. The refractive indices are as follows:
where is the antisymmetry coefficient of permittivities and the overbar means the arithmetic mean over ordinary and extraordinary permittivities:
Scale invariance of Maxwell’s Equation (3) and normalization of material parameters (see Supplement in [4]) reduces the structure to two crucial parameters: electric and magnetic anisotropies
3.1. The Case of Equal Anisotropies,
Consider the case of equal anisotropies . The clarity and fineness of this single-parametric set of structures should compensate the difficulty of their physical realization in the optical range for the reader [25]. The wavelength parameterizes the set of differential transfer matrixes (Equation (4)) in the way as eccentricity does to a set of conical cross-sections. The cholesteric eigenmode dispersion law is simplified due to the symmetry of permittivities
Without further prejudice to the generality, we assume the normalization and . Then, . In other words, the permittivity is normalized to the geometric mean of and : , and the arithmetic mean is not less than unity: . The second term in the right-hand part of the cholesteric eigenmode dispersion law becomes squared anisotropy . Anisotropy here acquires the meaning of the standard deviation of permittivities:
Unlike the parabolic approximation typical of periodic media, the dispersion curves have a hyperbolic shape, except for the stop band where they have the shape of a circle. The cholesteric eigenmode dispersion law (11) can be written for the refractive index as well as for the wave vector
This inversion symmetry of and dispersions indicates the symmetry of the longwave and shortwave limits. In the longwave limit, the medium is homogeneous and becomes isotropic. The negative optical activity ceases as the situation comes close to the static field case. In the shortwave limit, positive optical activity is supported by the Mauguin waveguide regime (Figure 3). This symmetry is destroyed when the anisotropies become unequal (). The ordinary and extraordinary waves can then be distinguished in the high-frequency limit equivalent to helix untwisting. Next, we focus on the circular Bragg diffraction, when and the refractive index for the fast wave acquires purely imaginary values. This is the case when the phase velocity becomes infinite and the group velocity becomes meaningless. It would be reasonable here to write down cholesteric eigenmode dispersion law (11) in the form of a trigonometric identity where some angle acts, instead of the wavelength:
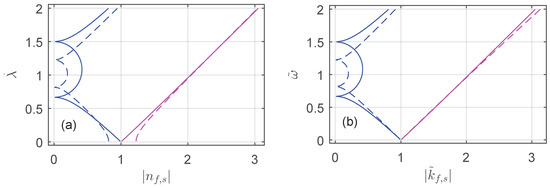
Figure 3.
Inversion symmetry of dispersion curves, Equation (12). (a) wavelength as a function of the refractive index . (b) frequency as a function of the wave number . The blue curve is the fast wave, the purple curve – slow wave. The solid curve is drawn for , . The semicircle refers to a diffracting wave for which the refractive index acquires purely imaginary values . The Mauguin regime, , is equivalent to homogenization according to the inversion symmetry of Equation (12). The symmetry is violated for the dashed line with .
This means that at wavelength
the refractive index of the fast wave describes full reflection in the cholesteric bulk. This wave is conventionally called a diffracting wave [1] and its polarization is derived from nontrivial solvability of Equation (6). Subtracting the refractive index from transfer matrix (4) yields the following identity:
where . We deal here with a manifest symmetry with respect to exchange between electric and magnetic fields and permittivities, . The equality of electric and magnetic permittivities is equivalent to the Umov–Pointing vector going to zero the same way as for conventional standing-wave nodes and antinodes. The electric and magnetic fields are linearly polarized at the same angle to the cholesteric director. This direction coincides with the x-axis for . Surface conditions for an ideal HPM are exactly the same—both the electric field and the magnetic field are linearly polarized along the magnetic axis of the mirror (Figure 2). Hence, the derived expression provides an exact description of COTS for a finite anisotropy.
3.2. The Case of Unequal Anisotropies,
In a general case, we denote the directions of electric and magnetic polarizations by the angles and . Generalized nontrivial solution of Equation (6) provides eigenvectors of the transfer matrix (4) and exact solutions for the angles [19]:
where the refractive index should be borrowed from cholesteric eigenmode dispersion law (7). It is evident that the polarizations are linear for the purely imaginary refractive index , whereas for the real refractive index , they are almost circular in the stop band. The cholesteric eigenmode dispersion law (14) can be generalized as
For a cholesteric without magnetic anisotropy (), we have
The eigenfrequency is:
This expression is more exact in comparison with the earlier obtained approximation (Equation (10) in [44]) and still there remains approximation. We have to use a unified angle between the cholesteric optical axis and HPM, hence the electric and magnetic polarizations are directed differently in a general case. This does not meet the condition on the HPM surface. The non-zero angle of polarization mismatch, , introduces a new non-local COTS component [19]. This enables the state to become a leaky mode (or resonance), acquiring finite relaxation time .
4. Relaxation Time and Spectral Manifestation
By definition, the time of relaxation of a vibrational state is the ratio of the stored energy to the lost power P taken with a positive sign:
Here, is the amplitude relaxation time, which is twice the energy relaxation time. Since the field does not penetrate into depth of an ideal HPM, the whole stored energy is the energy of diffracting waves inside the cholesteric layer. Let us find this energy by integrating its density over space in Gaussian units. The period-averaged densities of electric and magnetic energy components are equal because . Moreover, , where is the wave amplitude. Therefore, . A standing wave in the layer is formed by two waves travelling in opposite directions. Their constructive interference is compensated by a destructive one, and their energy densities add up. In the defect layer, . Integration yields
Here, is given by Equation (16). The power of leakage is proportional to the flow velocity and the energy density carried away by the travelling wave. The strength is governed by the boundary conditions:
We finally have [19]
Consider a cholesteric layer of finite thickness L embedded in a medium with permittivity . Instead of Equation (22), the power of leakage at the edge of the cholesteric is given by:
Note that, because of the cholesteric boundary condition, is twice as high as just exponentially decreasing by Equation (5). Then, the corresponding relaxation time is
which agrees with the expressions obtained in [10,19]. The last formula is also directly applicable when , assuming L being the optical density: .
4.1. Temporal Coupled-Mode Theory
By the temporal coupled-mode theory [58,71], the resonance is described by the cyclic eigenfrequency and complex amplitude A. This theory should not be confused with the spatial coupled-wave theory where the amplitudes of propagating waves are involved [63,70]. The resonance manifests itself through the amplitudes of incoming and outgoing energy fluxes:
Excitation via one of the ports yields the amplitude
Amplitudes of reflection from port ℓ into port form a scattering matrix
where is the Kronecker symbol. Reflections are observed as spectral peaks in the shape of Lorentzian profiles with full width at half maximum (FWHM)
Scaling from the cyclic frequency to the frequency yields a times narrower width of the peak:
This is sufficient to allow the spectral behavior of the state to be described in terms of temporal coupled-mode theory.
In the previous section, we dwelt in detail with ideal COTS with its eigenfrequency given by Equation (16). Relaxation times given by Equations (23) and (25) were used to express deviations from the ideal state associated with the angle and the layer thickness L, respectively. The other possibly large relaxation times from HPM and dissipation are easy to be incorporated into TCMT. Nevertheless, for the sake of simplicity, here we keep only two of them. This appears to be sufficient to fully describe COTS in terms of TCMT. The port of coupling via angle has the cross-handed circular polarization with respect to the cholesteric twist, while coupling via the cholesteric thickness L has the co-handed circular polarization. Equation (28) at the resonance frequency generates the following reflection matrix:
where , indices S and O stand for the same and the opposite circular polarizations, respectively. This matrix satisfies the energy conservation law. Maximum nondiagonal reflections occur at crossover when the relaxation times become equal .
An analytical expression for the length of crossover is obtained by equalizing relaxation times described by Equations (23) and (25), which yields:
This length, as is fairly noted in [24], is difficult to measure in the twist defect of a cholesteric because of the high and the high requirements of the experiment accuracy. In the case of COTS, the magnitude appears to be substantially larger because of the HPM imperfectness and the crossover length reduces, which should simplify its experimental measurement.
4.2. TCMT Applicability Limits
When using TCMT to tackle the problem of coupling between a localized state and waveguides, there are certain limits imposed such as linearity, time-invariant structural parameters, energy conservation, time-reversible energy flux and weak coupling [58]. The model chosen a priori meets the first four requirements. The fifth one incorporates, in fact, two requirements. First, the solution derived from Equation (26) ignores corrections with respect to a small parameter that is defined as a vibration period-to-relaxation time ratio [56]. Second, the waveguide dispersion should be small over the frequency range of the resonance Lorentz profile. For a fairly large relaxation time, the Lorentzian profile width approaches zero and this automatically takes care of the second requirement [58]. In this case, the cholesteric acts as a waveguide for waves with cross-handed circular polarization. Dispersion in the middle of the stop band is moderate. Thus, we believe the set of linear differential equations, Equation (26), provides an adequate description of the model when and . Beyond this approximation, the eigenfrequency depends on the cholesteric layer thickness and is possible to describe through the approach proposed in [10].
4.3. Numerical Results
Figure 4 shows that there is a Kopp–Genack effect observed for COTS. For definiteness, we took the helical pitch . For the parameters specified in the figure, the eigenfrequency is achieved at the angle and the mismatch angle . The crossover length agrees with Equation (33). For substantially thicker cholesteric layers, , the line width is and the quality factor saturates: . Note that for crossover, , the quality is half the magnitude.
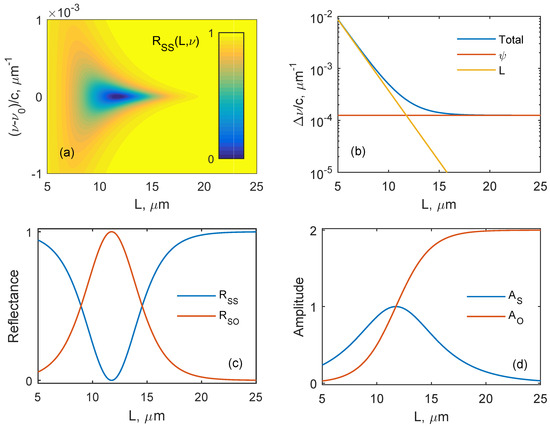
Figure 4.
The Kopp–Genack effect. The linewidth saturates with increasing cholesteric layer thickness. Polarization reversal of the optimal exciting light. (a) reflection spectrum, Equation (28). (b) spectral dip width, Equation (30). The cholesteric helix pitch is , electric anisotropy is ; there is no magnetic anisotropy, . (c) reflection at the resonance frequency , Equation (31). (d) state amplitude at the resonance frequency , Equation (27).
Figure 4a illustrates that for crossover , the structure reflects light as a conventional mirror; that is, the circular polarization handedness changes for the opposite one. The growing thickness of the cholesteric layer takes its polarization properties back to the HPM properties when , i.e., the circular polarization handedness no longer changes under reflection. Figure 4b proves that the co-handed and cross-handed (right and left) circular polarizations excite COTS equally efficiently when (crossover). Hence, the most efficient excitation occurs when both polarizations, with equal amplitudes and a certain phase difference, are superimposed to produce linearly polarized light. No COTS is excited by orthogonally polarized light. For thicker cholesterics, , excitation is only possible with cross-handed circularly polarized light as co-handed circularly polarized light is totally reflected from the cholesteric.
5. Conclusions
COTS can be considered strictly localized only provided the electric and magnetic permittivities are equal and the respective tensor axes coincide. Otherwise, COTS is observed as a polarized reflection resonance with two relaxation constants determined by the permittivity difference and the cholesteric layer thickness. COTS is closely connected with the twist defect of cholesteric and renders the Kopp–Genack crossover effect. A scattering matrix, where spectral peaks are described by Lorentzian profiles, has been found in terms of the temporal coupled-mode theory. It is for the first time, to the best of our knowledge, that a formula for the cholesteric crossover thickness has been suggested, which is equally suitable for COTS and for the twist defect. The analytical result agrees with the direct numerical one.
Acknowledgments
This work was financially sponsored by the Ministry of Science and Technology (MOST), Taiwan, under Grant No. 106-2923-M-009-002-MY3, the Russian Foundation for Basic Research, Government of Krasnoyarsk Territory, the Krasnoyarsk Region Science and Technology Support Fund to the research project No. 17-42-240464, the Scholarship of the President of the Russian Federation No. SP-227.2016.5 and by the Siberian Branch of the Russian Academy of Sciences under Complex Program II.2P (Project Nos. 0356-2015-0410 and 0356-2015-0411). The authors are thankful to A.F. Sadreev, E.N. Bulgakov, N.V. Rudakova, Y.-C. Hsiao and L.V. Pertseva for valuable discussions and comments.
Author Contributions
Ivan V. Timofeev and Stepan Ya. Vetrov conceived, designed, and performed the calculations and drafted the manuscript. Pavel S. Pankin helped check analytical expressions and applicability limits, and edited the manuscript. Vasily G. Arkhipkin and Wei Lee helped check the scientific content of the manuscript. Victor Ya. Zyryanov supervised the whole study and finalized the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| COTS | chiral optical Tamm state |
| TCMT | temporal coupled-mode theory |
| HPM | handedness-preserving mirror |
References
- Belyakov, V.A. Diffraction Optics of Complex-Structured Periodic Media; Springer: New York, NY, USA, 1992; p. 352. [Google Scholar]
- Faryad, M.; Lakhtakia, A. The circular Bragg phenomenon. Adv. Opt. Photonics 2014, 6, 225. [Google Scholar] [CrossRef]
- Xiang, J.; Li, Y.; Li, Q.; Paterson, D.A.; Storey, J.M.D.; Imrie, C.T.; Lavrentovich, O.D. Electrically Tunable Selective Reflection of Light from Ultraviolet to Visible and Infrared by Heliconical Cholesterics. Adv. Mater. 2015, 27, 3014–3018. [Google Scholar] [CrossRef] [PubMed]
- Avendaño, C.G.; Ponti, S.; Reyes, J.A.; Oldano, C. Multiplet structure of the defect modes in 1D helical photonic crystals with twist defects. J. Phys. A Math. Gen. 2005, 38, 8821–8840. [Google Scholar] [CrossRef]
- Haus, H.; Shank, C. Antisymmetric taper of distributed feedback lasers. IEEE J. Quantum Electron. 1976, 12, 532–539. [Google Scholar] [CrossRef]
- Lakhtakia, A.; McCall, M. Sculptured thin films as ultranarrow-bandpass circular-polarization filters. Opt. Commun. 1999, 168, 457–465. [Google Scholar] [CrossRef]
- Yang, Y.C.; Kee, C.S.; Kim, J.E.; Park, H.Y.; Lee, J.C.; Jeon, Y.J. Photonic defect modes of cholesteric liquid crystals. Phys. Rev. E 1999, 60, 6852–6854. [Google Scholar] [CrossRef]
- Shabanov, A.V.; Vetrov, S.Y.; Karneev, A.Y. Reflection spectrum of a cholesteric liquid crystal with structural defects. J. Exp. Theor. Phys. Lett. 2004, 80, 181–184. [Google Scholar] [CrossRef]
- Gevorgyan, A.H. The loss of the polarization dependence of diffraction reflection in chiral photonic crystals in the presence of anisotropic defects. Tech. Phys. Lett. 2006, 32, 698–702. [Google Scholar] [CrossRef]
- Belyakov, V.A.; Semenov, S.V. Optical defect modes in chiral liquid crystals. J. Exp. Theor. Phys. 2011, 112, 694–710. [Google Scholar] [CrossRef]
- Kiselev, A.D.; Chigrinov, V.G. Optics of short-pitch deformed-helix ferroelectric liquid crystals: Symmetries, exceptional points, and polarization-resolved angular patterns. Phys. Rev. E 2014, 90, 042504. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.C.; Wang, H.T.H.T.; Lee, W. Thermodielectric generation of defect modes in a photonic liquid crystal. Opt. Express 2014, 22, 3593–3599. [Google Scholar] [CrossRef] [PubMed]
- Rodarte, A.; Cisneros, F.; Hein, J.; Ghosh, S.; Hirst, L. Quantum Dot/Liquid Crystal Nanocomposites in Photonic Devices. Photonics 2015, 2, 855–864. [Google Scholar] [CrossRef]
- Lin, J.D.; Chu, C.L.; Lin, H.Y.; You, B.; Horng, C.T.; Huang, S.Y.; Mo, T.S.; Huang, C.Y.; Lee, C.R. Wide-band tunable photonic bandgaps based on nematic-refilling cholesteric liquid crystal polymer template samples. Opt. Mater. Express 2015, 5, 1419. [Google Scholar] [CrossRef]
- Kesaev, V.V.; Pozhidaev, E.P.; Kiselev, A.D. Modulation of unpolarized light in planar aligned subwavelength-pitch deformed-helix ferroelectric liquid crystals. Phys. Rev. E 2017, 95, 032705. [Google Scholar] [CrossRef]
- Hodgkinson, I.J.; Wu, Q.H.; Thorn, K.E.; Lakhtakia, A.; McCall, M.W. Spacerless circular-polarization spectral-hole filters using chiral sculptured thin films: Theory and experiment. Opt. Commun. 2000, 184, 57–66. [Google Scholar] [CrossRef]
- Kopp, V.I.; Genack, A.Z. Twist Defect in Chiral Photonic Structures. Phys. Rev. Lett. 2002, 89, 033901. [Google Scholar] [CrossRef] [PubMed]
- Oldano, C.; Reyes, J.A.; Ponti, S. Twist defects in helical sonic structures. Phys. Rev. E 2003, 67, 056624. [Google Scholar] [CrossRef] [PubMed]
- Becchi, M.; Ponti, S.; Reyes, J.; Oldano, C. Defect modes in helical photonic crystals: An analytic approach. Phys. Rev. B 2004, 70, 033103. [Google Scholar] [CrossRef]
- Schmidtke, J.; Stille, W. Photonic defect modes in cholesteric liquid crystal films. Eur. Phys. J. E Soft Matter 2003, 12, 553–564. [Google Scholar] [CrossRef] [PubMed]
- Schmidtke, J.; Stille, W.; Finkelmann, H. Defect Mode Emission of a Dye Doped Cholesteric Polymer Network. Phys. Rev. Lett. 2003, 90, 083902. [Google Scholar] [CrossRef] [PubMed]
- Ozaki, M.; Ozaki, R.; Matsui, T.; Yoshino, K. Twist-Defect-Mode Lasing in Photopolymerized Cholesteric Liquid Crystal. Jpn. J. Appl. Phys. 2003, 42, L472–L475. [Google Scholar] [CrossRef]
- Oldano, C. Comment on “Twist Defect in Chiral Photonic Structures”. Phys. Rev. Lett. 2003, 91, 259401. [Google Scholar] [CrossRef] [PubMed]
- Kopp, V.; Genack, A. Kopp and Genack Reply. Phys. Rev. Lett. 2003, 91, 259402. [Google Scholar] [CrossRef]
- Gevorgyan, A.H.; Rafayelyan, M.S. Optics of anisotropic metamaterial based structurally chiral photonic crystals. J. Opt. 2013, 15, 125103. [Google Scholar] [CrossRef]
- McCall, M.W.; Hodgkinson, I.J.; Wu, Q. Birefringent Thin Films and Polarizing Elements: 2nd Edition, 2nd revise ed.; Imperial College Press: London, UK, 2015. [Google Scholar]
- Belyakov, V.A.; Shilina, G.I. Surface Guided Electromagnetic Waves of Higher Diffraction Orders in Cholesterics. Mol. Cryst. Liq. Cryst. 1992, 223, 55–67. [Google Scholar] [CrossRef]
- Kavokin, A.; Shelykh, I.; Malpuech, G. Optical Tamm states for the fabrication of polariton lasers. Appl. Phys. Lett. 2005, 87, 261105. [Google Scholar] [CrossRef]
- Vinogradov, A.P.; Dorofeenko, A.V.; Merzlikin, A.M.; Lisyansky, A.A. Surface states in photonic crystals. Uspekhi Fizicheskikh Nauk 2010, 53, 243–256. [Google Scholar] [CrossRef]
- Iorsh, I.V.; Belov, P.A.; Zharov, A.A.; Shadrivov, I.V.; Kivshar, Y.S. Nonlinear Tamm states in nanostructured plasmonic metamaterials. Phys. Rev. A 2012, 86, 023819. [Google Scholar] [CrossRef]
- Afinogenov, B.I.; Bessonov, V.O.; Nikulin, A.A.; Fedyanin, A.A. Observation of hybrid state of Tamm and surface plasmon-polaritons in one-dimensional photonic crystals. Appl. Phys. Lett. 2013, 103, 061112. [Google Scholar] [CrossRef]
- Auguié, B.; Bruchhausen, A.; Fainstein, A. Critical coupling to Tamm plasmons. J. Opt. 2015, 17, 035003. [Google Scholar] [CrossRef]
- Chang, C.Y.; Chen, Y.H.; Tsai, Y.L.; Kuo, H.C.; Chen, K.P. Tunability and optimization of coupling efficiency in tamm plasmon modes. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 4600206. [Google Scholar] [CrossRef]
- Yang, Z.Y.; Ishii, S.; Yokoyama, T.; Dao, T.D.; Sun, M.g.; Nagao, T.; Chen, K.P. Tamm plasmon selective thermal emitters. Opt. Lett. 2016, 41, 4453. [Google Scholar] [CrossRef] [PubMed]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Abdulhalim, I. Unique optical properties of anisotropic helical structures in a Fabry-Perot cavity. Opt. Lett. 2006, 31, 3019. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, I.V.; Arkhipkin, V.G.; Vetrov, S.Y.; Zyryanov, V.Y.; Lee, W. Enhanced light absorption with a cholesteric liquid crystal layer. Opt. Mater. Express 2013, 3, 496. [Google Scholar] [CrossRef]
- Vetrov, S.Y.; Pyatnov, M.V.; Timofeev, I.V. Surface modes in “photonic cholesteric liquid crystal–phase plate–metal” structure. Opt. Lett. 2014, 39, 2743–2746. [Google Scholar] [CrossRef] [PubMed]
- Vetrov, S.Y.; Pyatnov, M.V.; Timofeev, I.V. Spectral and polarization properties of a ‘cholesteric liquid crystal—phase plate—metal’ structure. J. Opt. 2016, 18, 015103. [Google Scholar] [CrossRef]
- Zhuang, Z.; Patel, J.S. Behavior of cholesteric liquid crystals in a Fabry–Perot cavity. Opt. Lett. 1999, 24, 1759. [Google Scholar] [CrossRef] [PubMed]
- Isaacs, S.; Placido, F.; Abdulhalim, I. Investigation of liquid crystal Fabry–Perot tunable filters: Design, fabrication, and polarization independence. Appl. Opt. 2014, 53, H91. [Google Scholar] [CrossRef] [PubMed]
- Hsiao, Y.C.; Hou, C.T.C.T.; Zyryanov, V.Y.; Lee, W. Multichannel photonic devices based on tristable polymer-stabilized cholesteric textures. Opt. Express 2011, 19, 23952. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, I.V.; Lin, Y.T.; Gunyakov, V.A.; Myslivets, S.A.; Arkhipkin, V.G.; Vetrov, S.Y.; Lee, W.; Zyryanov, V.Y. Voltage-induced defect mode coupling in a one-dimensional photonic crystal with a twisted-nematic defect layer. Phys. Rev. E 2012, 85, 011705. [Google Scholar] [CrossRef] [PubMed]
- Timofeev, I.V.; Vetrov, S.Y. Chiral optical Tamm states at the boundary of the medium with helical symmetry of the dielectric tensor. JETP Lett. 2016, 104, 380–383. [Google Scholar] [CrossRef]
- Gunyakov, V.A.; Krakhalev, M.; Zyryanov, V.; Shabanov, V.; Loiko, V. Modulation of defect modes intensity by controlled light scattering in photonic crystal with liquid crystal domain structure. J. Quant. Spectrosc. Radiat. Transf. 2016, 178, 152–157. [Google Scholar] [CrossRef]
- Huang, K.C.; Hsiao, Y.C.; Timofeev, I.V.; Zyryanov, V.Y.; Lee, W. Photo-manipulated photonic bandgap devices based on optically tristable chiral-tilted homeotropic nematic liquid crystal. Opt. Express 2016, 24, 25019. [Google Scholar] [CrossRef] [PubMed]
- Plum, E.; Zheludev, N.I. Chiral mirrors. Appl. Phys. Lett. 2015, 106, 221901. [Google Scholar] [CrossRef]
- Fedotov, V.; Rogacheva, A.; Schwanecke, A.; Mladyonov, R.; Prosvirnin, S.; Cheni, Y.; Zheludev, N. ’Miracle’ mirror that does not change the phase of reflected wave. In Proceedings of the 2005 IEEE LEOS Annual Meeting Conference Proceedings, Sydney, Australia, 22–28 October 2005; Volume 2005, pp. 539–540. [Google Scholar]
- Ding, F.; Wang, Z.; He, S.; Shalaev, V.M.; Kildishev, A.V. Broadband high-efficiency half-wave plate: A supercell-based plasmonic metasurface approach. ACS Nano 2015, 9, 4111–4119. [Google Scholar] [CrossRef] [PubMed]
- Rudakova, N.V.; Timofeev, I.V.; Pankin, P.S.; Vetrov, S.Y. Polarization-Preserving Anisotropic Mirror on the Basis of Metal–Dielectric Nanocomposite. Bull. Russ. Acad. Sci. Phys. 2017, 81, 10–14. [Google Scholar] [CrossRef]
- Berreman, D.W. Optics in Stratified and Anisotropic Media: 4 x 4-Matrix Formulation. J. Opt. Soc. Am. 1972, 62, 502. [Google Scholar] [CrossRef]
- Oseen, C. The theory of liquid crystals. Trans. Faraday Soc. 1933, 29, 883–889. [Google Scholar] [CrossRef]
- De Vries, H. Rotatory power and other optical properties of certain liquid crystals. Acta Crystallogr. 1951, 4, 219–226. [Google Scholar] [CrossRef]
- Kats, E. Optical properties of cholesteric liquid crystals. J. Exp. Theor. Phys. 1971, 32, 1004–1007. [Google Scholar]
- Nityananda, R. On the Theory of Light Propagation in Cholesteric Liquid Crystals. Mol. Cryst. Liq. Cryst. 1973, 21, 315–331. [Google Scholar] [CrossRef]
- Haus, H.A. Waves and Fields in Optoelectronics; Prentice-Hall Series in Solid State Physical Electronics; Prentice Hall, Incorporated: Upper Saddle River, NJ, USA, 1983; p. 402. [Google Scholar]
- Manolatou, C.; Haus, H.A. Passive Components for Dense Optical Integration; Springer: Berlin, Germany, 2002; p. 173. [Google Scholar]
- Joannopoulos, J.D.; Johnson, S.G.; Winn, J.N.; Meade, R.D. Photonic Crystals: Molding the Flow of Light, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2008; p. 304. [Google Scholar]
- Fan, S.; Suh, W.; Joannopoulos, J.D. Temporal coupled-mode theory for the Fano resonance in optical resonators. J. Opt. Soc. Am. A 2003, 20, 569. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Y.; Lee, R.K.; Yariv, A. Scattering-theory analysis of waveguide-resonator coupling. Phys. Rev. E 2000, 62, 7389–7404. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Bliokh, Y.P.; Freilikher, V.; Savel’ev, S.; Nori, F. Colloquium : Unusual resonators: Plasmonics, metamaterials, and random media. Rev. Mod. Phys. 2008, 80, 1201–1213. [Google Scholar] [CrossRef]
- Lippmann, B.A.; Schwinger, J. Variational Principles for Scattering Processes. I. Phys. Rev. 1950, 79, 469–480. [Google Scholar] [CrossRef]
- Kogelnik, H. Coupled Wave Theory for Thick Hologram Gratings. Bell Syst. Tech. J. 1969, 48, 2909–2947. [Google Scholar] [CrossRef]
- Yariv, A. Coupled-mode theory for guided-wave optics. IEEE J. Quantum Electron. 1973, 9, 919–933. [Google Scholar] [CrossRef]
- Barybin, A.A.; Dmitriev, V.A. Modern Electrodynamics and Coupled-Mode Theory: Application To Guided-Wave Optics; Rinton Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Belyakov, V.A.; Dmitrienko, V.E. Theory of the optical properties of cholesteric liquid crystals. Sov. Phys. Solid State 1974, 15, 1811–1815. [Google Scholar]
- Belyakov, V.A.; Orlov, V.P.; Shilina, G.I. Surface guided electromagnetic modes in films with periodically modulated characteristics. J. Exp. Theor. Phys. 1992, 75, 189–194. [Google Scholar]
- McCall, M.W.; Lakhtakia, A. Development and assessment of coupled wave theory of axial propagation in thin-film helicoidal bianisotropic media. Part 1: Reflectances and transmittances. J. Mod. Opt. 2000, 47, 973–991. [Google Scholar] [CrossRef]
- Wang, F.; Lakhtakia, A. Optical crossover phenomenon due to a central 90-twist defect in a chiral sculptured thin film or chiral liquid crystal. Proc. R. Soc. A Math. Phys. Eng. Sci. 2005, 461, 2985–3004. [Google Scholar] [CrossRef]
- Pierce, J.R. Coupling of modes of propagation. J. Appl. Phys. 1954, 25, 179–183. [Google Scholar] [CrossRef]
- Manolatou, C.; Khan, M.; Fan, S.; Villeneuve, P.; Haus, H.; Joannopoulos, J.D. Coupling of modes analysis of resonant channel add-drop filters. IEEE J. Quantum Electron. 1999, 35, 1322–1331. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).