Comparative Interrelationship of the Structural, Nonlinear-Optical and Other Acentric Properties for Oxide, Borate and Carbonate Crystals
Abstract
:1. Introduction
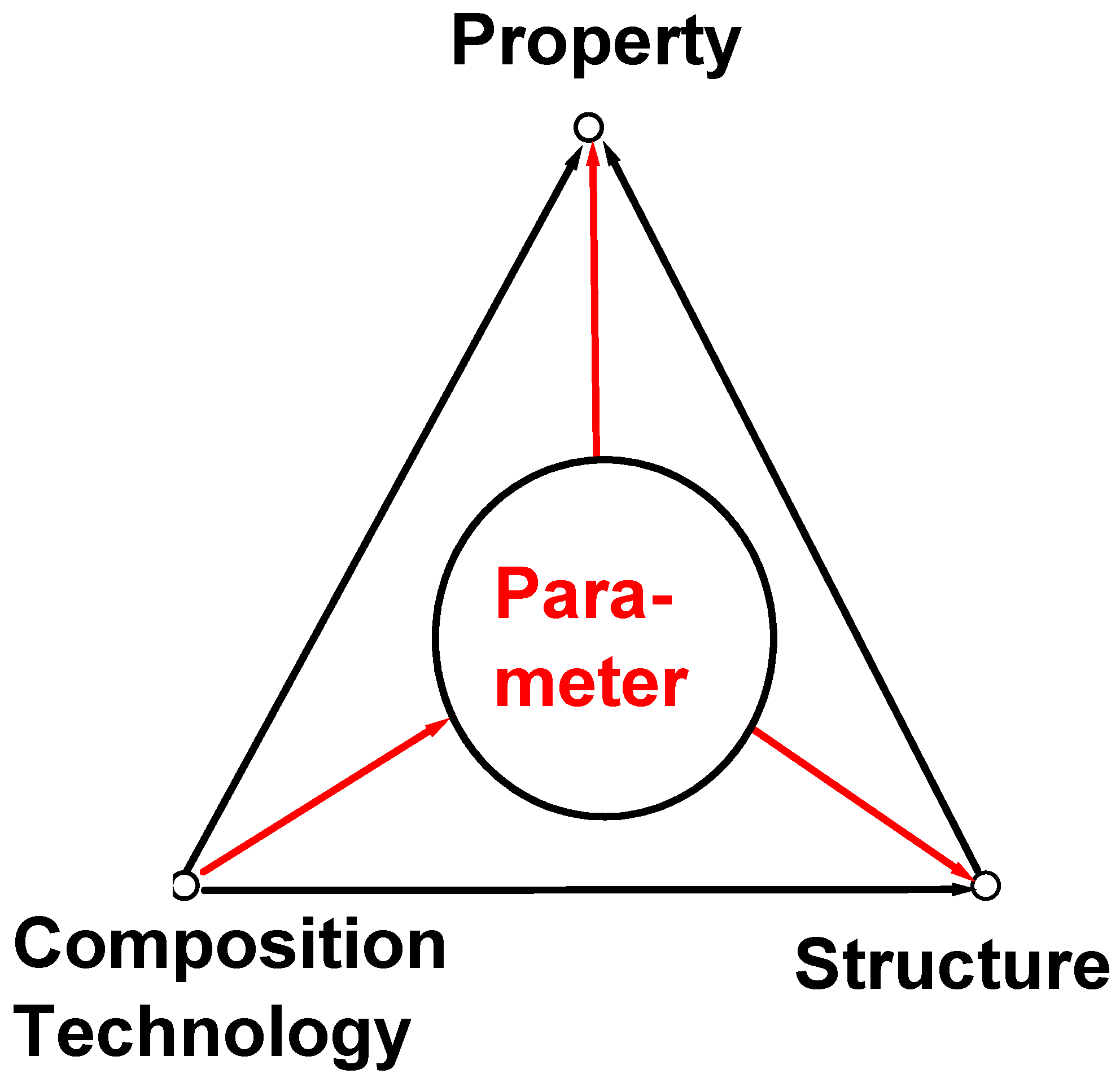
2. Triad of the Interrelationship “Composition-Structure-Property”
2.1. General View
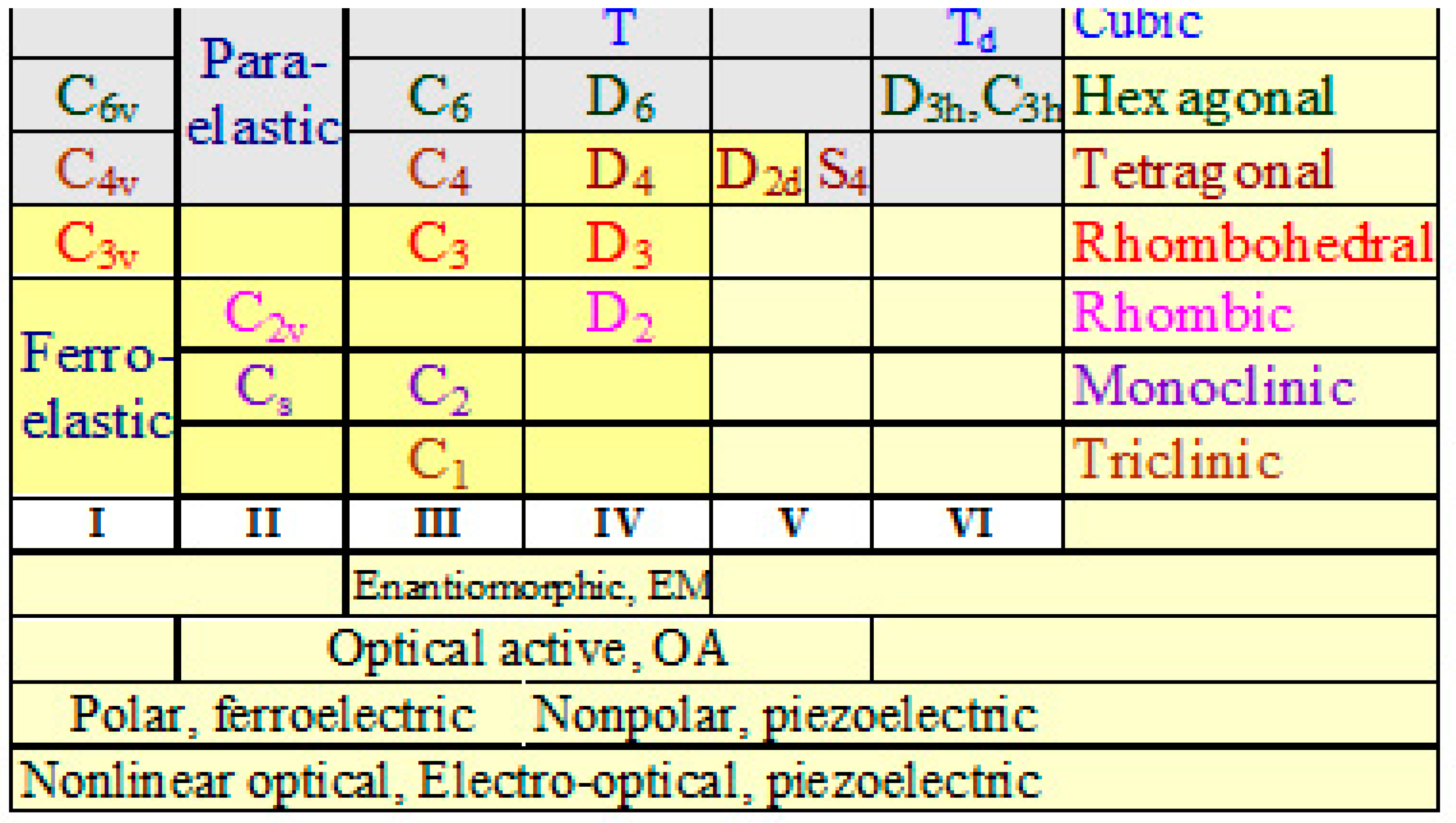
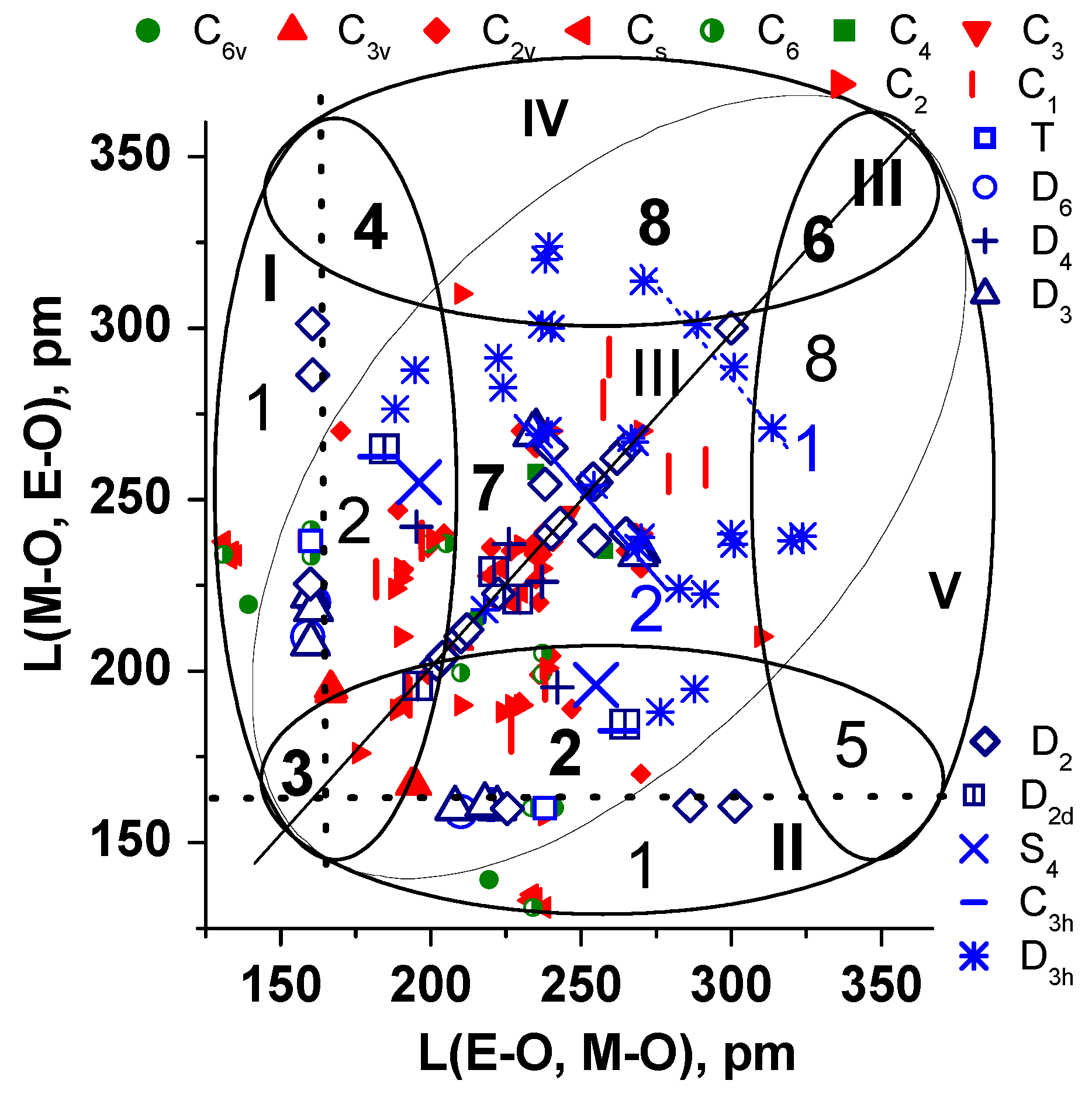
2.2. Relationship “Structure-Property” for Piezoelectric Crystals
3. Mutual Comparison of the Main Acentric Properties
3.1. General
3.2. Correlation between “Electro-Optical and Piezoelectric Properties”
3.3. Correlation between “Electro-Optical and Nonlinear Optical Properties”
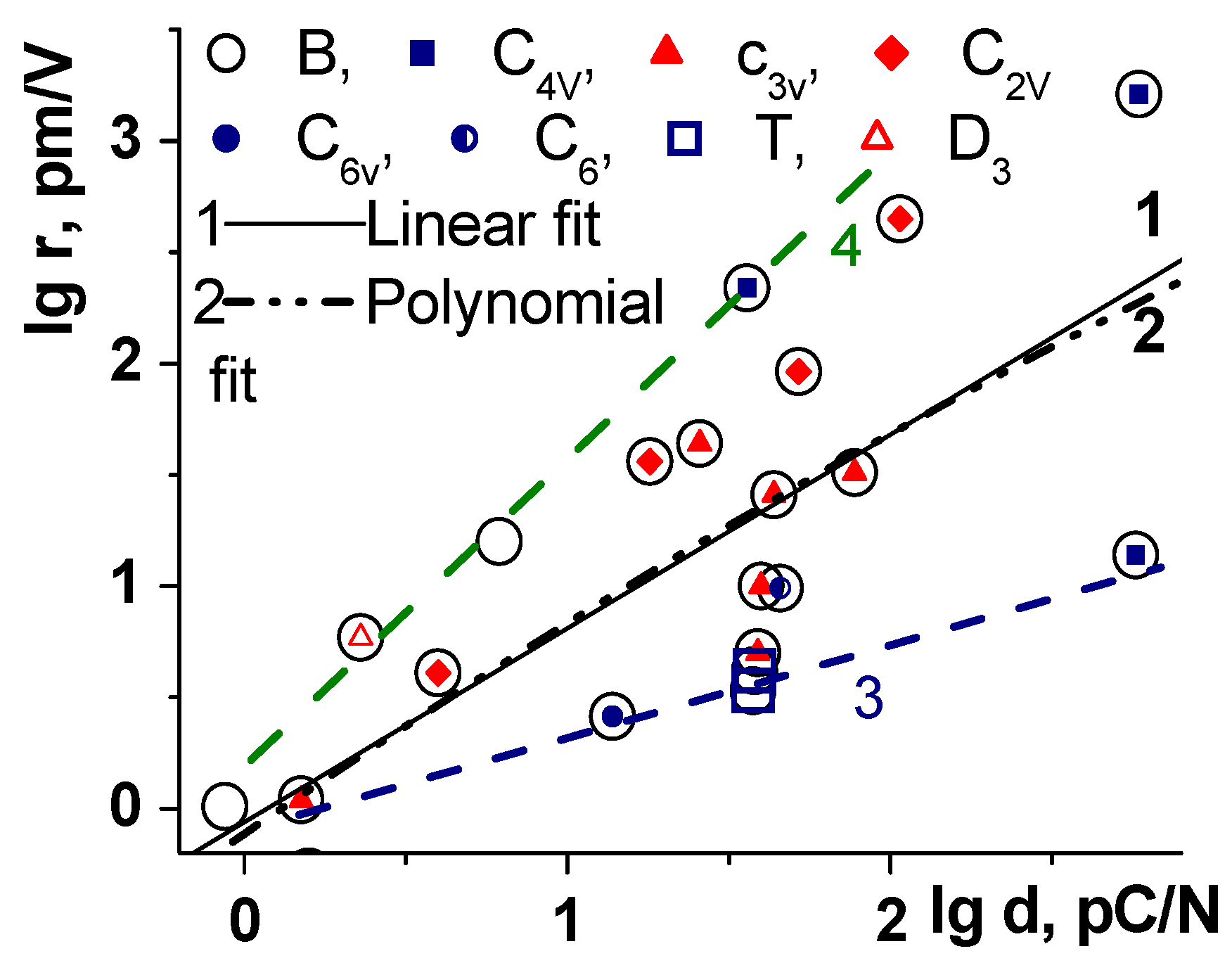
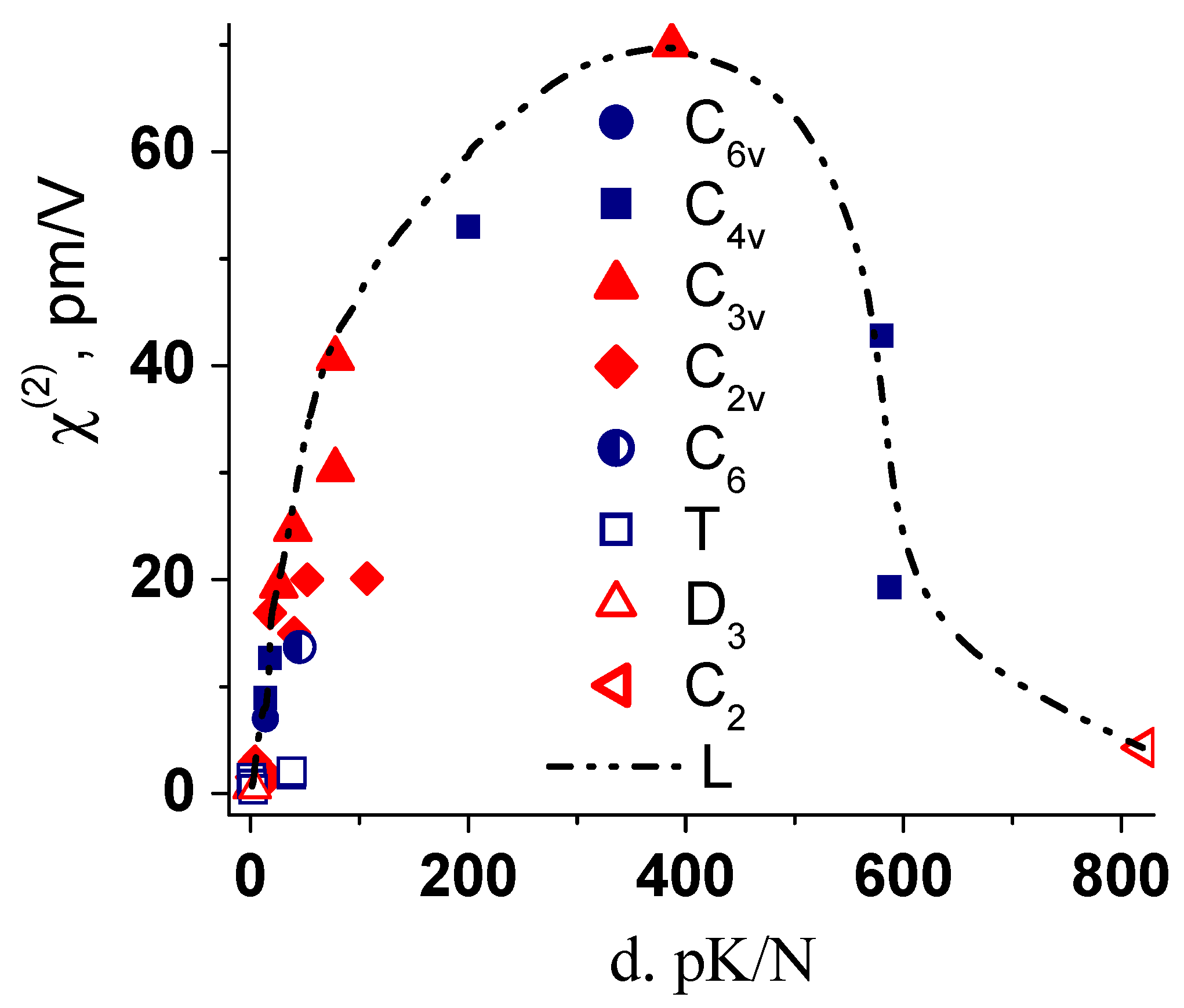
3.4. Correlation between “Piezoelectric and Nonlinear Optical Properties”
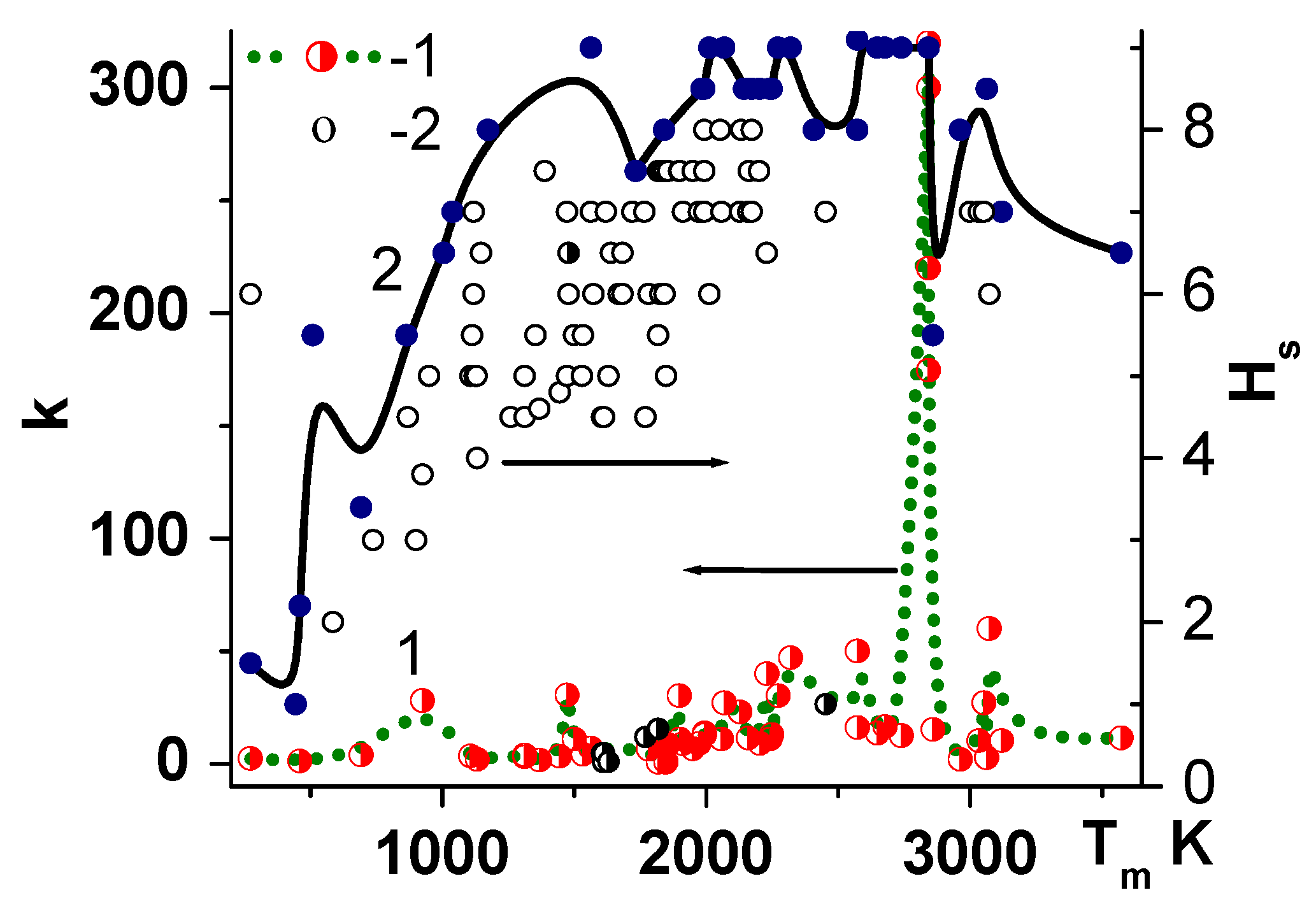
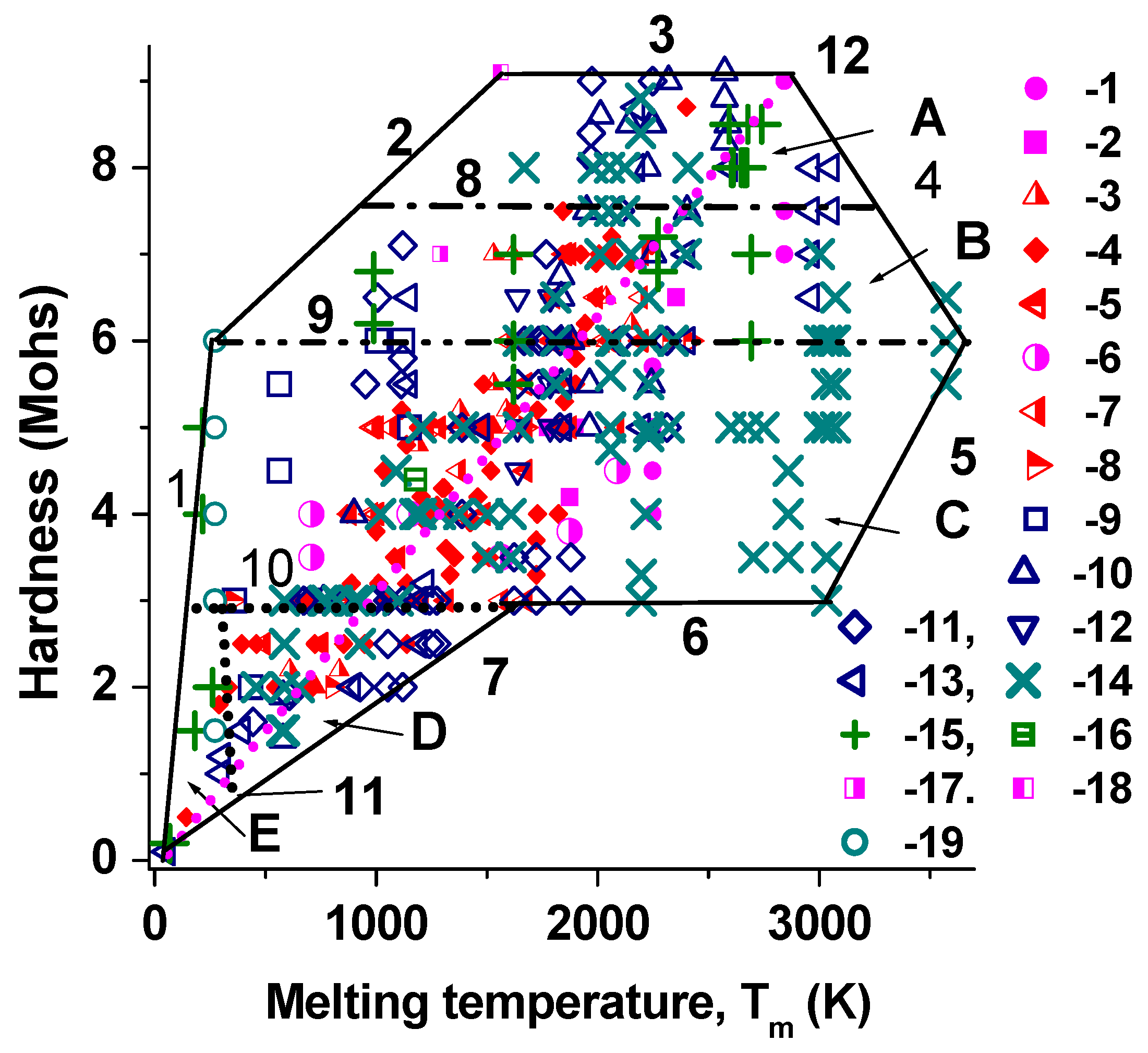
4. Interrelationship “Fusibility-Hardness-Thermal Conductivity”
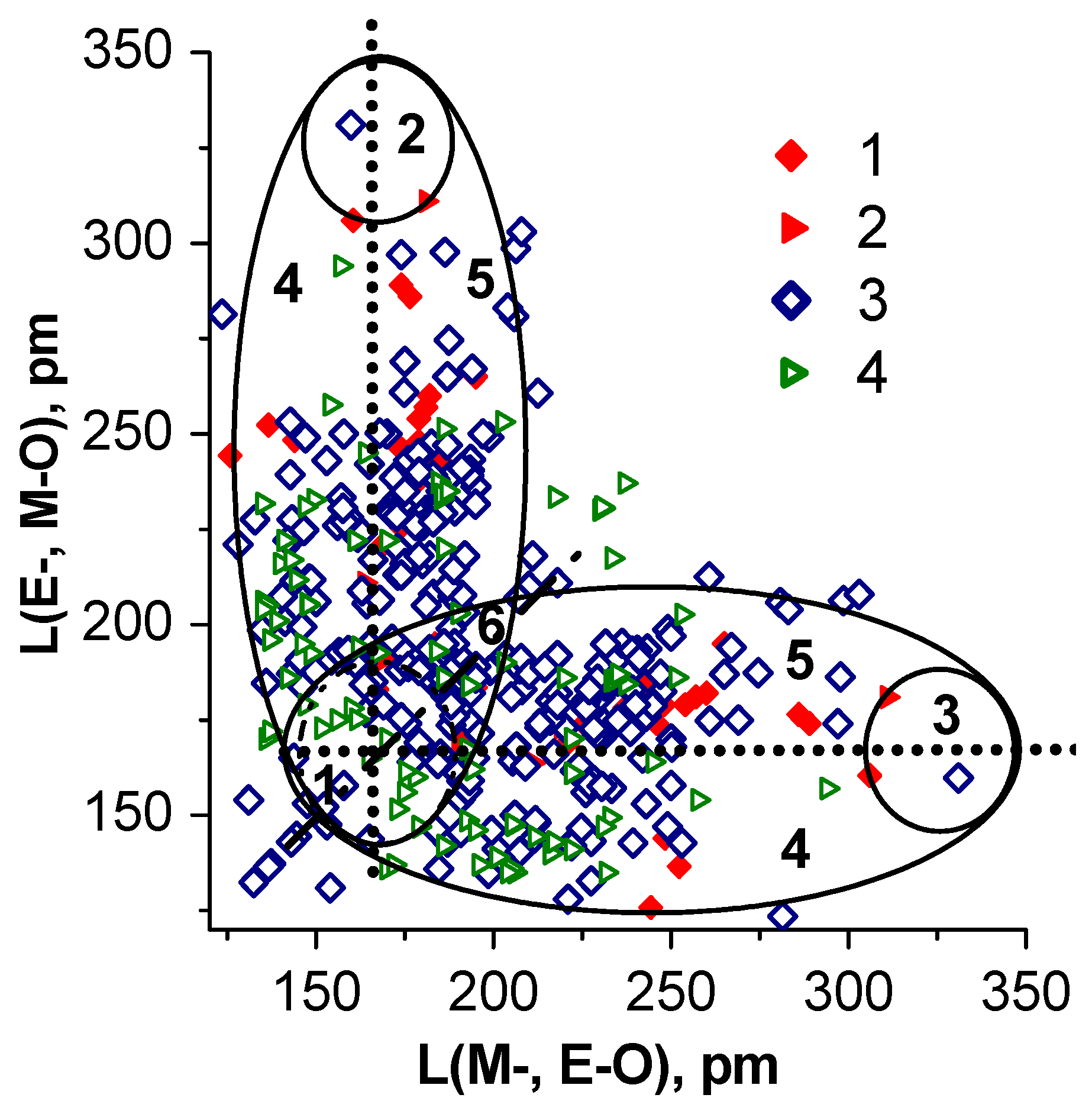
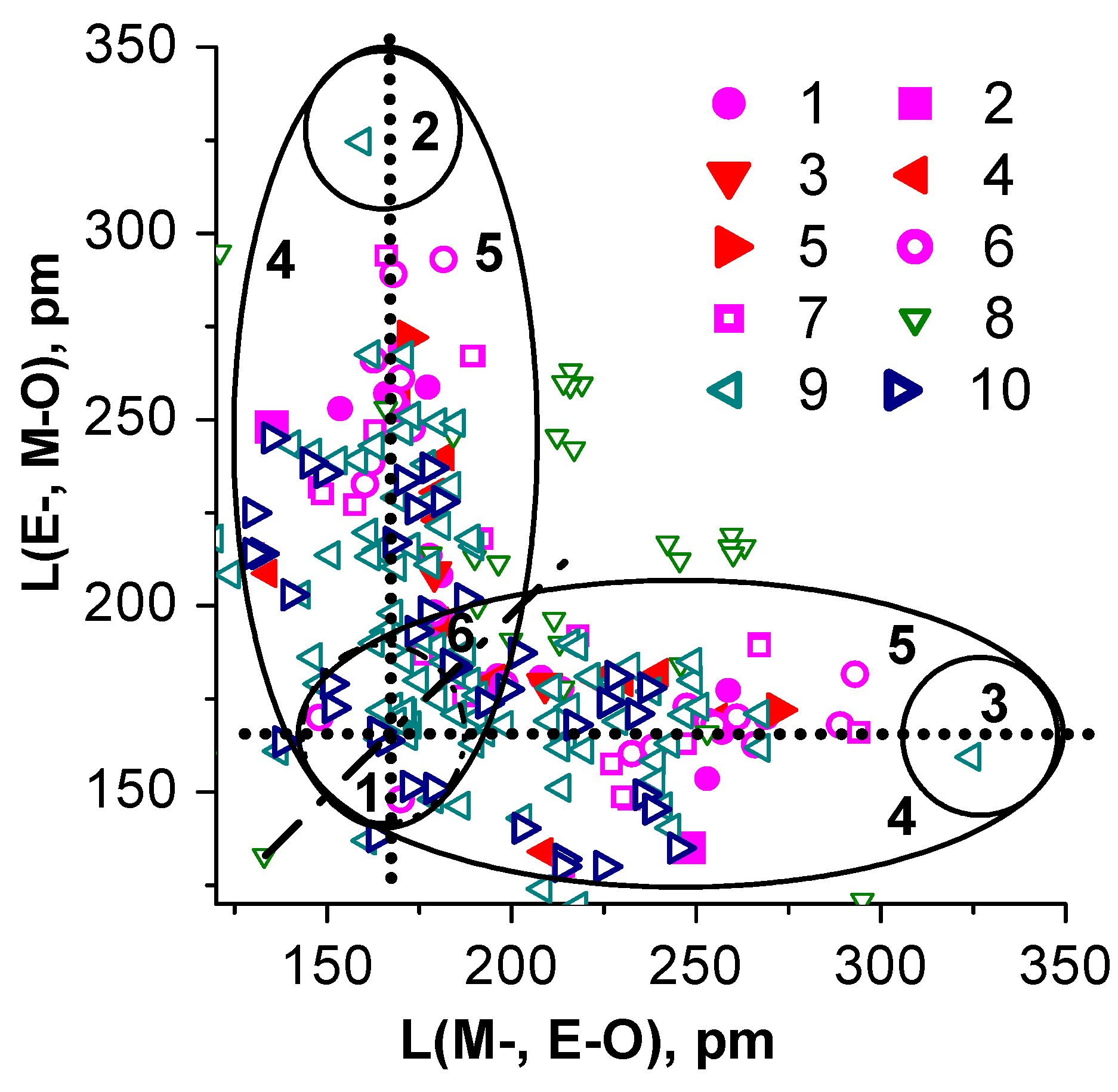
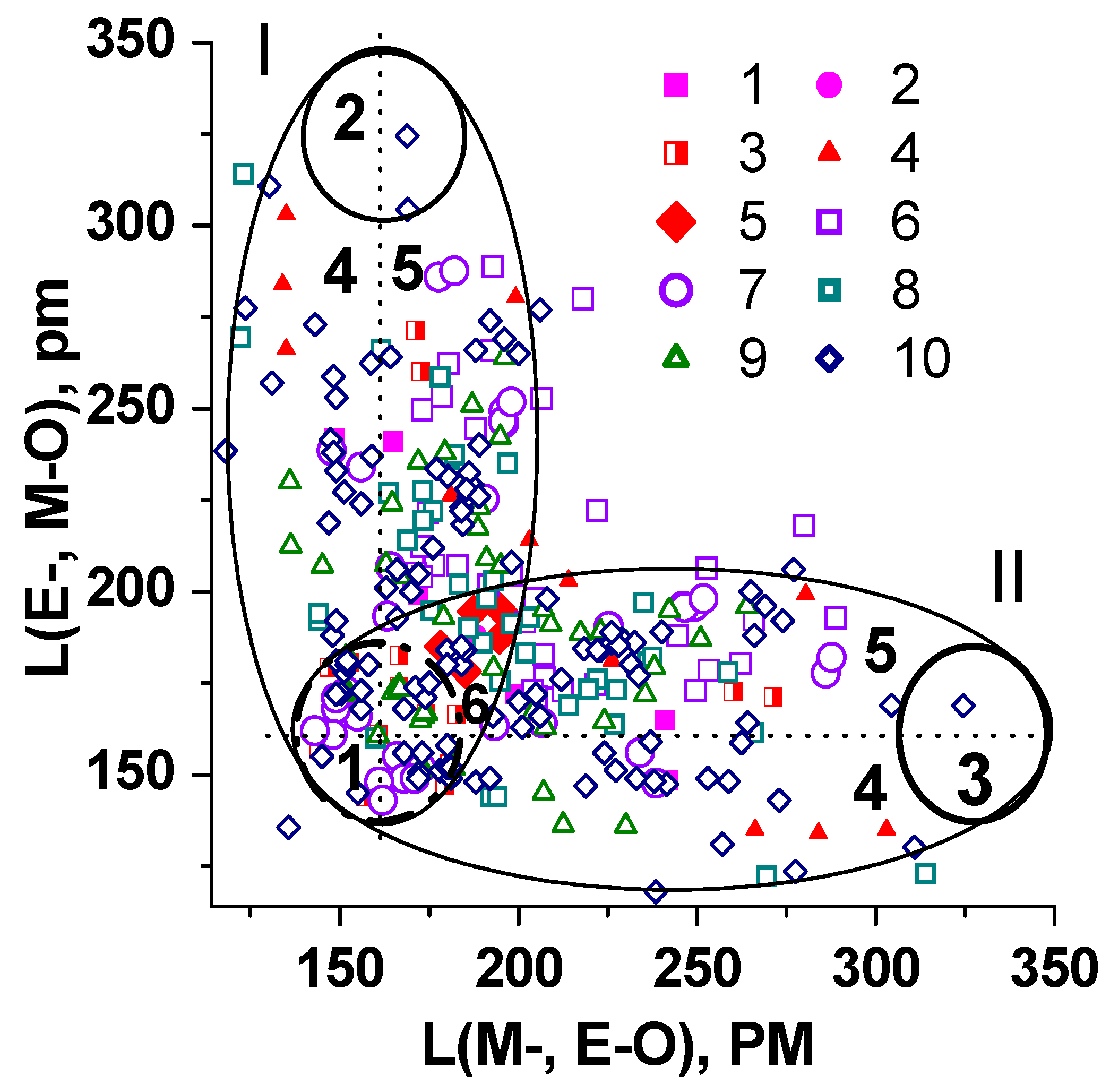
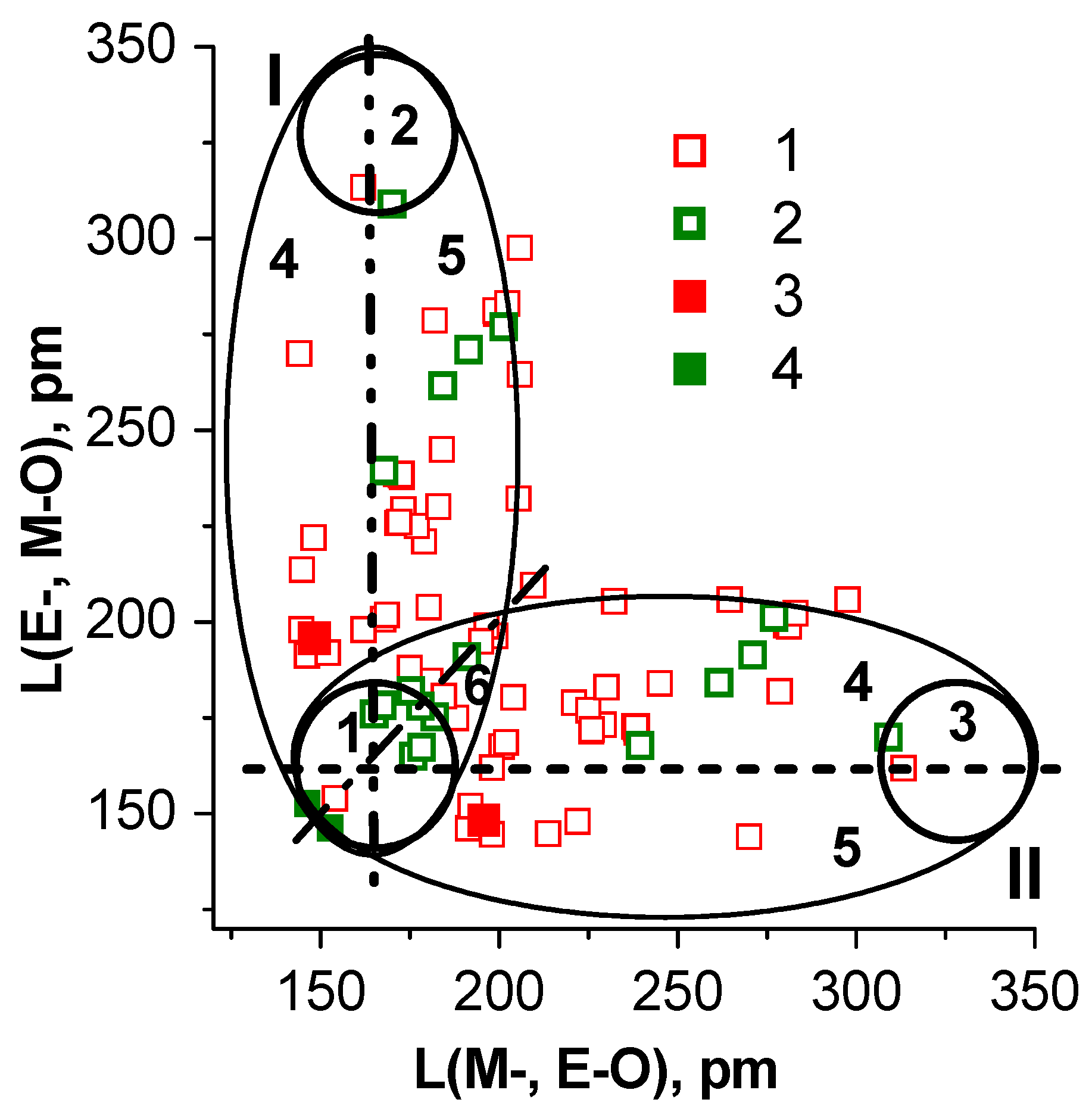
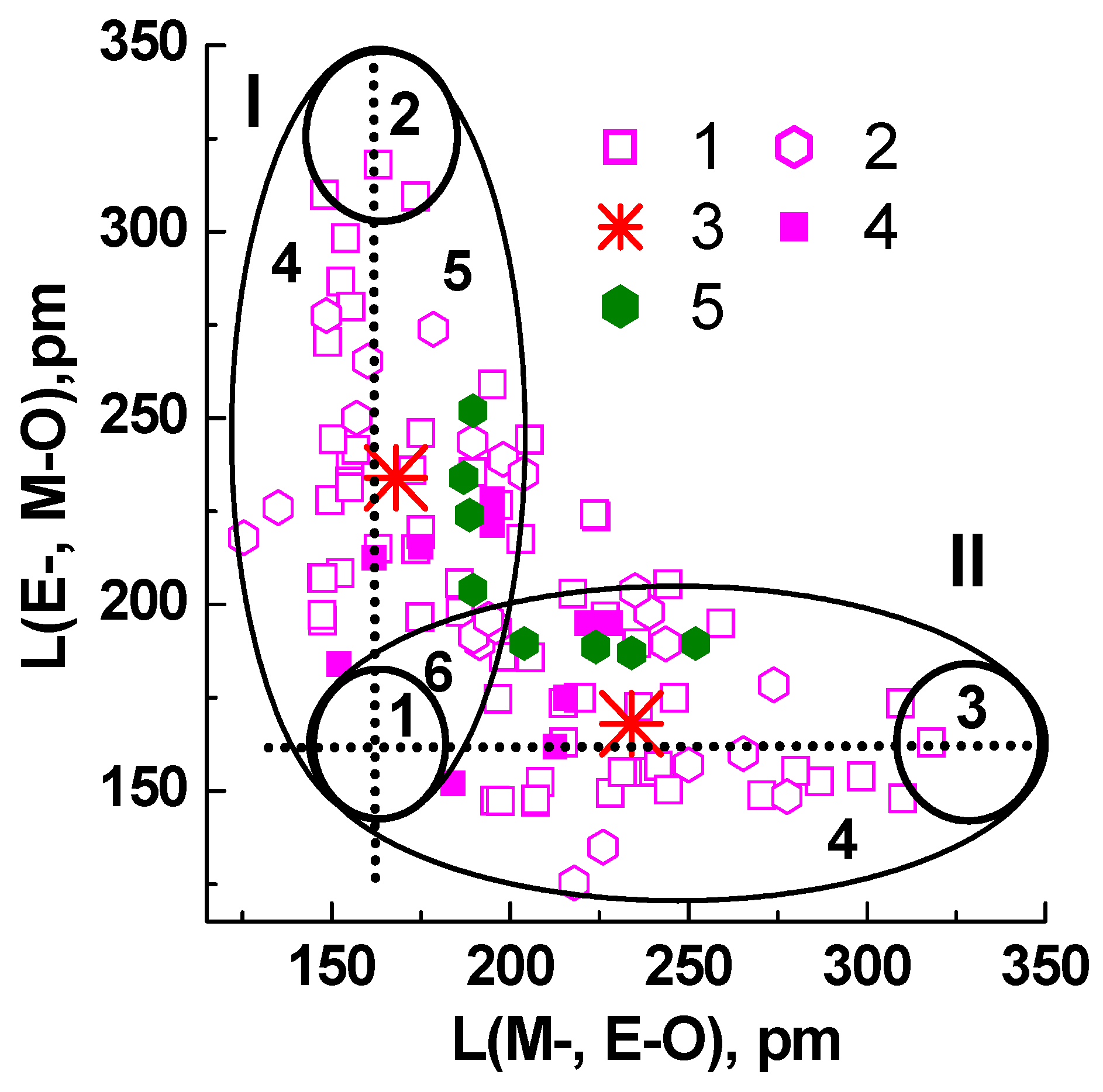
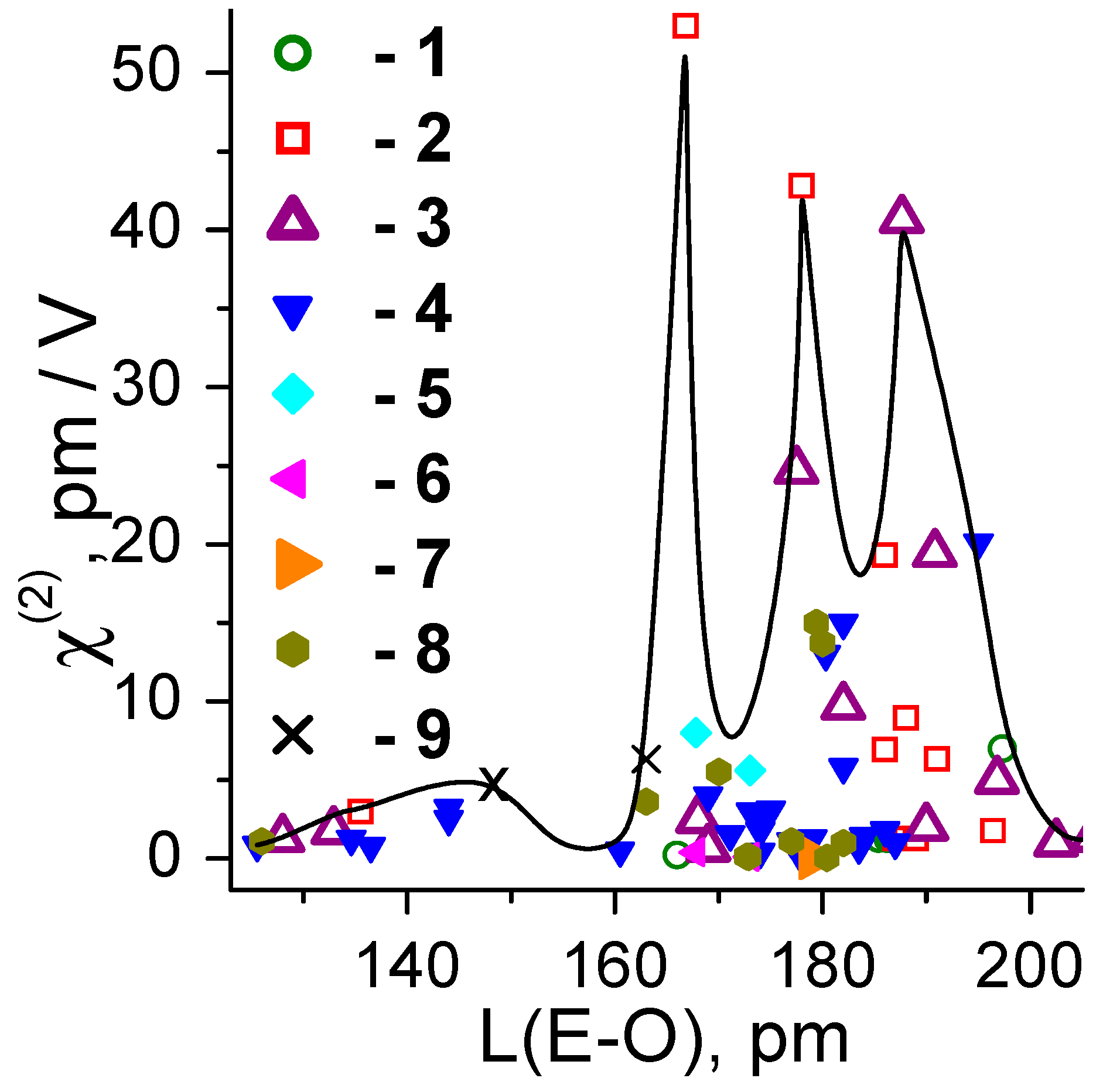
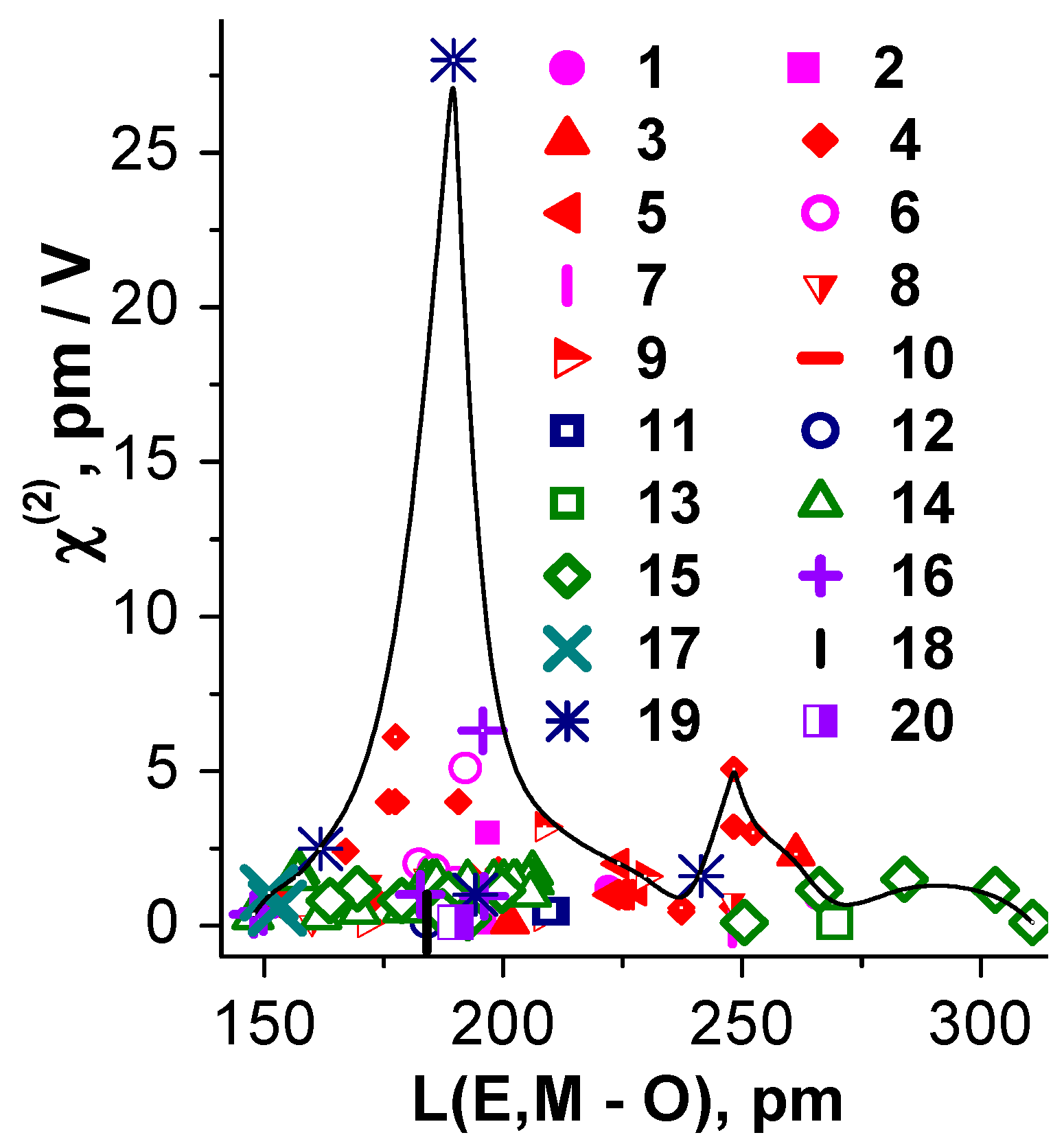
5. Interrelationship “Composition- Tructure–Oxide Bond Length-NLO-Susceptibility” for Binary Oxide Crystals
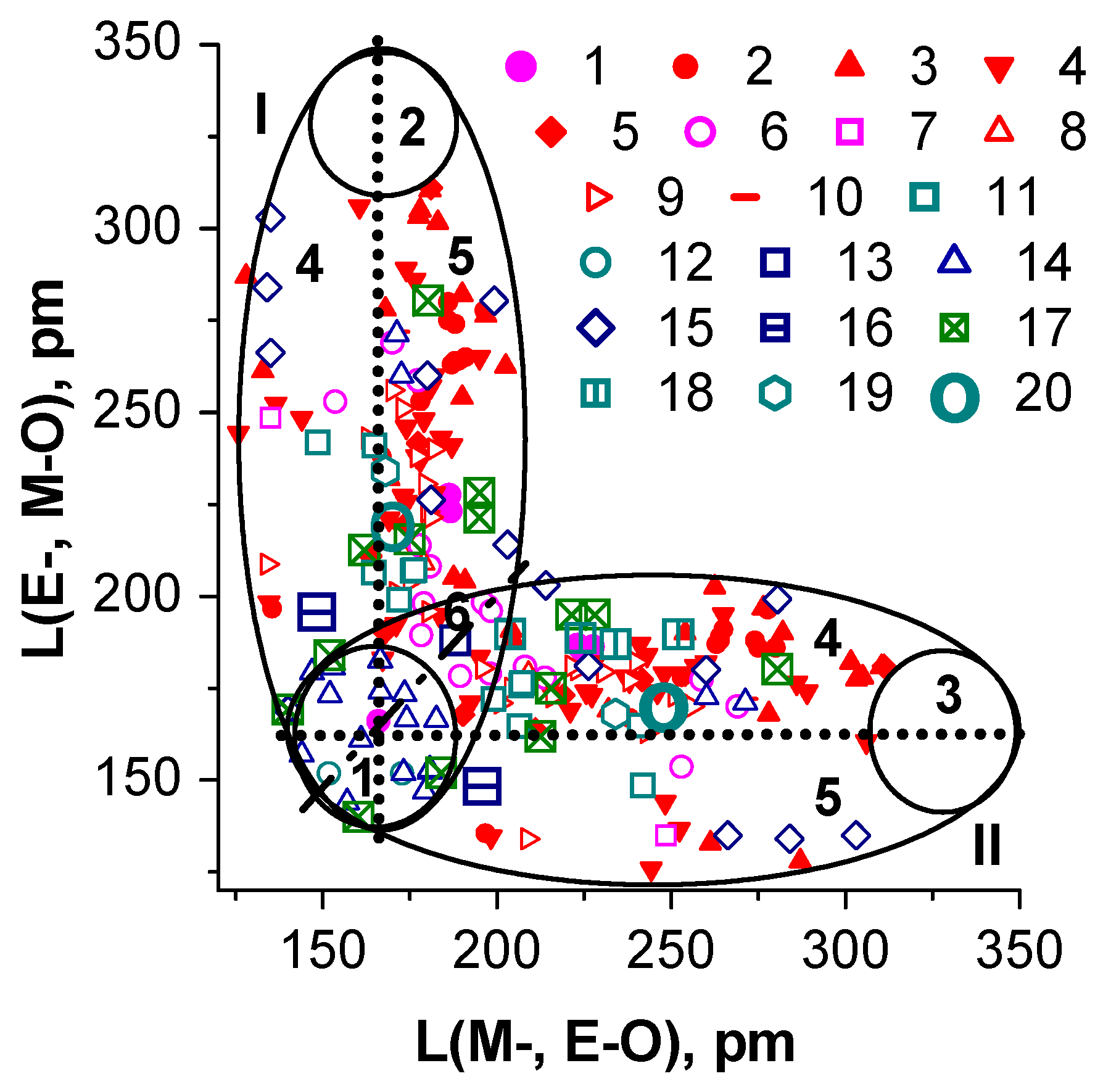
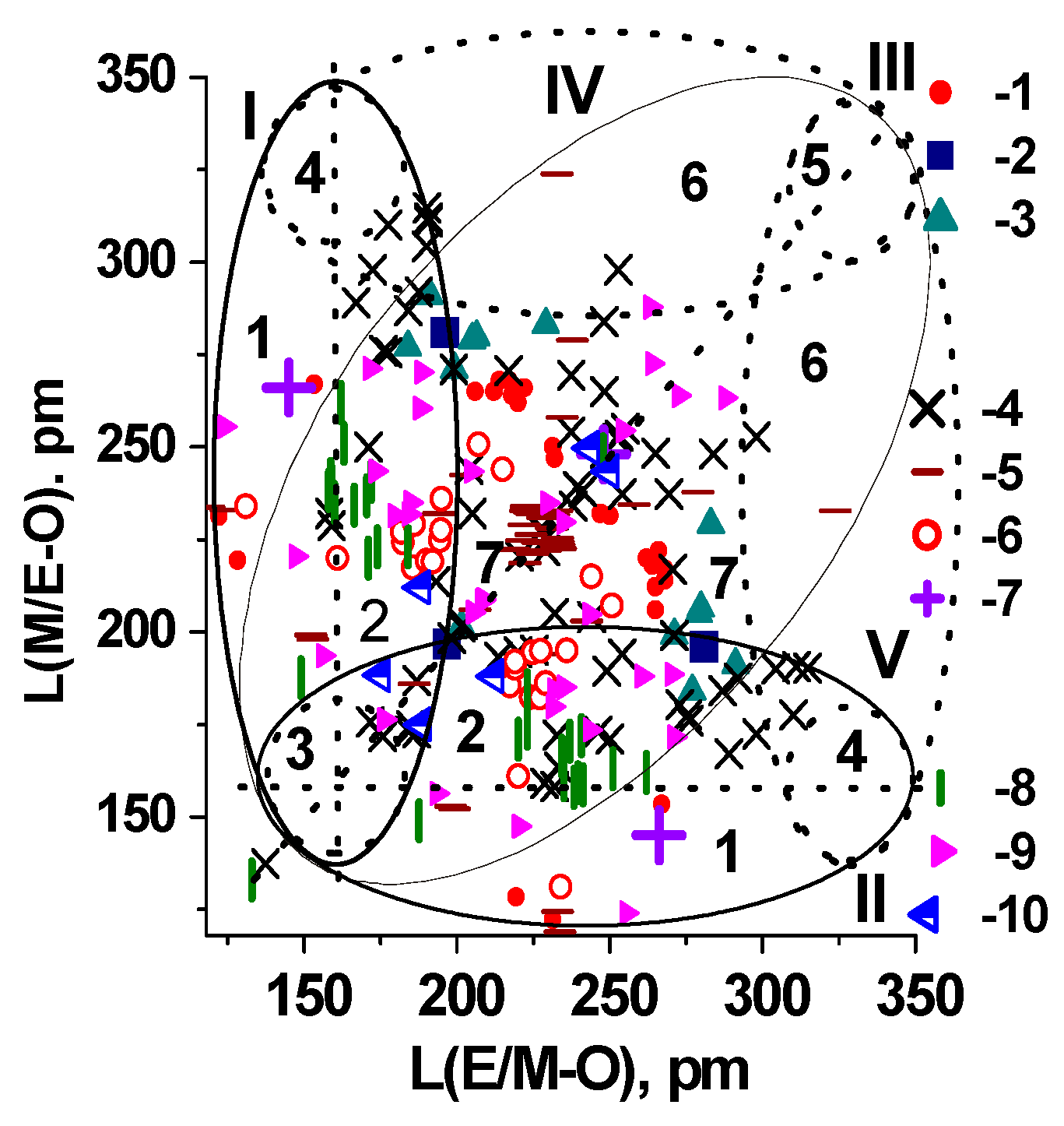
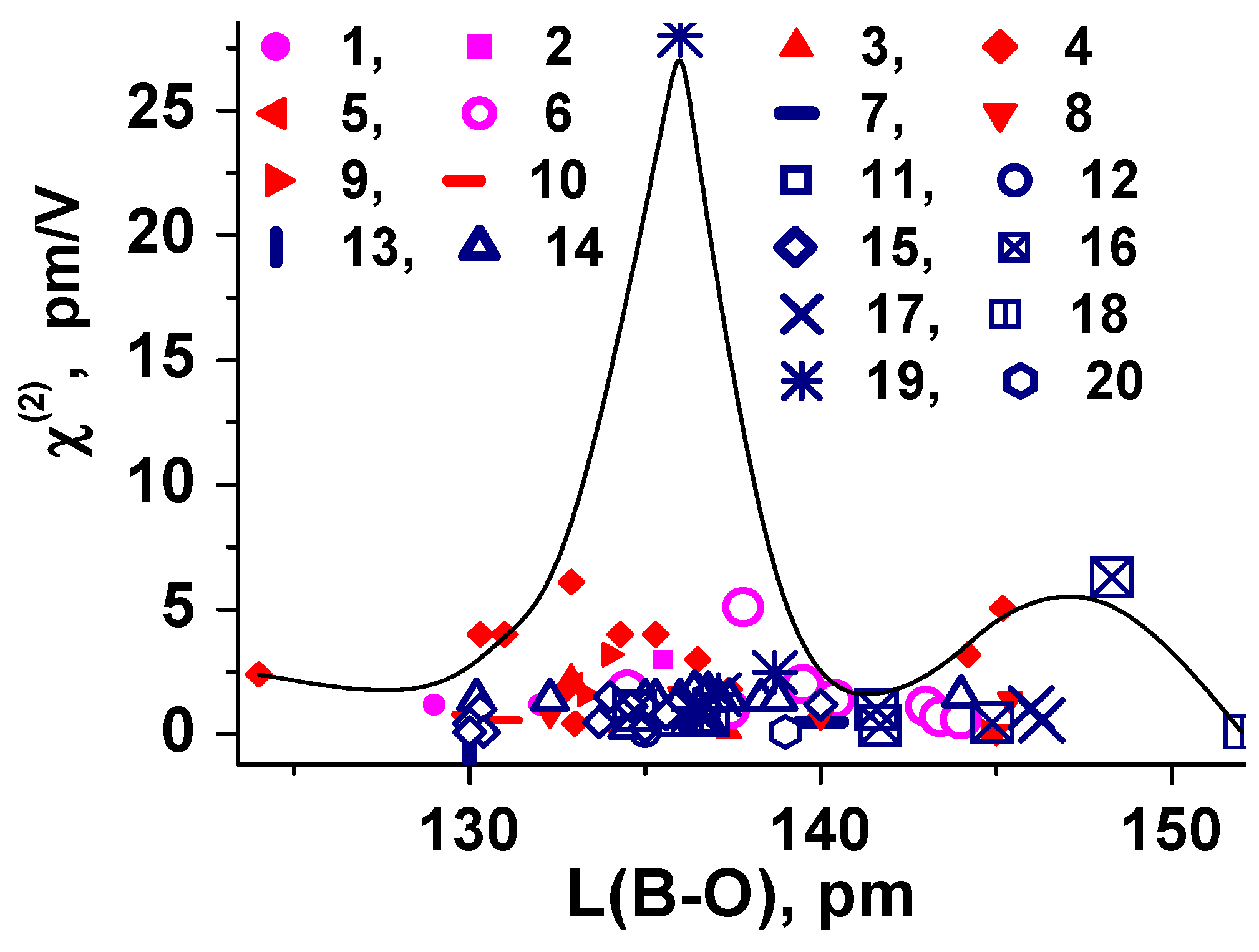
6. Interrelationship “Composition–Structure–Oxide Bond Length–NLO Susceptibility” for Simple and Binary Borate Crystals
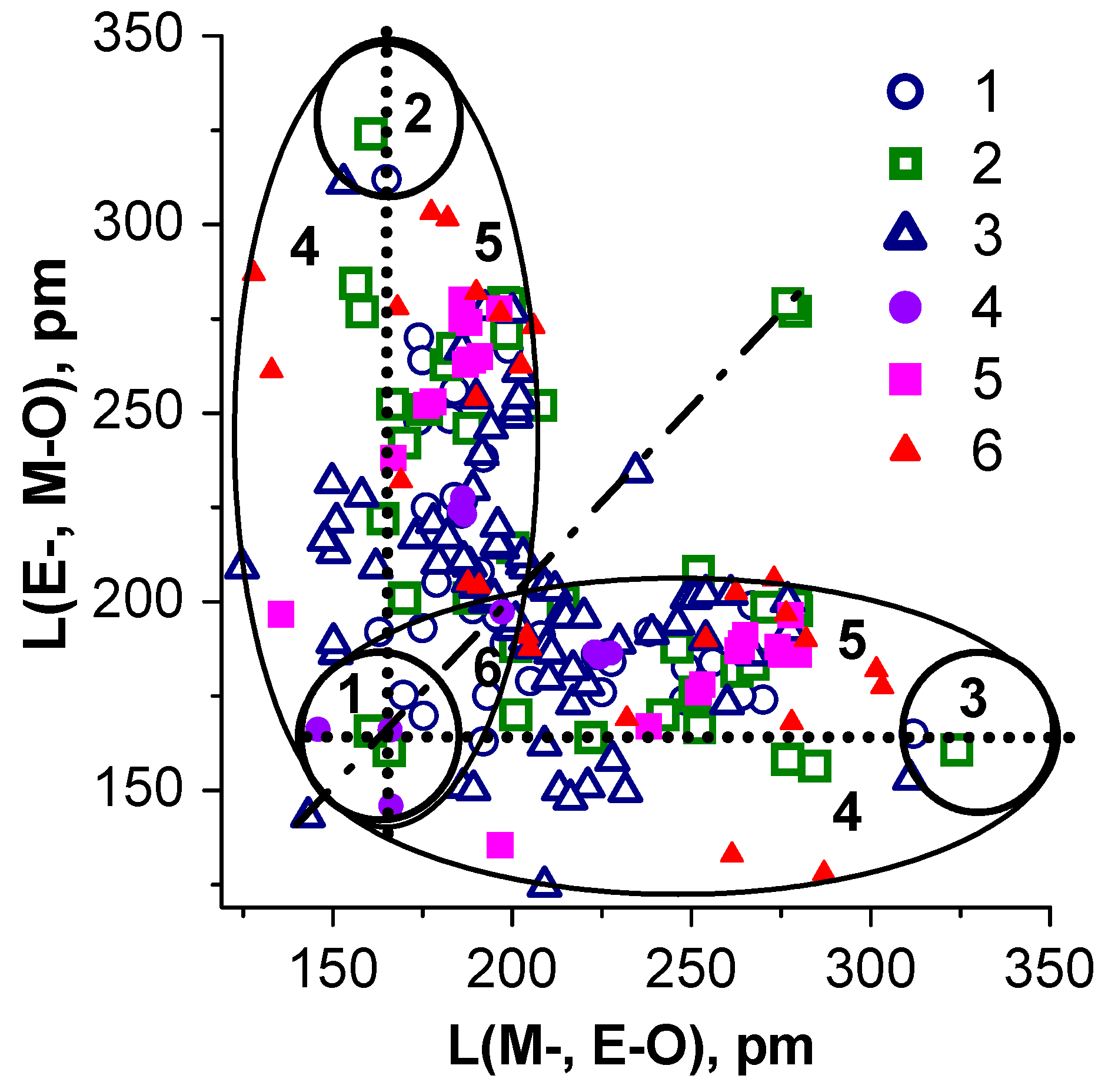
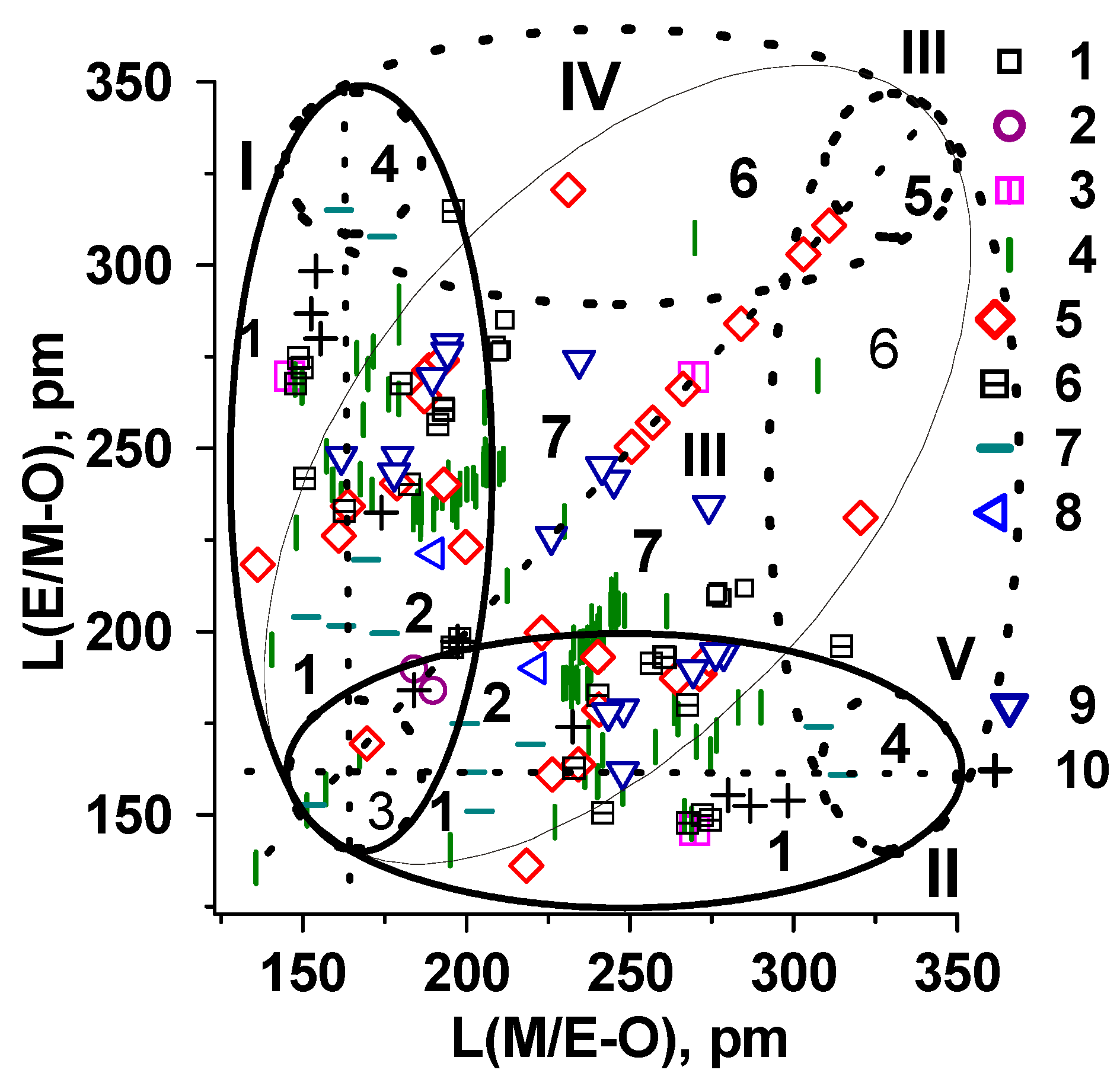
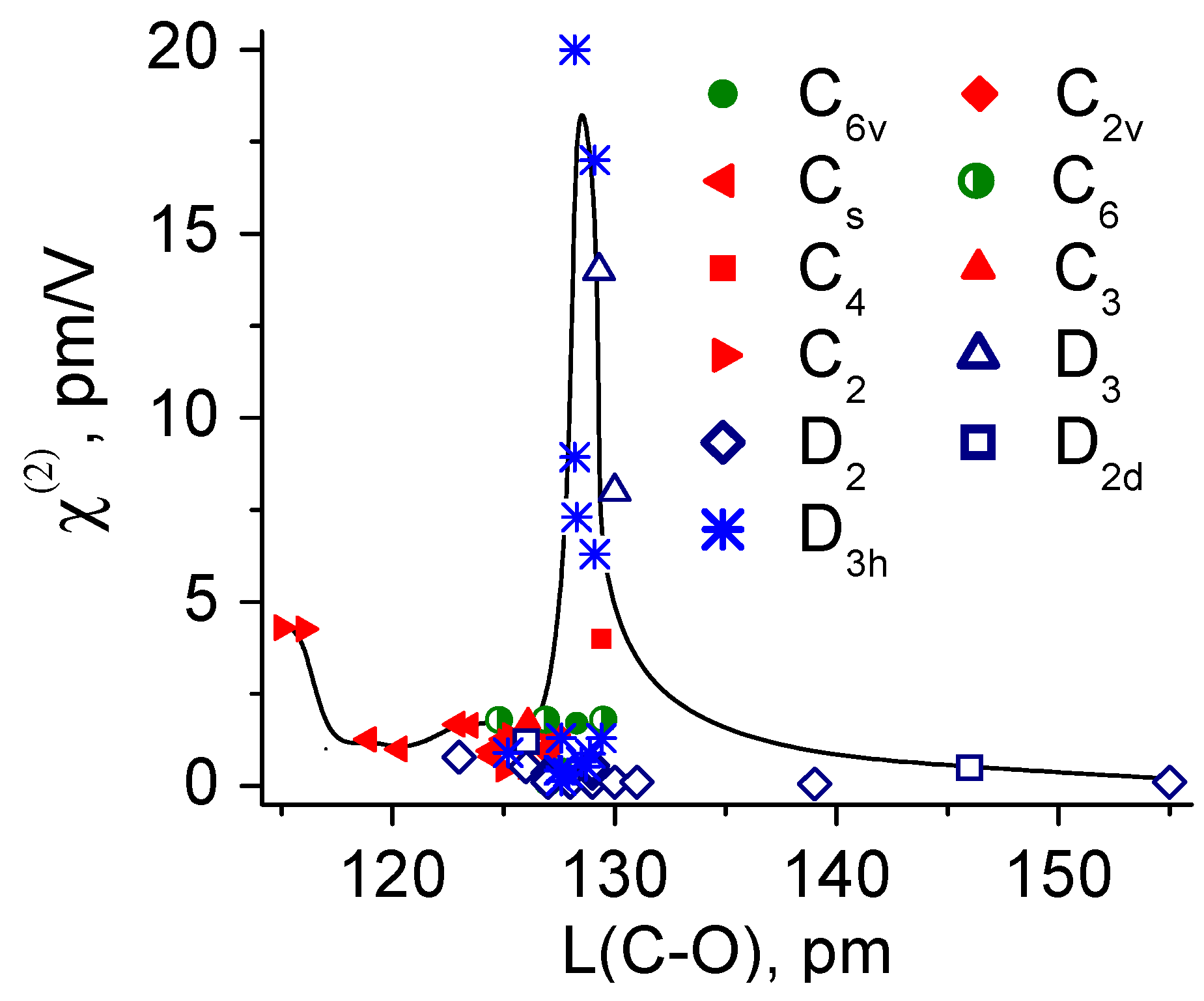
7. Interrelationship “Composition–Structure–Oxide Bond Length–NLO Susceptibility” for Simple and Binary Carbonate Crystals
8. Discussion and Conclusions
Supplementary Materials
Acknowledgments
Conflicts of Interest
References
- Gorelik, S.S. Again about the understanding of the notion “material science” and “material”. Mater. Electron. Technol. 2006, 2, 25–28. (In Russian) [Google Scholar]
- Rez, I.S.; Poplavko, Y.M. Dielectrics. Main Properties and Applications; Radio and Svyaz’: Moscow, Russia, 1989; p. 288. (In Russian) [Google Scholar]
- Jones, D.J.; Prasad, S.E. Wallace, J.B. Piezoelectric materials and their applications. Key Eng. Mater. 1996, 122, 71–143. [Google Scholar] [CrossRef]
- Kaminskii, A.A. Crystalline Lasers: Physical Processes and Operating Schemes; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Brenier, A. The self-doubling and summing lasers: Overview and modelling. J. Lumin. 2000, 91, 121–132. [Google Scholar] [CrossRef]
- Nikogosyan, D.N. Nonlinear Optical Crystals: A Complete Survey; Springer: New York, NY, USA, 2005; p. 427. [Google Scholar]
- Nowacki, W. Crystal Data; American Crystallographic Association: Buffulo, NY, USA, 1967. [Google Scholar]
- Arkhipenko, D.K.; Moroz, T.N. Refinement of the space group of the mineral based on analysis of vibration spectra selection rules. Crystallographiya 1996, 41, 975–978. (In Russian) [Google Scholar]
- Strunz, H. Mineralogische Tabellen; Akademische Verlaksgesselschaft Geest&Porting K.G.: Leipzig, Germany, 1957. [Google Scholar]
- Halasyamani, P.S.; Poeppelmeier, K.R. Nonventrosymmetric oxides. Chem. Mater. 1998, 10, 2753–2769. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V.; Pervukhina, N.V. Crystal structure-property relationship as a factor in the refinement of structural physical data. J. Struct. Chem. 2010, 51, 1119–1125. [Google Scholar] [CrossRef]
- Iona, F.; Shirane, D. Ferroelectric crystals. M. Mir. 1965, 555, 168. [Google Scholar]
- Lines, M.T.; Glass, M.L. Properties and Application of Ferroelectrics and Related Materials; Clarendon Press: Oxford, UK, 1977; p. 500. [Google Scholar]
- Chen, Ch.; Liu, G. Recent advances in nonlinear optical and electro-optical materials. Ann. Rev. Mater. Sci. 1986, 16, 203–243. [Google Scholar] [CrossRef]
- Chen, C.; Wu, Y.; Li, R. The anionic group theory of the nonlinear optical effect and its application in the development of new high quality NLO crystals in the borate series. Int. Rev. Phys. Chem. 1989, 8, 69–91. [Google Scholar] [CrossRef]
- Chen, C.; Ye, N.; Wu, B.; Zeng, W.; Chen, Q.; Zhang, Y. Design and Synthesis of New Nonlinear Optical Crystals. In Proceedings of the International Symposium on Laser and Nonlinear Optical Materials; Sasaki, T., Ed.; Data Storage Institute: Singapore, 1997; pp. 103–119. [Google Scholar]
- Chen, C.; Sasaki, T.; Li, R.; Wu, Z.; Lin, Z.; Mori, Y.; Hu, Z.; Wang, J.; Uda, S.; Yoshimura, M.; et al. Nonlinear Optical Borate Crystals, Principles and Applications; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2012; p. 387. [Google Scholar]
- Jiang, X.; Luo, S.; Kang, L.; Gong, P.; Huang, H.; Wang, S.; Lin, Z.; Chen, C. First-Principles Evaluation of the Alkali and/or Alkaline Earth Beryllium Borates in Deep Ultraviolet Nonlinear Optical Applications. ACS Photon. 2015, 2, 1183–1191. [Google Scholar] [CrossRef]
- Tran, T.T.; Yu, H.; Rondinelli, J.M.; Poeppelmeier, K.R.; Halasyamani, P.S. Deep Ultraviolet Nonlinear Optical Materials. Chem. Mater. 2016, 28, 5238–5258. [Google Scholar] [CrossRef]
- Zou, G.; Huang, L.; Ye, N.; Lin, C.; Cheng, W.; Huang, H. CsPbCO3F: A Strong Second-Harmonic Generation Material Derived from Enhancement via p−π Interaction. J. Am. Chem. Soc. 2013, 135, 18560–18566. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Halasyamani, P.S. New fluoride carbonates: Centrosymmetric KPb2(CO3)2F and non-centrosymmetric K2.70Pb5.15(CO3)5F3. Inorg. Chem. 2013, 52, 2466–2473. [Google Scholar] [CrossRef] [PubMed]
- Tran, T.T.; Halasyamani, P.S.; Rondinelli, J.M. Role of Acentric Displacements on the Crystal Structure and Second-Harmonic Generating Properties of RbPbCO3F and CsPbCO3F. Inorg. Chem. 2014, 53, 6241–6251. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Peng, G.; Ye, N.; Wang, J.; Luo, M.; Yan, T.; Zhou, Y. Structural Modulation of Anionic Group Architectures by Cations to Optimize SHG Effects: A Facile Route to New NLO Materials in the ATCO3F (A = K, Rb; T = Zn, Cd) Series. Chem. Mater. 2015, 27, 7520–7530. [Google Scholar] [CrossRef]
- Zou, G.; Nam, G.; Kim, H.G.; Jo, H.; You, T.S.; OK, K.M. ACdCO(3)F (A = K and Rb): New noncentrosymmetric materials with remarkably strong second-harmonic generation (SHG) responses enhanced via pi-interaction. RSC Adv. 2015, 5, 84754–84761. [Google Scholar] [CrossRef]
- Zou, G.; Ye, N.; Huang, L.; Lin, X.S. Alkaline-Alkaline Earth Fluoride Carbonate Crystals ABCO(3)F (A = K, Rb, Cs; B = Ca, Sr, Ba) as Nonlinear Optical Materials. J. Am. Chem. Soc. 2011, 133, 2001–2007. [Google Scholar] [CrossRef] [PubMed]
- Reference Book on Lasers; Prokhorov, A.M.; Sovetskoe, M. (Eds.) Sovetskoe Radio: Moscow, Russia, 1978; pp. 237–330. (In Russian) [Google Scholar]
- Kuz’minov, Y.S. Ferroelectric Crystals for Conversion of the Laser Radiation; Nauka: Moscow, Russia, 1982; p. 400. (In Russian) [Google Scholar]
- Prokhorov, A.V.; Kuz’minov, Y. Physics and Chemistry of Crystalline Lithium Niobate; dam Kluver. Bristol.: Bristol, ME, USA, 1990. [Google Scholar]
- Blistanov, A.A.; Bondarenko, V.S.; Perelomova, N.V.; Strizhevskaya, F.N.; Tchkalova, V.V.; Shaskolskaya, M.P. Acoustic Crystals, Reference Book; Nauka: Moscow, Russia, 1982; p. 632. (In Russian) [Google Scholar]
- Tressler, J.F.; Alkoy, S.; Newnham, R.E. Piezoelectric sensors and sensor materials. J. Electroceram. 1998, 2, 257–272. [Google Scholar] [CrossRef]
- Baettig, P.; Schelle, C.F.; LeSar, R.; Waghmare, U.V.; Spaldin, N.A. Theoretical prediction of new high-performance lead-free piezoelectrics. Chem. Mater. 2005, 17, 1376–1380. [Google Scholar] [CrossRef]
- Advanced Piezoelectric Materials. Science, and Technology; Uchino, K. (Ed.) Woodhead Publishing Limited: Cambridge, UK, 2010. [Google Scholar]
- Chen, X.; Deng, H.; Zhang, H.; Lin, D.; Zhao, X.; Luo, H. The growth and properties of lead free ferroelectrics single crystals. Crystals 2015, 5, 172–192. [Google Scholar]
- Shen, C.; Zhang, S.; Cao, W.; Cong, H.; Yu, H.; Wang, J.; Zhang, H. Thermal and electromechanical properties of melilite-type piezoelectric single crystals. J. Appl. Phys. 2015, 117, 064106. [Google Scholar] [CrossRef]
- Moure, C.; Peňa, O. Races Advances in Perovskites: Processing and Properties. Progr. Solid State Chem. 2015, 43, 123–148. [Google Scholar] [CrossRef]
- Cooper, R.V.; Voas, B.K.; Bridges, C.A.; Morris, J.R.; Beckman, S.P. First principles materials design of novel functional oxides. J. Adv. Dielectr. 2016, 6, 165001. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V. Universal crystal classification system “point symmetry-physical property”. Ferroelectrics 2007, 360, 96–99. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Kidyarov, B.I.; Pervukhina, N.V. Phenomenological modeling and design of new acentric crystal for optoelectronics. Comput. Mater. Sci. 2004, 30, 411–418. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Kidyarov, B.I.; Pervukhina, N.V. Shortest chemical bond length as a criteria for searching new noncentrosymmetric phosphate crystals. Ceram. Int. 2004, 30, 2005–2009. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Kidyarov, B.I.; Pervukhina, N.V. Shortest chemical bond lengths as a criteria for search new noncentrosymetric niobate and tantalate crystals with high optical nonlinearity. J. Cryst. Growth 2005, 275, e1941–e1946. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Kidyarov, B.I.; Pervukhina, N.V. Systematics and design of noncentrosymmetric sulphides and selenides for nonlinear optics. Comput. Mater. Sci. 2006, 32, 507–511. [Google Scholar] [CrossRef]
- Atuchin, V.V.; Kidyarov, B.I.; Pervukhina, N.V. Systematization and interrelationship of micro-, and macrostructure with physical properties of oxide crystals without inversion centre. II. Nonlinear property of binary oxide crystals. Nano-Micro-Syst. Technol. 2006, 5, 20–25. (In Russian) [Google Scholar]
- Kidyarov, B.I.; Atuchin, V.V. Interrelationship of micro-and macro-structure with physical properties of binary acentric oxide ferroelactic and paraelastic crystals. Ferroelectrics 2007, 360, 104–110. [Google Scholar] [CrossRef]
- Аtuchin, V.V.; Кidyarov, B.I.; Tsirkina, N.L. Classification of Noncentrosymmetric Oxides with Re3+ Ions Applicable for Self Frequency Doubling (SFD) Laser Crystals. In Proceedings of the SPIE International Conference on Nonlinear Optics, ICONO/LAT-2006, St. Petersburg, Russia, 25–30 June 2006; p. 6610w. [Google Scholar]
- Kidyarov, B.I.; Atuchin, V.V.; Pervukhina, N.V. Interrelation of the macrostructure and microstructure with the nonlinear optical properties of iodate and titanate crystals. Phys. Solid State 2009, 51, 1548–1552. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V. The simple and binary fluorides. Interrelationship “structure-nonlinear optical property” for halogenide crystals. Izvestiya Vuzov. Physics 2009, 3, 158–163. [Google Scholar]
- Atuchin, V.V.; Kidyarov, B.I.; Makukha, V.K. Interrelationship “Structure-Nonlinear Optical Properties” for Simple and Binary Acentric Chlorides. In Proceedings of the International Forum on Strategic Technologies, Ho Chi Minh City, Vietnam, 21–23 October 2009; Ho Chi Minh City Publishing House: Vietnam National University, Vietnam, 2009; pp. 162–164. [Google Scholar]
- Atuchin, V.V.; Kidyarov, B.I.; Makukha, V.K. Classification of Binary Acentric Tellurides. In Proceedings of the International Forum on Strategic Technologies, Ho Chi Minh City, Vietnam, 21–23 October 2009; Ho Chi Minh City Publishing House: Vietnam National University, Vietnam, 2009; pp. 58–60. [Google Scholar]
- Kidyarov, B.I.; Atuchin, V.V. Systematization of simple and binary silicates according to relationship “composition -structure-property”. Ferroelectrics 2010, 397, 169–176. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V. Interrelationship “composition-structure-nonlinear optical properties” in aluminate crystals. Ferroelectrics 2010, 397, 151–158. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V. Interrelationship of micro-and macrostructure with nonlinear optical properties of simple and binary acentric niobate crystals. Ferroelectrics 2010, 397, 159–168. [Google Scholar] [CrossRef]
- Zhang, L.; Atuchin, V.; Kidyarov, B.; Andreev, Y. Taxonomy, Chemical Bonding Relations, and Nonlinear Optical Properties of Noncentrosymmetric Sulfide Crystals. In Proceedings of the 2nd International Symposium on Laser Interaction with Matter (LIMIS 2012), Xi’an, China, 9 September 2013; Liu, J., Cao, J., Kaierle, S., Eds.; 2013; Volume 8796-2A. [Google Scholar]
- Kidyarov, B.I.; Atuchin, V.V. Interrelationship “Struсture-Property” for the Crystals of Noncentrosymmetric Tungstates. Ferroelectrics 2013, 444, 144–149. [Google Scholar] [CrossRef]
- Kidyarov, B.I.; Atuchin, V.V.; Troitskaia, I.B. Interrelationship of micro-and macrostructure with physical properties of germanates. Ferroelectrics 2013, 444, 137–143. [Google Scholar]
- Kidyarov, B.I.; Makukha, V.K. Interrelationship of the Structural and Nonlinear-Optical Properties of the Carbonate Crystals. In Proceedings of the 13th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE) (APEIE-2016), Novosibirsk, Russia, 5–6 October 2016; Volume 12, pp. 390–394. [Google Scholar]
- Kidyarov, B.I.; Makukha, V.K. Structural and Physical Systematization of the Nonlinear-Optical Borate Crystals. In Proceedings of the IFOST-2016, 11th International Forum on Strategic Technology (IFOST), Novosibirsk, Russia, 1–3 June 2016; Novosibirsk State Technical University Russia: Novosibirsk, Russia, 2016; pp. 539–543. [Google Scholar]
- Kidyarov, B.I.; Makukha, V.K. Comparison of the Acentric Properties for the Oxide Crystals. In Proceedings of the 12th International Conference on Actual Problems of Electronics Instrument Engineering (APEIE)–34006, Novosibirsk, Russia, 2–4 October 2014; Volume 7, pp. 61–63. [Google Scholar]
- Kidyarov, B.I.; Makukha, V.K. Interrelationship “structure-hardness-fusibility” for oxide crystals. In Proceedings of the 12th International Conference on Actual Problems of Electronics Instrument Engineering (APEIE)–34006, Novosibirsk, Russia, 2–4 October 2014; Volume 7, pp. 64–67. [Google Scholar]
- Katritzky, A.R.; Kuanar, M.; Slavov, S. Quantitative Correlation of Physical and Chemical Properties with Chemical Structure: Utility for Prediction. Chem. Rev. 2010, 110, 5714–5789. [Google Scholar] [CrossRef] [PubMed]
- Shanon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalkogenides. Acta Cryst. 1976, A32, 751–760. [Google Scholar] [CrossRef]
- Urusov, V.S. Theoretical Crystal-Chemistry; Moscow State University: Moscow, Russia, 1987; p. 275. [Google Scholar]
- Sirotin, Y.I.; Shaskolskaya, M.P. Fundamentals of Crystal Physics; Mir Publishers: Moscow, Russia, 1982; p. 680. [Google Scholar]
- Aizu, K. Possible species of “ferroelastic” crystals and of simultaneously ferroelectric and ferroelastic crystals. J. Phys. Soc. Jpn. 1969, 27, 387–396. [Google Scholar] [CrossRef]
- Rapoport, I.N. Electrooptic Effect on the Quadratic, and Cubic Nonlinearity. Ph.D. Thesis, Fare East State University for Means of Communication, Khabarovsk, Russia, 2000; p. 18. (In Russian). [Google Scholar]
- Kurtz, S.K.; Perry, T.T. A powder technique for evaluation of nonlinear optical materials. J. Appl. Phys. 1968, 39, 3798–3813. [Google Scholar] [CrossRef]
- Zhang, S.; Cheng, Z.; Lu, J.; Li, G.; Lu, J.; Shao, Z.; Chen, H. Studies on the effective nonlinear coefficient of GdCa4O(BO3)3 crystal. J. Cryst. Growth 1999, 205, 453–456. [Google Scholar] [CrossRef]
- Aka, G.; Mougel, F.; Augé, F.; Kahn-Harari, A.; Vivien, D.; Bénitez, J.M.; Salin, F.; Pelenc, D.; Balembois, F.; Georges, P.; et al. Overview of the laser and non-linear optical properties of calcium-gadolinium-oxo-borate Ca4GdO(BO3)3. J. Alloys Compd. 2000, 303–304, 401–408. [Google Scholar] [CrossRef]
- Belik, A.A.; Azuma, M.; Saito, T.; Shimakawa, Y.B. Crystallographic features, and tetragonal phase stability of PbVO3, a new member of PbTiO3 family. Chem. Mater. 2005, 17, 269–273. [Google Scholar] [CrossRef]
- Fukuda, T. Growth and crystallographic characteristic of K3Li2Nb5O15 single crystals. Jpn. J. Appl. Phys. 1969, 8, 122–126. [Google Scholar] [CrossRef]
- Adachi, M.; Kawabata, A. Elastic and piezoelectric properties of potassium lithium niobate (KLN) crystals. Jpn. J. Appl. Phys. 1978, 17, 1969–1973. [Google Scholar] [CrossRef]
- Xu, J.; Fan, S.; Xu, X. Bridgment growth and properties of potassium lithium niobate crystals. Progr. Cryst. Growth Character. Mater. 2000, 40, 137–144. [Google Scholar]
- Huang, L.Z.; Zhao, K.Y.; Ruan, W.; Ruan, X.Z.; Zhao, W.; Zeng, J.T.; Li, G.R. Enhancement of Рiezoelectric Properties of PMN-PT Based Ceramics in Low Temperatures. Abstracts Book. In Proceedings of the 11th Russia-CIS-Baltic-Japan Symposium on Ferroelectricity, Ekaterinburg, Russia, 20–24 August 2012; Ural Federal University: Ekaterinburg, Russia, 2012; p. 74. [Google Scholar]
- Fang, B.J.; Ding, C.L.; Wu, J. Preparation of Pb(Mg1/3Nb2/3)O-3-PbTiO3 ceramics by reaction-sintering method and their electrical properties. Eur. Phys. J. Appl. Phys. 2012, 57, 30101. [Google Scholar] [CrossRef]
- Srimathy, B.; Jayavel, R.; Ganesamoorthy, S. Crystal growth of PZN-PT single crystals and critical issues for higher piezoelectric coefficient. Cryst. Res. Technol. 2012, 47, 523–529. [Google Scholar] [CrossRef]
- Shvartsman, V.V.; Lupascu, D.C. Lead-Free Relaxor Ferroelectrics. J. Am. Ceram. Soc. 2012, 95, 1–26. [Google Scholar] [CrossRef]
- Inaguma, Y.; Aimi, A.; Shirako, Yu.; Sakurai, D.; Mori, D.; Kojitani, H.; Akaogi, M.; Nakayama, M. High pressure synthesis, crystal structure and phase stability relations of a LiNbO3 type polar titanate ZnTiO3 and its reinforced polarity by the second-order Jahn-Teller effect. J. Am. Chem. Soc. 2014, 136, 2748–2756. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Han, P. Growth and Characterization on PMN-PT-Based Single Crystals. Crystals 2014, 4, 331–341. [Google Scholar] [CrossRef]
- Fourquet, L.; Le Bail, A.; Gillet, P.A. LiNbWO6: Crystal structure of its two allotropic forms. Mater. Res. Bull. 1988, 23, 1163–1170. [Google Scholar] [CrossRef]
- Wiegel, M.; Blasse, G.; Ouwerkerk, M. Bond-orbital calculations of the non-linear optical response of lithium niobate-related compounds. J. Phys. Condens. Matter. 1995, 7, 675–683. [Google Scholar] [CrossRef]
- Eun, C.O.; Alberto, G.; Min, O.K.; Lei, Z.; Shiv, H.P. Synthesis, structures second-harmonic generating, and ferroelectric properties of tungsten bronzes: A6M2M'8O30 (A = Sr2+, Ba2+, or Pb2+; M = Ti4+, Zr4+, or Hf4+; M' = Nb5+ or Ta5+). Chem. Mater. 2004, 16, 3616–3622. [Google Scholar]
- Zheng, L.; Wang, J.; Huo, X.; Wang, R.; Sang, S.; Li, S.; Zheng, P.; Cao, W. Temperature dependence of dielectric and electromechanical properties of (KNa)(NbTa)O3 single crystals and corresponding domain structure evolution. J. Appl. Phys. 2014, 116, 041105. [Google Scholar] [CrossRef] [PubMed]
- Fu, X.; Víllora, E.G.; Matsushita, Y.; Kitanaka, Y.; Noguchi, Y.; Miyayama, M.; Shimamura, K.; Ohashi, N. Temperature dependence of electrical resistivity, dielectric and piezoelectric properties of Ca3TaGa3−xAlxSi2O14 single crystals as a function of Al content. J. Alloys Comp. 2016, 687, 797–803. [Google Scholar] [CrossRef]
- Yu, F.; Lu, Q.; Zhang, S.; Wang, H.; Cheng, X.; Zhao, X. High-performance, high-temperature piezoelectric BiB3O6 crystals. J. Mater. Chem. 2015, C3, 329–338. [Google Scholar]
- Belik, A.A.; Rusakov, D.A.; Furubayashi, T.; Takayama-Muromachi, E. BiGaO3-based perovskites: A large family of polar materials. Chem. Mater. 2012, 24, 3056–3064. [Google Scholar] [CrossRef]
- Kaczkowski, J. Electronic structure, ferroelectric properties, and phase stability of BiGaO3 under high pressure from first principles. J. Mater. Sci. 2016, 51, 9761–9770. [Google Scholar] [CrossRef]
- Kumar, A.; Rai, R.C.; Podraza, N.J.; Denev, S.R.; Chu, Y.-H.; Martin, L.W.; Ihlefeld, J.; Neeg, T.; Schubert, T.H.; Schlom, D.G.; et al. Linear and nonlinear properties of BiFeO3. Appl. Phys. Lett. 2008, 92, 121915. [Google Scholar] [CrossRef]
- Ma, D.L.; Ren, M.-L.; Dou, J.-H.; Li, Z.Y. Giant Enhancement of second harmonic generation at photonic gap edges. Chin. Phys. Lett. 2010, 27, 114209. [Google Scholar]
- Lottermoser, T.; Meier, D.; Pisarev, R.V.; Fiebig, M. Giant coupling of second-harmonic generation to a multiferroic polarization. Phys. Rev. 2009, B80, 100101. [Google Scholar] [CrossRef]
- Heimann, R.B.; Hengst, M.; Rossberg, M. Giant optical rotation in piezoelectric crystals with calcium gallium germanate structure. Phys. Status Solidi A Appl. Mater. Sci. 2003, 195, 468–474. [Google Scholar]
- Fan, Z.; Xiao, J.; Liu, H.; Yang, P.; Ke, Q.; Ji, W.; Yao, K.; Ong, K.P.; Zeng, K.; Wang, J. Stable ferroelectric perovskite structure with giant axial ratio and polarization in epitaxial BiFe0.6Ga0.4O3 thin films. ACS Appl. Mater. Interfaces 2015, 7, 2648–2653. [Google Scholar] [CrossRef] [PubMed]
- Flach, S.; Gorbach, A. Discrete breathers: Advances in theory and applications. Phys. Rep. 2008, 467, 1–116. [Google Scholar] [CrossRef]
- Yushkin, N.P. Mechanical Properties of Minerals; Nauka: Leningrad, Russia, 1971. (In Russian) [Google Scholar]
- Marfunin, А.S. Introduction in Mineral Physics; Nedra: Мoscow, Russia, 1974. (In Russian) [Google Scholar]
- Feklichev, V.G. Diagnostic Constants of Minerals; Nedra: Мoscow, Russia, 1989. (In Russian) [Google Scholar]
- Marfunin, A.S. Advanced Mineralogy. In V.1. Composition, Structure and Properties of Mineral Matter; Concepts, Results, and Problems; Springer: Berlin, Germany, 1994; p. 550. [Google Scholar]
- Okhotin, A.S.; Borovikova, R.P.; Nechaeva, T.V.; Pushkarskiii, A.S. Thermal Conductivity of Solid State; Energo-atomizdat: Moscow, Russia, 1984. (In Russian) [Google Scholar]
- Samsonov, G.V.; Bulankova, T.G.; Burykina, A.L. Physical and Chemical Properties of Oxides; Metallurghiya: Moscow, Russia, 1969. (In Russian) [Google Scholar]
- Bohaty, L.; Haussuhl, S.; Liebertz, J.; Stahr, S. Single crystal growth and physical property of cubic Zn4O(BO2)3. Z. Krist. 1982, 164, 157–158. [Google Scholar] [CrossRef]
- Gubina, Yu.K.; Belokoneva, E.L. The electronic density and chemical bond in the ultramarine crystals. Rep. Acad. Sci. 2001, 376, 662–666. (In Russian) [Google Scholar]
- Jiang, X.; Molokeev, M.S.; Gong, P.; Wang, W.; Wang, S.; Wu, S.; Wang, Y.; Huang, R.; Li, R.; Wu, Y.; et al. Near zero thermal expansion and high ultraviolet transparency in borate crystal of Zn4B6O13. Adv. Mater. 2016, 28, 7936–7940. [Google Scholar] [CrossRef] [PubMed]
- Korotkov, A.S. Correlation of optical properties of acentric crystals with chemical composition. Opt. Commun. 2013, 294, 218–222. [Google Scholar] [CrossRef]
- Hautier, G.; Fisher, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding nature’s missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 2010, 22, 3762–3767. [Google Scholar] [CrossRef]
- Song, J.L.; Hu, C.-L.; Xu, X. A facile synthetic route to a new SHG material with two types of parallel pi-conjugated planar triangular units. Angew. Chem. Int. Ed. 2015, 54, 3679–3682. [Google Scholar] [CrossRef] [PubMed]
- Ye, N. Structure design and crystal growth of UV nonlinear borate. Mater. Struct. Bond. 2012, 144, 181–222. [Google Scholar]
- Belokoneva, E.L.; Stefanovich, S.Y.; Borisova, T.A.; Dimitrova, O.V.; Vochenova, N.N.; Zubkova, N.V. Structure and nonlinear optical properties of the family of lead and barium nonaborates with zeolite-like framework. Crystallogr. Rep. 2009, 54, 814–821. [Google Scholar] [CrossRef]
- Abudoureheman, M.; Wang, L.; Zhang, X.; Yu, H.; Yang, Z.; Lei, C.; Han, J.; Pan, S. Pb7O(OH)3(BO3)CO3: First mixed borate and carbonate nonlinear optical material exhibiting large second harmonic generation response. Inorg. Chem. 2015, 54, 4138–4142. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Cheng, J.-W.; He, C.; Yang, G.-Y. An acentric calcium borate Ca2[B5O9]·(OH)·H2O. Synthesis, structure, and nonliner optical property. Inorg. Chem. 2014, 53, 11757–11763. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Pan, S.; Chang, L.; Hu, J.; Yu, Y. UV nonlinear optical crystal Ba−2[B6O9(OH)4].Featuring unique chiral layers with a new B18O42 circle based on BO3 and BO4 units. Inorg. Chem. 2012, 51, 1852–1858. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Hu, C.-L.; Xu, X.; Mao, J.-G. Series of SHG Materials Based on Lanthanide Borate–Acetate Mixed Anion Compounds. Inorg. Chem. 2015, 54, 7516–7523. [Google Scholar] [CrossRef] [PubMed]
- Barbier, J.; Cranswick, L.M.D. The non-centrosymmetric borate oxides, MBi2B2O7 (M = Ca, Sr). J. Solid State Chem. 2006, 179, 3932–3938. [Google Scholar] [CrossRef]
- Zhang, F.; Qun, J.; Zhang, F.; Pan, S.; Yang, Z.; Yan, J.; Yan, S. Sr4B10O18(OH)2 center dot 2H2O: A new UV nonlinear optical material with a [B10O23]16 building block. J. Mater. C 2013, 23, 667–674. [Google Scholar] [CrossRef]
- Belokoneva, E.L.; Topnikova, A.P.; Stefanovich, S.Yu; Dobretsova, E.A.; Volkov, A.S.; Dimitrova, O.V. New isoformula borates with similar structures and different properties–Acentric nonlinear optical KGd[B6O10(OH)2] and centrosymmetric KHo[B6O10(OH)2]. Solid State Sci. 2015, 46, 43–48. [Google Scholar] [CrossRef]
- Dong, L.; Pan, S.; Wang, Y. Synthesis and structural characterization of a new rubidium borosulfate, Rb5BS4O16. Mater. Res. Bull. 2015, 63, 93–98. [Google Scholar] [CrossRef]
- Becker, P. A contribution to borate crystal chemistry: Rules for the occurrence of polyborate anion types. Z. Crystallogr. 2001, 216, 523–533. [Google Scholar] [CrossRef]
- Frölich, R. Crystal structure of the low temperature form of BaB2O4. Z. Krist. 1984, 168, 109–112. [Google Scholar] [CrossRef]
- Chen, C.; Wu, B.; Jiang, A.; You, G. A new type ultraviolet SHG crystal BaB2O4. Sci. Sinica 1985, B38, 235–243. [Google Scholar]
- Jiang, A.; Cheng, F.; Lin, Q.; Cheng, G.; Zheng, Y. Flux growth of large single crystals of low temperature phase of barium metaborate. J. Cryst. Growth 1986, 79, 963–969. [Google Scholar]
- Ito, K.; Marumo, F.; Kuvano, Y. β-baium borate single crystal growth by a direct Czochralski method. J. Cryst. Growth 1990, 106, 728–731. [Google Scholar] [CrossRef]
- Kokh, A.E.; Bekker, T.B.; Vlezko, V.A.; Kokh, K.A. Development of β-BaB2O4 crystal growth technique in the heald field of thrre fold axis symmetry. J. Cryst. Growth 2011, 318, 602–605. [Google Scholar] [CrossRef]
- Wang, X.; Yan, X.; Luo, S.; Chen, C.T. Flux growth of KBe2BO3F2 crystals by localized spontaneous nucleation. J. Cryst. Growth 1995, 318, 610–612. [Google Scholar] [CrossRef]
- Mei, L.F.; Huang, X.; Wang, Y.B.; Wu, B.C.; Chen, C.T. Crystal structure of KBe2BO3F2. Z. Krist. New Cryst. Struct. 1995, 210, 93–95. [Google Scholar] [CrossRef]
- Wu, B.; Tang, D.; Ye, N.; Chen, C.T. Linear and nonlinear optical properties of the KBe2BO3F2 (KBBF) crystal. Opt. Mater. 1996, 5, 105–109. [Google Scholar] [CrossRef]
- Chen, C.T.; Wang, E.; Wu, B.; Wu, K.; Zeng, W.; Yu, L. Design and synthesis of an ultraviolet-transparent nonlinear optical crystal Sr2Be2B2O7 (SBBO). Nature 1995, 373, 322–324. [Google Scholar] [CrossRef]
- Hu, Z.G.; Yoshimura, M.; Muramatsu, K.; Mori, Y.; Sasaki, T. A new nonlinear optical crystals BaAlBO3F2 (BABF). Jpn. J. Appl. Phys. 2002, 41, L1131–L1133. [Google Scholar] [CrossRef]
- Yeliseyev, A.P.; Solntsev, V.P.; Jiang, X.; Bekker, T.B.; Lin, Z.; Fedorov, P.P. Electronic structure, magnetic and optical properties of the Ba7(BO3)4-xF2+3x crystals. J. Solid State Chem. 2015, 229, 358–365. [Google Scholar] [CrossRef]
- Chen, C.T.; Luo, S.Y.; Wang, X.Y.; Wen, X.H.; Wu, H.X.; Zhang, X.; Xu, Z.Y. Deep UV nonlinear optical crystal RbBe2BO3F2 (KBBF). J. Opt. Soc. Am. B 2009, 26, 1519–1525. [Google Scholar] [CrossRef]
- Wang, Y.; Pan, S. Recent development of metal borate halides: Crystal chemistry and application in second order NLO materials. Coord. Chem. Rev. 2016, 323, 15–35. [Google Scholar] [CrossRef]
- Yu, N.; Wang, S.; Ye, N.; Liang, F.; Lin, Z.; Luo, M.; Poeppelmeier, K.R. A deep ultra-violet nonlinear optical crystal: Strontium beryllium borate fluoride with planar Be(O/F)3 groups. Chem. Mater. 2016, 28, 4563–4571. [Google Scholar] [CrossRef]
- Bian, Q.; Yang, Z.; Wang, Y.; Cao, C.; Pan, S. Predicting global minimum in complex beryllium borate system for deep-ultraviolet functional optical application. Sci. Rep. 2016, 6, 34839. [Google Scholar] [CrossRef] [PubMed]
- Bashir, D.; Zhang, B.; Lei, B.-H.; Yang, Z.; Lee, M.-H.; Pan, S. DFT based theoretical study about the contribution of fluorine to nonlinear optical properties in borate fluoride crystals. Cryst. Growth Des. 2016, 16, 5067–5073. [Google Scholar] [CrossRef]
- Lin, Y.; Hu, C.-L.; Mao, J.-G. K2Pb3(CO3)3F2 and KCdCO3F: Novel Fluoride Carbonates with Layered and 3D Framework Structures. Inorg. Chem. 2015, 54, 10407–10414. [Google Scholar] [CrossRef] [PubMed]
- Luo, M.; Lin, C.; Zou, G.; Ye, N.; Cheng, W. Sodium rare earth carbonates with shorite structure and large second harmonic generation response. CrystEngComm 2014, 16, 4414–4421. [Google Scholar] [CrossRef]
- Yeung, H.H.-M.; Kosa, M.; Parrinello, M.; Cheetham, A.K. Chiral, racemic, and meso-lithium tartrate framework polymorphs: A detailed structural analysis. Cryst. Growth Des. 2013, 13, 3705–3715. [Google Scholar] [CrossRef]
- Weil, M. Crystal structure of lead(II) tartrate: A redetermination. Acta Crystallogr. Sect. E Crystallogr. Commun. 2015, E71, 82–89. [Google Scholar] [CrossRef] [PubMed]
- Cortese, A.J.; Wilkins, B.; Smith, M.D. Crystal Growth of Four Oxovanadium (IV) Tartrates Prepared via a Mild Two-Step Hydrothermal method: Observation of Spin-Dimer Behavior and Second Harmonic generation. Inorg. Chem. 2015, 54, 4011–4020. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Aguirre, L.C.; Pato-Doldan, B.; Stroppa, A.; Yaňez-Vilar, S.; Bayarjargal, L.; Winkler, B.; Castro-García, S.; Mira, J.; Sánchez-Anújar, M.; Señarís-Rodríguez, M.A. Room-temperature polar order in [NH4][Cd(HCOO)3]-a hybrid inorganic−organic compound with a unique perovskite architecture. Inorg. Chem. 2015, 54, 2109–2116. [Google Scholar] [CrossRef] [PubMed]
- Essid, M.; Rzaigui, M.; Marouani, H. Synthesis and physico-chemical studies of a new noncentrosymmetric Bis[N-(2-hydroxyethyl)piperazine-1,4-tetrakis(hydrogen oxalate) trihydrate; diium] [C6H16N2O]2 (HC2O4)4 H2O [C6H16N2O]2(HC2O4)4∙H2O. Inorg. Chem. 2015, 54, 2109–2116. [Google Scholar]
- Norby, P.; Dinnebier, R.; Fitch, A.N. Decomposition of silver carbonate; the crystal structure of two high-temperature modifications of Ag2CO3. Inorg. Chem. 2002, 41, 3628–3637. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Ma, Z.; Sa, R.; Zhang, Y.; Wu, K. A promising lead-free fluoride carbonate SHG material designed from a theoretical perspective. Dalton Trans. 2017, 46, 2635–2642. [Google Scholar] [CrossRef] [PubMed]
- Krivovichev, S.V.; Burns, P.C. Crystal chemistry of basic lead carbonates. II. Crystal structure of synthetic ‘plumbonacrite’. Mineral. Mag. 2000, 64, 1069–1075. [Google Scholar] [CrossRef]
- Hassan, I.; Buse, P.R. The origin of the superstructure and modulation in cancrinite. Can. Mineral. 1992, 30, 49–59. [Google Scholar]
- Schmidbaur, H.; Kumberger, О. Preparative, X-ray, and NMR studies of the interaction of beryllium with salicylic and o-cresotic acid: Crystal structures of (NH4)2[Be(C6H4OCO2)2] 2.25 H2O and Na3[Be(C7H6OCO2)(OH)(CO3) Be(C7H6OCO2)]∙8H2O. Chem. Ber. 1993, 126, 3–9. [Google Scholar] [CrossRef]
- Greaves, C.; Blower, S.K. Structural relationships between Bi2O2CO3 and β-Bi2O3. Mater. Res. Bull. 1988, 23, 1001–1008. [Google Scholar] [CrossRef]
- Kutlu, I.; Kalz, H.J.; Wartchow, R. Potassium lanthanoid carbonates, KM(CO3)2)(M = Nd, Gd, Dy, Ho Yb). Z. Anorg. Allg. Chem. 1997, 623, 1753–1758. [Google Scholar] [CrossRef]
- Labutina, M.L.; Marychev, M.O.; Portnov, V.N.; Somov, N.V.; Chuprunov, E.V. Second_Order Nonlinear Susceptibilities of the Crystals of Some Metal Tartrates. Crystallogr. Rep. 2011, 56, 72–74. (In Russian) [Google Scholar] [CrossRef]
- Zhang, G.; Liu, T.; Zhu, T.; Qin, J.; Wu, Y.; Chen, C. SbF3: A new second-order nonlinear optical material. Opt. Mater. 2008, 31, 110–113. [Google Scholar] [CrossRef]
- Wright, A.C. My borate life: An enigmatic journey. Int. J. Appl. Glass Sci. 2015, 145, 45–63. [Google Scholar] [CrossRef]
- Bengisu, M. Borate glasses for scientific and industrial application: A review. J. Mater. Sci. 2016, 51, 2199–2242. [Google Scholar] [CrossRef]
- Taziev, R.M. SAW excitation properties on YX-cut of CNGS and SNGS single crystals. IEEE Trans. Ultrason. Ferroelect. Freq. Control 2010, 57, 2370–2371. [Google Scholar] [CrossRef] [PubMed]
- Gazhulina, A.P.; Marychev, M.O. Pseudosymmetric features and nonlinear optical properties of potassium titanyl phosphate crystals. Cryst. Struct. Theory Appl. 2013, 2, 109–119. [Google Scholar] [CrossRef]
- Gazhulina, A.P.; Marychev, M.O. Structural electronic and nonlinear optical properties of B3 and B20 compounds: A first principles investigation within the LDA, GGA, and modified Becke Johnson exchange potential plus LDA. J. Alloy Comp. 2015, 623, 413–437. [Google Scholar] [CrossRef]
- Gazhulina, A.P.; Marychev, M.O. Pseudosymmetric features of non-centrosymmetric AB type crystals. J. Solid State Chem. 2016, 239, 170–177. [Google Scholar] [CrossRef]
- Arkhipov, S.G.; Boldyreva, E.V. Algorithm of existence detection and reproducible receiving of the single salt crystals and mixed crystals of amino acids, useful to roentgen-structure and CR-spectroscopy experimental studies. J. Struct. Chem. 2014, 55, 778–783. [Google Scholar] [CrossRef]
- Konstantinova, A.F.; Golovina, T.G.; Konstantinov, К.К. The manifestation of the optical activity in different substances. Crystallography 2014, 59, 509–528. [Google Scholar]
- Shvartsev, S.L. How the complexities are formed. Vestnik RAN 2014, 84, 618–628. [Google Scholar]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kidyarov, B.I. Comparative Interrelationship of the Structural, Nonlinear-Optical and Other Acentric Properties for Oxide, Borate and Carbonate Crystals. Crystals 2017, 7, 109. https://doi.org/10.3390/cryst7040109
Kidyarov BI. Comparative Interrelationship of the Structural, Nonlinear-Optical and Other Acentric Properties for Oxide, Borate and Carbonate Crystals. Crystals. 2017; 7(4):109. https://doi.org/10.3390/cryst7040109
Chicago/Turabian StyleKidyarov, Boris I. 2017. "Comparative Interrelationship of the Structural, Nonlinear-Optical and Other Acentric Properties for Oxide, Borate and Carbonate Crystals" Crystals 7, no. 4: 109. https://doi.org/10.3390/cryst7040109
APA StyleKidyarov, B. I. (2017). Comparative Interrelationship of the Structural, Nonlinear-Optical and Other Acentric Properties for Oxide, Borate and Carbonate Crystals. Crystals, 7(4), 109. https://doi.org/10.3390/cryst7040109




