Quantum Phenomena Emerging Near a Ferroelectric Critical Point in a Donor–Acceptor Organic Charge-Transfer Complex
Abstract
:1. Introduction
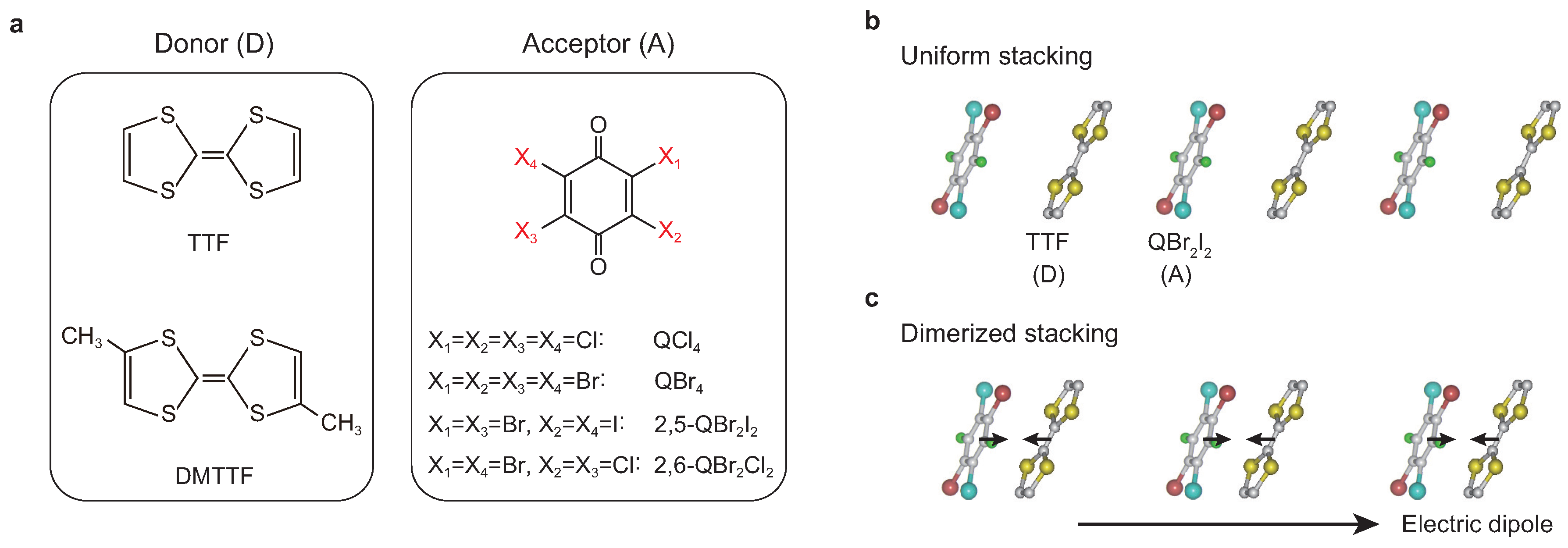
2. Crystal Structures
3. Quantum Effects on Thermo-Equilibrium Properties Near the Ferroelectric QCP
3.1. Phase Diagram
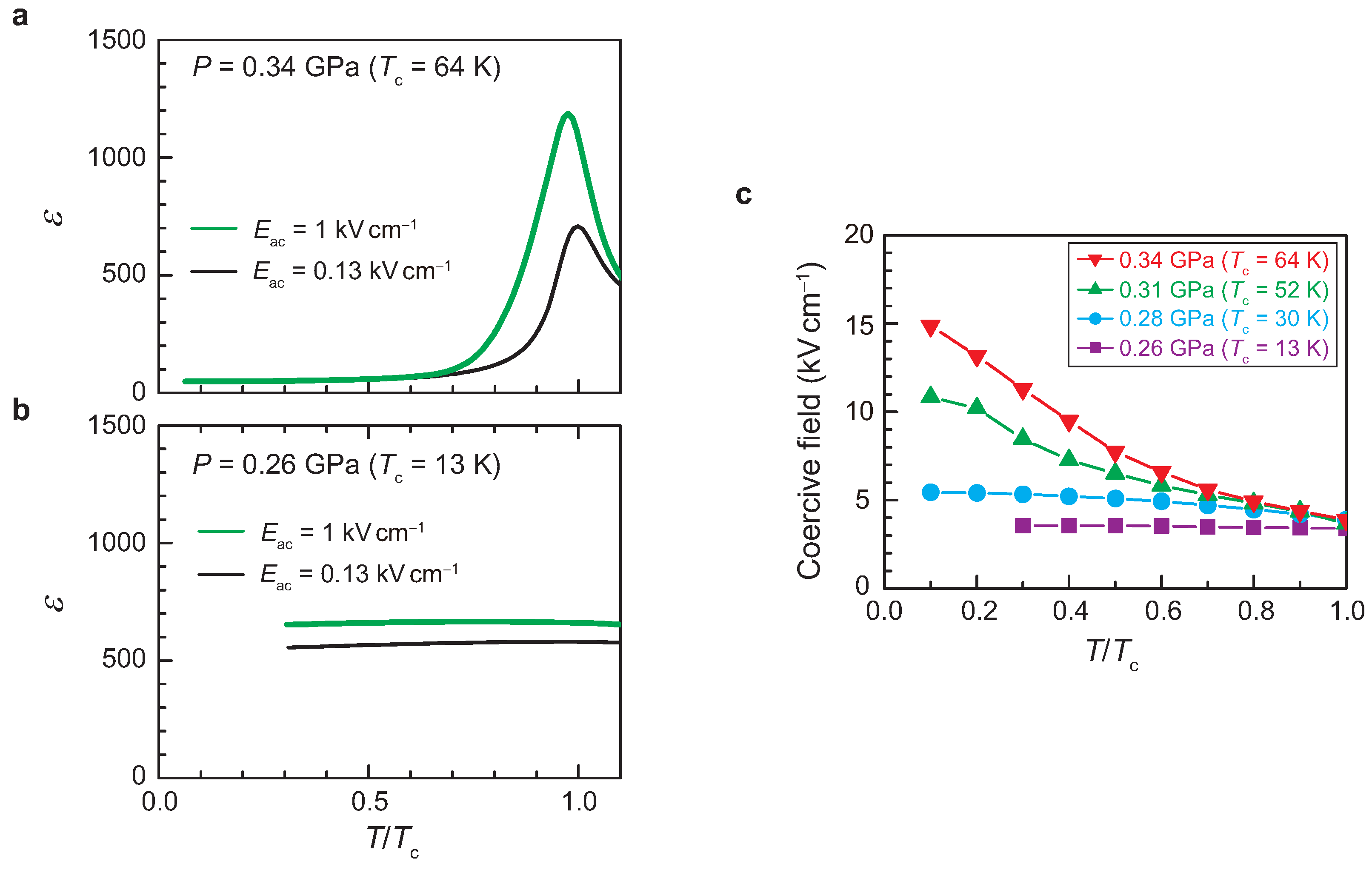
3.2. Quantum Criticality Seen in Order-Parameter-Related Quantities
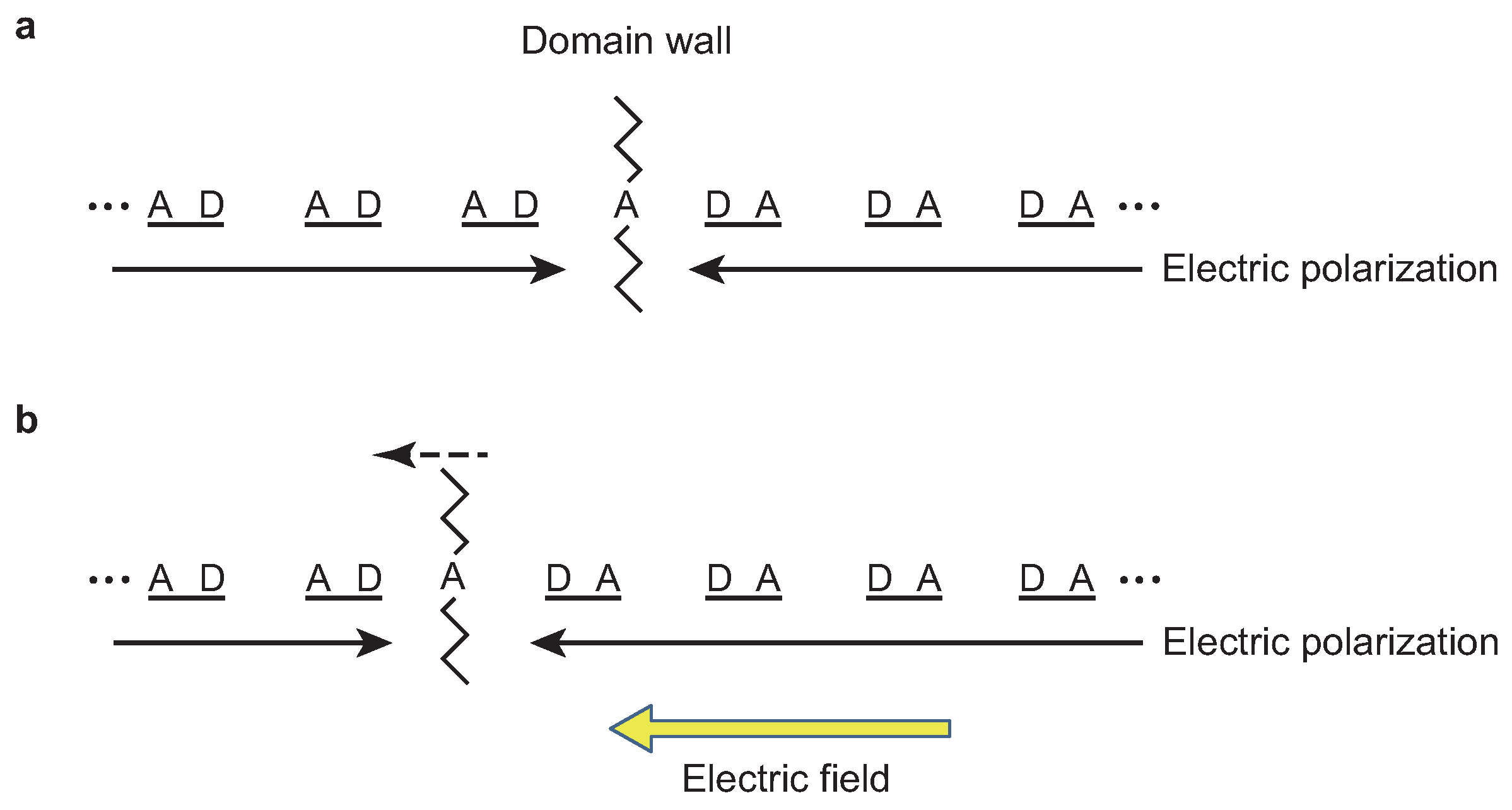
4. Quantum Effects on the Kinetics of Ferroelectric Domain Walls Near the Ferroelectric QCP
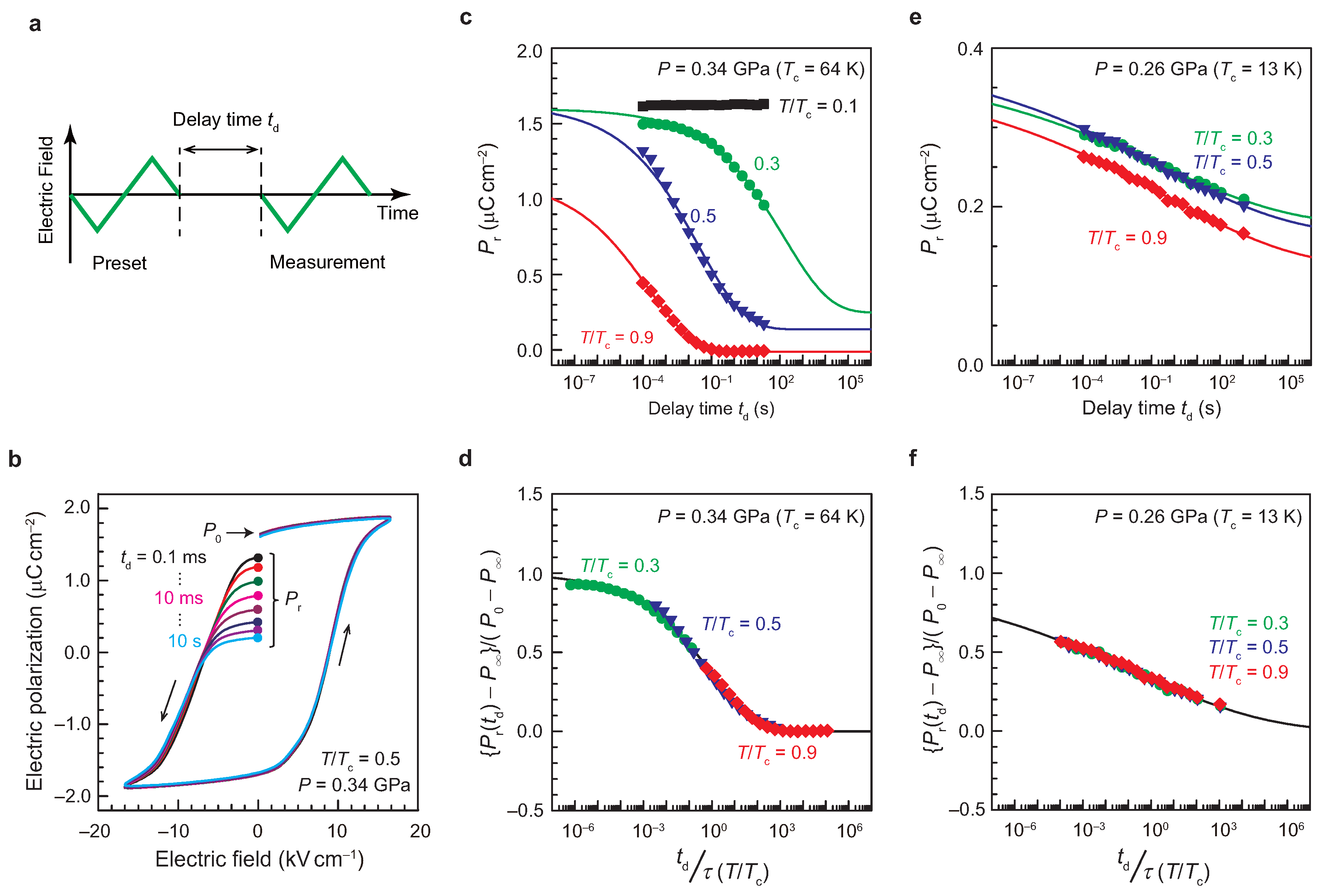
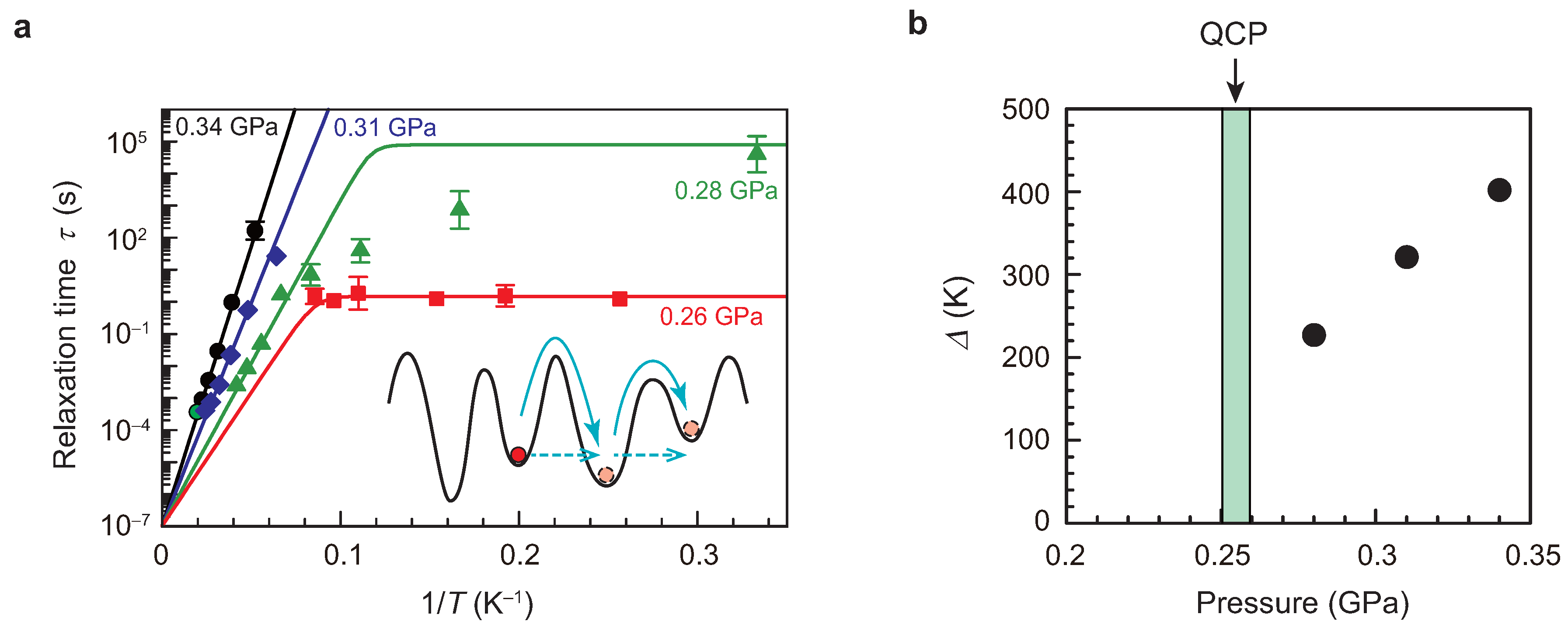
4.1. Athermal Creep Motion of Domain Walls Near the QCP
4.2. Effective Mass of the Ferroelectric Domain Wall Near the QCP
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Sachdev, S. Quantum Phase Transitions; Cambridge Univ. Press: Cambridge, UK, 1999. [Google Scholar]
- Coleman, P.; Schofield, A.J. Quantum criticality. Nature 2005, 433, 226–229. [Google Scholar] [CrossRef] [PubMed]
- Sachdev, S. Quantum criticality in heavy-fermion metals. Nat. Phys. 2008, 4, 173–185. [Google Scholar] [CrossRef]
- Gegenwart, P.; Si, Q.; Steglich, F. Quantum criticality in heavy-fermion metals. Nat. Phys. 2008, 4, 186–197. [Google Scholar] [CrossRef]
- Löhneysen, H.V.; Pietrus, T.; Portisch, G.; Schlager, H.G.; Schröder, A.; Sieck, M.; Trappmann, T. Non-Fermi-liquid behavior in a heavy-fermion alloy at a magnetic instability. Phys. Rev. Lett. 1994, 72, 3262–3265. [Google Scholar] [CrossRef] [PubMed]
- Custers, J.; Gegenwart, P.; Wilhelm, H.; Neumaier, K.; Tokiwa, Y.; Trovarelli, O.; Geibel, C.; Steglich, F.; Pépin, C.; Coleman, P. The break-up of heavy electrons at a quantum critical point. Nature 2003, 424, 524–527. [Google Scholar] [CrossRef] [PubMed]
- Mathur, N.D.; Grosche, F.M.; Julian, S.R.; Walker, I.R.; Freye, D.M.; Haselwimmer, R.K.W.; Lonzarich, G.G. Magnetically mediated superconductivity in heavy fermion compounds. Nature 1998, 394, 39–43. [Google Scholar]
- Park, T.; Ronning, F.; Yuan, H.Q.; Salamon, M.B.; Movshovich, R.; Sarrao, J.L.; Thompson, J.D. Hidden magnetism and quantum criticality in the heavy fermion superconductor CeRhIn5. Nature 2006, 440, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Löhneysen, H.V.; Rosch, A.; Vojta, M.; Wölfle, P. Fermi-liquid instabilities at magnetic quantum phase transitions. Rev. Mod. Phys. 2007, 79, 1015–1075. [Google Scholar] [CrossRef]
- Rowley, S.E.; Spalek, L.J.; Smith, R.P.; Dean, M.P.M.; Itoh, M.; Scott, J.F.; Lonzarich, G.G.; Saxena, S.S. Ferroelectric quantum criticality. Nat. Phys. 2014, 10, 367–372. [Google Scholar] [CrossRef]
- Rowley, S.E.; Hadjimichael, M.; Ali, M.N.; Durmaz, Y.C.; Lashley, J.C.; Cava, R.J.; Scott, J.F. Quantum Criticality in a uniaxial organic ferroelectric. J. Phys. Condens. Matter 2015, 27, 395901. [Google Scholar] [CrossRef] [PubMed]
- Rowley, S.E.; Chai, Y.-S.; Shen, S.-P.; Sun, Y.; Jones, A.T.; Watts, B.E.; Scott, J.F. Uniaxial ferroelectric quantum criticality in multiferroic hexaferrites BaFe12O19 and SrFe12O19. Sci. Rep. 2016, 6, 25724. [Google Scholar] [CrossRef] [PubMed]
- Morf, R.; Scheider, T.; Stoll, E. Nonuniversal critical behavior and its suppression by quantum fluctuations. Phys. Rev. B 1977, 16, 462–469. [Google Scholar] [CrossRef]
- Roussev, R.; Millis, A.J. Theory of the quantum paraelectric-ferroelectric transition. Phys. Rev. B 2003, 67, 014105. [Google Scholar] [CrossRef]
- Das, N.; Mishra, S.G. Fluctuations and criticality in quantum paraelectrics. J. Phys. Condens. Matter 2009, 21, 095901. [Google Scholar] [CrossRef] [PubMed]
- Pálová, L.; Chandra, P.; Coleman, P. Quantum critical paraelectrics and the Casimir effect in time. Phys. Rev. B 2009, 79, 075101. [Google Scholar] [CrossRef]
- Belitz, D.; Kirkpatrick, T.R.; Vojta, T. How generic scale invariance influences quantum and classical phase transitions. Rev. Mod. Phys. 2005, 77, 579–632. [Google Scholar] [CrossRef]
- Grigera, S.A.; Gegenwart, P.; Borzi, R.A.; Weickert, F.; Schofield, A.J.; Perry, R.S.; Tayama, T.; Sakakibara, T.; Maeno, Y.; Green, A.G.; Mackenzie, A.P. Disorder-Sensitive Phase Formation Linked to Metamagnetic Quantum Criticality. Science 2004, 306, 1154–1157. [Google Scholar] [CrossRef] [PubMed]
- Lester, C.; Ramos, S.; Perry, R.S.; Croft, T.P.; Bewley, R.I.; Guidi, T.; Manuel, P.; Khalyavin, D.D.; Forgan, E.M.; Hayden, S.M. Field-tunable spin-density-wave phases in Sr3Ru2O7. Nat. Mat. 2015, 14, 373–378. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Minami, N.; Kagawa, F.; Tokura, Y. Quantum ferroelectricity in charge-transfer complex crystals. Nat. Commun. 2016, 6, 16075. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Minami, N.; Horiuchi, S.; Tokura, Y. Athermal domain-wall creep near a ferroelectric quantum critical point. Nat. Commun. 2015, 6, 7469. [Google Scholar] [CrossRef] [PubMed]
- Horiuchi, S.; Okimoto, Y.; Kumai, R.; Tokura, Y. Quantum Phase Transition in Organic Charge-Transfer Complexes. Science 2003, 299, 229–232. [Google Scholar] [CrossRef] [PubMed]
- Nagaosa, N. Theory of Neutral-Ionic Transition in Organic Crystals. III. Effec of the Electron-Lattice Interaction. J. Phys. Soc. Jpn. 1986, 55, 2754–2764. [Google Scholar] [CrossRef]
- Soos, Z.G.; Bewick, S.A.; Peri, A.; Painelli, A. Dielectric response of modified Hubbard models with neutral-ionic and Peierls transitions. J. Chem. Phys. 2004, 120, 6712–6720. [Google Scholar] [CrossRef] [PubMed]
- Soos, Z.G.; Painelli, A. Metastable domains and potential energy surfaces in organic charge-transfer salts with neutral-ionic phase transitions. Phys. Rev. B 2007, 75, 155119. [Google Scholar] [CrossRef]
- Kagawa, F.; Horiuchi, S.; Tokunaga, M.; Fujioka, J.; Tokura, Y. Ferroelectricity in a one-dimensional organic quantum magnet. Nat. Phys. 2010, 6, 169–172. [Google Scholar] [CrossRef]
- Torrance, J.B.; Girlando, A.; Mayerle, J.J.; Crowley, J.I.; Lee, V.Y.; Batail, P.; LaPlaca, S.J. Anomalous Nature of Neutral-to-Ionic Phase Transition in Tetrathiafulvalene-Chloranil. Phys. Rev. Lett. 1981, 47, 1747–1750. [Google Scholar] [CrossRef]
- Kobayashi, K.; Horiuchi, S.; Kumai, R.; Kagawa, F.; Murakami, Y.; Tokura, Y. Electronic Ferroelectricity in a Molecular Crystal with Large Polarization Directing Antiparallel to Ionic Displacement. Phys. Rev. Lett. 2012, 108, 237601. [Google Scholar] [CrossRef] [PubMed]
- Girlando, A.; Pecile, C.; Torrance, J.B. A key to understanding ionic mixed stacked organic-solids—Tetrathiafulvalene-bromanil (TTF-BA). Solid State Commun. 1985, 54, 753–759. [Google Scholar] [CrossRef]
- García, P.; Dahaoui, S.; Fertey, P.; Wenger, E.; Lecomte, C. Crystallographic investigation of temperature-induced phase transition of the tetrathiafulvalene-p-bromanil, TTF-BA charge transfer complex. Phys. Rev. B 2005, 72, 104115. [Google Scholar] [CrossRef]
- Lemée-Cailleau, M.H.; Le Cointe, M.; Cailleau, H.; Luty, T.; Moussa, F.; Roos, J.; Brinkmann, D.; Toudic, B.; Ayache, C.; Karl, N. Thermodynamics of the Neutral-to-Ionic Transition as Condensation and Crystallization of Charge-Transfer Excitations. Phys. Rev. Lett. 1997, 79, 1690–1693. [Google Scholar] [CrossRef]
- Sadohara, R.; Matsuzaki, S. Neutral-ionic transition of charge transfer complexes of TTF and tetrahalo-p-benzoquinones. Mol. Cryst. Liq. Cryst. 1997, 296, 269–280. [Google Scholar] [CrossRef]
- Matsuzaki, S.; Hiejima, T.; Sano, M. Pressure-induced neutral-ionic phase transition of a tetrathiafulvalene-iodanil crystal. Bull. Chem. Soc. Jpn. 1991, 64, 2052–2057. [Google Scholar] [CrossRef]
- Horiuchi, S.; Kobayashi, K.; Kumai, R.; Ishibashi, S. Ionic versus Electronic Ferroelectricity in Donor-Acceptro Molecular Sequences. Chem. Lett. 2014, 43, 26–35. [Google Scholar] [CrossRef]
- Barrett, J.H. Dielectric constant in perovskite type crystals. Phys. Rev. 1952, 86, 118–120. [Google Scholar] [CrossRef]
- Miller, R.C.; Savage, A. Velocity of Sidewise 180 Domain-Wall Motion in BaTiO3 as a Function of Applied Electric Field. Phys. Rev. 1958, 112, 755–762. [Google Scholar] [CrossRef]
- Tybell, T.; Paruch, P.; Giamarchi, T.; Triscone, J.-M. Domain Wall Creep in Epitaxial Ferroelectric Pb(Zr0.2Ti0.8)O3 Thin Films. Phys. Rev. Lett. 2002, 89, 097601. [Google Scholar] [CrossRef] [PubMed]
- Jo, J.Y.; Yang, S.M.; Kim, T.H.; Lee, H.N.; Yoon, J.-G.; Park, S.; Jo, Y.; Jung, M.H.; Noh, T.W. Nonlinear Dynamics of Domain-Wall Propagation in Epitaxial Ferroelectric Thin Films. Phys. Rev. Lett. 2009, 102, 045701. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.L.; Tagantsev, A.K.; Damjanovic, D.; Setter, N. Giant domain wall contribution to the dielectric susceptibility in BaTiO3 single crystals. Appl. Phys. Lett. 2007, 91, 062905. [Google Scholar] [CrossRef]
- Shur, V.Y.; Rumyantsev, E.L.; Nikolaeva, E.V.; Shishkin, E.I. Formation and evolution of charged domain walls in congruent lithium niobate. Appl. Phys. Lett. 2000, 77, 3636–3638. [Google Scholar] [CrossRef]
- Balke, N.; Gajek, H.; Tagantsev, S.K.; Martin, L.W.; Chu, Y.-H.; Ramesh, R.; Kalinin, S.V. Direct Observation of Capacitor Switching Using Planar Electrodes. Adv. Funct. Mater. 2010, 20, 3466–3475. [Google Scholar] [CrossRef]
- Kagawa, F.; Horiuchi, S.; Minami, N.; Ishibashi, S.; Kobayashi, K.; Kumai, R.; Murakami, Y.; Tokura, Y. Polarization Switching Ability Dependent on Multidomain Topology in a Uniaxial Organic Ferroelectric. Nano Lett. 2014, 14, 239–243. [Google Scholar] [CrossRef] [PubMed]
- Chauve, P.; Giamarchi, T.; Le Doussal, P. Creep and depinning in disordered media. Phys. Rev. B 2000, 62, 6241–6267. [Google Scholar] [CrossRef]
- Shin, Y.-H.; Grinberg, I.; Chen, I.-W.; Rappe, A.M. Nucleation and growth mechanism of ferroelectric domain-wall motion. Nature 2007, 449, 881–884. [Google Scholar] [CrossRef] [PubMed]
- Kolton, A.B.; Rosso, A.; Giamarchi, T.; Krauth, W. Creep dynamics of elastic manifolds via exact transition pathways. Phys. Rev. B 2009, 79, 184207. [Google Scholar] [CrossRef]
- Kleemann, W. Universal Domain Wall Dynamics in Disordered Ferroic Materials. Annu. Rev. Mater. Res. 2007, 37, 415–448. [Google Scholar] [CrossRef]
- Braun, T.; Kleemann, W.; Dec, J.; Thomas, P.A. Creep and Relaxation Dynamics of Domain Walls in Periodically Poled KTiOPO4. Phys. Rev. Lett. 2005, 94, 117601. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Horiuchi, S.; Matsui, H.; Kumai, R.; Onose, Y.; Hasegawa, T.; Tokura, Y. Electric-Field Control of Solitons in a Ferroelectric Organic Charge-Transfer Salt. Phys. Rev. Lett. 2010, 104, 227602. [Google Scholar] [CrossRef] [PubMed]
- Kagawa, F.; Hatahara, K.; Horiuchi, S.; Tokura, Y. Domain-wall dynamics coupled to proton motion in a hydrogen-bonded organic ferroelectric. Phys. Rev. B 2012, 85, 220101. [Google Scholar] [CrossRef]
- Hemberger, J.; Lunkenheimer, P.; Viana, R.; Böhmer, R.; Loidl, A. Electric-field-dependent dielectric constant and nonlinear susceptibility in SrTiO3. Phys. Rev. B 1995, 52, 13159–13162. [Google Scholar] [CrossRef]
- Brooke, J.; Rosenbaum, T.F.; Aeppli, G. Tunable quantum tunneling of magnetic domain walls. Nature 2001, 413, 610–613. [Google Scholar] [CrossRef] [PubMed]
- Shpyrko, O.G.; Isaacs, E.D.; Logan, J.M.; Feng, Y.; Aeppli, G.; Jaramillo, R.; Kim, H.C.; Rosenbaum, T.F.; Zschack, P.; Sprung, M.; Narayanan, S.; Sandy, A.R. Direct measurement of antiferromagnetic domain fluctuations. Nature 2007, 447, 68–71. [Google Scholar] [CrossRef] [PubMed]
- Mehta, R.R.; Silverman, B.D.; Jacobs, J.T. Depolarization fields in thin ferroelectric films. J. Appl. Phys. 1973, 44, 3379–3385. [Google Scholar] [CrossRef]
- Benedetto, J.M.; Moore, R.A.; McLean, F.B. Effects of operating conditions on the fast-decay component of the retained polarization in lead zirconate titanate thin films. J. Appl. Phys. 1994, 75, 460–466. [Google Scholar] [CrossRef]
- Clemens, J.M.; Hochstrasser, R.M.; Trommsdorff, H.P. Direct studies of proton tunneling in hydrogen bonded mixed molecular crystals by optical excitation. J. Chem. Phys. 1984, 80, 1744–1753. [Google Scholar] [CrossRef]
- Neumann, M.; Brougham, D.F.; McGloin, C.J.; Johnson, M.R.; Horsewill, A.J.; Trommsdorff, H.P. Proton tunneling in benzoic acid crystals at intermediate temperatures: Nuclear magnetic resonance and neutron scattering studies. J. Chem. Phys. 1998, 109, 7300–7311. [Google Scholar] [CrossRef]
- Champagne, B.; Deumens, E.; Öhrn, Y. Vibrations and soliton dynamics of positively charged polyacetylene chains. J. Chem. Phys. 1997, 107, 5433–5444. [Google Scholar] [CrossRef]
- Heeger, A.J.; Kivelson, S.; Schrieffer, J.R.; Su, W.-P. Solitons in conducting polymers. Rev. Mod. Phys. 1988, 60, 781–850. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kagawa, F.; Horiuchi, S.; Tokura, Y. Quantum Phenomena Emerging Near a Ferroelectric Critical Point in a Donor–Acceptor Organic Charge-Transfer Complex. Crystals 2017, 7, 106. https://doi.org/10.3390/cryst7040106
Kagawa F, Horiuchi S, Tokura Y. Quantum Phenomena Emerging Near a Ferroelectric Critical Point in a Donor–Acceptor Organic Charge-Transfer Complex. Crystals. 2017; 7(4):106. https://doi.org/10.3390/cryst7040106
Chicago/Turabian StyleKagawa, Fumitaka, Sachio Horiuchi, and Yoshinori Tokura. 2017. "Quantum Phenomena Emerging Near a Ferroelectric Critical Point in a Donor–Acceptor Organic Charge-Transfer Complex" Crystals 7, no. 4: 106. https://doi.org/10.3390/cryst7040106
APA StyleKagawa, F., Horiuchi, S., & Tokura, Y. (2017). Quantum Phenomena Emerging Near a Ferroelectric Critical Point in a Donor–Acceptor Organic Charge-Transfer Complex. Crystals, 7(4), 106. https://doi.org/10.3390/cryst7040106




