Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation
Abstract
1. Introduction
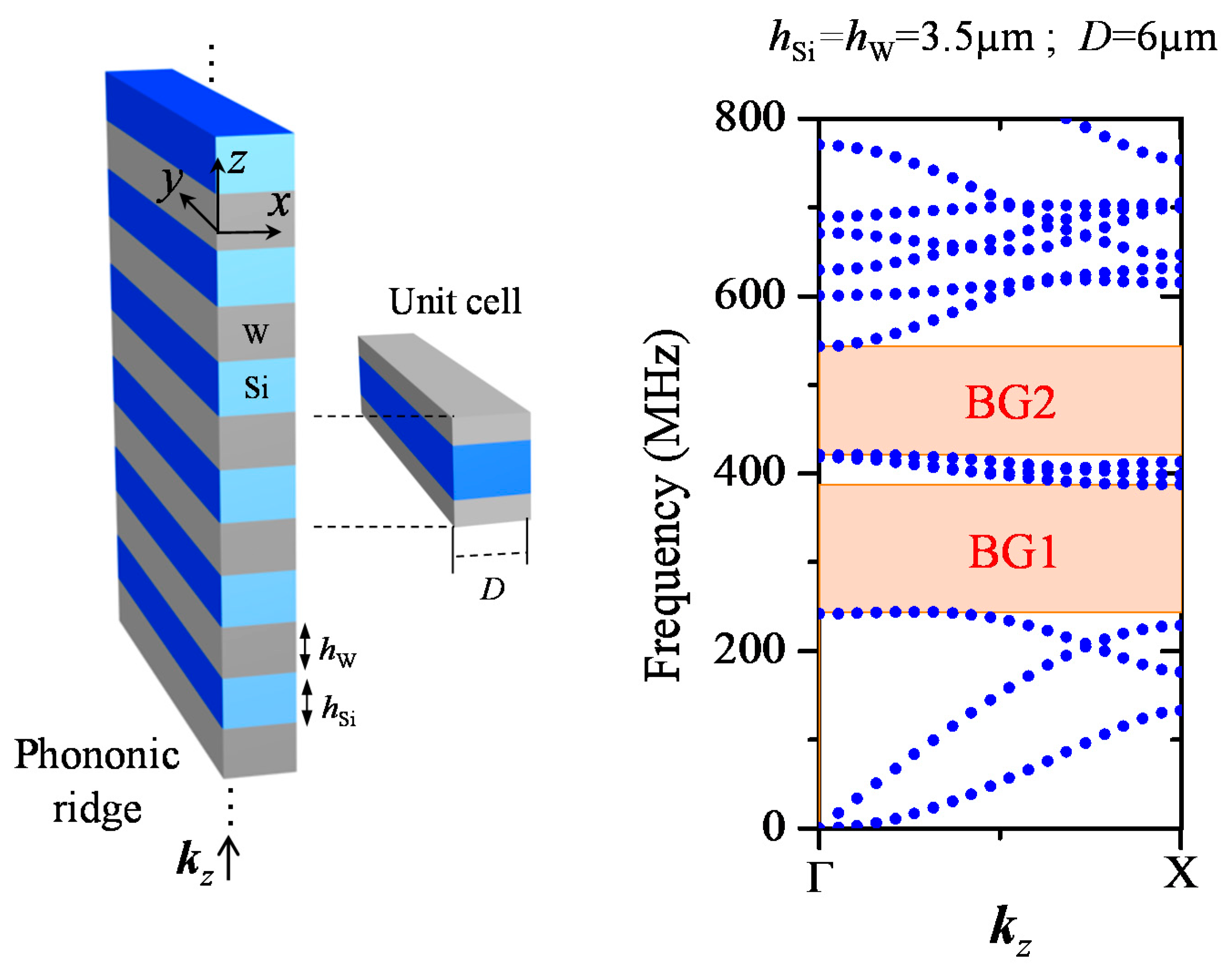
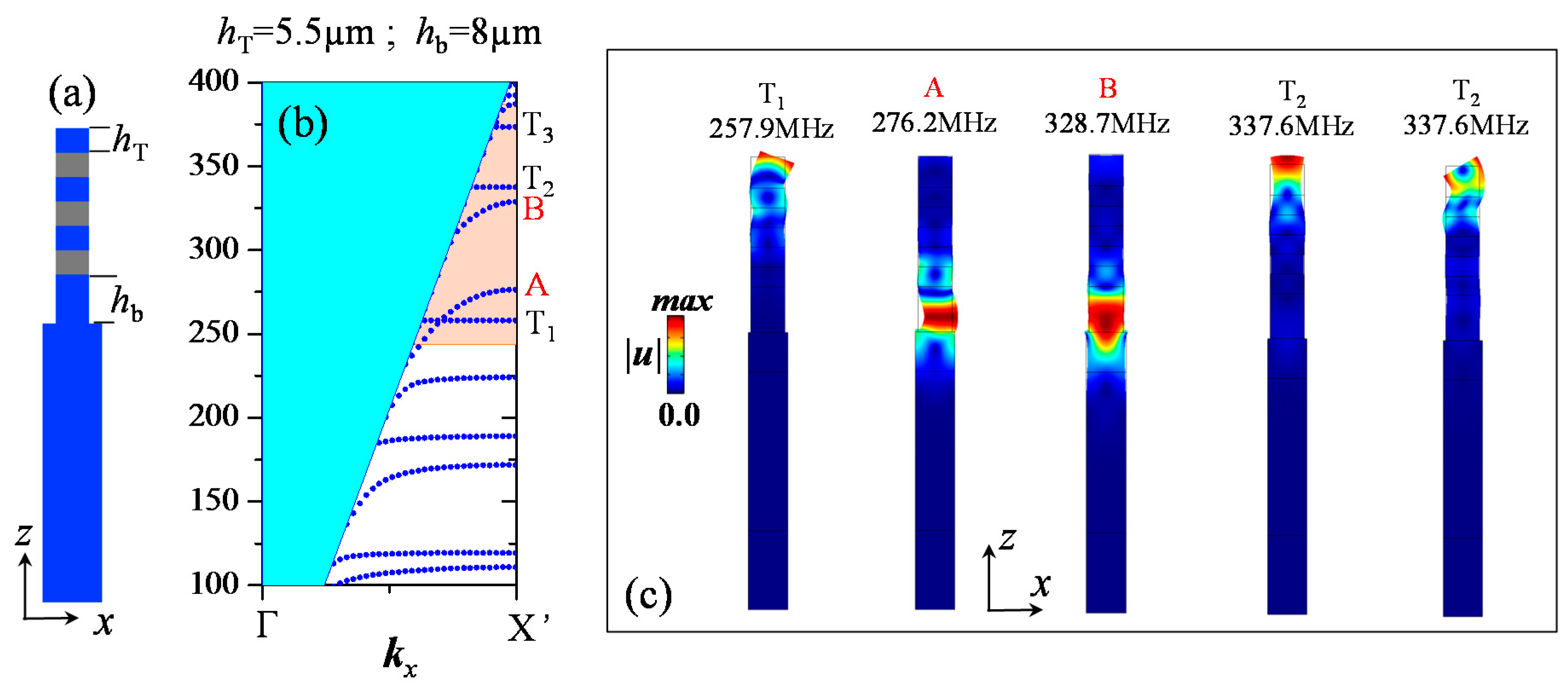
2. SAW Dispersion in the PC System with Phononic Ridges
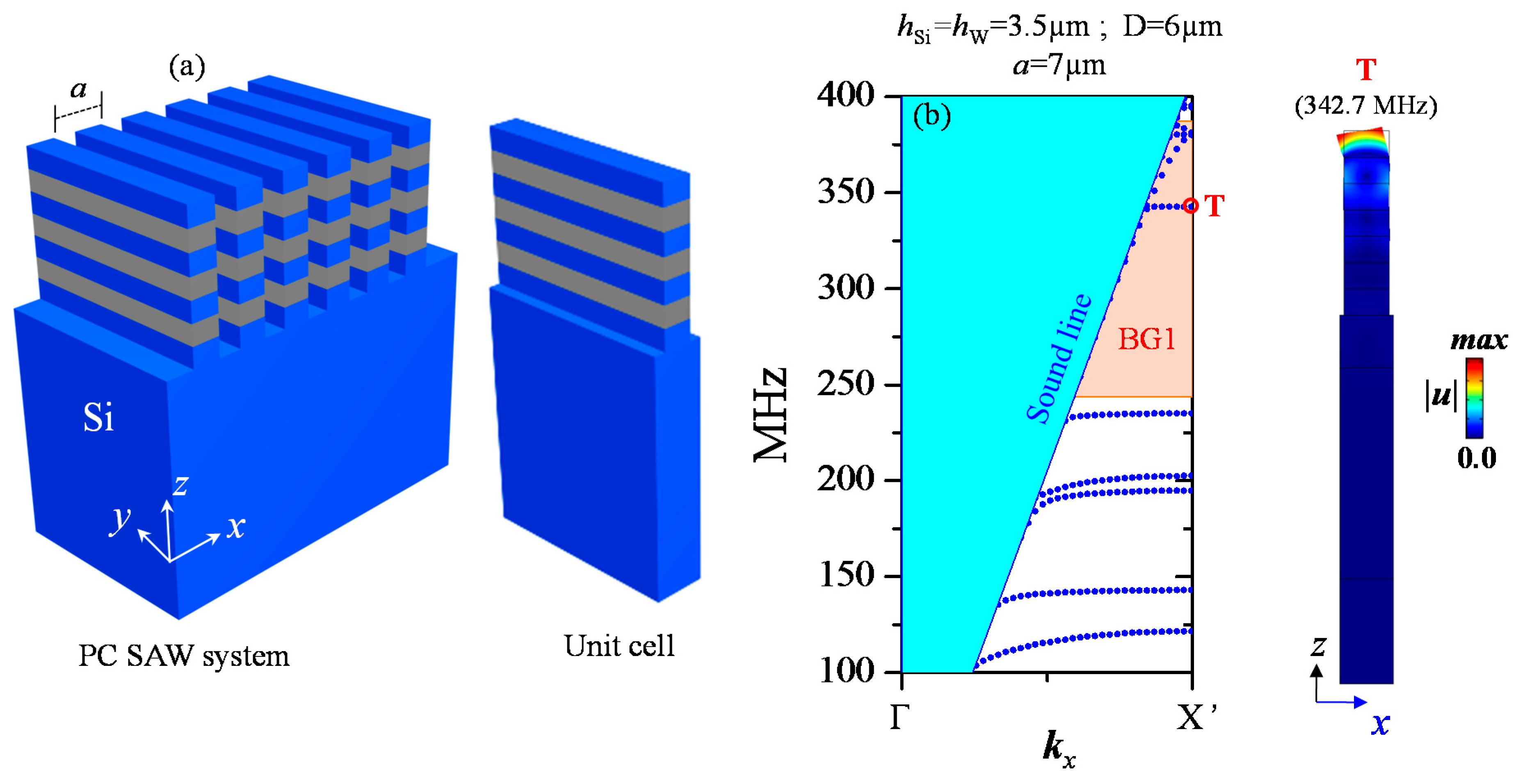
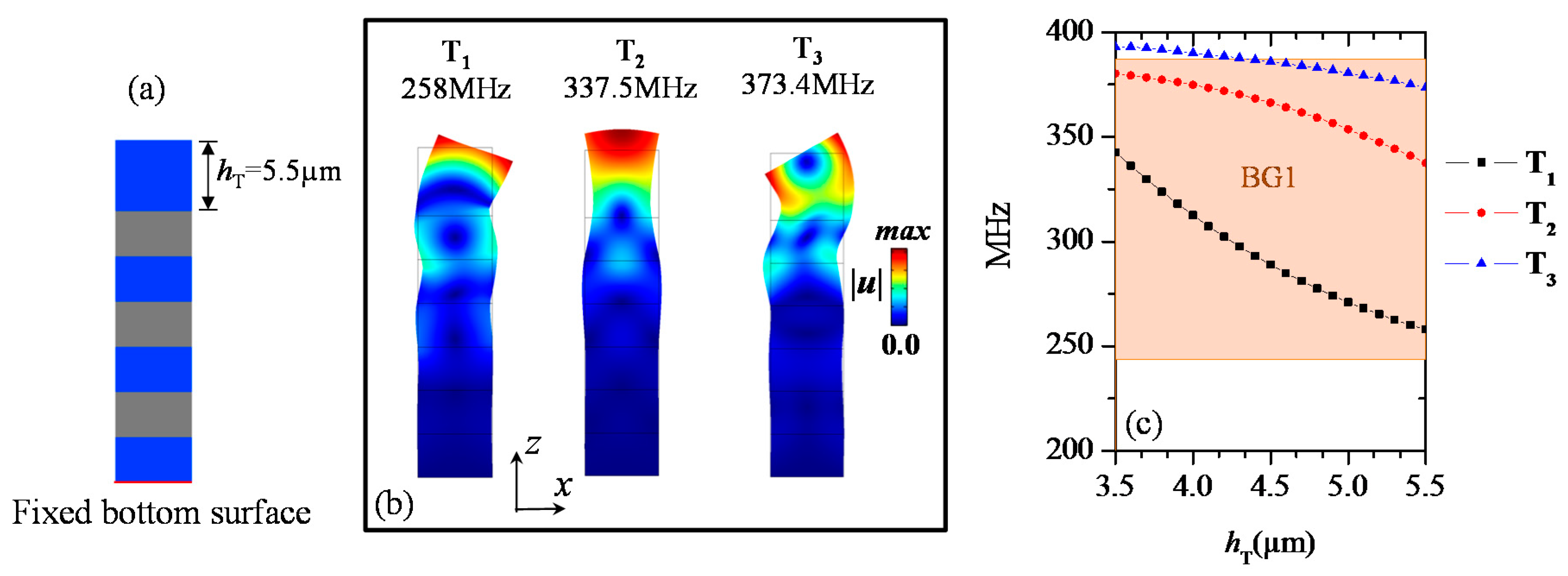
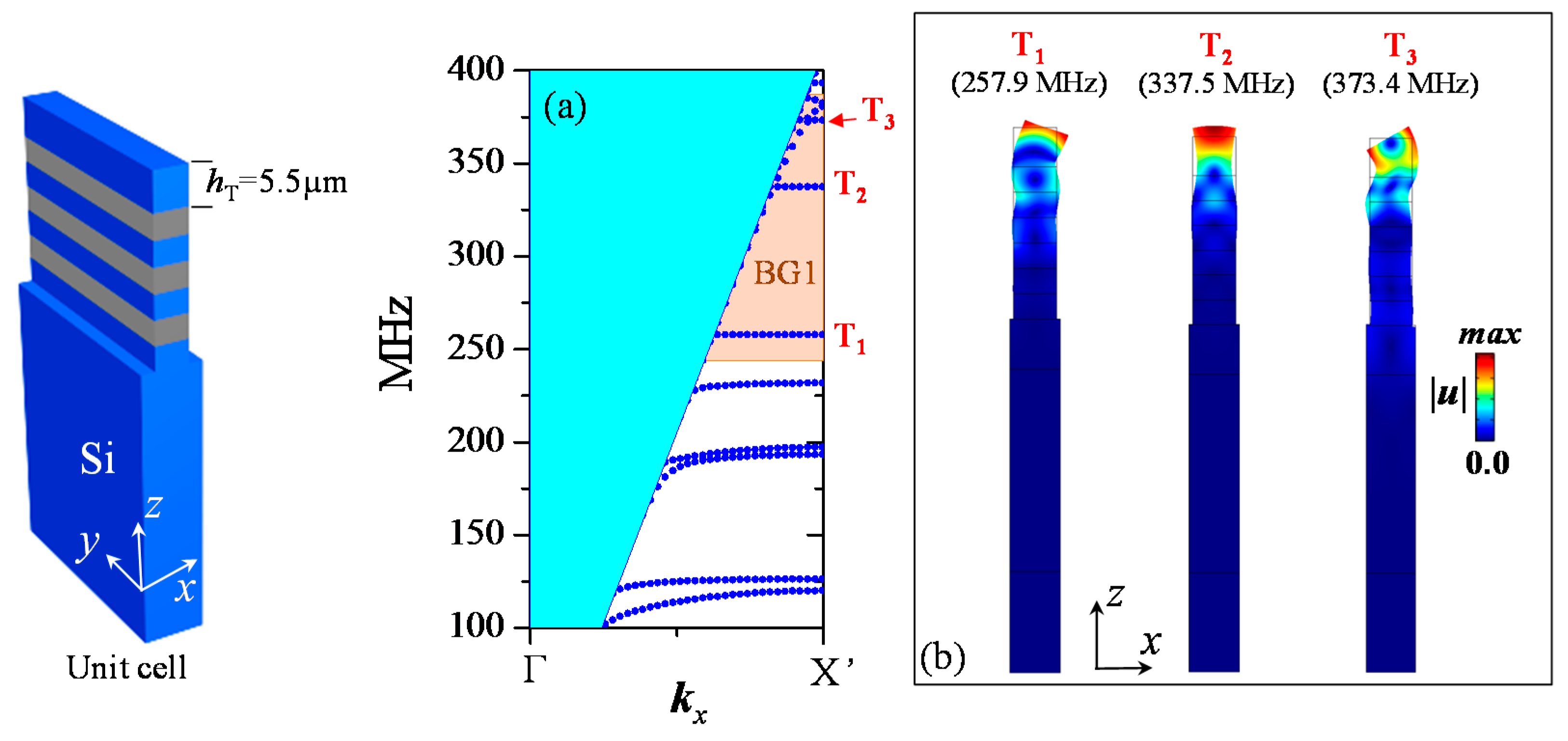
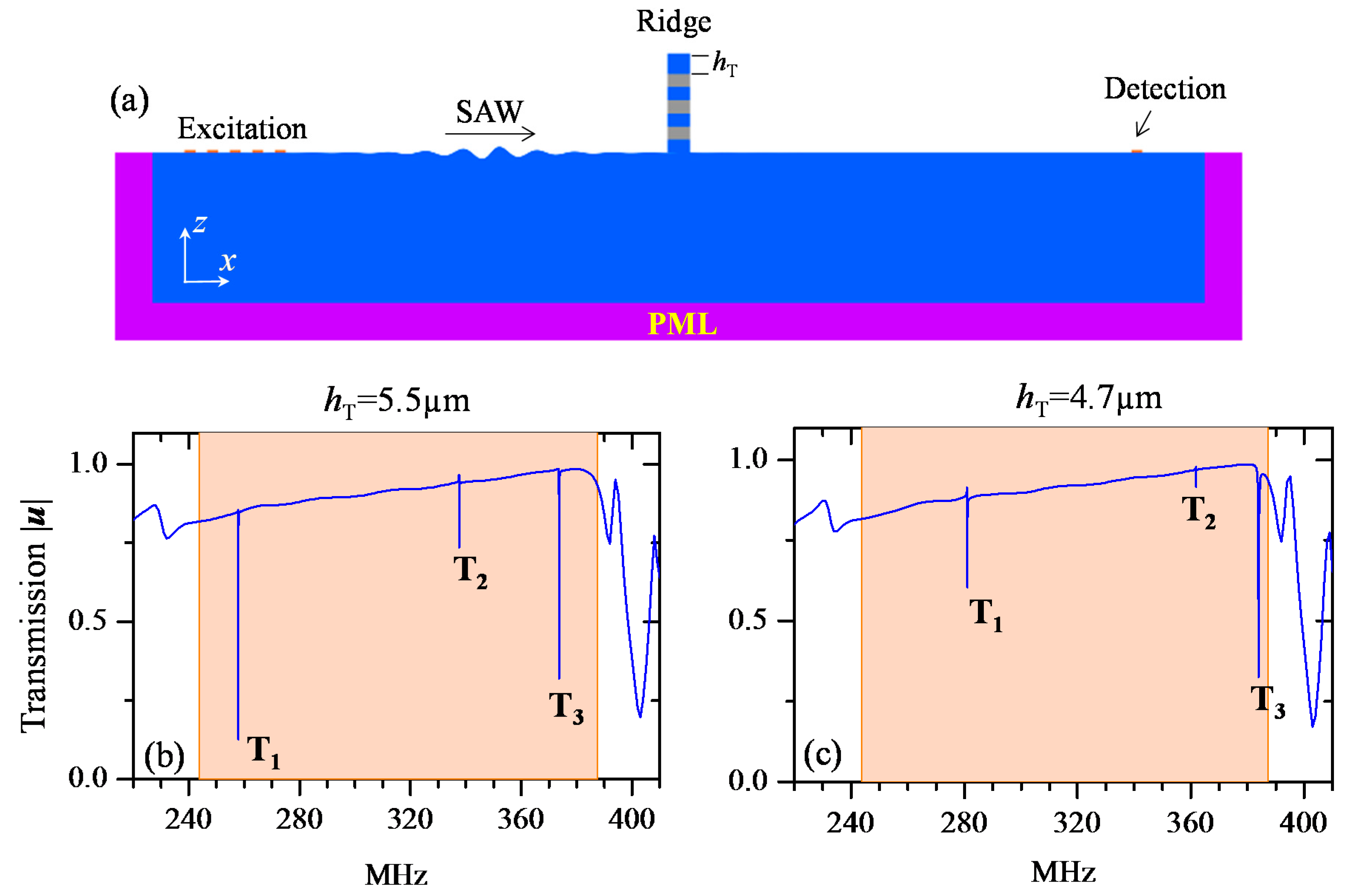
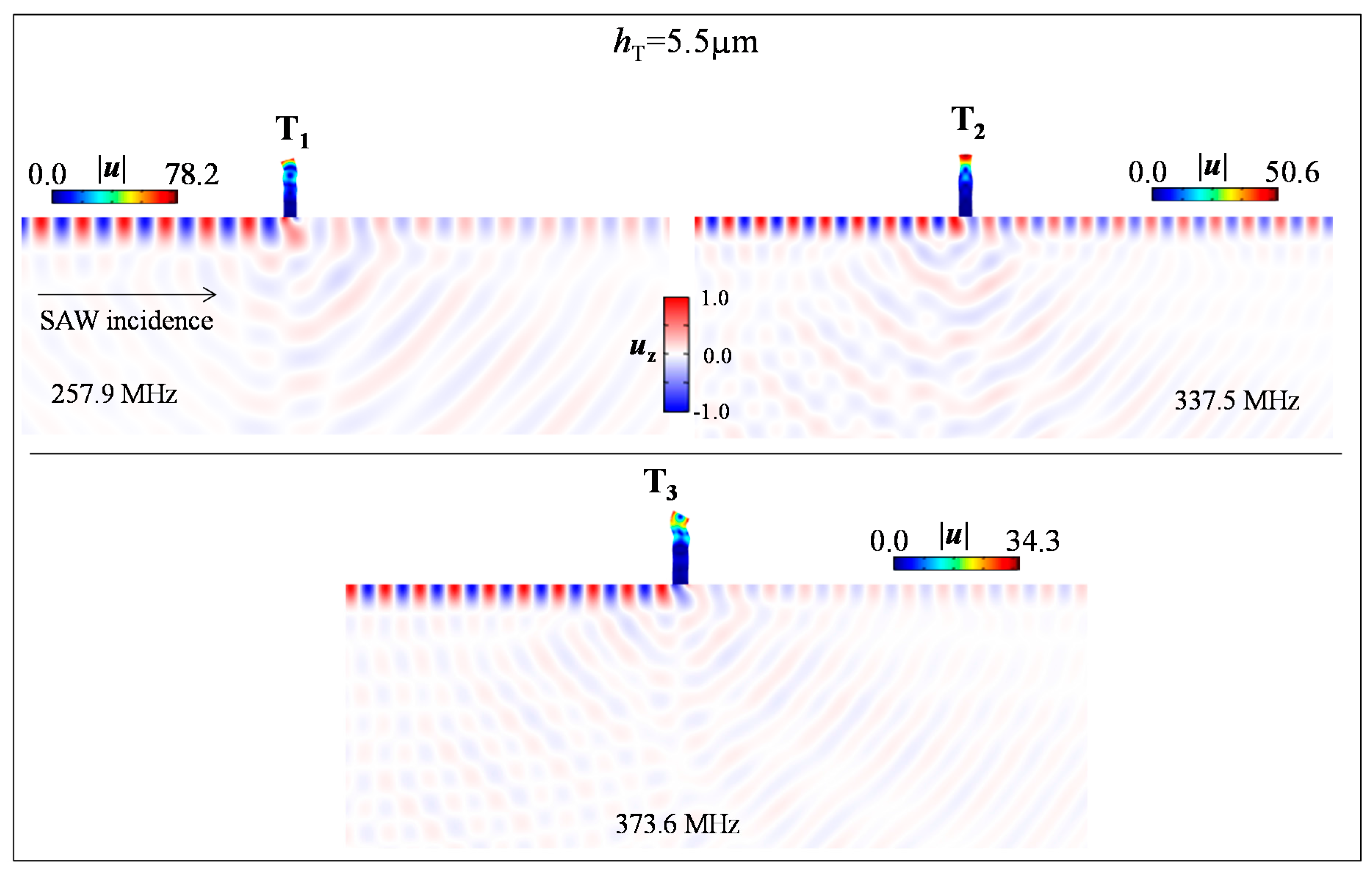
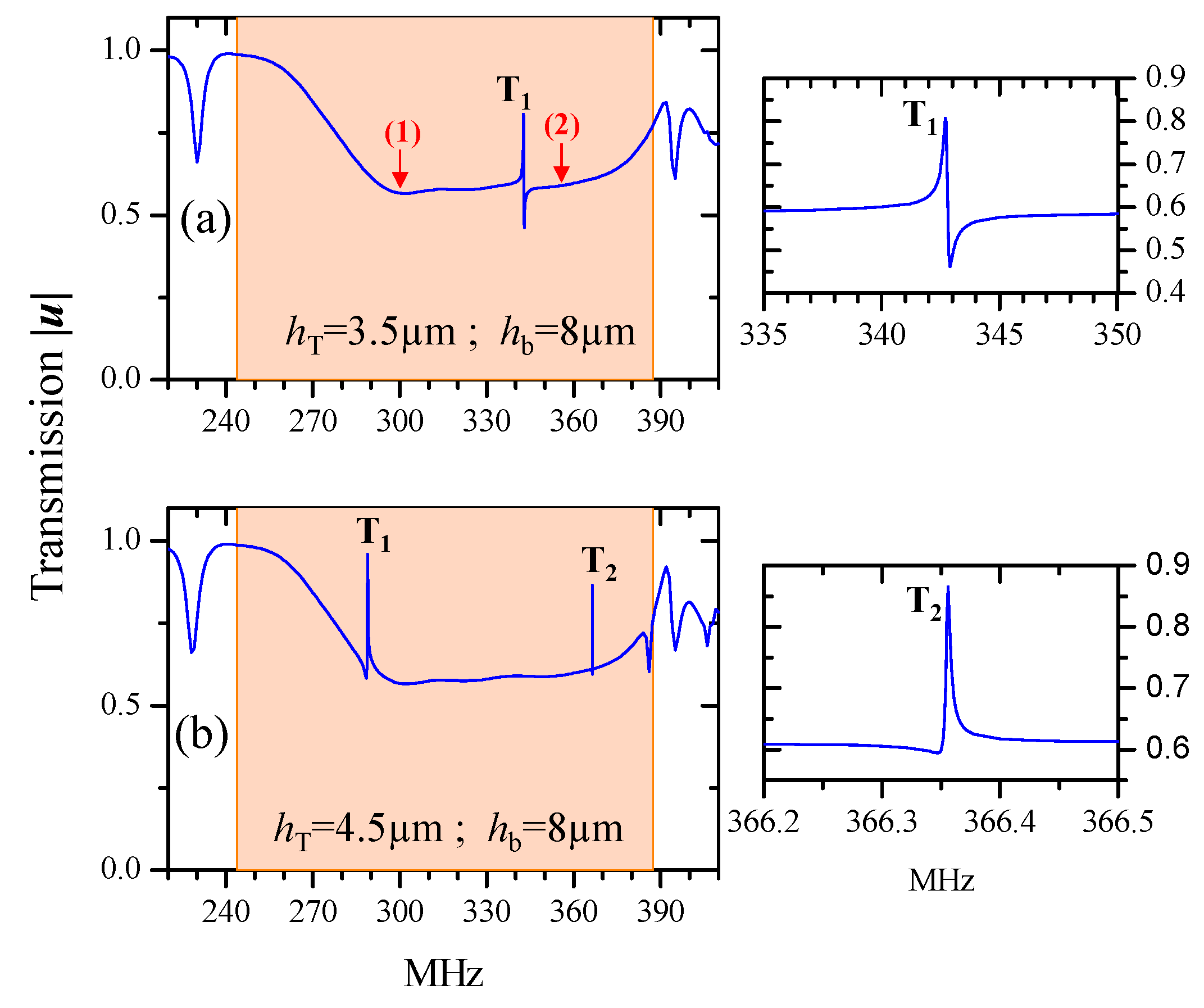
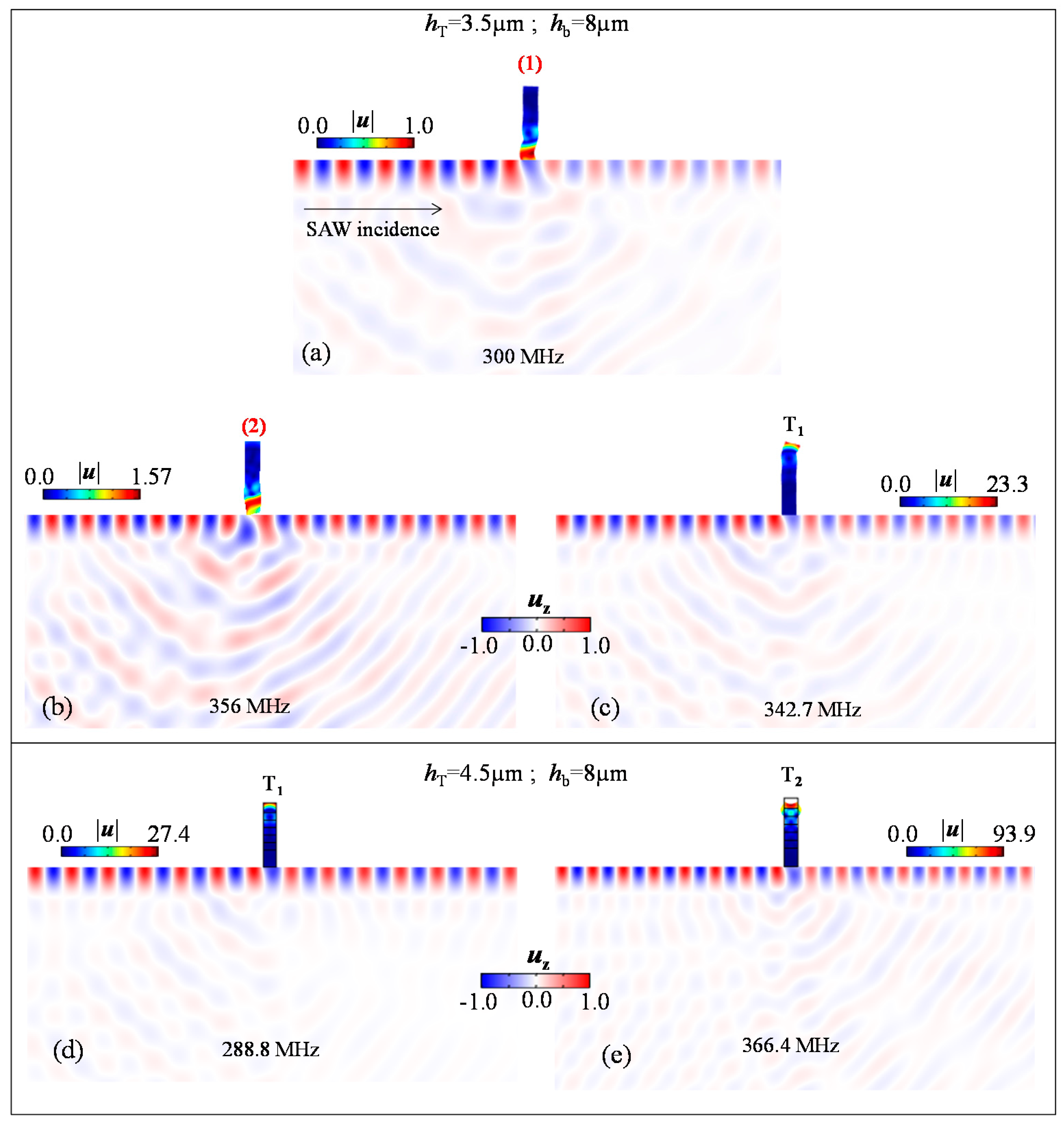
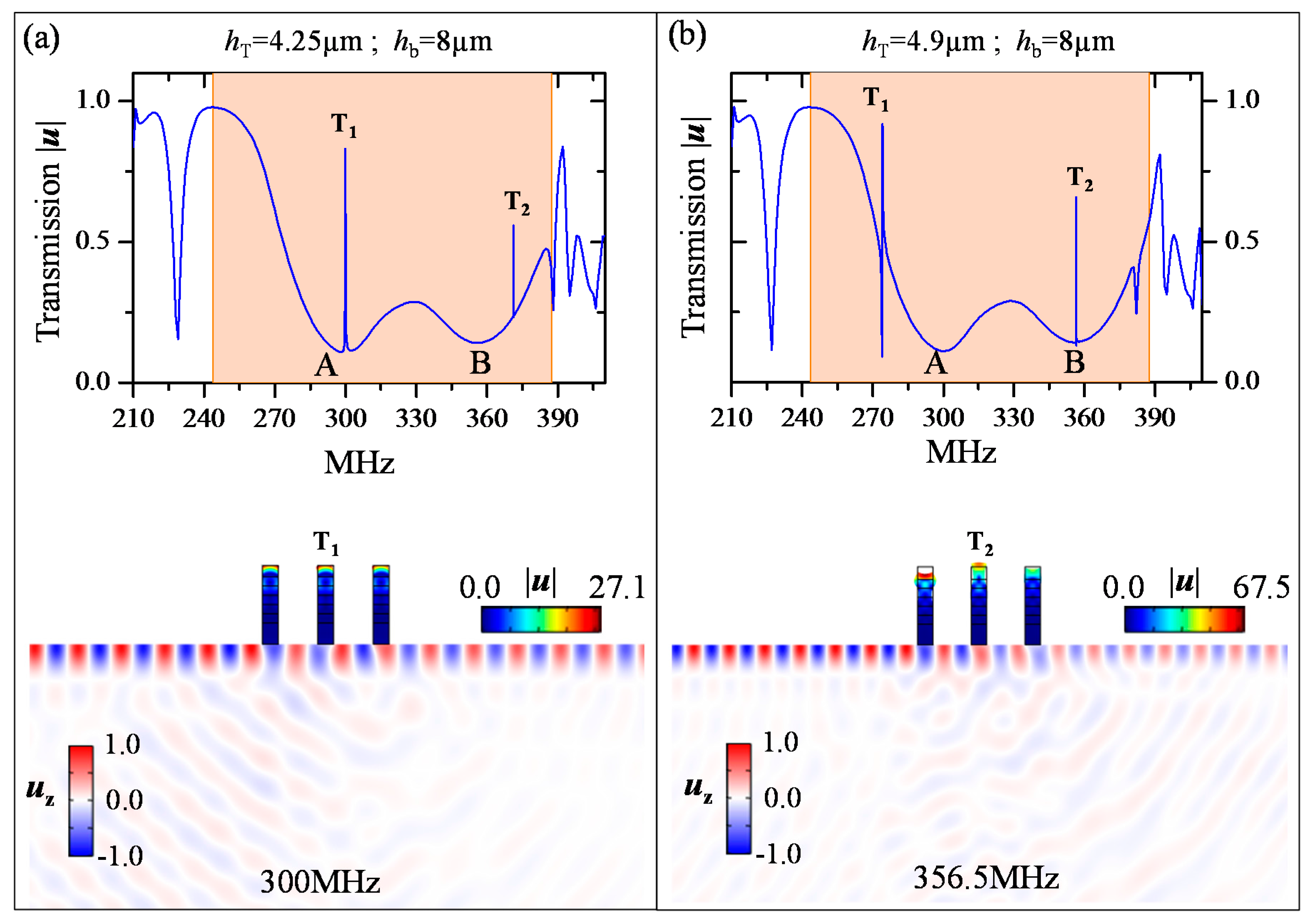
3. SAW Transmission through a Phononic Ridge
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Sigalas, M.; Economou, E.N. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Kafesaki, M.; Sigalas, M.M.; Garcia, N. Frequency modulation in the transmittivity of wave guides in elastic-wave band-gap materials. Phys. Rev. Lett. 2000, 85, 4044. [Google Scholar] [CrossRef] [PubMed]
- Qiu, C.; Liu, Z.; Mei, J.; Shi, J. Mode-selecting acoustic filter by using resonant tunneling of two-dimensional double phononic crystals. Appl. Phys. Lett. 2005, 87, 104101. [Google Scholar] [CrossRef]
- Wu, T.-T.; Wu, L.-C.; Huang, Z.-G. Frequency band-gap measurement of two-dimensional air/silicon phononic crystals using layered slanted finger interdigital transducers. J. Appl. Phys. 2005, 97, 094916. [Google Scholar] [CrossRef]
- Vasseur, J.O.; Deymier, P.A.; Djafari-Rouhani, B.; Pennec, Y.; Hladky-Hennion, A.-C. Absolute forbidden bands and waveguiding in two-dimensional phononic crystal plates. Phys. Rev. B 2008, 77, 085415. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari Rouhani, B.; Larabi, H.; Akjouj, A.; Gillet, J.N.; Vasseur, J.O.; Thabet, G. Phonon transport and waveguiding in a phononic crystal made up of cylindrical dots on a thin homogeneous plate. Phys. Rev. B 2009, 80, 144302. [Google Scholar] [CrossRef]
- Sun, J.-H.; Wu, T.-T. Propagation of surface acoustic waves through sharply bent two-dimensional phononic crystal waveguides using a finite-difference time-domain method. Phys. Rev. B 2006, 74, 174305. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.O.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 2004, 69, 046608. [Google Scholar] [CrossRef] [PubMed]
- Amoudache, S.; Moiseyenko, R.; Pennec, Y.; Djafari-Rouhani, B.; Khater, A.; Lucklum, R.; Tigrine, R. Optical and acoustic sensing using Fano-like resonances in dual phononic and photonic crystal plate. J. Appl. Phys. 2016, 119, 114502. [Google Scholar] [CrossRef]
- Wu, T.-T.; Chen, Y.-T.; Sun, J.-H.; Steven Lin, S.-C.; Huang, T.J. Focusing of the lowest antisymmetric Lamb wave in a gradient-index phononic crystal plate. Appl. Phys. Lett. 2011, 98, 171911. [Google Scholar] [CrossRef]
- Zhao, J.; Bonello, B.; Becerra, L.; Boyko, O.; Marchal, R. Focusing of Rayleigh waves with gradient-index phononic crystals. Appl. Phys. Lett. 2016, 108, 221905. [Google Scholar] [CrossRef]
- Zhao, J.; Bonello, B.; Marchal, R.; Boyko, O. Beam path and focusing of flexural Lamb waves within phononic crystal-based acoustic lenses. New J. Phys. 2014, 16, 063031. [Google Scholar] [CrossRef]
- Lin, S.-C.S.; Huang, T.J.; Sun, J.-H.; Wu, T.-T. Gradient-index phononic crystals. Phys. Rev. B 2009, 79, 094302. [Google Scholar] [CrossRef]
- Yang, Z.; Gao, F.; Shi, X.; Lin, X.; Gao, Z.; Chong, Y.; Zhang, B. Topological Acoustics. Phys. Rev. Lett. 2015, 114, 114301. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Ni, X.; Ge, H.; Sun, X.-C.; Chen, Y.-B.; Lu, M.-H.; Liu, X.-P.; Chen, Y.-F. Acoustic topological insulator and robust one-way sound transport. Nat. Phys. 2016, 12, 1124–1129. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally resonant sonic materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Chan, C.T. Double-negative acoustic metamaterial. Phys. Rev. E 2004, 70, 055602(R). [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Liu, Z.; Qiu, C.; Shi, J. Metamaterial with simultaneously negative bulk modulus and mass density. Phys. Rev. Lett. 2007, 99, 093904. [Google Scholar] [CrossRef] [PubMed]
- Oudich, M.; Djafari-Rouhani, B.; Pennec, Y.; Assouar, M.B.; Bonello, B. Negative effective mass density of acoustic metamaterial plate decorated with low frequency resonant pillars. J. Appl. Phys. 2014, 116, 184504. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Assouar, M.B.; Oudich, M. Subwavelength acoustic focusing by surface-wave-resonance enhanced transmission in doubly negative acoustic metamaterials. J. Appl. Phys. 2014, 116, 194501. [Google Scholar] [CrossRef]
- Zhou, X.; Assouar, M.B.; Oudich, M. Acoustic superfocusing by solid phononic crystals. Appl. Phys. Lett. 2014, 105, 233506. [Google Scholar] [CrossRef]
- Farhat, M.; Enoch, S.; Guenneau, S.; Movchan, A.B. Broadband cylindrical acoustic cloak for linear surface waves in a fluid. Phys. Rev. Lett. 2008, 101, 134501. [Google Scholar] [CrossRef] [PubMed]
- Khelif, A.; Aoubiza, B.; Mohammadi, S.; Adibi, A.; Laude, V. Complete band gaps in two-dimensional phononic crystal slabs. Phys. Rev. E 2006, 74, 046610. [Google Scholar] [CrossRef] [PubMed]
- Vasseur, J.O.; Hladky-Hennion, A.-C.; Djafari-Rouhani, B.; Duval, F.; Dubus, B.; Pennec, Y.; Deymier, P.A. Waveguiding in two-dimensional piezoelectric phononic crystal plates. Appl. Phys. Lett. 2007, 101, 114904. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.O.; Hladky-Hennion, A.C. Low-frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B 2008, 78, 104105. [Google Scholar] [CrossRef]
- Wu, T.-T.; Huang, Z.-G.; Tsai, T.-C.; Wu, T.-C. Evidence of complete band gap and resonances in a plate with periodic stubbed surface. Appl. Phys. Lett. 2008, 93, 111902. [Google Scholar] [CrossRef]
- Wu, T.-C.; Wu, T.-T.; Hsu, J.-C. Waveguiding and frequency selection of Lamb waves in a plate with a periodic stubbed surface. Phys. Rev. B 2009, 79, 104306. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, B.M.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 083049. [Google Scholar] [CrossRef]
- Assouar, M.B.; Oudich, M. Enlargement of a locally resonant sonic band gap by using double-sides stubbed phononic plates. Appl. Phys. Lett. 2012, 100, 123506. [Google Scholar] [CrossRef]
- Oudich, M.; Senesi, M.; Assouar, M.B.; Ruzzene, M.; Sun, J.-H.; Vincent, B.; Hou, Z.; Wu, T.-T. Experimental evidence of locally resonant sonic band gap in two-dimensional phononic stubbed plates. Phys. Rev. B 2011, 84, 165136. [Google Scholar] [CrossRef]
- Oudich, M.; Zhou, X.; Assouar, M.B. General analytical approach for sound transmission loss analysis through a thick metamaterial plate. J. Appl. Phys. 2014, 116, 193509. [Google Scholar] [CrossRef]
- Assouar, B.; Oudich, M.; Zhou, X. Acoustic metamaterials for sound mitigation. C. R. Phys. 2016, 17, 524–532. [Google Scholar] [CrossRef]
- Jin, Y.; Fernez, N.; Pennec, Y.; Bonello, B.; Moiseyenko, R.P.; Hémon, S.; Pan, Y.; Djafari-Rouhani, B. Tunable waveguide and cavity in a phononic crystal plate by controlling whispering-gallery modes in hollow pillars. Phys. Rev. B 2016, 93, 054109. [Google Scholar] [CrossRef]
- Jin, Y.; EI Boudouti, E.H.; Pennec, Y.; Djafari-Rouhani, B. Phononic crystal plate with hollow pillars connected by thin bars. J. Phys. D Appl. Phys. 2017, 50, 425304. [Google Scholar] [CrossRef]
- Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling. Crystals 2016, 6, 64. [Google Scholar] [CrossRef]
- Wang, T.-T.; Wang, Y.-F.; Wang, Y.-S.; Laude, V. Tunable fluid-filled phononic metastrip. Appl. Phys. Lett. 2017, 111, 041906. [Google Scholar] [CrossRef]
- Jin, Y.; Bonello, B.; Moiseyenko, R.P.; Pennec, Y.; Boyko, O.; Djafari-Rouhani, B. Pillar-type acoustic metasurface. Phys. Rev. B 2017, 96, 104311. [Google Scholar] [CrossRef]
- Assouar, M.B.; Senesi, M.; Oudich, M.; Ruzzene, M.; Hou, Z. Broadband plate-type acoustic metamaterial for low-frequency sound attenuation. Appl. Phys. Lett. 2012, 101, 173505. [Google Scholar] [CrossRef]
- Celli, P.; Gonella, S. Manipulating waves with LEGO® bricks: A versatile experimental platform for metamaterial architectures. Appl. Phys. Lett 2015, 107, 081901. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y. Tunable sub-wavelength acoustic energy harvesting with a metamaterial plate. J. Phys. D Appl. Phys. 2017, 50, 315104. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Lin, S. Surface and bulk acoustic waves in two-dimensional phononic crystal consisting of materials with general anisotropy. Phys. Rev. B 2004, 69, 094301. [Google Scholar] [CrossRef]
- Laude, V.; Wilm, M.; Benchabane, S.; Khelif, A. Full band gap for surface acoustic waves in a piezoelectric phononic crystal. Phys. Rev. E 2005, 71, 036607. [Google Scholar] [CrossRef] [PubMed]
- Benchabane, S.; Gaiffe, O.; Ulliac, G.; Salut, R.; Achaoui, Y.; Laude, V. Observation of surface-guided waves in holey hypersonic phononic crystal. Appl. Phys. Lett. 2011, 98, 171908. [Google Scholar] [CrossRef]
- Yudistira, D.; Pennec, Y.; Djafari Rouhani, B.; Dupont, S.; Laude, V. Non-radiative complete surface acoustic wave bandgap for finite-depth holey phononic crystal in lithium niobate. Appl. Phys. Lett. 2012, 100, 061912. [Google Scholar] [CrossRef]
- Khelif, A.; Achaoui, Y.; Benchabane, S.; Laude, V.; Aoubiza, B. Locally resonant surface acoustic wave band gaps in a two-dimensional phononic crystal of pillars on a surface. Phys. Rev. B 2010, 81, 214303. [Google Scholar] [CrossRef]
- Achaoui, Y.; Khelif, A.; Benchabane, S.; Robert, L.; Laude, V. Experimental observation of locally-resonant and Bragg band gaps for surface guided waves in a phononic crystal of pillars. Phys. Rev. B 2011, 83, 104201. [Google Scholar] [CrossRef]
- Robillard, J.F.; Devos, A.; Roch-Jeune, I. Time-resolved vibrations of two-dimensional hypersonic phononic crystals. Phys. Rev. B 2007, 76, 092301. [Google Scholar] [CrossRef]
- Giannetti, C.; Revaz, B.; Banfi, F.; Montagnese, M.; Ferrini, G.; Cilento, F.; Maccalli, S.; Vavassori, P.; Oliviero, G.; Bontempi, E.; et al. Thermomechanical behavior of surface acoustic waves in ordered arrays of nanodisks studied by near-infrared pump-probe diffraction experiments. Phys. Rev. B 2007, 76, 125413. [Google Scholar] [CrossRef]
- Yudistira, D.; Boes, A.; Graczykowski, B.; Alzina, F.; Yeo, L.Y.; Sotomayor Torres, C.M.; Mitchell, A. Nanoscale pillar hypersonic surface phononic crystals. Phys. Rev. B 2016, 94, 094304. [Google Scholar] [CrossRef]
- Ash, B.J.; Worsfold, S.R.; Vukusic, P.; Nash, G.R. A highly attenuating and frequency tailorable annular hole phononic crystal for surface acoustic waves. Nat. Commun. 2017, 8, 174. [Google Scholar] [CrossRef] [PubMed]
- Brûlé, S.; Javelaud, E.H.; Enoch, S.; Guenneau, S. Experiments on Seismic Metamaterials: Molding Surface Waves. Phys. Rev. Lett. 2014, 112, 133901. [Google Scholar] [CrossRef] [PubMed]
- Colombi, A.; Roux, P.; Guenneau, S.; Gueguen, P.; Craster, R.V. Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 2016, 6, 19238. [Google Scholar] [CrossRef] [PubMed]
- Al Lethawe, M.; Addouche, M.; Benchabane, S.; Laude, V.; Khelif, A. Guidance of surface elastic waves along a linear chain of pillars. AIP Adv. 2016, 6, 121708. [Google Scholar] [CrossRef]
- Benchabane, S.; Salut, R.; Gaiffe, O.; Soumann, V.; Addouche, M.; Laude, V.; Khelif, A. Sarah Benchabane, Roland Salut, Olivier Gaiffe, Valérie Soumann, Mahmoud Addouche, Vincent Laude, and Abdelkrim Khelif. Phys. Rev. Appl. 2017, 8, 034016. [Google Scholar] [CrossRef]
- Fano, U. Effects of Configuration Interaction on Intensities and Phase Shifts. Phys. Rev. 1961, 124, 1866. [Google Scholar] [CrossRef]
- Nardi, D.; Travagliati, M.; Siemens, M.E.; Li, Q.; Murnane, M.M.; Kapteyn, H.C.; Ferrini, G.; Parmigiani, F.; Banfi, F. Probing Thermomechanics at the Nanoscale: Impulsively Excited Pseudosurface Acoustic Waves in Hypersonic Phononic Crystals. Nano Lett. 2011, 11, 4126–4133. [Google Scholar] [CrossRef] [PubMed]
- Nardi, D.; Travagliati, M.; Murnane, M.M.; Kapteyn, H.C.; Ferrini, G.; Giannetti, C.; Banfi, F. Impulsively Excited Surface Phononic Crystals: A Route Toward Novel Sensing Schemes. IEEE Sens. J. 2015, 15, 5142–5150. [Google Scholar] [CrossRef]
- Boller, K.-J.; Imamoglu, A.; Harris, S.E. Observation of electromagnetically induced transparency. Phys. Rev. Lett. 1991, 66, 2593–2596. [Google Scholar] [CrossRef] [PubMed]
- Fleischhauer, M.; Imamoglu, A.; Marangos, J.P. Electromagnetically induced transparency: Optics in coherent media. Rev. Mod. Phys. 2005, 77, 633–673. [Google Scholar] [CrossRef]
- Dyer, G.C.; Aizin, G.R.; Allen, S.J.; Grine, A.D.; Bethke, D.; Reno, J.L.; Shaner, E.A. Induced transparency by coupling of Tamm and defect states in tunable terahertz plasmonic crystals. Nat. Photonics 2013, 7, 925–930. [Google Scholar] [CrossRef]
- Anguiano, S.; Bruchhausen, A.E.; Jusserand, B.; Favero, I.; Lamberti, F.R.; Lanco, L.; Sagnes, I.; Lemaître, A.; Lanzillotti-Kimura, N.D.; Senellart, P.; et al. Micropillar Resonators for Optomechanics in the Extremely High 19–95-GHz Frequency Range. Phys. Rev. Lett. 2017, 118, 263901. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, F.R.; Yao, Q.; Lanco, L.; Nguyen, D.T.; Esmann, M.; Fainstein, A.; Sesin, P.; Anguiano, S.; Villafañe, V.; Bruchhausen, A.; et al. Optomechanical properties of GaAs/AlAs micropillar resonators operating in the 18 GHz range. Opt. Express 2017, 25, 24437. [Google Scholar] [CrossRef] [PubMed]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oudich, M.; Djafari-Rouhani, B.; Bonello, B.; Pennec, Y.; Sarry, F. Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation. Crystals 2017, 7, 372. https://doi.org/10.3390/cryst7120372
Oudich M, Djafari-Rouhani B, Bonello B, Pennec Y, Sarry F. Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation. Crystals. 2017; 7(12):372. https://doi.org/10.3390/cryst7120372
Chicago/Turabian StyleOudich, Mourad, Bahram Djafari-Rouhani, Bernard Bonello, Yan Pennec, and Frédéric Sarry. 2017. "Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation" Crystals 7, no. 12: 372. https://doi.org/10.3390/cryst7120372
APA StyleOudich, M., Djafari-Rouhani, B., Bonello, B., Pennec, Y., & Sarry, F. (2017). Phononic Crystal Made of Multilayered Ridges on a Substrate for Rayleigh Waves Manipulation. Crystals, 7(12), 372. https://doi.org/10.3390/cryst7120372







