Simultaneous Guidance of Surface Acoustic and Surface Optical Waves in Phoxonic Crystal Slabs
Abstract
1. Introduction
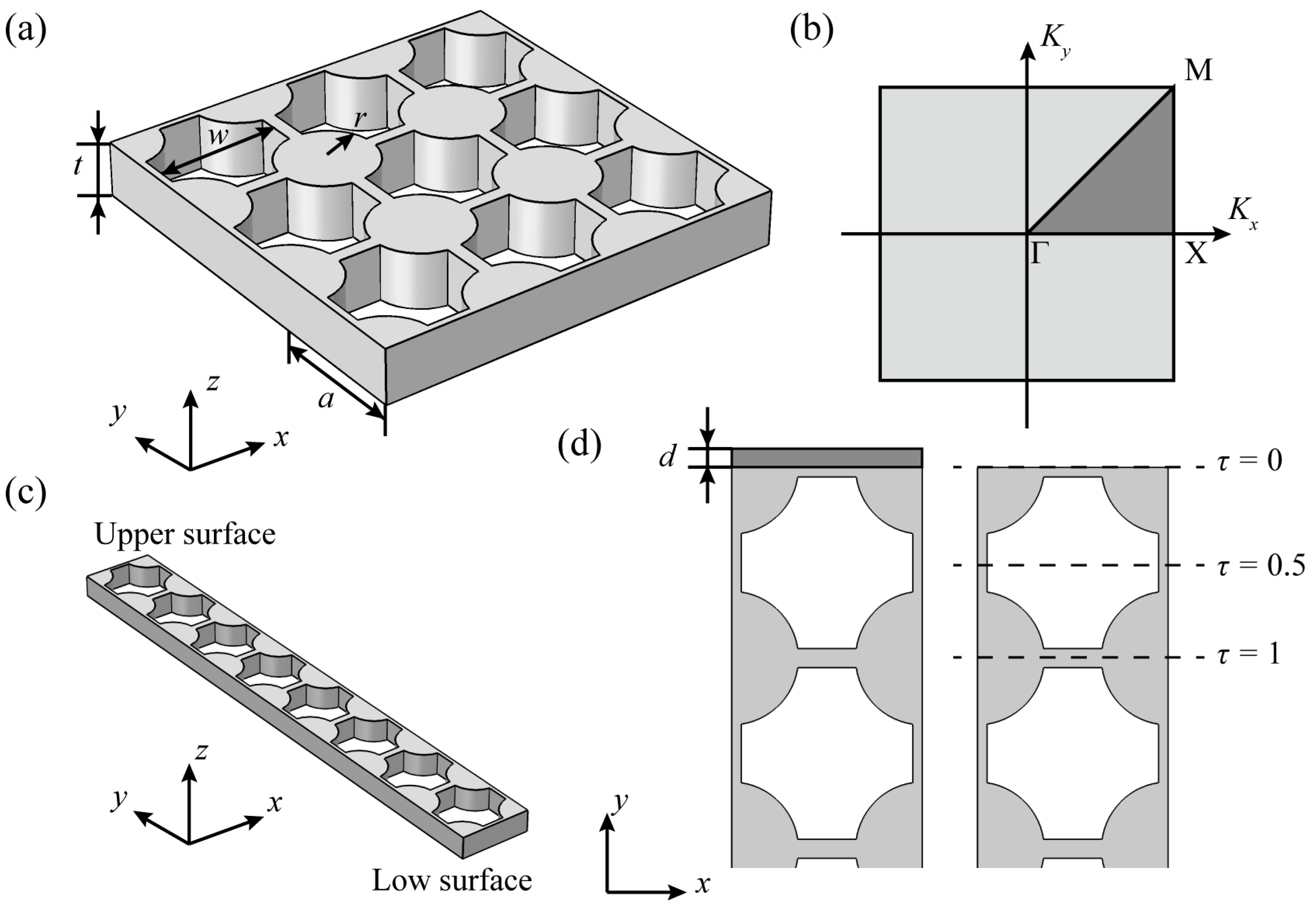
2. Structure and Method
3. Slab Modes
4. Surface Modes
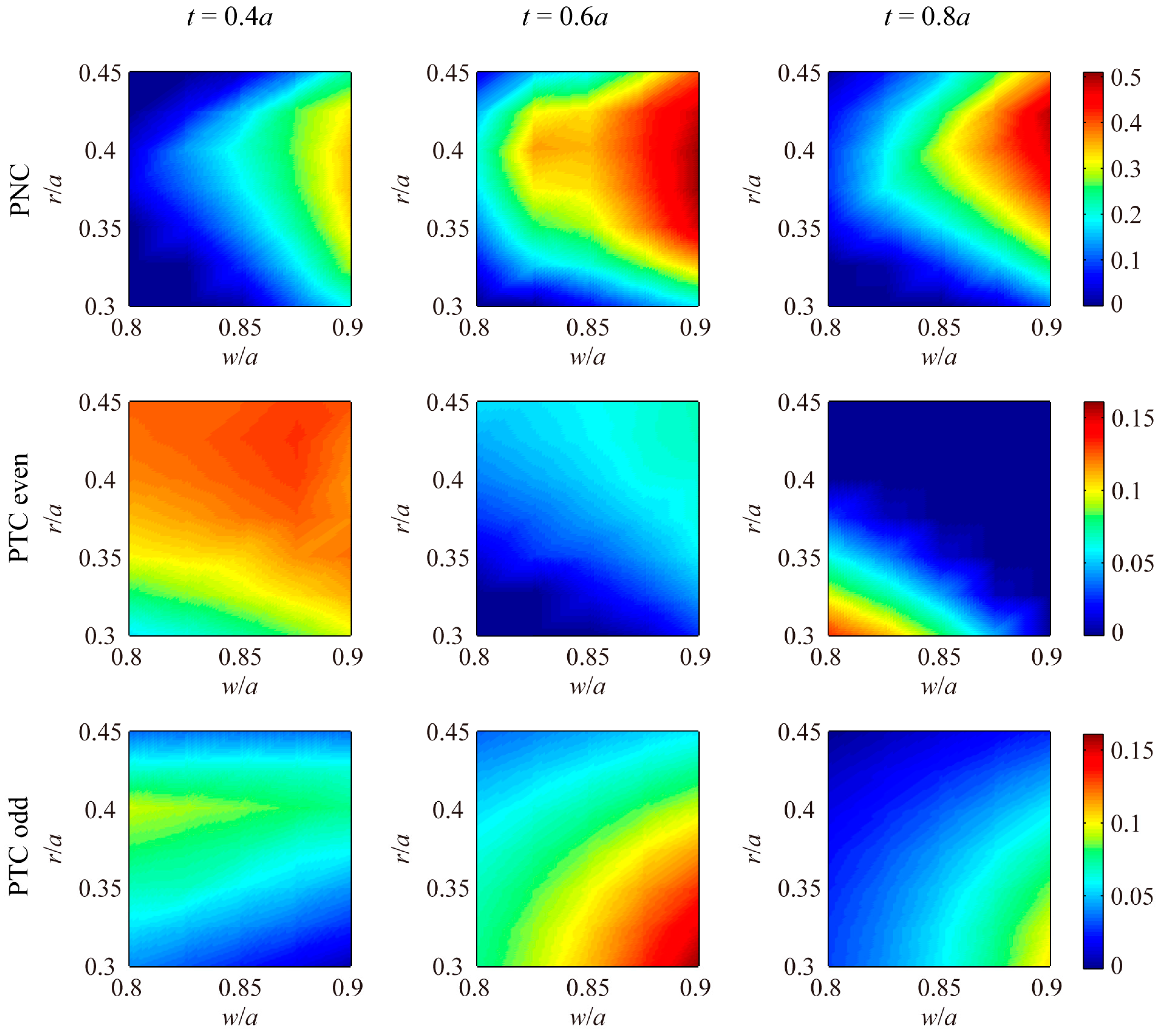
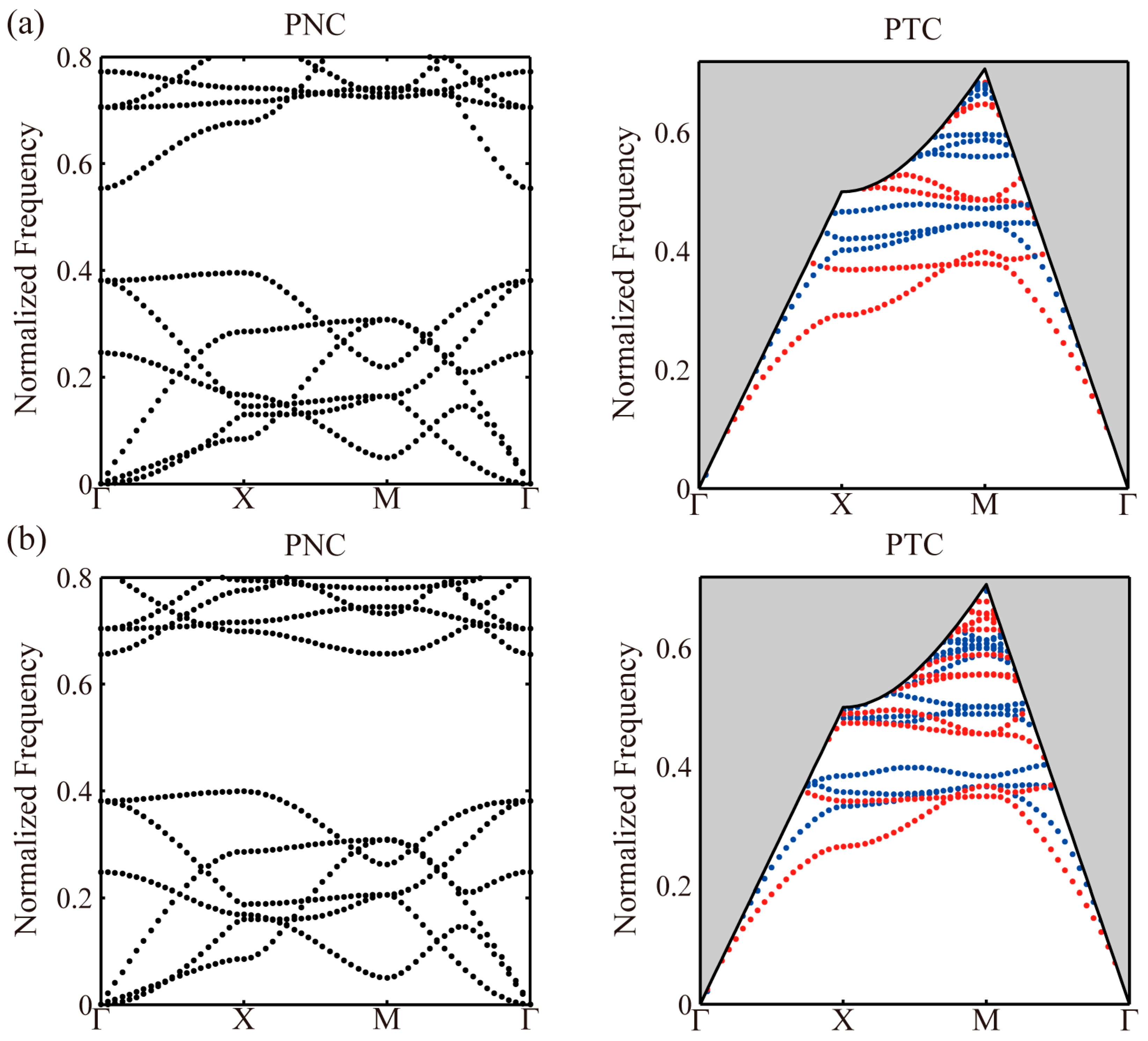
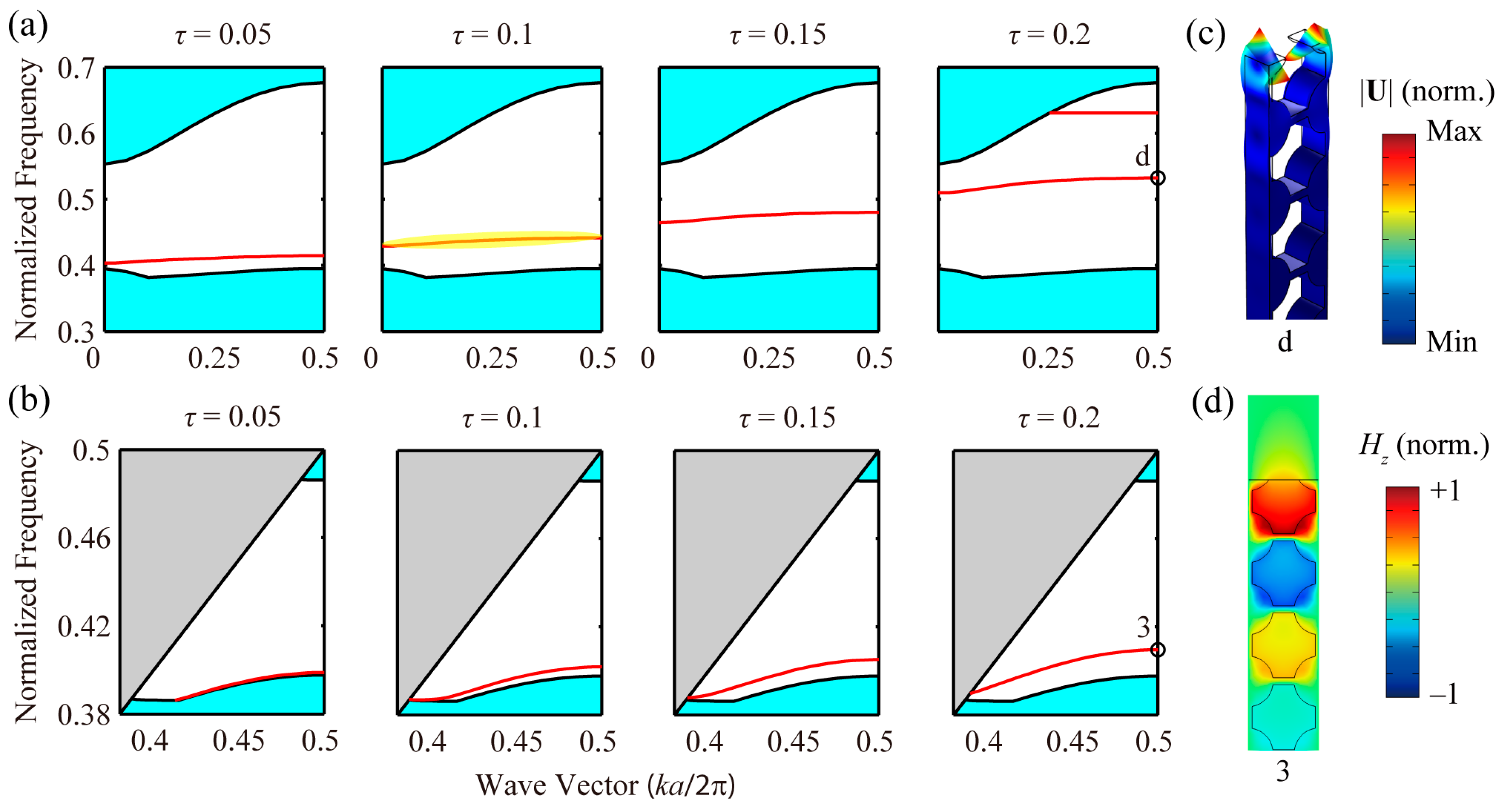
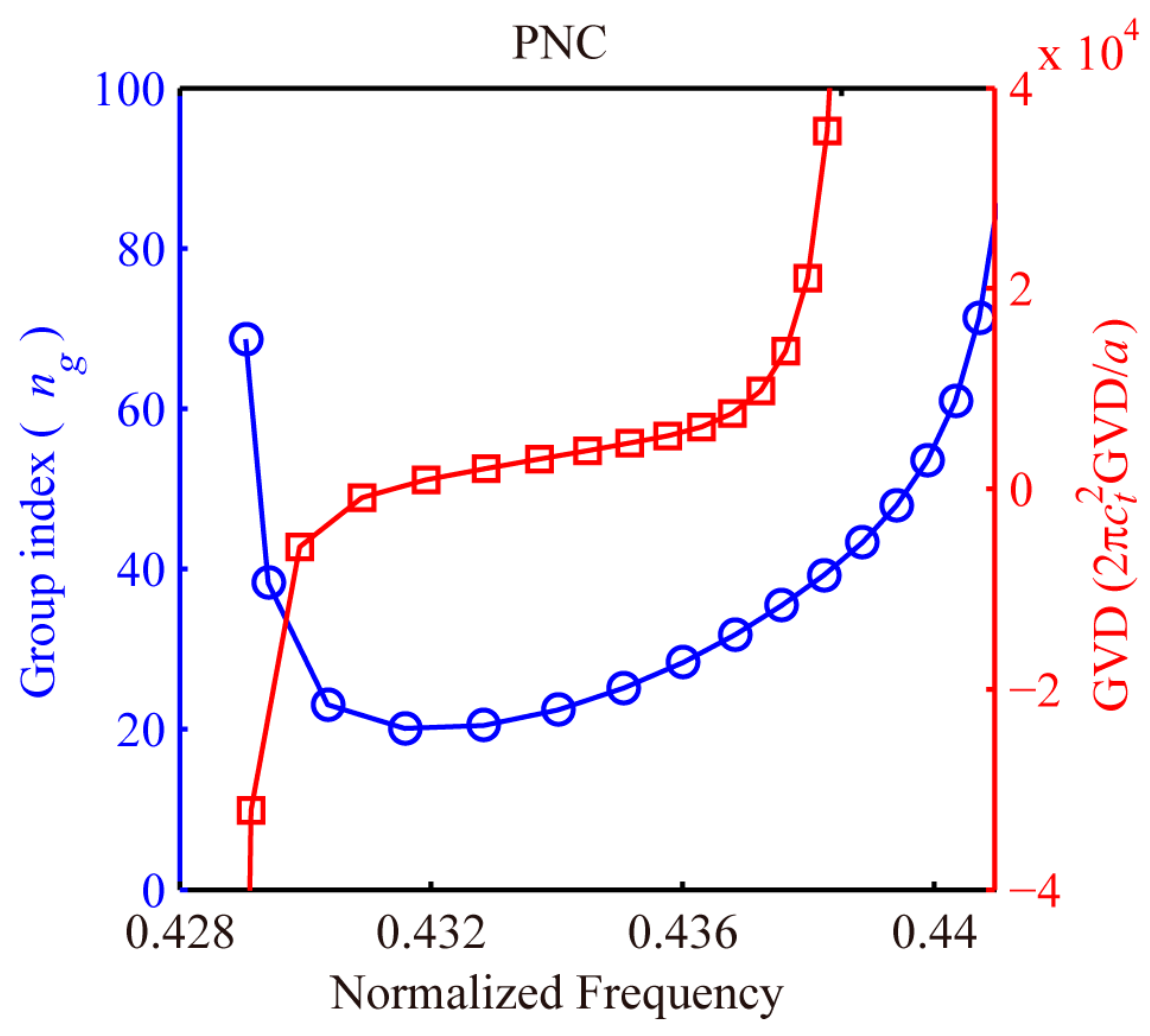
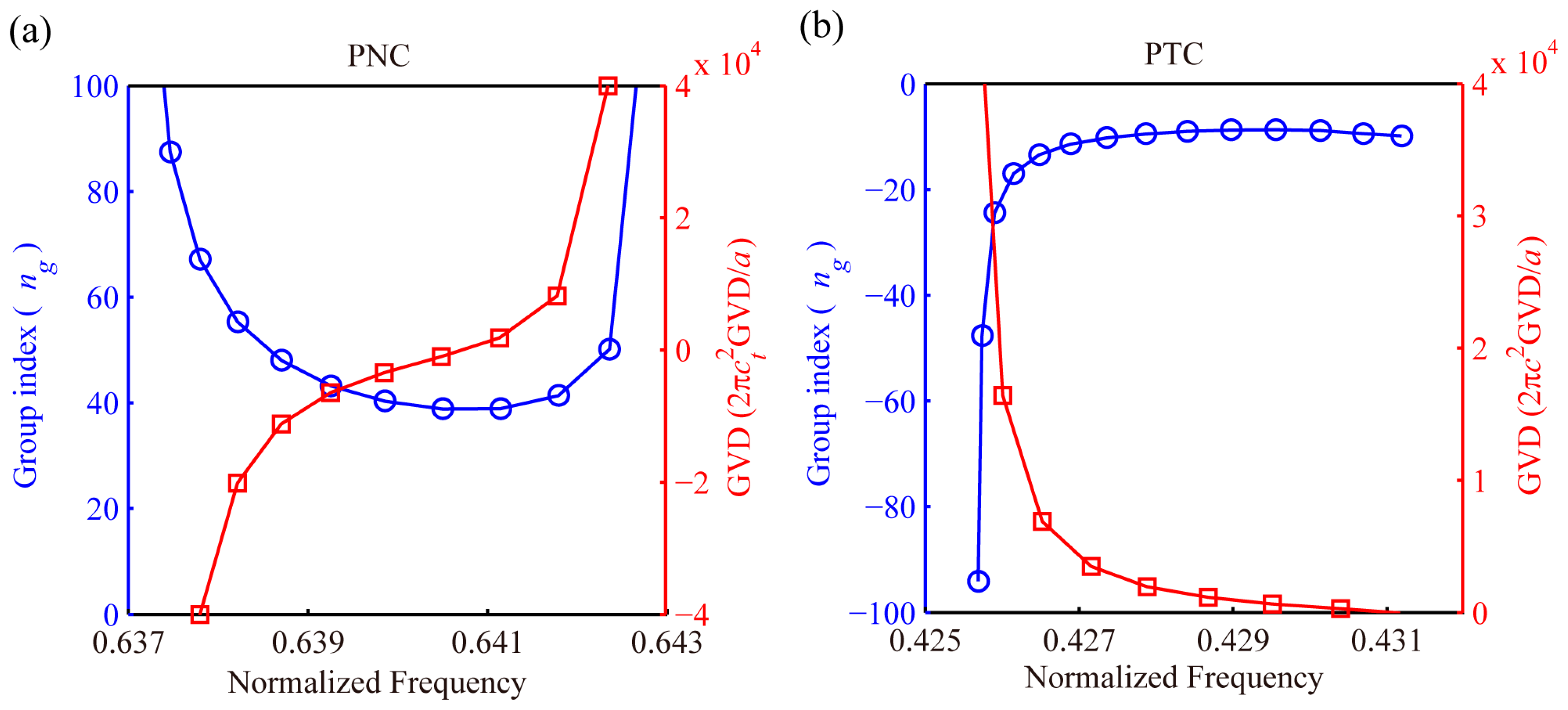
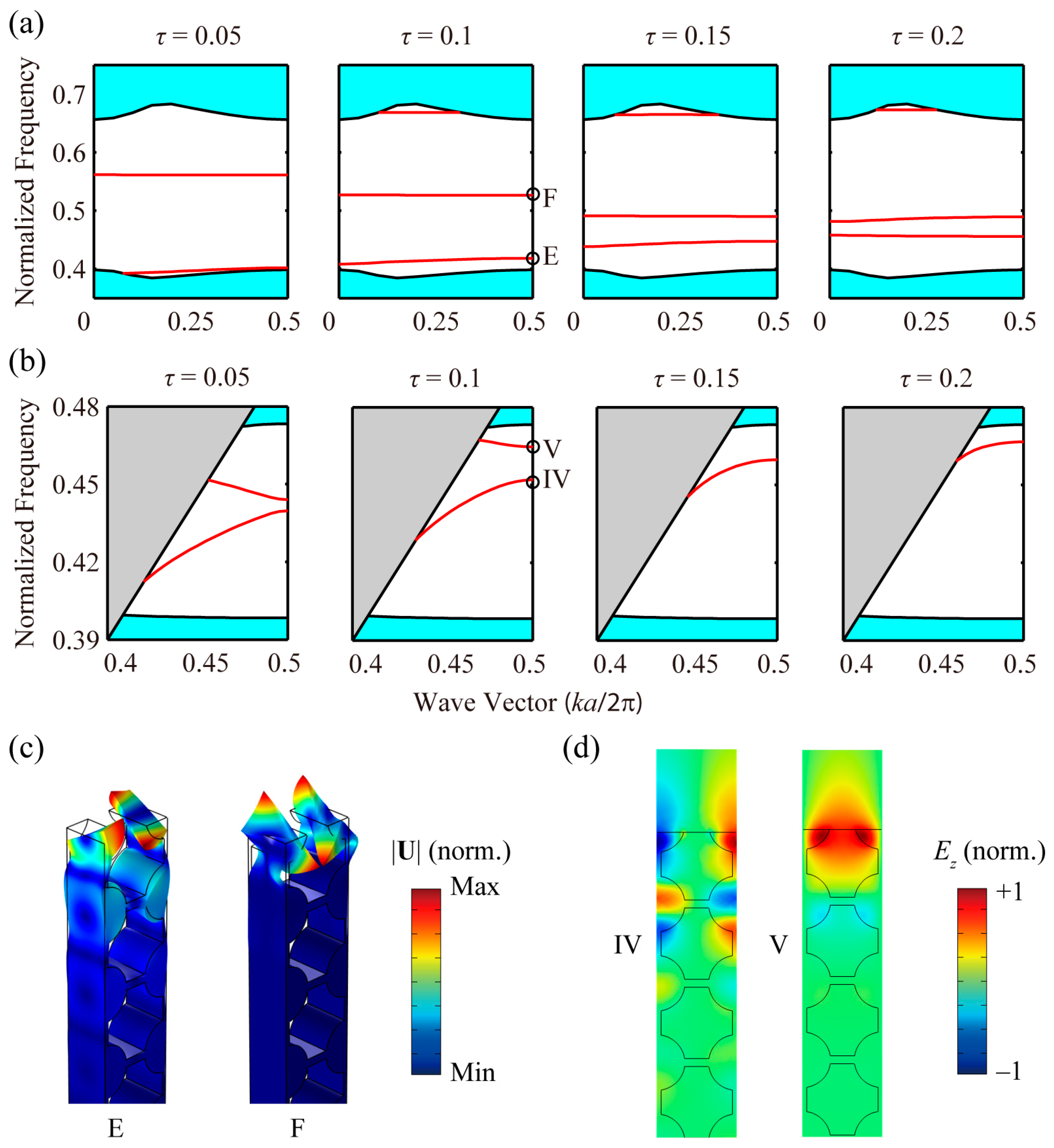
4.1. Phononic and Photonic Even Modes
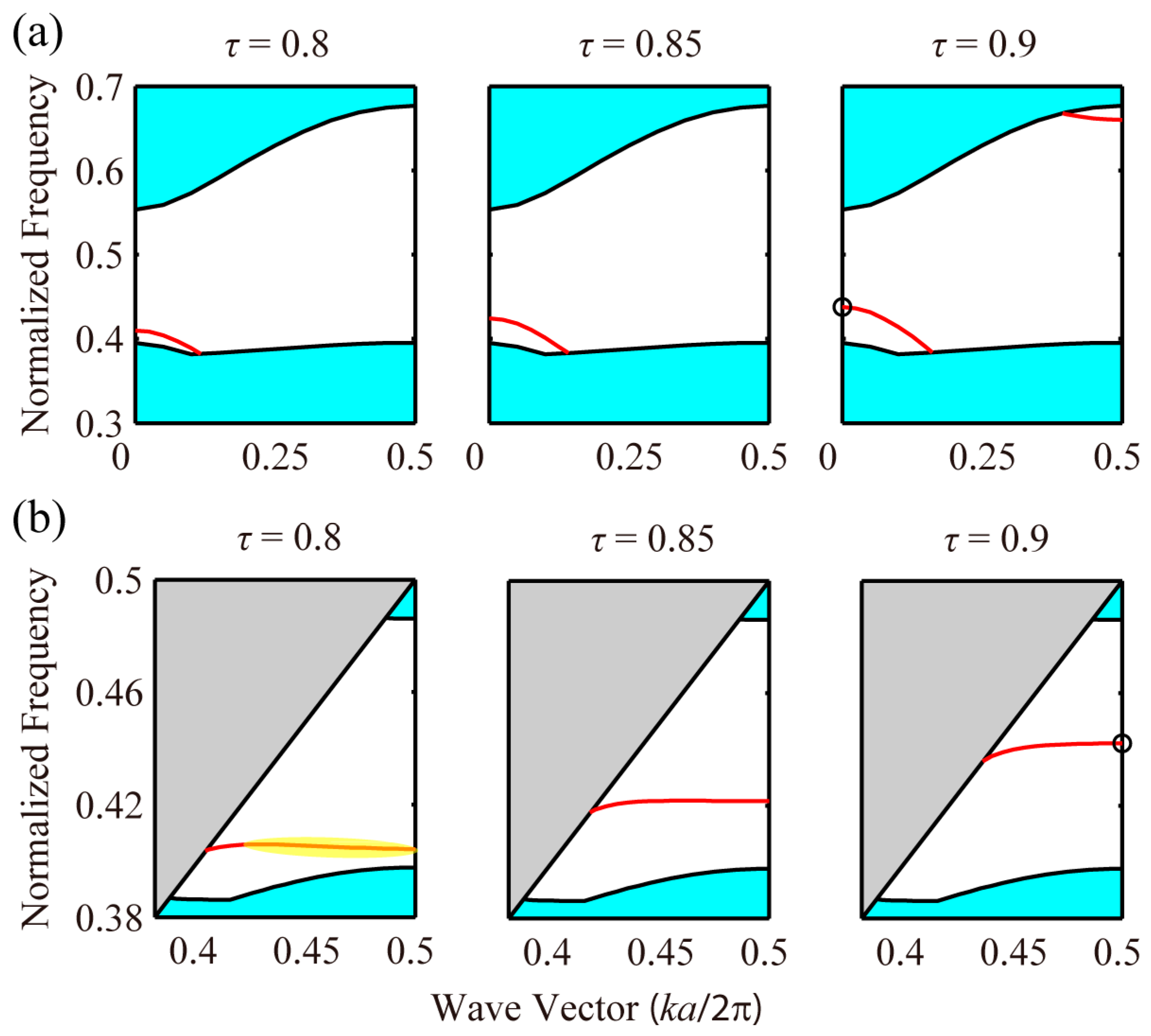
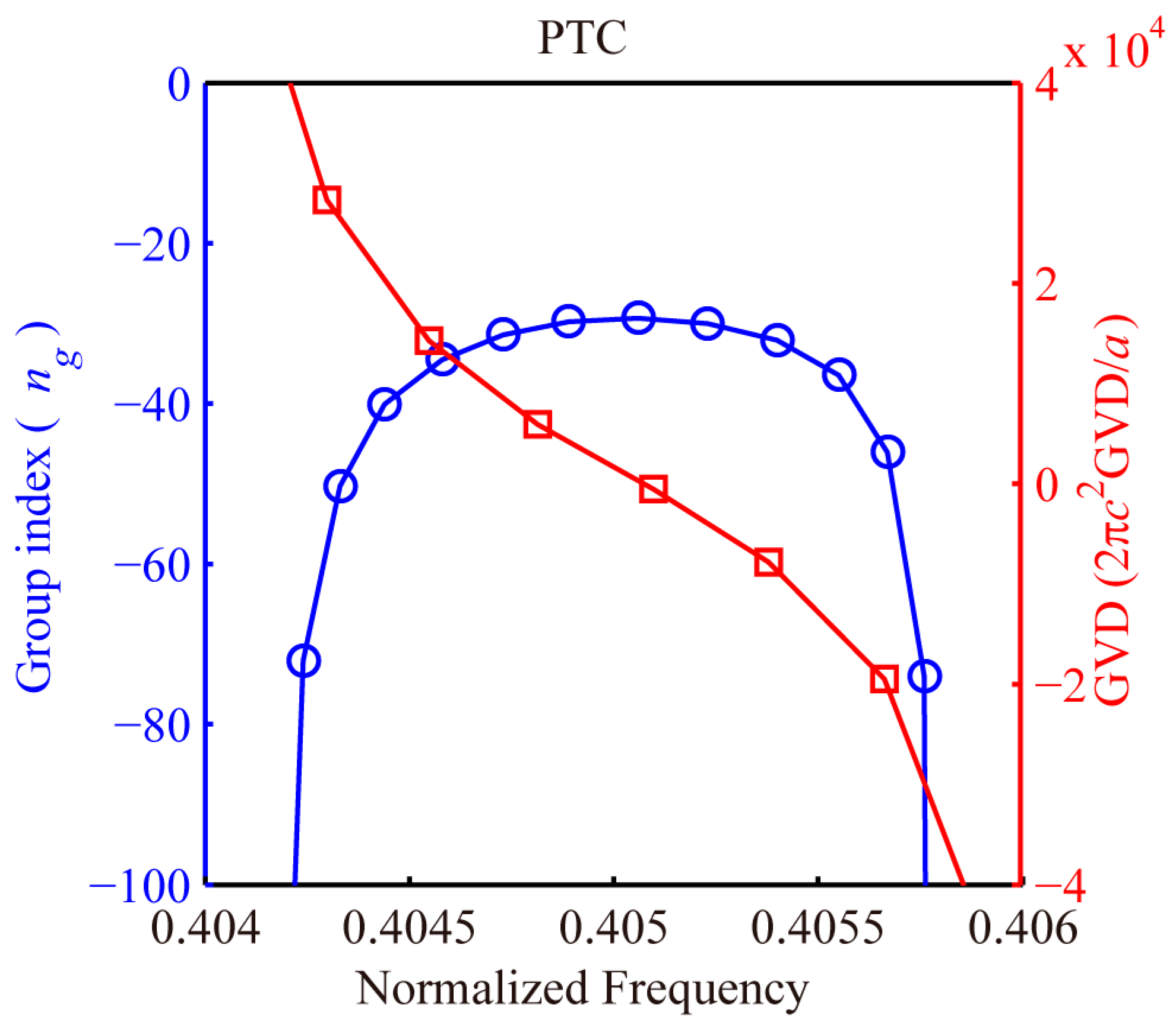
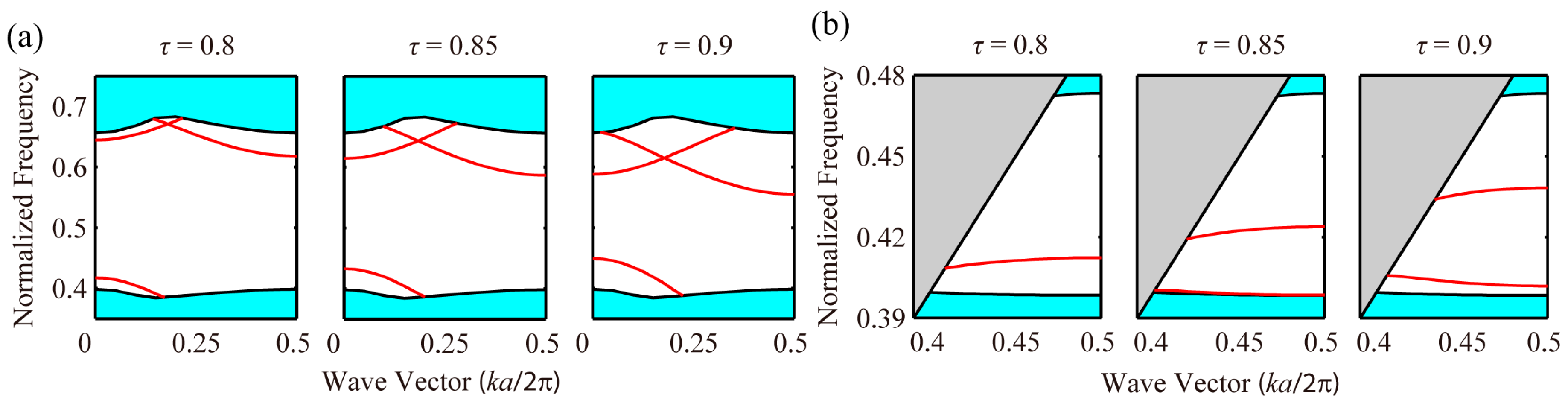
4.2. Phononic and Photonic Odd Modes
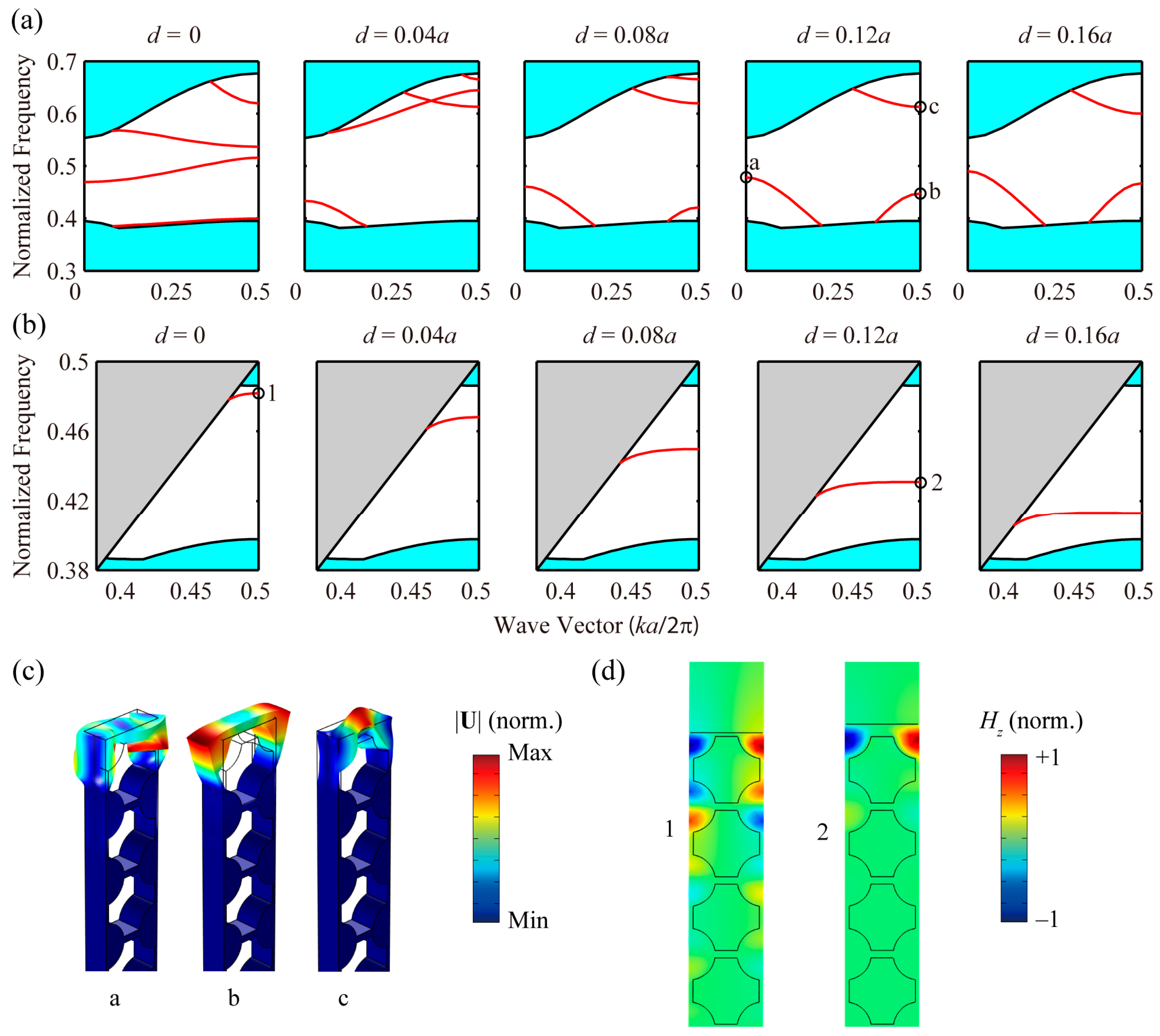
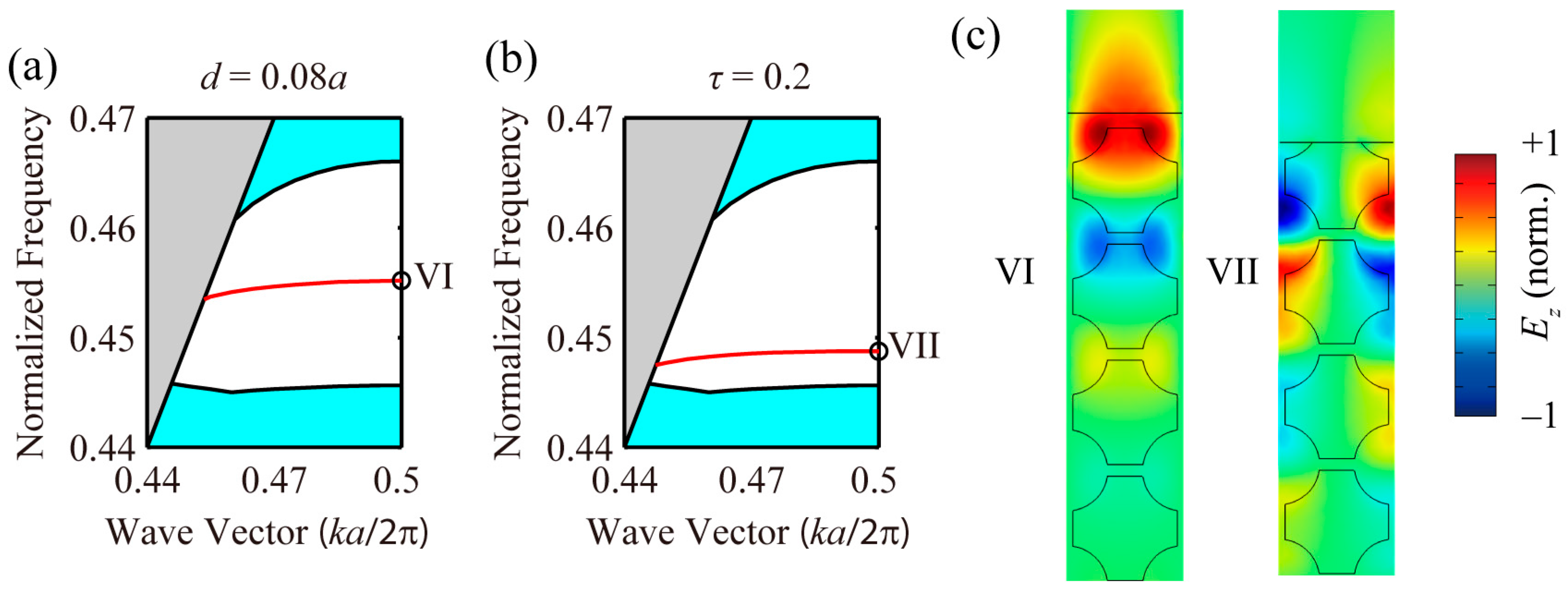
4.3. Phononic, Photonic Even and Odd Modes
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Pennec, Y.; Laude, V.; Papanikolaou, N.; Djafari-Rouhani, B.; Oudich, M.; El Jallal, S.; Beugnot, J.C.; Escalante, J.M.; Martínez, A. Modeling light-sound interaction in nanoscale cavities and waveguides. Nanophotonics 2014, 3, 413–440. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E.L. Simultaneous localization of photons and phonons in two-dimensional periodic structures. Appl. Phys. Lett. 2006, 88, 251907. [Google Scholar] [CrossRef]
- Maldovan, M.; Thomas, E.L. Simultaneous complete elastic and electromagnetic band gaps in periodic structures. Appl. Phys. B 2006, 83, 595–600. [Google Scholar] [CrossRef]
- Sadat-Saleh, S.; Benchabane, S.; Baida, F.I.; Bernal, M.P.; Laude, V. Tailoring simultaneous photonic and phononic band gaps. J. Appl. Phys. 2009, 106, 074912. [Google Scholar] [CrossRef]
- Papanikolaou, N.; Psarobas, I.E.; Stefanou, N. Absolute spectral gaps for infrared light and hypersound in three-dimensional metallodielectric phoxonic crystals. Appl. Phys. Lett. 2010, 96, 231917. [Google Scholar] [CrossRef]
- Mohammadi, S.; Eftekhar, A.A.; Khelif, A.; Adibi, A. Simultaneous two-dimensional phononic and photonic band gaps in opto-mechanical crystal slabs. Opt. Express 2010, 18, 9164–9172. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.X.; Wang, Y.S.; Wang, Y.F.; Su, X.X. Three-dimensional dielectric phoxonic crystals with network topology. Opt. Express 2013, 21, 2727–2732. [Google Scholar] [CrossRef] [PubMed]
- Rolland, Q.; Dupont, S.; Gazalet, J.; Kastelik, J.C.; Pennec, Y.; Djafari-Rouhani, B.; Laude, V. Simultaneous bandgaps in LiNbO3 phoxonic crystal slab. Opt. Express 2014, 22, 16288–16297. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.W.; Wang, Y.S.; Ma, T.X.; Su, X.X. Topology optimization of simultaneous photonic and phononic bandgaps and highly effective phoxonic cavity. J. Opt. Soc. Am. B 2014, 31, 2946–2955. [Google Scholar] [CrossRef]
- Laude, V.; Beugnot, J.C.; Benchabane, S.; Pennec, Y.; Djafari-Rouhani, B.; Papanikolaou, N.; Escalante, M.; Martinez, A. Simultaneous guidance of slow photons and slow acoustic phonons in silicon phoxonic crystal slabs. Opt. Express 2011, 19, 9690–9698. [Google Scholar] [CrossRef] [PubMed]
- Escalante, J.M.; Martínez, A.; Laude, V. Design of single-mode waveguides for enhanced light-sound interaction in honeycomb-lattice silicon slabs. J. Appl. Phys. 2014, 115, 064302. [Google Scholar] [CrossRef]
- Lucklum, R.; Zubtsov, M.; Oseev, A. Phoxonic crystals-a new platform for chemical and biochemical sensors. Anal. Bioanal. Chem. 2013, 405, 6497–6509. [Google Scholar] [CrossRef] [PubMed]
- Amoudache, S.; Pennec, Y.; Djafari Rouhani, B.; Khater, A.; Lucklum, R.; Tigrine, R. Simultaneous sensing of light and sound velocities of fluids in a two-dimensional phoXonic crystal with defects. J. Appl. Phys. 2014, 115, 134503. [Google Scholar] [CrossRef]
- Amoudache, S.; Moiseyenko, R.; Pennec, Y.; Djafari Rouhani, B.; Khater, A.; Lucklum, R.; Tigrine, R. Optical and acoustic sensing using Fano-like resonances in dual phononic and photonic crystal plate. J. Appl. Phys. 2016, 119, 114502. [Google Scholar] [CrossRef]
- Ma, T.X.; Wang, Y.S.; Zhang, C.; Su, X.X. Theoretical research on a two-dimensional phoxonic crystal liquid sensor by utilizing surface optical and acoustic waves. Sens. Actuators A 2016, 242, 123–131. [Google Scholar] [CrossRef]
- Chen, G.; Zhang, R.; Sun, J. On-chip optical mode conversion based on dynamic grating in photonic-phononic hybrid waveguide. Sci. Rep. 2015, 5, 10346. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.J.; Huo, S.Y. Investigation of dual acoustic and optical asymmetric propagation in two-dimensional phoxonic crystals with grating. Opt. Mater. Express 2017, 7, 1716–1724. [Google Scholar] [CrossRef]
- Almpanis, E.; Papanikolaou, N.; Stefanou, N. Breakdown of the linear acousto-optic interaction regime in phoxonic cavities. Opt. Express 2014, 22, 31595–31607. [Google Scholar] [CrossRef] [PubMed]
- Kipfstuhl, L.; Guldner, F.; Riedrich-Möller, J.; Becher, C. Modeling of optomechanical coupling in a phoxonic crystal cavity in diamond. Opt. Express 2014, 22, 12410–12423. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.C.; Lu, T.Y.; Lin, T.R. Acousto-optic coupling in phoxonic crystal nanobeam cavities with plasmonic behavior. Opt. Express 2015, 23, 25814–25826. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Cui, K.; Li, Y.; Feng, X.; Liu, F.; Zhang, W.; Huang, Y. Strong Optomechanical Coupling in Nanobeam Cavities based on Hetero Optomechanical Crystals. Sci. Rep. 2015, 5, 15964. [Google Scholar] [CrossRef] [PubMed]
- Chiu, C.C.; Chen, W.M.; Sung, K.W.; Hsiao, F.L. High-efficiency acousto-optic coupling in phoxonic resonator based on silicon fishbone nanobeam cavity. Opt. Express 2017, 25, 6076–6091. [Google Scholar] [CrossRef] [PubMed]
- Eichenfield, M.; Chan, J.; Camacho, R.M.; Vahala, K.J.; Painter, O. Optomechanical crystals. Nature 2009, 462, 78–82. [Google Scholar] [CrossRef] [PubMed]
- Psarobas, I.E.; Papanikolaou, N.; Stefanou, N.; Djafari-Rouhani, B.; Bonello, B.; Laude, V. Enhanced acousto-optic interactions in a one-dimensional phoxonic cavity. Phys. Rev. B 2010, 82, 174303. [Google Scholar] [CrossRef]
- Gomis-Bresco, J.; Navarro-Urrios, D.; Oudich, M.; El-Jallal, S.; Griol, A.; Puerto, D; Chavez, E.; Pennec, Y.; Djafari-Rouhani, B.; Alzina, F.; et al. A one-dimensional optomechanical crystal with a complete phononic band gap. Nat. Commun. 2014, 5, 4452. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Zheng, J.; Poot, M.; Wong, C.W.; Tang, H.X. Femtogram doubly clamped nanomechanical resonators embedded in a high-Q two-dimensional photonic crystal nanocavity. Nano Lett. 2012, 12, 2299–2305. [Google Scholar] [CrossRef] [PubMed]
- Safavi-Naeini, A.H.; Hill, J.T.; Meenehan, S.; Chan, J.; Gröblacher, S.; Painter, O. Two-dimensional phononic-photonic band gap optomechanical crystal cavity. Phys. Rev. Lett. 2014, 112, 153603. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Wang, Z.; Liu, W.; Wang, T.; Liu, N.; Liao, Q. Simultaneous large band gaps and localization of electromagnetic and elastic waves in defect-free quasicrystals. Opt. Express 2016, 24, 7951–7959. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liu, W.; Yu, T.; Wang, T. Simultaneous localization of photons and phonons within the transparency bands of LiNbO3 phoxonic quasicrystals. Opt. Express 2016, 24, 23353–23360. [Google Scholar] [CrossRef] [PubMed]
- Ishizaki, K.; Noda, S. Manipulation of photons at the surface of three-dimensional photonic crystals. Nature 2009, 460, 367–370. [Google Scholar] [CrossRef] [PubMed]
- Rahachou, A.I.; Zozoulenko, I.V. Waveguiding properties of surface states in photonic crystals. J. Opt. Soc. Am. B 2006, 23, 1679–1683. [Google Scholar] [CrossRef]
- Kramper, P.; Agio, M.; Soukoulis, C.M.; Birner, A.; Müller, F.; Wehrspohn, R.B.; Gösele, U.; Sandoghdar, V. Highly directional emission from photonic crystal waveguides of subwavelength width. Phys. Rev. Lett. 2004, 92, 113903. [Google Scholar] [CrossRef] [PubMed]
- Lu, T.W.; Hsiao, Y.H.; Ho, W.D.; Lee, P.T. High-index sensitivity of surface mode in photonic crystal hetero-slab-edge microcavity. Opt. Lett. 2010, 35, 1452–1454. [Google Scholar] [CrossRef] [PubMed]
- Hsu, J.C.; Hsu, C.H. Edge waves and resonances in two-dimensional phononic crystal plates. J. Appl. Phys. 2015, 117, 174504. [Google Scholar] [CrossRef]
- Ma, T.X.; Kui, Z.; Wang, Y.S.; Zhang, C.; Su, X.X. Acousto-optical interaction of surface acoustic and optical waves in a two-dimensional phoxonic crystal hetero-structure cavity. Opt. Express 2014, 22, 28443–28451. [Google Scholar] [CrossRef] [PubMed]
- Ma, T.X.; Wang, Y.S.; Zhang, C. Investigation of dual photonic and phononic bandgaps in two-dimensional phoxonic crystals with veins. Opt. Commun. 2014, 312, 68–72. [Google Scholar] [CrossRef]
- El-jallal, S.; Oudich, M.; Pennec, Y.; Djafari-Rouhani, B.; Makhoute, A.; Rolland, Q.; Dupont, S.; Gazalet, J. Optomechanical interactions in two-dimensional Si and GaAs phoXonic cavities. J. Phys. Condens. Matter 2014, 26, 015005. [Google Scholar] [CrossRef] [PubMed]
- Courjal, N.; Benchabane, S.; Dahdah, J.; Ulliac, G.; Gruson, Y.; Laude, V. Acousto-optically tunable lithium niobate photonic crystal. Appl. Phys. Lett. 2010, 96, 131103. [Google Scholar] [CrossRef]
- Hsiao, F.L.; Hsieh, C.Y.; Hsieh, H.Y.; Chiu, C.C. High-efficiency acousto-optical interaction in phoxonic nanobeam waveguide. Appl. Phys. Lett. 2012, 100, 171103. [Google Scholar] [CrossRef]
- Lin, T.R.; Lin, C.H.; Hsu, J.C. Enhanced acousto-optic interaction in two-dimensional phoxonic crystals with a line defect. J. Appl. Phys. 2013, 113, 053508. [Google Scholar] [CrossRef]
- Hou, J.; Gao, D.S.; Wu, H.M.; Hao, R.; Zhou, Z.P. Flat band slow light in symmetric line defect photonic crystal waveguides. IEEE Photonics Technol. Lett. 2009, 21, 1571–1573. [Google Scholar]
- Xu, Y.M.; Xiang, L.; Cassan, E.; Gao, D.S.; Zhang, X.L. Slow light in an alternative row of ellipse-hole photonic crystal waveguide. Appl. Opt. 2013, 52, 1155–1160. [Google Scholar] [CrossRef] [PubMed]
- Baba, T. Slow light in photonic crystals. Nat. Photonics 2008, 2, 465–473. [Google Scholar] [CrossRef]
- Cicek, A.; Kaya, O.A.; Yilmaz, M.; Ulug, B. Slow sound propagation in a sonic crystal linear waveguide. J. Appl. Phys. 2012, 111, 013522. [Google Scholar] [CrossRef]
- Malfanti, I.; Taschin, A.; Bartolini, P.; Torre, R. Evidence of slow acoustic surface waves on a 1D phononic surface by a pulsed laser spectroscopic technique resolved in time and space. EPL 2012, 97, 44010. [Google Scholar] [CrossRef]
- Qiu, W.; Rakich, P.T.; Shin, H.; Dong, H.; Soljačić, M.; Wang, Z. Stimulated Brillouin scattering in nanoscale silicon step-index waveguides: A general framework of selection rules and calculating SBS gain. Opt. Express 2013, 21, 31402–31419. [Google Scholar] [CrossRef] [PubMed]
- Van Laer, R.; Baets, R.; Van Thourhout, D. Unifying Brillouin scattering and cavity optomechanics. Phys. Rev. A 2016, 93, 053828. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, J. Design of silicon phoxonic crystal waveguides for slow light enhanced forward stimulated Brillouin scattering. J. Lightwave Technol. 2017, 35, 2917–2925. [Google Scholar] [CrossRef]
- Peano, V.; Brendel, C.; Schmidt, M.; Marquardt, F. Topological Phases of Sound and Light. Phys. Rev. X 2015, 5, 031011. [Google Scholar] [CrossRef]
- Brendela, C.; Peano, V.; Painter, O.J.; Marquardt, F. Pseudomagnetic fields for sound at the nanoscale. Proc. Natl. Acad. Sci. USA 2017, 114, E3390–E3395. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, T.-X.; Wang, Y.-S.; Zhang, C. Simultaneous Guidance of Surface Acoustic and Surface Optical Waves in Phoxonic Crystal Slabs. Crystals 2017, 7, 350. https://doi.org/10.3390/cryst7110350
Ma T-X, Wang Y-S, Zhang C. Simultaneous Guidance of Surface Acoustic and Surface Optical Waves in Phoxonic Crystal Slabs. Crystals. 2017; 7(11):350. https://doi.org/10.3390/cryst7110350
Chicago/Turabian StyleMa, Tian-Xue, Yue-Sheng Wang, and Chuanzeng Zhang. 2017. "Simultaneous Guidance of Surface Acoustic and Surface Optical Waves in Phoxonic Crystal Slabs" Crystals 7, no. 11: 350. https://doi.org/10.3390/cryst7110350
APA StyleMa, T.-X., Wang, Y.-S., & Zhang, C. (2017). Simultaneous Guidance of Surface Acoustic and Surface Optical Waves in Phoxonic Crystal Slabs. Crystals, 7(11), 350. https://doi.org/10.3390/cryst7110350






