FOX, Current State and Possibilities
Abstract
:1. Introduction
2. New Features in FOX
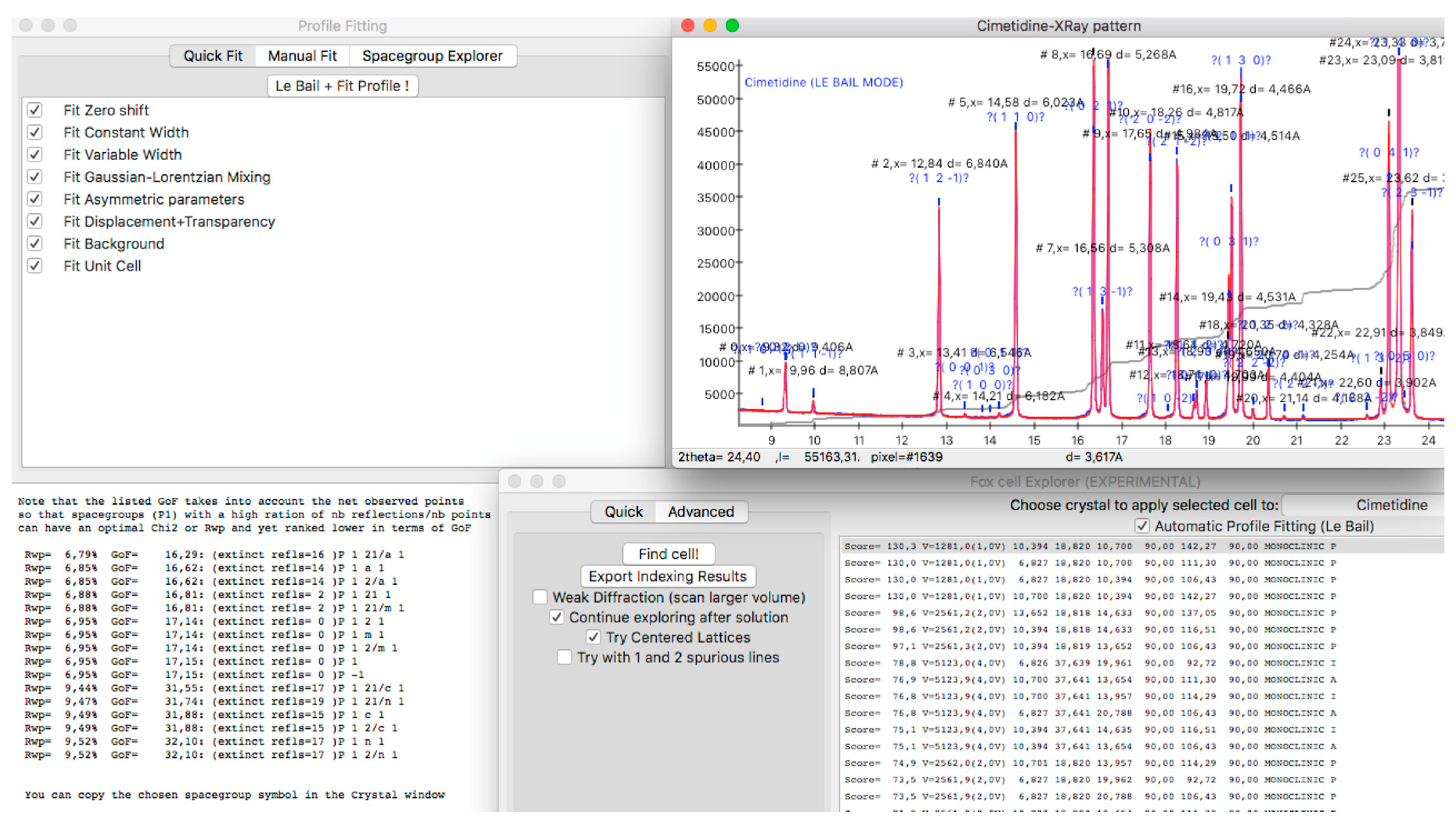
2.1. Preparation of Powder Diffraction Data
2.2. Global Optimization Features
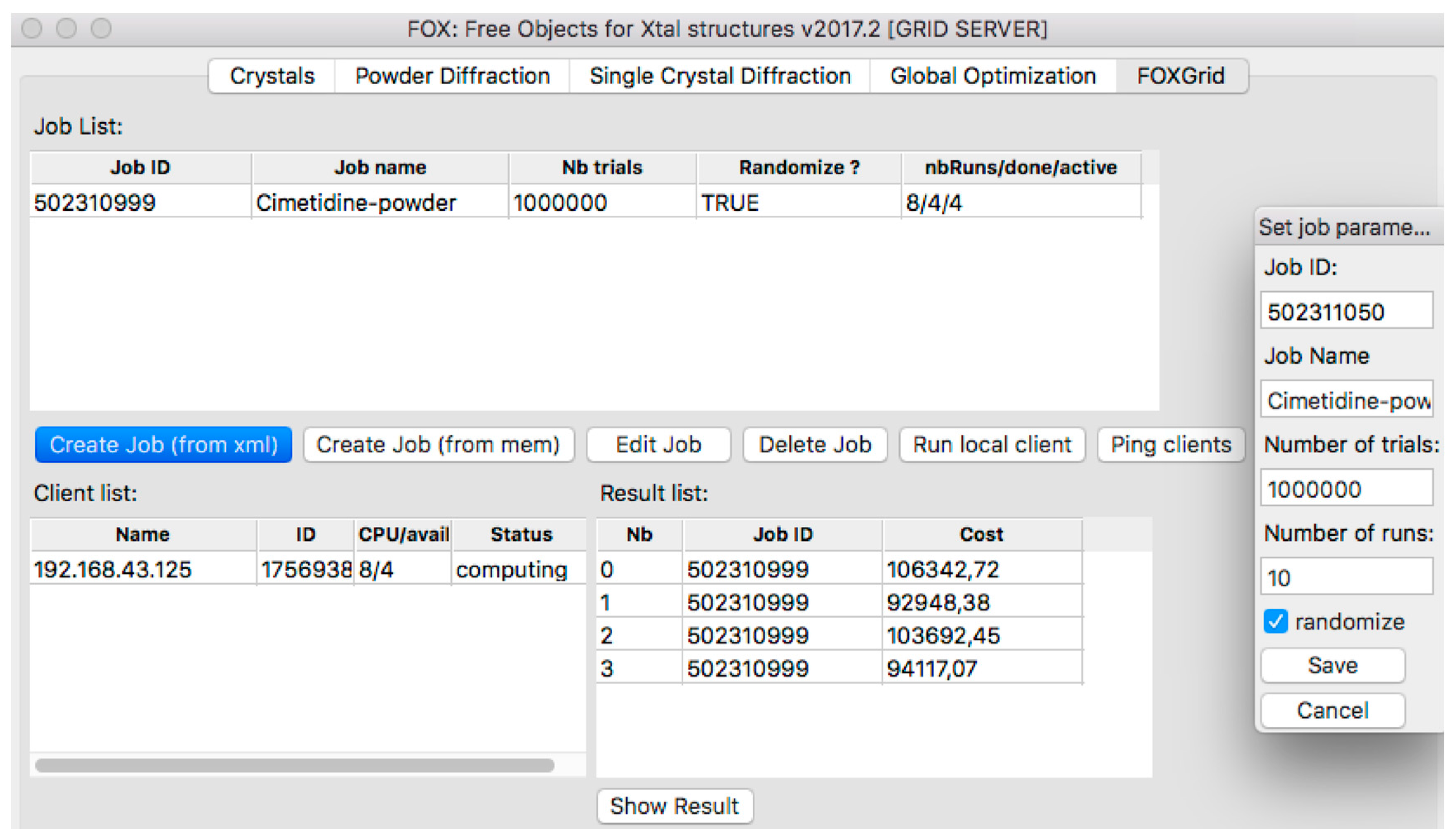
2.3. Distributed Computing
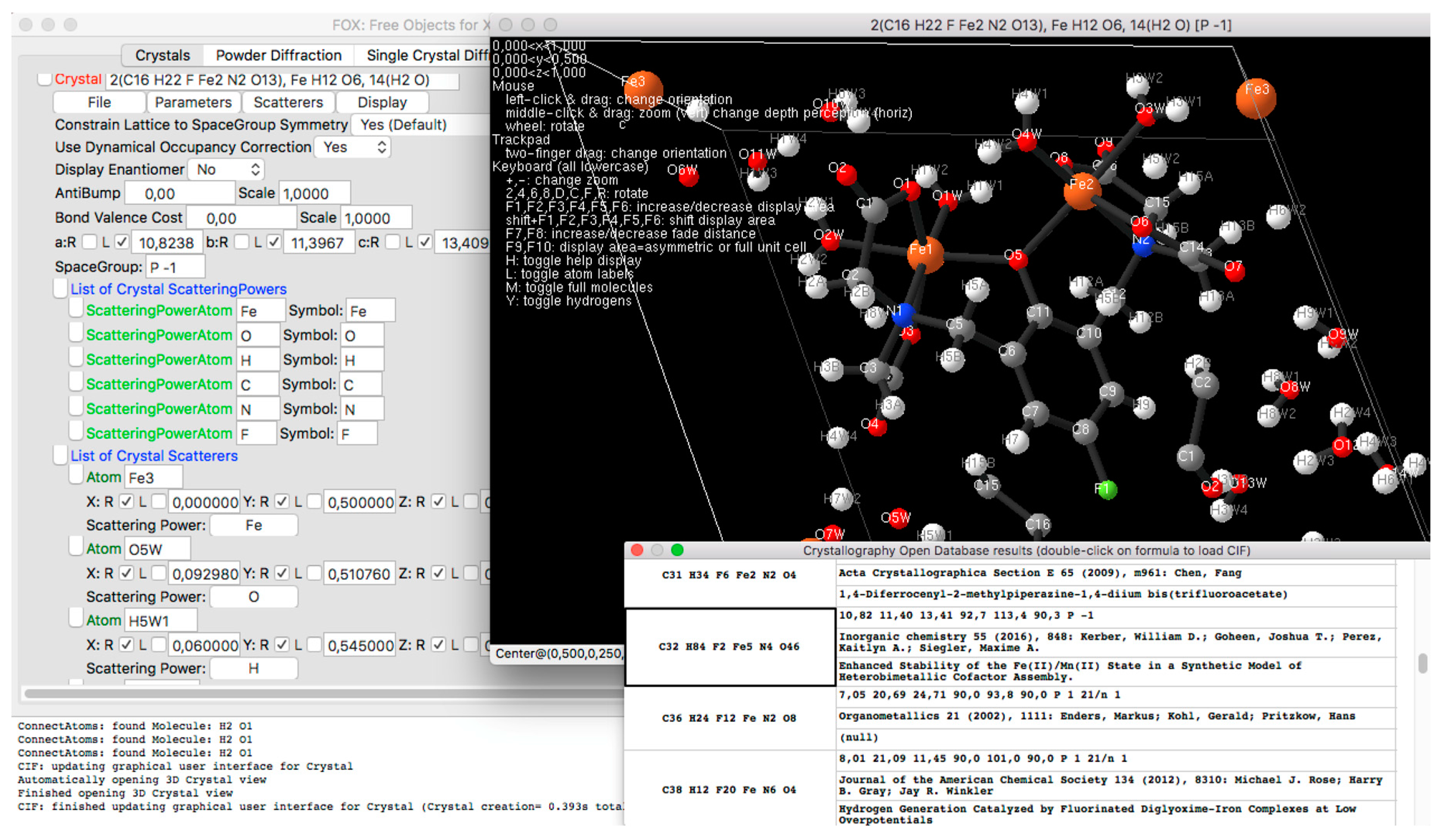
2.4. Import and Export, CIF and Crystallography Open Database
3. Examples
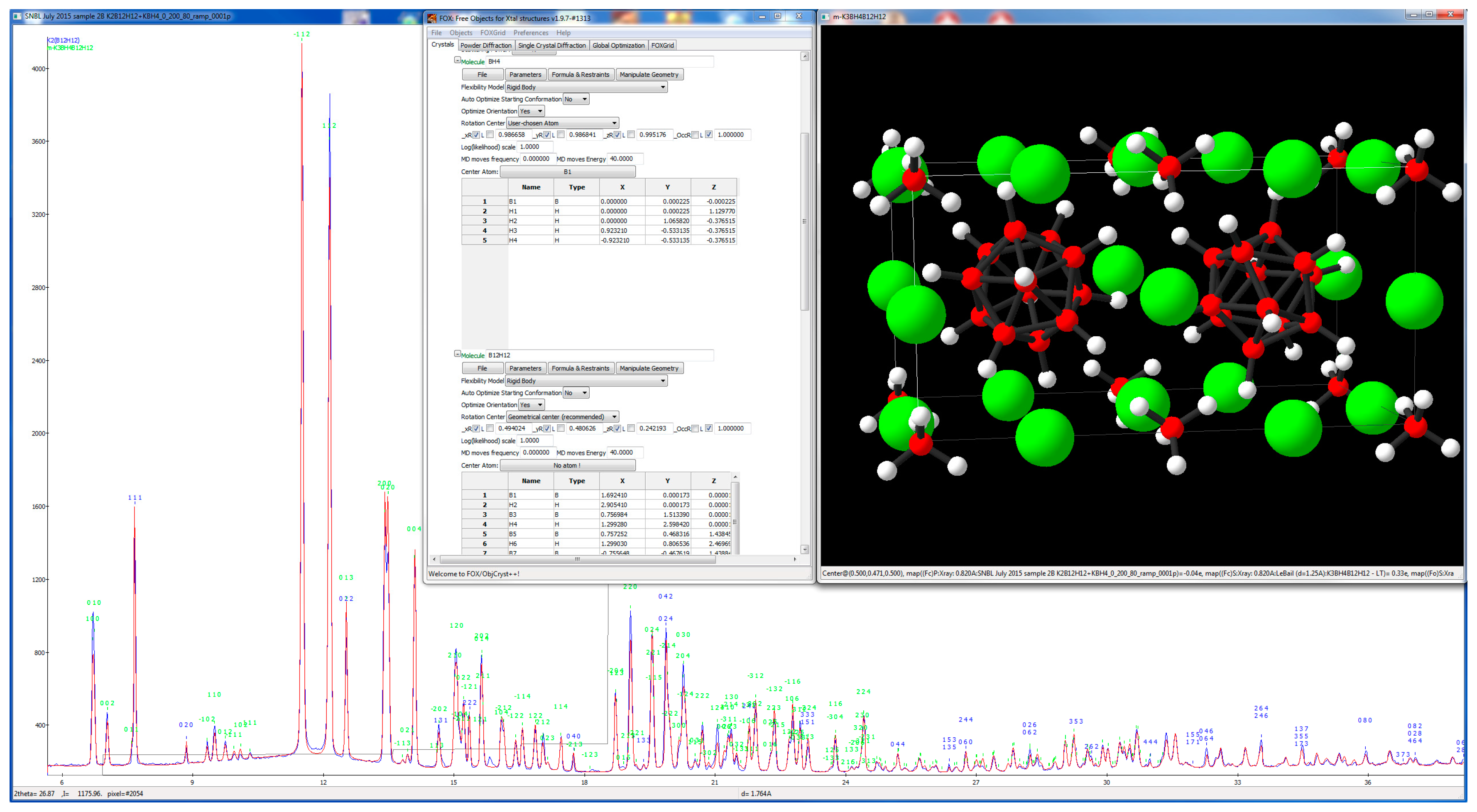
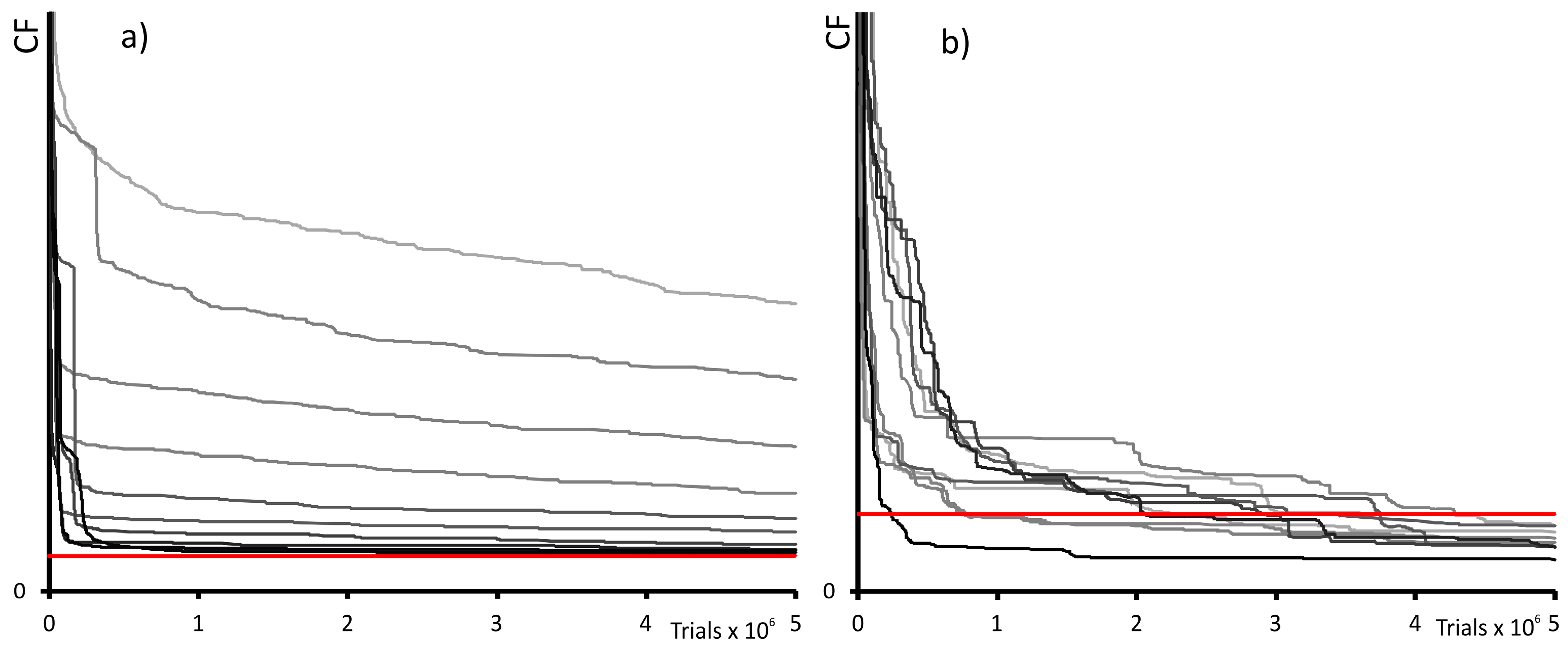
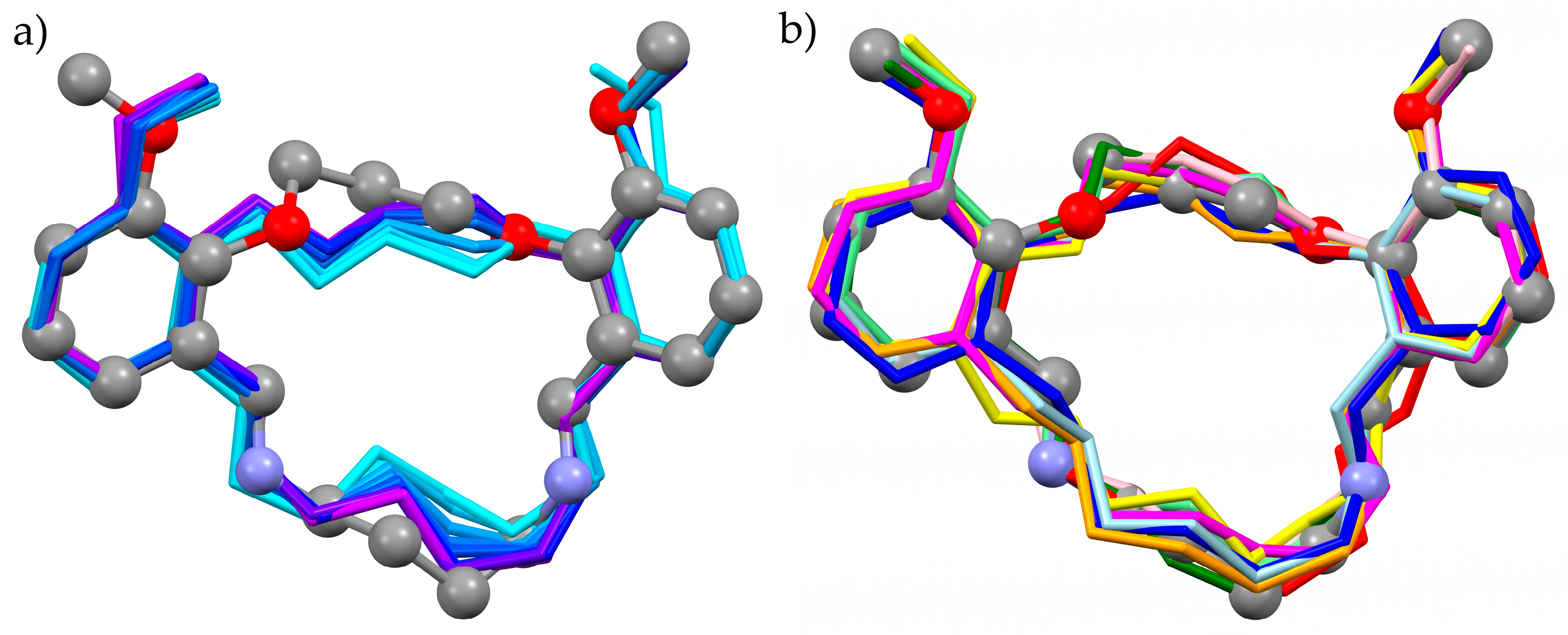
3.1. Inorganic Structure—Rigid Body and Orientation Disorder
3.2. Organic Structure—Molecule with Flexible Cycle
4. Availability of FOX
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Favre-Nicolin, V.; Černý, R. FOX, “Free Objects for Crystallography”: A modular approach to ab-initio structure determination from powder diffraction. J. Appl. Cryst. 2002, 35, 734–743. [Google Scholar] [CrossRef]
- Favre-Nicolin, V.; Černý, R. A better FOX: Using flexible modelling and maximum likelihood to improve direct-space ab initio structure determination from powder diffraction. Z. Kristallogr. 2004, 219, 847–856. [Google Scholar] [CrossRef]
- Update on ab-Initio Structure Determination Using FOX. Available online: http://www.iucr.org/__data/assets/pdf_file/0014/21623/cpd31.pdf (accessed on 24 October 2017).
- Černý, R.; Favre-Nicolin, V. FOX: A friendly tool to solve nonmolecular structures from powder diffraction. Powder Diffr. 2005, 20, 359–365. [Google Scholar] [CrossRef]
- FOX, Free Objects for Xtallography Version 1.7 (November 2005). Available online: http://www.iucr.org/__data/assets/pdf_file/0003/21657/CPD32.pdf (accessed on 24 October 2017).
- Černý, R.; Favre-Nicolin, V.; Rohlícek, J.; Hušák, M.; Matej, Z.; Kužel, R. Expanding FOX: Auto-indexing, grid computing, profile fitting. Comm. Powder Diffr. (IUCr) Newsl. 2007, 35, 16–19. [Google Scholar]
- David, W.I.F.; Sivia, D.S. Background estimation using a robust Bayesian analysis. J. Appl. Cryst. 2001, 34, 318–324. [Google Scholar] [CrossRef]
- Boultif, A.; Louër, D. Indexing of powder diffraction patterns for low-symmetry lattices by the successive dichotomy method. J. Appl. Cryst. 1991, 24, 987–993. [Google Scholar] [CrossRef]
- Boultif, A.; Louër, D. Powder pattern indexing with the dichotomy method. J. Appl. Cryst. 2004, 37, 724–731. [Google Scholar] [CrossRef]
- Louër, D.; Boultif, A. Powder pattern indexing and the dichotomy algorithm. Z. Kristallogr. Suppl. 2007, 26, 191–196. [Google Scholar] [CrossRef]
- De Wolff, P.M. The definition of the indexing figure of merit M20. J. Appl. Cryst. 1972, 5, 243. [Google Scholar] [CrossRef]
- Černý, R.; Filinchuk, Y. Complex inorganic structures from powder diffraction: Case of tetrahydroborates of light metals. Z. Kristallogr. 2011, 226, 882–891. [Google Scholar] [CrossRef]
- Le Bail, A. Whole powder pattern decomposition methods and applications: A retrospection. Powder Diffr. 2005, 20, 316–326. [Google Scholar] [CrossRef]
- McCusker, L.B.; Von Dreele, R.B.; Cox, D.E.; Louër, D.; Scardi, P. Rietveld refinement guidelines. J. Appl. Cryst. 1999, 32, 36–50. [Google Scholar] [CrossRef]
- Markvardsen, A.J.; David, W.I.F.; Johnson, J.C.; Shankland, K. A probabilistic approach to space-group determination from powder diffraction data. Acta Cryst. A 2001, 57, 47–54. [Google Scholar] [CrossRef]
- Pitt, M.P. In-situ Powder Diffraction Studies of Metal-Hydrogen Microstructures. Ph.D. Thesis, Griffith University, Nathan, Australia, 2003. [Google Scholar]
- Dollase, W.A. Correction of intensities for preferred orientation in powder diffractometry: Application of the March model. J. Appl. Cryst. 1986, 19, 267–272. [Google Scholar] [CrossRef]
- Falcioni, M.; Deem, M.W. A Biased Monte Carlo Scheme for Zeolite Structure Solution. J. Chem. Phys. 1999, 110, 1754–1766. [Google Scholar] [CrossRef]
- Earl, D.J.; Deem, M.W. Parallel tempering: Theory, applications, and new perspectives. Phys. Chem. Chem. Phys. 2005, 7, 3910–3916. [Google Scholar] [CrossRef] [PubMed]
- David, W.I.F.; Shankland, K.; Van de Streek, J.; Pidcock, E.; Motherwell, W.D.S.; Cole, J.C. DASH: A program for crystal structure determination from powder diffraction data. J. Appl. Cryst. 2006, 39, 910–915. [Google Scholar] [CrossRef]
- Johnston, J.C.; David, W.I.F.; Markvardsen, A.J.; Shankland, K. A hybrid Monte Carlo method for crystal structure determination from powder diffraction data. Acta Cryst. A 2002, 58, 441–447. [Google Scholar] [CrossRef]
- Markvardsen, A.J.; Shankland, K.; David, W.I.F.; Didlick, G. Characterization of a hybrid Monte Carlo search algorithm for structure determination. J. Appl. Cryst. 2005, 38, 107–111. [Google Scholar] [CrossRef]
- Turner, G.W.; Tedesco, E.; Harris, K.D.M.; Johnston, R.L.; Kariuki, B.M. Implementation of Lamarckian concepts in a Genetic Algorithm for structure solution from powder diffraction data. Chem. Phys. Lett. 2000, 321, 183–190. [Google Scholar] [CrossRef]
- Cernik, R.J.; Cheetham, A.K.; Prout, C.K.; Watkin, D.J.; Wilkinson, A.P.; Willis, B.T.M. The structure of cimetidine (C10H16N6S) solved from synchrotron-radiation X-ray powder diffraction data. J. Appl. Cryst. 1991, 24, 222–226. [Google Scholar] [CrossRef]
- Shankland, K.; Markvardsen, A.J.; Rowlatt, C.; Shankland, N.; David, W.I.F. A benchmark method for global optimization problems in structure determination from powder diffraction data. J. Appl. Cryst. 2010, 43, 401–406. [Google Scholar] [CrossRef]
- Fernandes, P.; Shankland, K.; David, W.I.F.; Markvardsen, A.J.; Florence, A.J.; Shankland, N.; Leech, C.K. A differential thermal expansion approach to crystal structure determination from powder diffraction data. J. Appl. Cryst. 2008, 41, 1089–1094. [Google Scholar] [CrossRef]
- Griffin, T.A.N.; Shankland, K.; Van de Streek, J.; Cole, J. GDASH: A grid-enabled program for structure solution from powder diffraction data. J. Appl. Cryst. 2009, 42, 356–359. [Google Scholar] [CrossRef]
- Spillman, M.J.; Shankland, K.; Williams, A.C.; Cole, J.C. CDASH: A cloud-enabled program for structure solution from powder diffraction data. J. Appl. Cryst. 2015, 48, 2033–2039. [Google Scholar] [CrossRef]
- Recent Developments of the Program FULLPROF. Available online: http://www.iucr.org/__data/assets/pdf_file/0019/21628/cpd26.pdf (accessed on 24 October 2017).
- Gražulis, S.; Chateigner, D.; Downs, R.T.; Yokochi, A.F.T.; Quirós, M.; Lutterotti, L.; Manakova, E.; Butkus, J.; Moeck, P.; Le Bail, A. Crystallography Open Database—An open-access collection of crystal structures. J. Appl. Cryst. 2009, 42, 726–729. [Google Scholar] [CrossRef] [PubMed]
- Paskevicius, M.; Jepsen, L.H.; Schouwink, P.; Černý, R.; Ravnsbaeck, D.; Filinchuk, Y.; Dornheim, M.; Besenbacher, F.; Jensen, T.R. Metal borohydrides and derivatives—Synthesis, structure and properties. Chem. Soc. Rev. 2017, 46, 1565–1634. [Google Scholar] [CrossRef] [PubMed]
- Sadikin, Y.; Skoryunov, R.V.; Babanova, O.A.; Soloninin, A.V.; Lodziana, Z.; Brighi, M.; Skripov, A.V.; Černý, R. Anion disorder in K3BH4B12H12 and its effect on cation mobility. J. Phys. Chem. C 2017, 121, 5503–5514. [Google Scholar] [CrossRef]
- Khalaji, A.D.; Ghoran, S.H.; Rohlíček, J.; Dušek, M. Characterization and crystal structure of a 17-membered macrocyclic Schiff base compound MeO-sal-pn-bn. J. Struct. Chem. 2015, 56, 259–265. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Černý, R.; Favre-Nicolin, V.; Rohlíček, J.; Hušák, M. FOX, Current State and Possibilities. Crystals 2017, 7, 322. https://doi.org/10.3390/cryst7100322
Černý R, Favre-Nicolin V, Rohlíček J, Hušák M. FOX, Current State and Possibilities. Crystals. 2017; 7(10):322. https://doi.org/10.3390/cryst7100322
Chicago/Turabian StyleČerný, Radovan, Vincent Favre-Nicolin, Jan Rohlíček, and Michal Hušák. 2017. "FOX, Current State and Possibilities" Crystals 7, no. 10: 322. https://doi.org/10.3390/cryst7100322
APA StyleČerný, R., Favre-Nicolin, V., Rohlíček, J., & Hušák, M. (2017). FOX, Current State and Possibilities. Crystals, 7(10), 322. https://doi.org/10.3390/cryst7100322




