1. Introduction
Oxide single crystals are the prerequisite for many applications, as e.g., hosts for lasers, frequency doublers in lasers, sensors exploiting the piezoelectric effect, and substrates for functional layers of oxides. In particular,
β-Ga
O
as a transparent semiconducting oxide has recently become of great interest for the design of new types of electronic devices [
1]. Bulk crystals of this material can act as a substrate not only for homoepitaxy (see e.g., [
2]), but also for epitaxy of mixed systems of (In
Ga
)
O
[
3] or (Al
Ga
)
O
[
4]. One way of growing single crystals of
β-Ga
O
is the Czochralski method, where the crystal is pulled from a melt hosted in an iridium crucible. Heat is induced in the crucible by electro-magnetic heating. Single crystals have been succesfully grown by this method [
5,
6,
7,
8]. The major issue associated with growing Ga
O
single crystals from the melt is its thermal instability at high temperatures leading to a strong decomposition. Applying a new approach [
5] allowed for growing two-inch diameter crystals with a weight of up to 1 kg. Additionally, free carrier absorption within a growing semiconducting crystal causes problems with heat removal from the growth interface, leading to its inversion from convex to concave and, consequently, to a spiral formation [
6]. Growing large crystal size enhances both decomposition (larger melt volume) and free carrier absorption (larger optical thickness of the crystal), and also thermal stresses, which may affect the structural quality, such as dislocation formation, twinning and cracking. Numerical calculations can contribute to a better understanding and eventually lead to improvements of the growth process.
The growth process of
β-Ga
O
includes all of the challenges for numerical modelling of oxide crystal growth, namely high melting point temperature causing radiation as an important heat transport mechanism, semitransparency of crystal depending on the doping, time dependent melt flow, formation of facets, and anisotropy of several properties. The latter three points usually require a 3D calculation and, thus, a high amount of computational resources. At first glance, for computing melt convection, a local calculation including the melt and maybe crucible and crystal is enough because the three -dimensionality results only from the flow instability. Oxide melts have a Prandtl number larger than 1 (
,
specific heat,
μ dynamic viscosity,
λ thermal conductivity), which means a significant heat transport by convection. In contrast to typical semi-conductor problems, the melt flow is time-dependent but far away from turbulence. Some researchers looked for the onset of the flow instability in oxide melts [
9], but the realistic conditions are far beyond the ones considered there. For more realistic Grashof numbers, 3D computations have been performed but only for the melt applying simple boundary conditions at its side, bottom and top [
10,
11]. The bottom was set adiabatic and a constant temperature was set at the side. At the melt/crystal interface, there was melting point temperature and the free melt surface at the top was also assumed to be adiabatic. Enger et al. [
11] performed computations for a melt of Prandtl number Pr = 10.5 and, later, Jing et al. [
10] performed runs for Pr = 13.6, as it is the Prandtl number of LiNbO
melt. The computations comprised buoyancy and Marangoni convection as well as crystal rotation and exhibited a time-dependent behaviour of the convection. The temperature distribution on the free melt surface showed a structure, which changed in time. The pattern depends on the rotation rate, as was found by Jing et al. However, there are strong restrictions in these computations because of the adiabatic assumption at the free surface of the melt. In real systems, a heat exchange by radiation takes place, adding another non-linearity (the radiation heat flux depends on
) the non-linearity of the Navier–Stokes equations governing the melt convection. Therefore, Tsukada et al. introduced a coupling of a global axisymmetric calculation with a local 3D one [
12]. In the local calculation comprising melt, crucible, and crystal, the time-dependent flow was computed using temperature boundary conditions from the global axisymmetric calculations. Afterwards, the time-averaged velocity field is used in the global calculation for updating the temperature field and the melt/crystal interface shape. In this study, we did not make any back coupling from 3D to axisymmetric calculations but included the complete inner part of the furnace in our 3D calculations. However, we used a rather high viscosity (
), which yields a nearly time-independent flow. The main focus is on the influence of the crystal orientation on the thermal stress. More detailed investigations of the melt convection are part of upcoming research.
The importance of the internal radiation was already shown by Xiao and Derby [
13] and, later, by Galazka et al. [
14]. The additional heat transport compared to an opaque crystal leads to conical interface deep into the melt. Later, Kobayashi et al. investigated the effect of different absorption coefficients on the thermal stress in the Czochralski growth of a LiNbO
crystal [
15]. Budenkova et al. applied the discrete ordinate method [
16] to compute the interface shape including facet formation [
17]. For simplicity, they only consider a central facet of the Bi
GeO
(BGO) crystal. A much more elaborated algorithm with a kinetic operator to compute the interface motion was applied by Weinstein and Miller in a fully 3D calculation [
18]. However, the internal radiation was neglected. Nevertheless, the experimentally observed influence of crystal rotation rate and pulling velocity on the facet formation [
19] was also found by their computations.
In our study, we assumed a completely transparent crystal. This is a reasonable approach if the
β-Ga
O
crystal is electrically insulating, e.g., by doping with Mg. For comparison, calculations of the temperature field have also been performed for an opaque and a semi-transparent crystal. Considering facets requires a different kind of numeric approach, which was not part of this study. The key point of this study is the anisotropy of the thermal conductivity, the thermal expansion, and the elasticity coefficients. Thus, for the same process, thermal stress might be different for different crystal orientation with respect to the pulling direction. Such effect has been studied some time ago for the Czochralski growth of Gd
SiO
[
20]. However, in that study, the thermal field was taken from the estimation for a different material. In this paper, we will present global axisymmetric and 3D calculations of the thermal field that enter the computation of the thermal stress.
3. Computation
A sketch of the furnace geometry is given on the left-hand side of
Figure 2. The heat is induced in the iridium crucible by the electric current with a frequency of
in the copper-made coil. This coil outside the insulation is water cooled, and we apply a fixed temperature of 300 K. All computations have been performed for crystal of 2″ diameter with a length of 91 mm plus a seed of 37 mm length. At this growth stage, the melt height was 62 mm in reference to the crucible bottom. The growth rate was 1.5 mm/h and the rotation rate of the crystal was 5 rpm.
In order to treat the anisotropies in the crystal, we have to perform 3D calculations and have to at least include the inner part where the radiative heat exchange with crystal takes place. In particular, we used the inner part including most all insulations as sketched in
Figure 2 (middle part). Thermal boundary conditions in terms of temperatures and the distribution of heat sources in the iridium crucible are taken from an axisymmetric calculation using CrysMAS [
34]. The final computation of thermal stress is done by applying the software tool comsol. For the latter step, we took only the crystal including seeds, applying the temperatures obtained in the 3D calculation with Ansys-cfx.
For comparison, various calculations have been done with CrysMAS and the software CGsim (
http://www.str-soft.com/). Regarding the numerical schemes of the different software tools, all tools used—CrysMAS, CGsim, and Ansys-cfx—apply finite volume schemes to solve the transport equations. The anisotropy of the thermal conductivity can be handled as follows:
CrysMAS and CGsim: different values for radial and vertical directions;
Ansys-cfx: different values for x-, y-, and z-directions;
comsol: full matrix.
In all runs, we solved the Navier–Stokes equation directly and did not use a turbulence model.
Both CrysMAS and CGsim solve the inverse problem of finding the required heater power, however in a different manner. CrysMAS uses the temperature difference at the three-phase junction ( versus current temperature) to adjust the heater power. CGsim applies along the entire interface and computes the latent heat required to fulfill this constraint. At the three-phase junction, the difference between the growth rate computed from the required latent heat and the given one is used for adjusting the heater power. In 3D, the computation of the inverse problem is not applicable because iterative relaxation of the temperature field takes too much time. However, the heat source distribution as obtained from CrysMAS is multiplied by a factor, which was adapted by hand from run to run.
As already mentioned, radiation is an important mechanism of heat transport. It is handled differently in the three software packages used. In cavities filled with transparent material, the wall-to-wall radiation is computed. The view factors are computed once before the run, and the computer time needed for the radiative heat transport is negligible. In CrysMAS, such a cavity can contain both gas and solid materials. Thus, in our case, a completely transparent crystal cavity for radiation is given by the crystal/melt interface, the crystal/holder boundary, the melt interface and the inner part of the furnace. In CGsim, only the gas is treated as transparent. The crystal can be treated as semi-transparent, solving the radiative transport by the discrete ordinate method [
35]. Transparency can be achieved by choosing small absorption and scattering coefficients (here, we chose
and
). However, the solid material still has a refractive index, which makes the problem different from a transparent cavity of gas and crystal together. Ansys-cfx uses the Monte Carlo method to compute the movements of photons. This is the most general approach but also the most time-consuming.
Different types of grids have been used in the different software tools:
CrysMAS: Unstructured triangles for the entire geometry—in regions with convection, a structured rectangular grid is used for solving the Navier–Stokes equation (not applied in this paper).
CGsim: Every domain can have an unstructured triangle or structured rectangular grid. At interfaces of domains, grids do not need to match, but values are interpolated. Only at the crystal melt must interface grids match. For the view factor calculation, an independent grid definition is used.
Ansys-cfx: We used a fully structured grid. In all computations presented in this paper, we had a total amount of 1,330,756 nodes. In the crystal, the number of grid elements was 140,676. In order to save computational time, for the Monte Carlo ray tracing, the number of grid points can be reduced. Treating the crystal as transparent, we reduced the number of elements for ray tracing to 19,810 in the crystal.
In the axisymmetric runs, the interface shape can be computed. Both CGsim and CrysMAS can adapt the crystal/melt interface shape to the isoline of the melting-point temperature. The node points on the interface are moved in the vertical direction, and the rest of the grid in adjacent domains is adjusted. In CrysMAS, the drawback is the fact that the view factors are not recomputed and, thus, might not fit to the new shape of the interface. This does not held for CGsim because here the discrete ordinate method is used for computing the heat transport by radiation. In 3D, the computation of the interface shape in our problem is currently beyond our capabilities. In fact, in order to include facet formation, we need to use a different program than Ansys-cfx (see [
18]). As we know the crystal shape from the experiment, we used this geometry for our 3D computations. At the crystal/melt boundary, we apply an additional heat flux (
) for latent heat release, corresponding to a growth rate of 1.5 mm/h.
The computation of the 3D thermal stresses were performed by using the software comsol Multiphysics (v. 5.2, COMSOL Multiphysics GmbH, Göttingen, Germany), i.e., by using the modules for linear elasticity and for heat transfer in solids, which were coupled by temperature and thermal expansion. The temperature data for all outer boundaries (crystal–melt interface, surface of cylinder, cone and seed) were taken from global modelling of the inner part of the crystal growth equipment (middle of
Figure 2) and set as a Dirichlet-type condition. Hence, the temperature distribution within the crystal was recomputed by using the same thermal conductivity as in the global modelling. For the mechanics, the displacements are set to zero at the ring boundary of the seed end wall where the crystal is fixed to the holder. The reference temperature is the temperature at the top of the seed. The Comsol procedure uses the finite element method, and we selected elements with quadratic shape function. The tensorial material properties such as thermal conductivity, thermal expansion coefficients and elasticity coefficients were treated by rotation operation in order to meet the crystal orientation.
The overall strategy is the following: in the first step (left side of
Figure 2), the temperature field is computed by a global simulation within a real growth furnace and chamber. For the calculations, measured temperature values at different points of the furnace were used as monitoring points.
In the first attempt, we performed a calculation using CrysMAS without melt convection and with a uniform thermal conductivity
. From this calculation, we extract the temperatures at the boundaries of the 3D domain (middle of
Figure 2). At the insulation (domain in magenta), the data from CrysMAS is directly used (interpolation to the grid used with Ansys-cfx). At the (virtual) outer boundary of the gas domain (blue), we approximate the temperature profile by
and
at the side and the top, respectively.
r is the radius and
z the vertical coordinate measured from the bottom of the inhousing. Then, we performed the 3D calculations as described in the next section. The 3D calculations of the thermal field were very time-consuming. Therefore, we did not update the boundary conditions by axisymmetric computations including melt convection, as we recently performed with CGsim. In the end, we used the temperature distribution at the crystal and seed boundary as input for the computation with Comsol. The thermal computations was repeated and afterwards the thermal stress was calculated.
4. Results
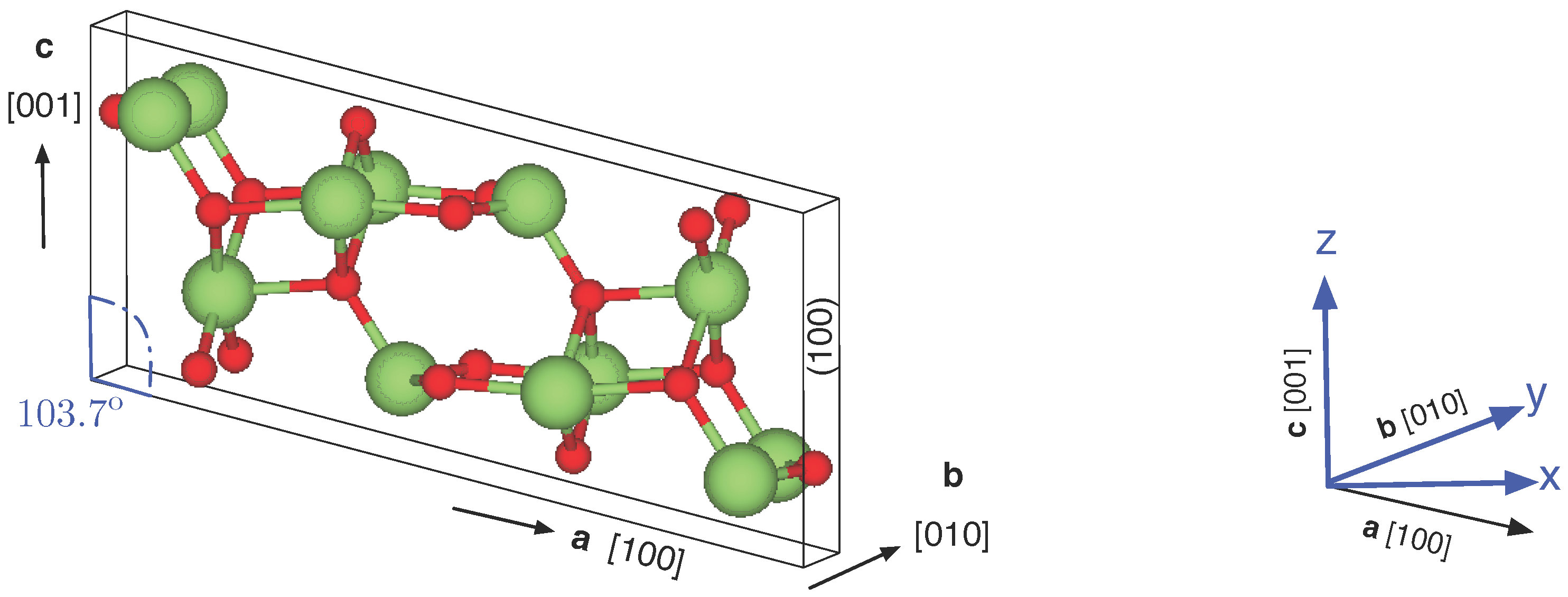
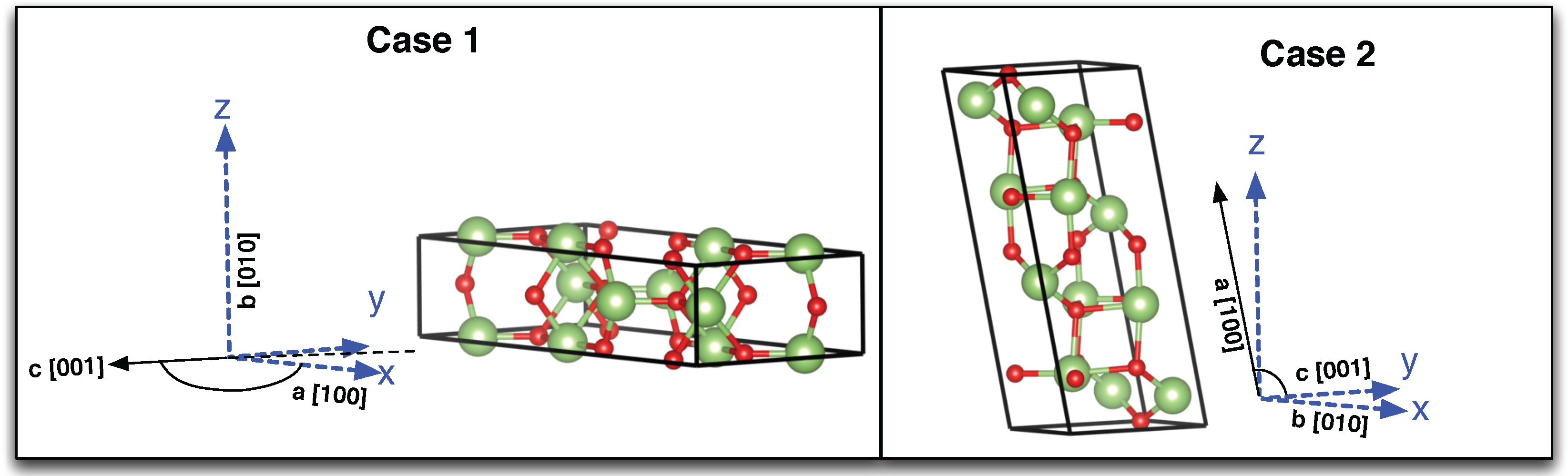
The main question we address is the influence of the crystal orientation on the von Mises stress. We used two orientations of the crystal: in Case 1, the growth direction is the
b-axis ((010) plane in the growth direction) as in all of our growth experiments by the Czochralski method; in Case 2, the growth direction is the
a*-axis ((100) plane in the growth direction). This orientation has not been used in the Czochralski growth but was observed in the vertical Bridgman growth [
25]. The two orientations are shown in
Figure 3. The thermal conductivities in
are:
| | Vertical | Horizontal |
| | | | | |
| Case 1 | 2.11 | 1.07 | 1.79 | 1.43 |
| Case 2 | 1.23 | 2.61 | 1.63 | 1.87 |
() has been computed from the tensor by appropriate rotations. and are used in the 3D computations. is used in the axisymmetric calculations and was computed as the average of and .
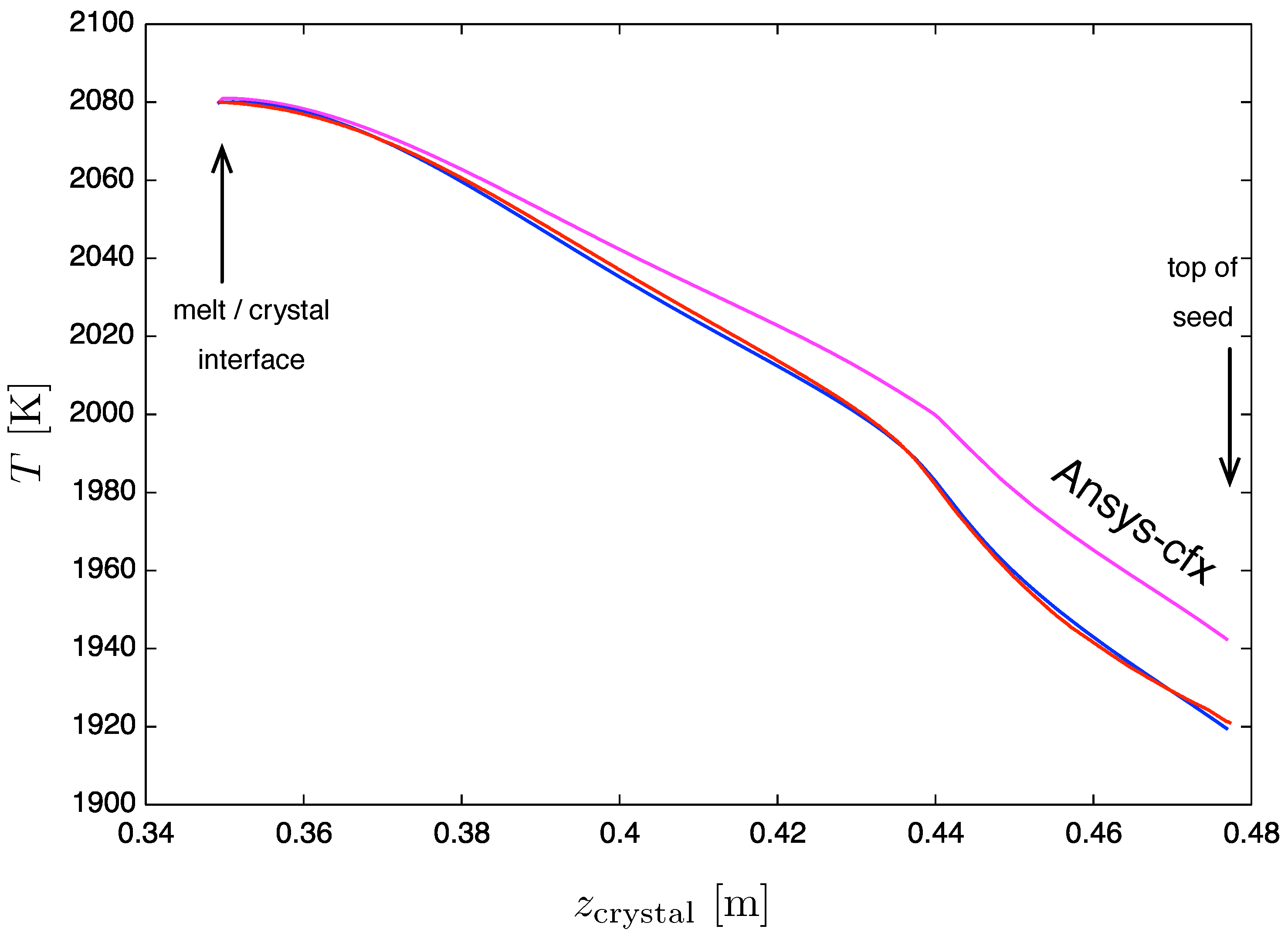
In the first step, we computed the temperature field. We compared the runs with different software tools (see
Figure 4). Please note that, as mentioned above, the 3D calculation was performed with temperature boundary conditions obtained from a CrysMAS run without melt convection. Therefore, the temperature at the top of the domain for Ansys-cfx (see
Figure 2) is about 100 K higher than in the case with melt convection. Thus, the temperature at the top of the seed is also higher in the case of the 3D calculation (about 20 K). The other point to be mentioned is that, in CGsim, the radiation within the crystal is computed by the discrete ordinate method with absorption and scattering coefficients of
and
, respectively.
In
Figure 5, the temperature profiles in melt, crystal and seed are shown for the two different crystal orientations. Only small differences occur, which can be seen in more detail in the temperature profile along the axis (plot on the right-hand side). In the melt, the advective heat transport can be clearly seen. Using the high viscosity (
), one large convection roll is established, transporting the heat from the lower part, where the induced heat in the crucible is the highest, towards the melt surface and the crystal–melt interface. We considered buoyancy convection and a crystal rotation of 5 rpm. The resulting convection causes a nearly uniform temperature on the crystal–melt interface. As already mentioned, the interface shape was fixed in the 3D calculations and, thus, the temperature at the interface is a result of the computations. The temperature variation is about 3 K (see also Figure 7).
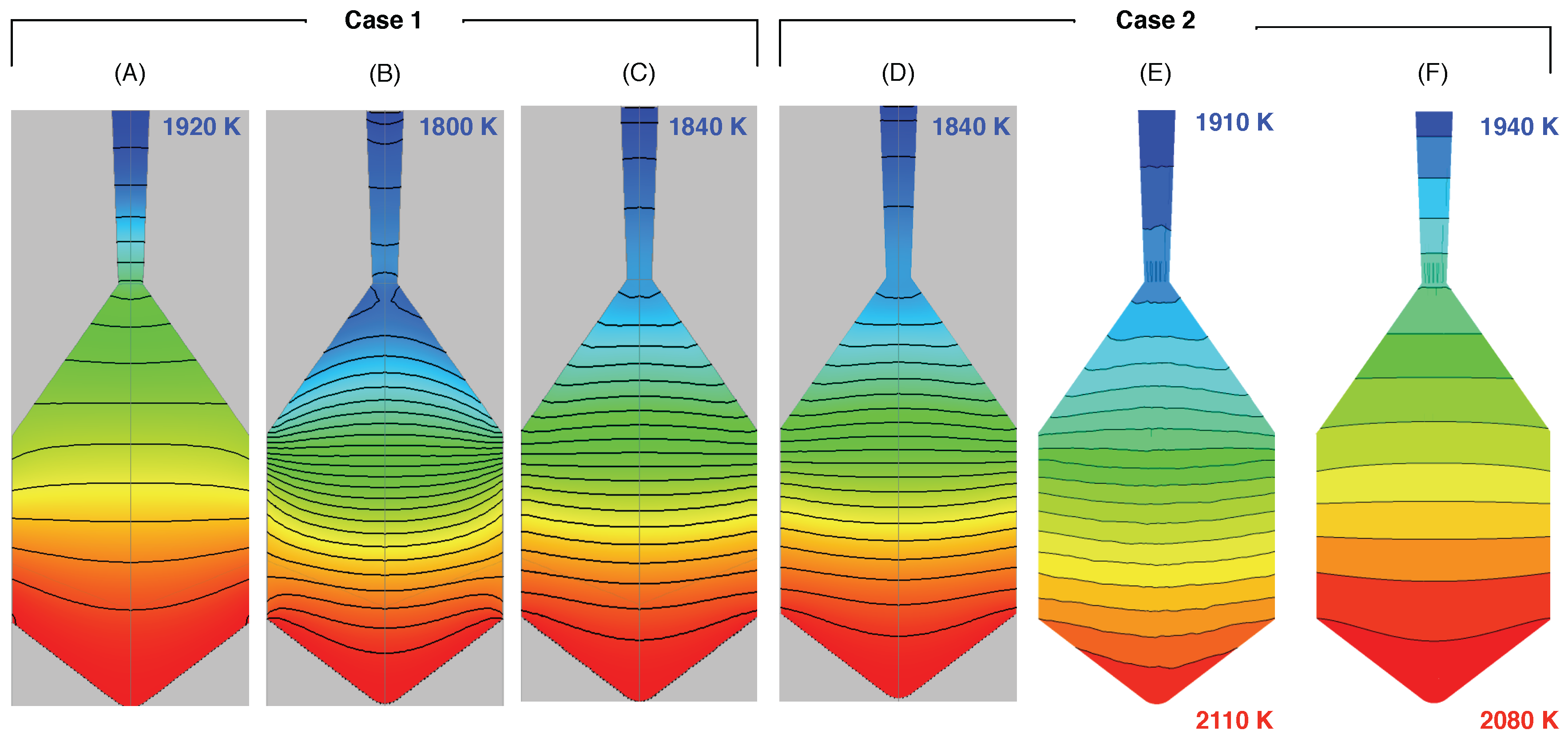
A more detailed analysis of the temperature in crystal and seed for different runs is given in
Figure 6. Four calculations have been performed with CGsim (figures with grey background). In
Figure 6A, the result of the run with
and
is shown (the refraction index was set to
.), i.e., for a quasi-transparent crystal. In complete contrast,
Figure 6B presents the result for an opaque crystal. Because there is no heat transport by radiation, all of the heat from the interface has to be removed by heat conduction, resulting in a much higher temperature gradient than in (A). For a semi-transparent crystal with
and
(C), the gradient is still higher than in case (A) but strongly reduced in comparison to (B). As already noticed from
Figure 5, there is not so much difference between Case 1 and Case 2, i.e., for the two different crystal orientations (compare
Figure 6C, D). Going to a 3D computation for the semi-transparent crystal, there is the difference that, in the axisymmetric calculation by CGsim, the temperature at the interface is fixed to
, whereas, in the 3D calculation, the latent heat release at the interface is fixed. Therefore, in the latter case (
Figure 6E), the maximum temperature is 2110 K, with a considerable temperature gradient in the lower part of the cone. In (F), there is again the case with a transparent crystal. The total temperature difference in crystal and seed is 140 K as compared to 200 K in the case with a semi-transparent crystal and seed (E). Thus, the conductive heat transport is about 1.4 times larger for semi-transparent crystal and seed.
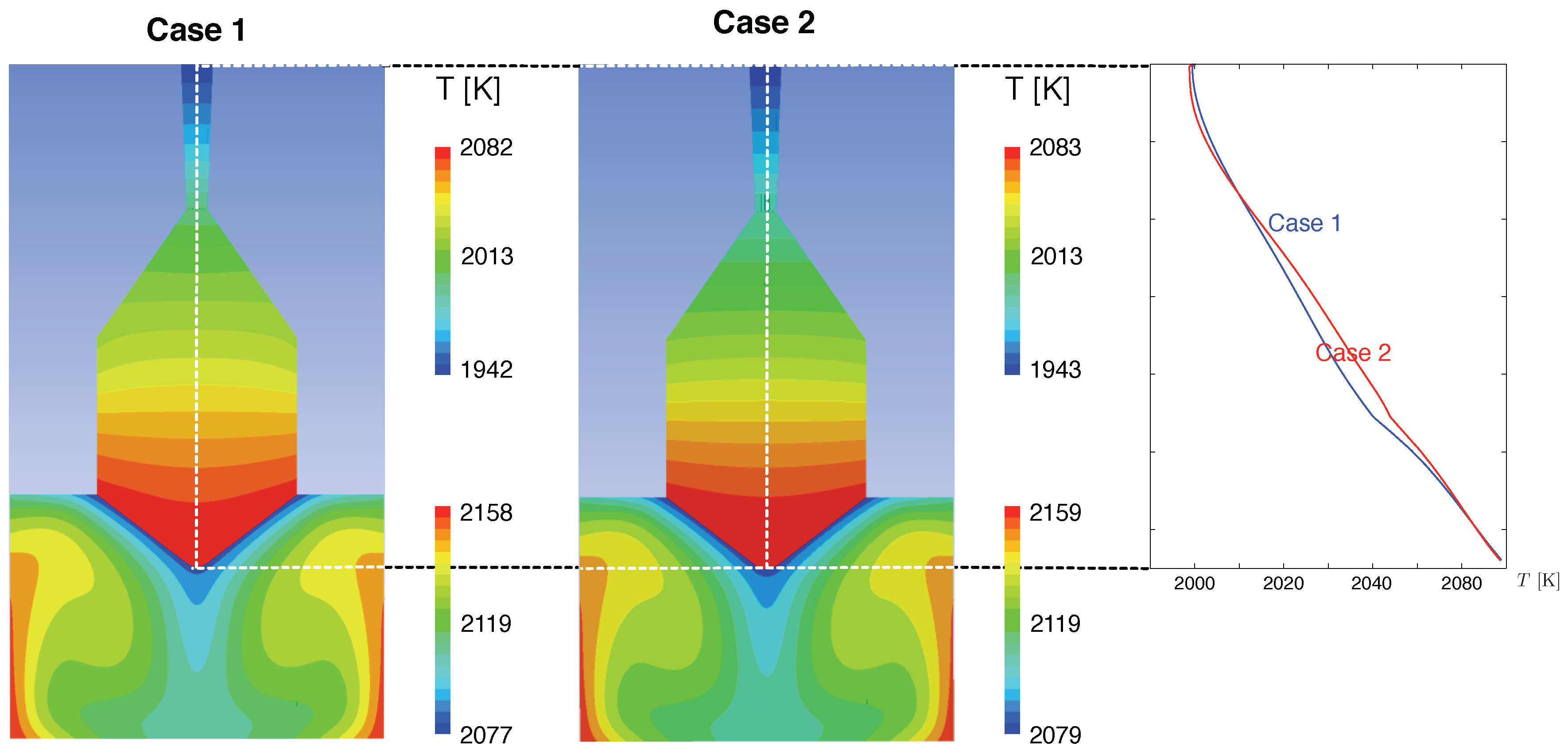
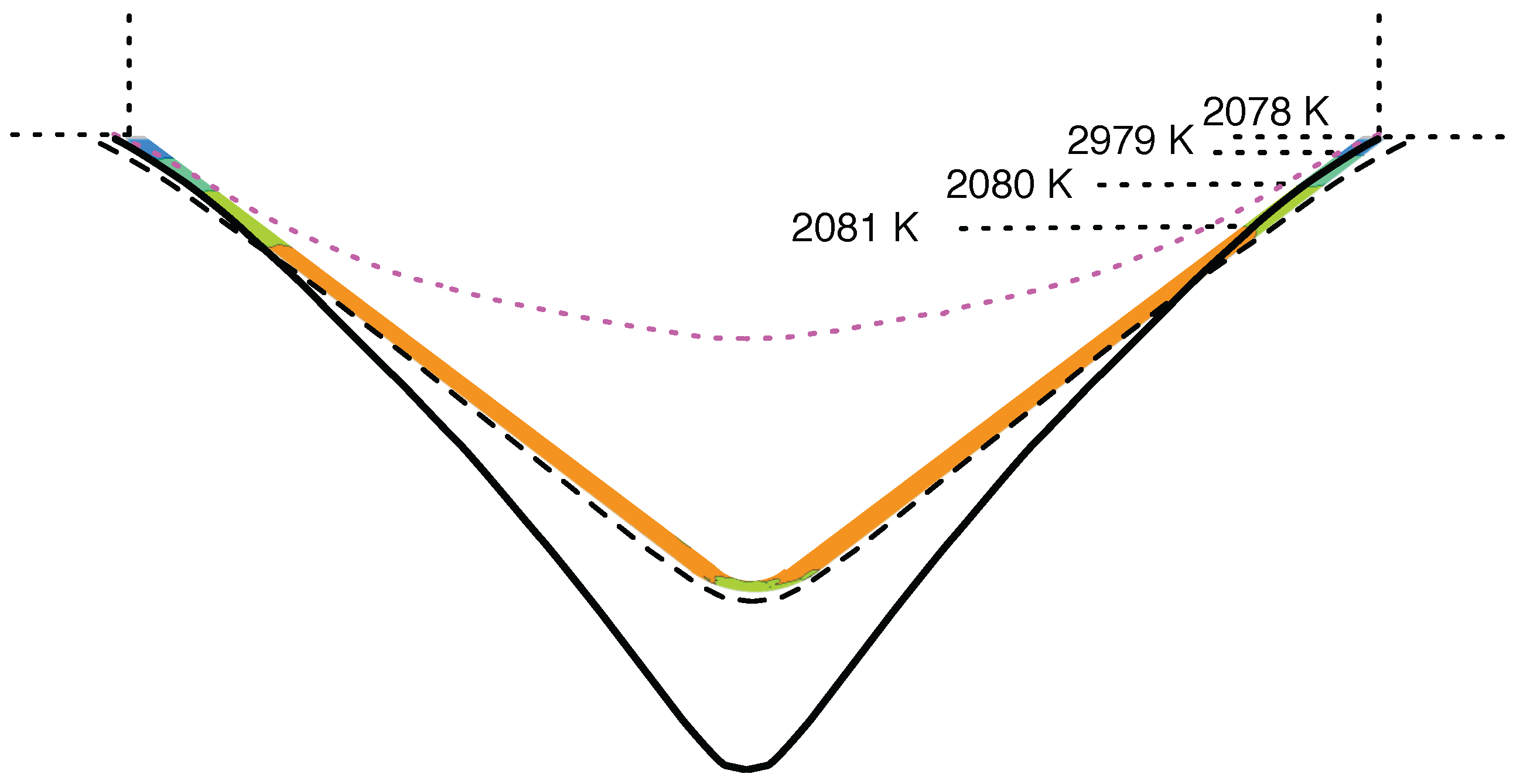
In the 3D calculation, the interface shape is fixed as taken from the typical shape in the growth experiments. This means that there is a temperature variation along the interface. When melt convection with
is applied, the temperature difference is about 3 K, as indicated by the colours along the interface in
Figure 7. The interface shape obtained in the axisymmetric calculation using CGsim is given by the black line in
Figure 7. It is much deeper compared with the shape used in the 3D calculation. It is also much deeper than the isoline of
(black dotted line) as obtained in the 3D computation. One has to keep in mind that the interface shape has an influence on the convection, and this is vice versa on the heat transport in the melt. However, without convection, the interface is much flatter as computed by CGsim (dotted line in magenta). This underlines the necessity to include melt convection to recover the interface shape as obtained by the real growth process.
The thermal stress was computed only for the temperature fields observed by the 3D calculations employing Ansys-cfx, as indicated in the sketch of
Figure 2. We used both the thermal expansion coefficients taken from [
22] and from our measurements. The results are completely different due to the strong coupling between [001] and [100] direction, in the case of the coefficients from [
22].
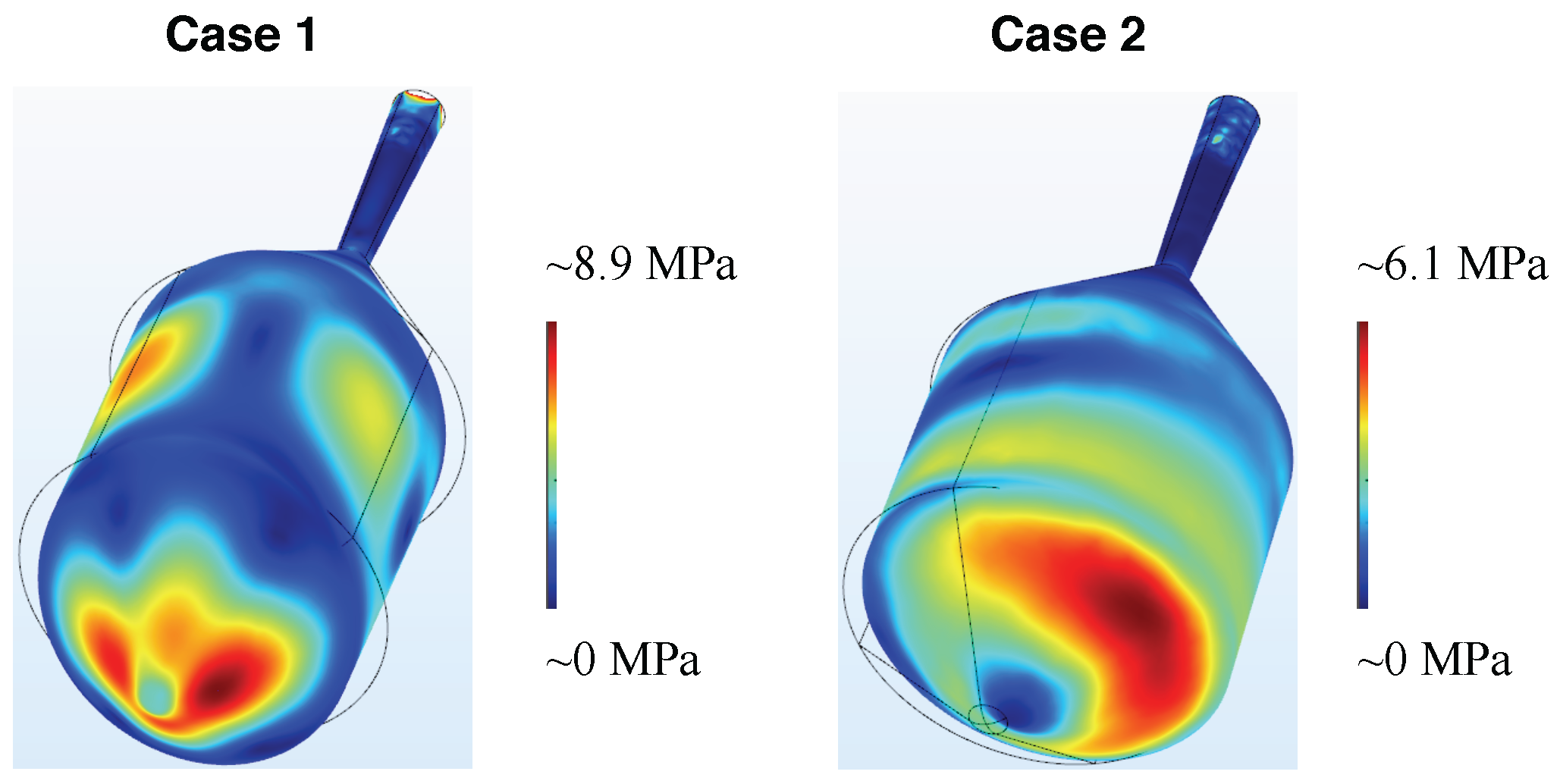
Figure 8 shows the results using the thermal expansion coefficients from [
22]: in Case 1, the crystal is shrinking in the radial direction and extending in the growth direction yielding in a high von Mises stress in the central part of the interface. In Case 2, the strong coupling via
leads to a skew growth of the crystal, which is visible by the magnified geometry deformation on the right-hand side of
Figure 8. The influence of the strong coupling is also visible in the high anisotropy of the stress distribution. As a result, the maximum of von Mises stress is higher in Case 1 (about 8.7 MPa) as compared to Case 2 (about 5.1 MPa).
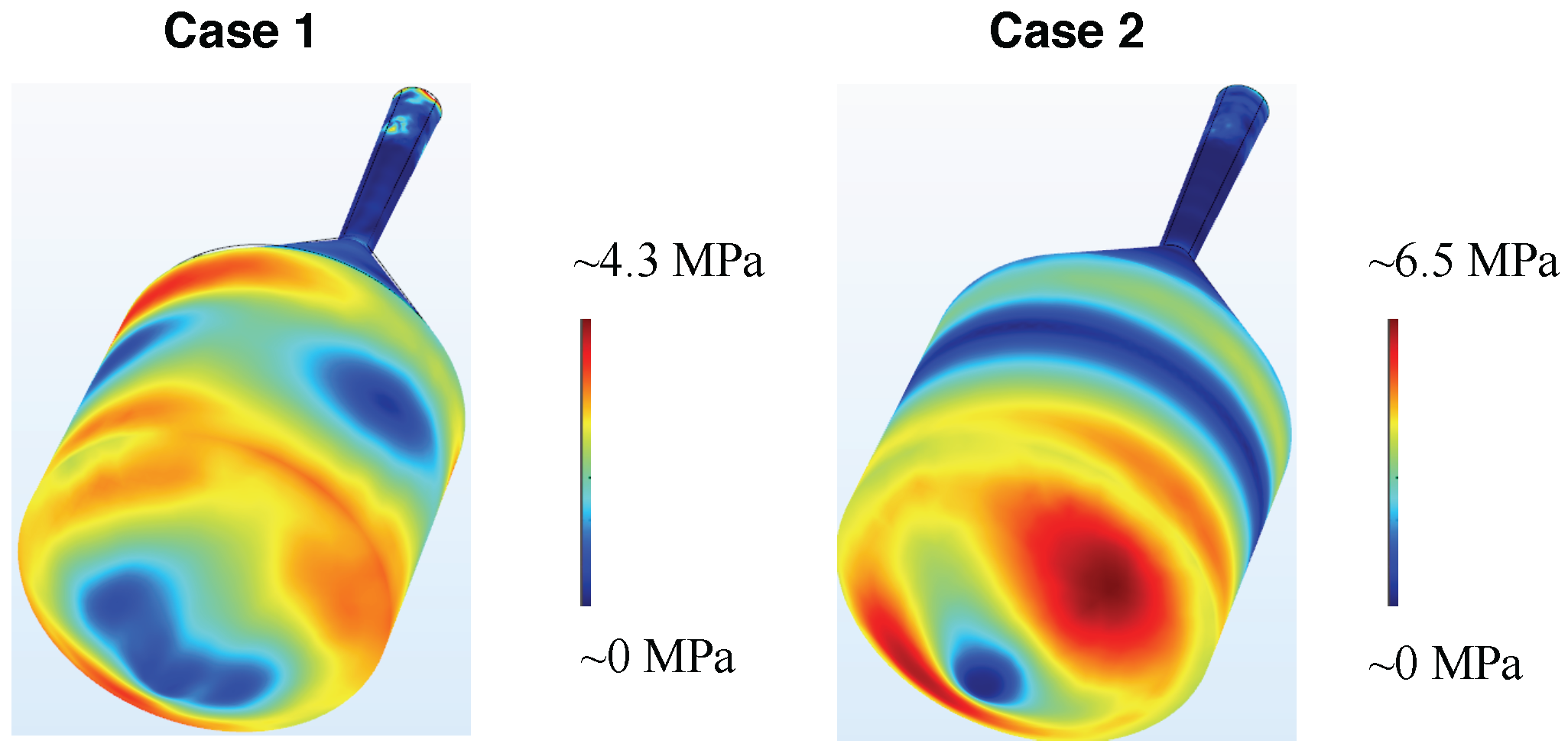
The field distribution of displacement and stress is very different when using the thermal expansion coefficient measured by us (see
Figure 9): the coupling via the off-diagonal thermal expansion is rather weak; therefore, in both cases, the crystal geometry nearly maintains its axisymmetry. However, a significant anisotropy in the von Mises stress can be observed. Firstly, we discuss Case 1. the blue stripe of minimal stress at the bottom of the crystal is in the
a* direction. The main cleavage plane, the (100) plane, is perpendicular to this direction, and, thus, feels a significant change of stress from its boundary towards its centre.
In Case 2, we have the b- and c-axis in the (100)-plane perpendicular to the growth direction. On the crystal–melt interface, we observe high stress in one direction going up to ≈6.4 close to the periphery. This is the direction of the c-axis. In the b-axis, the variation from the tip (low) towards the rim (higher) is much smaller.