Symmetry-Induced Light Confinement in a Photonic Quasicrystal-Based Mirrorless Cavity
Abstract
:1. Introduction
2. Results
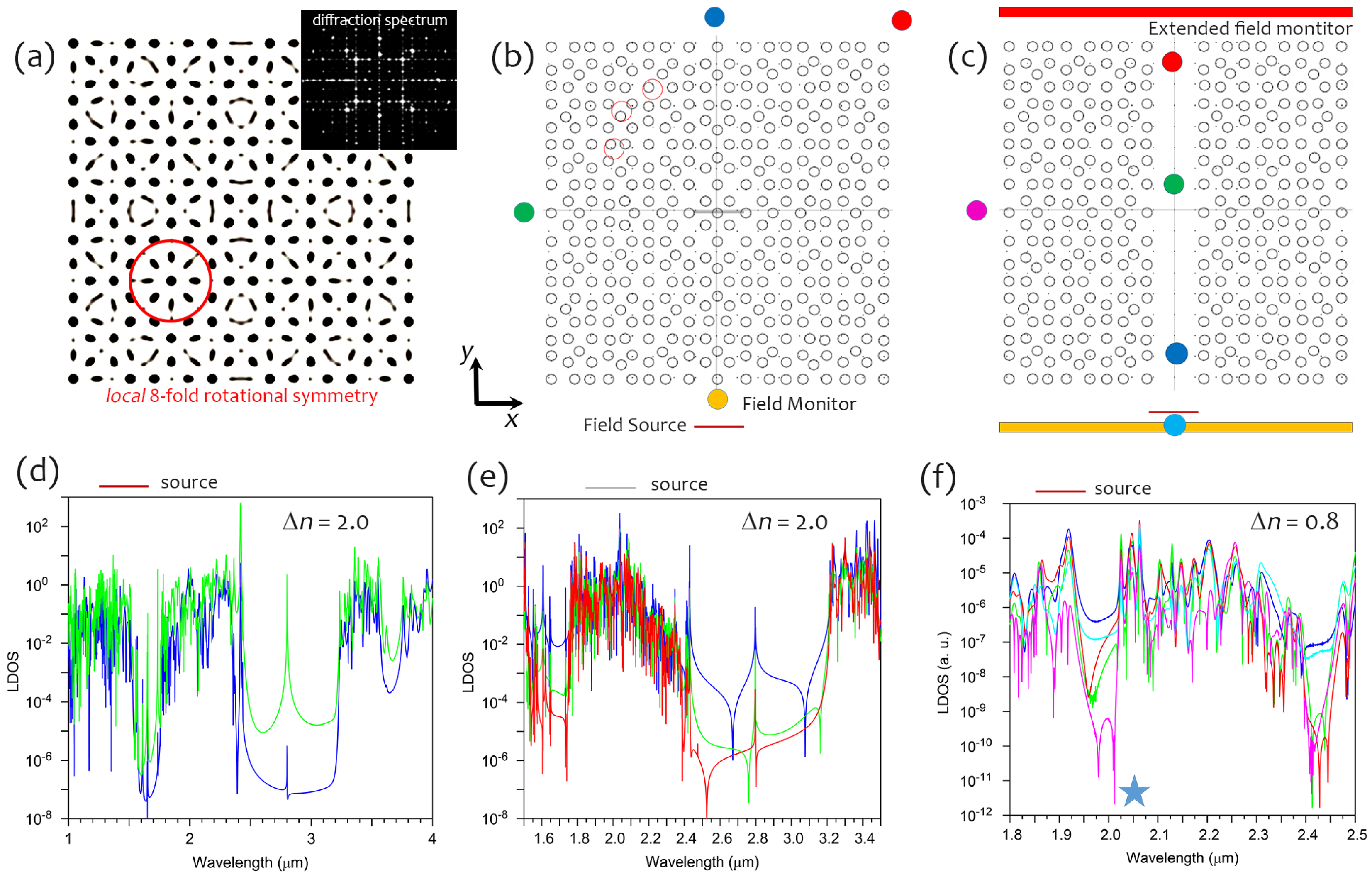
2.1. Octagonal-Based Holographic Tiling
2.2. Methods
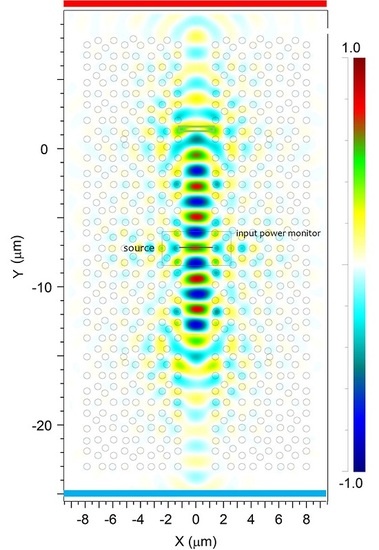
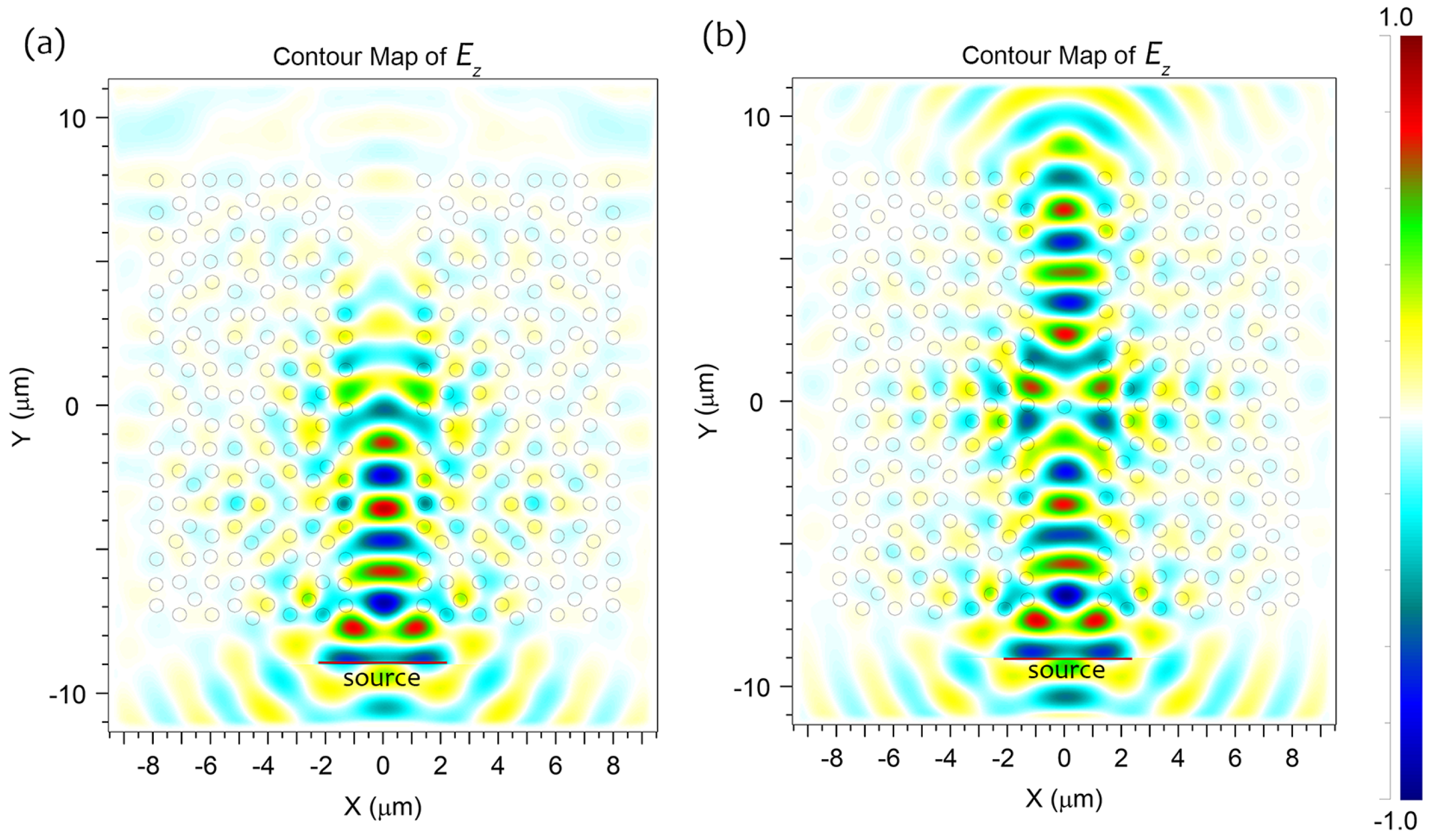
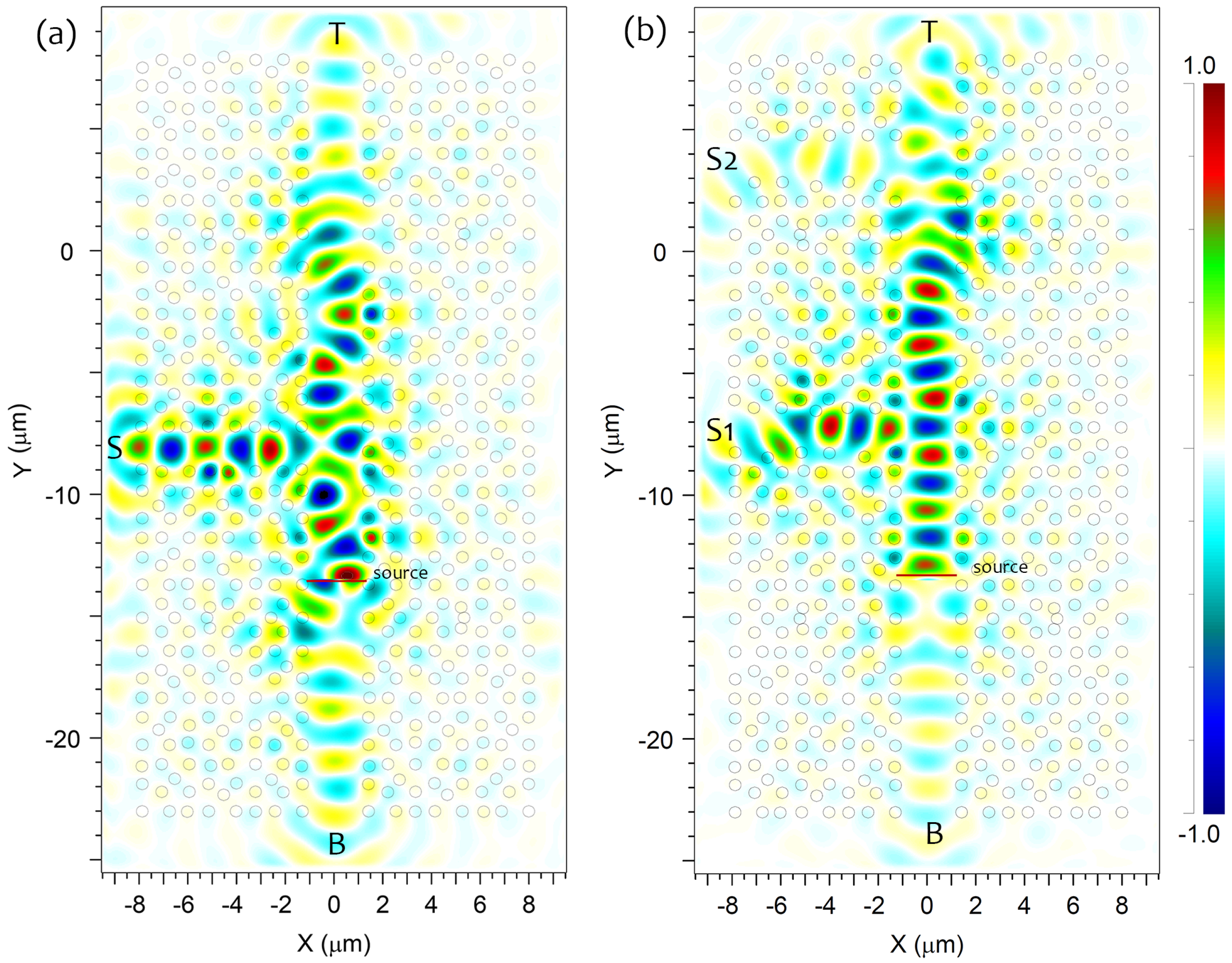
2.3. Mirrorless Cavity
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PQC | Photonic quasi-crystal |
| PBG | Photonic band gap |
| DFLM | Defect-free localized mode |
| HT | Holographic tiling |
References
- Yablonovitch, E. Inhibited spontaneous emission in solid-state physics and electronics. Phys. Rev. Lett. 1987, 58, 2059–2062. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486–2489. [Google Scholar] [CrossRef] [PubMed]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1953. [Google Scholar] [CrossRef]
- Zoorob, M.; Charlton, M.; Parker, G.; Baumberg, J.; Netti, M. Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature 2000, 404, 740–743. [Google Scholar] [PubMed]
- Della Villa, A.; Enoch, S.; Tayeb, G.; Pierro, V.; Galdi, V.; Capolino, F. Band gap formation and multiple scattering in photonic quasicrystals with a Penrose-type lattice. Phys. Rev. Lett. 2005, 94, 183903. [Google Scholar] [CrossRef] [PubMed]
- Zito, G.; Pepe, G.P.; De Nicola, S. Hidden translational symmetry in square–triangle-tiled dodecagonal quasicrystal. J. Opt. 2015, 17, 055103. [Google Scholar] [CrossRef]
- Senechal, M. Quasicrystals and Geometry; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Levine, D.; Steinhardt, P.J. Quasicrystals: A new class of ordered structures. Phys. Rev. Lett. 1984, 53, 2477–2480. [Google Scholar] [CrossRef]
- Wang, N.; Chen, H.; Kuo, K. Two-dimensional quasicrystal with eightfold rotational symmetry. Phys. Rev. Lett. 1987, 59, 1010–1013. [Google Scholar] [CrossRef] [PubMed]
- Mikhael, J.; Roth, J.; Helden, L.; Bechinger, C. Archimedean-like tiling on decagonal quasicrystalline surfaces. Nature 2008, 454, 501–504. [Google Scholar] [CrossRef] [PubMed]
- Bendersky, L. Quasicrystal with one-dimensional translational symmetry and a tenfold rotation axis. Phys. Rev. Lett. 1985, 55, 1461–1463. [Google Scholar] [CrossRef] [PubMed]
- Rose, P.T.; Di Gennaro, E.; Abbate, G.; Andreone, A. Isotropic properties of the photonic band gap in quasicrystals with low-index contrast. Phys. Rev. B 2011, 84, 125111. [Google Scholar]
- Zito, G.; Rose, P.T.; Di Gennaro, E.; Andreone, A.; Santamato, E.; Abbate, G. Bandgap properties of low-index contrast aperiodically ordered photonic quasicrystals. Microwa. Opt. Tech. Lett. 2009, 51, 2732–2737. [Google Scholar] [CrossRef]
- Zito, G.; Piccirillo, B.; Santamato, E.; Marino, A.; Tkachenko, V.; Abbate, G. Two-dimensional photonic quasicrystals by single beam computer-generated holography. Opt. Exp. 2008, 16, 5164–5170. [Google Scholar] [CrossRef]
- Zito, G.; Pissadakis, S. Holographic polymer-dispersed liquid crystal Bragg grating integrated inside a solid core photonic crystal fiber. Opt. Lett. 2013, 38, 3253–3256. [Google Scholar] [CrossRef] [PubMed]
- Zito, G.; Finizio, A.; De Nicola, S. Spatially resolved refractive index profiles of electrically switchable computer-generated holographic gratings. Opt. Exp. 2009, 17, 18843–18851. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. Exploiting quasiperiodic order in the design of optical devices. Phys. Rev. B 2001, 63, 205421. [Google Scholar] [CrossRef]
- Della Villa, A.; Enoch, S.; Tayeb, G.; Capolino, F.; Pierro, V.; Galdi, V. Localized modes in photonic quasicrystals with Penrose-type lattice. Opt. Exp. 2006, 14, 10021–10027. [Google Scholar] [CrossRef]
- Notomi, M.; Suzuki, H.; Tamamura, T.; Edagawa, K. Lasing action due to the two-dimensional quasiperiodicity of photonic quasicrystals with a Penrose lattice. Phys. Rev. Lett. 2004, 92, 123906. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Hu, X.; Xu, X.; Cheng, B.; Zhang, D. Localized modes in defect-free dodecagonal quasiperiodic photonic crystals. Phys. Rev. B 2003, 68, 165106. [Google Scholar] [CrossRef]
- Rose, P.; Zito, G.; Di Gennaro, E.; Abbate, G.; Andreone, A. Control of the light transmission through a quasiperiodic waveguide. Opt. Exp. 2012, 20, 26056–26061. [Google Scholar]
- Escuti, M.J.; Crawford, G.P. Holographic photonic crystals. Opt. Eng. 2004, 43, 1973–1987. [Google Scholar]
- Gorkhali, S.P.; Qi, J.; Crawford, G.P. Switchable quasi-crystal structures with five-, seven-, and ninefold symmetries. JOSA B 2006, 23, 149–158. [Google Scholar] [CrossRef]
- Roichman, Y.; Grier, D.G. Holographic assembly of quasicrystalline photonic heterostructures. Opt. Exp. 2005, 13, 5434–5439. [Google Scholar] [CrossRef]
- Lifshitz, R. Quasicrystals: A matter of definition. Found. Phys. 2003, 33, 1703–1711. [Google Scholar] [CrossRef]
- Elcoro, L.; Perez-Mato, J.M. Cubic superspace symmetry and inflation rules in metastable MgAl alloy. Eur. Phys. J. B 1999, 7, 85–89. [Google Scholar] [CrossRef]
- Obreja, P.; Cristea, D.; Purica, M.; Gavrila, R.; Comanescu, F. Polymers doped with metal oxide nanoparticles with controlled refractive index. Polimery 2007, 52, 679–685. [Google Scholar]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zito, G.; Rusciano, G.; Sasso, A.; De Nicola, S. Symmetry-Induced Light Confinement in a Photonic Quasicrystal-Based Mirrorless Cavity. Crystals 2016, 6, 111. https://doi.org/10.3390/cryst6090111
Zito G, Rusciano G, Sasso A, De Nicola S. Symmetry-Induced Light Confinement in a Photonic Quasicrystal-Based Mirrorless Cavity. Crystals. 2016; 6(9):111. https://doi.org/10.3390/cryst6090111
Chicago/Turabian StyleZito, Gianluigi, Giulia Rusciano, Antonio Sasso, and Sergio De Nicola. 2016. "Symmetry-Induced Light Confinement in a Photonic Quasicrystal-Based Mirrorless Cavity" Crystals 6, no. 9: 111. https://doi.org/10.3390/cryst6090111
APA StyleZito, G., Rusciano, G., Sasso, A., & De Nicola, S. (2016). Symmetry-Induced Light Confinement in a Photonic Quasicrystal-Based Mirrorless Cavity. Crystals, 6(9), 111. https://doi.org/10.3390/cryst6090111