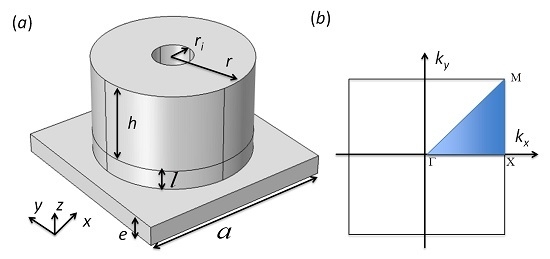
Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling
Abstract
:1. Introduction
2. Results and Discussion
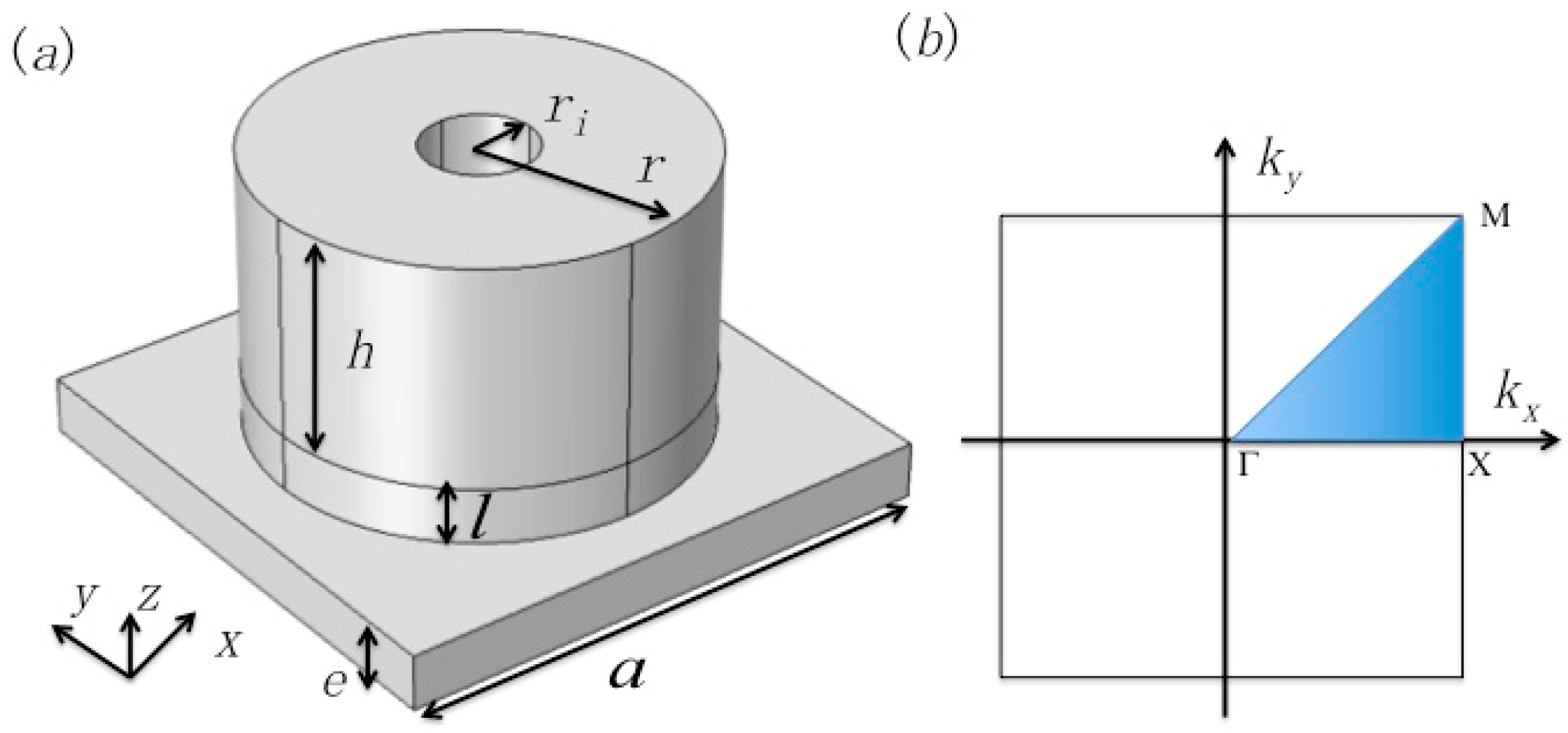
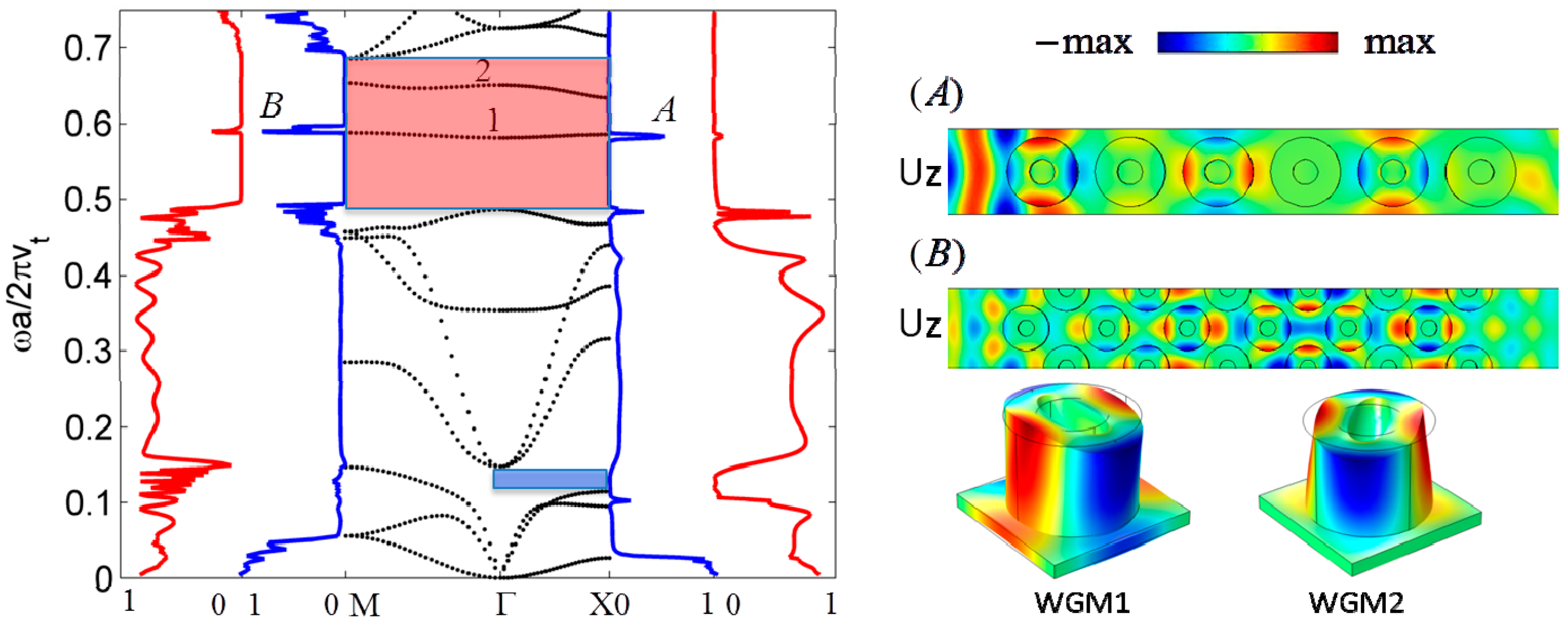
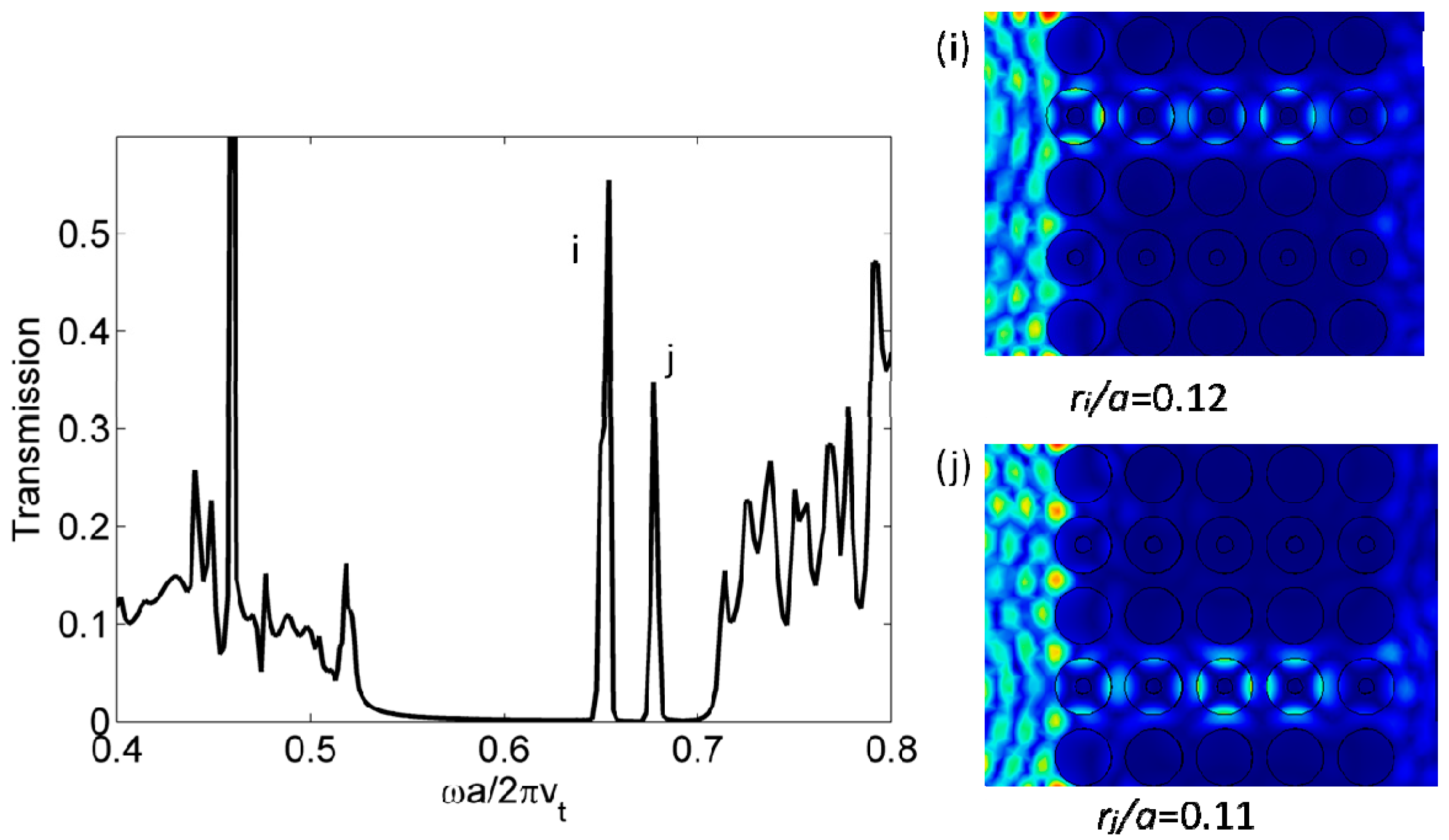
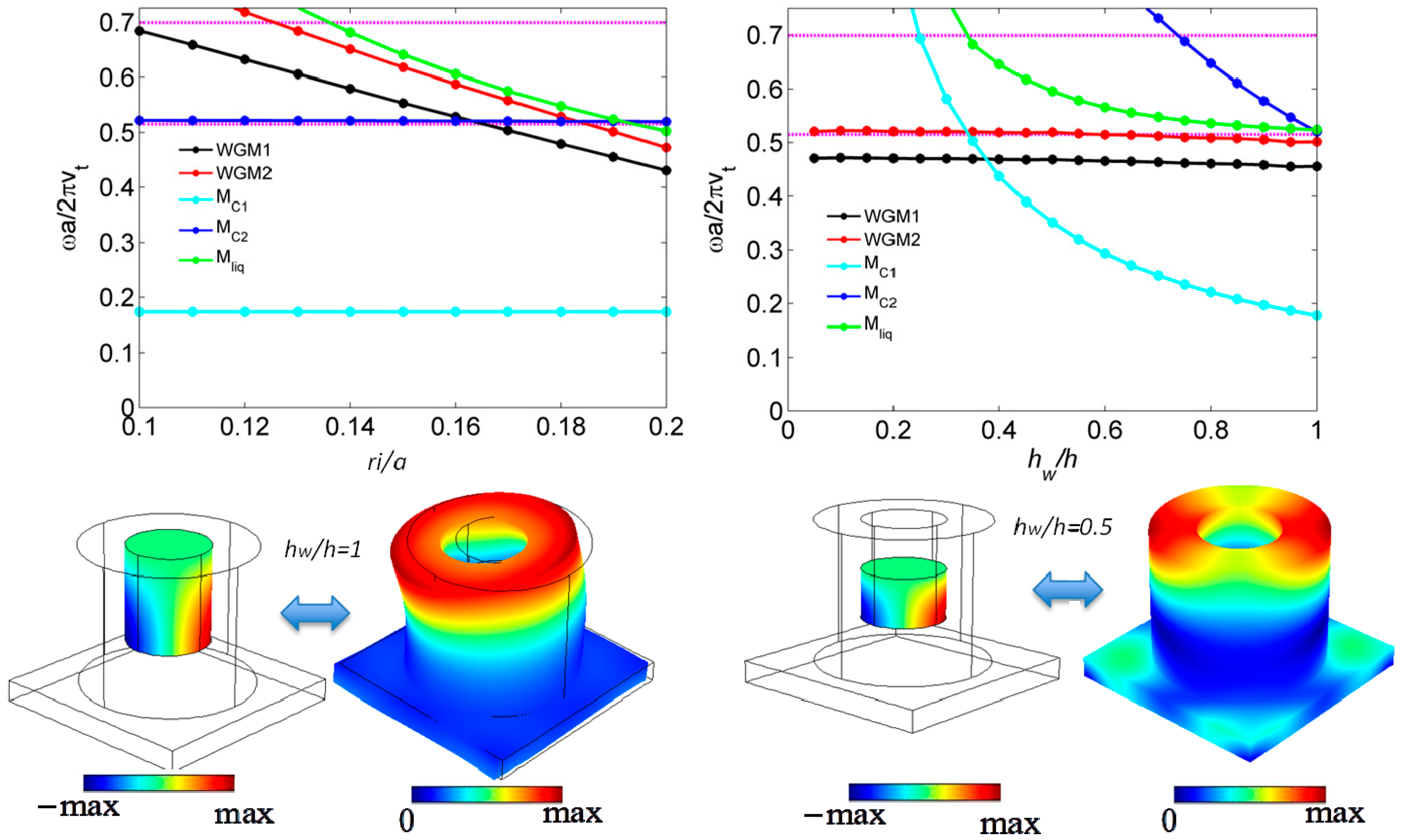
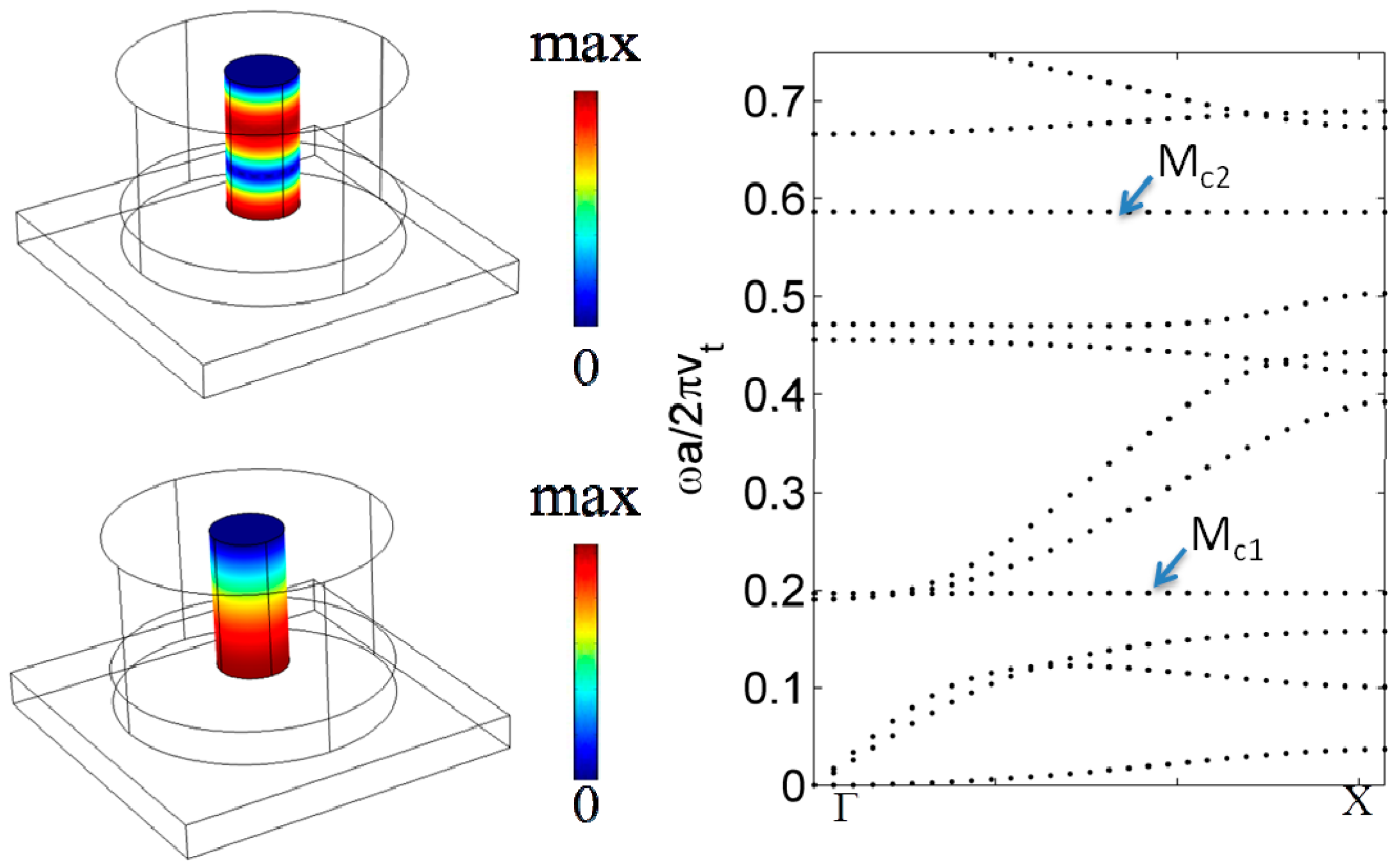
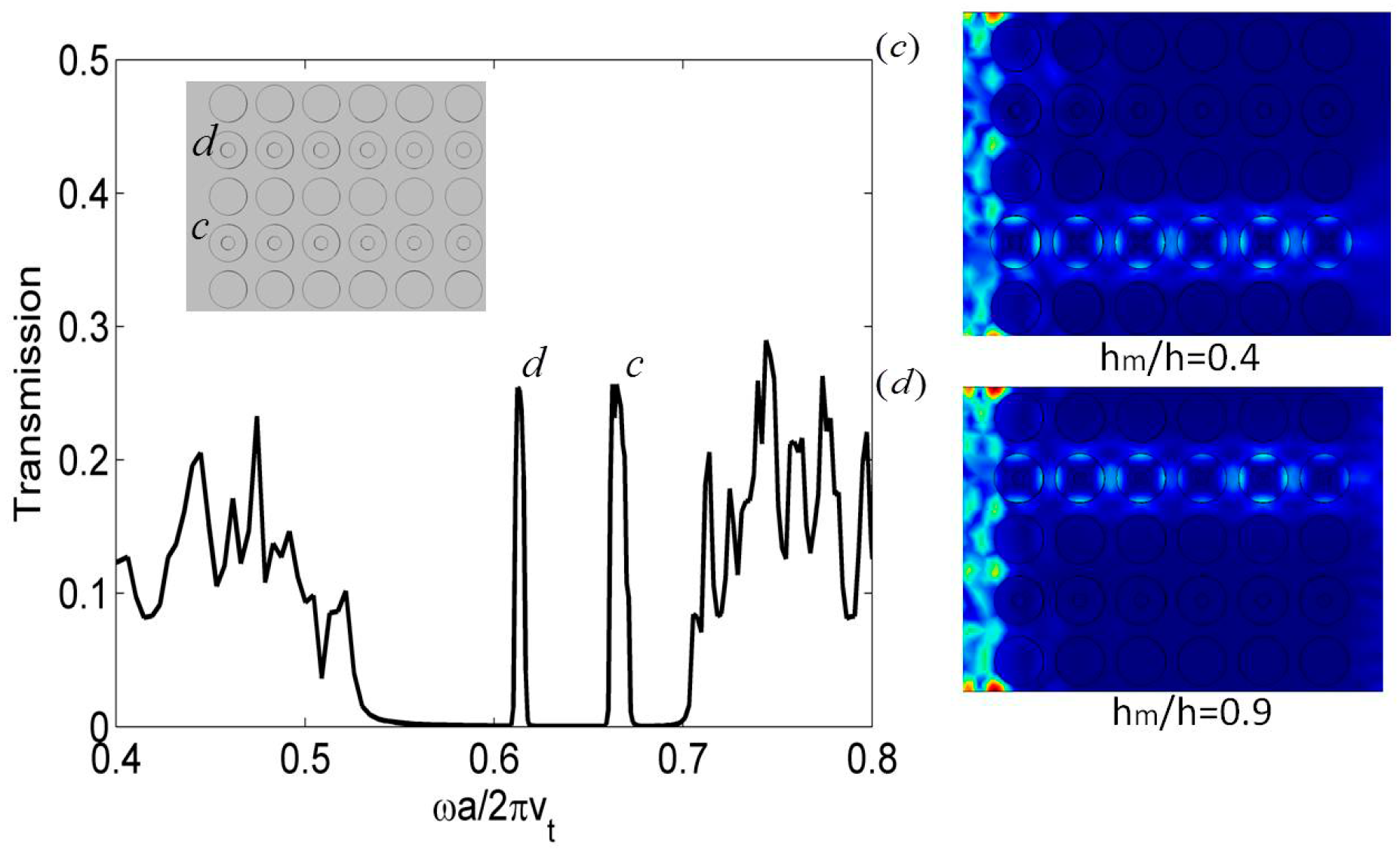
2.1. Whispering-Gallery Modes
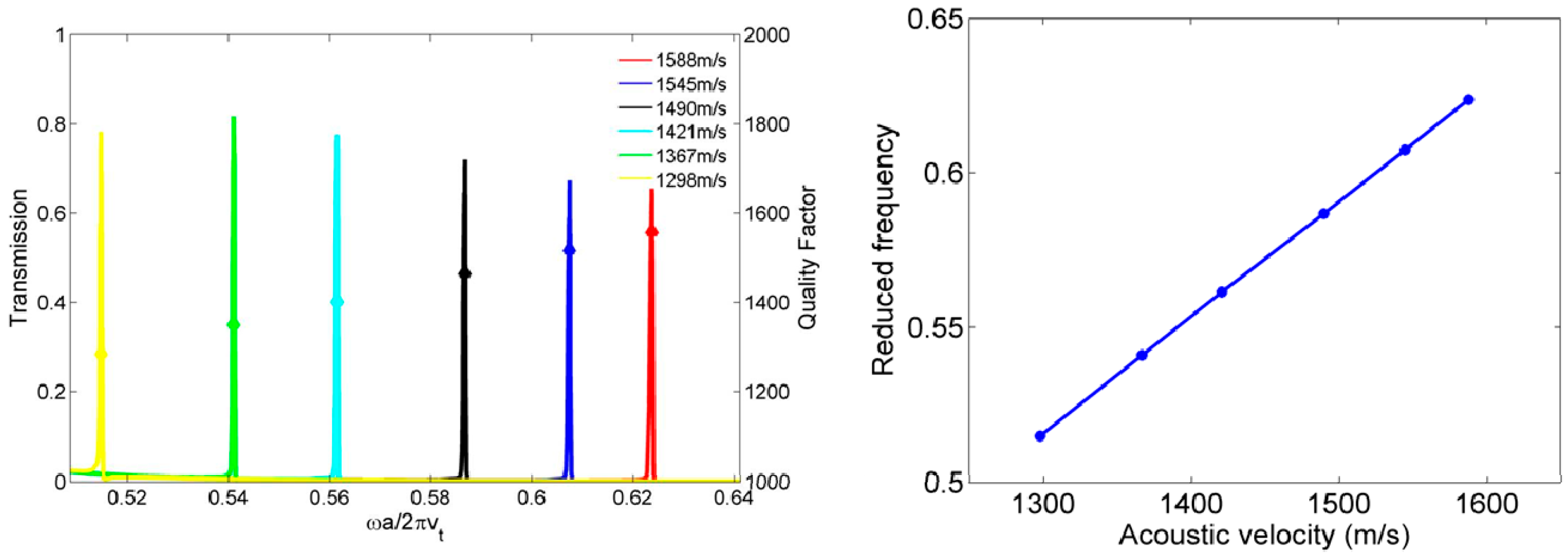
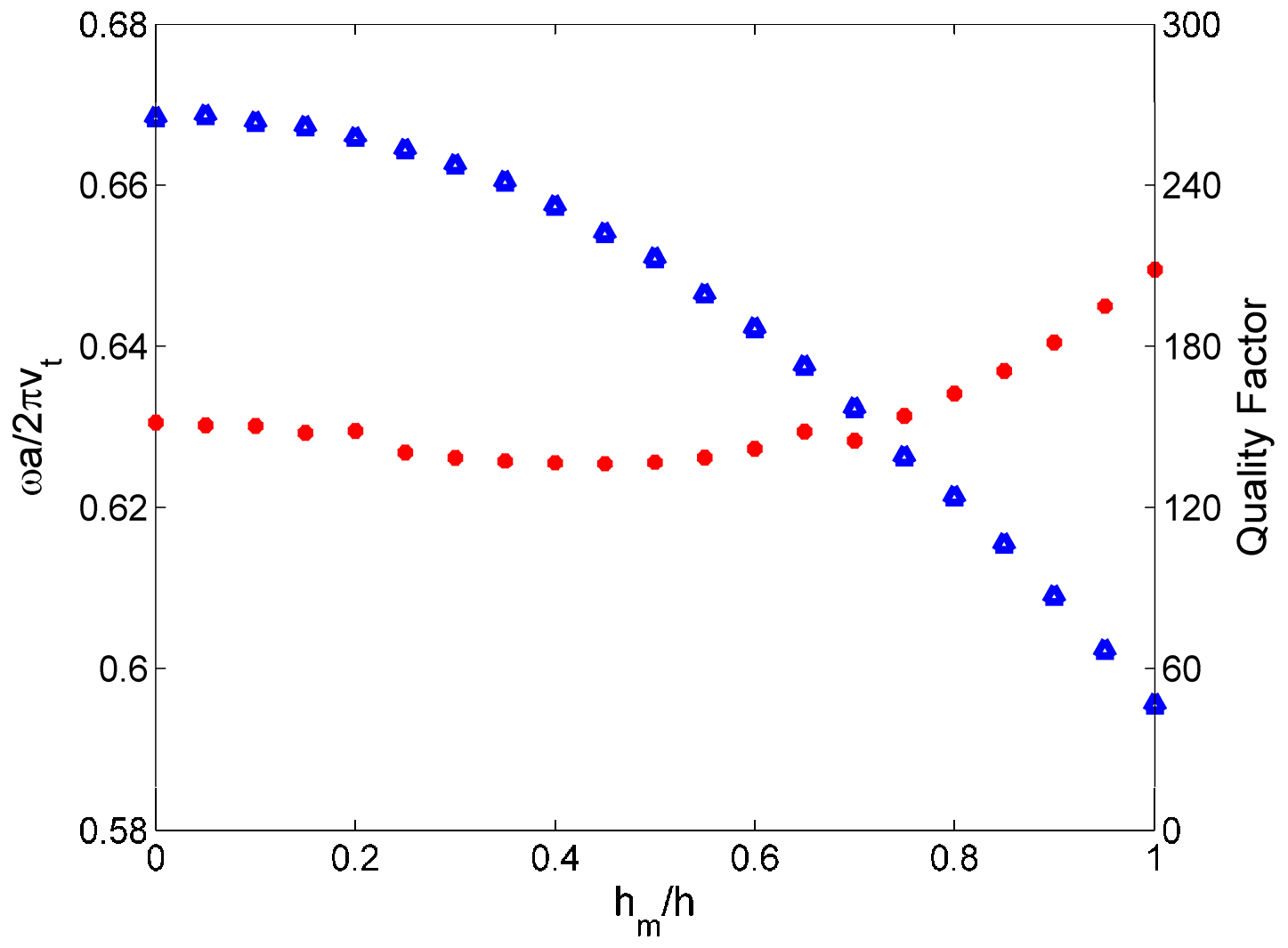
2.2. Active Control of the WGMs and New Localized Modes by Filling the Hollows with a Liquid
2.3. Compressional Modes along the Height of the Liquid
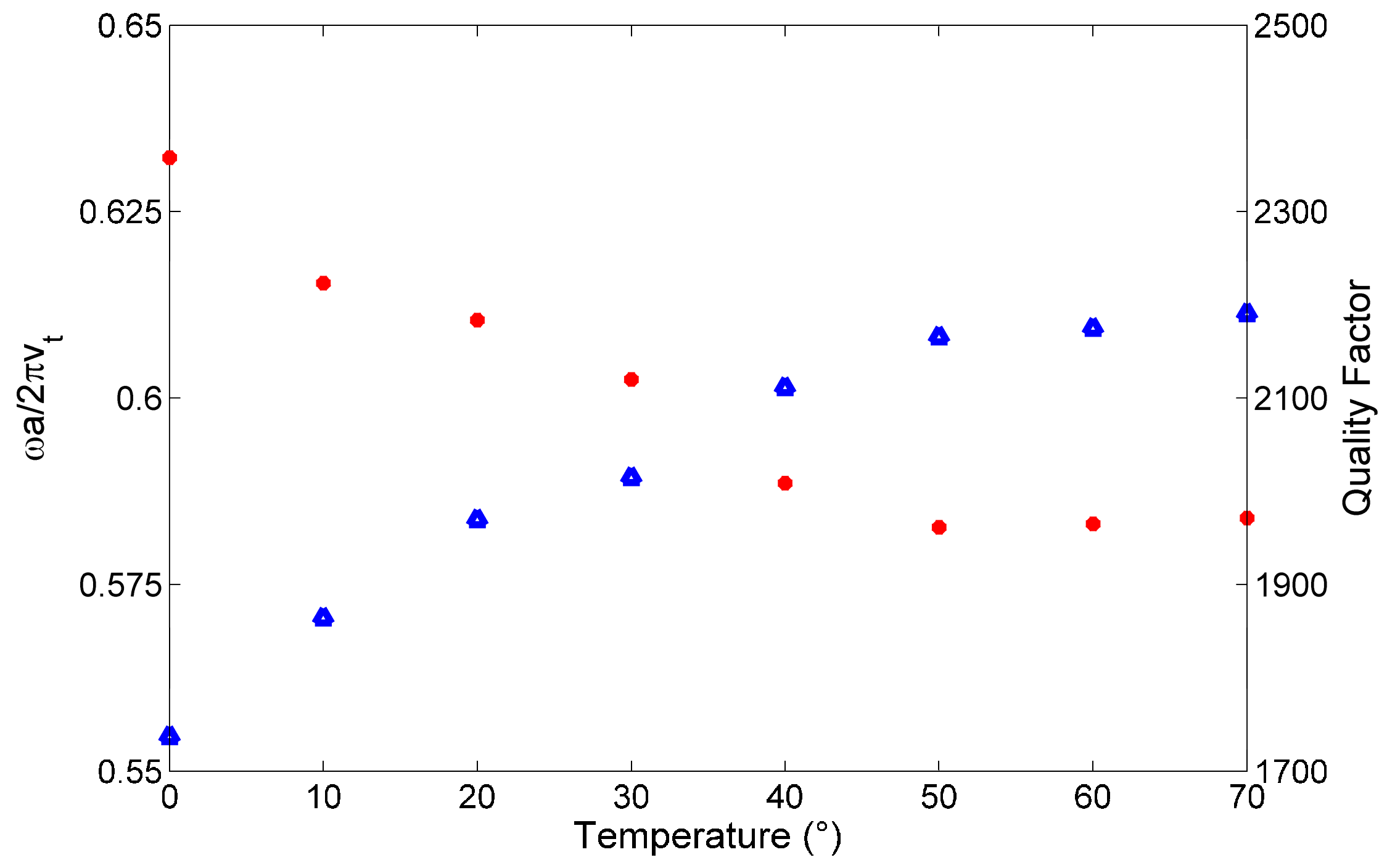
2.4. Influence of Filling the Holes with Mercury on Whispering Gallery Modes
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef] [PubMed]
- Sigalas, M.; Economou, E.N. Band structure of elastic waves in two dimensional systems. Solid State Commun. 1993, 86, 141–143. [Google Scholar] [CrossRef]
- Pennec, Y.; Vasseur, J.O.; Djafari-Rouhani, B.; Dobrzynski, L.; Deymier, P.A. Two-Dimensional phononic crystals: Examples and applications. Surf. Sci. Rep. 2010, 65, 229–291. [Google Scholar] [CrossRef]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress and future outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Khelif, A.; Choujaa, A.; Benchabane, S.; Djafari-Rouhani, B.; Laude, V. Guiding and bending of acoustic waves in highly confined phononic crystal waveguides. Appl. Phys. Lett. 2004, 84, 4400. [Google Scholar] [CrossRef]
- Sun, J.H.; Wu, T.T. Propagation of acoustic waves in Phononic-Crystal plates and waveguides using a finite-difference Time-Domain method. Phys. Rev. B 2007, 76, 104304. [Google Scholar] [CrossRef]
- Rostami-Dogolsara, B.; Moravvej-Farshi, M.K.; Nazari, F. Acoustic add-drop filters based on phononic crystal ring resonants. Phys. Rev. B 2016, 93, 014304. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Vasseur, J.O.; Khelif, A.; Deymier, P.A. Tunable filtering and demultiplexing in phononic crystals with hollow cylinders. Phys. Rev. E 2004, 69, 046608. [Google Scholar] [CrossRef] [PubMed]
- Lucklum, R.; Li, J. Phononic crystals for liquid sensor applications. Acoustic band structure of periodic elastic composites. Meas. Sci. Technol. 2009, 20, 124014. [Google Scholar] [CrossRef]
- Amoudache, S.; Pennec, Y.; Djafari-Rouhani, B.; Khater, A.; Lucklum, R.; Tigrine, R. Simultaneous sensing of light and sound velocities of fluids in a two-dimensional phoXonic crystal with defects. J. Appl. Phys. 2014, 115, 134503. [Google Scholar] [CrossRef]
- Yang, S.; Page, J.H.; Liu, Z.; Cowan, M.L.; Chan, C.T.; Sheng, P. Focusing of sound in a 3D phononic crystal. Phys. Rev. Lett. 2004, 93, 024301. [Google Scholar] [CrossRef] [PubMed]
- Jin, Y.; Torrent, D.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Simultaneous control of the S0 and A0 Lamb modes by graded phononic crystal plates. J. Appl. Phys. 2015, 117, 244904. [Google Scholar] [CrossRef]
- Jin, Y.; Torrent, D.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Gradient index devices for the full control of elastic waves in plates. Sci. Rep. 2016, 6, 24437. [Google Scholar] [CrossRef] [PubMed]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Vasseur, J.O.; Hladky-Henion, A.C. Low-Frequency gaps in a phononic crystal constituted of cylindrical dots deposited on a thin homogeneous plate. Phys. Rev. B. 2008, 78, 104105. [Google Scholar] [CrossRef]
- Wu, T.T.; Huang, Z.G.; Tsai, T.C.; Wu, T.C. Evidence of complete band gap and resonances in a plate with periodic stubbed surface. Appl. Phys. Lett. 2008, 93, 111902. [Google Scholar] [CrossRef]
- Pennec, Y.; Djafari-Rouhani, B.; Larabi, H.; Akjouj, A.; Gillet, J.N.; Vasseur, J.O.; Thabet, G. Phonon transport and waveguiding in a phononic crystal made up of cylindrical dots on a thin homogeneous plate. Phys. Rev. B 2009, 80, 144302. [Google Scholar] [CrossRef]
- Oudich, M.; Li, Y.; Assouar, M.B.; Hou, Z. A sonic band gap based on the locally resonant phononic plates with stubs. New J. Phys. 2010, 12, 083049. [Google Scholar] [CrossRef]
- Assouar, M.B.; Oudich, M. Enlargement of a locally resonant sonic band gap by using double-Sides stubbed phononic plates. Appl. Phys. Lett. 2012, 100, 123506. [Google Scholar] [CrossRef]
- Coffy, E.; Lavergne, T.; Addouche, M.; Euphrasie, S.; Vairac, P.; Khelif, A. Ultra-Wide acoustic band gaps in pillar-Based phononic crystal strips. J. Appl. Phys. 2015, 118, 214902. [Google Scholar] [CrossRef]
- Midtvedt, D.; Isacsson, A.; Croy, A. Nonlinear phononics using atomically thin membrances. Nat. Commun. 2014, 5, 4838. [Google Scholar] [CrossRef] [PubMed]
- Graczykowshi, B.; Sledzinska, M.; Alzina, F.; Gomis-Bresco, J.; Reparaz, J.S.; Wagner, M.R.; Sotomayor Torres, C.M. Phonon dispersion in hypersonic two-dimensional phononic crystal membranes. Phys. Rev. B 2015, 91, 075414. [Google Scholar] [CrossRef]
- Jin, Y.; Fernez, N.; Pennec, Y.; Bonello, B.; Moiseyenko, R.P.; Hemon, S.; Pan, Y.; Djafari-Rouhani, B. Tunable waveguide and cavity in a phononic crystal plate by controlling whispering-Gallery modes in hollow pillars. Phys. Rev. B 2016, 93, 054109. [Google Scholar] [CrossRef]
- Jin, Y.; Bonello, B.; Pan, Y. Acoustic metamaterials with piezoelectric resonant structures. J. Phys. D Appl. Phys. 2014, 47, 245301. [Google Scholar] [CrossRef]
- Popa, B.T.; Cummer, S.A. Non-Reciprocal and highly nonlinear active acoustic metamaterials. Nat. Commun. 2014, 5, 3398. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Casadei, F.; Shan, S.; Weaver, J.C.; Bertoldi, K. Harnessing buckling to design tunable locally resonant acoustic metamaterials. Phys. Rev. Lett. 2014, 113, 014301. [Google Scholar] [CrossRef] [PubMed]
- Sato, A.; Pennec, Y.; Shingne, N.; Thurn-Albrecht, T.; Knoll, W.; Steinhart, M.; Djafari-Rouhani, B.; Fytas, G. Tuning and switching the hypersonic phononic properties of elastic impedance contrast nanocomposites. ACS Nano 2010, 4, 3471. [Google Scholar] [CrossRef] [PubMed]
- Demirci, U.; Montesano, G. Single cell epitaxy by acoustic picolitre droplets. Lab Chip 2007, 7, 1139. [Google Scholar] [CrossRef] [PubMed]
- Tilli, M.; Motooka, T.; Airaksinen, V.; Franssila, S.; Paulasto-Krockel, M.; Lindroos, V. Handbook of Silicon Based MEMs Materials and Technologies, 2nd ed.; William Andrew: London, UK, 2015. [Google Scholar]


| Molar Ratio x | Density (kg·m−3) | Speed of Sound (ms−1) |
|---|---|---|
| 0 (water) | 998 | 1490 |
| 0.021 | 990 | 1545 |
| 0.056 | 974 | 1588 |
| 0.230 | 908 | 1421 |
| 0.347 | 881 | 1367 |
| 0.596 | 841 | 1298 |
| T (°C) | Mass Density (kg·m−3) | Speed of Sound (ms−1) |
|---|---|---|
| 0 | 999 | 1405 |
| 10 | 999 | 1447 |
| 20 | 998 | 1482 |
| 30 | 997 | 1497 |
| 40 | 992 | 1529 |
| 50 | 986 | 1547 |
| 60 | 983 | 1550 |
| 70 | 977 | 1554 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Pennec, Y.; Pan, Y.; Djafari-Rouhani, B. Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling. Crystals 2016, 6, 64. https://doi.org/10.3390/cryst6060064
Jin Y, Pennec Y, Pan Y, Djafari-Rouhani B. Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling. Crystals. 2016; 6(6):64. https://doi.org/10.3390/cryst6060064
Chicago/Turabian StyleJin, Yabin, Yan Pennec, Yongdong Pan, and Bahram Djafari-Rouhani. 2016. "Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling" Crystals 6, no. 6: 64. https://doi.org/10.3390/cryst6060064
APA StyleJin, Y., Pennec, Y., Pan, Y., & Djafari-Rouhani, B. (2016). Phononic Crystal Plate with Hollow Pillars Actively Controlled by Fluid Filling. Crystals, 6(6), 64. https://doi.org/10.3390/cryst6060064